Robust AOA-Based Target Localization for Uniformly Distributed Noise via ℓp-ℓ1 Optimization
Abstract
:1. Introduction
- The sparse regularized robust model based on the - optimization is proposed for the target localization in the presence of uniformly distributed noise, which enables the joint estimation of outliers and target position;
- The optimization algorithm for introducing the proximal operator into the framework of alternating direction method of multipliers (POADMM) is developed to solve the model effectively when ;
- To derive a convergent algorithm, a smoothed POADMM (SPOADMM) optimization algorithm is presented by a smoothing strategy for the nonconvex case of .
2. Related Work
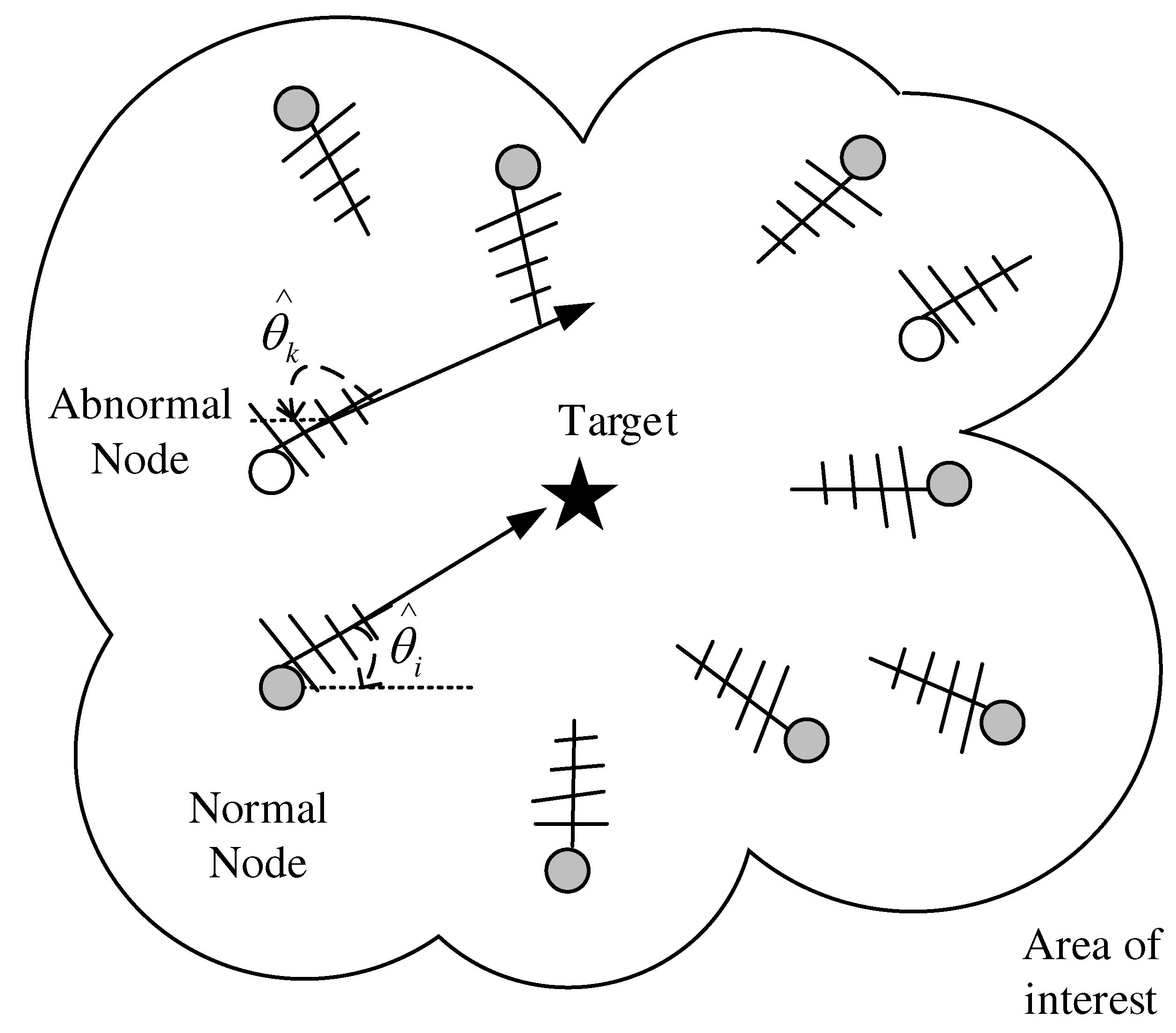
3. AOA-Based Localization Methods and Problem Statement
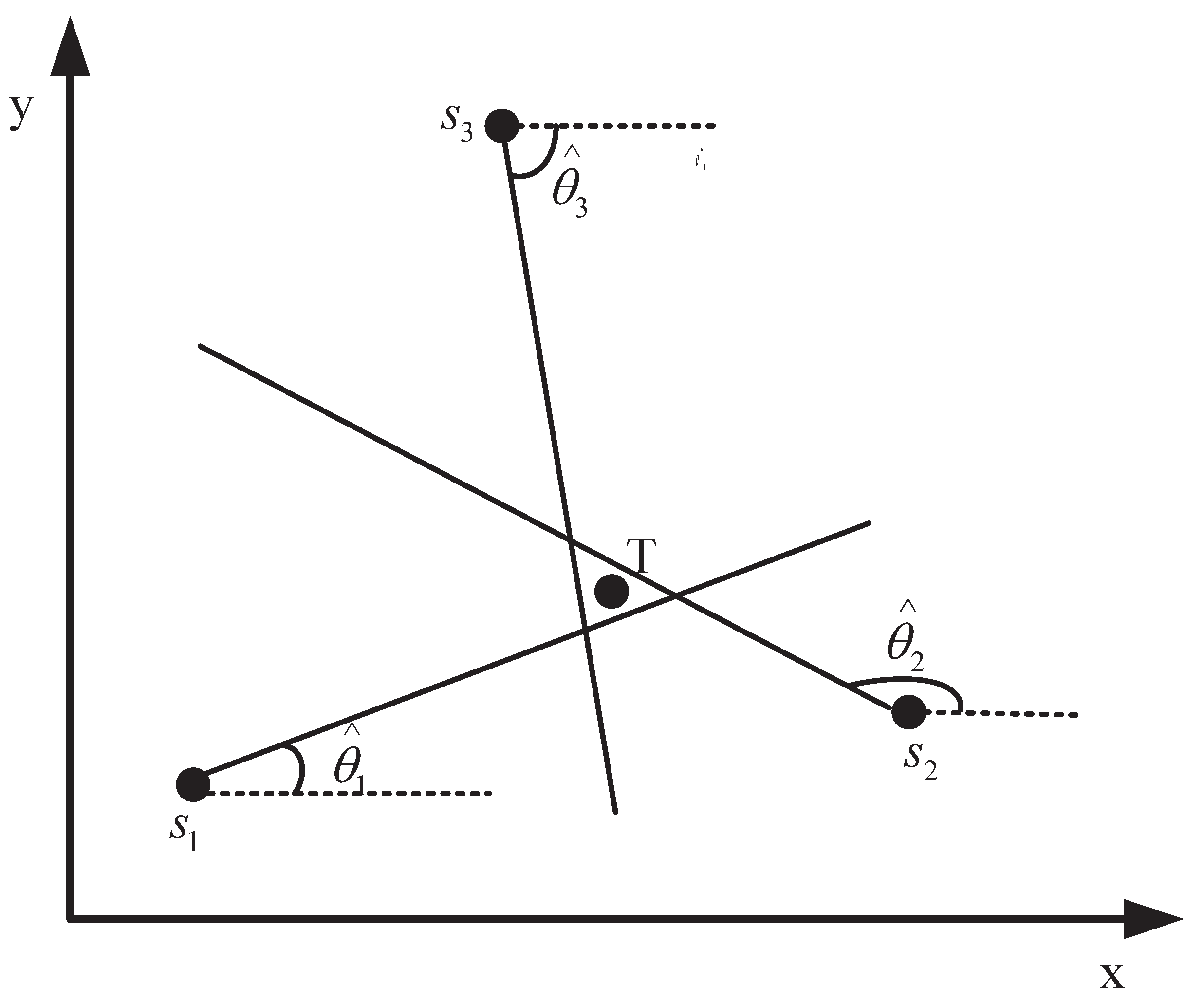
3.1. Angle of Arrival Model
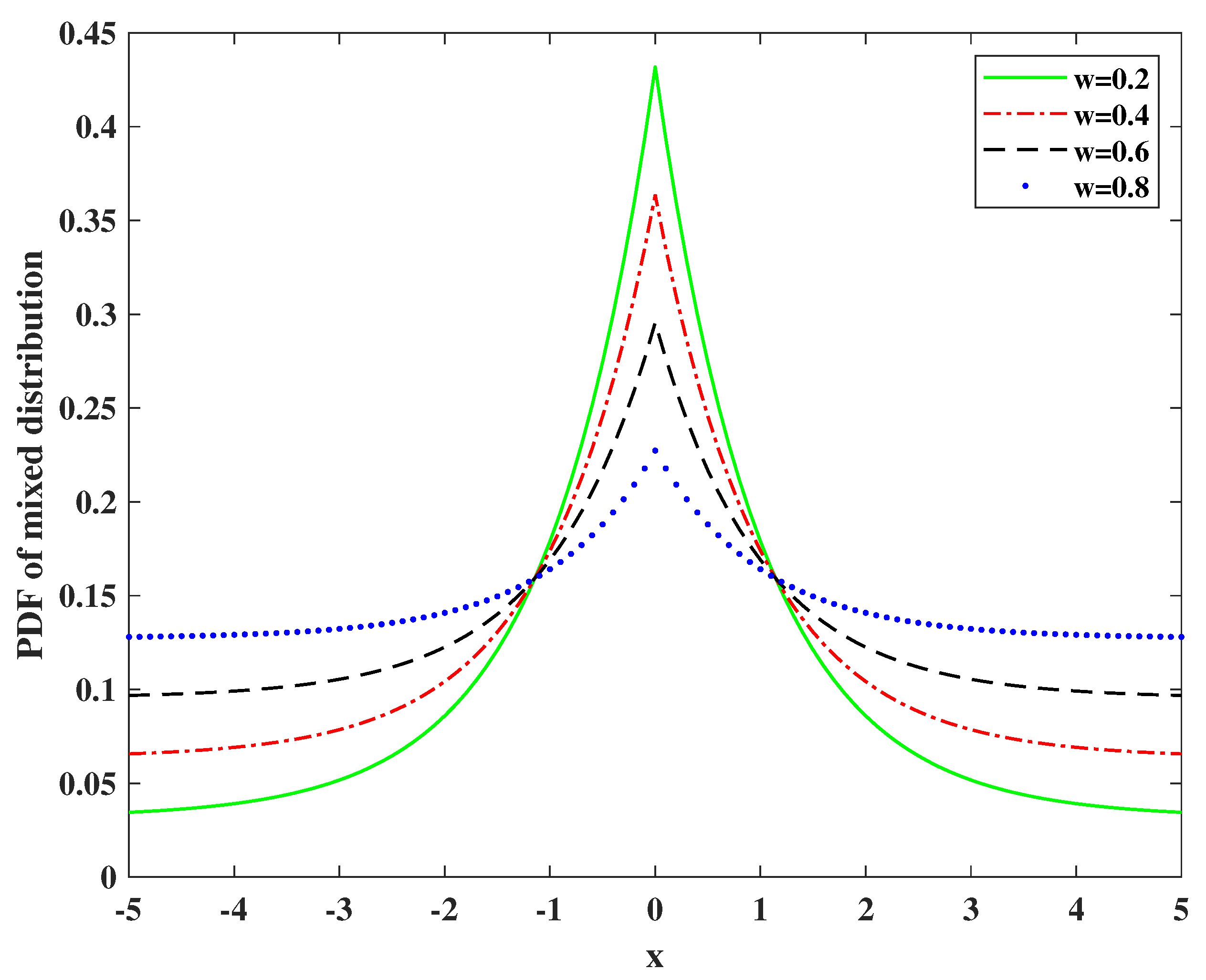
3.2. Problem Statement
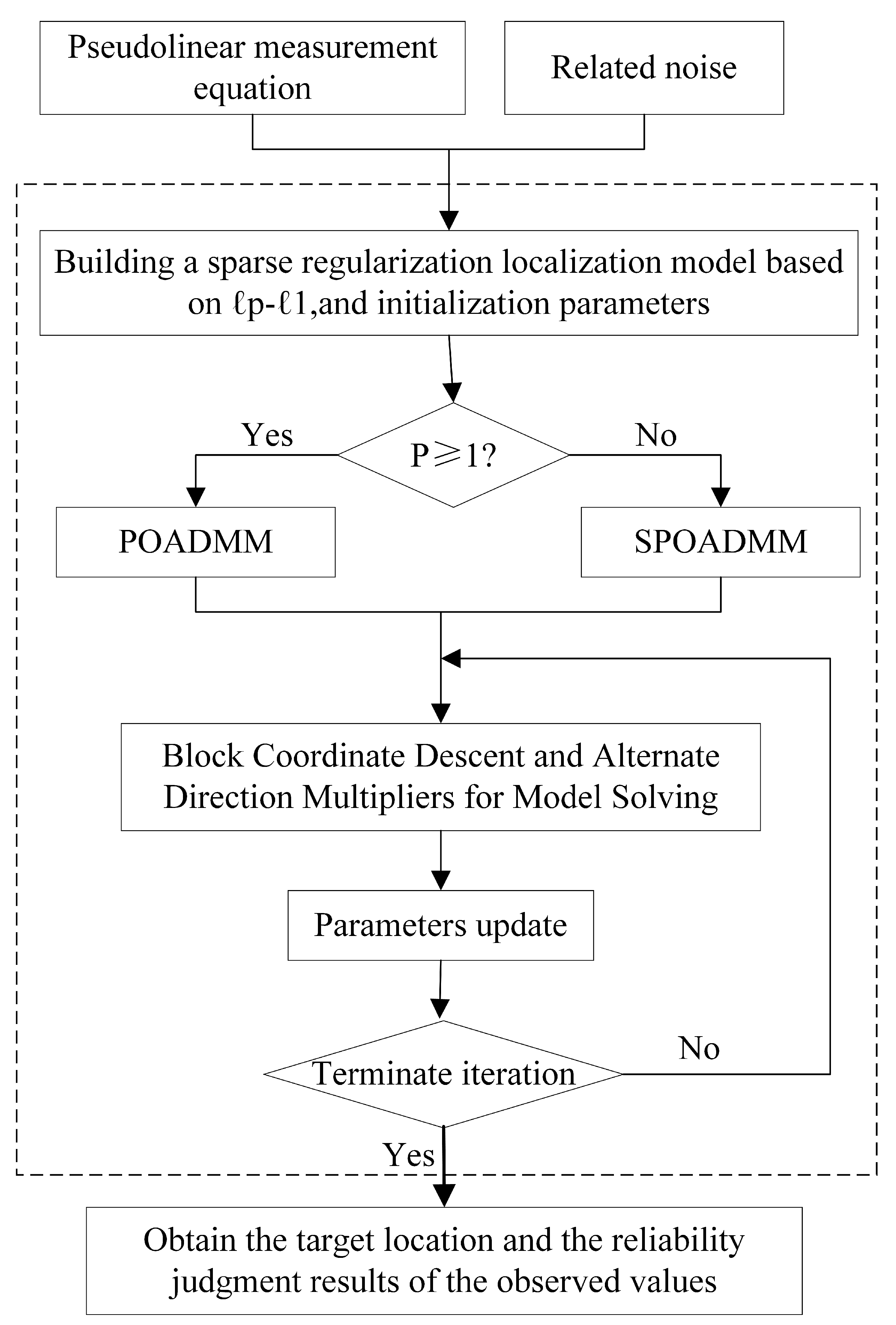
4. Proposed Estimators
4.1. POADMM Estimator
4.2. SPOADMM Estimator
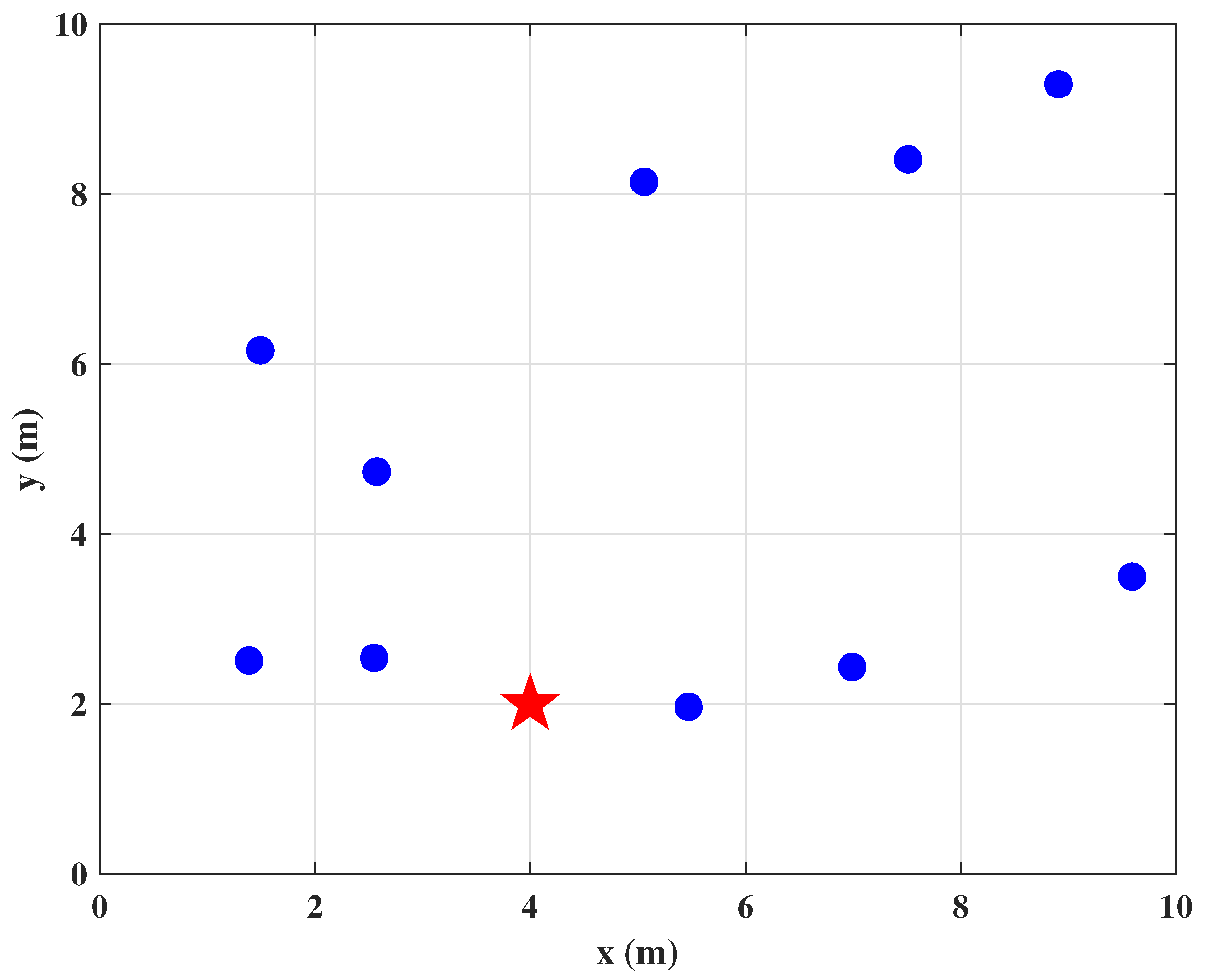
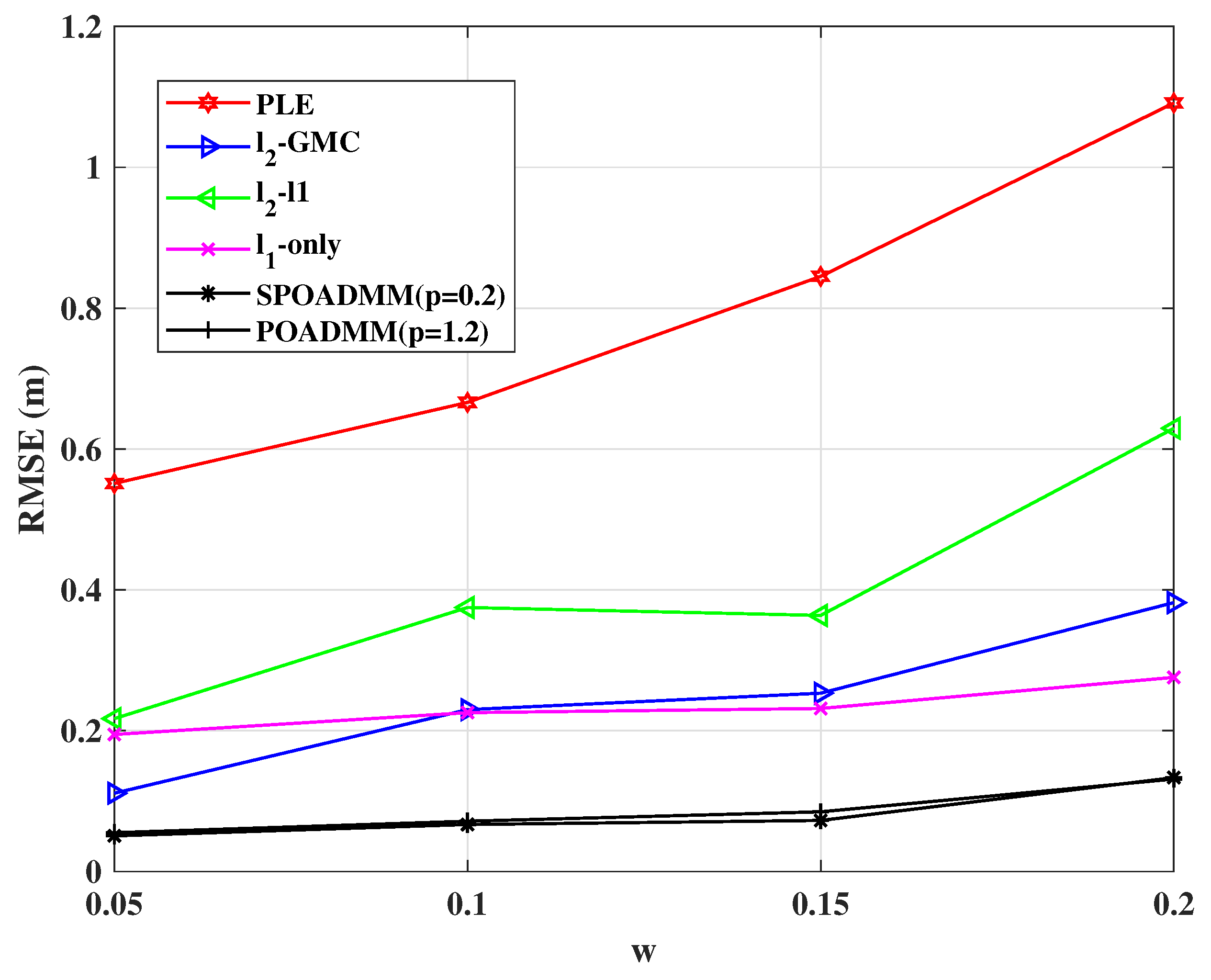
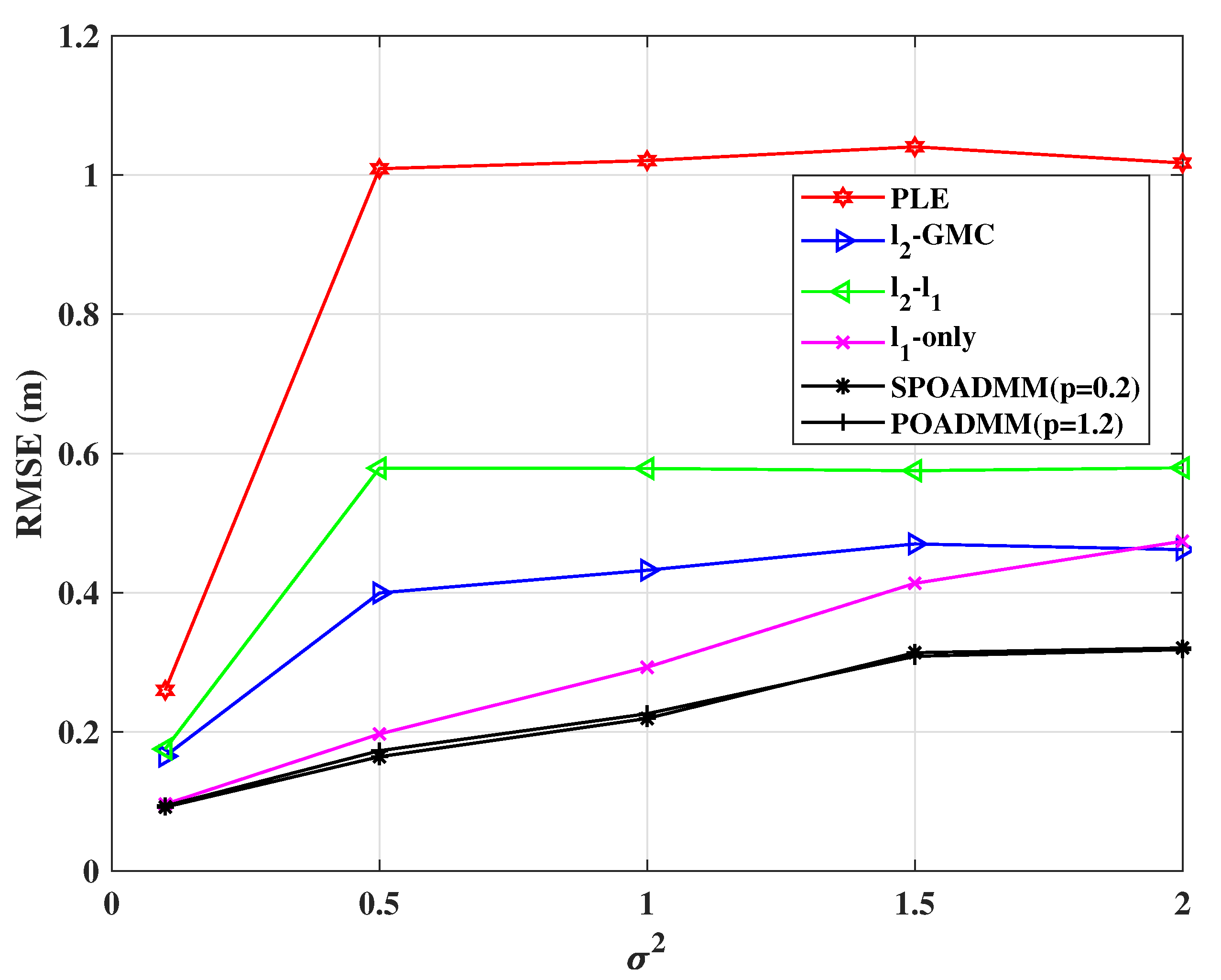
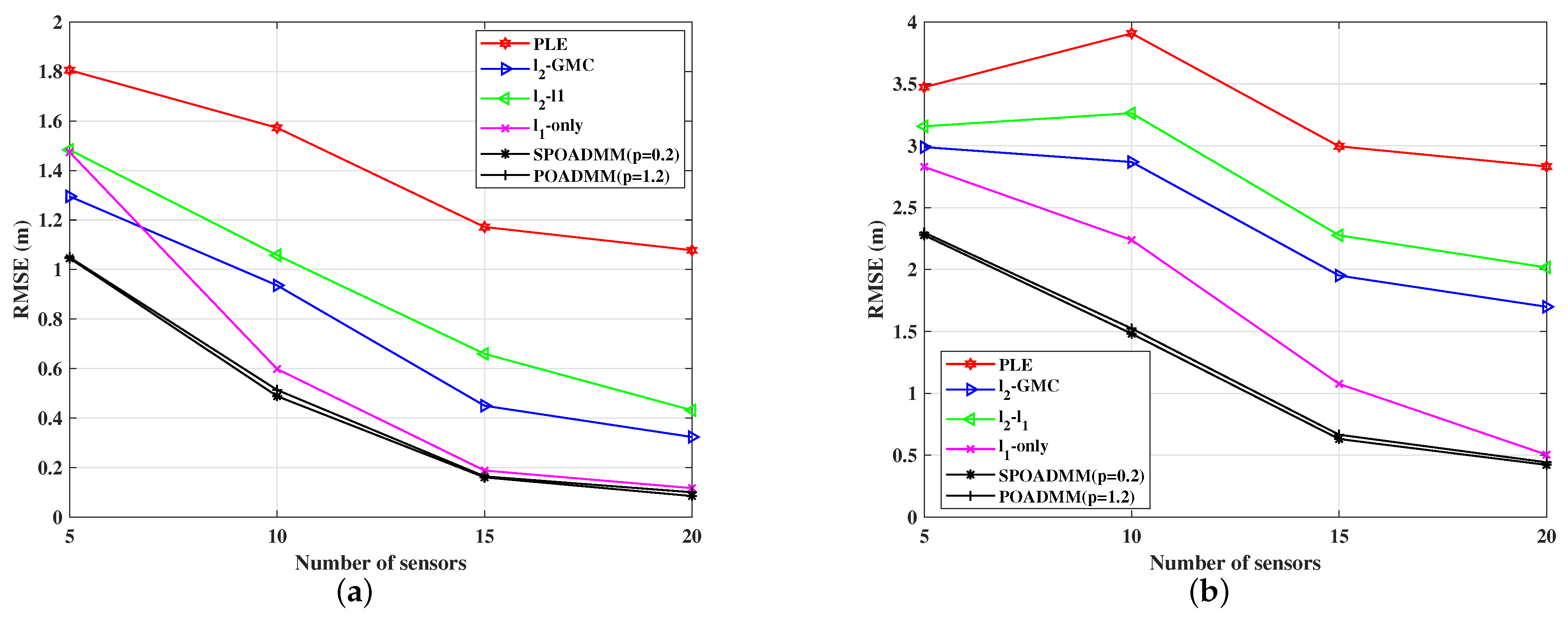
5. Simulation Experiments
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Symbol Description | |
| lowercase bold notation | column vectors |
| uppercase bold notation | matrices |
| an identity matrix | |
| inner product | |
| matrix transpose operators | |
| matrix inverse operators | |
| the -norm of , | |
| the -norm of , | |
| the -norm of , | |
| the gradient of the function f | |
| the Hessian of the function f | |
| w | the outlier occurrence probability |
| the variance of the measurement noise | |
| the regularization parameter |
References
- Poulose, A.; Eyobu, O.S.; Kim, M.; Han, D.S. Localization Error Analysis of Indoor Positioning System Based on UWB Measurements. In Proceedings of the 2019 Eleventh International Conference on Ubiquitous and Future Networks (ICUFN), Zagreb, Croatia, 2–5 July 2019; pp. 84–88. [Google Scholar] [CrossRef]
- Khelifi, F.; Bradai, A.; Benslimane, A.; Rawat, P.; Atri, M. A Survey of Localization Systems in Internet of Things. Mob. Netw. Appl. 2019, 24, 761–785. [Google Scholar] [CrossRef]
- Zafari, F.; Gkelias, A.; Leung, K.K. A Survey of Indoor Localization Systems and Technologies. IEEE Commun. Surv. Tutor. 2019, 21, 2568–2599. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, H.; Lu, T.; Gulliver, T.A. Cooperative RSS-Based Localization in Wireless Sensor Networks Using Relative Error Estimation and Semidefinite Programming. IEEE Trans. Veh. Technol. 2019, 68, 483–497. [Google Scholar] [CrossRef]
- Sun, Y.; Yang, S.; Wang, G.; Chen, H. Robust RSS-Based Source Localization with Unknown Model Parameters in Mixed LOS/NLOS Environments. IEEE Trans. Veh. Technol. 2021, 70, 3926–3931. [Google Scholar] [CrossRef]
- Zheng, R.; Wang, G.; Ho, K.C. Accurate semidefinite relaxation method for elliptic localization with unknown transmitter position. IEEE Trans. Wirel. Commun. 2021, 20, 2746–2760. [Google Scholar] [CrossRef]
- Chen, H.; Wang, G.; Wu, X. Cooperative Multiple Target Nodes Localization Using TOA in Mixed LOS/NLOS Environments. IEEE Sens. J. 2020, 20, 1473–1484. [Google Scholar] [CrossRef]
- Wang, G.; Zhu, W.; Ansari, N. Robust TDOA-Based Localization for IoT via Joint Source Position and NLOS Error Estimation. IEEE Internet Things 2019, 6, 8529–8541. [Google Scholar] [CrossRef]
- Liu, Y.; Guo, F.; Yang, L.; Jiang, W. An Improved Algebraic Solution for TDOA Localization with Sensor Position Errors. IEEE Commun. Lett. 2015, 19, 2218–2221. [Google Scholar] [CrossRef]
- Xu, S.; Doğançay, K. Optimal Sensor Placement for 3-D Angle-of-Arrival Target Localization. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 1196–1211. [Google Scholar] [CrossRef]
- Zheng, Y.; Sheng, M.; Liu, J.; Li, J. Exploiting AoA Estimation Accuracy for Indoor Localization: A Weighted AoA-Based Approach. IEEE Wirel. Commun. Lett. 2019, 8, 65–68. [Google Scholar] [CrossRef]
- BniLam, N.; Joosens, D.; Aernouts, M.; Steckel, J.; Weyn, M. LoRay: AoA Estimation System for Long Range Communication Networks. IEEE Trans. Wirel. Commun. 2020, 20, 2005–2018. [Google Scholar] [CrossRef]
- Tomic, S.; Beko, M.; Dinis, R. 3-D Target Localization in Wireless Sensor Networks Using RSS and AoA Measurements. IEEE Trans. Veh. Technol. 2017, 66, 3197–3210. [Google Scholar] [CrossRef]
- Li, J.; He, Y.; Zhang, X.; Wu, Q. Simultaneous Localization of Multiple Unknown Emitters Based on UAV Monitoring Big Data. IEEE Trans. Ind. Inform. 2021, 17, 6303–6313. [Google Scholar] [CrossRef]
- Noroozi, A.; Sebt, M.A. lgebraic solution for three-dimensional TDOA/AOA localisation in multiple-input–multiple-output passive radar. IET Radar Sonar Navig. 2018, 12, 21–29. [Google Scholar] [CrossRef]
- Gabbrielli, A.; Xiong, W.; Schott, D.J.; Fischer, G.; Wendeberg, J.; Höflinger, F.; Reindl, L.M.; Schindelhauer, C.; Rupitsch, S.J. An echo suppression delay estimator for angle of arrival ultrasonic indoor localization. IEEE Trans. Instrum. Meas. 2021, 70, 6503612. [Google Scholar] [CrossRef]
- Gavish, M.; Weiss, A.J. Performance analysis of bearing-only target location algorithms. IEEE Trans. Aerosp. Electron. Syst. 1992, 28, 817–828. [Google Scholar] [CrossRef]
- Lingren, A.G.; Gong, K.F. Position and Velocity Estimation Via Bearing Observations. IEEE Trans. Aerosp. Electron. Syst. 1978, AES-14, 564–577. [Google Scholar] [CrossRef]
- Doǧançay, K. Bearings-only target localization using total least squares. Signal Process. 2005, 85, 1695–1710. [Google Scholar] [CrossRef]
- Wen, F.; Liu, P.; Liu, Y.; Qiu, R.C.; Yu, W. Robust Sparse Recovery in Impulsive Noise via ℓp-ℓ1 Optimization. IEEE Trans. Signal Process. 2017, 65, 105–118. [Google Scholar] [CrossRef]
- Xu, S.; Ou, Y.; Wu, X. Learning-based Adaptive Estimation for AOA Target Tracking with Non-Gaussian White Noise. In Proceedings of the 2019 IEEE International Conference on Robotics and Biomimetics (ROBIO), Dali, China, 6–8 December 2019; pp. 2233–2238. [Google Scholar]
- Nguyen, N.H.; Doğançay, K.; Kuruoğlu, E.E. An iteratively reweighted instrumental-variable estimator for robust 3-D AOA localization in impulsive noise. IEEE Trans. Signal Process. 2019, 67, 4795–4808. [Google Scholar] [CrossRef]
- Zhang, R.; Xia, W.; Yan, F.; Shen, L. A single-site positioning method based on TOA and DOA estimation using virtual stations in NLOS environment. China Commun. 2019, 16, 146–159. [Google Scholar] [CrossRef]
- Fang, W.; Zhang, W.; Chen, W.; Pan, T.; Ni, Y.; Yang, Y. Trust-based attack and defense in wireless sensor networks: A survey. Wirel. Commun. Mob. Comput. 2020, 2020, 2643546. [Google Scholar] [CrossRef]
- Gharamaleki, M.M.; Babaie, S. A New Distributed Fault Detection Method for Wireless Sensor Networks. IEEE Syst. J. 2020, 14, 4883–4890. [Google Scholar] [CrossRef]
- Xiong, W.; Bordoy, J.; Gabbrielli, A.; Fischer, G.; Schott, D.J.; Hoflinger, F.; Wendeberg, J.; Schindelhauer, C.; Rupitsch, S.J. Two Efficient and Easy-to-Use NLOS Mitigation Solutions to Indoor 3-D AOA-Based Localization. In Proceedings of the 2021 International Conference on Indoor Positioning and Indoor Navigation (IPIN), Lloret de Mar, Spain, 29 November–2 December 2021; pp. 1–8. [Google Scholar]
- Yan, L.; Lu, Y.; Zhang, Y. An Improved NLOS Identification and Mitigation Approach for Target Tracking in Wireless Sensor Networks. IEEE Access 2017, 5, 2798–2807. [Google Scholar] [CrossRef]
- Yan, Q.; Chen, J.; Ottoy, G.; Cox, B.; De Strycker, L. An accurate AOA localization method based on unreliable sensor detection. In Proceedings of the 2018 IEEE Sensors Applications Symposium (SAS), Seoul, Korea, 12–14 March 2018; pp. 1–6. [Google Scholar]
- Yan, Q.; Chen, J.; Ottoy, G.; Strycker, L.D. Robust AOA based acoustic source localization method with unreliable measurements. Signal Process 2008, 152, 13–21. [Google Scholar] [CrossRef]
- Wu, H.; Chen, S.; Zhang, Y.; Zhang, H.; Ni, J. Robust structured total least squares algorithm for passive location. J. Syst. Eng. Electron. 2015, 26, 946–953. [Google Scholar] [CrossRef]
- Yan, Q.; Chen, J.; Zhang, J.; Zhang, W. Robust AOA-based source localization using outlier sparsity regularization. Digit. Signal Process. 2021, 112, 103006. [Google Scholar] [CrossRef]
- Yan, Q.; Chen, J. Robust AOA-Based Source Localization in Correlated Measurement Noise via Nonconvex Sparse Optimization. IEEE Commun. Lett. 2021, 25, 1529–1533. [Google Scholar] [CrossRef]
- Giménez-Febrer, P.; Pagès-Zamora, A.; Pereira, S.S.; López-Valcarce, R. Distributed AOA-based source positioning in NLOS with sensor networks. In Proceedings of the 2015 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), South Brisbane, QLD, Australia, 19–24 April 2015; pp. 3197–3201. [Google Scholar]
- Liu, Y.; Hu, Y.H.; Pan, Q. Distributed, Robust Acoustic Source Localization in a Wireless Sensor Network. IEEE Trans. Signal Process. 2012, 60, 4350–4359. [Google Scholar] [CrossRef]
- Naseri, M.; Amiri, H. A novel bearing-only localization for generalized Gaussian noise. Signal Process. 2021, 189, 108248. [Google Scholar] [CrossRef]
- Trump, T. A robust detector for uniformly distributed noise. In Proceedings of the 2010 IEEE International Conference on Acoustics, Speech and Signal Processing, Dallas, TX, USA, 14–19 March 2010; pp. 3870–3873. [Google Scholar] [CrossRef]
- Wang, H.M.; Jiang, J.C.; Wang, Y.N. Model Refinement Learning and an Example on Channel Estimation with Universal Noise Model. IEEE J. Sel. Areas Commun. 2021, 39, 31–46. [Google Scholar] [CrossRef]
- Dong, J.; Zheng, H.; Lian, L. Low-Rank Laplacian-Uniform Mixed Model for Robust Face Recognition. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 11897–11906. [Google Scholar]
- Selesnick, I. Sparse Regularization via Convex Analysis. IEEE Trans. Signal Process. 2017, 65, 4481–4494. [Google Scholar] [CrossRef]
- Boyd, S.; Parikh, N.; Chu, E.; Peleato, B.; Eckstein, J. Distributed optimization and statistical learning via the alternating direction method of multipliers. In Foundations and Trends® in Machine Learning; Now Publishers: Delft, The Netherlands, 2011; Volume 3, pp. 1–122. ISBN 978-1-60198-460-9. [Google Scholar]
- Bauschke, H.H.; Combettes, P.L. Convex Analysis and Monotone Operator Theory in Hilbert Spaces; Springer: New York, NY, USA, 2011; Volume 408, ISBN 978-3-319-48311-5. [Google Scholar]
- Combettes, P.L.; Pesquet, J.C. Proximal splitting methods in signal processing. In Fixed-Point Algorithms for Inverse Problems in Science and Engineering; Bauschke, H., Burachik, R., Combettes, P., Elser, V., Luke, D., Wolkowicz, H., Eds.; Springer: New York, NY, USA, 2011; pp. 185–212. [Google Scholar]
- Beck, A.; Teboulle, M. A fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM J. Imaging Sci. 2009, 2, 183–202. [Google Scholar] [CrossRef]
- She, Y.; Owen, A.B. Outlier detection using nonconvex penalized regression. J. Am. Stat. Assoc. 2011, 106, 626–639. [Google Scholar] [CrossRef]
- Marjanovic, G.; Solo, V. On ℓq Optimization and Matrix Completion. IEEE Trans. Signal Process. 2012, 60, 5714–5724. [Google Scholar] [CrossRef]
- Luo, J.; Fang, F.; Shi, Y.; Han, S.; Guo, Y. L1-Norm and Lp-Norm Optimization for Bearing-Only Positioning in Presence of Unreliable Measurements. In Proceedings of the 2020 Chinese Control And Decision Conference (CCDC), Hefei, China, 22–24 August 2020; pp. 1201–1205. [Google Scholar]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Wang, C.; Yan, Q. Robust AOA-Based Target Localization for Uniformly Distributed Noise via ℓp-ℓ1 Optimization. Entropy 2022, 24, 1259. https://doi.org/10.3390/e24091259
Chen Y, Wang C, Yan Q. Robust AOA-Based Target Localization for Uniformly Distributed Noise via ℓp-ℓ1 Optimization. Entropy. 2022; 24(9):1259. https://doi.org/10.3390/e24091259
Chicago/Turabian StyleChen, Yanping, Chunmei Wang, and Qingli Yan. 2022. "Robust AOA-Based Target Localization for Uniformly Distributed Noise via ℓp-ℓ1 Optimization" Entropy 24, no. 9: 1259. https://doi.org/10.3390/e24091259




