Investigation of the JPA-Bandwidth Improvement in the Performance of the QTMS Radar
Abstract
:1. Introduction
2. Preliminaries
2.1. Quantum Radar (QR)
- Using a pump and a signal generator, we produce a current of entangled photon pairs (signal/idler) using quantum sources.
- To send a signal to the target, we need to amplify the signal with low-noise amplifiers, and to determine the presence of the target, we have to record the idler.
- After receiving the signal reflected from the target by the receiver antenna, the signal and idler are amplified again, and an analog-to-digital conversion (ADC) is applied.
- Using a suitable detector, the presence or absence of a target can be inferred. Figure 1 depicts the general block diagram of a quantum radar.
2.1.1. QTMS Radar
- Utilize the JPA to generate a pair of entangled signals (signal and idler). Amplify both the signal and the idler. Transmit the signal through the free space forward to the target. Perform a heterodyne measurement on the idler, and hold a record of the results in the form of a time series of I and Q voltages.
- Receive a reflected signal. Fulfill a heterodyne measurement on it to create a time series of I and Q voltages.
- Correlate the I and Q voltages of the signal and idler.
- If the correlation surpasses a preset threshold, notify a detection.
2.2. Two-Photon Entanglement
3. Results and Discussion
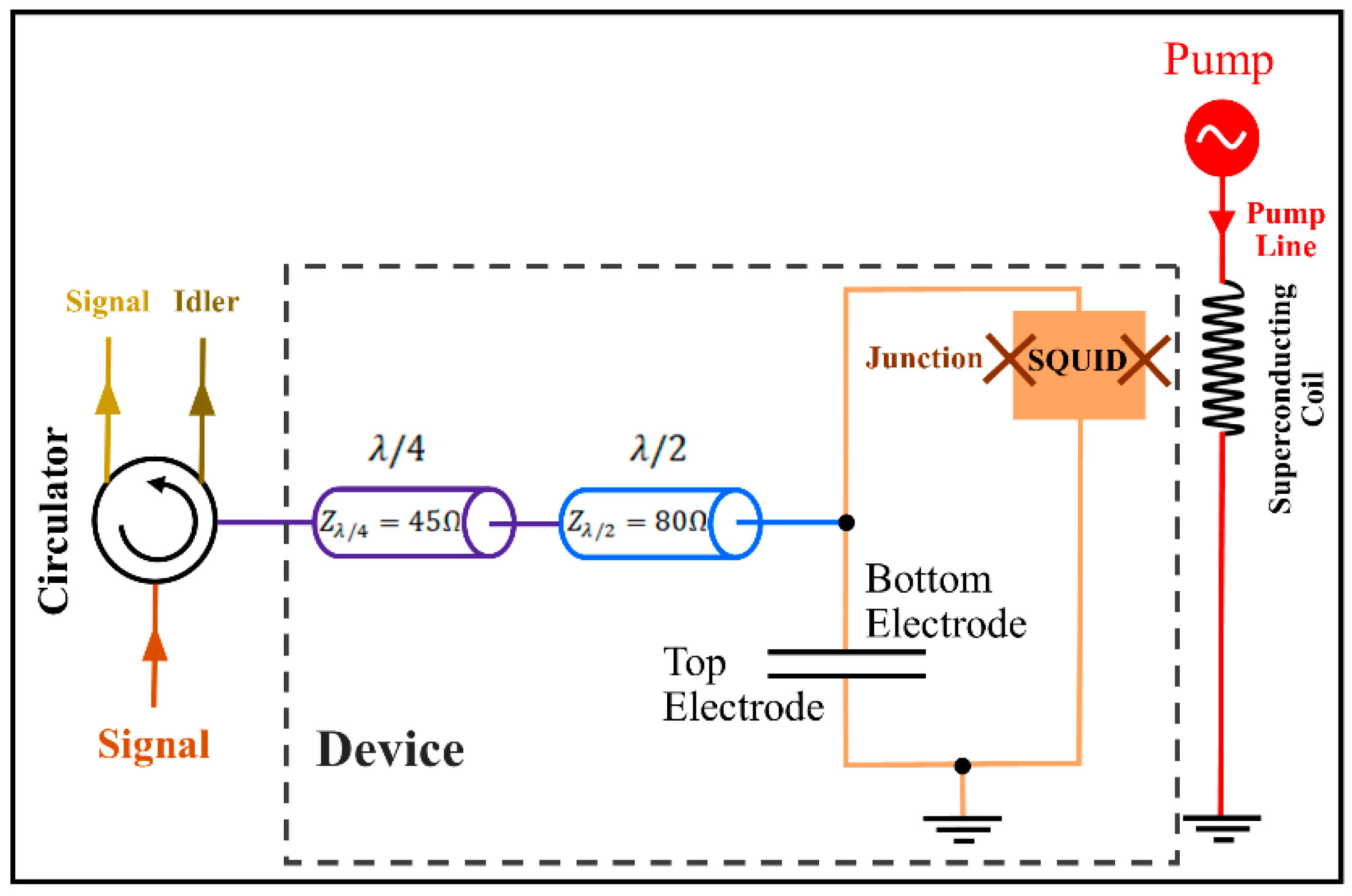
3.1. Engineering JPA (EJPA)
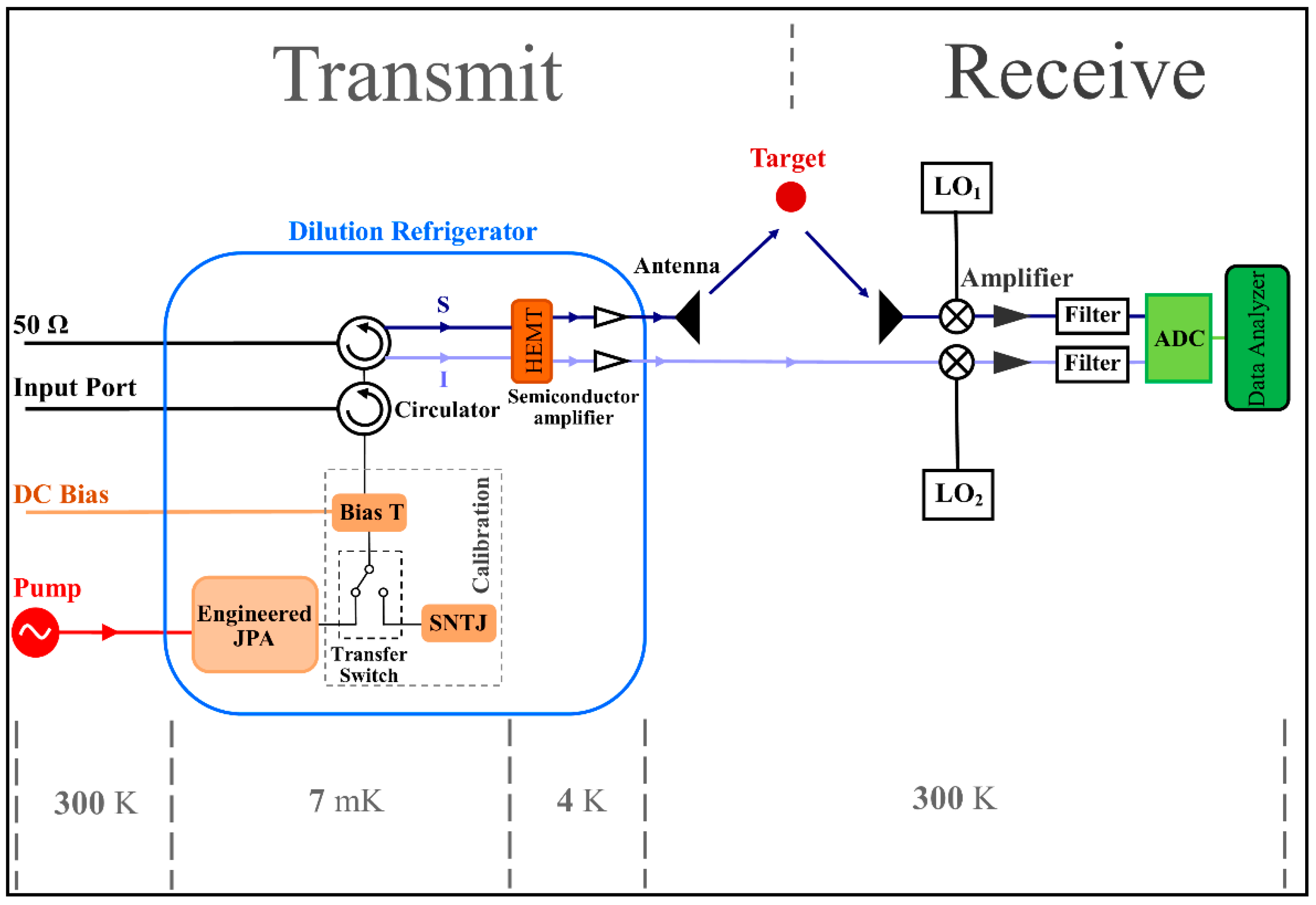
3.2. A Proposed QTMS Radar Design with EJPA
3.3. Post-Processing
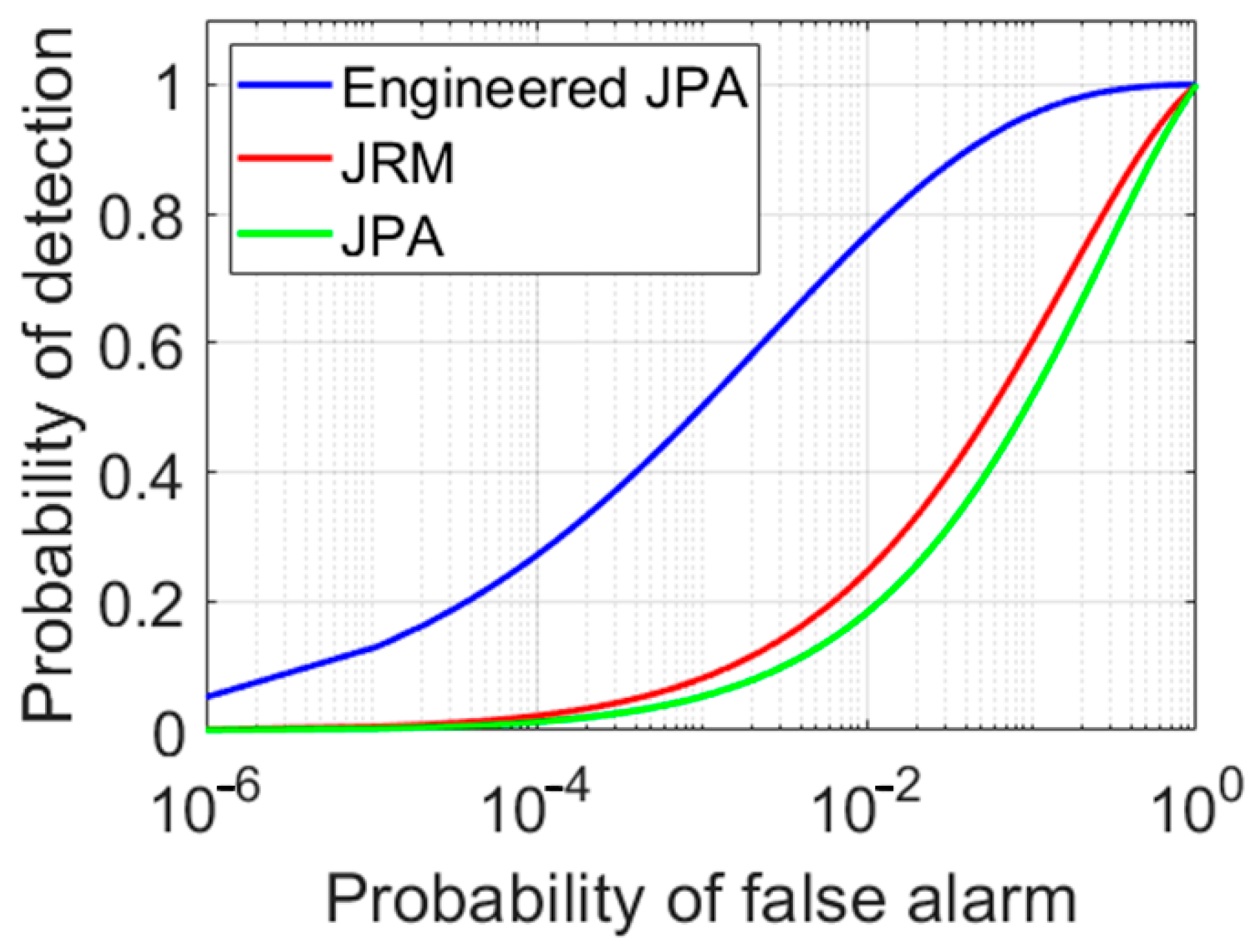
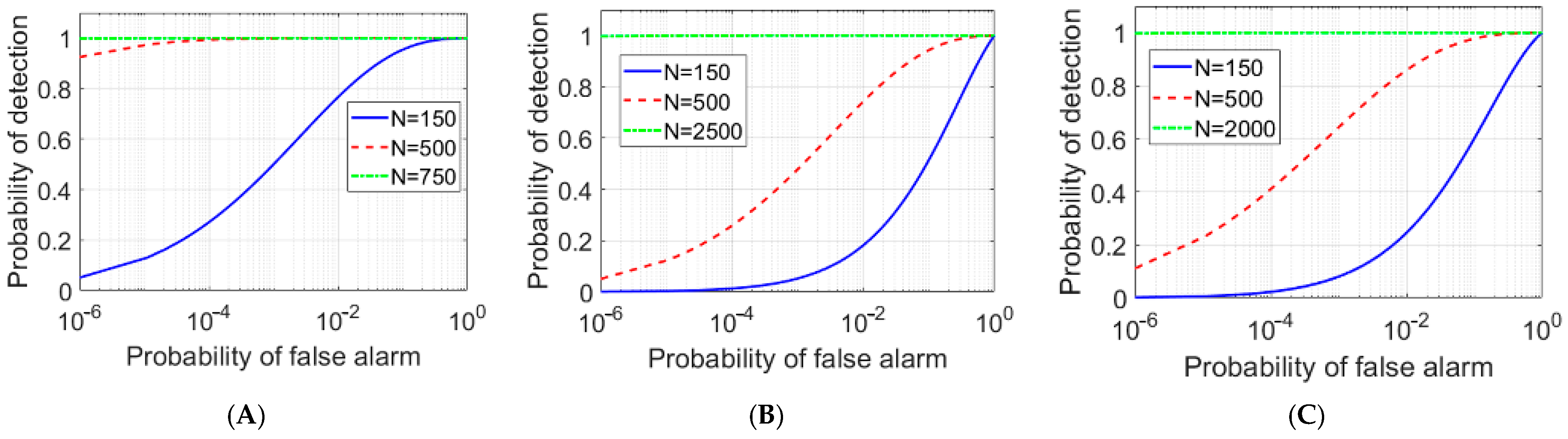
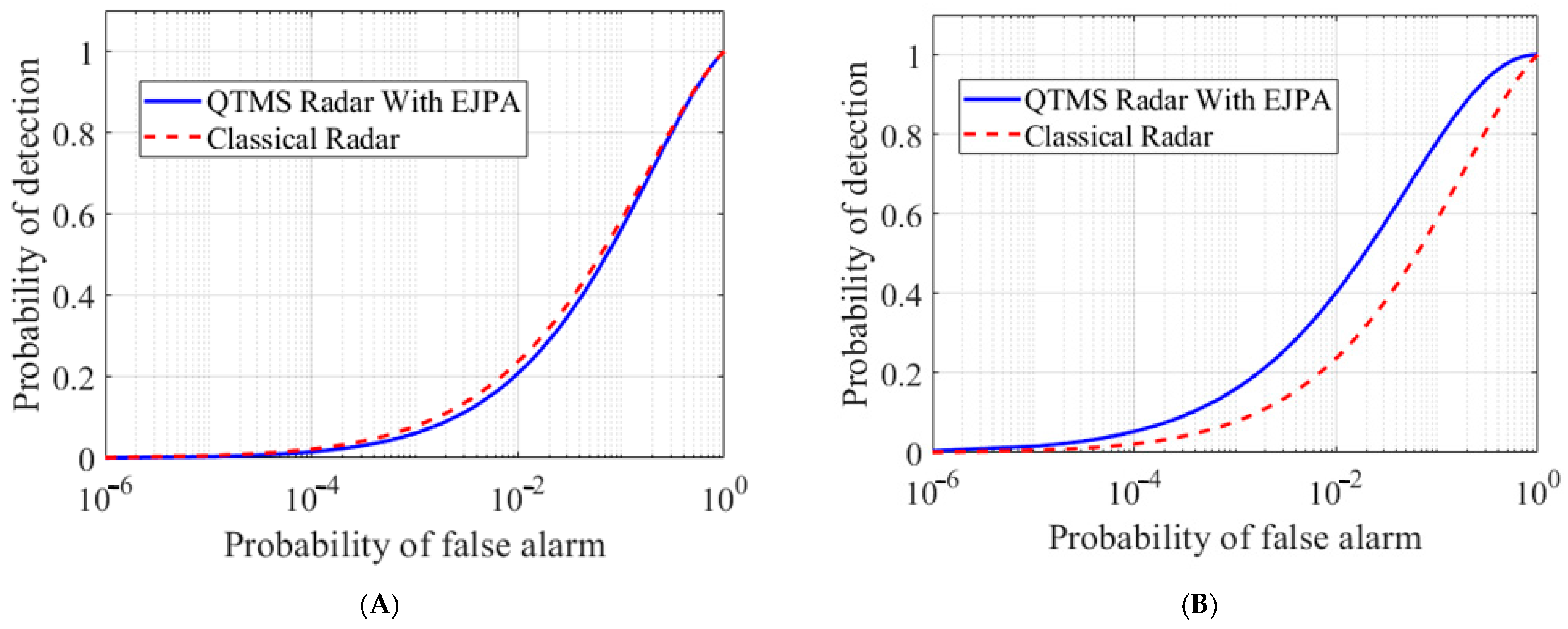
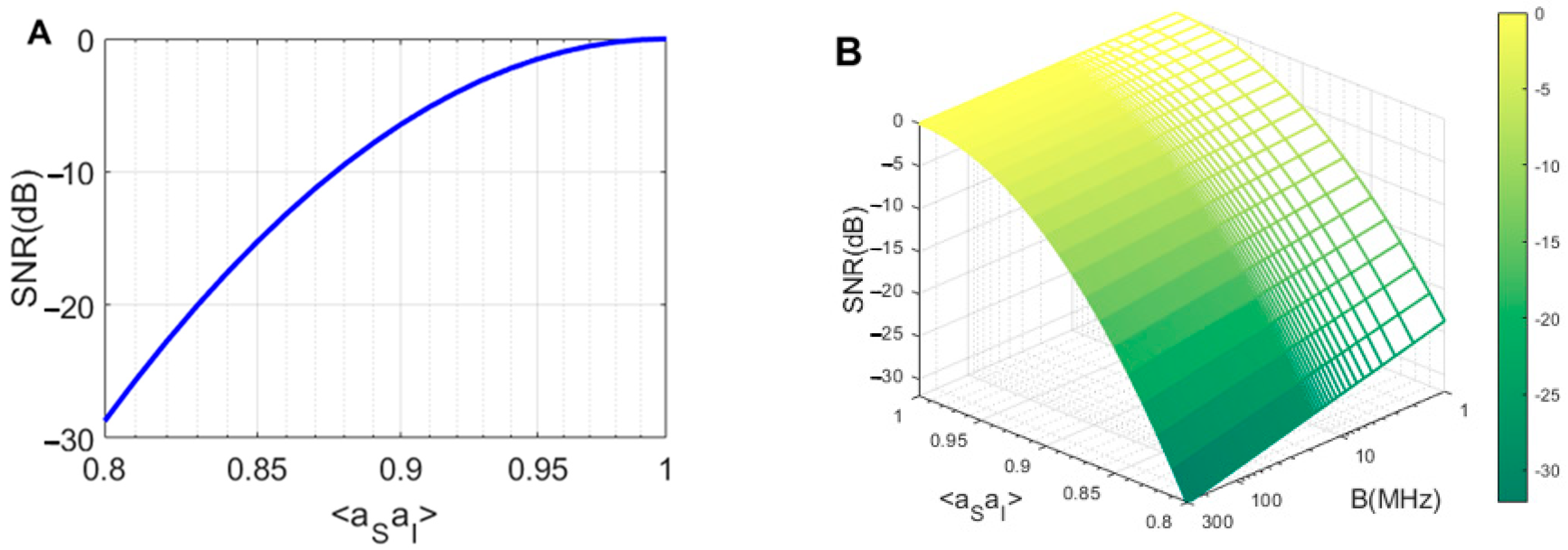
3.3.1. SNR and ROC
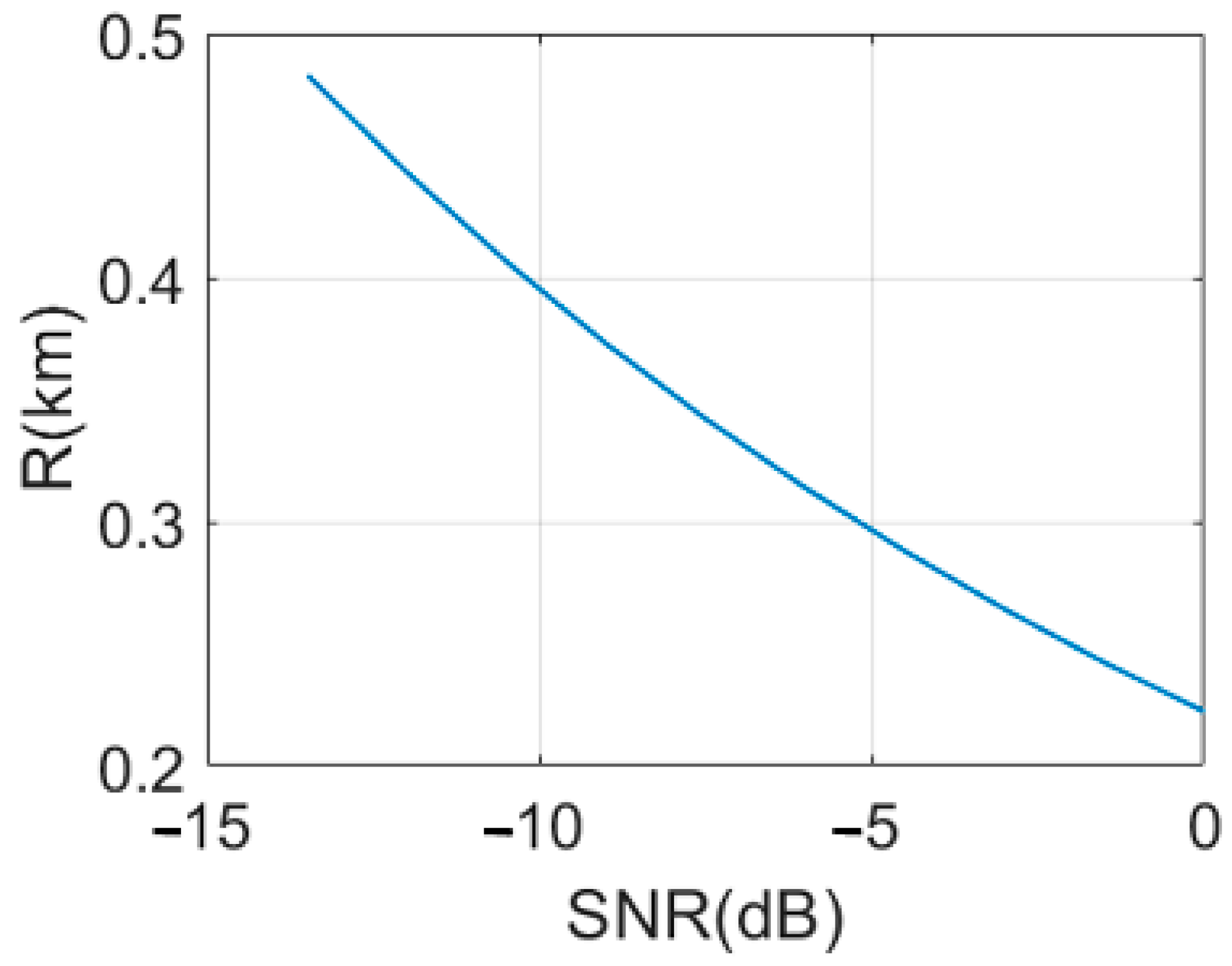
3.3.2. QTMS Radar Range
3.4. Simulation Methodology
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
Appendix A
References
- Luong, D.; Chang, C.W.S.; Vadiraj, A.M.; Damini, A.; Wilson, C.M.; Balaji, B. Receiver operating characteristics for a prototype quantum two-mode squeezing radar. IEEE Trans. Aerosp. Electron. Syst. 2019, 56, 2041–2060. [Google Scholar] [CrossRef]
- Chang, C.S.; Vadiraj, A.M.; Bourassa, J.; Balaji, B.; Wilson, C.M. Quantum-enhanced noise radar. Appl. Phys. Lett. 2019, 114, 112601. [Google Scholar] [CrossRef]
- Luong, D.; Balaji, B.; Chang, C.W.S.; Rao, V.M.A.; Wilson, C.M. Microwave Quantum Radar: An Experimental Validation. In Proceedings of the 2018 International Carnahan Conference on Security Technology (ICCST), Montreal, QC, Canada, 22–25 October 2018; pp. 1–5. [Google Scholar]
- Shapiro, J.H. The quantum illumination story. IEEE Trans. Aerosp. Electron. Syst. Mag. 2020, 35, 8–20. [Google Scholar] [CrossRef]
- Luong, D.; Rajan, S.; Balaji, B. Quantum Monopulse Radar. In Proceedings of the 2020 International Applied Computational Electromagnetics Society Symposium, Monterey, CA, USA, 27–31 July 2020; pp. 1–2. [Google Scholar]
- Luong, D.; Rajan, S.; Balaji, B. Entanglement-based quantum radar: From myth to reality. IEEE Trans. Aerosp. Electron. Syst. Mag. 2020, 35, 22–35. [Google Scholar] [CrossRef]
- Liu, H.; Helmy, A.; Balaji, B. Inspiring radar from quantum-enhanced LiDAR. In Proceedings of the 2020 IEEE International Radar Conference (RADAR), Washington, DC, USA, 28–30 April 2020; pp. 964–968. [Google Scholar]
- Luong, D.; Rajan, S.; Balaji, B. Are quantum radar arrays possible? In Proceedings of the 2019 IEEE International Symposium on Phased Array System & Technology (PAST), Waltham, MA, USA, 15–18 October 2019; pp. 1–4. [Google Scholar]
- Luong, D.; Balaji, B. Quantum Radar, Quantum Networks, Not-so-Quantum Hackers. In Signal Processing, Sensor/Information Fusion, and Target Recognition XXVIII; International Society for Optics and Photonics: Bellingham, DC, USA, 2019; Volume 11018, p. 110181E. [Google Scholar]
- Frasca, M.; Farina, A. Multiple Input-Multiple Output Quantum Radar. In Proceedings of the 2020 IEEE Radar Conference (RadarConf20), Florence, Italy, 21–25 September 2020; pp. 1–4. [Google Scholar]
- Daum, F. Quantum radar cost and practical issues. IEEE Trans. Aerosp. Electron. Syst. Mag. 2020, 35, 8–20. [Google Scholar] [CrossRef]
- Daum, F. A system engineering perspective on quantum radar. In Proceedings of the 2020 IEEE Radar Conference (RadarConf20), Florence, Italy, 21–25 September 2020; pp. 958–963. [Google Scholar]
- Torromé, R.G.; Bekhti-Winkel, N.B.; Knott, P. Introduction to quantum radar. arXiv 2020, arXiv:2006.14238. [Google Scholar]
- Barzanjeh, S.; Guha, S.; Weedbrook, C.; Vitali, D.; Shapiro, J.H.; Pirandola, S. Microwave quantum illumination. Phys. Rev. Lett. 2015, 114, 080503. [Google Scholar] [CrossRef]
- Barzanjeh, S.; Pirandola, S.; Vitali, D.; Fink, J.M. Microwave quantum illumination using a digital receiver. Sci. Adv. 2020, 6, eabb0451. [Google Scholar] [CrossRef]
- Maccone, L.; Ren, C. Quantum radar. Phys. Rev. Lett. 2020, 124, 200503. [Google Scholar] [CrossRef]
- Pirandola, S.; Bardhan, B.R.; Gehring, T.; Weedbrook, C.; Lloyd, S. Advances in photonic quantum sensing. Nat. Photonics 2018, 12, 724–733. [Google Scholar] [CrossRef]
- Tan, S.-H.; Erkmen, B.I.; Giovannetti, V.; Guha, S.; Lloyd, S.; Maccone, L.; Pirandola, S.; Shapiro, J.H. Quantum illumination with Gaussian states. Phys. Rev. Lett. 2008, 101, 253601. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Balaji, B.; Helmy, A.S. Target detection aided by quantum temporal correlations: Theoretical analysis and experimental validation. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 3529–3544. [Google Scholar] [CrossRef]
- Zhuang, Q.; Shapiro, J.H. Ultimate accuracy limit of quantum pulse-compression ranging. Phys. Rev. Lett. 2022, 128, 1010501. [Google Scholar] [CrossRef] [PubMed]
- Lanzagorta, M. Quantum Radar. In Synthesis Lectures on Quantum Computing; Morgan & Claypool Publishers: San Rafael, CA, USA, 2011; Volume 3, pp. 1–139. [Google Scholar]
- Grebel, J.; Bienfait, A.; Dumur, É.; Chang, H.-S.; Chou, M.-H.; Conner, C.R.; Peairs, G.A.; Povey, R.G.; Zhong, Y.P.; Cleland, A.N. Flux-pumped impedance-engineered broadband Josephson parametric amplifier. Appl. Phys. Lett. 2021, 118, 142601. [Google Scholar] [CrossRef]
- Barnett, S.; Radmore, P.M. Methods in Theoretical Quantum Optics; Oxford University Press: Oxford, UK, 2002. [Google Scholar]
- Nielsen, M.A.; Chuang, I. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2002; pp. 558–559. [Google Scholar]
- Zubairy, M.S. Quantum state measurement via Autler-Townes spectroscopy. Phys. Lett. A 1996, 222, 91–96. [Google Scholar] [CrossRef]
- Nakahara, M. Quantum Computing: From Linear Algebra to Physical Realizations; CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar]
- Weedbrook, C.; Pirandola, S.; Thompson, J.; Vedral, V.; Gu, M. How discord underlies the noise resilience of quantum illumination. New J. Phys. 2016, 18, 043027. [Google Scholar] [CrossRef]
- Salmanogli, A.; Gokcen, D. Entanglement sustainability improvement using optoelectronic converter in quantum radar (interferometric object-sensing). IEEE Sens. J. 2021, 21, 9054–9062. [Google Scholar] [CrossRef]
- Salmanogli, A.; Gokcen, D.; Gecim, H.S. Entanglement sustainability in quantum radar. IEEE J. Sel. Top. Quantum Electron. 2020, 26, 1–11. [Google Scholar] [CrossRef]
- Xiangbin, W.; Hiroshima, T.; Tomita, A.; Hayashi, M. Quantum information with Gaussian states. Phys. Rep. 2007, 448, 1–11. [Google Scholar]
- Sebastian, K.; Storz, S.; Kurpiers, P.; Magnard, P.; Heinsoo, J.; Keller, R.; Luetolf, J.; Eichler, C.; Wallraff, A. Engineering cryogenic setups for 100-qubit scale superconducting circuit systems. EPJ Quantum Technol. 2019, 6, 2. [Google Scholar]
- Luong, D.; Balaji, B. Quantum two-mode squeezing radar and noise radar: Covariance matrices for signal processing. IET Radar Sonar Navig. 2020, 14, 97–104. [Google Scholar] [CrossRef]
- Luong, D.; Rajan, S.; Balaji, B. Quantum two-mode squeezing radar and noise radar: Correlation coefficients for target detection. IEEE Sens. J. 2020, 20, 5221–5228. [Google Scholar] [CrossRef]
- Cai, Q.; Liao, J.; Shen, B.; Guo, G.; Zhou, Q. Microwave quantum illumination via cavity magnonics. Phys. Rev. A 2021, 103, 052419. [Google Scholar] [CrossRef]
- Luong, D.; Balaji, B.; Rajan, S. Performance prediction for coherent noise radars using the correlation coefficient. IEEE Access 2022, 10, 8627–8633. [Google Scholar] [CrossRef]
- Luong, D.; Balaji, B.; Rajan, S. A likelihood ratio detector for QTMS radar and noise radar. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 3011–3020. [Google Scholar] [CrossRef]
- Braunstein, S.L.; Loock, P.V. Quantum information with continuous variables. Rev. Mod. Phys. 2005, 77, 513. [Google Scholar] [CrossRef]
- Cai, Q.; Liao, J.; Zhou, Q. Stationary entanglement between light and microwave via ferromagnetic magnons. Ann. Phys. 2020, 532, 2000250. [Google Scholar] [CrossRef]
- Barzanjeh, S.; Redchenko, E.S.; Peruzzo, M.; Wulf, M.; Lewis, D.P.; Arnold, G.; Fink, J.M. Stationary entangled radiation from micromechanical motion. Nature 2019, 570, 480–483. [Google Scholar] [CrossRef]
- Li, J.; Gröblacher, S. Entangling the vibrational modes of two massive ferromagnetic spheres using cavity magnomechanics. Quantum Sci. Technol. 2021, 6, 024005. [Google Scholar] [CrossRef]
- Weedbrook, C.; Pirandola, S.; García-Patrón, R.; Cerf, N.J.; Ralph, T.C.; Shapiro, J.H.; Lloyd, S. Gaussian quantum information. Rev. Mod. Phys. 2012, 84, 621. [Google Scholar] [CrossRef]
- Vidal, G.; Werner, R.F. Computable measure of entanglement. Phys. Rev. A 2002, 65, 032314. [Google Scholar] [CrossRef]
- Plenio, M. Logarithmic negativity: A full entanglement monotone that is not convex. Phys. Rev. Lett. 2005, 95, 090503. [Google Scholar] [CrossRef] [PubMed]
- Boura, H.A.; Isar, A. Logarithmic negativity of two bosonic modes in the two thermal reservoir model. Rom. J. Phys. 2015, 60, 1278. [Google Scholar]
- Wang, X.; Wilde, M.M. α-logarithmic negativity. Phys. Rev. A 2020, 102, 032416. [Google Scholar] [CrossRef]
- Hosseiny, S.M.; Norouzi, M.; Seyed-Yazdi, J.; Irannezhad, F. Purity in the QTMS radar. Phys. Scr. 2023, 98, 055105. [Google Scholar] [CrossRef]
- Hosseiny, S.M.; Norouzi, M.; Seyed-Yazdi, J.; Irannezhad, F. Performance improvement factors in quantum radar/illumination. Commun. Theor. Phys. 2023, 75, 055101. [Google Scholar] [CrossRef]
- Salmanogli, A.; Gokcen, D.; Gecim, H.S. Entanglement of optical and microcavity modes by means of an optoelectronic system. Phys. Rev. Appl. 2019, 11, 024075. [Google Scholar] [CrossRef]
- Mahafza, B.R. Radar Signal Analysis and Processing Using MATLAB; Chapman and Hall: Strand, London; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]




| Quantity | EJPA [This Work] | JRM [15] | JPA [1] | Unit |
|---|---|---|---|---|
| Antenna | C-band | X-band | X-band | --- |
| Antenna gain (G) | 6.4 | 15 * | 15 | dB |
| Antenna effective area (Ae) | 8.8 × 10−5 | - | - | m2 |
| Target radar cross-section (σ) | 1.0 | - | - | m2 |
| Bandwidth (B) | 300 ‡ | 20 | 1.0 | MHz |
| JPA or JPC power gain (Gp) | 20 | 30 | 20 † | dB |
| HEMT gain (at 4 K) (GHEMT) | 38 | 36 | 36 † | dB |
| Signal gain (GS) | 83.98 | 93.98 | ~96 † | dB |
| Detection gain (GD) | 16.82 | 16.82 | 16.82 † | dB |
| Amplifier gain (GA) | 67.16 | 77.16 | 79.18 † | dB |
| Signal power (Ps) | 5 ‡ | −128 * | −82 | dBm |
| Pump power (Pp) | 6 ‡ | −97 | - | dBm |
| Noise power (Pn) | −145 | 4 | −94 | dBm |
| Pump frequency ωp = ωs + ωi | 10.62 | 16.89 | 13.6821 † | GHz |
| Signal frequency (ωs) | 5.31 | 10.09 | 7.5376 | GHz |
| Idler frequency (ωi) | 5.31 | 6.8 | 6.1445 | GHz |
| Signal-to-noise ratio (SNRQR) | −13.48 | −18 | −19 | dB |
| Range (R) (Ns = 0.1, η = 1 dB) | 482 with signal transmission to target | 1 with signal transmission to target (a low-power short-range radar) | 0.5 without signal transmission to target (a low-power prototype radar) | m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Norouzi, M.; Seyed-Yazdi, J.; Hosseiny, S.M.; Livreri, P. Investigation of the JPA-Bandwidth Improvement in the Performance of the QTMS Radar. Entropy 2023, 25, 1368. https://doi.org/10.3390/e25101368
Norouzi M, Seyed-Yazdi J, Hosseiny SM, Livreri P. Investigation of the JPA-Bandwidth Improvement in the Performance of the QTMS Radar. Entropy. 2023; 25(10):1368. https://doi.org/10.3390/e25101368
Chicago/Turabian StyleNorouzi, Milad, Jamileh Seyed-Yazdi, Seyed Mohammad Hosseiny, and Patrizia Livreri. 2023. "Investigation of the JPA-Bandwidth Improvement in the Performance of the QTMS Radar" Entropy 25, no. 10: 1368. https://doi.org/10.3390/e25101368






