Classical Information and Collapse in Wigner’s Friend Setups
Abstract
:1. Introduction
2. Classical Information and Collapse
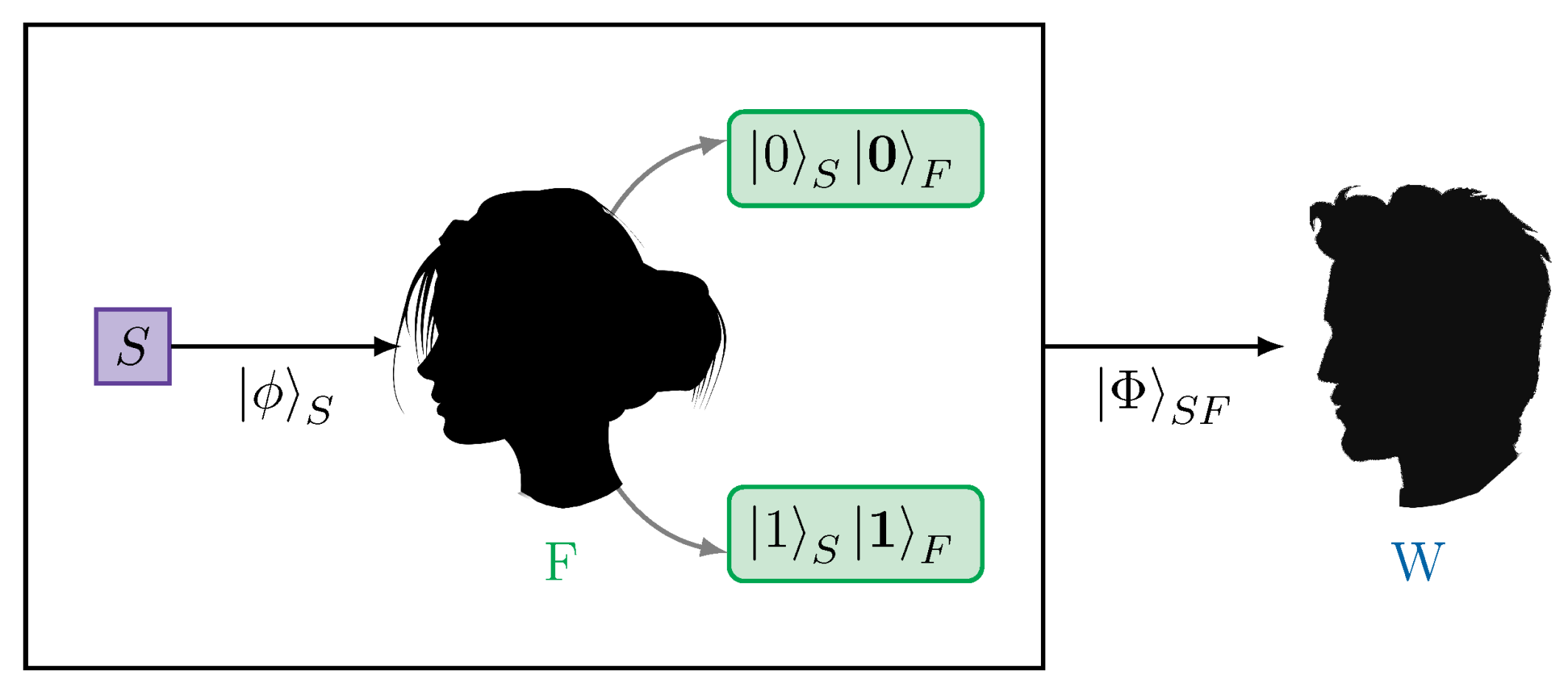
2.1. Effective Collapse
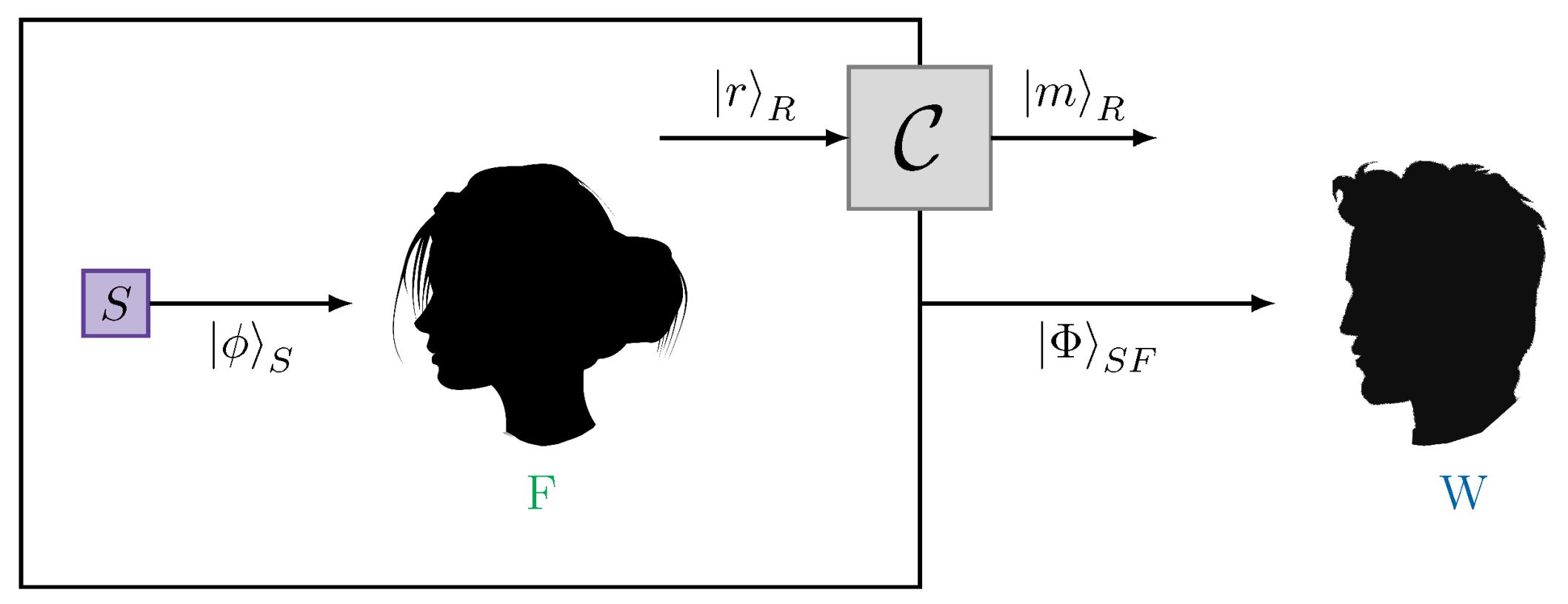
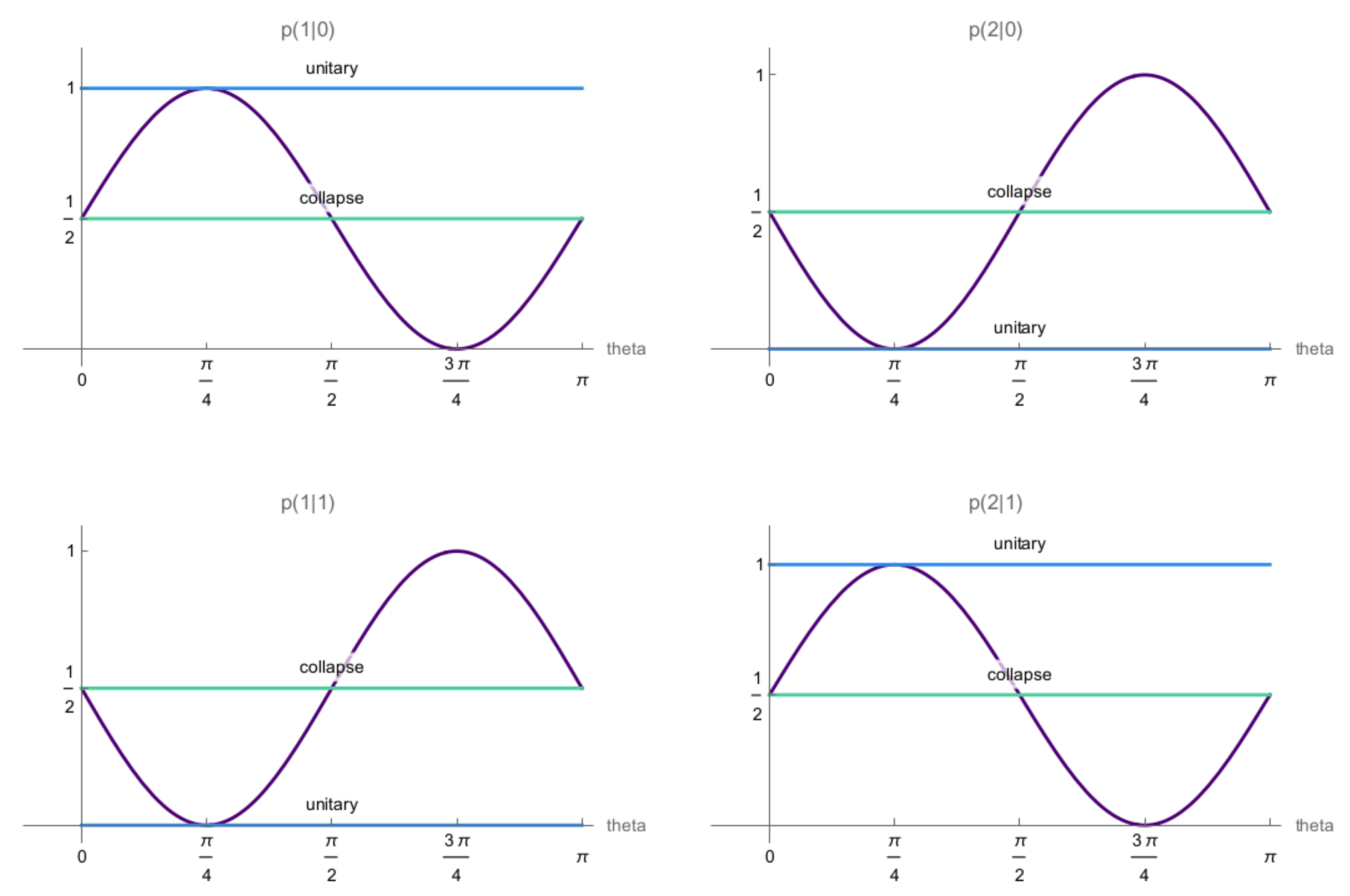
2.2. Partial Collapse
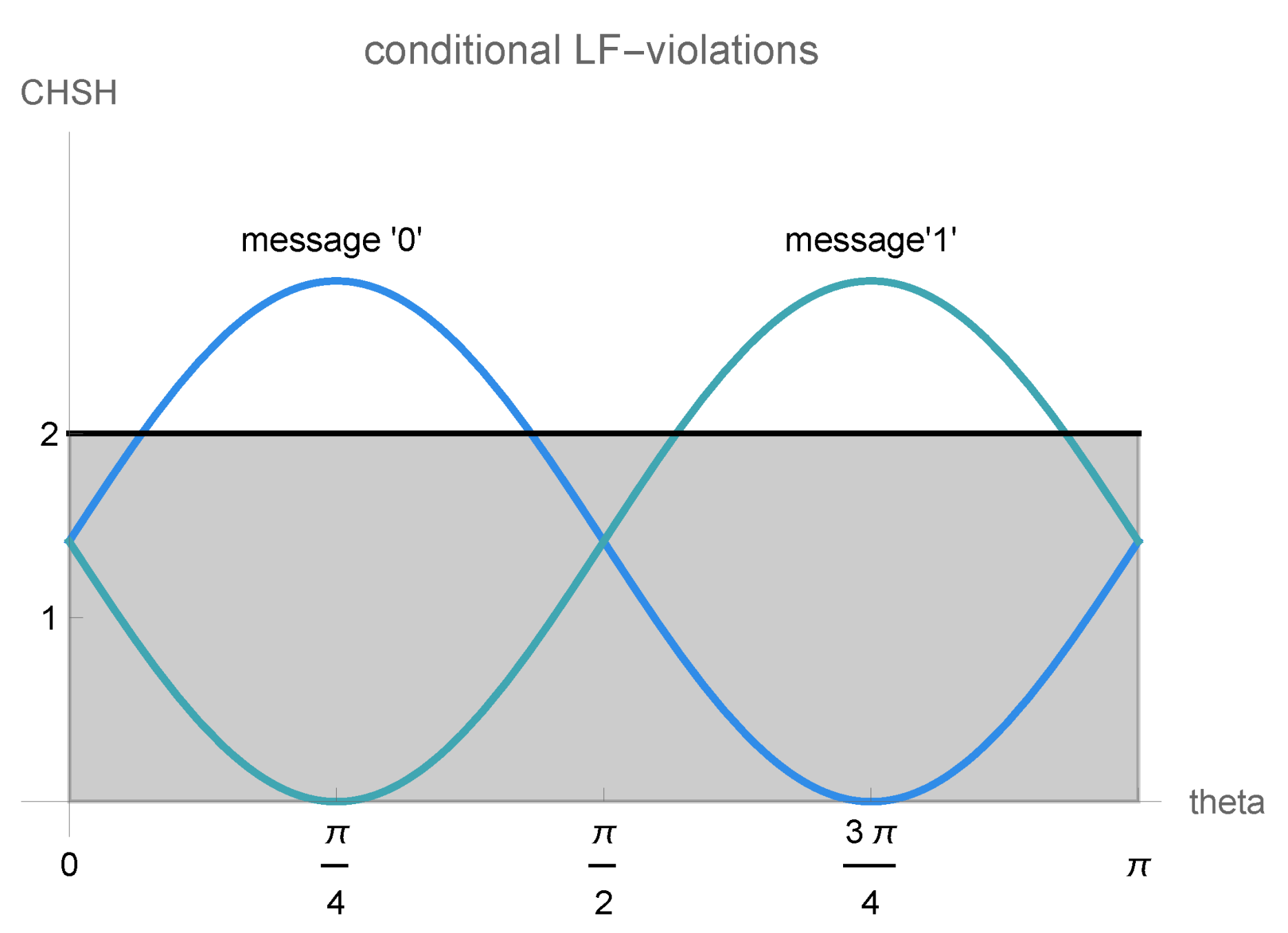
2.3. Local Friendliness Inequalities and Communication
3. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wigner, E.P. The problem of measurement. Am. J. Phys. 1963, 31, 6–15. [Google Scholar] [CrossRef]
- Bub, J.; Pitowsky, I. Two dogmas about quantum mechanics. In Many Worlds?: Everett, Quantum Theory, & Reality; Oxford University Press: Oxford, UK, 2010; pp. 433–459. [Google Scholar]
- Busch, P.; Lahti, P.J.; Mittelstaedt, P. The Quantum Theory of Measurement; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Maudlin, T. Three measurement problems. Topoi 1995, 14, 7–15. [Google Scholar] [CrossRef]
- Deutsch, D. Quantum theory as a universal physical theory. Int. J. Theor. Phys. 1985, 24, 1–41. [Google Scholar] [CrossRef]
- Baumann, V.; Wolf, S. On formalisms and interpretations. Quantum 2021, 2, 99. [Google Scholar] [CrossRef]
- Cavalcanti, E.G. The view from a wigner bubble. Found. Phys. 2021, 51, 39. [Google Scholar] [CrossRef]
- Baumann, V.; Brukner, Č. Wigner’s friend as a rational agent. In Quantum, Probability, Logic; Springer: Berlin/Heidelberg, Germany, 2020; pp. 91–99. [Google Scholar]
- Guérin, P.A.; Baumann, V.; Santo, F.D.; Brukner, Č. A no-go theorem for the persistent reality of wigner’s friend’s perception. arXiv 2020. [Google Scholar]
- Haddara, M.; Cavalcanti, E.G. A possibilistic no-go theorem on the wigner’s friend paradox. arXiv 2022, arXiv:2205.12223. [Google Scholar] [CrossRef]
- Ormrod, N.; Barrett, J. A no-go theorem for absolute observed events without inequalities or modal logic. arXiv 2022, arXiv:2209.03940. [Google Scholar]
- Leegwater, G. When greenberger, horne and zeilinger meet wigner’s friend. Found. Phys. 2022, 52, 2022. [Google Scholar] [CrossRef]
- Żukowski, M.; Markiewicz, M. Even performed pre-measurements have no results. arXiv 2020, arXiv:2003.07464. [Google Scholar]
- Bong, K.-W.; Utreras-Alarcón, A.; Ghafari, F.; Liang, Y.-C.; Tischler, N.; Cavalcanti, E.G.; Pryde, G.J.; Wiseman, H.M. A strong no-go theorem on the Wigner’s friend paradox. Nat. Phys. 2020, 16, 1199–1205. [Google Scholar] [CrossRef]
- Brukner, Č. A no-go theorem for observer-independent facts. Entropy 2018, 20, 350. [Google Scholar] [CrossRef] [PubMed]
- Frauchiger, D.; Renner, R. Quantum theory cannot consistently describe the use of itself. Nat. Commun. 2018, 9, 3711. [Google Scholar] [CrossRef] [PubMed]
- Brukner, Č. On the quantum measurement problem. In Quantum [Un] Speakables II; Springer: Berlin/Heidelberg, Germany, 2017; pp. 95–117. [Google Scholar]
- Vilasini, V.; Nurgalieva, N.; del Rio, L. Multi-agent paradoxes beyond quantum theory. New J. Phys. 2019, 21, 113028. [Google Scholar] [CrossRef]
- Vilasini, V.; Woods, M.P. A general framework for consistent logical reasoning in wigner’s friend scenarios: Subjective perspectives of agents within a single quantum circuit. arXiv 2022, arXiv:2209.09281. [Google Scholar]
- Proietti, M.; Pickston, A.; Graffitti, F.; Barrow, P.; Kundys, D.; Branciard, C.; Ringbauer, M.; Fedrizzi, A. Experimental test of local observer independence. Sci. Adv. 2019, 5, eaaw9832. [Google Scholar] [CrossRef]
- Brukner, Č. Qubits are not observers–a no-go theorem. arXiv 2021, arXiv:2107.03513. [Google Scholar]
- Wiseman, H.M.; Cavalcanti, E.G.; Rieffel, E.G. A “thoughtful” local friendliness no-go theorem: A prospective experiment with new assumptions to suit. arXiv 2022, arXiv:2209.08491. [Google Scholar] [CrossRef]
- Zurek, W.H. Quantum reversibility is relative, or does a quantum measurement reset initial conditions? Philos. Trans. R. Soc. Math. Phys. Eng. Sci. 2018, 376, 20170315. [Google Scholar] [CrossRef]
- Elouard, C.; Lewalle, P.; Manikandan, S.K.; Rogers, S.; Frank, A.; Jordan, A.N. Quantum erasing the memory of wigner’s friend. Quantum 2021, 5, 498. [Google Scholar] [CrossRef]
- Matzkin, A.; Sokolovski, D. Wigner’s friend, Feynman’s paths and material records. Europhys. Lett. 2020, 131, 40001. [Google Scholar] [CrossRef]
- Holevo, A.S. Quantum coding theorems. Russ. Math. Surv. 1998, 53, 1295. [Google Scholar] [CrossRef]
- Matzkin, A.; Sokolovski, D. Wigner-friend scenarios with noninvasive weak measurements. Phys. Rev. A 2020, 102, 062204. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baumann, V. Classical Information and Collapse in Wigner’s Friend Setups. Entropy 2023, 25, 1420. https://doi.org/10.3390/e25101420
Baumann V. Classical Information and Collapse in Wigner’s Friend Setups. Entropy. 2023; 25(10):1420. https://doi.org/10.3390/e25101420
Chicago/Turabian StyleBaumann, Veronika. 2023. "Classical Information and Collapse in Wigner’s Friend Setups" Entropy 25, no. 10: 1420. https://doi.org/10.3390/e25101420
APA StyleBaumann, V. (2023). Classical Information and Collapse in Wigner’s Friend Setups. Entropy, 25(10), 1420. https://doi.org/10.3390/e25101420





