On the Optimal Error Exponent of Type-Based Distributed Hypothesis Testing †
Abstract
:1. Introduction
2. Problem Formulations
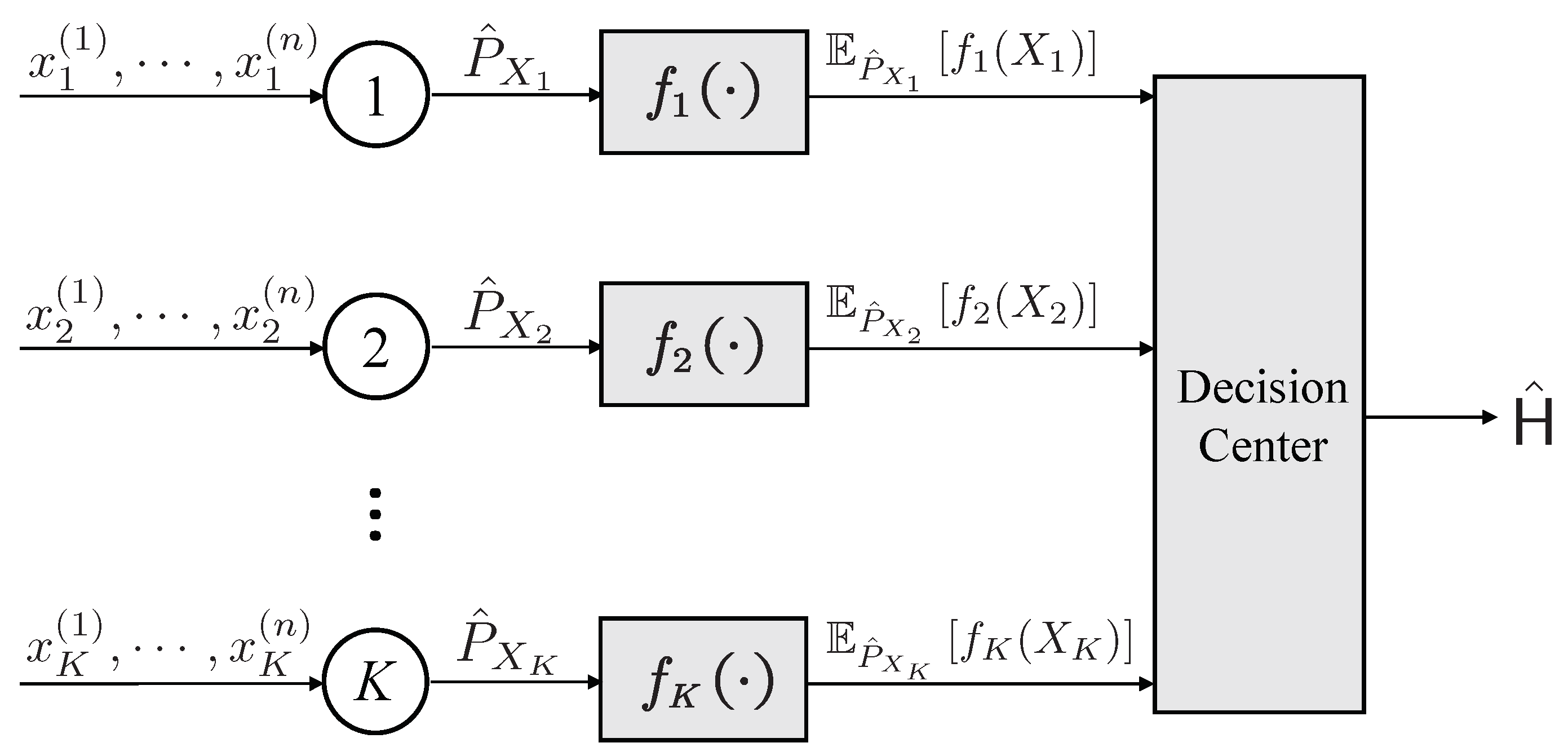
2.1. Type-Based Hypothesis Testing over Noiseless Channels
2.2. Type-Based Hypothesis Testing over AWGN Channels
3. Related Works
4. Type-Based Hypothesis Testing over Noiseless Channels
4.1. Optimal Feature
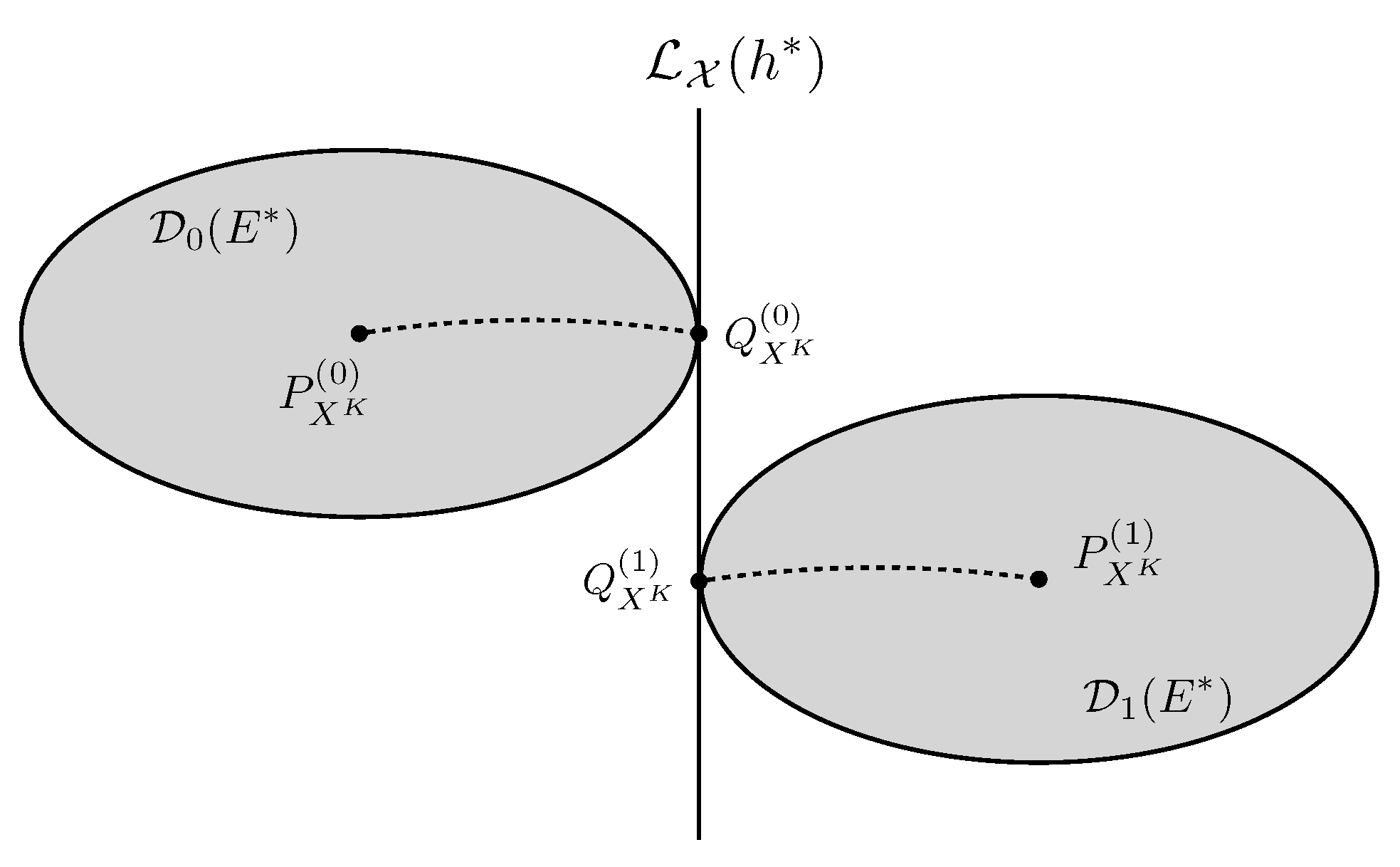
4.2. General Geometric Structure
4.3. Local Information Geometric Analysis
5. Type-Based Hypothesis Testing over AWGN Channels
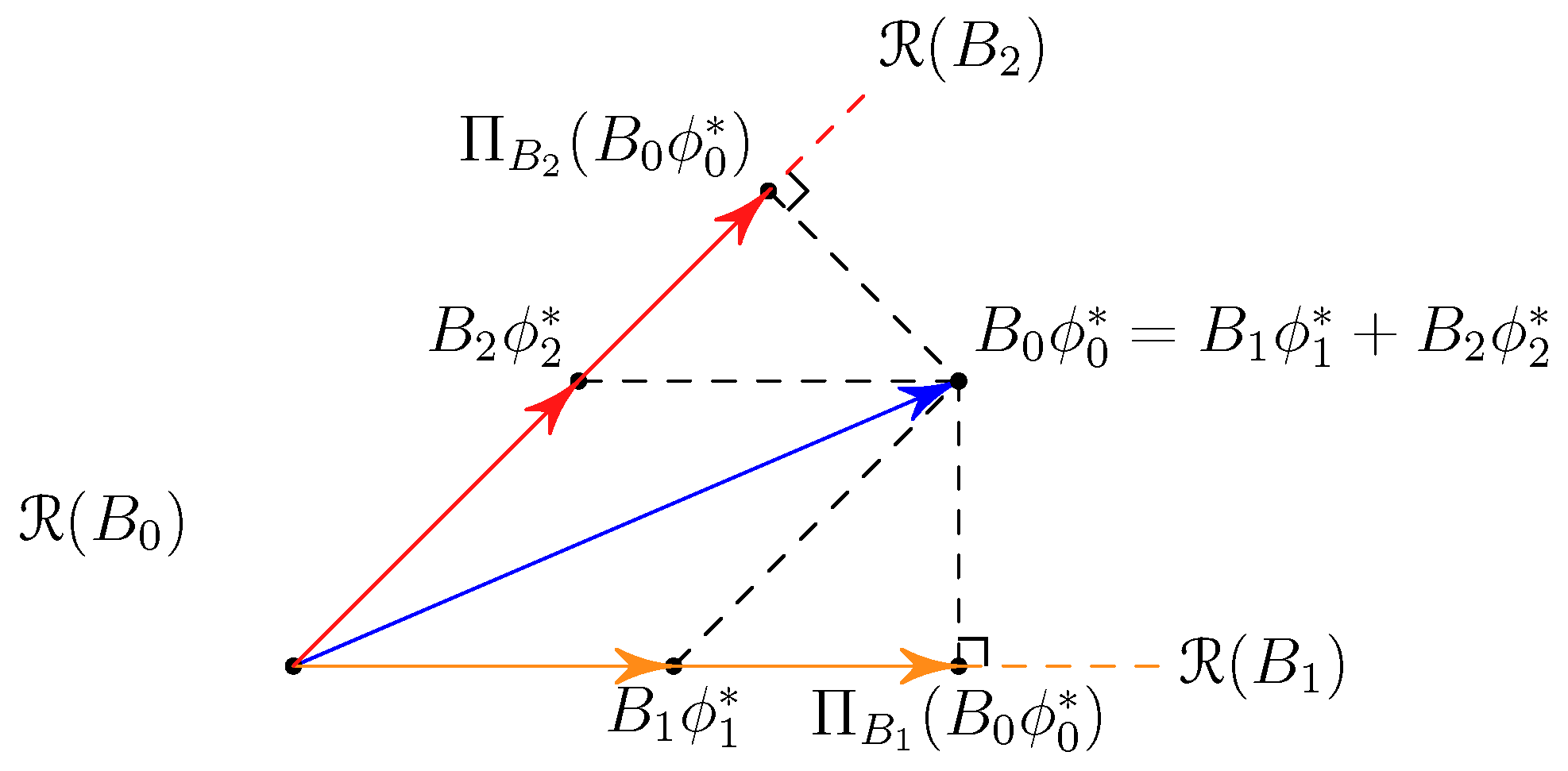
5.1. The Coding Strategy for Distributed Nodes
- Decode-and-forward regime:
- Amplify-and-forward regime:
5.2. Decision Rule and Achievable Error Exponent
5.3. The Converse Result
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| DHT | Distributed hypothesis testing |
| AWGN | Additive white Gaussian noise |
| BPSK | Binary phase shift keying |
| LLRT | Log-likelihood ratio test |
| PAM | Pulse amplitude modulation |
Appendix A. Proof of Lemma 2
Appendix B. Proof of Proposition 1
Appendix C. Proof of Theorem 1
Appendix D. Proof of Theorem 2
Appendix E. Proof of Proposition 2
Appendix F. Proof of Proposition 3
Appendix G. Proof of Proposition 4
Appendix H. Proof of Proposition 6
Appendix I
References
- Han, T.S.; Amari, S. Statistical inference under multiterminal data compression. IEEE Trans. Inf. Theory 1998, 44, 2300–2324. [Google Scholar] [CrossRef]
- Ahlswede, R.; Csiszár, I. Hypothesis testing with communication constraints. IEEE Trans. Inf. Theory 1986, 32, 533–542. [Google Scholar] [CrossRef]
- Han, T.S.; Kobayashi, K. Exponential-type error probabilities for multiterminal hypothesis testing. IEEE Trans. Inf. Theory 1989, 35, 2–14. [Google Scholar] [CrossRef]
- Amari, S.I.; Han, T.S. Statistical inference under multiterminal rate restrictions: A differential geometric approach. IEEE Trans. Inf. Theory 1989, 35, 217–227. [Google Scholar] [CrossRef]
- Watanabe, S. Neyman–Pearson test for zero-rate multiterminal hypothesis testing. IEEE Trans. Inf. Theory 2017, 64, 4923–4939. [Google Scholar] [CrossRef]
- Shimokawa, H.; Han, T.S.; Amari, S. Error bound of hypothesis testing with data compression. In Proceedings of the 1994 IEEE International Symposium on Information Theory, Trondheim, Norway, 27 June–1 July 1994; p. 114. [Google Scholar] [CrossRef]
- Xu, X.; Huang, S.L. On Distributed Learning with Constant Communication Bits. IEEE J. Sel. Areas Inf. Theory 2022, 3, 125–134. [Google Scholar] [CrossRef]
- Sreekumar, S.; Gündüz, D. Strong Converse for Testing Against Independence over a Noisy channel. In Proceedings of the 2020 IEEE International Symposium on Information Theory (ISIT), Los Angeles, CA, USA, 21–26 June 2020; pp. 1283–1288. [Google Scholar] [CrossRef]
- McMahan, B.; Moore, E.; Ramage, D.; Hampson, S.; Arcas, B.A.Y. Communication-Efficient Learning of Deep Networks from Decentralized Data. In Proceedings of the 20th International Conference on Artificial Intelligence and Statistics, Fort Lauderdale, FL, USA, 20–22 April 2017; Volume 54, pp. 1273–1282. [Google Scholar]
- Vapnik, V. Principles of Risk Minimization for Learning Theory. In Proceedings of the 4th International Conference on Neural Information Processing Systems, San Francisco, CA, USA, 2–5 December 1991; pp. 831–838. [Google Scholar]
- Srivastava, N.; Salakhutdinov, R. Multimodal learning with deep boltzmann machines. J. Mach. Learn. Res. 2014, 15, 2949–2980. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory (Wiley Series in Telecommunications and Signal Processing); Wiley-Interscience: Hoboken, NJ, USA, 2006. [Google Scholar]
- Huang, S.L.; Makur, A.; Wornell, G.W.; Zheng, L. On universal features for high-dimensional learning and inference. arXiv 2019, arXiv:1911.09105. [Google Scholar]
- Han, T.S. Hypothesis testing with multiterminal data compression. IEEE Trans. Inf. Theory 1987, 33, 759–772. [Google Scholar] [CrossRef]
- Scardapane, S.; Wang, D.; Panella, M.; Uncini, A. Distributed learning for random vector functional-link networks. Inf. Sci. 2015, 301, 271–284. [Google Scholar]
- Georgopoulos, L.; Hasler, M. Distributed machine learning in networks by consensus. Neurocomputing 2014, 124, 2–12. [Google Scholar] [CrossRef]
- Tsitsiklis, J.; Athans, M. On the complexity of decentralized decision making and detection problems. IEEE Trans. Autom. Control 1985, 30, 440–446. [Google Scholar] [CrossRef]
- Tsitsiklis, J.N. Decentralized detection by a large number of sensors. Math. Control. Signals Syst. 1988, 1, 167–182. [Google Scholar] [CrossRef]
- Tenney, R.R.; Sandell, N.R. Detection with distributed sensors. IEEE Trans. Aerosp. Electron. Syst. 1981, AES-17, 501–510. [Google Scholar] [CrossRef]
- Shalaby, H.M.; Papamarcou, A. Multiterminal detection with zero-rate data compression. IEEE Trans. Inf. Theory 1992, 38, 254–267. [Google Scholar] [CrossRef]
- Zhao, W.; Lai, L. Distributed testing with zero-rate compression. In Proceedings of the 2015 IEEE International Symposium on Information Theory (ISIT), Hong Kong, China, 14–19 June 2015; pp. 2792–2796. [Google Scholar]
- Sreekumar, S.; Gündüz, D. Distributed hypothesis testing over noisy channels. In Proceedings of the 2017 IEEE International Symposium on Information Theory (ISIT), Aachen, Germany, 25–30 June 2017; pp. 983–987. [Google Scholar]
- Zaidi, A. Hypothesis Testing Against Independence Under Gaussian Noise. In Proceedings of the 2020 IEEE International Symposium on Information Theory (ISIT), Los Angeles, CA, USA, 21–26 June 2020; pp. 1289–1294. [Google Scholar] [CrossRef]
- Salehkalaibar, S.; Wigger, M.A. Distributed hypothesis testing over a noisy channel. In Proceedings of the International Zurich Seminar on Information and Communication (IZS 2018), Zurich, Switzerland, 21–23 February 2018; pp. 25–29. [Google Scholar]
- Weinberger, N.; Kochman, Y.; Wigger, M. Exponent trade-off for hypothesis testing over noisy channels. In Proceedings of the 2019 IEEE International Symposium on Information Theory (ISIT), Paris, France, 7–12 July 2019; pp. 1852–1856. [Google Scholar]
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Csiszár, I.; Shields, P.C. Information Theory and Statistics: A Tutorial; Now Publishers Inc.: Delft, The Netherlands, 2004. [Google Scholar]
- Csiszár, I. The method of types [information theory]. IEEE Trans. Inf. Theory 1998, 44, 2505–2523. [Google Scholar] [CrossRef]
- Huang, S.L.; Xu, X.; Zheng, L. An information-theoretic approach to unsupervised feature selection for high-dimensional data. IEEE J. Sel. Areas Inf. Theory 2020, 1, 157–166. [Google Scholar] [CrossRef]
- Horn, R.A.; Johnson, C.R. Matrix Analysis; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Graham, R.L.; Knuth, D.E.; Patashnik, O.; Liu, S. Concrete mathematics: A foundation for computer science. Comput. Phys. 1989, 3, 106–107. [Google Scholar] [CrossRef]
- Blair, J.; Edwards, C.; Johnson, J.H. Rational Chebyshev approximations for the inverse of the error function. Math. Comput. 1976, 30, 827–830. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tong, X.; Xu, X.; Huang, S.-L. On the Optimal Error Exponent of Type-Based Distributed Hypothesis Testing. Entropy 2023, 25, 1434. https://doi.org/10.3390/e25101434
Tong X, Xu X, Huang S-L. On the Optimal Error Exponent of Type-Based Distributed Hypothesis Testing. Entropy. 2023; 25(10):1434. https://doi.org/10.3390/e25101434
Chicago/Turabian StyleTong, Xinyi, Xiangxiang Xu, and Shao-Lun Huang. 2023. "On the Optimal Error Exponent of Type-Based Distributed Hypothesis Testing" Entropy 25, no. 10: 1434. https://doi.org/10.3390/e25101434
APA StyleTong, X., Xu, X., & Huang, S.-L. (2023). On the Optimal Error Exponent of Type-Based Distributed Hypothesis Testing. Entropy, 25(10), 1434. https://doi.org/10.3390/e25101434





