Entanglement Degradation in Two Interacting Qubits Coupled to Dephasing Environments
Abstract
:1. Introduction
2. The Model and Solution
3. Dynamics of Entanglement
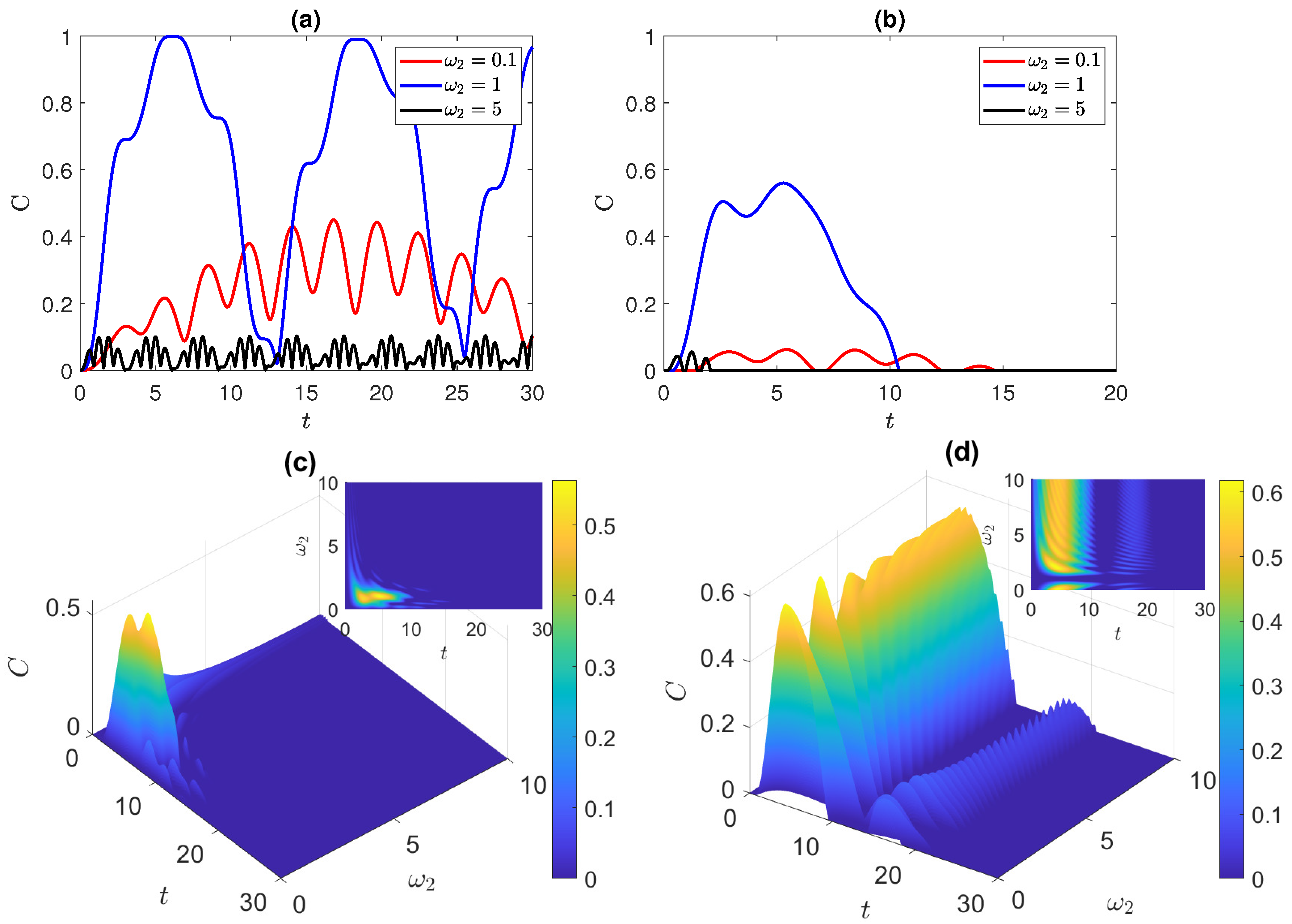
3.1. Disentangled State
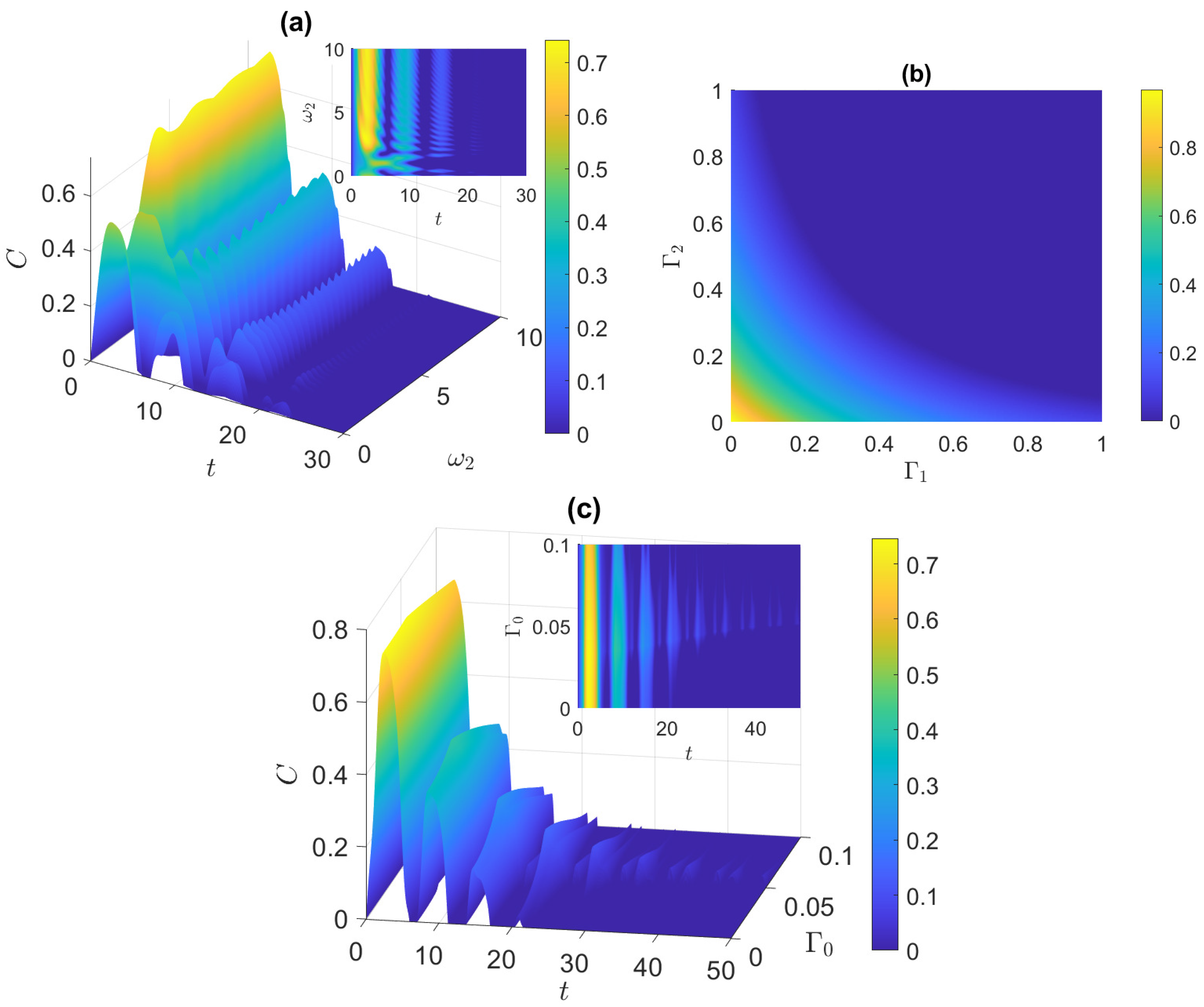
3.2. Correlated Bell State
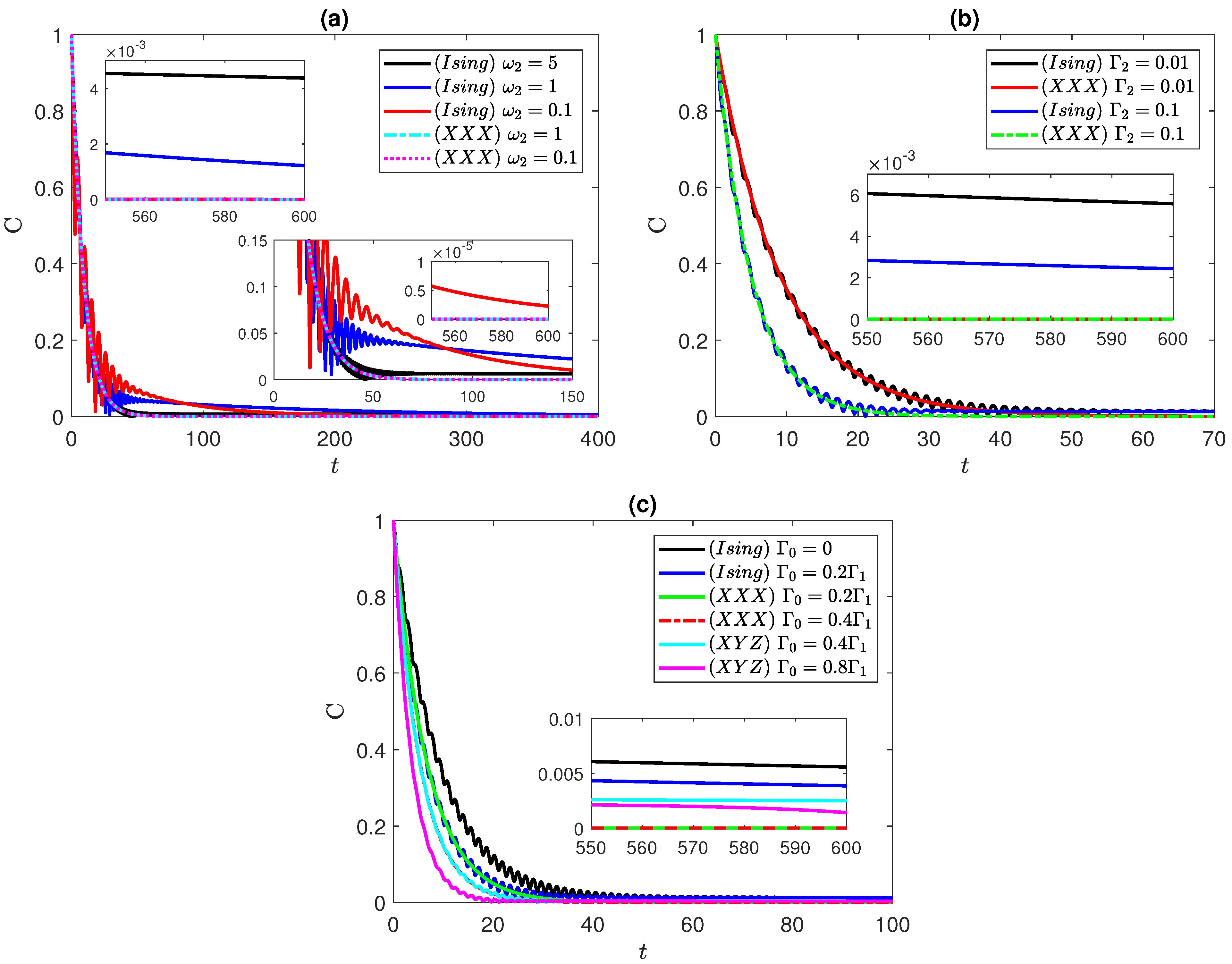
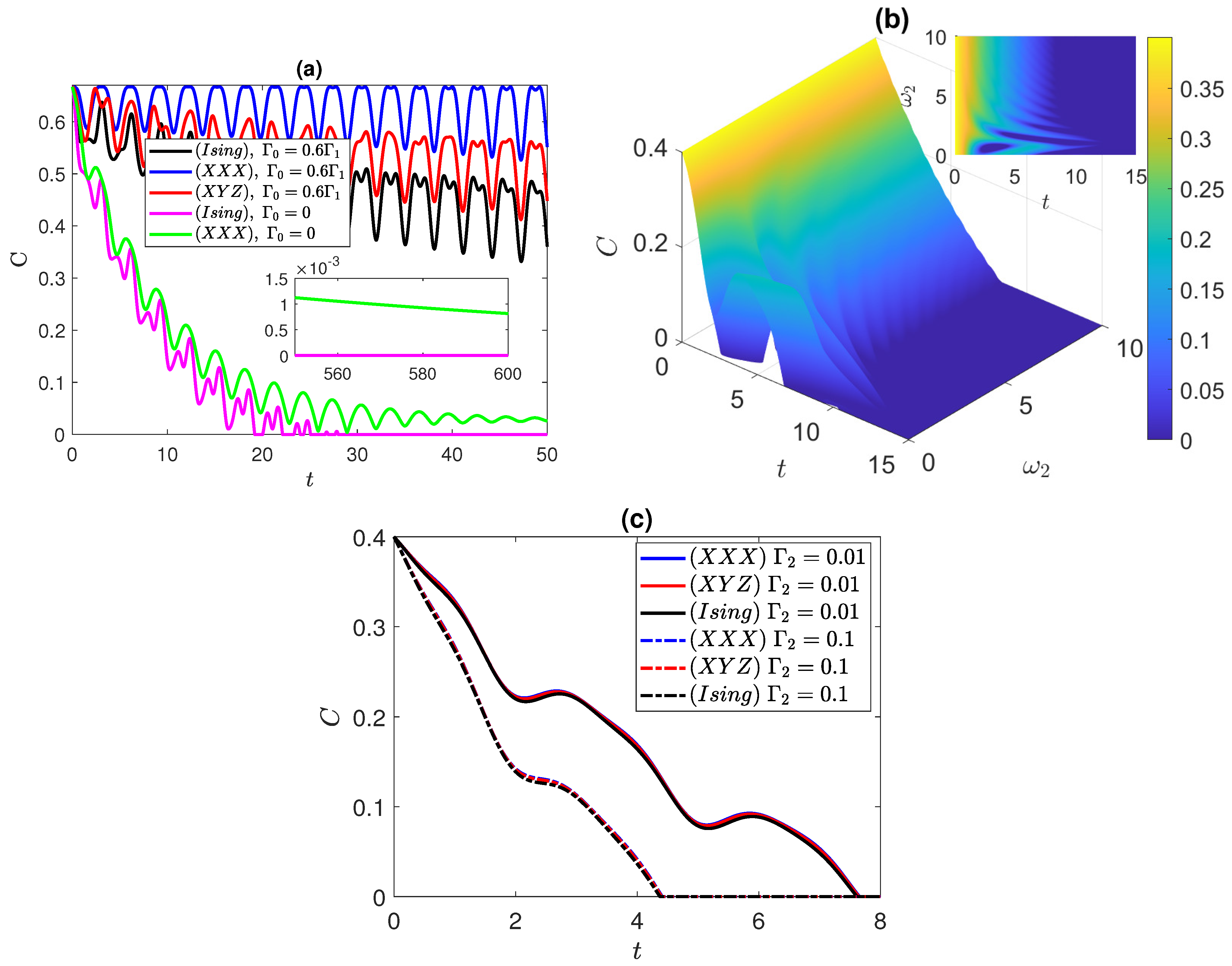
3.3. Anti-Correlated Bell State
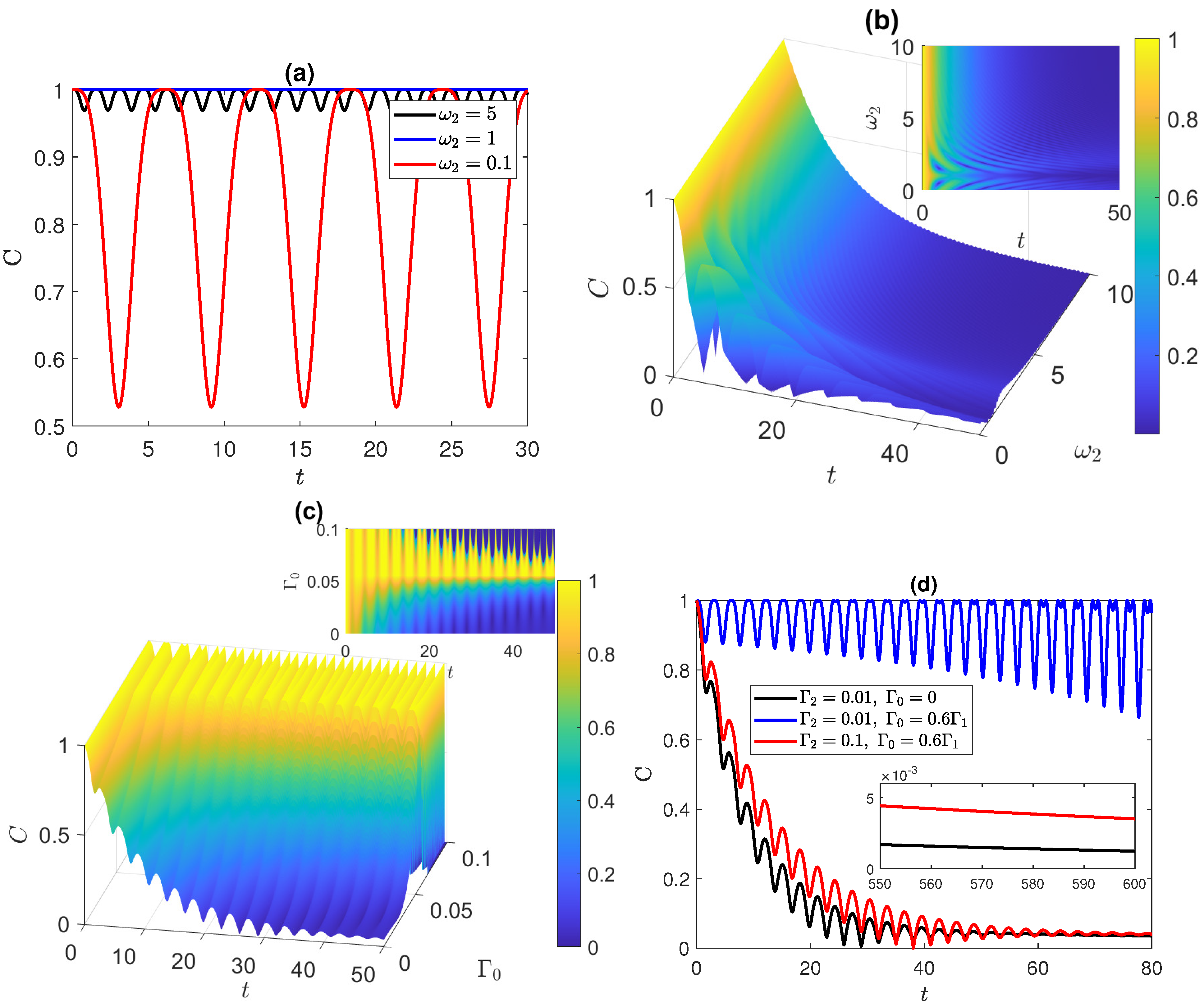
3.4. W and Werner States
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Nielsen, M.; Chuang, I. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Breuer, H.P.; Petruccione, F. The Theory of Open Quantum Systems; Oxford University Press: Oxford, UK, 2002. [Google Scholar]
- Knill, E.; Laflamme, R.; Zurek, W. Resilient quantum computation: Error models and thresholds. R. Soc. Lond. A 1998, 454, 365–384. [Google Scholar] [CrossRef]
- Paz-Silva, G.; Lidar, D. Optimally combining dynamical decoupling and quantum error correction. Sci. Rep. 2013, 3, 1530. [Google Scholar] [CrossRef]
- Paz-Silva, G.; Lee, S.W.; Green, T.; Viola, L. Dynamical decoupling sequences for multi-qubit dephasing suppression and long-time quantum memory. New J. Phys. 2016, 18, 073020. [Google Scholar] [CrossRef]
- Qiu, J.; Zhou, Y.; Hu, C.K.; Yuan, J.; Zhang, L.; Chu, J.; Huang, W.; Liu, W.; Luo, K.; Ni, Z.; et al. Suppressing Coherent Two-Qubit Errors via Dynamical Decoupling. Phys. Rev. Appl. 2021, 16, 054047. [Google Scholar] [CrossRef]
- Shor, P. Scheme for reducing decoherence in quantum computer memory. Phys. Rev. A 1995, 52, R2493(R). [Google Scholar] [CrossRef]
- Calderbank, A.; Shor, P. Good quantum error-correcting codes exist. Phys. Rev. A 1996, 54, 1098. [Google Scholar] [CrossRef]
- Lidar, D.; Chuang, I.; Whaley, K. Decoherence-Free Subspaces for Quantum Computation. Phys. Rev. Lett. 1998, 81, 2594. [Google Scholar] [CrossRef]
- Bacon, D.; Lidar, D.; Whaley, K. Robustness of decoherence-free subspaces for quantum computation. Phys. Rev. A 1999, 60, 1944. [Google Scholar] [CrossRef]
- Harrow, A.; Nielsen, M. Robustness of quantum gates in the presence of noise. Phys. Rev. A 2003, 68, 012308. [Google Scholar] [CrossRef]
- Das, S.; Agarwal, G. Bright and dark periods in the entanglement dynamics of interacting qubits in contact with the environment. J. Phys. B At. Mol. Opt. Phys. 2009, 42, 141003. [Google Scholar] [CrossRef]
- Liu, Z.D.; Lyyra, H.; Sun, Y.N.; Liu, B.H.; Li, C.F.; Guo, G.C.; Maniscalco, S.; Piilo, J. Experimental implementation of fully controlled dephasing dynamics and synthetic spectral densities. Nat. Commun. 2018, 9, 3453. [Google Scholar] [CrossRef] [PubMed]
- Guo, Q.; Zheng, S.B.; Wang, J.; Song, C.; Zhang, P.; Li, K.; Liu, W.; Deng, H.; Huang, K.; Zheng, D.; et al. Dephasing-Insensitive Quantum Information Storage and Processing with Superconducting Qubits. Phys. Rev. Lett. 2018, 121, 130501. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Bae, Y.; Heinrich, A. Harnessing the Quantum Behavior of Spins on Surfaces. Adv. Mater. 2022, 35, 2107534. [Google Scholar] [CrossRef] [PubMed]
- Kaplan, H.; Guo, L.; Tan, W.; De, A.; Marquardt, F.; Pagano, G.; Monroe, C. Many-Body Dephasing in a Trapped-Ion Quantum Simulator. Phys. Rev. Lett. 2020, 125, 120605. [Google Scholar] [CrossRef] [PubMed]
- Zheng, R.H.; Ning, W.; Yang, Z.B.; Xia, Y.; Zheng, S.B. Demonstration of dynamical control of three-level open systems with a superconducting qutrit. New J. Phys. 2022, 24, 063031. [Google Scholar] [CrossRef]
- Moskalenko, I.; Simakov, I.; Abramov, N.; Grigorev, A.; Moskalev, D.; Pishchimova, A.; Smirnov, N.; Zikiy, E.; Rodionov, I.; Besedin, I. High fidelity two-qubit gates on fluxoniums using a tunable coupler. npj Quantum Inf. 2022, 8, 130. [Google Scholar] [CrossRef]
- Mercurio, A.; Abo, S.; Mauceri, F.; Russo, E.; Macrì, V.; Miranowicz, A.; Savasta, S.; Stefano, O. Pure Dephasing of Light-Matter Systems in the Ultrastrong and Deep-Strong Coupling Regimes. Phys. Rev. Lett. 2023, 130, 123601. [Google Scholar] [CrossRef]
- Tahira, R.; Ikram, M.; Azim, T.; Zubairy, S. Entanglement dynamics of a pure bipartite system in dissipative environments. J. Phys. B At. Mol. Opt. Phys. 2008, 41, 205501. [Google Scholar] [CrossRef]
- Ikram, M.; Li, F.L.; Zubairy, M. Disentanglement in a two-qubit system subjected to dissipation environments. Phys. Rev. A 2007, 75, 062336. [Google Scholar] [CrossRef]
- Hu, M.L.; Xi, X.Q.; Lian, H.L. Thermal and phase decoherence effects on entanglement dynamics of the quantum spin systems. Phys. B 2009, 404, 3499–3506. [Google Scholar] [CrossRef]
- Orth, P.; Roosen, D.; Hofstetter, W.; Hur, K. Dynamics, synchronization, and quantum phase transitions of two dissipative spins. Phys. Rev. B 2010, 82, 144423. [Google Scholar] [CrossRef]
- Ghasemian, E.; Tavassoly, M.K. Generation of Werner-like states via a two-qubit system plunged in a thermal reservoir and their application in solving binary classification problems. Sci. Rep. 2021, 11, 3554. [Google Scholar] [CrossRef] [PubMed]
- Man, Z.X.; Xia, Y.J.; An, N. Manipulating entanglement of two qubits in a common environment by means of weak measurements and quantum measurement reversals. Phys. Rev. A 2012, 86, 012325. [Google Scholar] [CrossRef]
- Lashin, E.I.; Sadiek, G.; Abdalla, M.S.; Aldufeery, E. Two driven coupled qubits in a time varying magnetic field: Exact approximate solutions. Appl. Math. Inf. Sci. 2014, 8, 1071. [Google Scholar] [CrossRef]
- Obada, A.; Shaheen, M. Influence of Various Environments on Information and Entanglement Dynamics for Two Interacting Qubits. J. Russ. Laser Res. 2015, 36, 24–34. [Google Scholar] [CrossRef]
- Nourmandipour, A.; Tavassoly, M. Dynamics and protecting of entanglement in two-level systems interacting with a dissipative cavity: The Gardiner–Collett approach. J. Phys. B At. Mol. Opt. Phys. 2015, 48, 165502. [Google Scholar] [CrossRef]
- Zare, F.; Tavassoly, M. Decoherence attenuation in the Tavis-Cummings model via transition frequency modulation with dipole–dipole interaction and multi-photon transitions. Optik 2020, 217, 164841. [Google Scholar] [CrossRef]
- Musavi, S.; Tavassoly, M.; Salimian, S. Entanglement dynamics and population inversion of a two-qubit system in two cavities coupled with optical fiber in the presence of two-photon transition. Mod. Phys. Lett. A 2023, 38, 2350026. [Google Scholar] [CrossRef]
- Nourmandipour, A.; Tavassoly, M.; Bolorizadeh, M. Quantum Zeno and anti-Zeno effects on the entanglement dynamics of qubits dissipating into a common and non-Markovian environment. J. Opt. Soc. Am. B 2016, 33, 1723–1730. [Google Scholar] [CrossRef]
- Yu, T.; Eberly, J. Finite-Time Disentanglement Via Spontaneous Emission. Phys. Rev. Lett. 2004, 93, 140404. [Google Scholar] [CrossRef]
- Yu, T.; Eberly, J. Sudden death of entanglement: Classical noise effects. Opt. Commun. 2006, 264, 393–397. [Google Scholar] [CrossRef]
- Das, S.; Agarwal, G. Decoherence effects in interacting qubits under the influence of various environments. J. Phys. B At. Mol. Opt. Phys. 2009, 42, 205502. [Google Scholar] [CrossRef]
- Shan, C.J.; Liu, J.B.; Cheng, W.W.; Liu, T.K.; Huang, Y.X.; Li, H. Entanglement Dynamics of Two-Qubit System in Different Types of Noisy Channels. Commun. Theor. Phys. 2009, 51, 1013. [Google Scholar] [CrossRef]
- Jiang, L.N.; Ma, J.; Yu, S.Y.; Tan, L.Y.; Ran, Q.W. Entanglement Evolution of the Extended Werner-like State under the Influence of Different Noisy Channels. Int. J. Theor. Phys. 2015, 54, 440–449. [Google Scholar] [CrossRef]
- Rossi, M.; Benedetti, C.; Paris, M. Engineering decoherence for two-qubit systems interacting with a classical environment. Int. J. Quantum Inf. 2014, 12, 15600035. [Google Scholar] [CrossRef]
- Yang, C.; Guo, Y.N.; Peng, H.P.; Lu, Y.B. Dynamics of local quantum uncertainty for a two-qubit system under dephasing noise. Laser Phys. 2020, 30, 015203. [Google Scholar] [CrossRef]
- Chirolli, L.; Burkard, G. Decoherence in solid-state qubits. Taylor Fr. 2008, 57, 225–285. [Google Scholar] [CrossRef]
- Trauzettel, B.; Borhani, M.; Trif, M.; Loss, D. Theory of spin qubits in nanostructures. J. Phys. Soc. Jpn. 2008, 77, 031012. [Google Scholar] [CrossRef]
- Jing, J.; Wu, L.A. Decoherence and control of a qubit in spin baths: An exact master equation study. Sci. Rep. 2018, 8, 1471. [Google Scholar] [CrossRef]
- Malkoc, O.; Stano, P.; Loss, D. Charge-Noise-Induced Dephasing in Silicon Hole-Spin Qubits. Phys. Rev. Lett. 2022, 129, 247701. [Google Scholar] [CrossRef]
- Kakuyanagi, K.; Meno, T.; Saito, S.; Nakano, H.; Semba, K.; Takayanagi, H.; Deppe, F.; Shnirman, A. Dephasing of a Superconducting Flux Qubit. Phys. Rev. Lett. 2007, 98, 047004. [Google Scholar] [CrossRef] [PubMed]
- Anton, S.; Müller, C.; Birenbaum, J.; O’Kelley, S.; Fefferman, A.; Golubev, D.; Hilton, G.; Cho, H.; Irwin, K.; Wellstood, F.; et al. Pure dephasing in flux qubits due to flux noise with spectral density scaling as 1/fα. Phys. Rev. B 2012, 85, 224505. [Google Scholar] [CrossRef]
- Spilla, S.; Hassler, F.; Splettstoesser, J. Measurement and dephasing of a flux qubit due to heat currents. New J. Phys. 2014, 16, 045020. [Google Scholar] [CrossRef]
- Hutchings, M.D.; Hertzberg, J.B.; Liu, Y.; Bronn, N.T.; Keefe, G.A.; Brink, M.; Chow, J.M.; Plourde, B.T. Tunable Superconducting Qubits with Flux-Independent Coherence. Phys. Rev. Appl. 2017, 8, 044003. [Google Scholar] [CrossRef]
- Filipp, S.; Goppl, M.; Fink, J.M.; Baur, M.; Bianchetti, R.; Steffen, L.; Wallraff, A. Multimode mediated qubit–qubit coupling and dark-state symmetries in circuit quantum electrodynamics. Phys. Rev. A 2011, 83, 063827. [Google Scholar] [CrossRef]
- Yang, C.P.; Su, Q.P.; Zheng, S.B.; Nori, F. Entangling superconducting qubits in a multi-cavity system. New J. Phys 2016, 18, 013025. [Google Scholar] [CrossRef]
- Scarlino, P.; van Woerkom, D.J.; Mendes, U.C.; Koski, J.V.; Landig, A.J.; Andersen, C.K.; Gasparinetti, S.; Reichl, C.; Wegscheider, W.; Ensslin, K.; et al. Coherent microwave-photon-mediated coupling between a semiconductor and a superconducting qubit. Nat. Commun. 2019, 10, 3011. [Google Scholar] [CrossRef]
- Sedov, D.; Kozin, V.; Iorsh, I. Chiral Waveguide Optomechanics: First Order Quantum Phase Transitions with Z3 Symmetry Breaking. Phys. Rev. Lett. 2020, 125, 263606. [Google Scholar] [CrossRef]
- Fortunato, E.M.; Viola, L.; Hodges, J.; Teklemariam, G.; Cory, D.G. Implementation of universal control on a decoherence-free qubit. New J. Phys. 2002, 4, 5. [Google Scholar] [CrossRef]
- Singh, H.; Arvind Kavita, D. Experimentally freezing quantum discord in a dephasing environment using dynamical decoupling. EPL 2017, 118, 50001. [Google Scholar] [CrossRef]
- Blatt, R.; Wineland, D. Entangled states of trapped atomic ions. Nature 2008, 453, 1008–1015. [Google Scholar] [CrossRef] [PubMed]
- Hensen, B.; Bernien, H.; Dréau, A.E.; Reiserer, A.; Kalb, N.; Blok, M.S.; Ruitenberg, J.; Vermeulen, R.L.; Schouten, R.N.; Abellán, C.; et al. Loophole-free Bell inequality violation using electron spins separated by 1.3 kilometres. Nature 2015, 526, 682–686. [Google Scholar] [CrossRef] [PubMed]
- Giustina, M.; Versteegh, M.M.; Wengerowsky, S.; Handsteiner, J.; Hochrainer, A.; Phelan, K.; Steinlechner, F.; Kofler, J.; Larsson, J.K.; Abellán, C.; et al. Significant-loophole-free test of Bell’s theorem with entangled photons. Phys. Rev. Lett. 2015, 115, 250401. [Google Scholar] [CrossRef]
- Li, M.H.; Wu, C.; Zhang, Y.; Liu, W.Z.; Bai, B.; Liu, Y.; Zhang, W.; Zhao, Q.; Li, H.; Wang, Z.; et al. Test of local realism into the past without detection and locality loopholes. Phys. Rev. Lett. 2018, 121, 080404. [Google Scholar] [CrossRef] [PubMed]
- Rosenfeld, W.; Burchardt, D.; Garthoff, R.; Redeker, K.; Ortegel, N.; Rau, M.; Weinfurter, H. Event-Ready Bell Test Using Entangled Atoms Simultaneously Closing Detection and Locality Loopholes. Phys. Rev. Lett. 2017, 119, 010402. [Google Scholar] [CrossRef]
- Storz, S.; Schär, J.; Kulikov, A.; Magnard, P.; Kurpiers, P.; Lütolf, J.; Walter, T.; Copetudo, A.; Reuer, K.; Akin, A.; et al. Loophole-free Bell inequality violation with superconducting circuits. Nature 2023, 617, 265–270. [Google Scholar] [CrossRef]
- Zhang, Y.; Huang, Y.; Li, C.; Guo, G. Experimental preparation of the Werner state via spontaneous parametric down-conversion. Phys. Rev. A 2002, 66, 062315. [Google Scholar] [CrossRef]
- Liu, T.; Wang, C.; Li, J.; Wang, Q. Experimental preparation of an arbitrary tunable Werner state. EPL 2017, 119, 14002. [Google Scholar] [CrossRef]
- Lindblad, G. On the generators of quantum dynamical semigroups. Commun. Math. Phys. 1976, 48, 119–130. [Google Scholar] [CrossRef]
- Sadiek, G.; Almalki, S. Entanglement dynamics in Heisenberg spin chains coupled to a dissipative environment at finite temperature. Phys. Rev. A 2016, 94, 012341. [Google Scholar] [CrossRef]
- Wootters, W.K. Entanglement of Formation of an Arbitrary State of Two Qubits. Phys. Rev. Lett. 1998, 80, 2245–2248. [Google Scholar] [CrossRef]
- Buluta, I.; Ashhab, S.; Nori, F. Natural and artificial atoms for quantum computation. Rep. Prog. Phys. 2011, 74, 104401. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdelmagid, R.; Alshehhi, K.; Sadiek, G. Entanglement Degradation in Two Interacting Qubits Coupled to Dephasing Environments. Entropy 2023, 25, 1458. https://doi.org/10.3390/e25101458
Abdelmagid R, Alshehhi K, Sadiek G. Entanglement Degradation in Two Interacting Qubits Coupled to Dephasing Environments. Entropy. 2023; 25(10):1458. https://doi.org/10.3390/e25101458
Chicago/Turabian StyleAbdelmagid, Rahma, Khadija Alshehhi, and Gehad Sadiek. 2023. "Entanglement Degradation in Two Interacting Qubits Coupled to Dephasing Environments" Entropy 25, no. 10: 1458. https://doi.org/10.3390/e25101458
APA StyleAbdelmagid, R., Alshehhi, K., & Sadiek, G. (2023). Entanglement Degradation in Two Interacting Qubits Coupled to Dephasing Environments. Entropy, 25(10), 1458. https://doi.org/10.3390/e25101458






