Gaussian and Lerch Models for Unimodal Time Series Forcasting
Abstract
:1. Introduction
2. Probabilistic Interpretation of LAD Regression
3. LAD Regression Analysis Using Weighted Median
3.1. Weighted Median
3.1.1. Back to Our Proposed LAD Regression
3.1.2. Comparison of the Minimizers of the Map and the Minimizers of the Map
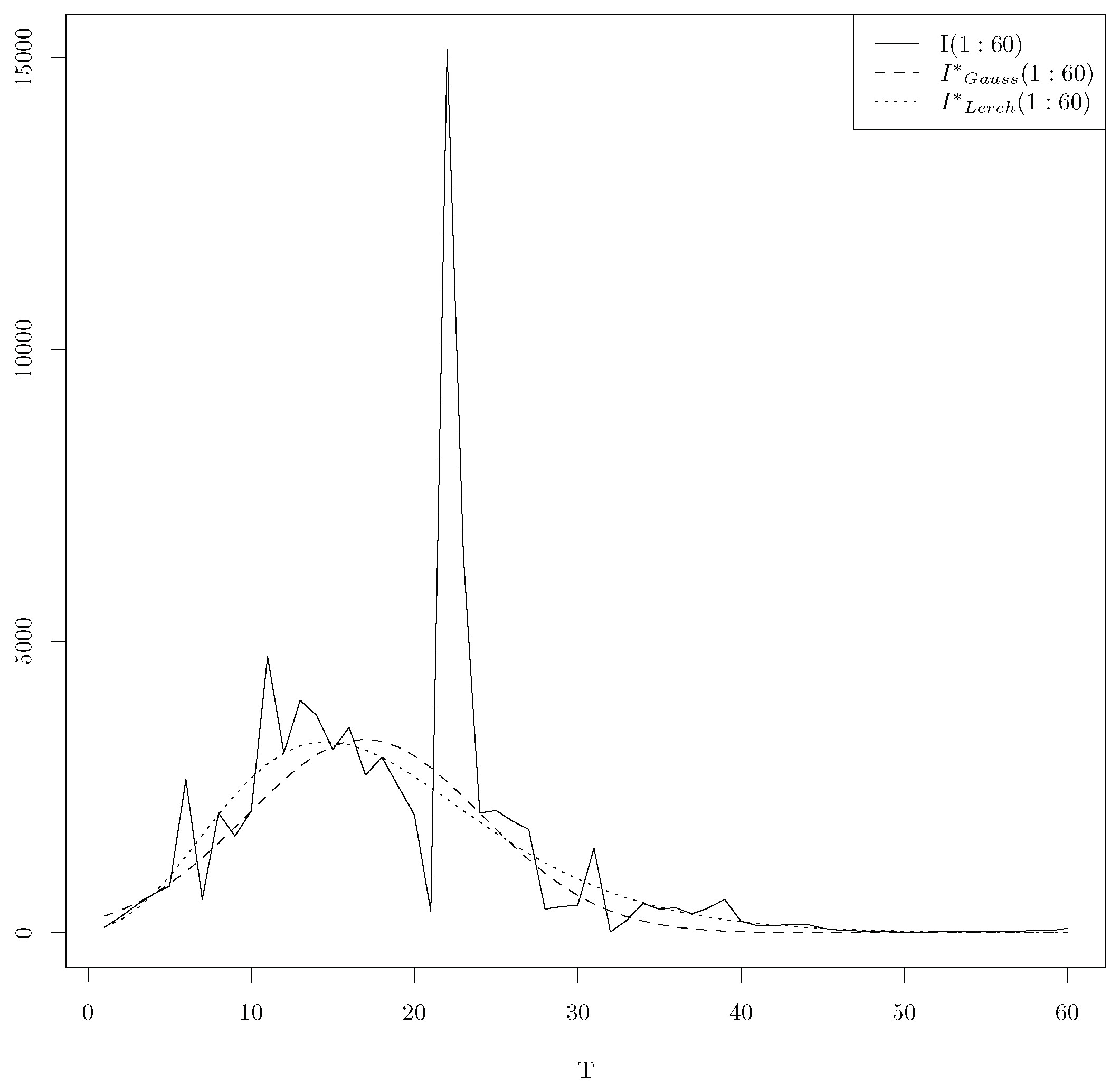
4. Numerical Results
4.1. LAD Regression Using Gaussian Model with
| Algorithm 1 The output of the iteration of optim function until convergence | |
| Input: Fonction F | |
| 1: | initialization , |
| 2: | while do |
| 3: | optim // optim function applied to F with the initialization . |
| 4: | end while |
| output: and . | |
4.2. Confidence Intervals Using Six minimas with T = 10 in the Gaussian Model
4.3. LAD Regression Using the Lerch Model with
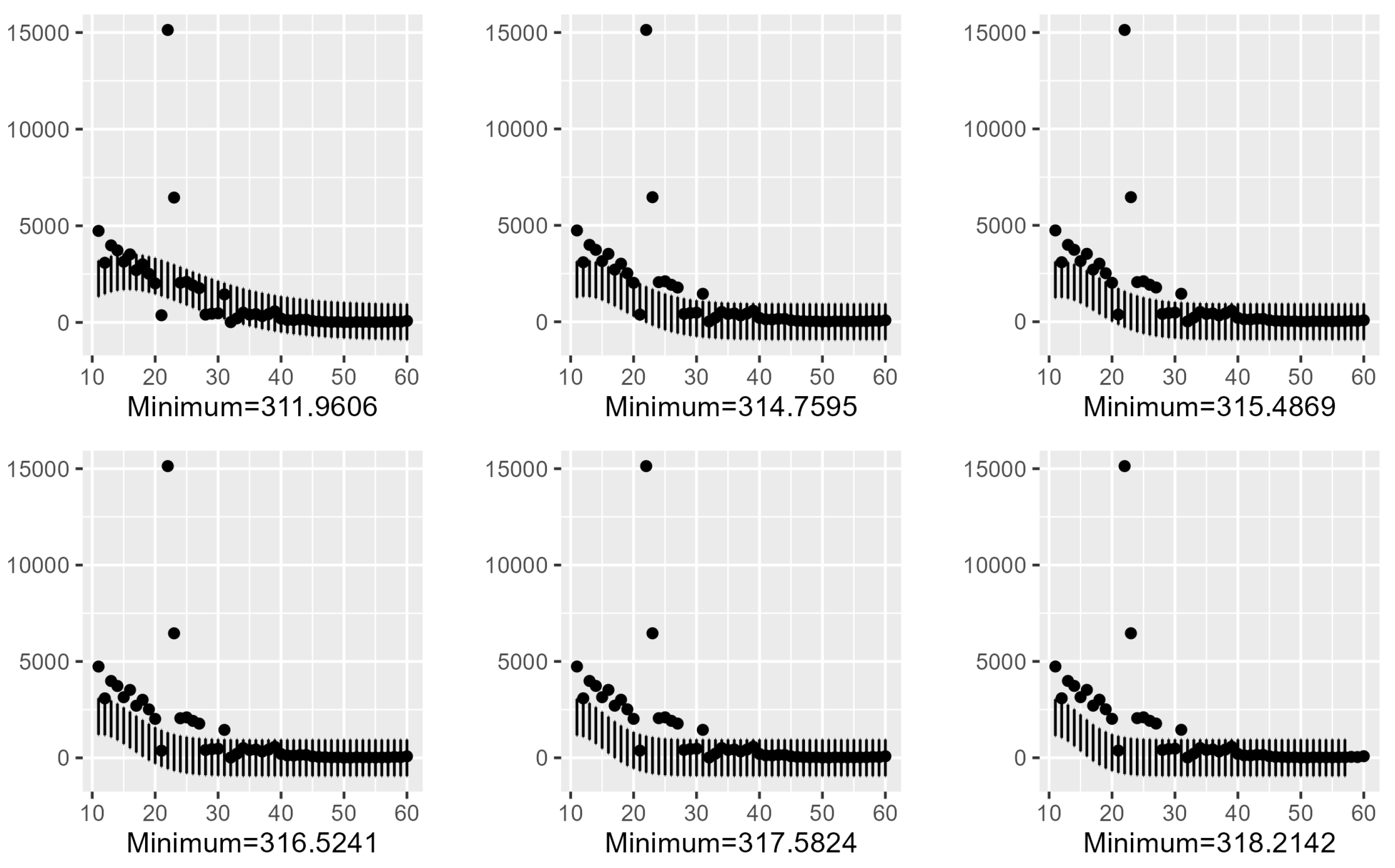
4.4. Confidence Intervals Using Six Minimas with in the Lerch Model
5. The Case T > 10
6. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. R Source Code
Appendix A.1. opt() Function
Appendix A.2. Confidence Intervals Plot
References
- Bloomfield, P.; Steiger, W.L. Least Absolute Deviations Curve-Fitting. SIAM J. Sci. Stat. Comput. 1980, 2, 290–301. [Google Scholar] [CrossRef]
- Eisenhart, C. Boscovitch and the combination of observations. In Roger Joseph Boscovitch; Whyte, L.L., Ed.; Fordham University Press: New York, NY, USA, 1961. [Google Scholar]
- Koenker, R.; Bassett, G. On Boscovich’s estimator. Ann. Stat. 1985, 13, 1625–1628. [Google Scholar] [CrossRef]
- Rhodes, E.C. Reducing observations by the method of minima deviations. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1930, 9, 974–992. [Google Scholar] [CrossRef]
- Karst, O.J. Linear curve fitting using least deviations. J. Am. Stat. Assoc. 1958, 53, 118–132. [Google Scholar] [CrossRef]
- Sadovski, A.N. Algorithm As 74. L1-norm fit of straight line. J. R. Stat. Soc. Ser. C Appl. Stat. 1974, 23, 244–248. [Google Scholar] [CrossRef]
- Dielman, T.E. Least absolute value regression: Recent contributions. J. Stat. Comput. Simul. 2005, 75, 263–286. [Google Scholar] [CrossRef]
- Li, Y.; Arce, G.R. A maximum likelihood approach to least absolute deviation regression. EURASIP J. Appl. Signal Process. 2004, 12, 1762–1769. [Google Scholar] [CrossRef]
- Barmparis, G.D.; Tsironis, G.P. Estimating the infection horizon of COVID-19 in eight countries with a data-driven approach. Chaos Solitons Fractals 2020, 135, 109842. [Google Scholar] [CrossRef] [PubMed]
- Aksenov, S.V.; Savageau, M.A. Some properties of the Lerch family of discrete distributions. arXiv 2005, arXiv:math/0504485. [Google Scholar]
- Dermoune, A.; Ounaissi, D.; Slaoui, Y. Confidence intervals from local minimas of objective function. Stat. Optim. Inf. Comput. 2023, 11, 798–810. [Google Scholar] [CrossRef]
- Gao, F.; Lixing, H. Implementing the Nelder-Mead simplex algorithm with adaptive parameters. Comput. Optim. Appl. 2010, 51, 259–277. [Google Scholar] [CrossRef]
- Lagarias, J.C.; Reeds, J.A.; Wright, M.W.; Wright, P.E. Convergence properties of the Nelder–Mead simplex method in low dimensions. SIAM J. Optim. 1998, 9, 112–147. [Google Scholar] [CrossRef]
- Nelder, J.A.; Mead, R. A simplex method for function minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
- Johnson, N.L.; Kotz, S.; Balakrishnan, N. Continuous Univariate Distributions; Wiley: Hoboken, NJ, USA, 1994. [Google Scholar]
- Ord, J.K. Laplace Distribution, in Encyclopedia of Statistical Science; Kotz, S., Johnson, N.L., Read, C.B., Eds.; Wiley: New York, NY, USA, 1983; Volume 4, p. 473475. [Google Scholar]
- Novoselac, V. The Component Weighted Median Absolute Deviations Problem. Eur. J. Pure Appl. Math. 2020, 13, 964–976. [Google Scholar] [CrossRef]
- Croux, C.; Rousseeuw, P.J.; Van Bael, A. Positive-breakdown regression by minimizing nested scale estimators. J. Stat. Plan. Inference 1996, 53, 197–235. [Google Scholar] [CrossRef]

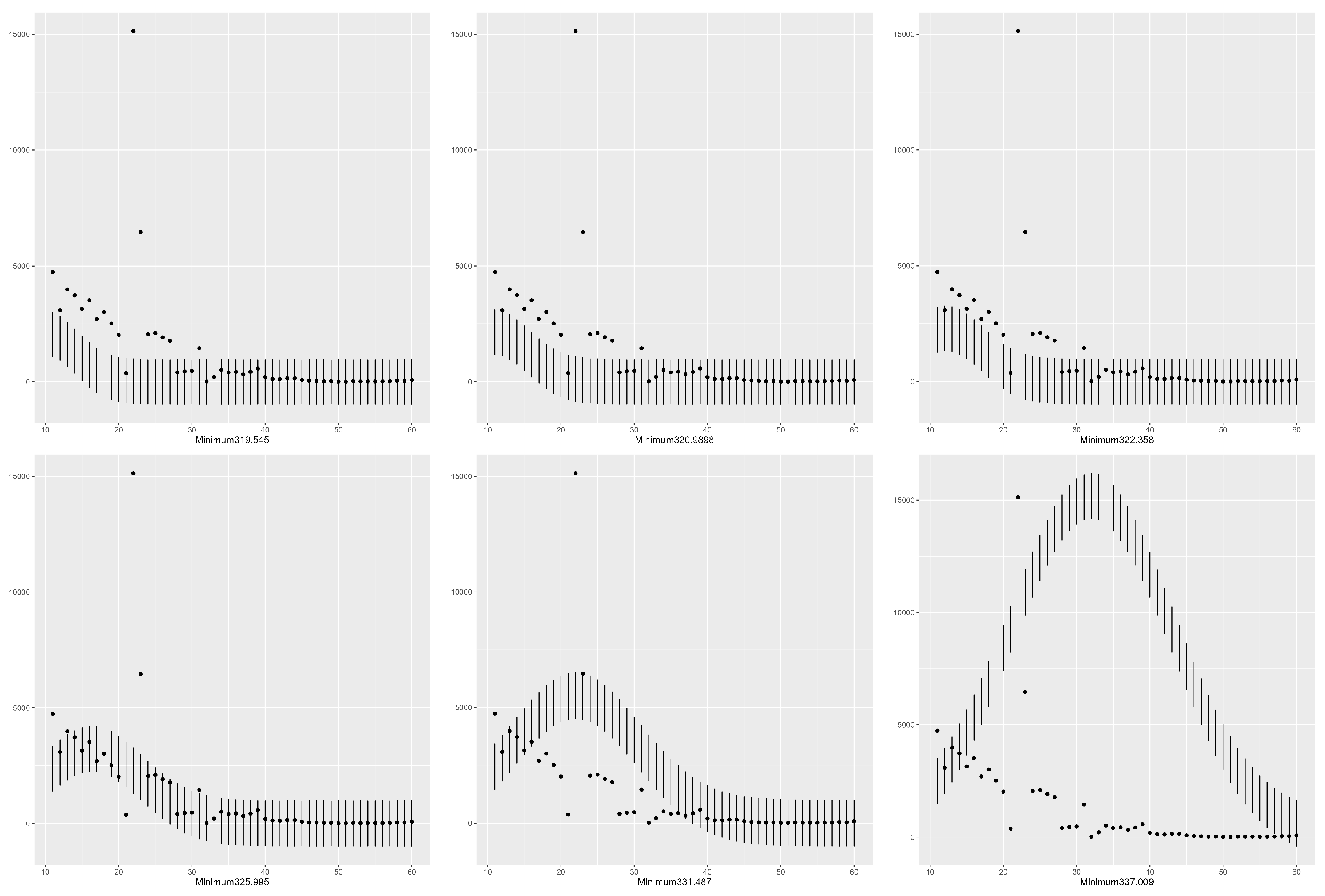

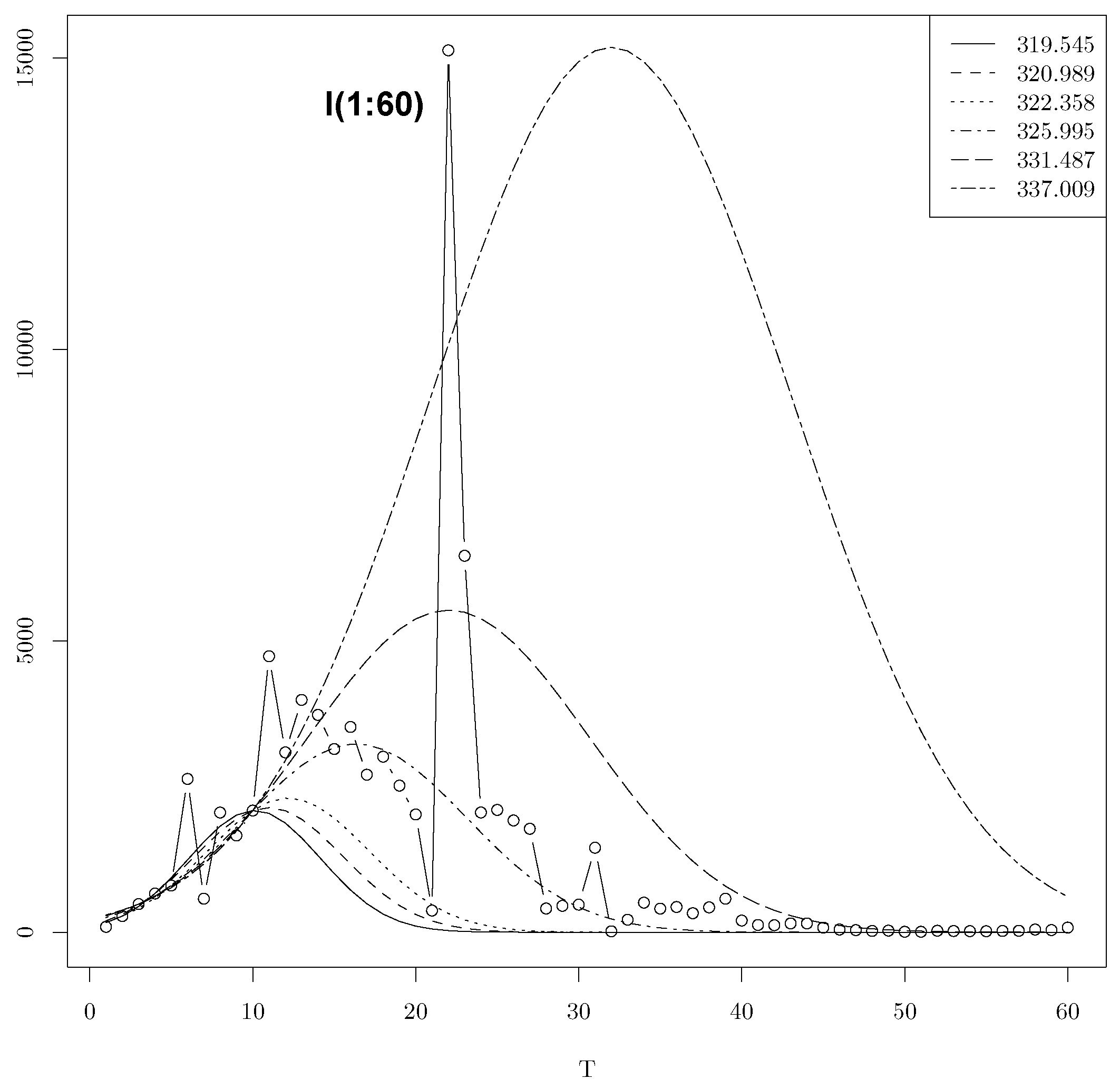
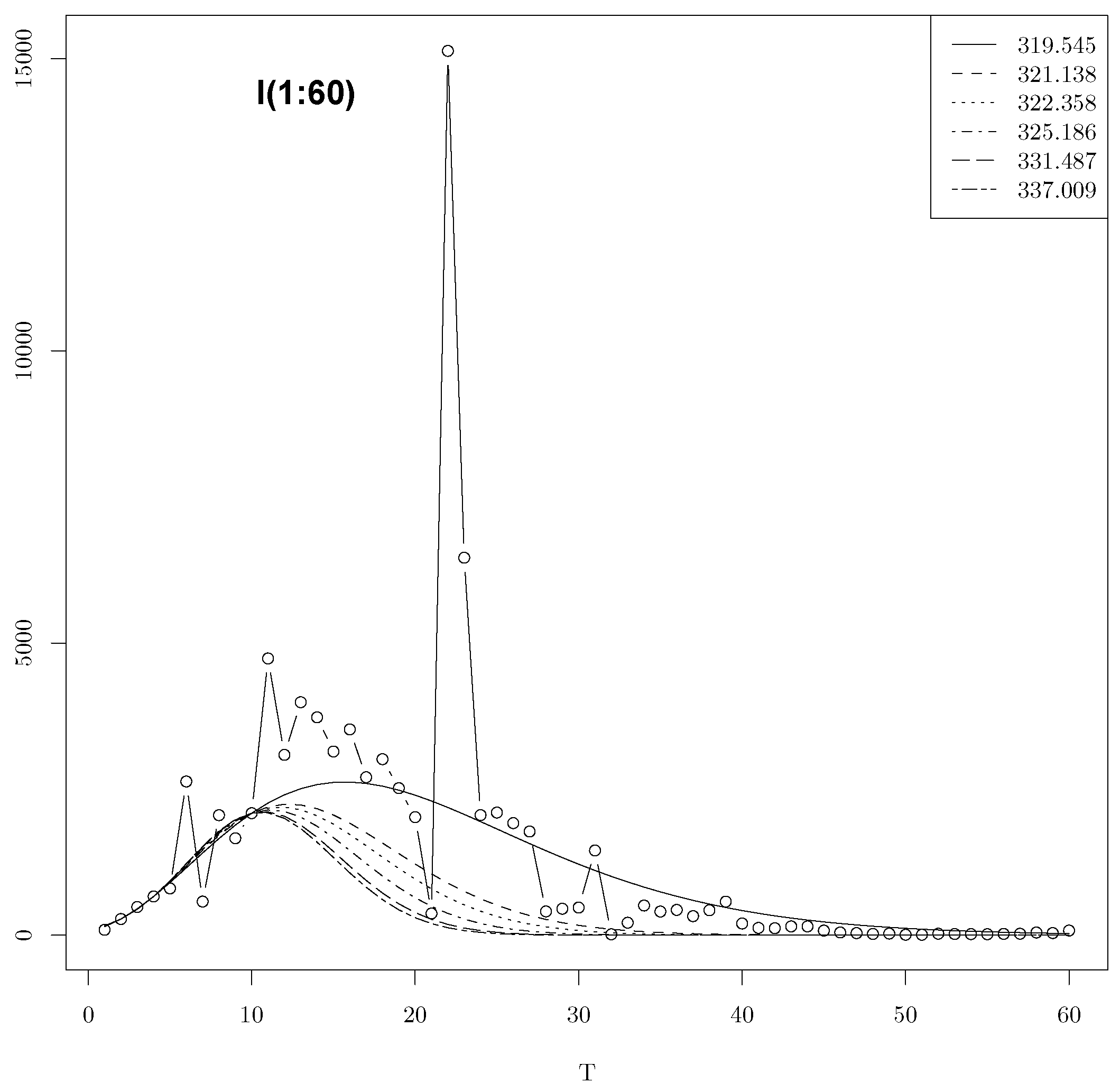
| minima | % Predictions | |||
|---|---|---|---|---|
| 2088.911 | 10.119 | 5.712 | 319.545 | 0.66 |
| 2137.277 | 10.98621 | 6.457 | 320.9898 | 0.66 |
| 2301.818 | 12.186 | 7 | 322.358 | 0.68 |
| 3229.843 | 16.346 | 9.609 | 325.995 | 0.88 |
| 5526.387 | 22.018 | 12.183 | 331.487 | 0.60 |
| 15,185.797 | 31.994 | 15.614 | 337.009 | 0.12 |
| Minima | % Predictions | ||||
|---|---|---|---|---|---|
| 5.990886 | 0.81023163 | 3.201870 | −3.976447 | 311.9606 | 0.84 |
| 1.354215 | 0.59318684 | 8.174956 | −10.683932 | 314.7595 | 0.70 |
| 1.555525 | 0.50711308 | 10.701817 | −15.255833 | 315.4869 | 0.68 |
| 8.235320 | 0.35420137 | 16.512305 | −28.741171 | 316.5241 | 0.66 |
| 2.185815 | 0.1647315 | 28.956740 | −71.553876 | 317.5824 | 0.66 |
| 7.23785 | 0.05804243 | 45.948388 | −160.673224 | 318.2142 | 0.66 |
| Mode Position | Amplitude | ||||
|---|---|---|---|---|---|
| 5.990886 | 0.81023163 | 3.201870 | −3.976447 | 16.19885 | 2618.210 |
| 1.354215 | 0.59318684 | 8.174956 | −10.683932 | 12.78678 | 2236.537 |
| 1.555525 | 0.50711308 | 10.701817 | −15.255833 | 12.26928 | 2186.184 |
| 8.235320 | 0.35420137 | 16.512305 | −28.741171 | 11.68264 | 2134.780 |
| 2.185815 | 0.1647315 | 28.956740 | −71.553876 | 11.22172 | 2101.053 |
| 7.23785 | 0.05804243 | 45.948388 | −160.673224 | 11.05461 | 2090.932 |
| Minima | % Predictions | ||||
|---|---|---|---|---|---|
| 4.366541 × 10−268 | 0.1073967 | 55.31169 | −154.51447 | 392.5692 | 0.825 |
| 3.422419 × 10−262 | 0.1387492 | 47.81770 | −121.91023 | 393.5286 | 0.825 |
| 2.572282 × 10−256 | 0.1708497 | 41.39999 | −97.69044 | 394.7033 | 0.825 |
| 1.155039 × 10−253 | 0.1860852 | 38.76658 | −88.52397 | 395.2740 | 0.825 |
| 3.035334 × 10−234 | 0.3069971 | 23.34634 | −43.86187 | 400.4082 | 0.825 |
| 4.970115 × 10−230 | 0.3344249 | 20.71433 | −37.77693 | 401.7952 | 0.825 |
| 1.667726 × 10−233 | 0.3634773 | 22.30914 | −36.60867 | 403.6049 | 0.825 |
| Minima | % Predictions | |||
|---|---|---|---|---|
| 3712.1297 | 14.2556 | 7.60744 | 386.0318 | 0.80 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dermoune, A.; Ounaissi, D.; Slaoui, Y. Gaussian and Lerch Models for Unimodal Time Series Forcasting. Entropy 2023, 25, 1474. https://doi.org/10.3390/e25101474
Dermoune A, Ounaissi D, Slaoui Y. Gaussian and Lerch Models for Unimodal Time Series Forcasting. Entropy. 2023; 25(10):1474. https://doi.org/10.3390/e25101474
Chicago/Turabian StyleDermoune, Azzouz, Daoud Ounaissi, and Yousri Slaoui. 2023. "Gaussian and Lerch Models for Unimodal Time Series Forcasting" Entropy 25, no. 10: 1474. https://doi.org/10.3390/e25101474
APA StyleDermoune, A., Ounaissi, D., & Slaoui, Y. (2023). Gaussian and Lerch Models for Unimodal Time Series Forcasting. Entropy, 25(10), 1474. https://doi.org/10.3390/e25101474








