A Novel Intelligent Fault Diagnosis Method for Self-Priming Centrifugal Pumps
Abstract
:1. Introduction
- (1)
- The introduction of a novel intelligent fault diagnosis method tailored for self-priming centrifugal pumps, which integrates the refined time-shift multiscale fluctuation dispersion entropy, cosine pairwise-constrained supervised manifold mapping, and adaptive chaotic Aquila optimization support vector machine;
- (2)
- The practical application of the proposed intelligent fault diagnosis method within the context of analyzing a self-priming centrifugal pump case. This endeavor serves the purpose of validating the method’s effectiveness;
- (3)
- A comprehensive comparative analysis involving the proposed fault diagnosis method, various feature extraction techniques, feature dimensionality reduction methods, and existing intelligent fault diagnosis approaches. This comparative assessment is aimed at substantiating the method’s superior performance.
2. Intelligent Fault Diagnosis Model for Self-Priming Centrifugal Pump
2.1. Proposed Intelligent Fault Diagnosis Model
- (1)
- Signal acquisition. A single sensor obtains the self-priming centrifugal pump signal under different operating conditions;
- (2)
- Feature extraction. The RTSMFDE extracts the entropy features of each group of signal samples and constructs the fault feature vector in the entropy domain;
- (3)
- Dimensionality reduction. The dimensionality of the extracted high-dimensional fault feature set from the RTSMFDE is reduced by the CPCSMM method, resulting in an entropy-manifold feature set that exhibits a high degree of fault differentiation;
- (4)
- Fault identification. The training set is constructed by randomly selecting entropy-manifold feature vectors from the samples. Conversely, the remaining samples’ entropy-manifold feature vectors are considered as the test set. Both the training and test sets undergo normalization. The normalized training set is used to construct the predictive model. Subsequently, the normalized test set is fed into the predictive model for intelligent fault diagnosis self-priming centrifugal pumps.
2.2. Refined Time-Shift Multiscale Fluctuation Dispersion Entropy
- (1)
- Under the scale factor s, h time-shift multiscale decomposition sequences X are constructed:
- (2)
- The normal cumulative distribution function is used to decompose the time-shift multiscale subsequences mapping to :
- (3)
- is mapped to an integer index from 1 to c using a linear transformation :
- (4)
- The reconstructed sequence is obtained using phase space reconstruction:
- (5)
- Fluctuation dispersion analysis for the reconstructed sequence:
- (6)
- The relative frequency of each fluctuation dispersion mode is calculated as follows:
- (7)
- The average relative frequency of multiple time-shift multiscale decomposition sequences with scale factor s is calculated in a refined way:
- (8)
- The RTSMFDE can be expressed as follows:
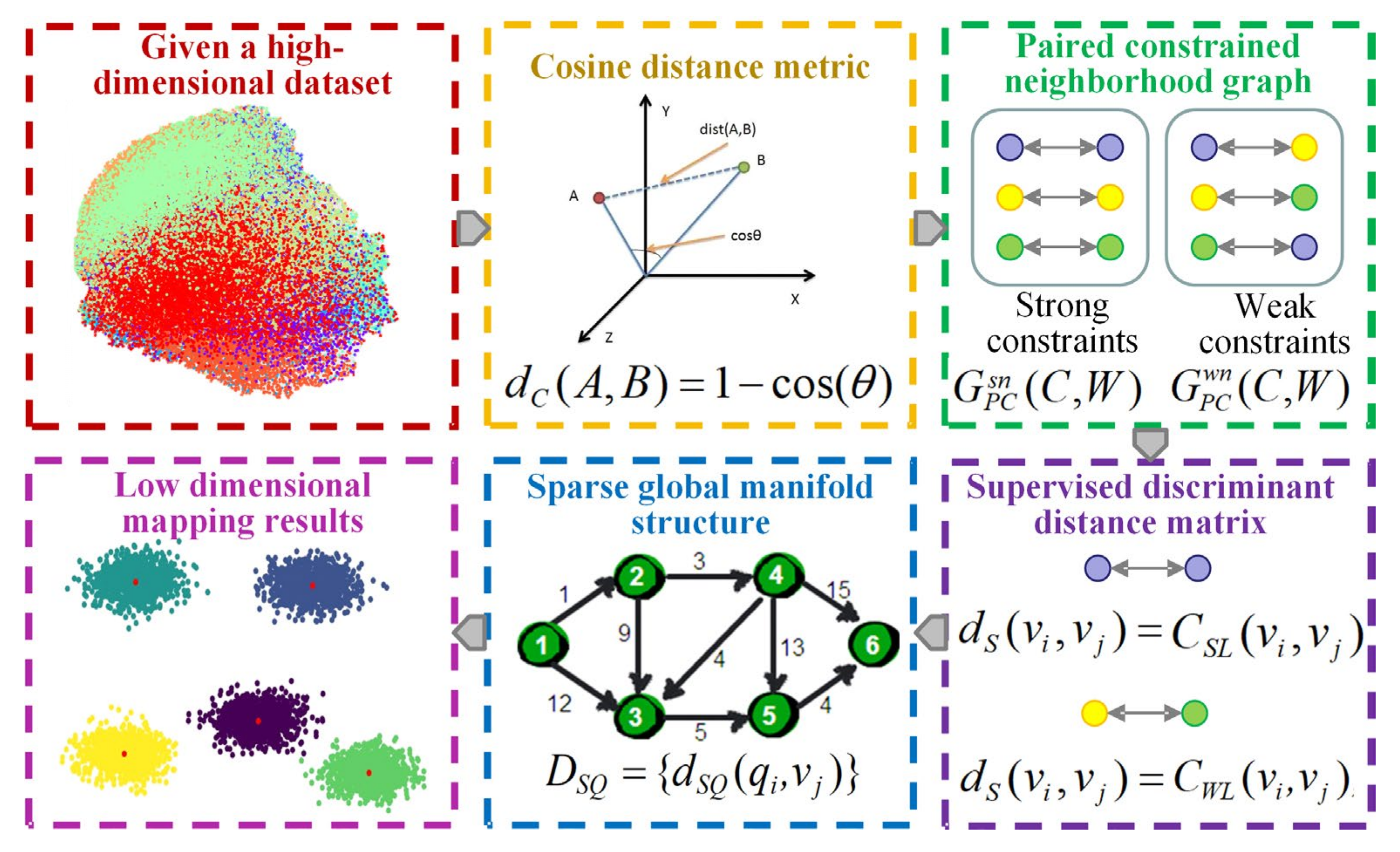
2.3. Cosine Pairwise-Constrained Supervised Manifold Mapping
- (1)
- Cosine distance measurement
- (2)
- Pairwising the constrained neighborhood graph
- (3)
- Supervising the discriminant distance matrix
- (4)
- Sparse global manifold structure
- (5)
- Low-dimensional mapping results
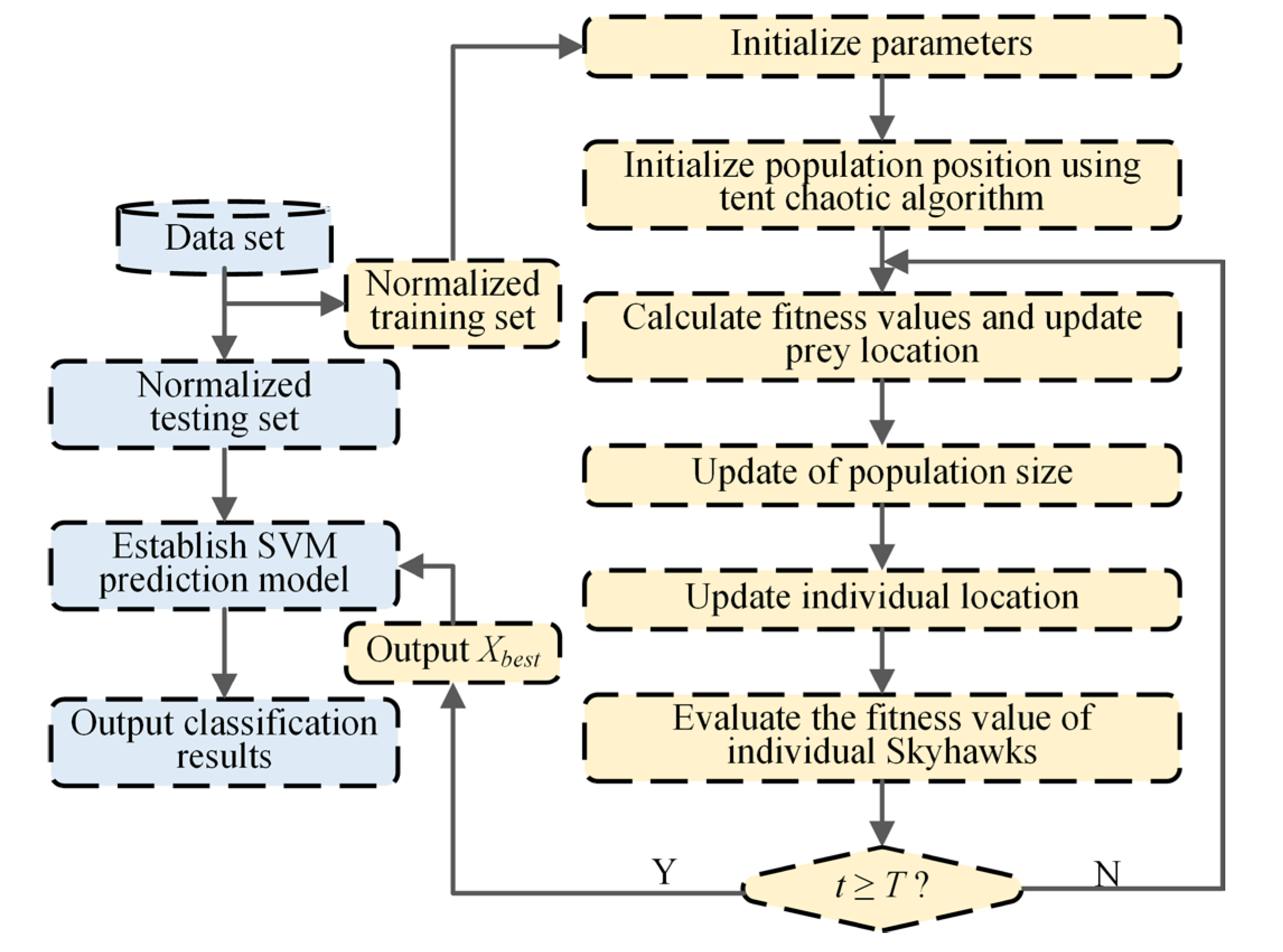
2.4. Adaptive Chaotic Aquila Optimization Support Vector Machine
- (1)
- Data preprocessing. The training and test sets are created by randomly dividing the input feature set. In addition, is used to normalize the training and test sets to [0, 1]. and v represents the normalized eigenvalues and the original, and min and max represent the minimum and maximum eigenvalues;
- (2)
- Initializing the ACAO method parameters. The minimum population size Pmin is 5, the maximum population size Pmax is 30, the maximum number of initial iterations T is 200, the upper limit UB of the optimization problem is [0.001, 0.001], the lower limit LB of the optimization problem is [100, 100], and the individual position of the Aquila is ();
- (3)
- The population location is initialized by the tent chaotic mapping method (details shown in Equations (20) and (21)). In the Dim-dimension space, generates the tent chaotic sequence with different trajectories:
- (4)
- Adaptive updating of Aquila’s population size. Aquila’s population size is adaptively updated using the linear reduction method (Equation (22)). The computational complexity of the Aquila optimizer (AO) is determined by the maximum number of iterations T, the optimization solution dimension Dim, and the population size P. Thus, to enhance the operational efficiency of the AO, the original constant population size strategy is replaced with a linear reduction adaptive population size update method;
- (5)
- The fitness value of each Aquila individual is calculated in the current iteration. The fitness value is defined as the average error classification rate after conducting a three-fold cross-validation on the training set. To achieve this, the training set is normalized and divided into three groups. One group is randomly selected as the sub-validation set, while the remaining two groups are treated as the training set, resulting in the creation of three models. The fitness value is obtained by calculating the average error classification rate of each model on its corresponding validation set. The current target prey position is identified as the position of the Aquila individual with the lowest fitness value in the current iteration. Consequently, the optimization process of the SVM classifier parameters aims to discover the global minimum fitness value;
- (6)
- Updating the individual position of the Aquila. The strategies include soaring at high altitudes with vertical dives, glide attacks at close range, contour flying, slow descent attacks at low altitudes, and stalking and capturing prey, as detailed in Equations (23)–(26):
- (7)
- Evaluating the position of individual Aquilas and the prey. In the present iteration, if either the fitness values of the individual or the prey surpass their historical values, the original positions of the individual or the prey should be replaced with the updated positions. Alternatively, if the historical positions of either the individual or the prey are superior in terms of fitness values, these historical positions are retained;
- (8)
- Determining whether the iteration is terminated. If the maximum number of iterations is reached, the entire cycle is halted. Otherwise, steps (4)–(7) are iteratively repeated until the specified condition is satisfied;
- (9)
- Determining the final prey location. At the termination of the iteration, the final captured prey position is determined by outputting the location of the best individual in the Aquila population;
- (10)
- Establishing the SVM prediction model. The SVM prediction model is established according to the parameter optimization result ;
- (11)
- Sample classification. The normalized test set is fed into the SVM prediction model for intelligent classification, which then generates the predicted fault type for the test samples.
3. Experimental Validation
3.1. Self-Priming Centrifugal Pump Experiment Platform and Data Collection
3.2. Fault Diagnosis Results and Comparative Analysis
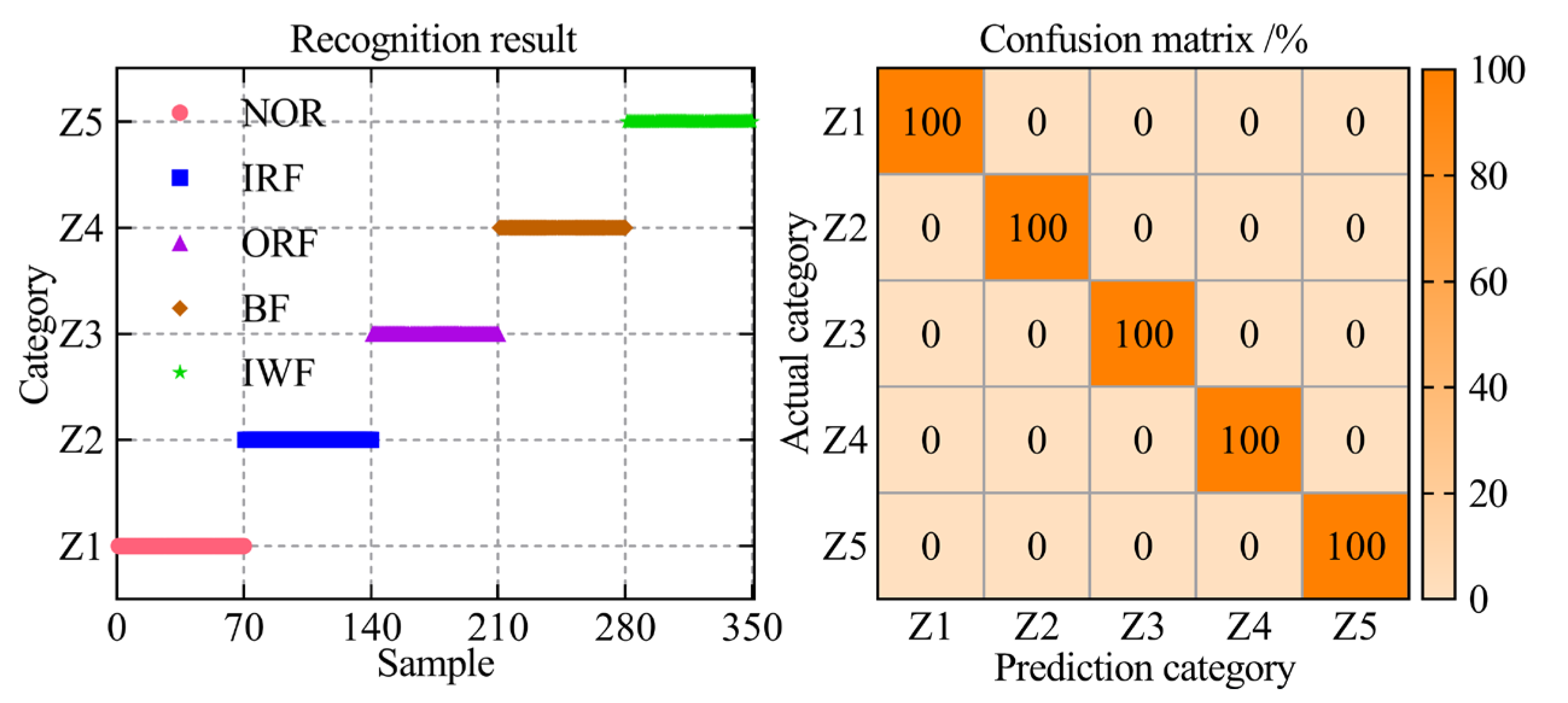
3.2.1. Fault Diagnosis Results
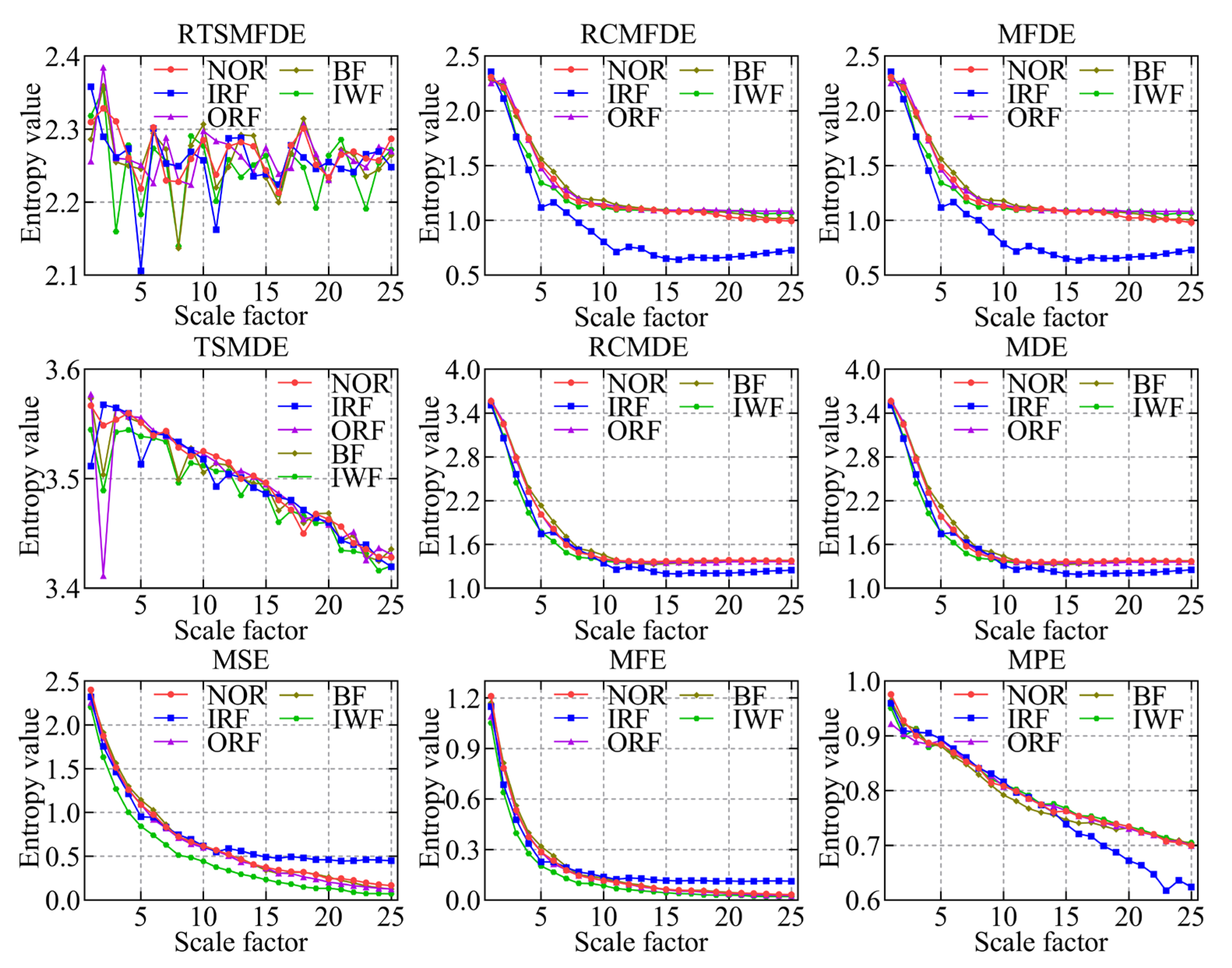
3.2.2. Comparative Experiments of Different Fault Feature Extraction Methods
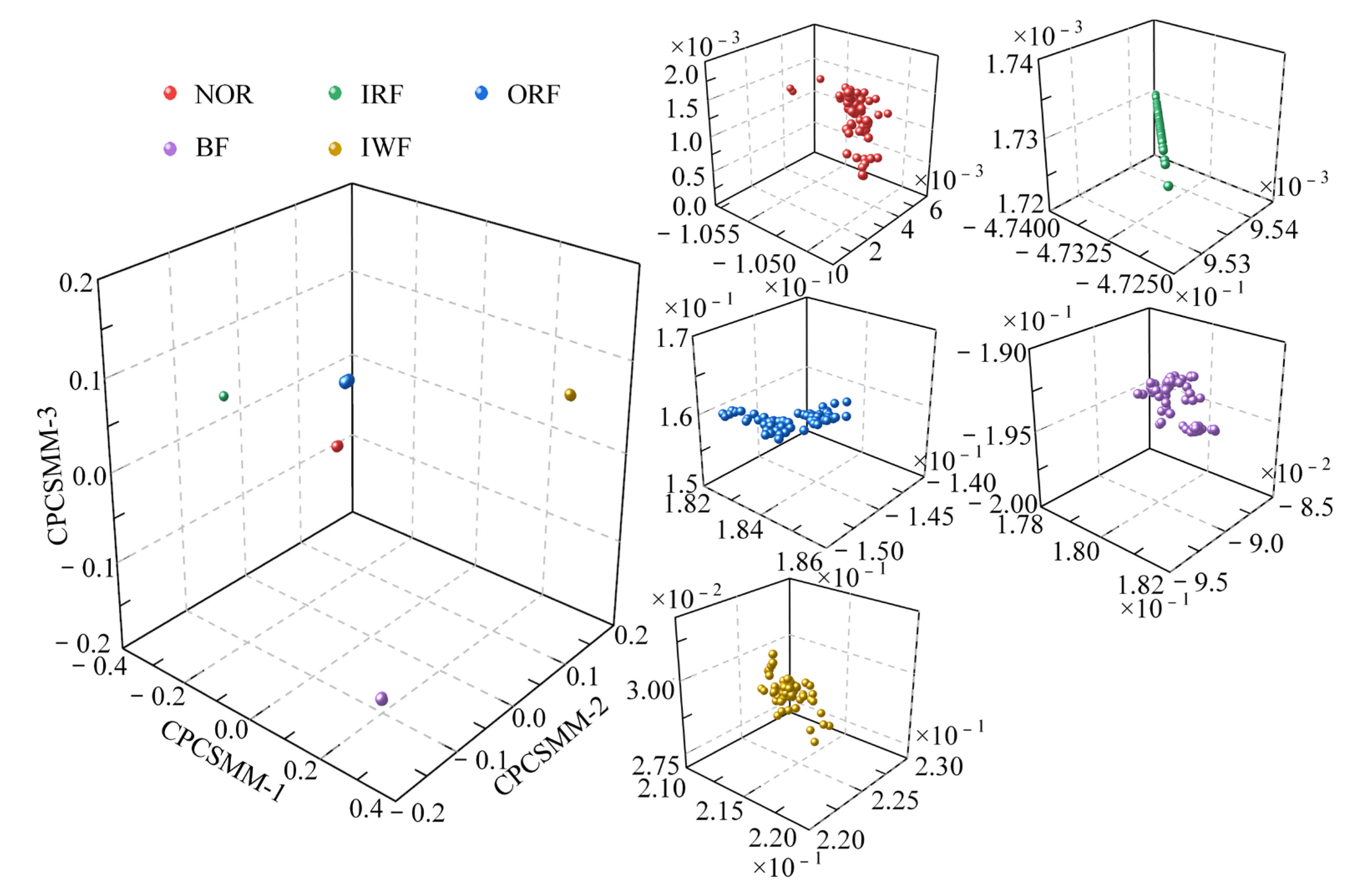
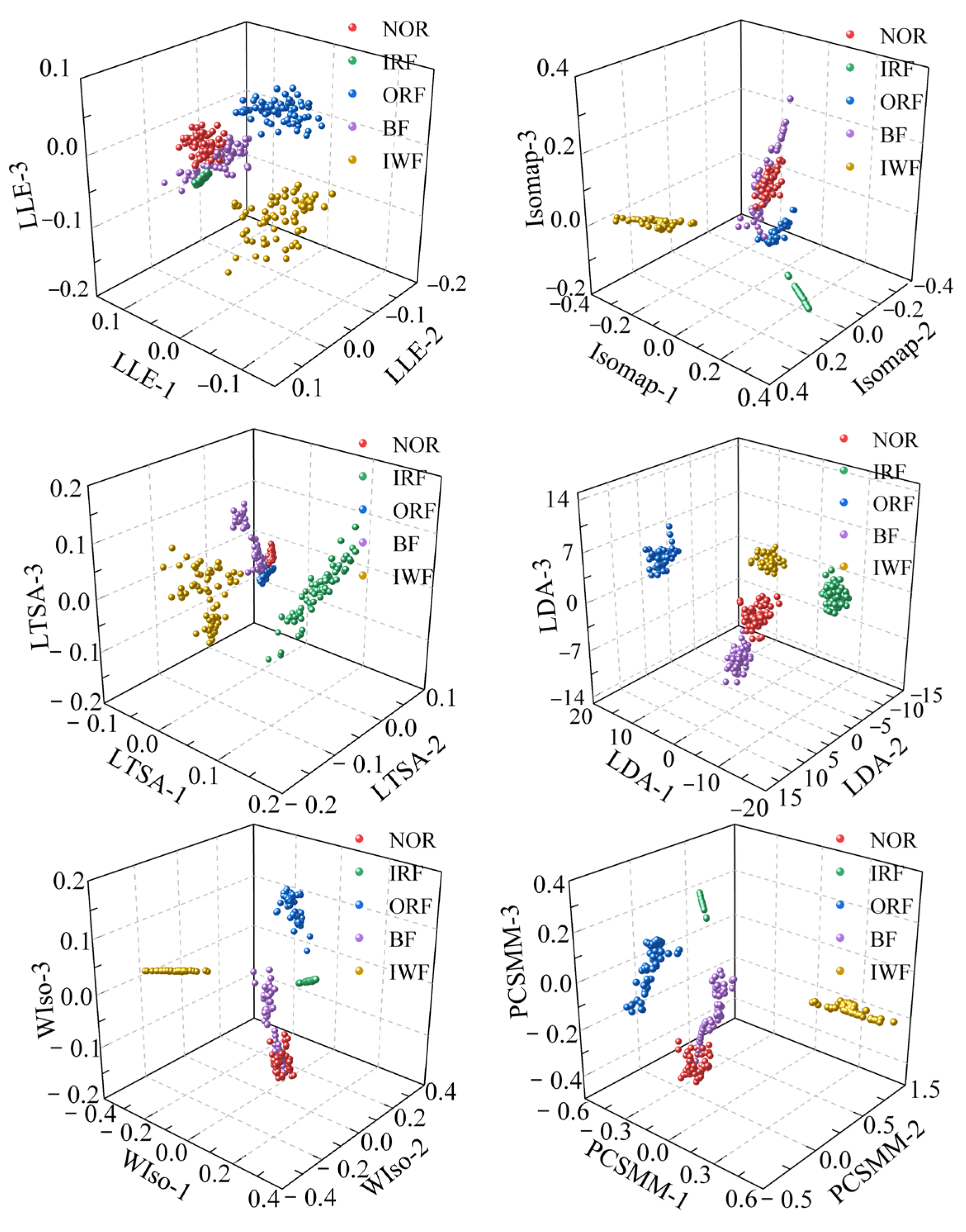
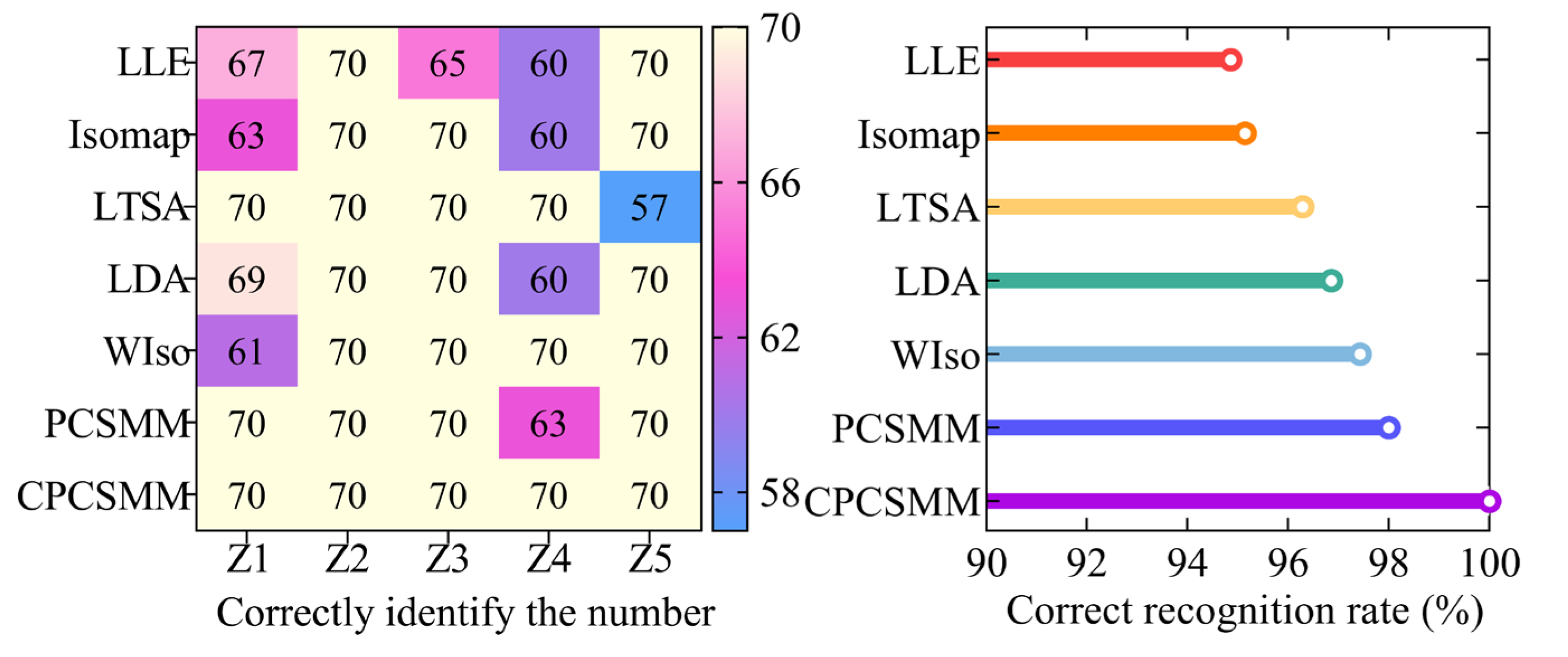
3.2.3. Comparative Experiments of Different DR Methods
- (1)
- Visual comparison experiment
- (2)
- Comparison experiment of DR performance index
- (3)
- Comparison experiment of correct recognition rate
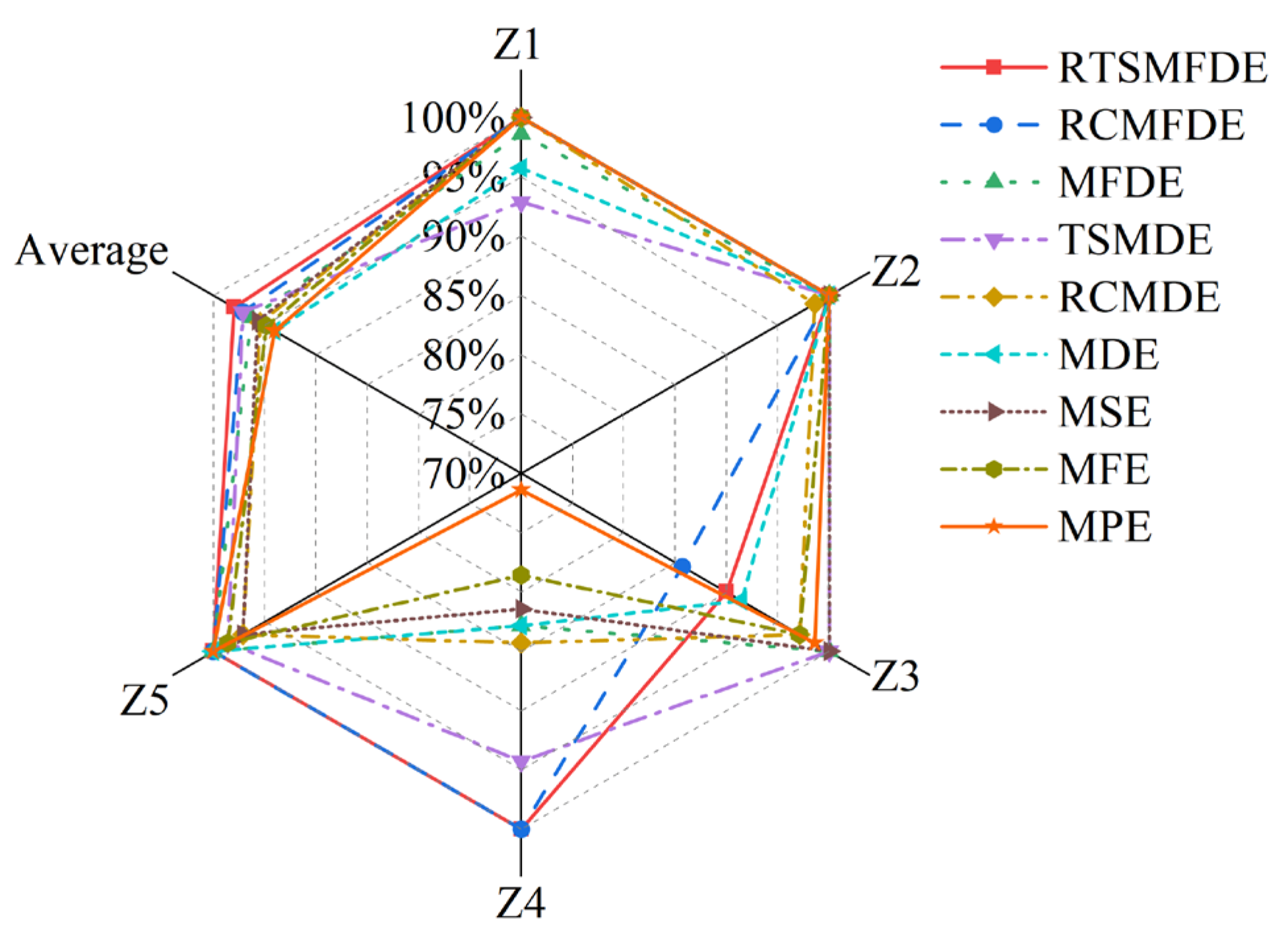
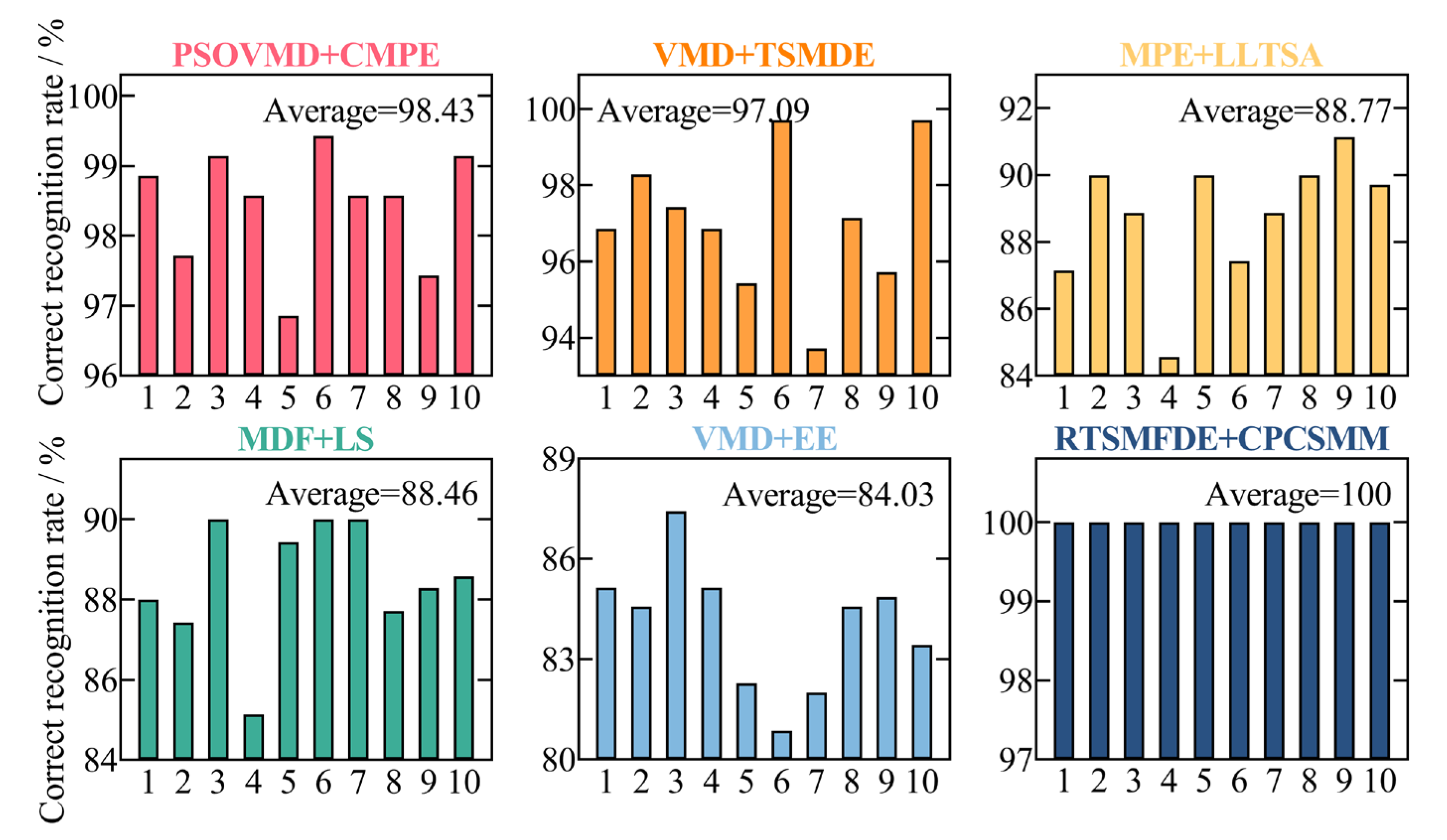
3.2.4. Comparative Experiments of Different Intelligent Fault Diagnosis Methods
4. Conclusions
- (1)
- With a recognition rate of 100%, the proposed intelligent fault diagnosis methods, RTSMFDE, CPCSMM, and ACAO-SVM, accurately identify the fault type for self-priming centrifugal pumps. Furthermore, the average correct recognition rate of the proposed methods surpasses that of the existing five intelligent fault diagnosis methods by up to 15.97%;
- (2)
- The fault feature information of self-priming centrifugal pumps can be effectively extracted by the RTSMFDE method. When compared to eight existing fault feature extraction methods, namely MPE, MFE, MSE, MDE, RCMDE, TSMDE, MFDE, and RCMFDE, the correct recognition rate of the RTSMFDE can be improved by up to 4.00%;
- (3)
- The CPCSMM method has the optimal visualization effect, the optimal DR performance index, and the highest correct recognition rate compared to the six DR methods (LLE, Isomap, LTSA, LDA, WIso, and PCSMM).
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AO | Aquila optimizer |
| ACAO | adaptive chaotic Aquila optimization |
| ACAO-SVM | adaptive chaotic Aquila optimization support vector machine |
| BF | ball fault |
| CPCSMM | cosine pairwise-constrained supervised manifold mapping |
| CMPE | composite multiscale permutation entropy |
| DR | dimensionality reduction |
| EE | energy entropy |
| IRF | inner ting fault |
| Isomap | isometric mapping |
| IWF | impeller wear fault |
| LE | Laplacian Eigenmaps |
| LDA | linear discriminant analysis |
| LLE | locally linear embedding |
| LTSA | local tangent space alignment |
| LLTSA | linear local tangent space alignment |
| LS | Laplace score |
| MDE | multiscale dispersion entropy |
| MDF | multi-domain features |
| MFDE | multiscale fluctuation dispersion entropy |
| MFE | multiscale fuzzy entropy |
| MPE | multiscale permutation entropy |
| MSE | multiscale sample entropy |
| NOR | normal |
| ORF | outer ring fault |
| PCSMM | pairwise-constrained supervised manifold mapping |
| PSO-VMD | particle swarm optimization-based variational mode decomposition |
| RCMDE | refined composite multiscale dispersion entropy |
| RCMFDE | refined composite multiscale fluctuation dispersion entropy |
| RTSMFDE | refined time-shift multiscale fluctuation dispersion entropy |
| SVM | support vector machine |
| TSMDE | time-shift multiscale dispersion entropy |
| VMD | variational mode decomposition |
| WIso | weighted isometric mapping |
References
- Li, Z.; Jiang, W.; Zhang, S.; Sun, Y.; Zhang, S. A hydraulic pump fault diagnosis method based on the modified ensemble empirical mode decomposition and wavelet kernel extreme learning machine methods. Sensors 2021, 21, 2599. [Google Scholar] [CrossRef] [PubMed]
- Peng, Y.; Sakai, Y.; Nakagawa, K.; Funabora, Y.; Aoyama, T.; Yokoe, K.; Doki, S. Funabot-Suit: A bio-inspired and McKibben muscle-actuated suit for natural kinesthetic perception. Biomim. Intell. Robot. 2023, 100127. [Google Scholar] [CrossRef]
- Mao, Z.; Peng, Y.; Hu, C.; Ding, R.; Yamada, Y.; Maeda, S. Soft computing-based predictive modeling of flexible electrohydrodynamic pumps. Biomim. Intell. Robot. 2023, 3, 100114. [Google Scholar] [CrossRef]
- Zhou, K.; Diehl, E.; Tang, J. Deep convolutional generative adversarial network with semi-supervised learning enabled physics elucidation for extended gear fault diagnosis under data limitations. Mech. Syst. Signal Process. 2023, 185, 109772. [Google Scholar] [CrossRef]
- Han, T.; Liu, C.; Wu, R.; Jiang, D. Deep transfer learning with limited data for machinery fault diagnosis. Appl. Soft Comput. 2021, 103, 107150. [Google Scholar] [CrossRef]
- Wu, Z.; Jiang, H.; Zhao, K.; Li, X. An adaptive deep transfer learning method for bearing fault diagnosis. Measurement 2020, 151, 107227. [Google Scholar] [CrossRef]
- Wang, Z.; Li, G.; Yao, L.; Qi, X.; Zhang, J. Data-driven fault diagnosis for wind turbines using modified multiscale fluctuation dispersion entropy and cosine pairwise-constrained supervised manifold mapping. Knowl.-Based Syst. 2021, 228, 107276. [Google Scholar] [CrossRef]
- Dong, Z.; Zhao, D.; Cui, L. Non-negative wavelet matrix factorization-based bearing fault intelligent classification method. Meas. Sci. Technol. 2023, 34, 115013. [Google Scholar] [CrossRef]
- Chen, S.; Peng, Z.; Zhou, P. Review of signal decomposition theory and its applications in machine fault diagnosis. J. Mech. Eng. 2020, 56, 91. [Google Scholar]
- Wang, Z.; Li, G.; Yao, L.; Cai, Y.; Lin, T.; Zhang, J.; Dong, H. Intelligent fault detection scheme for constant-speed wind turbines based on improved multiscale fuzzy entropy and adaptive chaotic Aquila optimization-based support vector machine. ISA Trans. 2023, 138, 582–602. [Google Scholar] [CrossRef]
- Wang, Z.; Shang, P. Generalized entropy plane based on multiscale weighted multivariate dispersion entropy for financial time series. Chaos Solitons Fractals 2021, 142, 110473. [Google Scholar] [CrossRef]
- Sharma, S.; Tiwari, S.K. A novel feature extraction method based on weighted multiscale fluctuation based dispersion entropy and its application to the condition monitoring of rotary machines. Mech. Syst. Signal Process. 2022, 171, 108909. [Google Scholar] [CrossRef]
- Geng, D.; Yang, D.; Cai, M.; Zheng, L. A novel microwave treatment for sleep disorders and classification of sleep stages using multi-scale entropy. Entropy 2020, 22, 347. [Google Scholar] [CrossRef] [PubMed]
- Aremu, O.O.; Hyland-Wood, D.; McAree, P.R. A machine learning approach to circumventing the curse of dimensionality in discontinuous time series machine data. Reliab. Eng. Syst. Saf. 2020, 195, 106706. [Google Scholar] [CrossRef]
- Wei, L.; Zhou, R.; Yin, J.; Zhu, C.; Zhang, X.; Liu, H. Latent graph-regularized inductive robust principal component analysis. Knowl.-Based Syst. 2019, 177, 68–81. [Google Scholar] [CrossRef]
- Li, C.-N.; Shao, Y.-H.; Wang, Z.; Deng, N.-Y.; Yang, Z.-M. Robust Bhattacharyya bound linear discriminant analysis through an adaptive algorithm. Knowl.-Based Syst. 2019, 183, 104858. [Google Scholar] [CrossRef]
- Han, H.; Teng, J.; Xia, J.; Wang, Y.; Guo, Z.; Li, D. Predict high-frequency trading marker via manifold learning. Knowl.-Based Syst. 2021, 213, 106662. [Google Scholar] [CrossRef]
- Zhang, S.; Ma, Z.; Tan, H. On the equivalence of HLLE and LTSA. IEEE Trans. Cybern. 2017, 48, 742–753. [Google Scholar] [CrossRef]
- Shao, H.; Jiang, H.; Li, X.; Liang, T. Rolling bearing fault detection using continuous deep belief network with locally linear embedding. Comput. Ind. 2018, 96, 27–39. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, D.; Li, C.; Wang, Y.; Yang, J.; Jiang, Q. Fault diagnosis of subway plug door based on Isomap and GWO-SVM. In Proceedings of the 2020 15th IEEE Conference on Industrial Electronics and Applications (ICIEA), Kristiansand, Norway, 9–13 November 2020; pp. 106–110. [Google Scholar]
- Chen, F.; Tang, B.; Song, T.; Li, L. Multi-fault diagnosis study on roller bearing based on multi-kernel support vector machine with chaotic particle swarm optimization. Measurement 2014, 47, 576–590. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, Y.; Yu, Z.; Zeng, M. Incremental supervised locally linear embedding for machinery fault diagnosis. Eng. Appl. Artif. Intell. 2016, 50, 60–70. [Google Scholar] [CrossRef]
- Wang, X.; Yang, S.; Zhao, Y.; Wang, Y. Lithology identification using an optimized KNN clustering method based on entropy-weighed cosine distance in Mesozoic strata of Gaoqing field, Jiyang depression. J. Pet. Sci. Eng. 2018, 166, 157–174. [Google Scholar] [CrossRef]
- Djeziri, M.A.; Djedidi, O.; Morati, N.; Seguin, J.-L.; Bendahan, M.; Contaret, T. A temporal-based SVM approach for the detection and identification of pollutant gases in a gas mixture. Appl. Intell. 2022, 52, 6065–6078. [Google Scholar] [CrossRef]
- Sun, B.; Chen, H. A survey of k nearest neighbor algorithms for solving the class imbalanced problem. Wirel. Commun. Mob. Comput. 2021, 2021, 5520990. [Google Scholar] [CrossRef]
- Elshenawy, L.M.; Chakour, C.; Mahmoud, T.A. Fault detection and diagnosis strategy based on k-nearest neighbors and fuzzy C-means clustering algorithm for industrial processes. J. Frankl. Inst. 2022, 359, 7115–7139. [Google Scholar] [CrossRef]
- Aljemely, A.H.; Xuan, J.; Xu, L.; Jawad, F.K.J.; Al-Azzawi, O. Wise-local response convolutional neural network based on Naïve Bayes theorem for rotating machinery fault classification. Appl. Intell. 2021, 51, 6932–6950. [Google Scholar] [CrossRef]
- Peng, B.; Xia, H.; Lv, X.; Annor-Nyarko, M.; Zhu, S.; Liu, Y.; Zhang, J. An intelligent fault diagnosis method for rotating machinery based on data fusion and deep residual neural network. Appl. Intell. 2022, 52, 3051–3065. [Google Scholar] [CrossRef]
- Bazan, G.H.; Scalassara, P.R.; Endo, W.; Goedtel, A.; Palacios, R.H.C.; Godoy, W.F. Stator short-circuit diagnosis in induction motors using mutual information and intelligent systems. IEEE Trans. Ind. Electron. 2018, 66, 3237–3246. [Google Scholar] [CrossRef]
- Zhao, Y.-P.; Huang, G.; Hu, Q.-K.; Li, B. An improved weighted one class support vector machine for turboshaft engine fault detection. Eng. Appl. Artif. Intell. 2020, 94, 103796. [Google Scholar] [CrossRef]
- Xing, S.; Lei, Y.; Wang, S.; Jia, F. Distribution-invariant deep belief network for intelligent fault diagnosis of machines under new working conditions. IEEE Trans. Ind. Electron. 2020, 68, 2617–2625. [Google Scholar] [CrossRef]
- She, B.; Wang, X. A hidden feature label propagation method based on deep convolution variational autoencoder for fault diagnosis. Meas. Sci. Technol. 2022, 33, 055107. [Google Scholar] [CrossRef]
- Wang, Z.; Yao, L.; Cai, Y.; Zhang, J. Mahalanobis semi-supervised mapping and beetle antennae search based support vector machine for wind turbine rolling bearings fault diagnosis. Renew. Energy 2020, 155, 1312–1327. [Google Scholar] [CrossRef]
- Zhou, R.; Wang, X.; Wan, J.; Xiong, N. EDM-Fuzzy: An euclidean distance based multiscale fuzzy entropy technology for diagnosing faults of industrial systems. IEEE Trans. Ind. Inform. 2021, 17, 4046–4054. [Google Scholar] [CrossRef]
- Yan, X.; Jia, M. Intelligent fault diagnosis of rotating machinery using improved multiscale dispersion entropy and mRMR feature selection. Knowl.-Based Syst. 2019, 163, 450–471. [Google Scholar] [CrossRef]
- Azami, H.; Rostaghi, M.; Abásolo, D.; Escudero, J. Rerefined composite multiscale dispersion entropy and its application to biomedical signals. IEEE Trans. Biomed. Eng. 2017, 64, 2872–2879. [Google Scholar] [PubMed]
- Shao, K.; Fu, W.; Tan, J.; Wang, K. Coordinated approach fusing time-shift multiscale dispersion entropy and vibrational Harris hawks optimization-based SVM for fault diagnosis of rolling bearing. Measurement 2021, 173, 108580. [Google Scholar] [CrossRef]
- Azami, H.; Arnold, S.E.; Sanei, S.; Chang, Z.; Sapiro, G.; Escudero, J.; Gupta, A.S. Multiscale fluctuation-based dispersion entropy and its applications to neurological diseases. IEEE Access 2019, 7, 68718–68733. [Google Scholar] [CrossRef]
- Anowar, F.; Sadaoui, S.; Selim, B. Conceptual and empirical comparison of dimensionality reduction algorithms (PCA, KPCA, LDA, MDS, SVD, LLE, ISOMAP, LE, ICA, t-SNE). Comput. Sci. Rev. 2021, 40, 100378. [Google Scholar] [CrossRef]
- Vlachos, M.; Domeniconi, C.; Gunopulos, D.; Kollios, G.; Koudas, N. Nonlinear dimensionality reduction techniques for classification and visualization. In Proceedings of the Eighth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Edmonton, AB, Canada, 23–26 July 2002; pp. 645–651. [Google Scholar]
- He, C.; Wu, T.; Gu, R.; Jin, Z.; Ma, R.; Qu, H. Rolling bearing fault diagnosis based on composite multiscale permutation entropy and reverse cognitive fruit fly optimization algorithm–extreme learning machine. Measurement 2021, 173, 108636. [Google Scholar] [CrossRef]
- Ye, Y.; Zhang, Y.; Wang, Q.; Wang, Z.; Teng, Z.; Zhang, H. Fault diagnosis of high-speed train suspension systems using multiscale permutation entropy and linear local tangent space alignment. Mech. Syst. Signal Process. 2020, 138, 106565. [Google Scholar] [CrossRef]
- Yan, X.; Jia, M. A novel optimized SVM classification algorithm with multi-domain feature and its application to fault diagnosis of rolling bearing. Neurocomputing 2018, 313, 47–64. [Google Scholar] [CrossRef]
- Chen, X.; Yang, Y.; Cui, Z.; Shen, J. Vibration fault diagnosis of wind turbines based on variational mode decomposition and energy entropy. Energy 2019, 174, 1100–1109. [Google Scholar] [CrossRef]


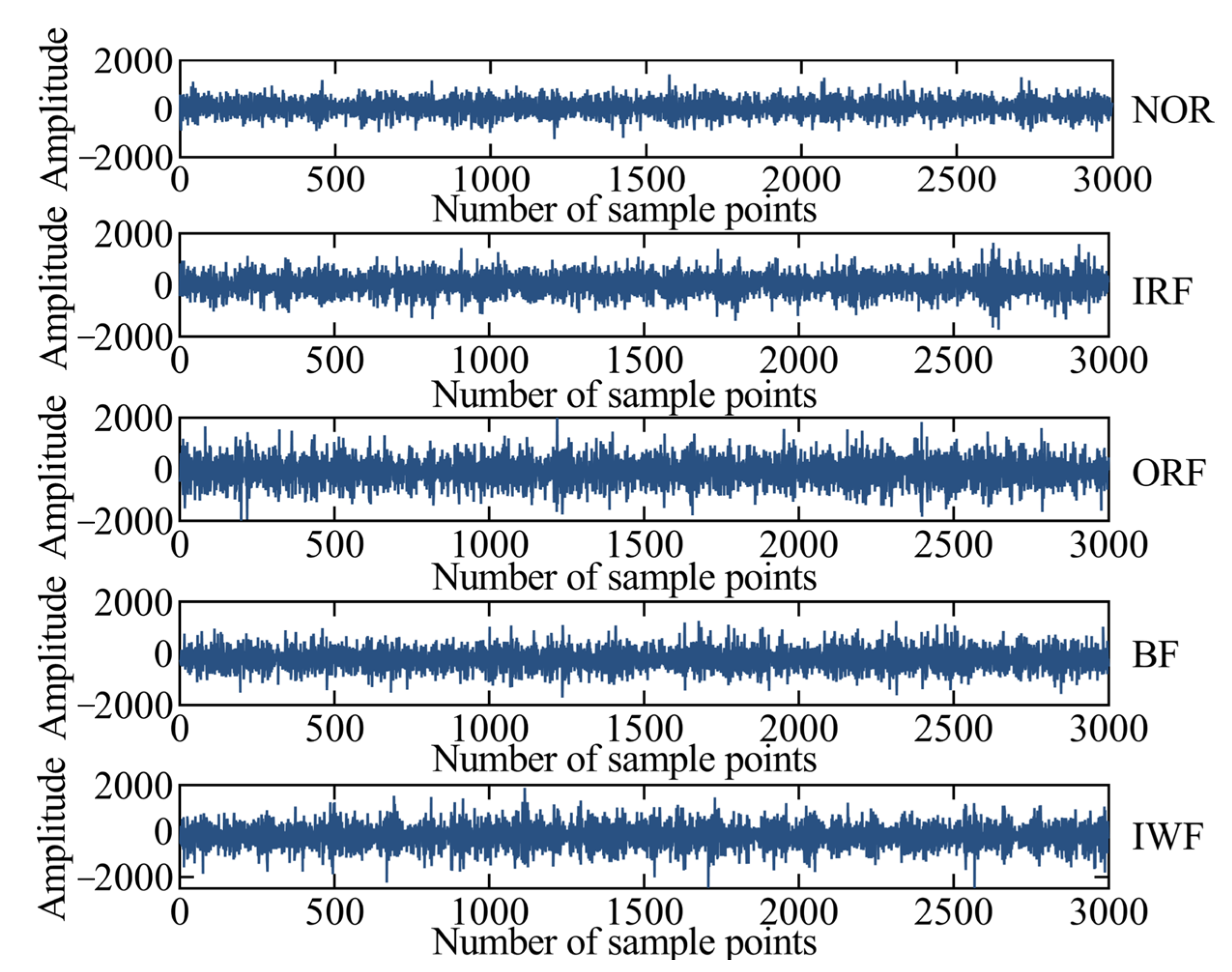



| Status | Tag | Number of Training Samples | Number of Testing Samples | Sample Count |
|---|---|---|---|---|
| Normal (NOR) | Z1 | 20 | 70 | 90 |
| Inner-ring fault (IRF) | Z2 | 20 | 70 | 90 |
| Outer-ring fault (ORF) | Z3 | 20 | 70 | 90 |
| Bearing fault (BF) | Z4 | 20 | 70 | 90 |
| Impeller wear fault (IWF) | Z5 | 20 | 70 | 90 |
| Entropy Method | Parameter Setting |
|---|---|
| MPE | N = 3000, m = 6, t = 1, s = 25 |
| MFE | N = 3000, m = 2, r = 0.15SD, n = 2, t = 1, s = 25 |
| MSE | N = 3000, m = 2, r = 0.15SD, t = 1, s = 25 |
| MDE | N = 3000, m = 2, c = 6, t = 1, s = 25 |
| RCMDE | |
| TSMDE | |
| MFDE | |
| RCMFDE | |
| RTSMFDE |
| DR Method | Type | Parameter Setting |
|---|---|---|
| LLE | Unsupervised | d = 3, K = 81 |
| Isomap | Unsupervised | d = 3, K = 52 |
| LTSA | Unsupervised | d = 3, K = 91 |
| LDA | Supervised | d = 3 |
| WIso | Supervised | d = 3, K = 49, w = 0.76 |
| PCSMM (Euclidean distance) | Supervised | d = 3, K = 55, = 0.55 |
| CPCSMM (cosine distance) | Supervised | d = 3, K = 81, = 0.45 |
| DR Method | DR Performance Indicators | DR Time(s) | ||
|---|---|---|---|---|
| Divergence between Classes | Intra-Class Divergence | Ratio | ||
| LLE | 5.03 × 10−3 | 1.63 × 10−3 | 3.09 | 0.47 |
| Isomap | 6.76 × 10−2 | 4.20 × 10−3 | 1.61 × 101 | 1.94 |
| LTSA | 4.60 × 10−3 | 2.06 × 10−3 | 2.23 | 0.72 |
| LDA | 1.65 × 102 | 6.50 | 2.54 × 101 | 0.04 |
| WIso | 5.51 × 10−2 | 1.85 × 10−3 | 2.98 × 101 | 1.78 |
| PCSMM | 2.58 × 10−1 | 7.87 × 10−3 | 3.28 × 101 | 0.52 |
| CPCSMM | 9.85 × 10−2 | 1.81 × 10−6 | 5.44 × 104 | 0.72 |
| Model | Feature Extraction | Parameter Setting |
|---|---|---|
| Model 1 | PSOVMD+CMPE | P = 50, T = 100, c1 = c2 = 2, m = 6, , s = 12 |
| Model 2 | VMD+TSMDE | Decomposition number = 4, a = 2000, m = 3, , c = 6, s = 20 |
| Model 3 | MPE+LLTSA | m = 4, , s = 12, d = 3, K = 27 |
| Model 4 | MDF+LS | Decomposition number = 4, a = 2000, m = 3, |
| Model 5 | VMD+EE | Decomposition number = 4, a = 2000 |
| Model 6 | RTSMFDE+CPCSMM | c = 6, m = 2, t = 1, s = 25, d = 3, K = 81, = 0.45 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, B.; Wang, Z.; Yao, L.; Luo, B. A Novel Intelligent Fault Diagnosis Method for Self-Priming Centrifugal Pumps. Entropy 2023, 25, 1501. https://doi.org/10.3390/e25111501
Zhang B, Wang Z, Yao L, Luo B. A Novel Intelligent Fault Diagnosis Method for Self-Priming Centrifugal Pumps. Entropy. 2023; 25(11):1501. https://doi.org/10.3390/e25111501
Chicago/Turabian StyleZhang, Bo, Zhenya Wang, Ligang Yao, and Biaolin Luo. 2023. "A Novel Intelligent Fault Diagnosis Method for Self-Priming Centrifugal Pumps" Entropy 25, no. 11: 1501. https://doi.org/10.3390/e25111501
APA StyleZhang, B., Wang, Z., Yao, L., & Luo, B. (2023). A Novel Intelligent Fault Diagnosis Method for Self-Priming Centrifugal Pumps. Entropy, 25(11), 1501. https://doi.org/10.3390/e25111501







