Causal Factor Disentanglement for Few-Shot Domain Adaptation in Video Prediction
Abstract
:1. Introduction
- We generate and make available SMS-TRIS, a new benchmark for evaluating few-shot domain adaptation for next-frame prediction under the Sparse Mechanism Shift assumption (The code to generate the datasets and reproduce our experiments as well as links to the dataset artifacts can be found at https://github.com/Natithan/SMS-TRIS (accessed on 21 August 2023.)
- We show that encouraging disentanglement during pretraining for few-shot domain adaptation can benefit prediction accuracy, but only if the disentanglement encouragement succeeds in leading to strong disentanglement.
- We show that an external baseline (Deep CORAL) does not improve over a naïve baseline, underlining the need for customized algorithms to exploit the Sparse Mechanism Shift assumption.
2. Related Work
2.1. Causal/Disentangled Representation Learning
2.2. Causality for Distribution Shifts
2.3. Domain Adaptation
3. Methodology
3.1. Problem Setup
- : A distribution from which the set of true, unobserved causal factors at the first time are sampled, where is the dimension of factor ;
- : A distribution from which the rendering noise is sampled at each timestep, where is the dimension of ;
- : A distribution from which the set of factor noises is sampled at each timestep, where is the dimension of . The are assumed to be independent of each other: ;
- : The true causal mechanisms that determine how factors evolve: . They are stationary;
- : The observed video frame at time t, deterministically ‘rendered’ from a combination of and by some observation function h: .
- An invertible encoder , with inverse function , that maps between and a latent representation , .
- A transition prior that predicts the next timestep in the latent space: .
3.2. Our Method: Causal Mechanism Disentanglement for Few-Shot Domain Adaptation
3.2.1. Causal Mechanism Disentanglement
- An Encoder-Transition Model M with encoder and transition prior ;
- A Mechanisms-Induced Distribution D;
- An assignment function that assigns dimensions of to an index k in . In other words, partitions the dimensions of into K subsets, where each subset is assigned to one of the K true factors.For a certain , we can consider as the composition of two parts:
- -
- : A shared part whose parameters affect all dimensions of ;
- -
- : A set of K parts, where the parameters of the part with index k affect only the dimensions of that are assigned to factor k.
3.2.2. Relevance to Few-Shot Next-Frame Prediction
3.2.3. Shared Parameters
4. Experimental Setup
4.1. Datasets
4.1.1. TRIS Datasets
4.1.2. SMS-TRIS Benchmark
4.2. Models
4.2.1. Backbones
4.2.2. CITRIS CFD Extensions
4.2.3. Deep CORAL
4.3. Evaluation
4.3.1. Causal Factor Disentanglement (CFD)
4.3.2. Prediction Error
5. Results and Discussion
5.1. Causal Factor Disentanglement (CFD)
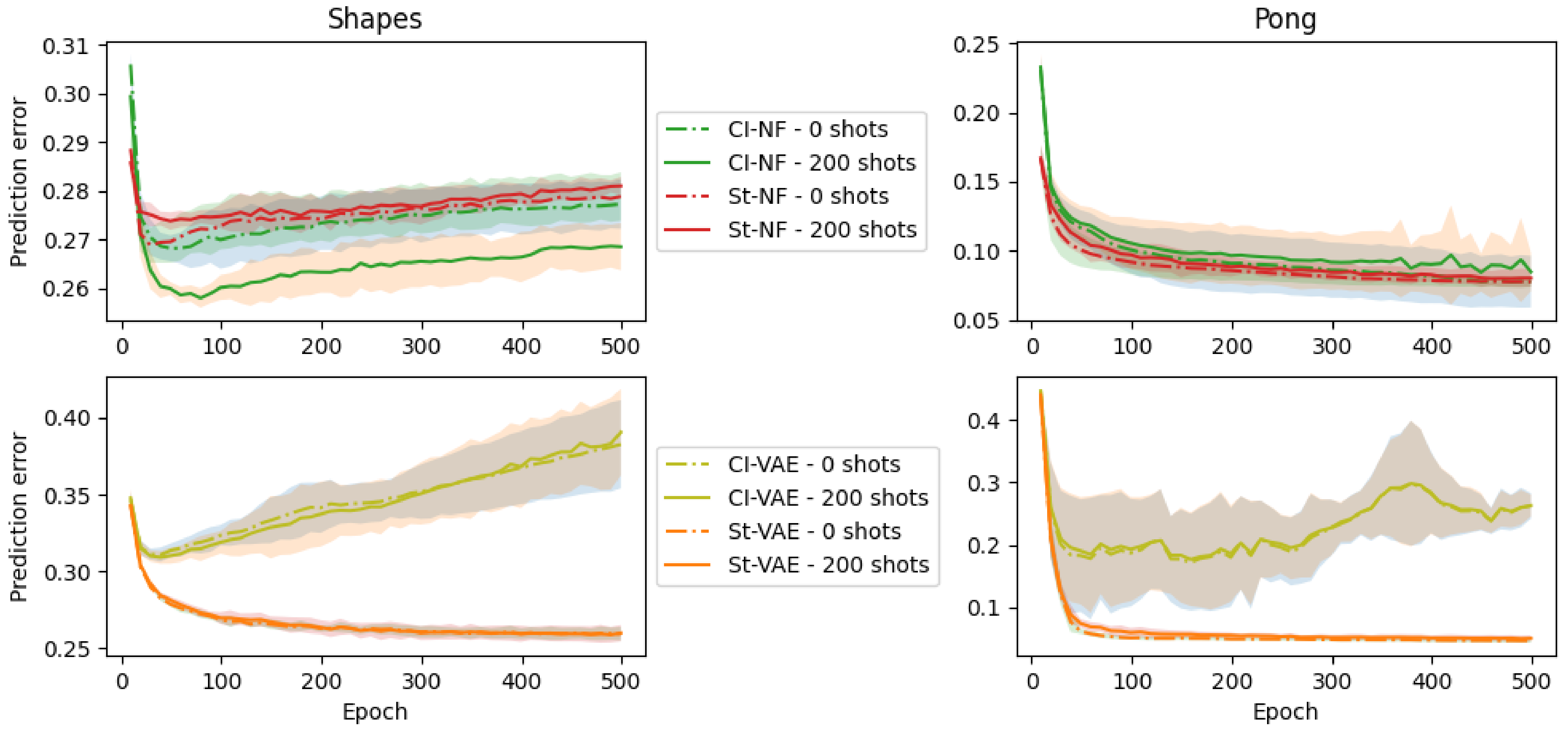
5.2. Prediction Error
5.2.1. Varying Pretraining Epoch
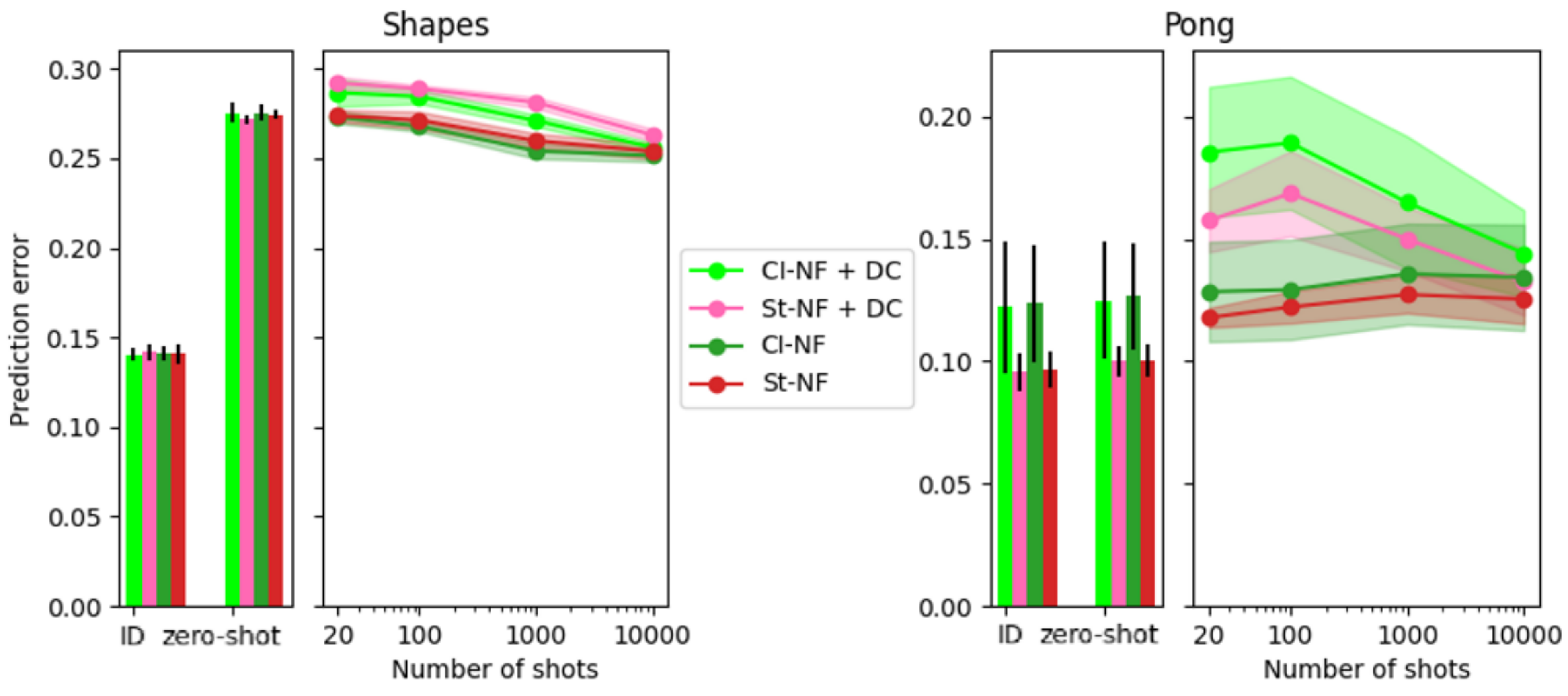
5.2.2. Varying Number of Shots
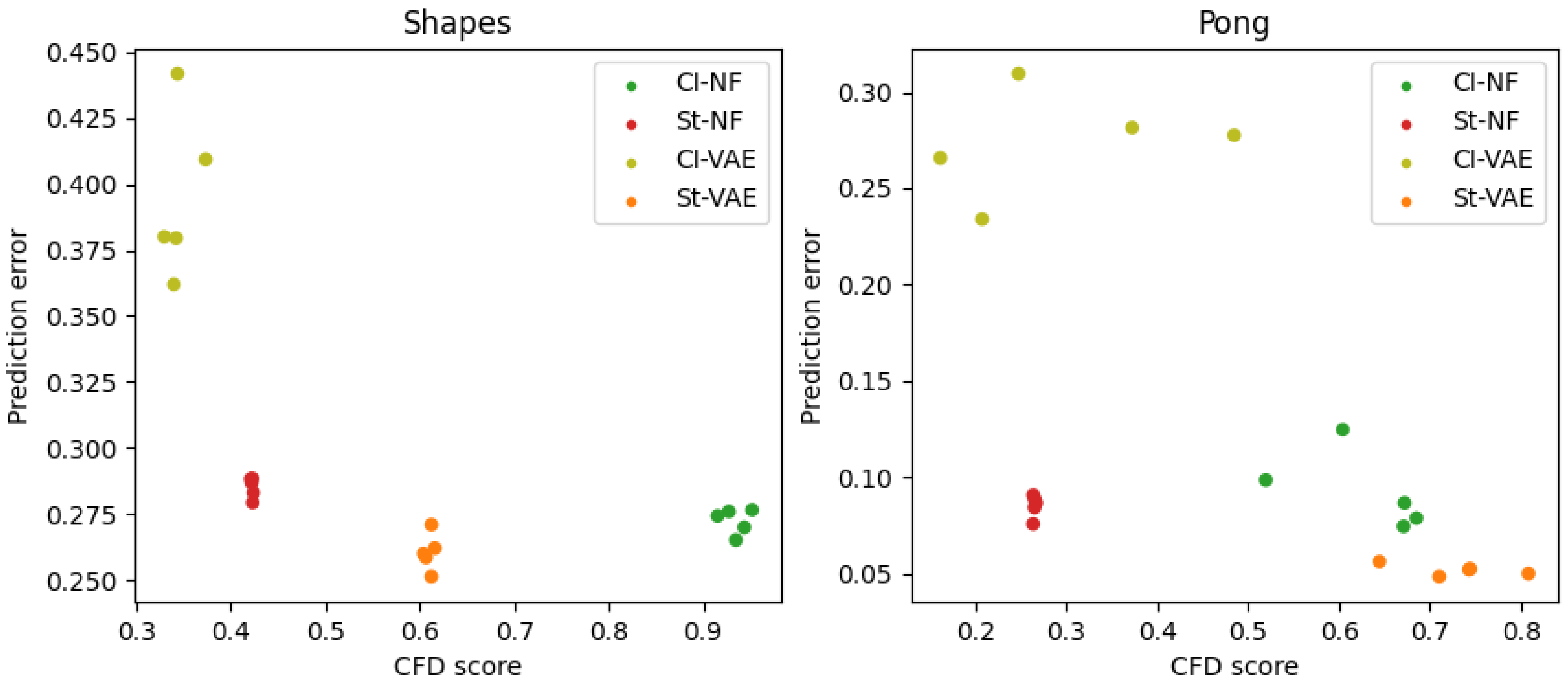
5.3. Causal Factor Disentanglement versus Prediction Error
5.4. Comparison to Deep CORAL
5.5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Example Subsequence of Shapes and Pong Datasets


References
- Filos, A.; Tigkas, P.; McAllister, R.; Rhinehart, N.; Levine, S.; Gal, Y. Can autonomous vehicles identify, recover from, and adapt to distribution shifts? In Proceedings of the International Conference on Machine Learning, PMLR, Virtual, 13–18 July 2020; pp. 3145–3153. [Google Scholar]
- Guariso, G.; Nunnari, G.; Sangiorgio, M. Multi-step solar irradiance forecasting and domain adaptation of deep neural networks. Energies 2020, 13, 3987. [Google Scholar] [CrossRef]
- Rothfuss, J.; Ferreira, F.; Aksoy, E.E.; Zhou, Y.; Asfour, T. Deep Episodic Memory: Encoding, Recalling, and Predicting Episodic Experiences for Robot Action Execution. IEEE Robot. Autom. Lett. 2018, 3, 4007–4014. [Google Scholar] [CrossRef]
- Teshima, T.; Sato, I.; Sugiyama, M. Few-shot Domain Adaptation by Causal Mechanism Transfer. In Proceedings of the 37th International Conference on Machine Learning, PMLR, Virtual, 13–18 July 2020; pp. 9458–9469. [Google Scholar]
- Arjovsky, M.; Bottou, L.; Gulrajani, I.; Lopez-Paz, D. Invariant Risk Minimization. arXiv 2019, arXiv:1907.02893. [Google Scholar]
- Liu, C.; Sun, X.; Wang, J.; Tang, H.; Li, T.; Qin, T.; Chen, W.; Liu, T.Y. Learning causal semantic representation for out-of-distribution prediction. Adv. Neural Inf. Process. Syst. 2021, 34, 6155–6170. [Google Scholar]
- Wang, R.; Yi, M.; Chen, Z.; Zhu, S. Out-of-distribution Generalization with Causal Invariant Transformations. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, CVPR 2022, New Orleans, LA, USA, 18–24 June 2022; pp. 375–385. [Google Scholar] [CrossRef]
- Schölkopf, B.; Locatello, F.; Bauer, S.; Ke, N.R.; Kalchbrenner, N.; Goyal, A.; Bengio, Y. Toward causal representation learning. Proc. IEEE 2021, 109, 612–634. [Google Scholar] [CrossRef]
- Kozhubaev, Y.; Ovchinnikova, E.; Viacheslav, I.; Krotova, S. Incremental Machine Learning for Soft Pneumatic Actuators with Symmetrical Chambers. Symmetry 2023, 15, 1206. [Google Scholar] [CrossRef]
- Lopez, R.; Tagasovska, N.; Ra, S.; Cho, K.; Pritchard, J.; Regev, A. Learning Causal Representations of Single Cells via Sparse Mechanism Shift Modeling. In Proceedings of the Second Conference on Causal Learning and Reasoning, PMLR, Tübingen, Germany, 11–14 April 2023; pp. 662–691. [Google Scholar]
- Lippe, P.; Magliacane, S.; Löwe, S.; Asano, Y.M.; Cohen, T.; Gavves, S. Citris: Causal identifiability from temporal intervened sequences. In Proceedings of the International Conference on Machine Learning, PMLR, Baltimore, MD, USA, 17–23 July 2022; pp. 13557–13603. [Google Scholar]
- Bengio, Y.; Deleu, T.; Rahaman, N.; Ke, N.R.; Lachapelle, S.; Bilaniuk, O.; Goyal, A.; Pal, C.J. A Meta-Transfer Objective for Learning to Disentangle Causal Mechanisms. In Proceedings of the 8th International Conference on Learning Representations, ICLR 2020, Addis Ababa, Ethiopia, 26–30 April 2020. [Google Scholar]
- Sun, B.; Saenko, K. Deep CORAL: Correlation Alignment for Deep Domain Adaptation. In Proceedings of the Computer Vision—ECCV 2016 Workshops, Amsterdam, The Netherlands, 8–10, 15–16 October 2016. [Google Scholar]
- Khemakhem, I.; Kingma, D.P.; Monti, R.P.; Hyvärinen, A. Variational Autoencoders and Nonlinear ICA: A Unifying Framework. In Proceedings of the 23rd International Conference on Artificial Intelligence and Statistics, Online, 26–28 August 2020; Chiappa, S., Calandra, R., Eds.; Volume 108, pp. 2207–2217. [Google Scholar]
- Kim, H.; Mnih, A. Disentangling by Factorising. In Proceedings of the 35th International Conference on Machine Learning, ICML 2018, Stockholm, Sweden, 10–15 July 2018; Dy, J.G., Krause, A., Eds.; Volume 80, pp. 2654–2663. [Google Scholar]
- Lu, C.; Wu, Y.; Hernández-Lobato, J.M.; Schölkopf, B. Nonlinear Invariant Risk Minimization: A Causal Approach. arXiv 2021, arXiv:2102.12353. [Google Scholar]
- Krueger, D.; Caballero, E.; Jacobsen, J.H.; Zhang, A.; Binas, J.; Zhang, D.; Priol, R.L.; Courville, A. Out-of-Distribution Generalization via Risk Extrapolation (REx). In Proceedings of the 38th International Conference on Machine Learning. PMLR, Virtual, 18–24 July 2021; pp. 5815–5826. [Google Scholar]
- Rojas-Carulla, M.; Scholkopf, B.; Turner, R.; Peters, J. Invariant Models for Causal Transfer Learning. J. Mach. Learn. Res. 2018, 19, 1–34. [Google Scholar]
- Shu, R.; Bui, H.H.; Narui, H.; Ermon, S. A DIRT-T Approach to Unsupervised Domain Adaptation. In Proceedings of the 6th International Conference on Learning Representations, ICLR 2018, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Yoon, J.; Kang, D.; Cho, M. Semi-supervised domain adaptation via sample-to-sample self-distillation. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 3–8 January 2022; pp. 1978–1987. [Google Scholar]
- Peng, K.; Wen, D.; Schneider, D.; Zhang, J.; Yang, K.; Sarfraz, M.S.; Stiefelhagen, R.; Roitberg, A. FeatFSDA: Towards Few-shot Domain Adaptation for Video-based Activity Recognition. arXiv 2023, arXiv:2305.08420. [Google Scholar] [CrossRef]
- Xu, Y.; Yang, J.; Zhou, Y.; Chen, Z.; Wu, M.; Li, X. Augmenting and Aligning Snippets for Few-Shot Video Domain Adaptation. arXiv 2023, arXiv:2303.10451. [Google Scholar]
- Jiang, J.; Ji, Y.; Wang, X.; Liu, Y.; Wang, J.; Long, M. Regressive domain adaptation for unsupervised keypoint detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 6780–6789. [Google Scholar]
- Lang, C.; Cheng, G.; Tu, B.; Li, C.; Han, J. Base and meta: A new perspective on few-shot segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 10669–10686. [Google Scholar] [CrossRef] [PubMed]
- Tian, Z.; Zhao, H.; Shu, M.; Yang, Z.; Li, R.; Jia, J. Prior guided feature enrichment network for few-shot segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 44, 1050–1065. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Tam, D.; Muqeeth, M.; Mohta, J.; Huang, T.; Bansal, M.; Raffel, C. Few-Shot Parameter-Efficient Fine-Tuning is Better and Cheaper than In-Context Learning. In Proceedings of the NeurIPS, New Orleans, LA, USA, 28 November–9 December 2022. [Google Scholar]
- Crane, K. Keenan’s 3D Model Repository. Available online: https://www.cs.cmu.edu/~kmcrane/Projects/ModelRepository/ (accessed on 1 January 2021).
- Rusinkiewicz, S.; DeCarlo, D.; Finkelstein, A.; Santella, A. Suggestive Contour Gallery. Available online: https://gfx.cs.princeton.edu/proj/sugcon/models/ (accessed on 1 January 2021).
- Curless, B.; Levoy, M. A volumetric method for building complex models from range images. In Proceedings of the 23rd Annual Conference on Computer Graphics and Interactive Techniques, New Orleans, LA, USA, 4–9 August 1996; pp. 303–312. [Google Scholar]
- Turk, G.; Levoy, M. Zippered polygon meshes from range images. In Proceedings of the 21st Annual Conference on Computer Graphics and Interactive Techniques, Orlando, FL, USA, 24–29 July 1994; pp. 311–318. [Google Scholar]
- Krishnamurthy, V.; Levoy, M. Fitting smooth surfaces to dense polygon meshes. In Proceedings of the 23rd Annual Conference on Computer Graphics and Interactive Techniques, New Orleans, LA, USA, 4–9 August 1996; pp. 313–324. [Google Scholar]
- Praun, E.; Finkelstein, A.; Hoppe, H. Lapped textures. In Proceedings of the 27th Annual Conference on Computer Graphics and Interactive Techniques, New Orleans, LA, USA, 23–28 July 2000; pp. 465–470. [Google Scholar]
- Newell, M.E. The Utilization of Procedure Models in Digital Image Synthesis. Ph.D. Thesis, The University of Utah, Salt Lake City, UT, USA, 1975. [Google Scholar]
- Bellemare, M.G.; Naddaf, Y.; Veness, J.; Bowling, M. The arcade learning environment: An evaluation platform for general agents. J. Artif. Intell. Res. 2013, 47, 253–279. [Google Scholar] [CrossRef]
- Wright, S. Correlation and causation. J. Agric. Res. 1921, 20, 557–585. [Google Scholar]
- Spearman, C. The proof and measurement of association between two things. Am. J. Psychol. 1987, 100, 441–471. [Google Scholar] [CrossRef] [PubMed]



| Factor | ID Mechanism | OOD Mechanism |
|---|---|---|
| Object Shape | ID Object Hue Goal | OOD Object Hue Goal |
|---|---|---|
| Teapot | 0 | |
| Armadillo | 0 | |
| Hare | avg(hue spot, hue back) | avg(hue spot, hue back) + |
| Cow | ||
| Dragon | avg(hue spot, hue back) + | avg(hue spot, hue back) |
| Head | ||
| Horse |
| Factor | OOD Mechanism Change |
|---|---|
| Ball x-position | The ball now teleports horizontally over a middle section whose width is half the inter-paddle horizontal distance. |
| Ball y-position | The ball now teleports vertically over a middle section whose width is one-fifth of the inter-wall vertical distance. |
| Ball velocity direction | When a ball collides with a paddle, instead of only having the x-component of its velocity direction flipped, now the y-component also flips, flipping the velocity direction by 180 degrees. |
| Ball velocity magnitude | Ball velocity is doubled when in the lower half of the playing field. |
| Paddle left y-position | After a paddle–ball collision, the paddle now teleports a distance equal to half the inter-wall vertical distance up, if the collision was in the lower half, and down, if the collision was in the upper half. |
| Paddle right y-position | Same as for paddle left y-position. |
| Score left | When a score of 5 is reached, the score now resets to 1 instead of 0. |
| Score right | Same as for score left. |
| Model | Diag ↑ | Sep ↓ | Sp Diag ↑ | Sp Sep ↓ | Triplet Mean ↓ | CFD Score ↑ | |
|---|---|---|---|---|---|---|---|
| Shapes | CITRIS-NF | 0.95 ± 0.011 | 0.08 ± 0.020 | 0.95 ± 0.017 | 0.10 ± 0.016 | 0.05 ± 0.008 | 0.93 ± 0.014 |
| Standard-NF | 0.26 ± 0.001 | 0.62 ± 0.003 | 0.29 ± 0.001 | 0.61 ± 0.004 | 0.21 ± 0.000 | 0.42 ± 0.001 | |
| CITRIS-VAE | 0.63 ± 0.022 | 0.25 ± 0.062 | 0.63 ± 0.028 | 0.28 ± 0.050 | 0.34 ± 0.010 | 0.68 ± 0.031 | |
| Standard-VAE | 0.60 ± 0.016 | 0.46 ± 0.015 | 0.61 ± 0.014 | 0.47 ± 0.004 | 0.23 ± 0.001 | 0.61 ± 0.005 | |
| Pong | CITRIS-NF | 0.64 ± 0.064 | 0.39 ± 0.046 | 0.62 ± 0.068 | 0.41 ± 0.045 | 0.31 ± 0.168 | 0.63 ± 0.070 |
| Standard-NF | 0.13 ± 0.004 | 0.85 ± 0.006 | 0.13 ± 0.003 | 0.85 ± 0.002 | 0.25 ± 0.001 | 0.26 ± 0.001 | |
| CITRIS-VAE | 0.77 ± 0.085 | 0.25 ± 0.118 | 0.77 ± 0.086 | 0.31 ± 0.136 | 0.26 ± 0.030 | 0.75 ± 0.081 | |
| Standard-VAE | 0.83 ± 0.124 | 0.37 ± 0.081 | 0.83 ± 0.115 | 0.39 ± 0.054 | 0.25 ± 0.001 | 0.73 ± 0.060 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cornille, N.; Laenen, K.; Sun, J.; Moens, M.-F. Causal Factor Disentanglement for Few-Shot Domain Adaptation in Video Prediction. Entropy 2023, 25, 1554. https://doi.org/10.3390/e25111554
Cornille N, Laenen K, Sun J, Moens M-F. Causal Factor Disentanglement for Few-Shot Domain Adaptation in Video Prediction. Entropy. 2023; 25(11):1554. https://doi.org/10.3390/e25111554
Chicago/Turabian StyleCornille, Nathan, Katrien Laenen, Jingyuan Sun, and Marie-Francine Moens. 2023. "Causal Factor Disentanglement for Few-Shot Domain Adaptation in Video Prediction" Entropy 25, no. 11: 1554. https://doi.org/10.3390/e25111554
APA StyleCornille, N., Laenen, K., Sun, J., & Moens, M.-F. (2023). Causal Factor Disentanglement for Few-Shot Domain Adaptation in Video Prediction. Entropy, 25(11), 1554. https://doi.org/10.3390/e25111554








