Relevant Analytic Spontaneous Magnetization Relation for the Face-Centered-Cubic Ising Lattice
Abstract
:1. Introduction
2. Methods and Results
2.1. Expansion of the Callen–Suzuki Identity
2.2. Derivation of the Analytic Relation for the Spontaneous Magnetization
2.3. Spontaneous Magnetization through MC Simulation
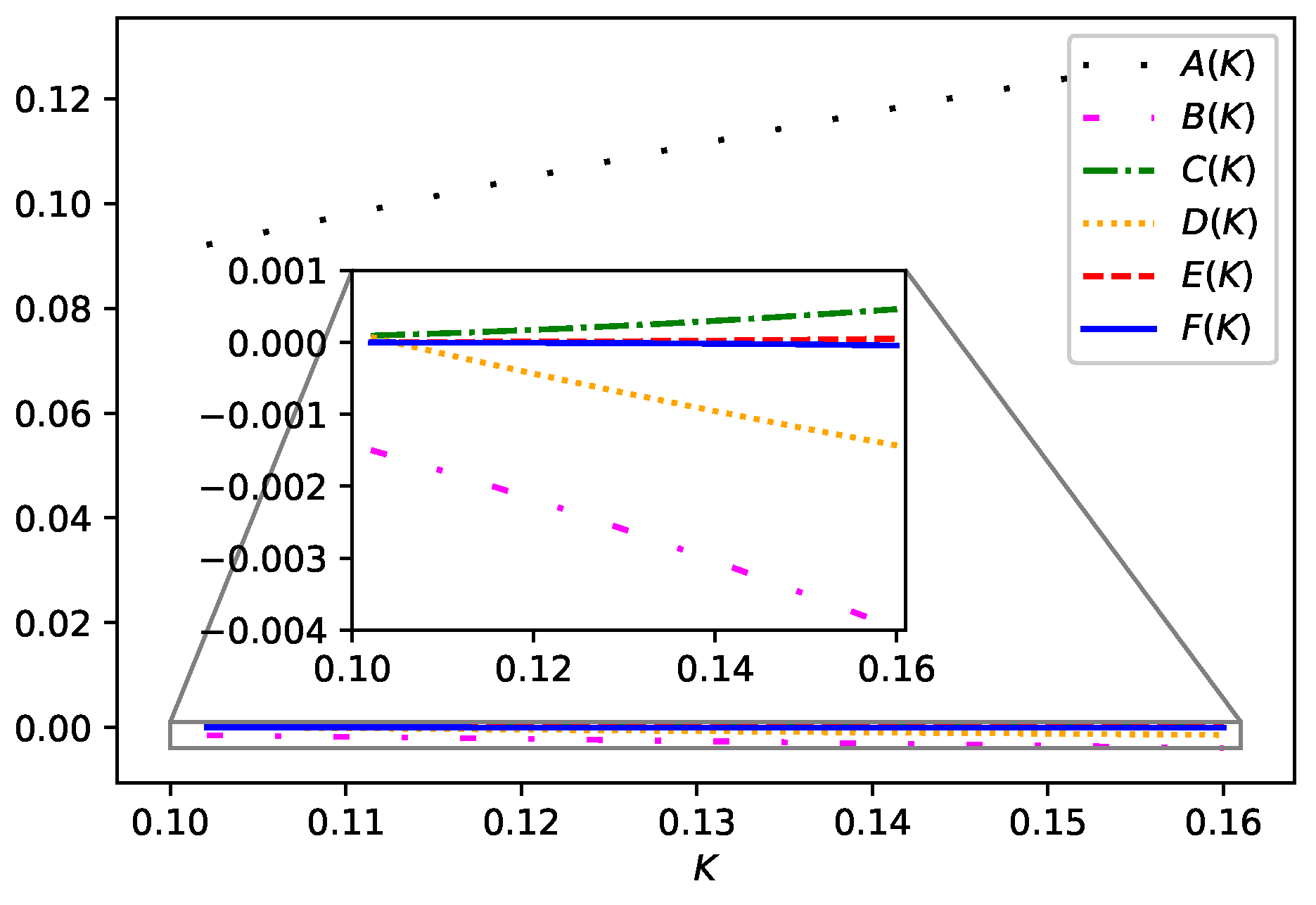
3. Discussion and Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Stanley, H. Introduction to Phase Transitions and Critical Phenomena; International Series of Monographs on Physics; Oxford University Press: New York, NY, USA, 1971. [Google Scholar]
- Ising, E. Contribution to the Theory of Ferromagnetism. Z. Phys. 1925, 31, 253–258. [Google Scholar] [CrossRef]
- Smits, J.; Stoof, H.T.C.; van der Straten, P. Spontaneous breaking of a discrete time-translation symmetry. Phys. Rev. A 2021, 104, 023318. [Google Scholar] [CrossRef]
- Onsager, L. Crystal Statistics. I. A Two-Dimensional Model with an Order-Disorder Transition. Phys. Rev. 1944, 65, 117–149. [Google Scholar] [CrossRef]
- Yang, C.N. The Spontaneous Magnetization of a Two-Dimensional Ising Model. Phys. Rev. 1952, 85, 808–816. [Google Scholar] [CrossRef]
- Baxter, R.J. Onsager and Kaufman’s Calculation of the Spontaneous Magnetization of the Ising Model: II. J. Stat. Phys. 2012, 149, 1164–1167. [Google Scholar] [CrossRef] [Green Version]
- Houtappel, R. Order-disorder in hexagonal lattices. Physica 1950, 16, 425–455. [Google Scholar] [CrossRef]
- Husimi, K.; Syôzi, I. The statistics of honeycomb and triangular lattice. I. Prog. Theor. Phys. 1950, 5, 177–186. [Google Scholar] [CrossRef]
- Syozi, I. The statistics of honeycomb and triangular lattice. II. Prog. Theor. Phys. 1950, 5, 341–351. [Google Scholar] [CrossRef]
- Newell, G.F. Crystal Statistics of a Two-Dimensional Triangular Ising Lattice. Phys. Rev. 1950, 79, 876–882. [Google Scholar] [CrossRef]
- Temperley, H. Statistical mechanics of the two-dimensional assembly. Proc. R. Soc. Lond. A Math. Phys. Sci. 1950, 202, 202–207. [Google Scholar] [CrossRef]
- Wannier, G.H. Antiferromagnetism. The Triangular Ising Net. Phys. Rev. 1950, 79, 357–364. [Google Scholar] [CrossRef] [Green Version]
- Potts, R.B. Combinatorial Solution of the Triangular Ising Lattice. Proc. Phys. Soc. A 1955, 68, 145–148. [Google Scholar] [CrossRef]
- Naya, S. On the Spontaneous Magnetizations of Honeycomb and Kagomé Ising Lattices. Prog. Theor. Phys. 1954, 11, 53–62. [Google Scholar] [CrossRef]
- Potts, R.B. Spontaneous Magnetization of a Triangular Ising Lattice. Phys. Rev. 1952, 88, 352. [Google Scholar] [CrossRef]
- Lin, K.Y.; Ma, W.J. Two-dimensional Ising model on a ruby lattice. J. Phys. A Math. Gen. 1983, 16, 3895–3898. [Google Scholar] [CrossRef]
- Zhang, Z.D. Conjectures on the exact solution of three-dimensional (3D) simple orthorhombic Ising lattices. Phil. Mag. 2007, 87, 5309–5419. [Google Scholar] [CrossRef] [Green Version]
- Wu, F.; McCoy, B.; Fisher, M.; Chayes, L. Comment on a recent conjectured solution of the three-dimensional Ising model. Phil. Mag. 2008, 88, 3093–3095. [Google Scholar] [CrossRef]
- Perk, J.H. Comment on ‘Conjectures on exact solution of three-dimensional (3D) simple orthorhombic Ising lattices’. Phil. Mag. 2009, 89, 761–764. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z. Response to the Comment on ‘Conjectures on exact solution of three-dimensional (3D) simple orthorhombic Ising lattices’. Phil. Mag. 2009, 89, 765–768. [Google Scholar] [CrossRef] [Green Version]
- Perk, J.H.H. Erroneous solution of three-dimensional (3D) simple orthorhombic Ising lattices. Bull. Société Sci. Lettres LÓDZ 2012, 62, 45–59. [Google Scholar]
- Zhang, Z.D. Mathematical structure of the three-dimensional (3D) Ising model. Chin. Phys. B 2013, 22, 030513. [Google Scholar] [CrossRef]
- Perk, J.H.H. Comment on ‘Mathematical structure of the three-dimensional (3D) Ising model’. Chin. Phys. B 2013, 22, 080508. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Suzuki, O.; March, N.H. Clifford algebra approach of 3D Ising model. Adv. Appl. Clifford Algebras 2019, 29, 12. [Google Scholar] [CrossRef] [Green Version]
- Suzuki, O.; Zhang, Z. A Method of Riemann–Hilbert Problem for Zhang’s Conjecture 1 in a Ferromagnetic 3D Ising Model: Trivialization of Topological Structure. Mathematics 2021, 9, 776. [Google Scholar] [CrossRef]
- Zhang, Z.; Suzuki, O. A Method of the Riemann–Hilbert Problem for Zhang’s Conjecture 2 in a Ferromagnetic 3D Ising Model: Topological Phases. Mathematics 2021, 9, 2936. [Google Scholar] [CrossRef]
- Zhang, Z. Topological Quantum Statistical Mechanics and Topological Quantum Field Theories. Symmetry 2022, 14, 323. [Google Scholar] [CrossRef]
- Viswanathan, G.M.; Portillo, M.A.G.; Raposo, E.P.; da Luz, M.G.E. What Does It Take to Solve the 3D Ising Model? Minimal Necessary Conditions for a Valid Solution. Entropy 2022, 24, 1665. [Google Scholar] [CrossRef]
- Domb, C. On the theory of cooperative phenomena in crystals. Adv. Phys. 1960, 9, 245–361. [Google Scholar] [CrossRef]
- Wilson, K.G. Renormalization Group and Critical Phenomena. I. Renormalization Group and the Kadanoff Scaling Picture. Phys. Rev. B 1971, 4, 3174–3183. [Google Scholar] [CrossRef] [Green Version]
- Wilson, K.G. Renormalization Group and Critical Phenomena. II. Phase-Space Cell Analysis of Critical Behavior. Phys. Rev. B 1971, 4, 3184–3205. [Google Scholar] [CrossRef] [Green Version]
- Wilson, K.G. The renormalization group and critical phenomena. Rev. Mod. Phys. 1983, 55, 583–600. [Google Scholar] [CrossRef]
- Goldenfeld, N. Lectures on Phase Transitions and the Renormalization Group; CRC Press: Boca Raton, FL, USA, 1992. [Google Scholar]
- Butera, P.; Comi, M. Critical universality and hyperscaling revisited for Ising models of general spin using extended high-temperature series. Phys. Rev. B 2002, 65, 144431. [Google Scholar] [CrossRef] [Green Version]
- Salman, Z.; Adler, J. High and low temperature series estimates for the critical temperature of the 3D Ising model. Int. J. Mod. Phys. C 1998, 9, 195–209. [Google Scholar] [CrossRef]
- Jasch, F.; Kleinert, H. Fast-convergent resummation algorithm and critical exponents of ϕ4-theory in three dimensions. J. Math. Phys. 2001, 42, 52–73. [Google Scholar] [CrossRef] [Green Version]
- El-Showk, S.; Paulos, M.F.; Poland, D.; Rychkov, S.; Simmons-Duffin, D.; Vichi, A. Solving the 3D Ising model with the conformal bootstrap. Phys. Rev. D 2012, 86, 025022. [Google Scholar] [CrossRef] [Green Version]
- El-Showk, S.; Paulos, M.F.; Poland, D.; Rychkov, S.; Simmons-Duffin, D.; Vichi, A. Solving the 3d Ising Model with the Conformal Bootstrap II. c-Minimization and Precise Critical Exponents. J. Stat. Phys. 2014, 157, 869–914. [Google Scholar] [CrossRef] [Green Version]
- Landau, D.P.; Binder, K. A Guide to Monte Carlo Simulations in Statistical Physics, 4th ed.; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. Equation of State Calculations by Fast Computing Machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef] [Green Version]
- Swendsen, R.H.; Wang, J.S. Nonuniversal critical dynamics in Monte Carlo simulations. Phys. Rev. Lett. 1987, 58, 86–88. [Google Scholar] [CrossRef]
- Wolff, U. Collective Monte Carlo Updating for Spin Systems. Phys. Rev. Lett. 1989, 62, 361–364. [Google Scholar] [CrossRef]
- Hasenbusch, M. Monte Carlo studies of the three-dimensional Ising model in equilibrium. Int. J. Mod. Phys. C 2001, 12, 911–1009. [Google Scholar] [CrossRef]
- Blöte, H.W.J.; Heringa, J.R.; Hoogland, A.; Meyer, E.W.; Smit, T.S. Monte Carlo Renormalization of the 3D Ising Model: Analyticity and Convergence. Phys. Rev. Lett. 1996, 76, 2613–2616. [Google Scholar] [CrossRef] [PubMed]
- Gupta, R.; Tamayo, P. Critical Exponents of the 3-D Ising Model. Int. J. Mod. Phys. C 1996, 7, 305–319. [Google Scholar] [CrossRef] [Green Version]
- Murase, Y.; Ito, N. Dynamic critical exponents of three-dimensional Ising models and two-dimensional three-states Potts models. J. Phys. Soc. Jpn. 2007, 77, 014002. [Google Scholar] [CrossRef]
- Lundow, P.H.; Markström, K.; Rosengren, A. The Ising model for the bcc, fcc and diamond lattices: A comparison. Phil. Mag. 2009, 89, 2009–2042. [Google Scholar] [CrossRef]
- Yu, U. Critical temperature of the Ising ferromagnet on the fcc, hcp, and dhcp lattices. Phys. A Stat. Mech. Appl. 2015, 419, 75–79. [Google Scholar] [CrossRef]
- Ferrenberg, A.M.; Xu, J.; Landau, D.P. Pushing the limits of Monte Carlo simulations for the three-dimensional Ising model. Phys. Rev. E 2018, 97, 043301. [Google Scholar] [CrossRef] [Green Version]
- Netz, R.R.; Berker, A.N. Monte Carlo mean-field theory and frustrated systems in two and three dimensions. Phys. Rev. Lett. 1991, 66, 377–380. [Google Scholar] [CrossRef]
- Wang, L. Discovering phase transitions with unsupervised learning. Phys. Rev. B 2016, 94, 195105. [Google Scholar] [CrossRef] [Green Version]
- Torlai, G.; Melko, R.G. Learning thermodynamics with Boltzmann machines. Phys. Rev. B 2016, 94, 165134. [Google Scholar] [CrossRef] [Green Version]
- Carrasquilla, J.; Melko, R.G. Machine learning phases of matter. Nat. Phys. 2017, 13, 431–434. [Google Scholar] [CrossRef] [Green Version]
- Hu, W.; Singh, R.R.P.; Scalettar, R.T. Discovering phases, phase transitions, and crossovers through unsupervised machine learning: A critical examination. Phys. Rev. E 2017, 95, 062122. [Google Scholar] [CrossRef]
- Chung, J.H.; Kao, Y.J. Neural Monte Carlo renormalization group. Phys. Rev. Res. 2021, 3, 023230. [Google Scholar] [CrossRef]
- Carleo, G.; Cirac, I.; Cranmer, K.; Daudet, L.; Schuld, M.; Tishby, N.; Vogt-Maranto, L.; Zdeborová, L. Machine learning and the physical sciences. Rev. Mod. Phys. 2019, 91, 045002. [Google Scholar] [CrossRef] [Green Version]
- Hu, C.K. Historical review on analytic, Monte Carlo, and renormalization group approaches to critical phenomena of some lattice Models. Chin. J. Phys. 2014, 52, 1–76. [Google Scholar] [CrossRef]
- Strecka, J.; Jaščur, M. A brief account of the Ising and Ising-like models: Mean-field, effective-field and exact results. Acta Phys. Slovaca 2015, 65, 235–367. [Google Scholar]
- McCoy, B. Advanced Statistical Mechanics; International Series of Monographs on Physics; Oxford University Press: New York, NY, USA, 2009. [Google Scholar]
- Kardar, M. Statistical Physics of Fields; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- McCoy, B.M.; Wu, T.T. The two-Dimensional Ising Model; Courier Corporation: New York, NY, USA, 2014. [Google Scholar]
- Baxter, R.J. Exactly Solved Models in Statistical Mechanics; Academic Press: London, UK, 1982. [Google Scholar]
- Pelissetto, A.; Vicari, E. Critical phenomena and renormalization-group theory. Phys. Rep. 2002, 368, 549–727. [Google Scholar] [CrossRef] [Green Version]
- Kramers, H.A.; Wannier, G.H. Statistics of the Two-Dimensional Ferromagnet. Part I. Phys. Rev. 1941, 60, 252–262. [Google Scholar] [CrossRef]
- Fisher, M.E. Transformations of Ising Models. Phys. Rev. 1959, 113, 969–981. [Google Scholar] [CrossRef]
- Kaufman, B. Crystal Statistics. II. Partition Function Evaluated by Spinor Analysis. Phys. Rev. 1949, 76, 1232–1243. [Google Scholar] [CrossRef]
- Kaufman, B.; Onsager, L. Crystal Statistics. III. Short-Range Order in a Binary Ising Lattice. Phys. Rev. 1949, 76, 1244–1252. [Google Scholar] [CrossRef]
- Perk, J. Quadratic identities for Ising model correlations. Phys. Lett. A 1980, 79, 3–5. [Google Scholar] [CrossRef]
- Callen, H. A note on Green functions and the Ising model. Phys. Lett. 1963, 4, 161. [Google Scholar] [CrossRef]
- Yang, C.N. Journey through Statistical Mechanics. Int. J. Mod. Phys. B 1988, 2, 1325–1329. [Google Scholar] [CrossRef]
- Kac, M.; Ward, J.C. A Combinatorial Solution of the Two-Dimensional Ising Model. Phys. Rev. 1952, 88, 1332–1337. [Google Scholar] [CrossRef]
- Hurst, C.A.; Green, H.S. New Solution of the Ising Problem for a Rectangular Lattice. J. Chem. Phys. 1960, 33, 1059–1062. [Google Scholar] [CrossRef]
- Montroll, E.W.; Potts, R.B.; Ward, J.C. Correlations and Spontaneous Magnetization of the Two-Dimensional Ising Model. J. Math. Phys. 1963, 4, 308–322. [Google Scholar] [CrossRef]
- Bornholdt, S.; Wagner, F. Stability of money: Phase transitions in an Ising economy. Phys. A Stat. Mech. Appl. 2002, 316, 453–468. [Google Scholar] [CrossRef] [Green Version]
- Sornette, D.; Zhou, W.X. Importance of positive feedbacks and overconfidence in a self-fulfilling Ising model of financial markets. Phys. A Stat. Mech. Appl. 2006, 370, 704–726. [Google Scholar] [CrossRef] [Green Version]
- Stauffer, D. Social applications of two-dimensional Ising models. Am. J. Phys. 2008, 76, 470–473. [Google Scholar] [CrossRef] [Green Version]
- Weber, M.; Buceta, J. The cellular Ising model: A framework for phase transitions in multicellular environments. J. R. Soc. Interface 2016, 13, 20151092. [Google Scholar] [CrossRef]
- Matsuda, H. The Ising Model for Population Biology. Prog. Theor. Phys. 1981, 66, 1078–1080. [Google Scholar] [CrossRef] [Green Version]
- Castellano, C.; Fortunato, S.; Loreto, V. Statistical physics of social dynamics. Rev. Mod. Phys. 2009, 81, 591–646. [Google Scholar] [CrossRef]
- Schneidman, E.; Berry, M.J.; Segev, R.; Bialek, W. Weak pairwise correlations imply strongly correlated network states in a neural population. Nature 2006, 440, 1007–1012. [Google Scholar] [CrossRef] [Green Version]
- Amit, D.J. Modeling Brain Function: The World of Attractor Neural Networks; Cambridge University Press: Cambridge, UK, 1989. [Google Scholar]
- Decelle, A.; Furtlehner, C. Restricted Boltzmann machine: Recent advances and mean-field theory. Chin. Phys. B 2021, 30, 040202. [Google Scholar] [CrossRef]
- Engel, A.; Van den Broeck, C. Statistical Mechanics of Learning; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Kaya, T. Relevant spontaneous magnetization relations for the triangular and the cubic lattice Ising model. Chin. J. Phys. 2022, 77, 2676–2683. [Google Scholar] [CrossRef]
- Kaya, T. Analytic average magnetization expression for the body-centered cubic Ising lattice. Eur. Phys. J. Plus 2022, 137, 1130. [Google Scholar] [CrossRef]
- Kaya, T. Relevant alternative analytic average magnetization calculation method for the square and the honeycomb Ising lattices. Chin. J. Phys. 2022, 77, 747–752. [Google Scholar] [CrossRef]
- Suzuki, M. Generalized exact formula for the correlations of the Ising model and other classical systems. Phys. Lett. 1965, 19, 267–268. [Google Scholar] [CrossRef]
- Suzuki, M. Correlation identities and application. Int. J. Mod. Phys. B 2002, 16, 1749–1765. [Google Scholar] [CrossRef]
- Baxter, R. Triplet order parameter of the triangular Ising model. J. Phys. A Math. Gen. 1975, 8, 1797–1805. [Google Scholar] [CrossRef]
- Barry, J.; Múnera, C.; Tanaka, T. Exact solutions for Ising model odd-number correlations on the honeycomb and triangular lattices. Phys. A Stat. Mech. Appl. 1982, 113, 367–387. [Google Scholar] [CrossRef]
- Pink, D.A. Three-site correlation functions of the two-dimensional Ising model. Can. J. Phys. 1968, 46, 2399–2405. [Google Scholar] [CrossRef]
- Enting, I.G. Triplet order parameters in triangular and honeycomb Ising models. J. Phys. A Math. Gen. 1977, 10, 1737–1743. [Google Scholar] [CrossRef]
- Barber, M.N. On the nature of the critical point in the three-spin triangular Ising model. J. Phys. A Math. Gen. 1976, 9, L171–L174. [Google Scholar] [CrossRef]
- Wood, D.W.; Griffiths, H.P. Triplet order parameters for three-dimensional Ising models. J. Phys. A Math. Gen. 1976, 9, 407–411. [Google Scholar] [CrossRef]
- Taggart, G.B. Effective field model for Ising ferromagnets: Influence of triplet correlations. J. Appl. Phys. 1982, 53, 1907–1909. [Google Scholar] [CrossRef] [Green Version]
- Baxter, R.J.; Choy, T.C. Local three-spin correlations in the free-fermion and planar Ising models. Proc. R. Soc. Lond. A Math. Phys. Sci. 1989, 423, 279–300. [Google Scholar] [CrossRef]
- Kaya, T. Exact three spin correlation function relations for the square and the honeycomb Ising lattices. Chin. J. Phys. 2020, 66, 415–421. [Google Scholar] [CrossRef]
- Lin, K.Y. Three-spin correlation of the Ising model on the generalized checkerboard lattice. J. Stat. Phys. 1989, 56, 631–643. [Google Scholar] [CrossRef]
- Lin, K.Y.; Chen, B.H. Three-spin correlation of the Ising model on a Kagome lattice. Int. J. Mod. Phys. B 1990, 04, 123–130. [Google Scholar] [CrossRef]
- Talapov, A.L.; Blöte, H.W.J. The magnetization of the 3D Ising model. J. Phys. A Math. Gen. 1996, 29, 5727–5733. [Google Scholar] [CrossRef] [Green Version]
- Newell, G.F.; Montroll, E.W. On the Theory of the Ising Model of Ferromagnetism. Rev. Mod. Phys. 1953, 25, 159. [Google Scholar] [CrossRef]
- Binder, K.; Luijten, E. Monte Carlo tests of renormalization-group predictions for critical phenomena in Ising models. Phys. Rep. 2001, 344, 179–253. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tambaş, B. Relevant Analytic Spontaneous Magnetization Relation for the Face-Centered-Cubic Ising Lattice. Entropy 2023, 25, 197. https://doi.org/10.3390/e25020197
Tambaş B. Relevant Analytic Spontaneous Magnetization Relation for the Face-Centered-Cubic Ising Lattice. Entropy. 2023; 25(2):197. https://doi.org/10.3390/e25020197
Chicago/Turabian StyleTambaş, Başer. 2023. "Relevant Analytic Spontaneous Magnetization Relation for the Face-Centered-Cubic Ising Lattice" Entropy 25, no. 2: 197. https://doi.org/10.3390/e25020197
APA StyleTambaş, B. (2023). Relevant Analytic Spontaneous Magnetization Relation for the Face-Centered-Cubic Ising Lattice. Entropy, 25(2), 197. https://doi.org/10.3390/e25020197





