Measurement-Based Quantum Thermal Machines with Feedback Control
Abstract
:1. Introduction
2. Model
3. Quantum Maxwell’s Demon
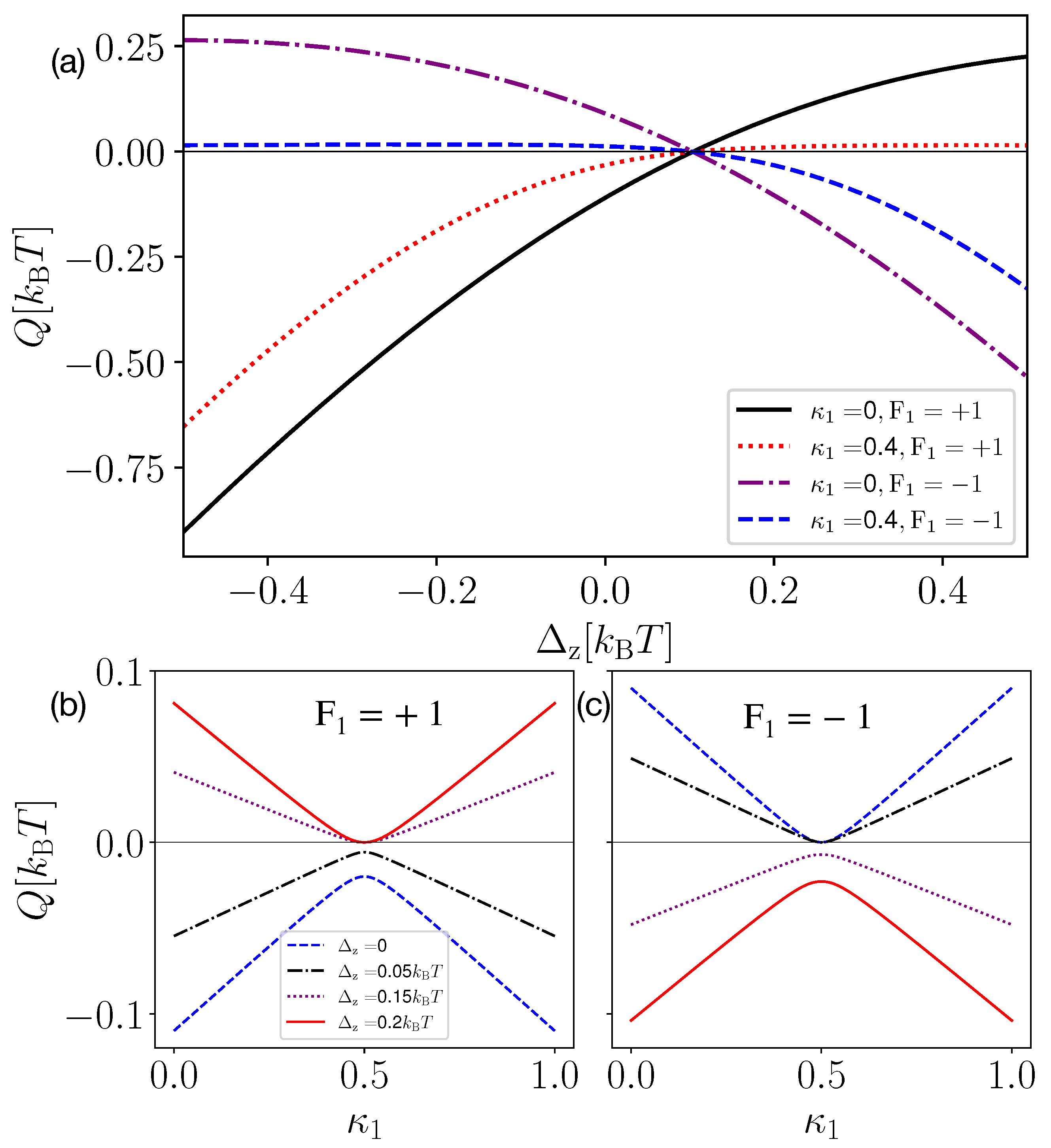
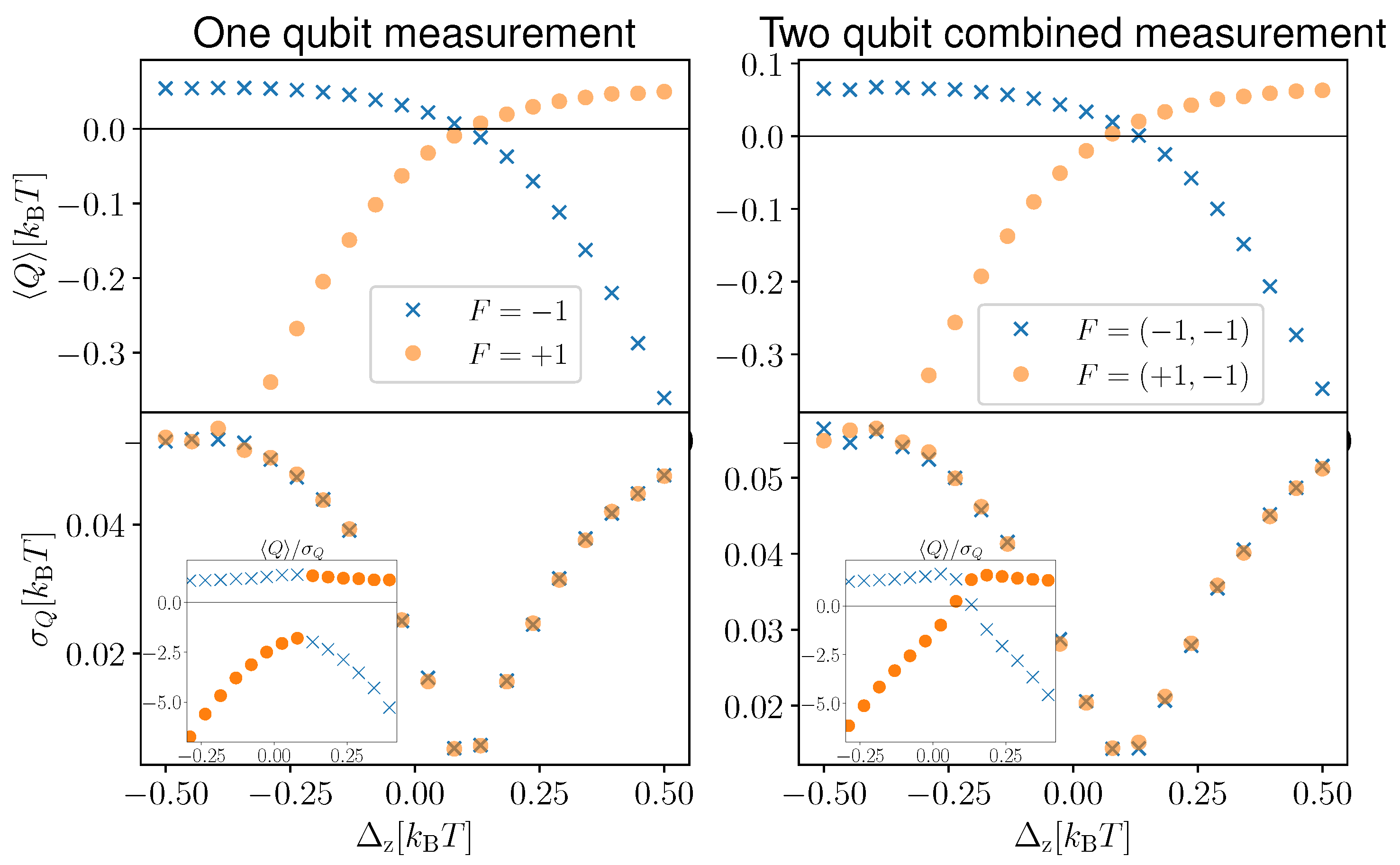
3.1. Discrete One-Qubit Measurement
3.2. Discrete Two-Qubit Combined Measurement
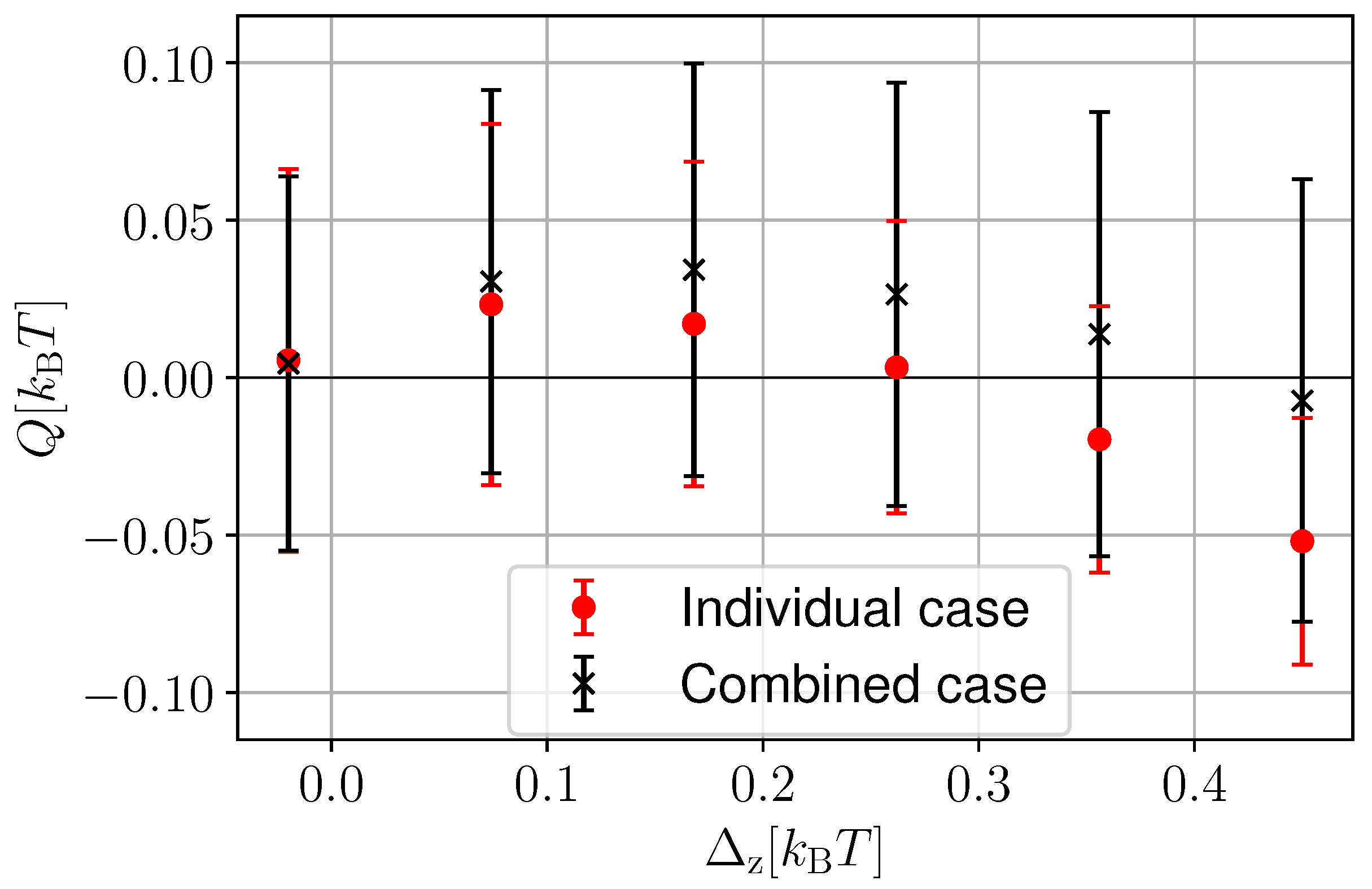
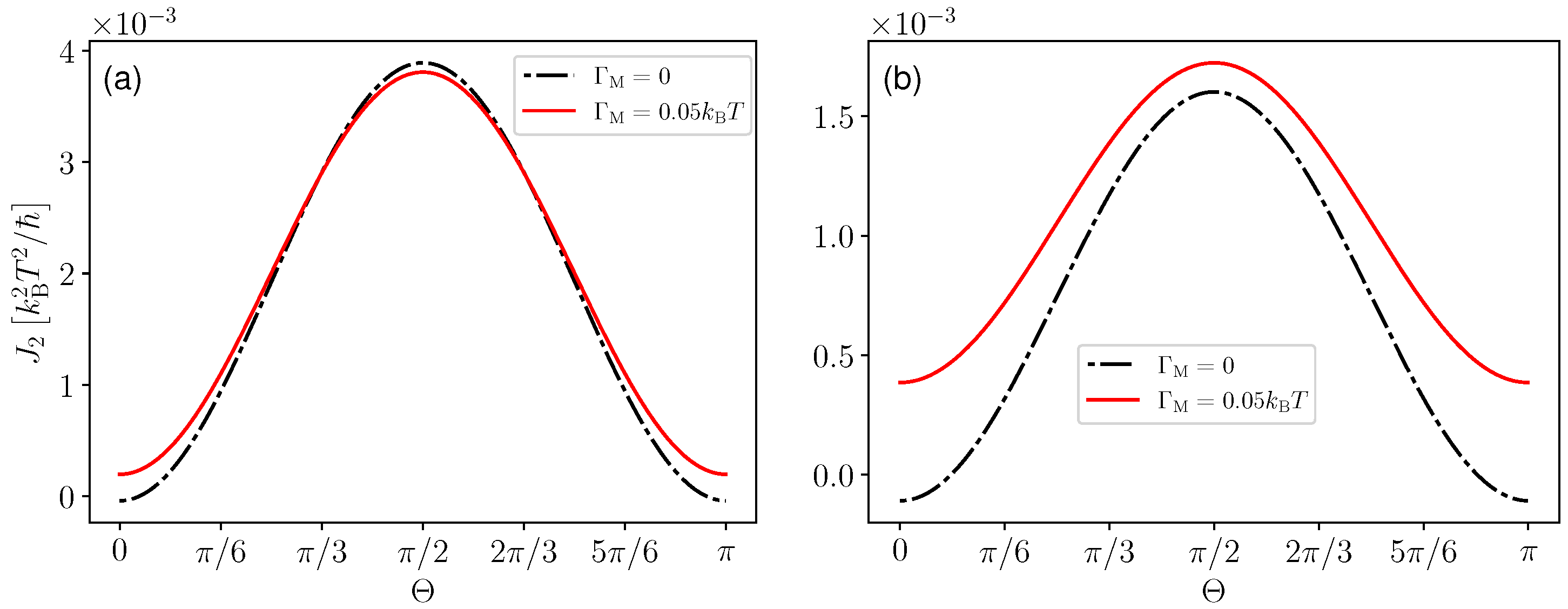
3.3. Continuous One- and Two-Qubit Measurement
4. Measurement-Assisted Refrigerator
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
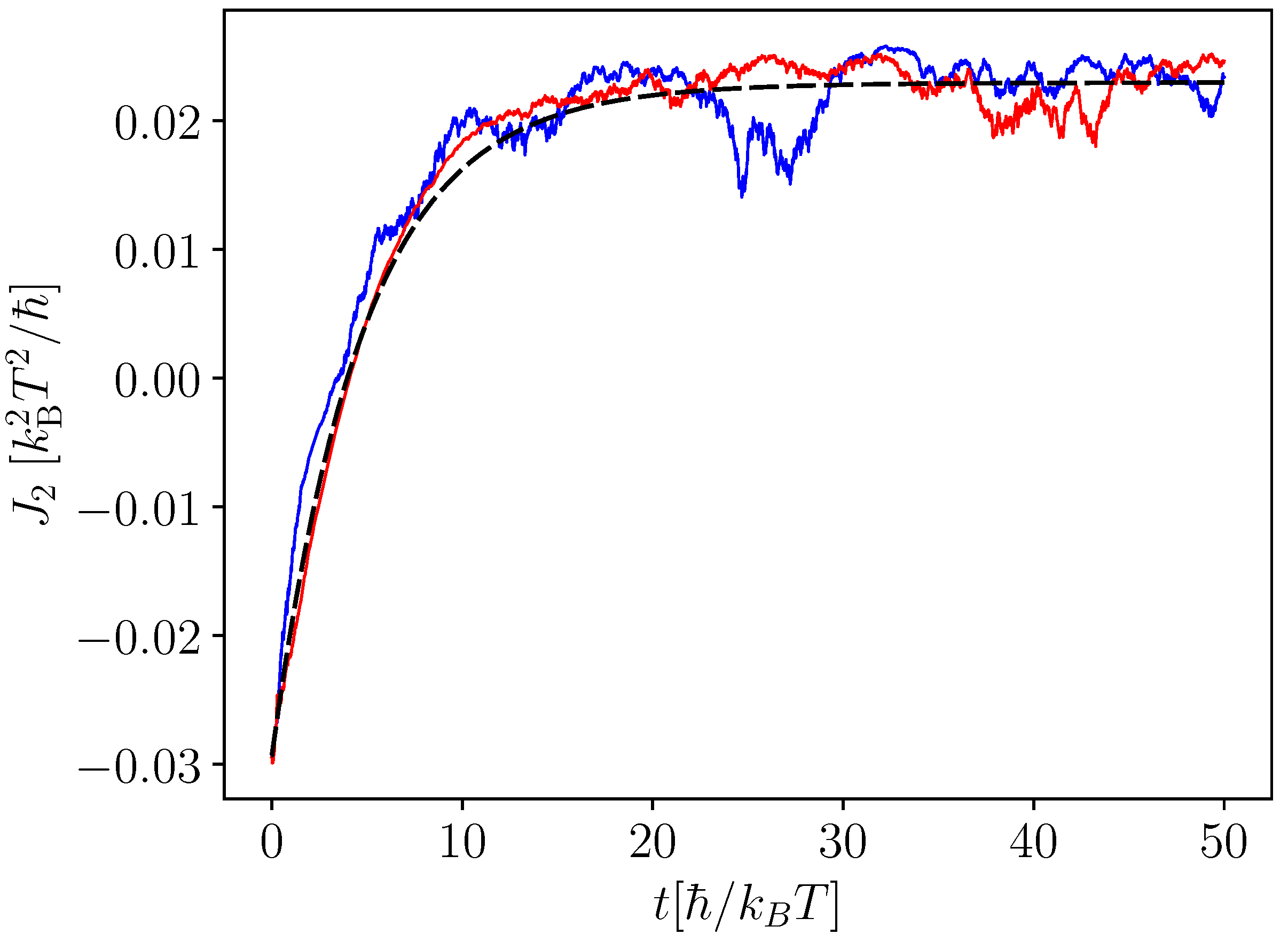
Appendix A. Quantum Master Equation
References
- Pekola, J.P. Towards quantum thermodynamics in electronic circuits. Nat. Phys. 2015, 11, 118. [Google Scholar] [CrossRef] [Green Version]
- Vinjanampathy, S.; Anders, J. Quantum thermodynamics. Contemp. Phys. 2016, 57, 545. [Google Scholar] [CrossRef] [Green Version]
- Benenti, G.; Casati, G.; Saito, K.; Whitney, R.S. Fundamental aspects of steady-state conversion of heat to work at the nanoscale. Phys. Rep. 2017, 694, 1. [Google Scholar] [CrossRef] [Green Version]
- Binder, F.; Correa, L.; Gogolin, C.; Anders, J.; Adesso, G. Thermodynamics in the Quantum Regime: Fundamental Aspects and New Directions; Fundamental Theories of Physics; Springer International Publishing: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Landi, G.T.; Paternostro, M. Irreversible entropy production: From classical to quantum. Rev. Mod. Phys. 2021, 93, 035008. [Google Scholar] [CrossRef]
- Pekola, J.P.; Karimi, B. Colloquium: Quantum heat transport in condensed matter systems. Rev. Mod. Phys. 2021, 93, 041001. [Google Scholar] [CrossRef]
- Koski, J.V.; Maisi, V.F.; Pekola, J.P.; Averin, D.V. Experimental realization of a Szilard engine with a single electron. Proc. Natl. Acad. Sci. USA 2014, 111, 13786–13789. [Google Scholar] [CrossRef] [Green Version]
- Koski, J.V.; Maisi, V.F.; Sagawa, T.; Pekola, J.P. Experimental Observation of the Role of Mutual Information in the Nonequilibrium Dynamics of a Maxwell Demon. Phys. Rev. Lett. 2014, 113, 030601. [Google Scholar] [CrossRef] [Green Version]
- Martínez, I.A.; Roldán, É.; Dinis, L.; Petrov, D.; Parrondo, J.M.; Rica, R.A. Brownian carnot engine. Nat. Phys. 2016, 12, 67. [Google Scholar] [CrossRef]
- Roßnagel, J.; Dawkins, S.T.; Tolazzi, K.N.; Abah, O.; Lutz, E.; Schmidt-Kaler, F.; Singer, K. A single-atom heat engine. Science 2016, 352, 325. [Google Scholar] [CrossRef] [Green Version]
- Ronzani, A.; Karimi, B.; Senior, J.; Chang, Y.C.; Peltonen, J.T.; Chen, C.; Pekola, J.P. Tunable photonic heat transport in a quantum heat valve. Nat. Phys. 2018, 14, 991–995. [Google Scholar] [CrossRef]
- Josefsson, M.; Svilans, A.; Burke, A.M.; Hoffmann, E.A.; Fahlvik, S.; Thelander, C.; Leijnse, M.; Linke, H. A quantum-dot heat engine operating close to the thermodynamic efficiency limits. Nat. Nanotechnol. 2018, 13, 920. [Google Scholar] [CrossRef] [Green Version]
- Prete, D.; Erdman, P.A.; Demontis, V.; Zannier, V.; Ercolani, D.; Sorba, L.; Beltram, F.; Rossella, F.; Taddei, F.; Roddaro, S. Thermoelectric conversion at 30 K in InAs/InP nanowire quantum dots. Nano Lett. 2019, 19, 3033–3039. [Google Scholar] [CrossRef] [Green Version]
- Maillet, O.; Erdman, P.A.; Cavina, V.; Bhandari, B.; Mannila, E.T.; Peltonen, J.T.; Mari, A.; Taddei, F.; Jarzynski, C.; Giovannetti, V.; et al. Optimal Probabilistic Work Extraction beyond the Free Energy Difference with a Single-Electron Device. Phys. Rev. Lett. 2019, 122, 150604. [Google Scholar] [CrossRef] [Green Version]
- Senior, J.; Gubaydullin, A.; Karimi, B.; Peltonen, J.T.; Ankerhold, J.; Pekola, J.P. Heat rectification via a superconducting artificial atom. Commun. Phys. 2020, 3, 40. [Google Scholar] [CrossRef] [Green Version]
- Scovil, H.E.D.; Schulz-DuBois, E.O. Three-Level Masers as Heat Engines. Phys. Rev. Lett. 1959, 2, 262–263. [Google Scholar] [CrossRef]
- Geusic, J.E.; Schulz-DuBios, E.O.; Scovil, H.E.D. Quantum Equivalent of the Carnot Cycle. Phys. Rev. 1967, 156, 343–351. [Google Scholar] [CrossRef]
- Alicki, R. The quantum open system as a model of the heat engine. J. Phys. A Math. Gen. 1979, 12, L103–L107. [Google Scholar] [CrossRef]
- Pendry, J.B. Quantum limits to the flow of information and entropy. J. Phys. A Math. Gen. 1983, 16, 2161. [Google Scholar] [CrossRef] [Green Version]
- Geva, E.; Kosloff, R. On the classical limit of quantum thermodynamics in finite time. J. Chem. Phys. 1992, 97, 4398–4412. [Google Scholar] [CrossRef] [Green Version]
- Allahverdyan, A.E.; Nieuwenhuizen, T.M. Extraction of Work from a Single Thermal Bath in the Quantum Regime. Phys. Rev. Lett. 2000, 85, 1799–1802. [Google Scholar] [CrossRef]
- Schwab, K.; Henriksen, E.; Worlock, J.; Roukes, M.L. Measurement of the quantum of thermal conductance. Nature 2000, 404, 974. [Google Scholar] [CrossRef] [PubMed]
- Kieu, T.D. The Second Law, Maxwell’s Demon, and Work Derivable from Quantum Heat Engines. Phys. Rev. Lett. 2004, 93, 140403. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Meschke, M.; Guichard, W.; Pekola, J.P. Single-mode heat conduction by photons. Nature 2006, 444, 187. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pekola, J.P.; Hekking, F.W.J. Normal-Metal-Superconductor Tunnel Junction as a Brownian Refrigerator. Phys. Rev. Lett. 2007, 98, 210604. [Google Scholar] [CrossRef] [Green Version]
- Blickle, V.; Bechinger, C. Realization of a micrometre-sized stochastic heat engine. Nat. Phys. 2012, 8, 143. [Google Scholar] [CrossRef] [Green Version]
- Horodecki, M.; Oppenheim, J. Fundamental limitations for quantum and nanoscale thermodynamics. Nat. Commun. 2013, 4, 2059. [Google Scholar] [CrossRef] [Green Version]
- Koski, J.; Sagawa, T.; Saira, O.; Yoon, Y.; Kutvonen, A.; Solinas, P.; Möttönen, M.; Ala-Nissila, T.; Pekola, J. Distribution of entropy production in a single-electron box. Nat. Phys. 2013, 9, 644. [Google Scholar] [CrossRef] [Green Version]
- Brantut, J.P.; Grenier, C.; Meineke, J.; Stadler, D.; Krinner, S.; Kollath, C.; Esslinger, T.; Georges, A. A thermoelectric heat engine with ultracold atoms. Science 2013, 342, 713. [Google Scholar] [CrossRef] [Green Version]
- Thierschmann, H.; Sánchez, R.; Sothmann, B.; Arnold, F.; Heyn, C.; Hansen, W.; Buhmann, H.; Molenkamp, L.W. Three-terminal energy harvester with coupled-quantum dots. Nat. Nanotechnol. 2015, 10, 854. [Google Scholar] [CrossRef]
- Campisi, M.; Fazio, R. The power of a critical heat engine. Nat. Commun. 2016, 7, 11895. [Google Scholar] [CrossRef]
- Partanen, M.; Tan, K.Y.; Govenius, J.; Lake, R.E.; Mäkelä, M.K.; Tanttu, T.; Möttönen, M. Quantum-limited heat conduction over macroscopic distances. Nat. Phys. 2016, 12, 460–464. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kosloff, R.; Rezek, Y. The Quantum Harmonic Otto Cycle. Entropy 2017, 19, 136. [Google Scholar] [CrossRef] [Green Version]
- Tan, K.Y.; Partanen, M.; Lake, R.E.; Govenius, J.; Masuda, S.; Möttönen, M. Quantum-circuit refrigerator. Nat. Commun. 2017, 8, 1. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Marchegiani, G.; Virtanen, P.; Giazotto, F. On-chip cooling by heating with superconducting tunnel junctions. EPL (Europhys. Lett.) 2018, 124, 48005. [Google Scholar] [CrossRef] [Green Version]
- Erdman, P.A.; Bhandari, B.; Fazio, R.; Pekola, J.P.; Taddei, F. Absorption refrigerators based on Coulomb-coupled single-electron systems. Phys. Rev. B 2018, 98, 045433. [Google Scholar] [CrossRef] [Green Version]
- Bhandari, B.; Fazio, R.; Taddei, F.; Arrachea, L. From nonequilibrium Green’s functions to quantum master equations for the density matrix and out-of-time-order correlators: Steady-state and adiabatic dynamics. Phys. Rev. B 2021, 104, 035425. [Google Scholar] [CrossRef]
- Bhandari, B.; Jordan, A.N. Minimal two-body quantum absorption refrigerator. Phys. Rev. B 2021, 104, 075442. [Google Scholar] [CrossRef]
- Terrén Alonso, P.; Abiuso, P.; Perarnau-Llobet, M.; Arrachea, L. Geometric Optimization of Nonequilibrium Adiabatic Thermal Machines and Implementation in a Qubit System. PRX Quantum 2022, 3, 010326. [Google Scholar] [CrossRef]
- Hajiloo, F.; Sánchez, R.; Whitney, R.S.; Splettstoesser, J. Quantifying nonequilibrium thermodynamic operations in a multiterminal mesoscopic system. Phys. Rev. B 2020, 102, 155405. [Google Scholar] [CrossRef]
- Juergens, S.; Haupt, F.; Moskalets, M.; Splettstoesser, J. Thermoelectric performance of a driven double quantum dot. Phys. Rev. B 2013, 87, 245423. [Google Scholar] [CrossRef]
- Erdman, P.A.; Cavina, V.; Fazio, R.; Taddei, F.; Giovannetti, V. Maximum power and corresponding efficiency for two-level heat engines and refrigerators: Optimality of fast cycles. New J. Phys. 2019, 21, 103049. [Google Scholar] [CrossRef] [Green Version]
- Brandner, K.; Saito, K. Thermodynamic Geometry of Microscopic Heat Engines. Phys. Rev. Lett. 2020, 124, 040602. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bhandari, B.; Alonso, P.T.; Taddei, F.; von Oppen, F.; Fazio, R.; Arrachea, L. Geometric properties of adiabatic quantum thermal machines. Phys. Rev. B 2020, 102, 155407. [Google Scholar] [CrossRef]
- Abiuso, P.; Perarnau-Llobet, M. Optimal Cycles for Low-Dissipation Heat Engines. Phys. Rev. Lett. 2020, 124, 110606. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Erdman, P.A.; Noé, F. Identifying optimal cycles in quantum thermal machines with reinforcement-learning. Npj Quantum Inf. 2022, 8, 1–11. [Google Scholar] [CrossRef]
- Wiseman, H.M.; Milburn, G.J. Quantum Measurement and Control; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Jacobs, K. Quantum Measurement Theory and Its Applications; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Biele, R.; Rodríguez-Rosario, C.A.; Frauenheim, T.; Rubio, A. Controlling heat and particle currents in nanodevices by quantum observation. Npj Quant. Mater. 2017, 2, 38. [Google Scholar] [CrossRef] [Green Version]
- Buffoni, L.; Solfanelli, A.; Verrucchi, P.; Cuccoli, A.; Campisi, M. Quantum Measurement Cooling. Phys. Rev. Lett. 2019, 122, 070603. [Google Scholar] [CrossRef] [Green Version]
- Caves, C.M.; Milburn, G.J. Quantum-mechanical model for continuous position measurements. Phys. Rev. A 1987, 36, 5543–5555. [Google Scholar] [CrossRef] [Green Version]
- Weber, S.; Chantasri, A.; Dressel, J.; Jordan, A.N.; Murch, K.; Siddiqi, I. Mapping the optimal route between two quantum states. Nature 2014, 511, 570–573. [Google Scholar] [CrossRef] [Green Version]
- Dressel, J.; Chantasri, A.; Jordan, A.N.; Korotkov, A.N. Arrow of time for continuous quantum measurement. Phys. Rev. Lett. 2017, 119, 220507. [Google Scholar] [CrossRef]
- Lewalle, P.; Chantasri, A.; Jordan, A.N. Prediction and characterization of multiple extremal paths in continuously monitored qubits. Phys. Rev. A 2017, 95, 042126. [Google Scholar] [CrossRef] [Green Version]
- Monroe, J.T.; Yunger Halpern, N.; Lee, T.; Murch, K.W. Weak Measurement of a Superconducting Qubit Reconciles Incompatible Operators. Phys. Rev. Lett. 2021, 126, 100403. [Google Scholar] [CrossRef] [PubMed]
- Maruyama, K.; Nori, F.; Vedral, V. Colloquium: The physics of Maxwell’s demon and information. Rev. Mod. Phys. 2009, 81, 1–23. [Google Scholar] [CrossRef] [Green Version]
- Cottet, N.; Jezouin, S.; Bretheau, L.; Campagne-Ibarcq, P.; Ficheux, Q.; Anders, J.; Auffèves, A.; Azouit, R.; Rouchon, P.; Huard, B. Observing a quantum Maxwell demon at work. Proc. Natl. Acad. Sci. USA 2017, 114, 7561–7564. [Google Scholar] [CrossRef] [Green Version]
- Jacobs, K. Quantum measurement and the first law of thermodynamics: The energy cost of measurement is the work value of the acquired information. Phys. Rev. E 2012, 86, 040106. [Google Scholar] [CrossRef] [Green Version]
- Naghiloo, M.; Tan, D.; Harrington, P.M.; Alonso, J.J.; Lutz, E.; Romito, A.; Murch, K.W. Heat and Work Along Individual Trajectories of a Quantum Bit. Phys. Rev. Lett. 2020, 124, 110604. [Google Scholar] [CrossRef] [Green Version]
- Jayaseelan, M.; Manikandan, S.K.; Jordan, A.N.; Bigelow, N.P. Quantum measurement arrow of time and fluctuation relations for measuring spin of ultracold atoms. Nat. Commun. 2021, 12, 1847. [Google Scholar] [CrossRef]
- Bresque, L.; Camati, P.A.; Rogers, S.; Murch, K.; Jordan, A.N.; Aufféves, A. Two-Qubit Engine Fueled by Entanglement and Local Measurements. Phys. Rev. Lett. 2021, 126, 120605. [Google Scholar] [CrossRef]
- Manikandan, S.K.; Elouard, C.; Murch, K.W.; Auffèves, A.; Jordan, A.N. Efficiently fueling a quantum engine with incompatible measurements. Phys. Rev. E 2022, 105, 044137. [Google Scholar] [CrossRef]
- Yanik, K.; Bhandari, B.; Manikandan, S.K.; Jordan, A.N. Thermodynamics of quantum measurement and Maxwell’s demon’s arrow of time. Phys. Rev. A 2022, 106, 042221. [Google Scholar] [CrossRef]
- Bhandari, B.; Jordan, A.N. Continuous measurement boosted adiabatic quantum thermal machines. Phys. Rev. Res. 2022, 4, 033103. [Google Scholar] [CrossRef]
- Yamamoto, T.; Tokura, Y.; Kato, T. Heat transport through a two-level system under continuous quantum measurement. Phys. Rev. B 2022, 106, 205419. [Google Scholar] [CrossRef]
- Pekola, J.P.; Golubev, D.S.; Averin, D.V. Maxwell’s demon based on a single qubit. Phys. Rev. B 2016, 93, 024501. [Google Scholar] [CrossRef] [Green Version]
- Elouard, C.; Herrera-Martí, D.; Huard, B.; Auffeves, A. Extracting work from quantum measurement in Maxwell’s demon engines. Phys. Rev. Lett. 2017, 118, 260603. [Google Scholar] [CrossRef] [Green Version]
- Miller, H.J.D.; Guarnieri, G.; Mitchison, M.T.; Goold, J. Quantum Fluctuations Hinder Finite-Time Information Erasure near the Landauer Limit. Phys. Rev. Lett. 2020, 125, 160602. [Google Scholar] [CrossRef]
- Johnson, M.A.I.; Madzik, M.T.; Hudson, F.E.; Itoh, K.M.; Jakob, A.M.; Jamieson, D.N.; Dzurak, A.; Morello, A. Beating the Thermal Limit of Qubit Initialization with a Bayesian Maxwell’s Demon. Phys. Rev. X 2022, 12, 041008. [Google Scholar] [CrossRef]
- Annby-Andersson, B.; Samuelsson, P.; Maisi, V.F.; Potts, P.P. Maxwell’s demon in a double quantum dot with continuous charge detection. Phys. Rev. B 2020, 101, 165404. [Google Scholar] [CrossRef] [Green Version]
- Jacobs, K. Second law of thermodynamics and quantum feedback control: Maxwell’s demon with weak measurements. Phys. Rev. A 2009, 80, 012322. [Google Scholar] [CrossRef] [Green Version]
- Yi, J.; Talkner, P.; Kim, Y.W. Single-temperature quantum engine without feedback control. Phys. Rev. E 2017, 96, 022108. [Google Scholar] [CrossRef] [Green Version]
- Chand, S.; Biswas, A. Measurement-induced operation of two-ion quantum heat machines. Phys. Rev. E 2017, 95, 032111. [Google Scholar] [CrossRef]
- Chand, S.; Biswas, A. Critical-point behavior of a measurement-based quantum heat engine. Phys. Rev. E 2018, 98, 052147. [Google Scholar] [CrossRef] [Green Version]
- Ding, X.; Yi, J.; Kim, Y.W.; Talkner, P. Measurement-driven single temperature engine. Phys. Rev. E 2018, 98, 042122. [Google Scholar] [CrossRef] [Green Version]
- Solfanelli, A.; Buffoni, L.; Cuccoli, A.; Campisi, M. Maximal energy extraction via quantum measurement. J. Stat. Mech. Theory Exp. 2019, 2019, 094003. [Google Scholar] [CrossRef] [Green Version]
- Das, A.; Ghosh, S. Measurement based quantum heat engine with coupled working medium. Entropy 2019, 21, 1131. [Google Scholar] [CrossRef] [Green Version]
- Debarba, T.; Manzano, G.; Guryanova, Y.; Huber, M.; Friis, N. Work estimation and work fluctuations in the presence of non-ideal measurements. New J. Phys. 2019, 21, 113002. [Google Scholar] [CrossRef] [Green Version]
- Seah, S.; Nimmrichter, S.; Scarani, V. Maxwell’s Lesser Demon: A Quantum Engine Driven by Pointer Measurements. Phys. Rev. Lett. 2020, 124, 100603. [Google Scholar] [CrossRef] [Green Version]
- Hasegawa, Y. Quantum Thermodynamic Uncertainty Relation for Continuous Measurement. Phys. Rev. Lett. 2020, 125, 050601. [Google Scholar] [CrossRef]
- Anka, M.F.; de Oliveira, T.R.; Jonathan, D. Measurement-based quantum heat engine in a multilevel system. Phys. Rev. E 2021, 104, 054128. [Google Scholar] [CrossRef]
- Annby-Andersson, B.; Bakhshinezhad, F.; Bhattacharyya, D.; De Sousa, G.; Jarzynski, C.; Samuelsson, P.; Potts, P.P. Quantum Fokker-Planck Master Equation for Continuous Feedback Control. Phys. Rev. Lett. 2022, 129, 050401. [Google Scholar] [CrossRef]
- Elouard, C.; Jordan, A.N. Efficient Quantum Measurement Engines. Phys. Rev. Lett. 2018, 120, 260601. [Google Scholar] [CrossRef]
- Gherardini, S.; Campaioli, F.; Caruso, F.; Binder, F.C. Stabilizing open quantum batteries by sequential measurements. Phys. Rev. Res. 2020, 2, 013095. [Google Scholar] [CrossRef] [Green Version]
- Yao, Y.; Shao, X.Q. Optimal charging of open spin-chain quantum batteries via homodyne-based feedback control. Phys. Rev. E 2022, 106, 014138. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Liu, Y.X.; Wu, R.B.; Jacobs, K.; Nori, F. Quantum feedback: Theory, experiments, and applications. Phys. Rep. 2017, 679, 1–60. [Google Scholar] [CrossRef] [Green Version]
- Jacobs, K. How to project qubits faster using quantum feedback. Phys. Rev. A 2003, 67, 030301(R). [Google Scholar] [CrossRef] [Green Version]
- Carmichael, H. An Open Systems Approach to Quantum Optics: Lectures Presented at the Université Libre de Bruxelles, October 28 to November 4, 1991; Springer Science & Business Media: Berlin, Germany, 2009; Volume 18. [Google Scholar]
- Murch, K.; Weber, S.; Macklin, C.; Siddiqi, I. Observing single quantum trajectories of a superconducting quantum bit. Nature 2013, 502, 211–214. [Google Scholar] [CrossRef] [Green Version]
- Vijay, R.; Macklin, C.; Slichter, D.; Weber, S.; Murch, K.; Naik, R.; Korotkov, A.N.; Siddiqi, I. Stabilizing Rabi oscillations in a superconducting qubit using quantum feedback. Nature 2012, 490, 77–80. [Google Scholar] [CrossRef] [Green Version]
- Livingston, W.P.; Blok, M.S.; Flurin, E.; Dressel, J.; Jordan, A.N.; Siddiqi, I. Experimental demonstration of continuous quantum error correction. Nat. Commun. 2022, 13, 2307. [Google Scholar] [CrossRef]
- Hekking, F.W.J.; Pekola, J.P. Quantum Jump Approach for Work and Dissipation in a Two-Level System. Phys. Rev. Lett. 2013, 111, 093602. [Google Scholar] [CrossRef] [Green Version]
- Barato, A.C.; Seifert, U. Thermodynamic Uncertainty Relation for Biomolecular Processes. Phys. Rev. Lett. 2015, 114, 158101. [Google Scholar] [CrossRef] [Green Version]
- Gingrich, T.R.; Horowitz, J.M.; Perunov, N.; England, J.L. Dissipation Bounds All Steady-State Current Fluctuations. Phys. Rev. Lett. 2016, 116, 120601. [Google Scholar] [CrossRef]
- Pietzonka, P.; Seifert, U. Universal Trade-Off between Power, Efficiency, and Constancy in Steady-State Heat Engines. Phys. Rev. Lett. 2018, 120, 190602. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Guarnieri, G.; Landi, G.T.; Clark, S.R.; Goold, J. Thermodynamics of precision in quantum nonequilibrium steady states. Phys. Rev. Res. 2019, 1, 033021. [Google Scholar] [CrossRef] [Green Version]
- Timpanaro, A.M.; Guarnieri, G.; Goold, J.; Landi, G.T. Thermodynamic Uncertainty Relations from Exchange Fluctuation Theorems. Phys. Rev. Lett. 2019, 123, 090604. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Falasco, G.; Esposito, M.; Delvenne, J.C. Unifying thermodynamic uncertainty relations. New J. Phys. 2020, 22, 053046. [Google Scholar] [CrossRef]
- Friedman, H.M.; Agarwalla, B.K.; Shein-Lumbroso, O.; Tal, O.; Segal, D. Thermodynamic uncertainty relation in atomic-scale quantum conductors. Phys. Rev. B 2020, 101, 195423. [Google Scholar] [CrossRef]
- Miller, H.J.D.; Mohammady, M.H.; Perarnau-Llobet, M.; Guarnieri, G. Thermodynamic Uncertainty Relation in Slowly Driven Quantum Heat Engines. Phys. Rev. Lett. 2021, 126, 210603. [Google Scholar] [CrossRef]
- Potts, P.P.; Samuelsson, P. Thermodynamic uncertainty relations including measurement and feedback. Phys. Rev. E 2019, 100, 052137. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Campisi, M.; Pekola, J.; Fazio, R. Feedback-controlled heat transport in quantum devices: Theory and solid-state experimental proposal. New J. Phys. 2017, 19, 053027. [Google Scholar] [CrossRef]
- Breuer, H.P.; Petruccione, F. The Theory of Open Quantum Systems; Oxford University Press: Oxford, UK, 2002. [Google Scholar]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bhandari, B.; Czupryniak, R.; Erdman, P.A.; Jordan, A.N. Measurement-Based Quantum Thermal Machines with Feedback Control. Entropy 2023, 25, 204. https://doi.org/10.3390/e25020204
Bhandari B, Czupryniak R, Erdman PA, Jordan AN. Measurement-Based Quantum Thermal Machines with Feedback Control. Entropy. 2023; 25(2):204. https://doi.org/10.3390/e25020204
Chicago/Turabian StyleBhandari, Bibek, Robert Czupryniak, Paolo Andrea Erdman, and Andrew N. Jordan. 2023. "Measurement-Based Quantum Thermal Machines with Feedback Control" Entropy 25, no. 2: 204. https://doi.org/10.3390/e25020204
APA StyleBhandari, B., Czupryniak, R., Erdman, P. A., & Jordan, A. N. (2023). Measurement-Based Quantum Thermal Machines with Feedback Control. Entropy, 25(2), 204. https://doi.org/10.3390/e25020204





