Coarse-Grained Effective Hamiltonian via the Magnus Expansion for a Three-Level System
Abstract
1. Introduction
2. Methods
2.1. Effective Hamiltonian by the Magnus Expansion
2.2. Validation of the Effective Hamiltonian
3. Application to Adiabatic Elimination
3.1. Adiabatic Elimination: Ambiguities and Limitations
- If we add to H a term that is an irrelevant uniform shift of all the energy levels, the procedure yields an that depends on in a non-trivial way. Thus, the procedure is affected by a gauge ambiguity. By comparing the exact numerical result with an analytic approximation based on the resolvent method a “best choice”, has been proposed [13].
- AE completely disregards the state . However, although apparently confining the dynamics to the relevant subspace, the procedure yields that and depend on time. Thus, on the one hand, the approximation misses leakage to ; on the other, it does not guarantee that the normalization of states of the relevant subspace is conserved. In Ref. [14], the problem of normalization is overcome by writing separated differential equations in the relevant and in non-relevant subspaces.
- The residual population in as given by the approximate may undergo very fast oscillations with angular frequency . This is not consistent with the initial assumption that . In Ref. [14], the assumption is supported by arguing that it holds at the coarse-grained level, which averages out the dynamics at time-scales of or faster.
- Standard AE is not a reliable approximation for larger two-photon detunings or larger external pulses, and it is not clear how to systematically improve its validity.
3.2. Magnus Expansion in the Regime of Large Detunings
3.2.1. Comparison of the Results at the Second-Order Level
3.2.2. Higher-Order Effective Hamiltonian
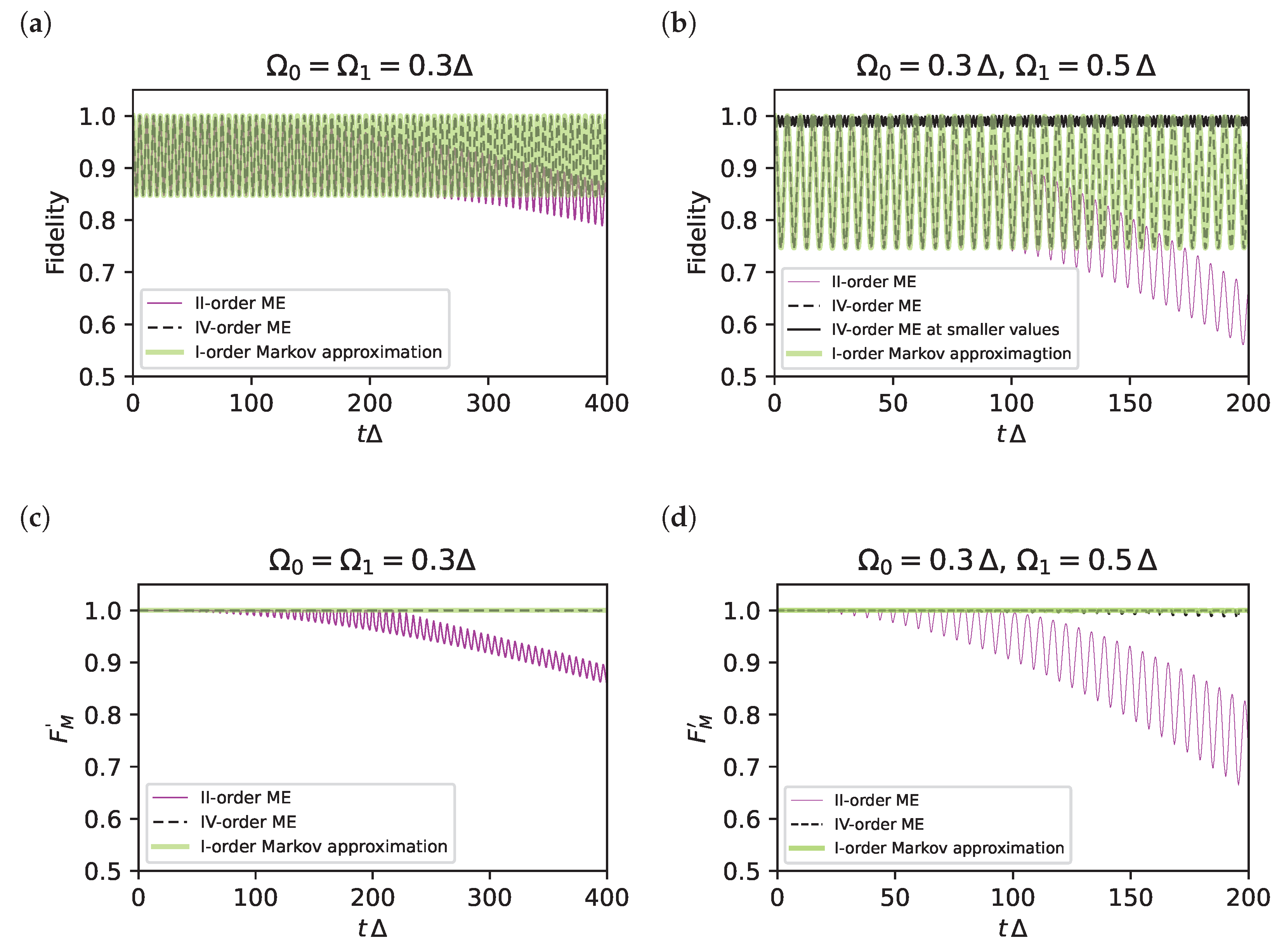
3.2.3. Validation of the Results at Fourth-Order
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ME | Magnus expansion |
| AE | Adiabatic elimination |
Appendix A. More on the ME
Appendix A.1. Third and Fourth-Order Terms
Appendix A.2. Convergence
Appendix A.3. Structure of the Series for the Lambda Hamiltonian
Appendix B. Integrals
References
- Dowling, J.P.; Milburn, G.J. Quantum technology: The second quantum revolution. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 2003, 361, 1655–1674. [Google Scholar] [CrossRef] [PubMed]
- Deutsch, I.H. Harnessing the power of the second quantum revolution. PRX Quantum 2020, 1, 020101. [Google Scholar] [CrossRef]
- Koch, C.P.; Boscain, U.; Calarco, T.; Dirr, G.; Filipp, S.; Glaser, S.J.; Kosloff, R.; Montangero, S.; Schulte-Herbrüggen, T.; Sugny, D.; et al. Quantum Optimal Control in Quantum Technologies. Strategic Report on Current Status, Visions and Goals for Research in Europe. EPJ Quantum Technol. 2022, 9, 19. [Google Scholar] [CrossRef]
- Nielsen, M.A.; Chuang, I. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Gisin, N.; Thew, R. Quantum communication. Nat. Photonics 2007, 1, 165–171. [Google Scholar] [CrossRef]
- Benenti, G.; D’Arrigo, A.; Falci, G. Enhancement of Transmission Rates in Quantum Memory Channels with Damping. Phys. Rev. Lett. 2009, 103, 020502. [Google Scholar] [CrossRef] [PubMed]
- Degen, C.L.; Reinhard, F.; Cappellaro, P. Quantum sensing. Rev. Mod. Phys. 2017, 89, 035002. [Google Scholar] [CrossRef]
- Bongs, K.; Holynski, M.; Vovrosh, J.; Bouyer, P.; Condon, G.; Rasel, E.; Schubert, C.; Schleich, W.P.; Roura, A. Taking atom interferometric quantum sensors from the laboratory to real-world applications. Nat. Rev. Phys. 2019, 1, 731–739. [Google Scholar] [CrossRef]
- Theis, L.; Motzoi, F.; Wilhelm, F. Simultaneous gates in frequency-crowded multilevel systems using fast, robust, analytic control shapes. Phys. Rev. A 2016, 93, 012324. [Google Scholar] [CrossRef]
- Li, B.; Calarco, T.; Motzoi, F. Nonperturbative Analytical Diagonalization of Hamiltonians with Application to Circuit QED. PRX Quantum 2022, 3, 030313. [Google Scholar] [CrossRef]
- Goerz, M.H.; Reich, D.M.; Koch, C.P. Optimal Control Theory for a Unitary Operation under Dissipative Evolution. New J. Phys. 2014, 16, 055012. [Google Scholar] [CrossRef]
- Blanes, S.; Casas, F.; Oteo, J.; Ros, J. The Magnus expansion and some of its applications. Phys. Rep. 2009, 470, 151–238. [Google Scholar] [CrossRef]
- Brion, E.; Pedersen, L.H.; Mølmer, K. Adiabatic elimination in a lambda system. J. Phys. Math. Theor. 2007, 40, 1033–1043. [Google Scholar] [CrossRef]
- Paulisch, V.; Rui, H.; Ng, H.K.; Englert, B.G. Beyond adiabatic elimination: A hierarchy of approximations for multi-photon processes. Eur. Phys. J. Plus 2014, 129, 12. [Google Scholar] [CrossRef]
- Bravyi, S.; DiVincenzo, D.P.; Loss, D. Schrieffer–Wolff transformation for quantum many-body systems. Ann. Phys. 2011, 326, 2793–2826. [Google Scholar] [CrossRef]
- Bukov, M.; Kolodrubetz, M.; Polkovnikov, A. Schrieffer-Wolff transformation for periodically driven systems: Strongly correlated systems with artificial gauge fields. Phys. Rev. Lett. 2016, 116, 125301. [Google Scholar] [CrossRef] [PubMed]
- Blanes, S.; Casas, F.; Oteo, J.; Ros, J. A pedagogical approach to the Magnus expansion. Eur. J. Phys. 2010, 31, 907. [Google Scholar] [CrossRef]
- Petiziol, F.; Arimondo, E.; Giannelli, L.; Mintert, F.; Wimberger, S. Optimized Three-Level Quantum Transfers Based on Frequency-Modulated Optical Excitations. Sci. Rep. 2020, 10, 2185. [Google Scholar] [CrossRef] [PubMed]
- Vandersypen, L.M.; Chuang, I.L. NMR techniques for quantum control and computation. Rev. Mod. Phys. 2005, 76, 1037. [Google Scholar] [CrossRef]
- Zhao, Q.; Zhou, Y.; Shaw, A.F.; Li, T.; Childs, A.M. Hamiltonian simulation with random inputs. arXiv 2021, arXiv:2111.04773. [Google Scholar] [CrossRef]
- An, D.; Fang, D.; Lin, L. Time-dependent unbounded Hamiltonian simulation with vector norm scaling. Quantum 2021, 5, 459. [Google Scholar] [CrossRef]
- Rajput, A.; Roggero, A.; Wiebe, N. Hybridized methods for quantum simulation in the interaction picture. Quantum 2022, 6, 780. [Google Scholar] [CrossRef]
- Haah, J.; Hastings, M.B.; Kothari, R.; Low, G.H. Quantum algorithm for simulating real time evolution of lattice Hamiltonians. SIAM J. Comput. 2021, FOCS18–250. [Google Scholar] [CrossRef]
- Tran, M.C.; Guo, A.Y.; Su, Y.; Garrison, J.R.; Eldredge, Z.; Foss-Feig, M.; Childs, A.M.; Gorshkov, A.V. Locality and digital quantum simulation of power-law interactions. Phys. Rev. X 2019, 9, 031006. [Google Scholar] [CrossRef] [PubMed]
- Berry, D.W.; Childs, A.M.; Su, Y.; Wang, X.; Wiebe, N. Time-dependent Hamiltonian simulation with L1-norm scaling. Quantum 2020, 4, 254. [Google Scholar] [CrossRef]
- Vitanov, N.; Fleischhauer, M.; Shore, B.; Bergmann, K. Coherent manipulation of atoms and molecules by sequential laser pulses. Adv. At. Mol. Opt. Phys. 2001, 46, 55–190. [Google Scholar] [CrossRef]
- Falci, G.; Di Stefano, P.; Ridolfo, A.; D’Arrigo, A.; Paraoanu, G.; Paladino, E. Advances in quantum control of three-level superconducting circuit architectures. Fort. Phys. 2017, 65, 1600077. [Google Scholar] [CrossRef]
- Vitanov, N.V.; Rangelov, A.A.; Shore, B.W.; Bergmann, K. Stimulated Raman adiabatic passage in physics, chemistry, and beyond. Rev. Mod. Phys. 2017, 89, 015006. [Google Scholar] [CrossRef]
- Siewert, J.; Brandes, T.; Falci, G. Advanced control with a Cooper-pair box: Stimulated Raman adiabatic passage and Fock-state generation in a nanomechanical resonator. Phys. Rev. B 2009, 79, 024504. [Google Scholar] [CrossRef]
- Falci, G.; Ridolfo, A.; Di Stefano, P.; Paladino, E. Ultrastrong coupling probed by Coherent Population Transfer. Sci. Rep. 2019, 9, 9249. [Google Scholar] [CrossRef] [PubMed]
- Di Stefano, P.G.; Paladino, E.; D’Arrigo, A.; Falci, G. Population transfer in a Lambda system induced by detunings. Phys. Rev. B 2015, 91, 224506. [Google Scholar] [CrossRef]
- Zeuch, D.; Hassler, F.; Slim, J.J.; DiVincenzo, D.P. Exact rotating wave approximation. Ann. Phys. 2020, 423, 168327. [Google Scholar] [CrossRef]
- Burgarth, D.; Facchi, P.; Nakazato, H.; Pascazio, S.; Yuasa, K. Eternal adiabaticity in quantum evolution. Phys. Rev. A 2021, 103, 032214. [Google Scholar] [CrossRef]
- Burgarth, D.; Facchi, P.; Gramegna, G.; Yuasa, K. One bound to rule them all: From Adiabatic to Zeno. Quantum 2022, 6, 737. [Google Scholar] [CrossRef]
- Vepsäläinen, A.; Danilin, S.; Paladino, E.; Falci, G.; Paraoanu, G.S. Quantum Control in Qutrit Systems Using Hybrid Rabi-STIRAP Pulses. Photonics 2016, 3, 62. [Google Scholar] [CrossRef]
- Earnest, N.; Chakram, S.; Lu, Y.; Irons, N.; Naik, R.K.; Leung, N.; Ocola, L.; Czaplewski, D.A.; Baker, B.; Lawrence, J.; et al. Realization of a Lambda System with Metastable States of a Capacitively Shunted Fluxonium. Phys. Rev. Lett. 2018, 120, 150504. [Google Scholar] [CrossRef]
- Hays, M.; Fatemi, V.; Bouman, D.; Cerrillo, J.; Diamond, S.; Serniak, K.; Connolly, T.; Krogstrup, P.; Nygård, J.; Levy Yeyati, A.; et al. Coherent manipulation of an Andreev spin qubit. Science 2021, 373, 430–433. [Google Scholar] [CrossRef]
- Pellegrino, F.; Falci, G.; Paladino, E. 1/f critical current noise in short ballistic graphene Josephson junctions. Commun. Phys. 2020, 3, 6. [Google Scholar] [CrossRef]
- Di Stefano, P.; Paladino, E.; Pope, T.; Falci, G. Coherent manipulation of noise-protected superconducting artificial atoms in the Lambda scheme. Phys. Rev. A 2016, 93, 051801. [Google Scholar] [CrossRef]
- Brown, J.; Sgroi, P.; Giannelli, L.; Paraoanu, G.S.; Paladino, E.; Falci, G.; Paternostro, M.; Ferraro, A. Reinforcement learning-enhanced protocols for coherent population-transfer in three-level quantum systems. N. J. Phys. 2021, 23, 093035. [Google Scholar] [CrossRef]
- Giannelli, L.; Sgroi, P.; Brown, J.; Paraoanu, G.S.; Paternostro, M.; Paladino, E.; Falci, G. A tutorial on optimal control and reinforcement learning methods for quantum technologies. Phys. Lett. A 2022, 2022, 128054. [Google Scholar] [CrossRef]
- Casas, F. Sufficient conditions for the convergence of the Magnus expansion. J. Phys. Math. Theor. 2007, 40, 15001. [Google Scholar] [CrossRef]
- Brinkmann, A. Introduction to average Hamiltonian theory. I. Basics. Concepts Magn. Reson. Part A 2016, 45, e21414. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Macrì, N.; Giannelli, L.; Paladino, E.; Falci, G. Coarse-Grained Effective Hamiltonian via the Magnus Expansion for a Three-Level System. Entropy 2023, 25, 234. https://doi.org/10.3390/e25020234
Macrì N, Giannelli L, Paladino E, Falci G. Coarse-Grained Effective Hamiltonian via the Magnus Expansion for a Three-Level System. Entropy. 2023; 25(2):234. https://doi.org/10.3390/e25020234
Chicago/Turabian StyleMacrì, Nicola, Luigi Giannelli, Elisabetta Paladino, and Giuseppe Falci. 2023. "Coarse-Grained Effective Hamiltonian via the Magnus Expansion for a Three-Level System" Entropy 25, no. 2: 234. https://doi.org/10.3390/e25020234
APA StyleMacrì, N., Giannelli, L., Paladino, E., & Falci, G. (2023). Coarse-Grained Effective Hamiltonian via the Magnus Expansion for a Three-Level System. Entropy, 25(2), 234. https://doi.org/10.3390/e25020234






