Robust Superpixel Segmentation for Hyperspectral-Image Restoration
Abstract
:1. Introduction
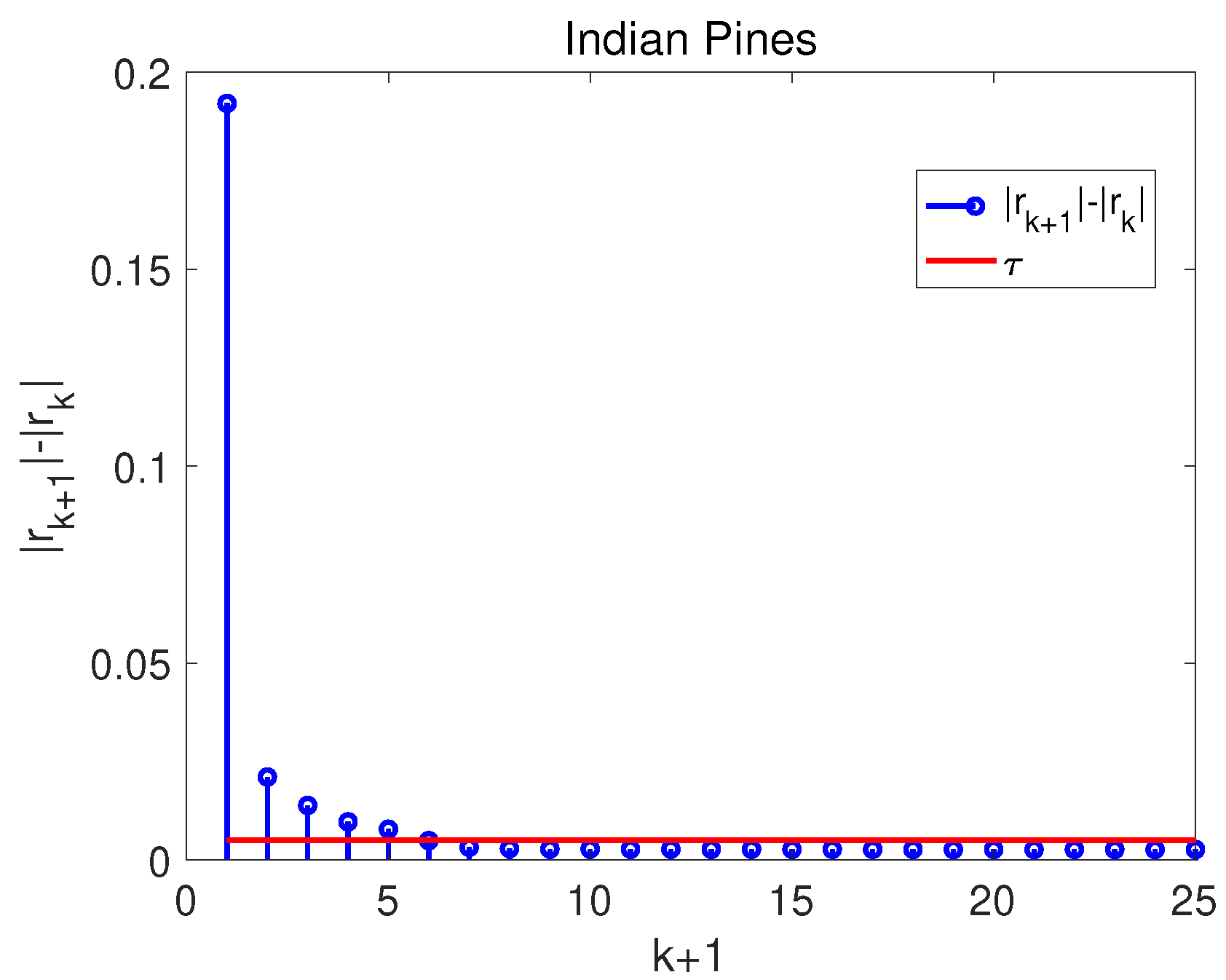
- Combining the superpixel segmentation with principal component analysis, we propose a robust superpixel segmentation strategy to better divide the HSI. A “first small jump” scheme in the robust superpixel segmentation is devised to select the PCs. The selected PCs include most of the important information of the HSI. The superpixel segmentation result based on the selected PCs is relatively accurate.
- The weighted nuclear norm is used to characterize the low-rank attribute of superpixel fibers. In particular, we summarize the weighted nuclear norm by three types of weighting in the HSI restoration model.
- The alternating direction method (ADM) is used to solve the weighted-nuclear-norm-based HSI restoration model, and the corresponding iterative optimization process is derived. We adopt three operators in one frame to solve the subproblem with the weighted nuclear norm. The experimental results obtained by different operators are displayed.
2. Materials and Methods
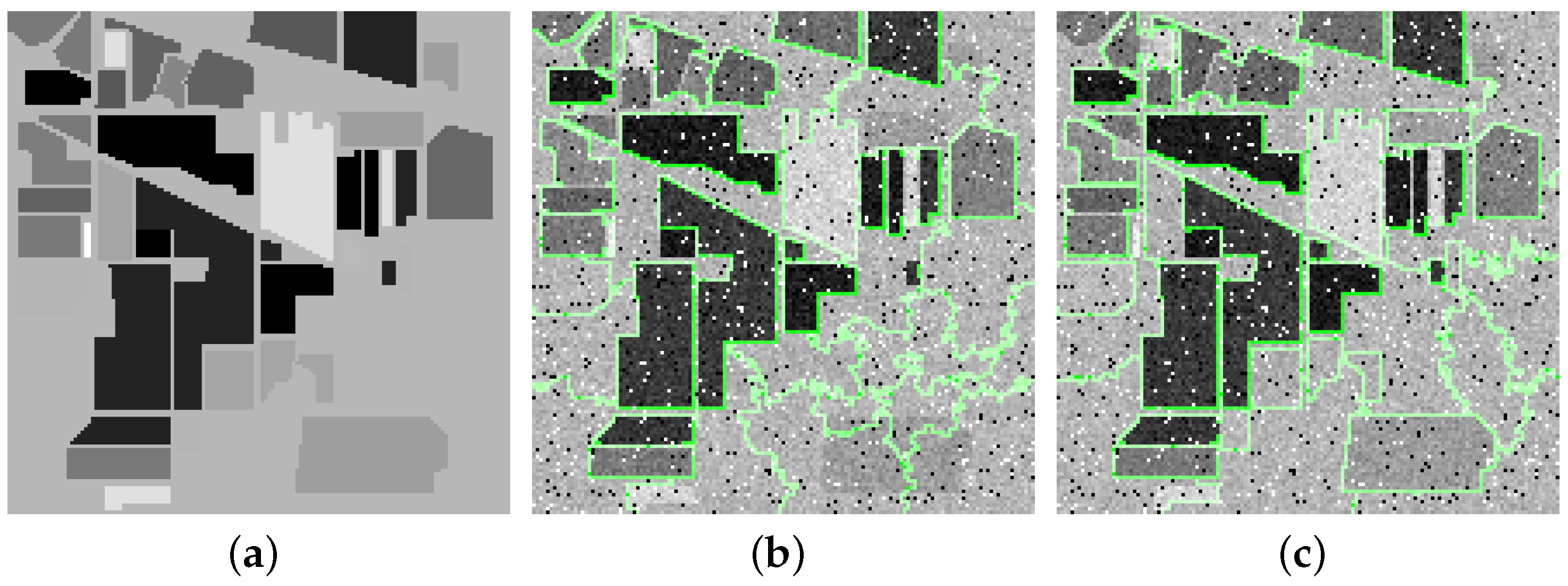
2.1. Robust Superpixel Segmentation
2.2. The HSI Restoration Model Based on Low-Rank Superpixel Fiber
- . is non-negative, where is a constant and is to avoid dividing by zero.
- . The weighted nuclear norm is reduced to the standard nuclear norm, i.e., .
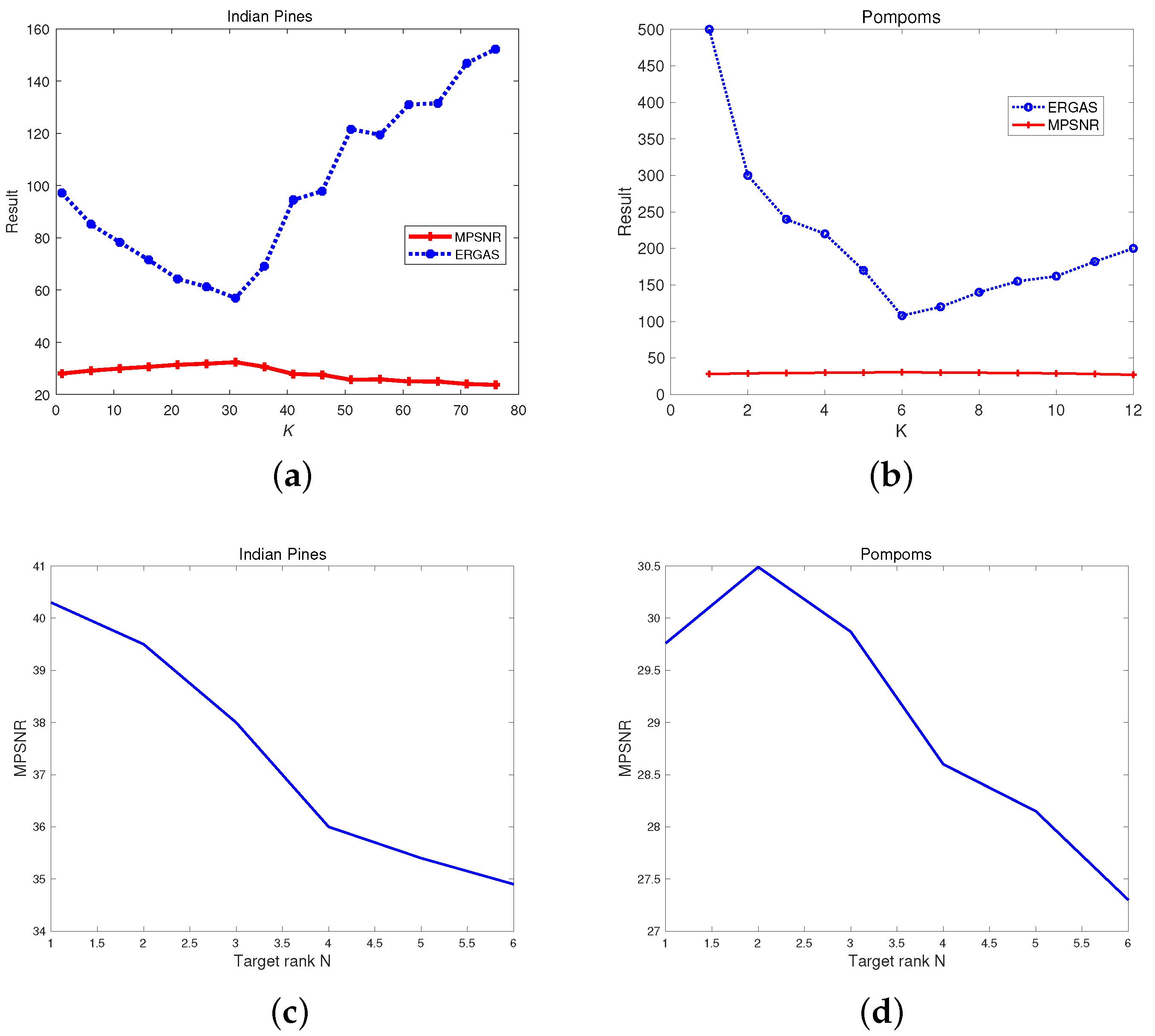
- . The weighted nuclear norm becomes the partial sum of singular values, i.e.,where N is the target rank of matrix [34].
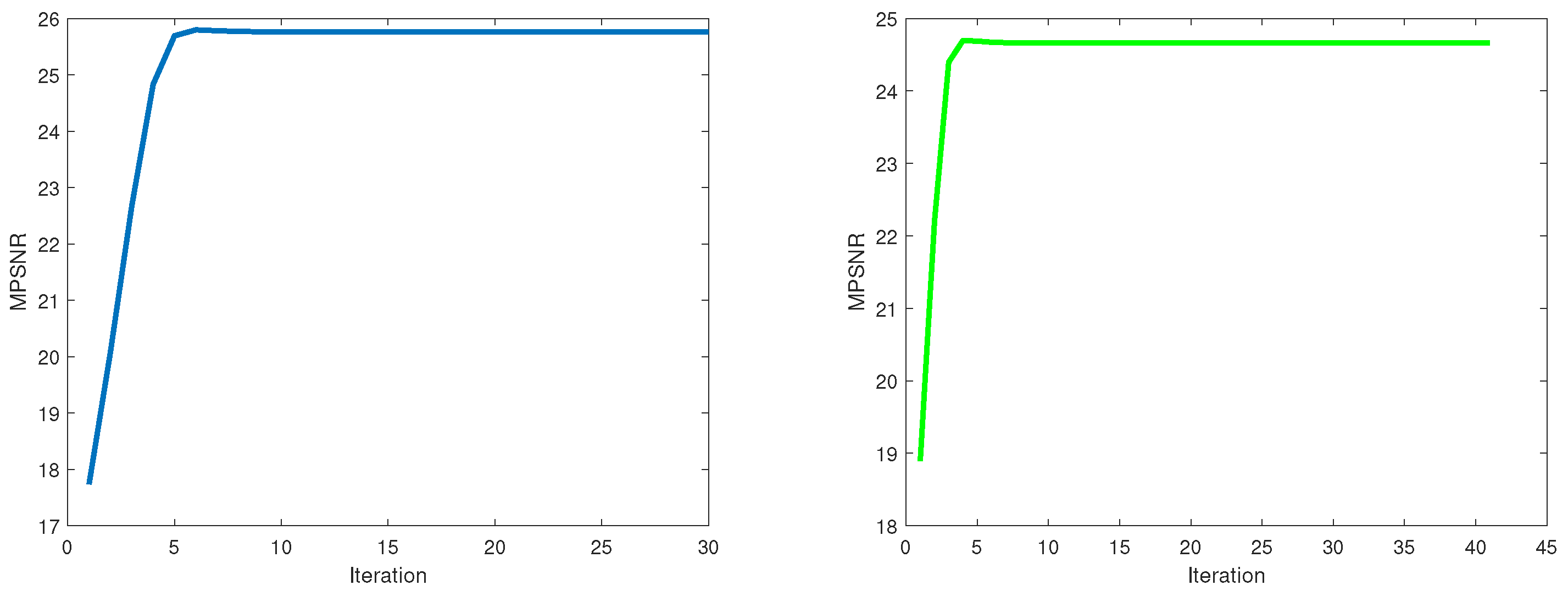
3. Optimization Algorithm
- For ,wherewhere is the singular value decomposition (SVD) of matrix and . is the weighted singular value thresholding (WSVT) operator [33].
- Forwherewhere is an identity matrix with the same size of . is the operator to solve standard nuclear norm.
- For andwherewhereis the partial singular value thresholding (PSVT) operator [34].
| Algorithm 1: The HSI restoration algorithm based on low-rank superpixel fiber |
| Input: the observed HSI y, the number of superpixel fibers K, the target rank N; |
| Output: the restored HSI x and the sparse noise e; |
| 1. Divide y by robust superpixel segmentation into K superpixel fibers |
| and vectorize them as K matrices , like Figure 1; |
| 2. For do |
| Initialize: , , parameters , ; |
| 3. Repeat |
| ; |
| or ; |
| or ; |
| ; |
| ; |
| Until convergence criterion is satisfied; |
| 4. Return , ; |
| End |
| 5. Merge all into the restored HSI x. |
4. Experiments
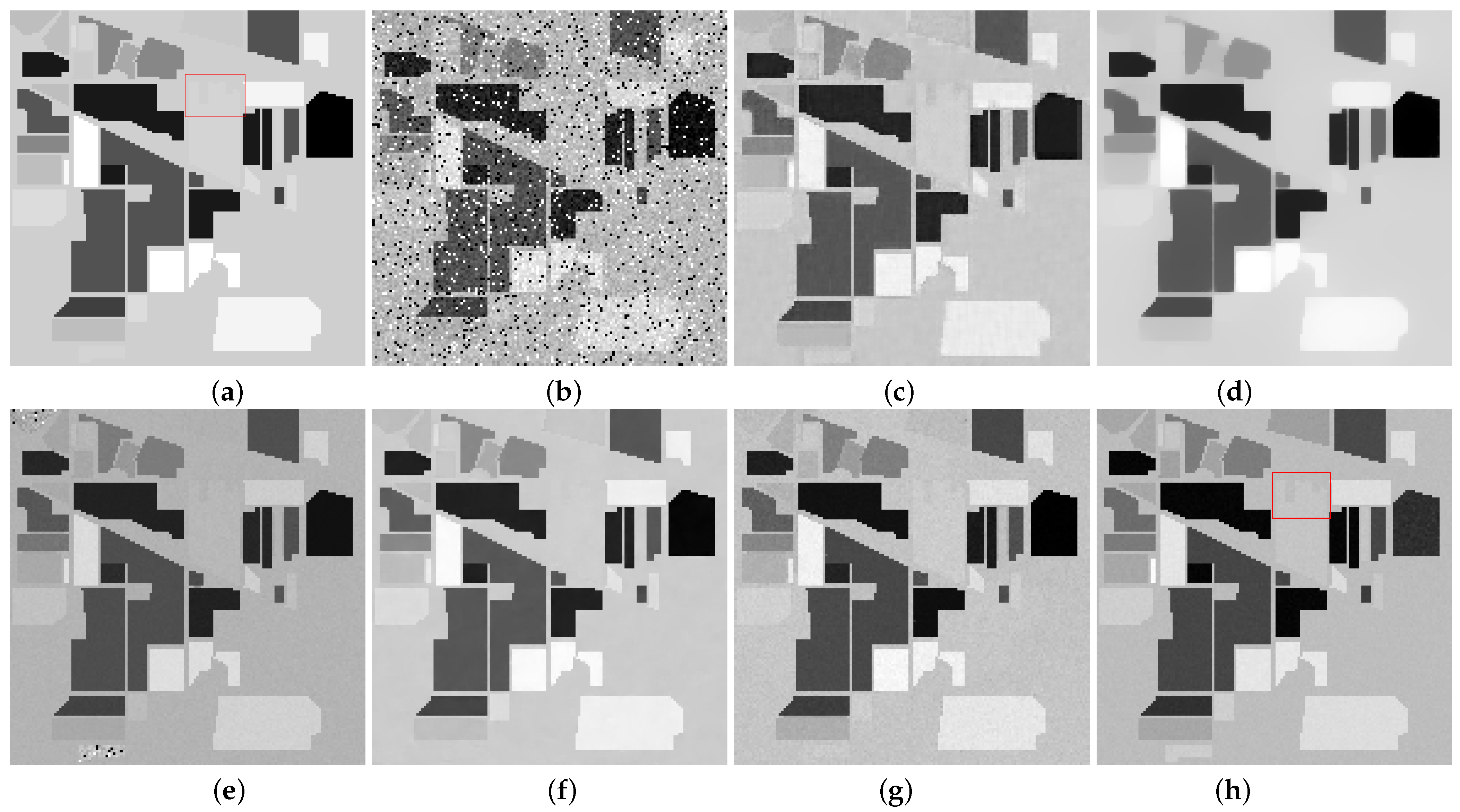
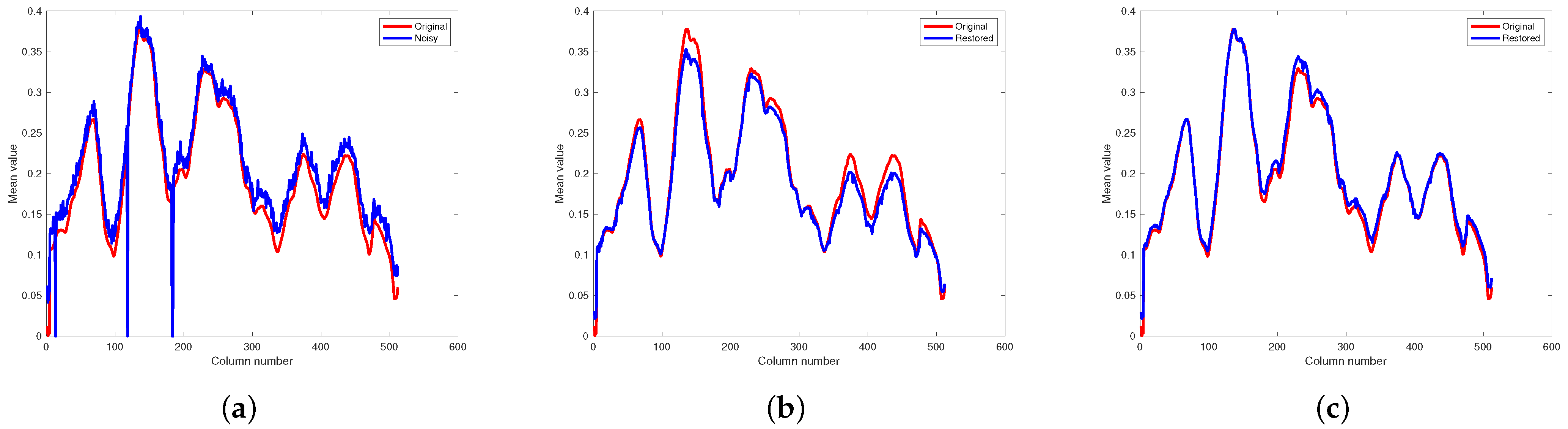
4.1. Simulation Experiment
- Case 1:
- (Gaussian Noise + Impulse Noise) Both Gaussian noise with the variance of 0.1 and impulse noise with the percentage of 0.1 are added to the Indian Pines data.
- Case 2:
- (Gaussian Noise + Impulse Noise + Dead Lines) Both Gaussian noise with the variance of 0.1, impulse noise with the percentage of 0.1, and dead lines from band 10 to band 25 are added into pompoms data.
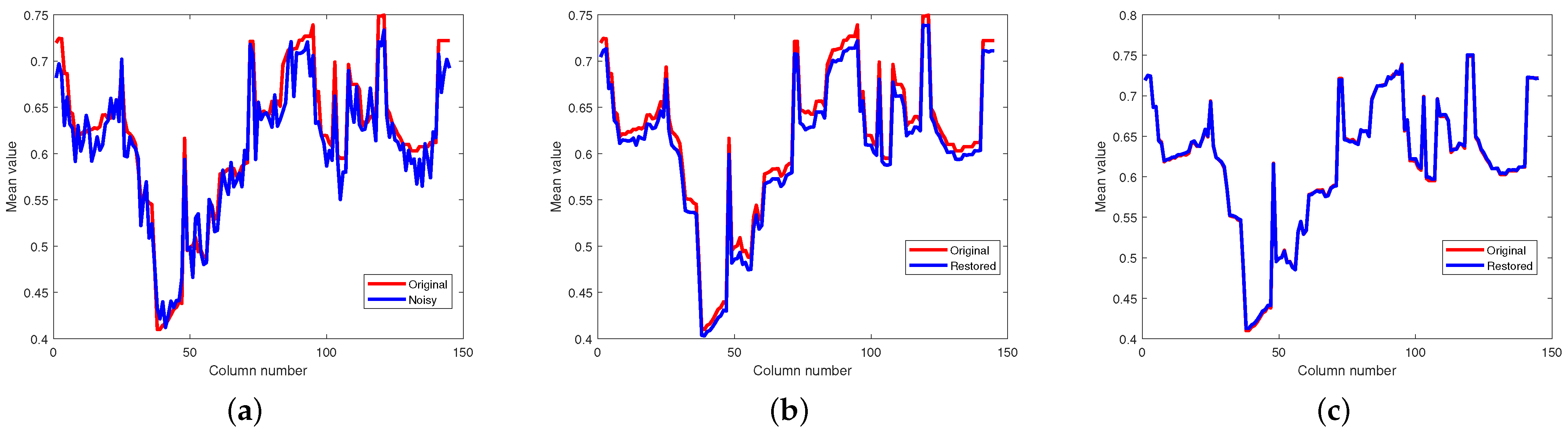
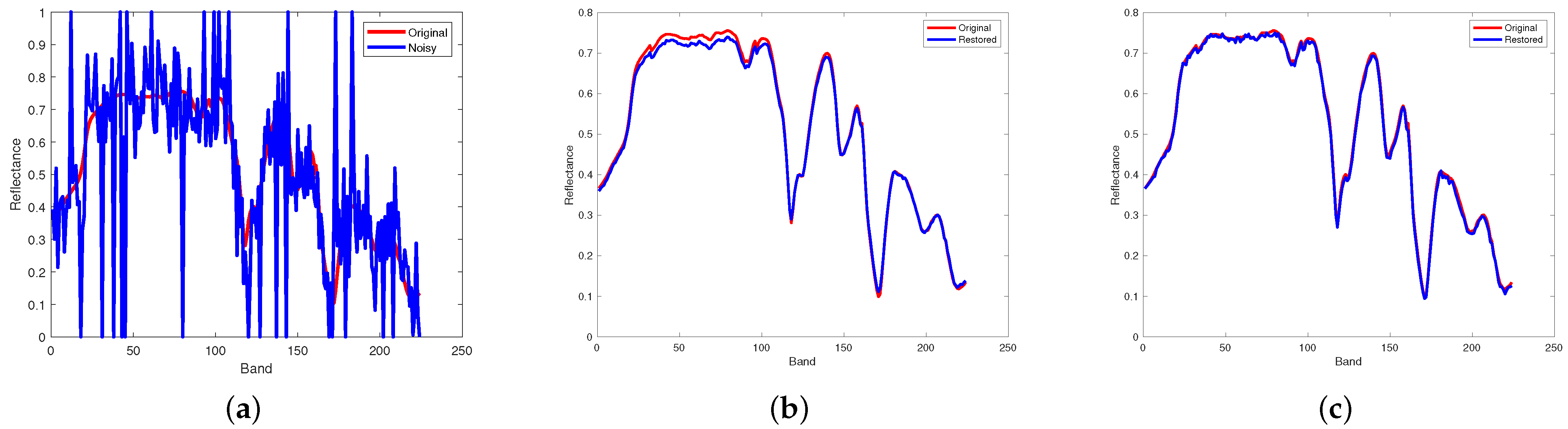
4.2. Real Data Experiment
5. Discussion
6. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Luo, F.; Zhang, L.; Du, B.; Zhang, L. Dimensionality reduction with enhanced hybrid-graph discriminant learning for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2020, 58, 5336–5353. [Google Scholar] [CrossRef]
- Dong, Y.; Liang, T.; Zhang, Y.; Du, B. Spectral-spatial weighted kernel manifold embedded distribution alignment for remote sensing image classification. IEEE Trans. Cybern. 2020, 51, 3185–3197. [Google Scholar] [CrossRef] [PubMed]
- Hong, D.; Yokoya, N.; Nan, G.; Chanussot, J.; Xiao, X.Z. Learnable Manifold Alignment (LeMA): A semi-supervised cross-modality learning framework for land cover and land use classification. ISPRS J. Photogramm. Remote Sens. 2019, 147, 193–205. [Google Scholar] [CrossRef] [PubMed]
- He, W.; Zhang, H.; Zhang, L. Total variation regularized reweighted sparse nonnegative matrix factorization for hyperspectral unmixing. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3909–3921. [Google Scholar] [CrossRef]
- Huang, J.; Huang, T.Z.; Deng, L.J.; Zhao, X.L. Joint-sparse-blocks and low-rank representation for hyperspectral unmixing. IEEE Trans. Geosci. Remote Sens. 2018, 57, 2419–2438. [Google Scholar] [CrossRef]
- Feng, X.; Han, L.; Dong, L. Weighted group sparsity-constrained tensor factorization for hyperspectral unmixing. Remote Sens. 2022, 14, 383. [Google Scholar] [CrossRef]
- Zhao, X.; Li, W.; Zhang, M.; Tao, R.; Ma, P. Adaptive iterated shrinkage thresholding-based Lp-norm sparse representation for hyperspectral imagery target detection. Remote Sens. 2020, 12, 3991. [Google Scholar] [CrossRef]
- Guo, T.; Luo, F.; Fang, L.; Zhang, B. Meta-pixel-driven embeddable discriminative target and background dictionary pair learning for hyperspectral target detection. Remote Sens. 2022, 14, 481. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, L.; Shen, H. A super-resolution reconstruction algorithm for hyperspectral images. Signal Process. 2012, 92, 2082–2096. [Google Scholar] [CrossRef]
- Deng, L.J.; Vivone, G.; Guo, W.; Dalla Mura, M.; Chanussot, J. A variational pansharpening approach based on reproducible kernel Hilbert space and Heaviside function. IEEE Trans. Image Process. 2018, 27, 4330–4344. [Google Scholar] [CrossRef]
- Yuan, Q.; Zhang, L.; Shen, H. Hyperspectral image denoising employing a spectral-spatial adaptive total variation model. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3660–3677. [Google Scholar] [CrossRef]
- Qian, Y.; Ye, M. Hyperspectral imagery restoration using nonlocal spectral-spatial structured sparse representation with noise estimation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 6, 499–515. [Google Scholar] [CrossRef]
- Xu, Y.; Qian, Y. Group sparse nonnegative matrix factorization for hyperspectral image denoising. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Beijing, China, 10–15 July 2016. [Google Scholar]
- Chang, Y.; Yan, L.; Zhong, S. Hyperspectral image denoising via spectral and spatial low-rank approximation. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Fort Worth, TX, USA, 23–28 July 2017. [Google Scholar]
- Hong, D.; Yokoya, N.; Chanussot, J.; Xu, J.; Zhu, X.X. Learning to propagate labels on graphs: An iterative multitask regression framework for semi-supervised hyperspectral dimensionality reduction. ISPRS J. Photogramm. Remote Sens. 2019, 158, 35–49. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; He, W.; Zhang, L.; Shen, H.; Yuan, Q. Hyperspectral-image restoration using low-rank matrix recovery. IEEE Trans. Geosci. Remote Sens. 2013, 52, 4729–4743. [Google Scholar] [CrossRef]
- Wu, Z.; Wang, Q.; Jin, J.; Shen, Y. Structure tensor total variation-regularized weighted nuclear norm minimization for hyperspectral image mixed denoising. Signal Process. 2017, 131, 202–219. [Google Scholar] [CrossRef]
- Huang, X.; Du, B.; Tao, D.; Zhang, L. Spatial-spectral weighted nuclear norm minimization for hyperspectral image denoising. Neurocomputing 2020, 399, 271–284. [Google Scholar] [CrossRef]
- Guo, X.; Huang, X.; Zhang, L.; Zhang, L. Hyperspectral image noise reduction based on rank-1 tensor decomposition. ISPRS J. Photogramm. Remote Sens. 2013, 83, 50–63. [Google Scholar] [CrossRef]
- Du, B.; Zhang, M.; Zhang, L.; Hu, R.; Tao, D. PLTD: Patch-based low-rank tensor decomposition for hyperspectral images. IEEE Trans. Multimed. 2016, 19, 67–79. [Google Scholar] [CrossRef]
- Wang, Y.; Peng, J.; Zhao, Q.; Leung, Y.; Zhao, X.L.; Meng, D. Hyperspectral-image restoration via total variation regularized low-rank tensor decomposition. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 1227–1243. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; He, W.; Yokoya, N.; Huang, T.Z. Weighted group sparsity regularized low-rank Tensor Decomposition for hyperspectral-image restoration. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019. [Google Scholar]
- Luo, Y.S.; Zhao, X.L.; Jiang, T.X.; Chang, Y.; Ng, M.K.; Li, C. Self-supervised nonlinear transform-based tensor nuclear norm for multi-dimensional image recovery. IEEE Trans. Image Process. 2022, 31, 3793–3808. [Google Scholar] [CrossRef]
- Zhang, H.; Zhao, X.L.; Jiang, T.X.; Ng, M.K.; Huang, T.Z. Multiscale feature tensor train rank minimization for multidimensional image recovery. IEEE Trans. Cybern. 2021, 52, 13395–13410. [Google Scholar] [CrossRef]
- Zhao, X.L.; Yang, J.H.; Ma, T.H.; Jiang, T.X.; Ng, M.K.; Huang, T.Z. Tensor completion via complementary global, local, and nonlocal priors. IEEE Trans. Image Process. 2022, 31, 984–999. [Google Scholar] [CrossRef]
- Fan, F.; Ma, Y.; Li, C.; Mei, X.; Huang, J.; Ma, J. Hyperspectral image denoising with superpixel segmentation and low-rank representation. Inf. Sci. 2017, 397, 48–68. [Google Scholar] [CrossRef]
- Liu, M.Y.; Tuzel, O.; Ramalingam, S.; Chellappa, R. Entropy rate superpixel segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Colorado Springs, CO, USA, 20–25 June 2011; IEEE: New York, NY, USA, 2011; pp. 2097–2104. [Google Scholar]
- Fan, Y.R.; Huang, T.Z. Hyperspectral-image restoration via superpixel segmentation of smooth band. Neurocomputing 2021, 455, 340–352. [Google Scholar] [CrossRef]
- Liu, Y.; Shan, C.; Gao, Q.; Gao, X.; Han, J.; Cui, R. Hyperspectral image denoising via minimizing the partial sum of singular values and superpixel segmentation. Neurocomputing 2019, 330, 465–482. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Chen, Y. Multiscale weighted adjacent superpixel-based composite kernel for hyperspectral image classification. Remote Sens. 2021, 13, 820. [Google Scholar] [CrossRef]
- Wang, Y.; Yin, W. Sparse signal reconstruction via iterative support detection. SIAM J. Imaging Sci. 2010, 3, 462–491. [Google Scholar] [CrossRef] [Green Version]
- Fan, Y.R.; Wang, Y.; Huang, T.Z. Enhanced joint sparsity via iterative support detection. Inf. Sci. 2017, 415–416, 298–318. [Google Scholar] [CrossRef] [Green Version]
- Gu, S.; Zhang, L.; Zuo, W.; Feng, X. Weighted nuclear norm minimization with application to image denoising. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 2862–2869. [Google Scholar]
- Oh, T.H.; Tai, Y.W.; Bazin, J.C.; Kim, H.; Kweon, I.S. Partial sum minimization of singular values in robust PCA: Algorithm and applications. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 744–758. [Google Scholar] [CrossRef] [Green Version]
- Yuan, X.; Yang, J. Sparse and low-rank matrix decomposition via alternating direction method. Pac. J. Optim. 2013, 9, 167–180. [Google Scholar]
- Peng, Y.; Meng, D.; Xu, Z.; Gao, C.; Yang, Y.; Zhang, B. Decomposable nonlocal tensor dictionary learning for multispectral image denoising. In Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 2949–2956. [Google Scholar] [CrossRef]
- He, W.; Zhang, H.; Zhang, L.; Shen, H. Total-variation-regularized low-rank matrix factorization for hyperspectral-image restoration. IEEE Trans. Geosci. Remote Sens. 2016, 54, 178–188. [Google Scholar] [CrossRef]
- Peng, J.; Xie, Q.; Zhao, Q.; Wang, Y.; Yee, L.; Meng, D. Enhanced 3DTV regularization and its applications on HSI denoising and compressed sensing. IEEE Trans. Image Process. 2020, 29, 7889–7903. [Google Scholar] [CrossRef]
- Wald, L. Data Fusion: Definitions and Architectures: Fusion of Images of Different Spatial Resolutions; Presses des MINES: Paris, France, 2002. [Google Scholar]
- Dou, H.X.; Pan, X.M.; Wang, C.; Shen, H.Z.; Deng, L.J. Spatial and spectral-channel attention network for denoising on hyperspectral remote sensing image. Remote Sens. 2022, 14, 3338. [Google Scholar] [CrossRef]
- Zhuang, L.; Ng, M.K.; Fu, X. Hyperspectral image mixed-noise removal using subspace representation and deep CNN image prior. Remote Sens. 2021, 13, 4098. [Google Scholar] [CrossRef]
- Dong, W.; Shi, G.; Li, X.; Ma, Y.; Huang, F. Compressive sensing via nonlocal low-rank regularization. IEEE Trans. Image Process. 2014, 23, 3618–3632. [Google Scholar] [CrossRef] [PubMed]










| Method | MPSNR | MSSIM | ERGAS | Time |
|---|---|---|---|---|
| TDL | 28.71 | 0.925 | 87.59 | 6.58 |
| LRTV | 26.51 | 0.908 | 113.05 | 81.16 |
| SSLRR | 30.48 | 0.960 | 70.48 | 11.37 |
| E3DTV | 28.84 | 0.978 | 91.67 | 46.58 |
| proposed (WSVT) | 31.50 | 0.980 | 46.26 | 19.12 |
| proposed (PSVT) | 32.27 | 0.996 | 30.10 | 24.87 |
| Method | MPSNR | MSSIM | ERGAS | Time |
|---|---|---|---|---|
| TDL | 24.39 | 0.737 | 220.45 | 185.22 |
| LRTV | 24.17 | 0.735 | 224.89 | 351.51 |
| SSLRR | 24.93 | 0.651 | 208.47 | 8.39 |
| E3DTV | 29.93 | 0.904 | 144.23 | 55.93 |
| proposed (WSVT) | 28.84 | 0.909 | 149.54 | 63.58 |
| proposed (PSVT) | 30.47 | 0.948 | 108.10 | 32.00 |
| Noisy Indian Pines | Noisy Pompoms | ||
|---|---|---|---|
| Number of PC | MPSNR | Number of PC | MPSNR |
| 1 | 30.41 | 1 | 24.41 |
| 3 | 31.39 | 2 | 30.24 |
| 5 | 32.27 | 3 | 30.47 |
| 6 | 32.24 | 4 | 30.41 |
| 7 | 32.01 | 5 | 30.39 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, Y.-R. Robust Superpixel Segmentation for Hyperspectral-Image Restoration. Entropy 2023, 25, 260. https://doi.org/10.3390/e25020260
Fan Y-R. Robust Superpixel Segmentation for Hyperspectral-Image Restoration. Entropy. 2023; 25(2):260. https://doi.org/10.3390/e25020260
Chicago/Turabian StyleFan, Ya-Ru. 2023. "Robust Superpixel Segmentation for Hyperspectral-Image Restoration" Entropy 25, no. 2: 260. https://doi.org/10.3390/e25020260
APA StyleFan, Y.-R. (2023). Robust Superpixel Segmentation for Hyperspectral-Image Restoration. Entropy, 25(2), 260. https://doi.org/10.3390/e25020260






