Discussion on Electron Temperature of Gas-Discharge Plasma with Non-Maxwellian Electron Energy Distribution Function Based on Entropy and Statistical Physics
Abstract
1. Introduction
2. Theoretical Backgrounds
2.1. Thermodynamics and Statistical Physics of Electrons
2.2. Confirmation of the Boltzmann Equation to Be Solved
2.3. Calculation of EEPF of Oxygen Plasma—Self-Consistent Simultaneous Solution with Rate Equations of Major Excited Species
2.4. Calculation of EEPF of Nitrogen Plasma—Self-Consistent Simultaneous Solution with the Vibrational Distribution Function of N Electronically Ground State
3. Results and Discussion
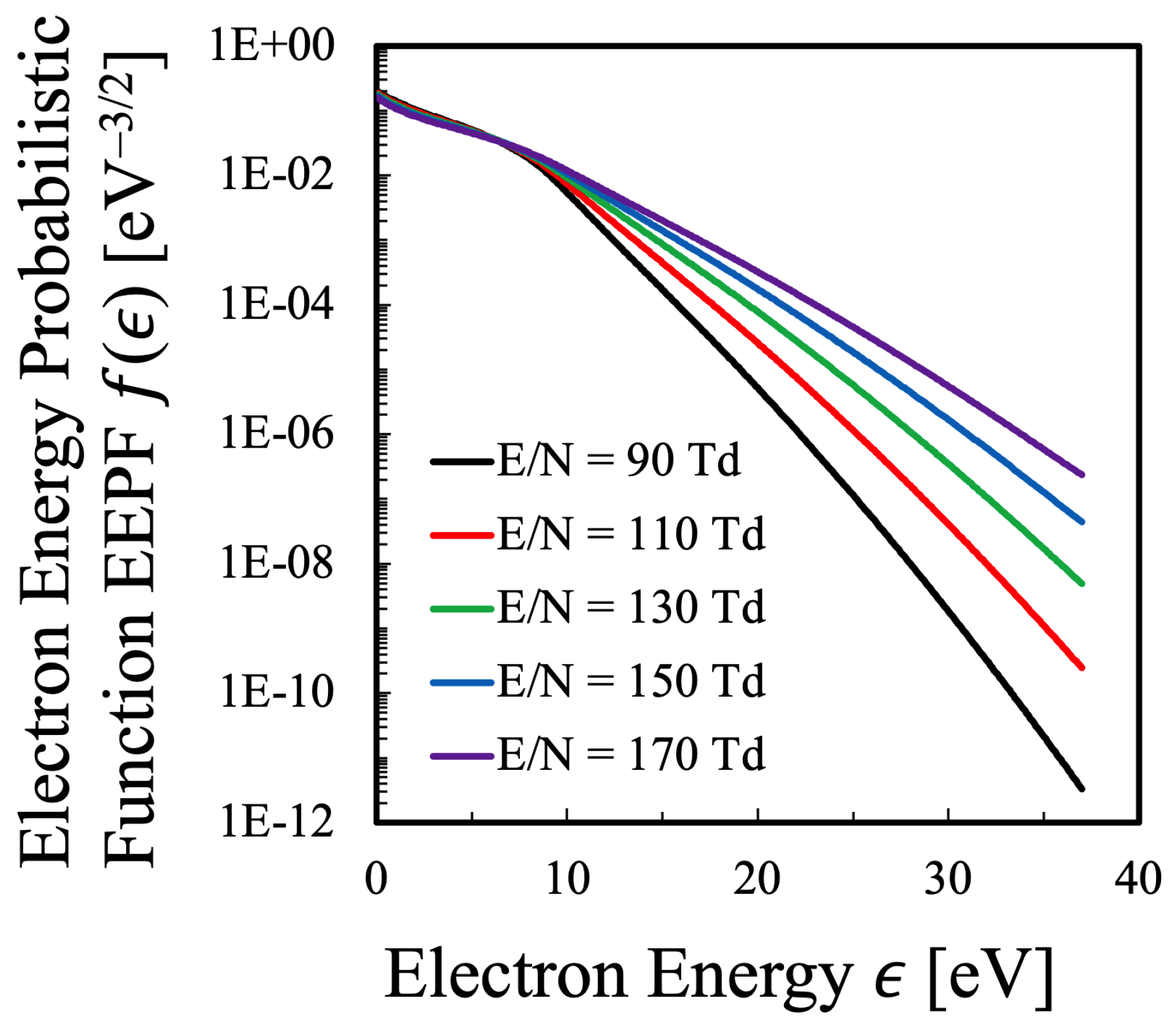
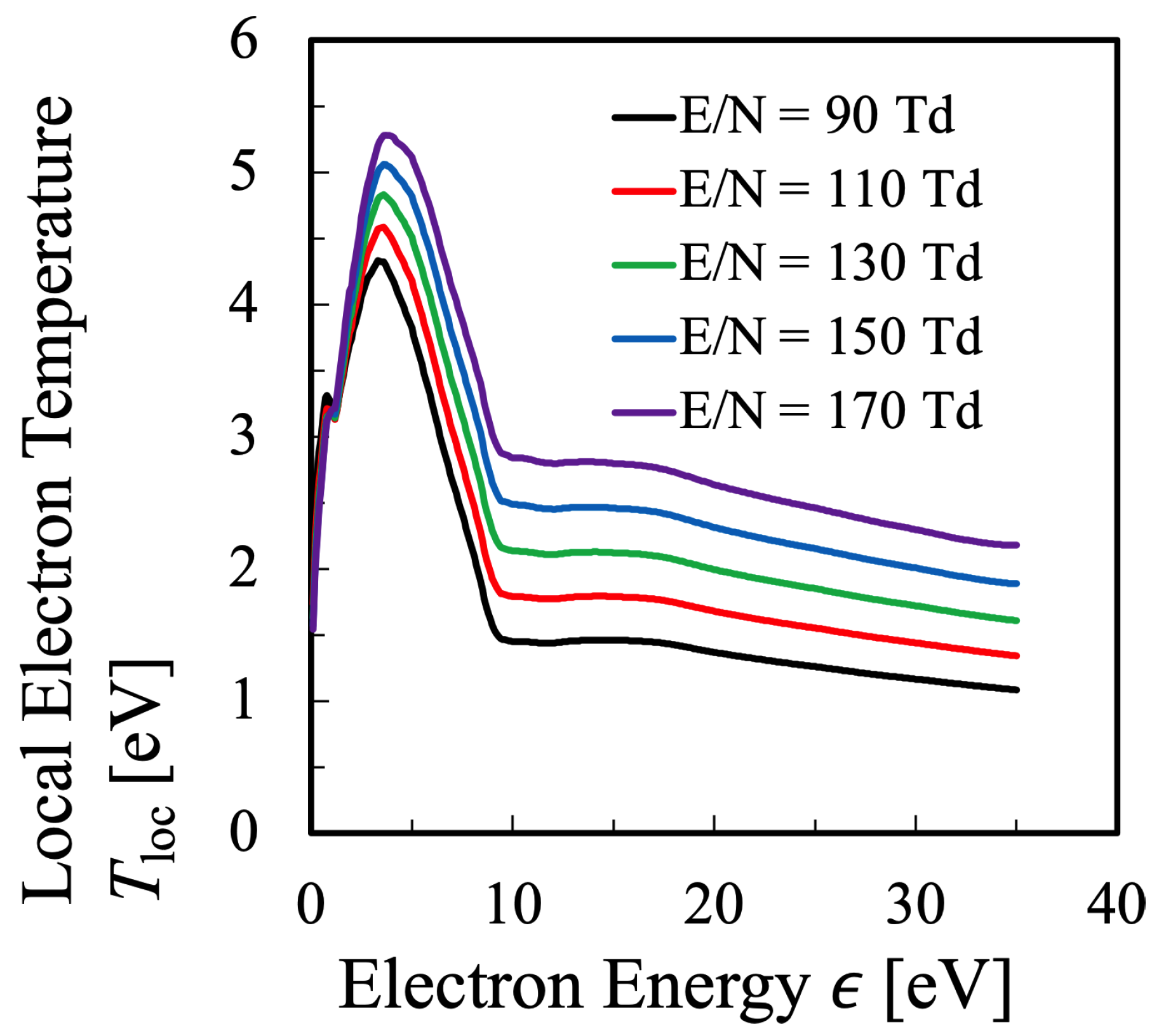
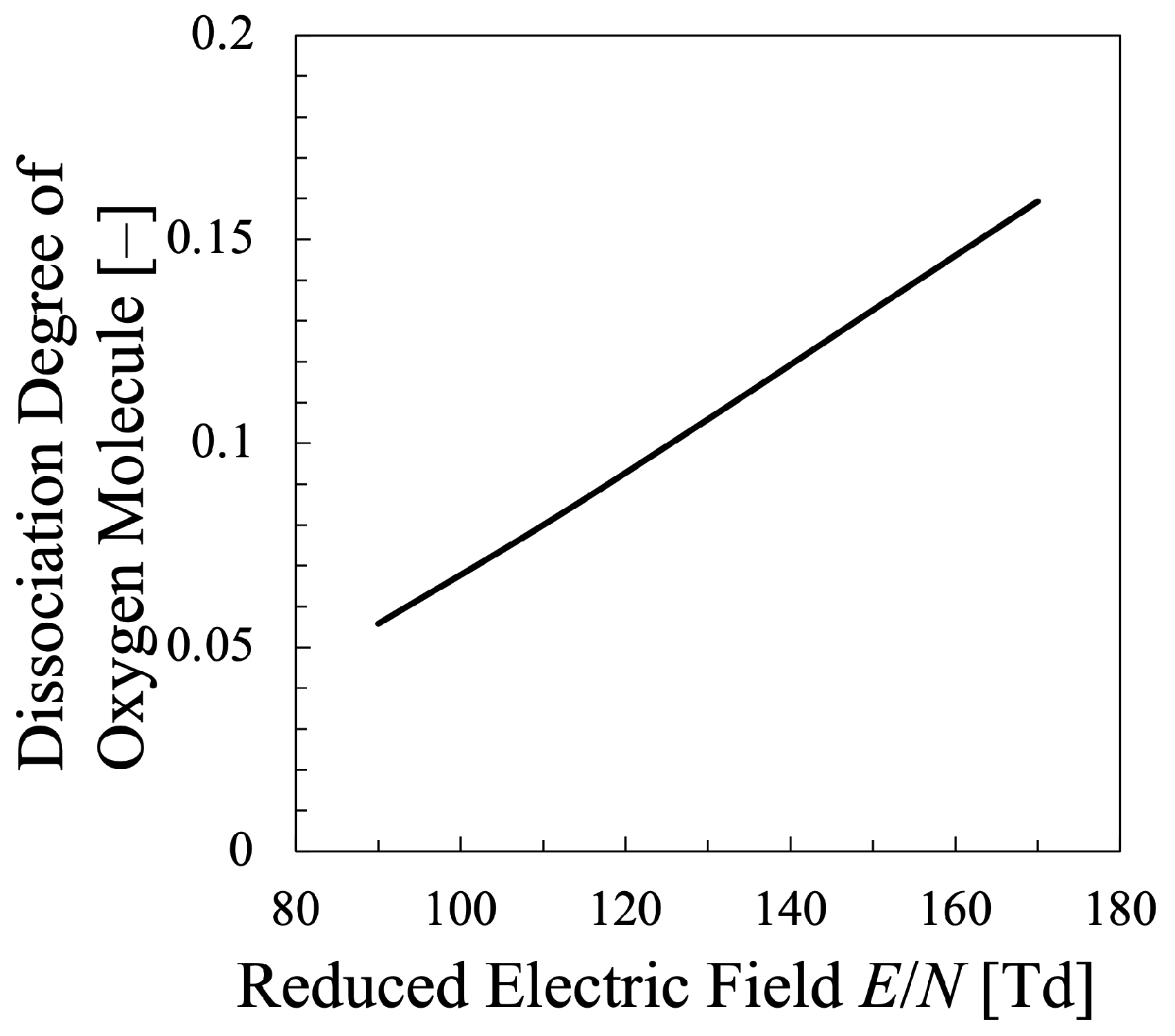
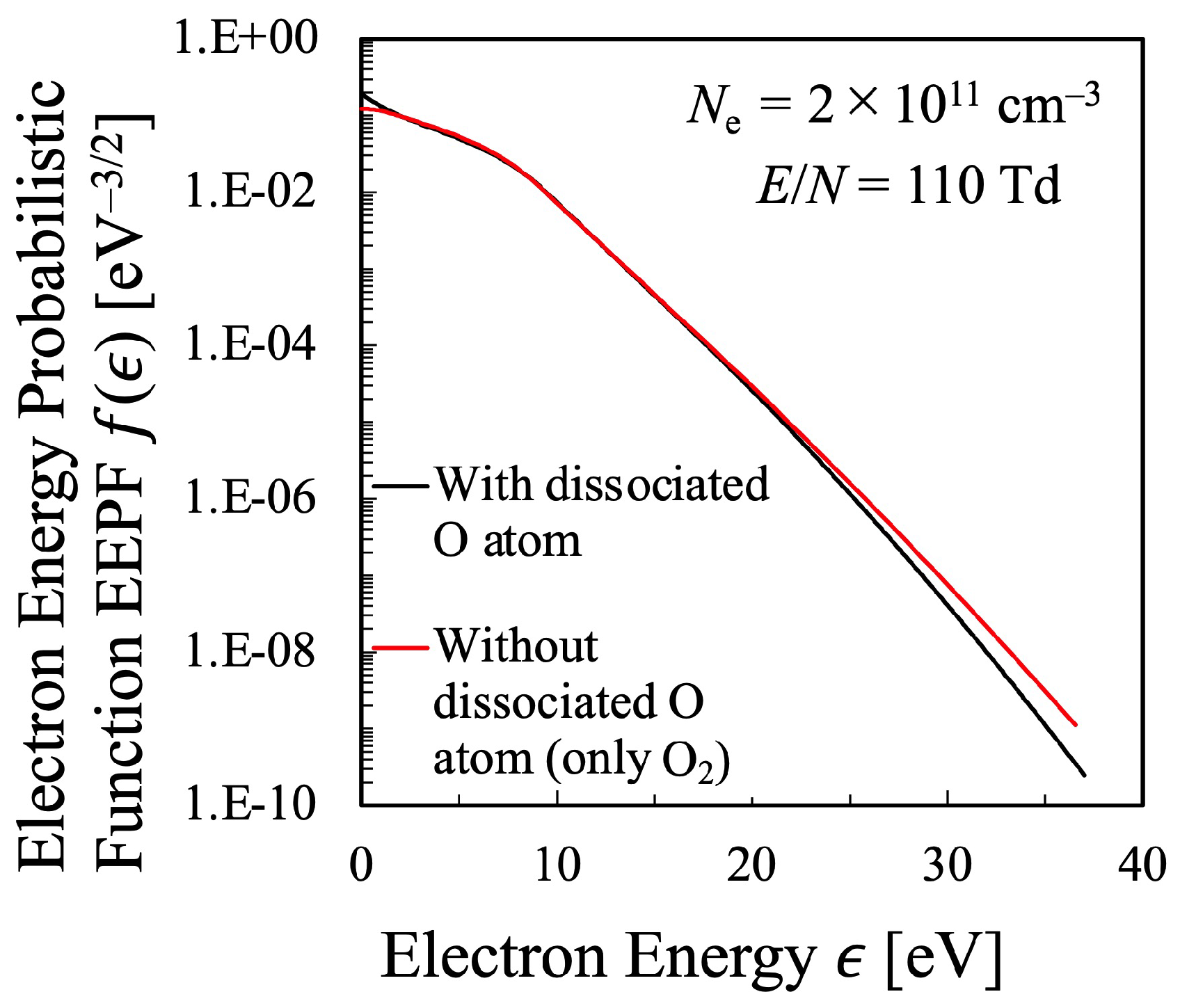
3.1. Oxygen Plasma
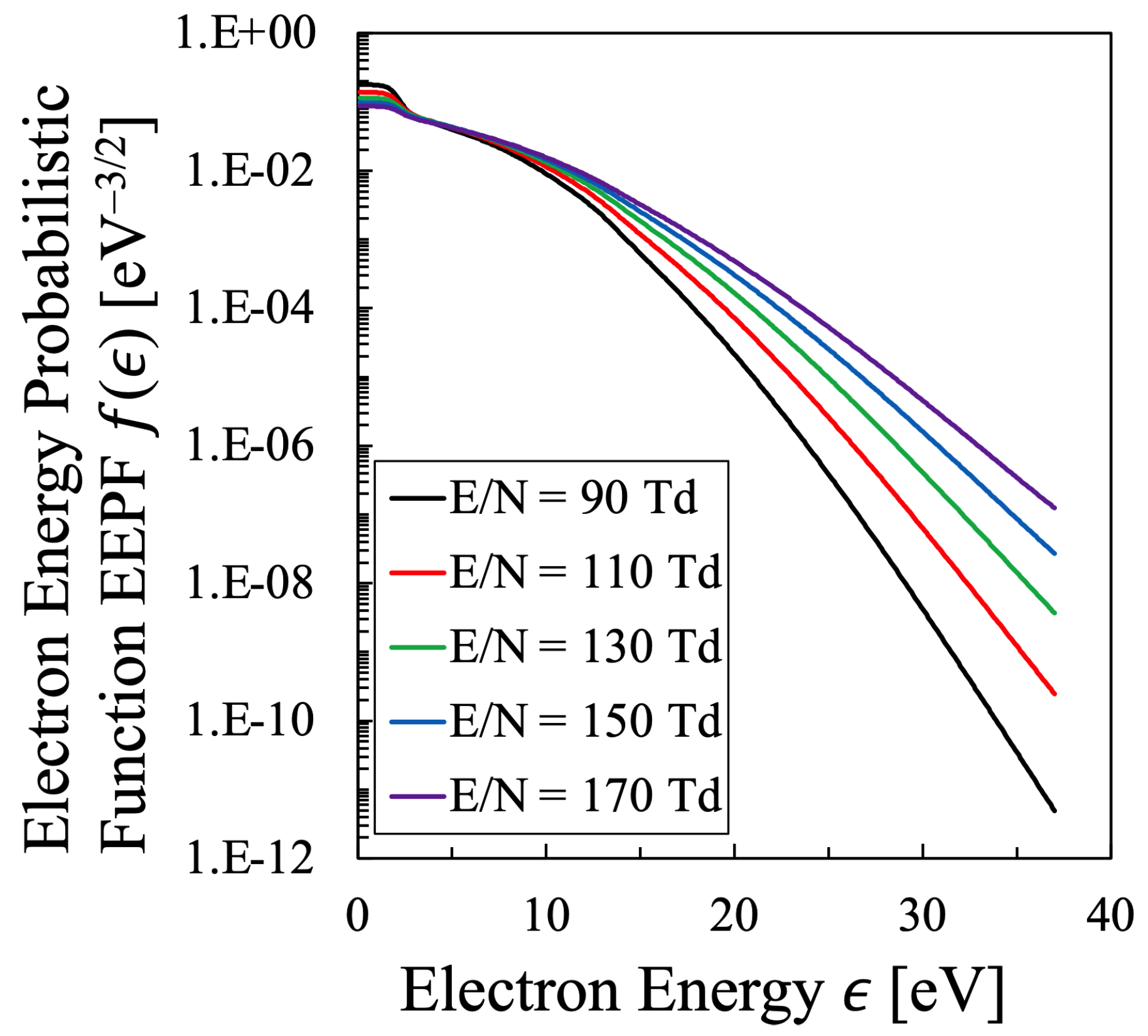
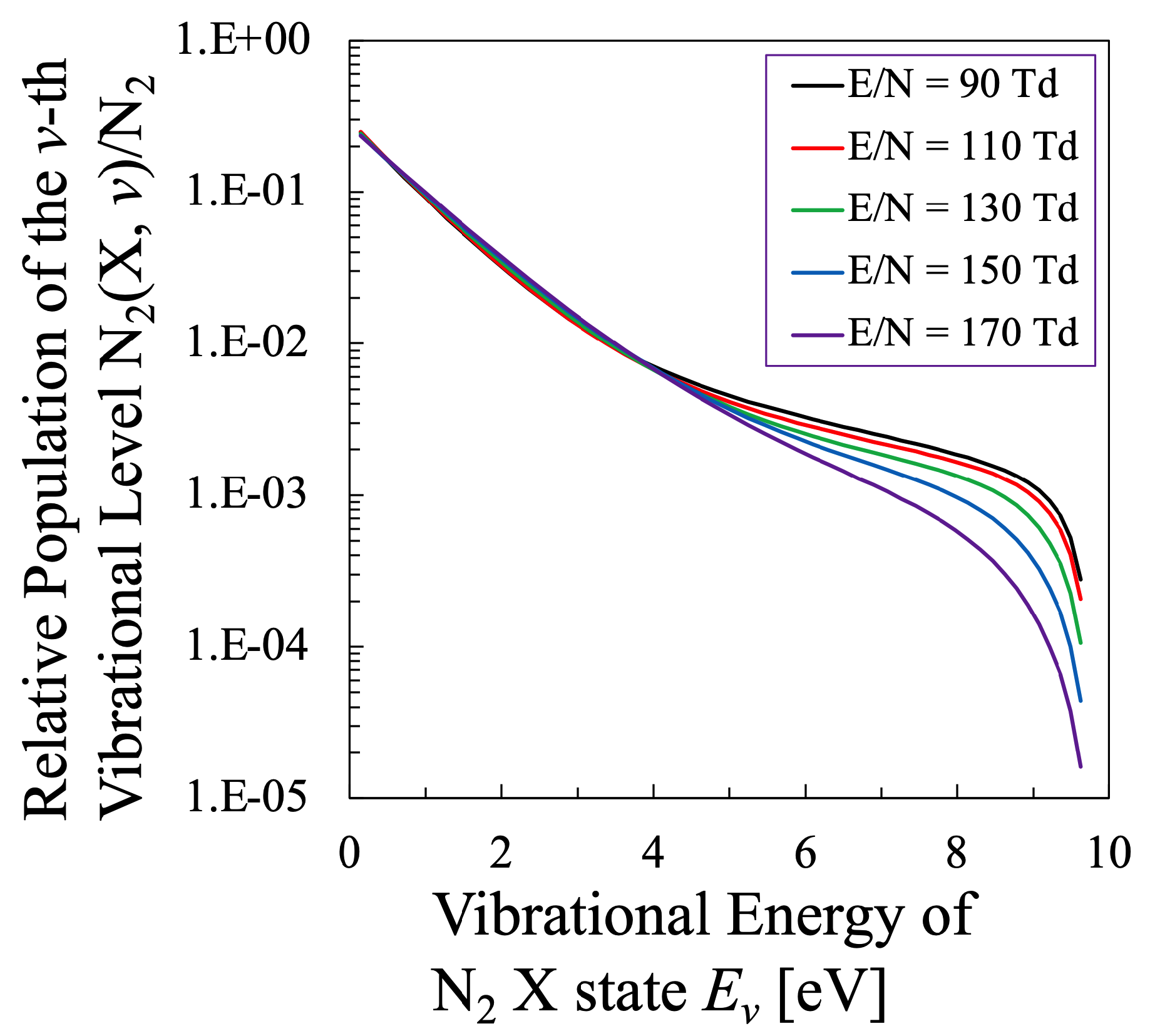
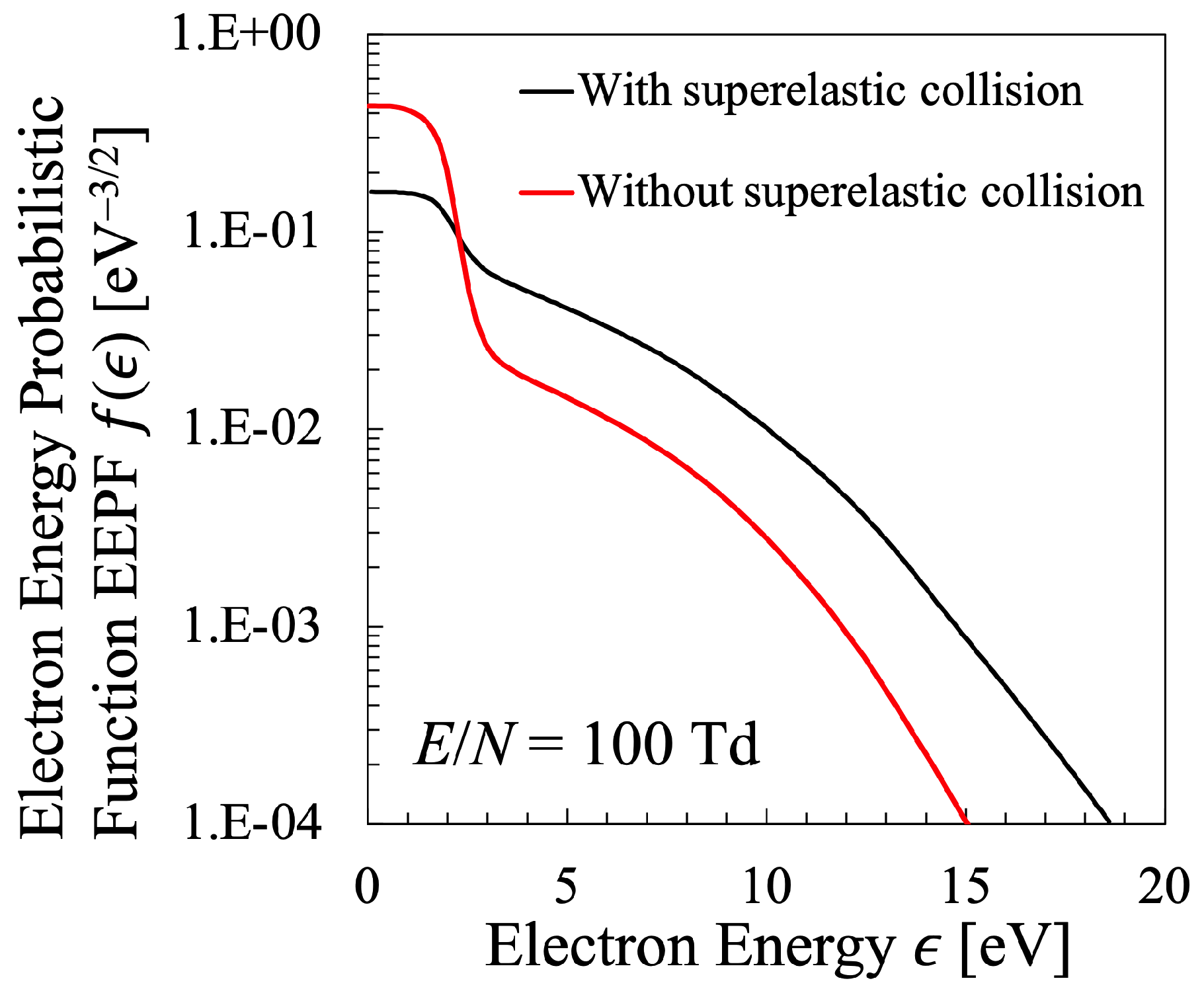
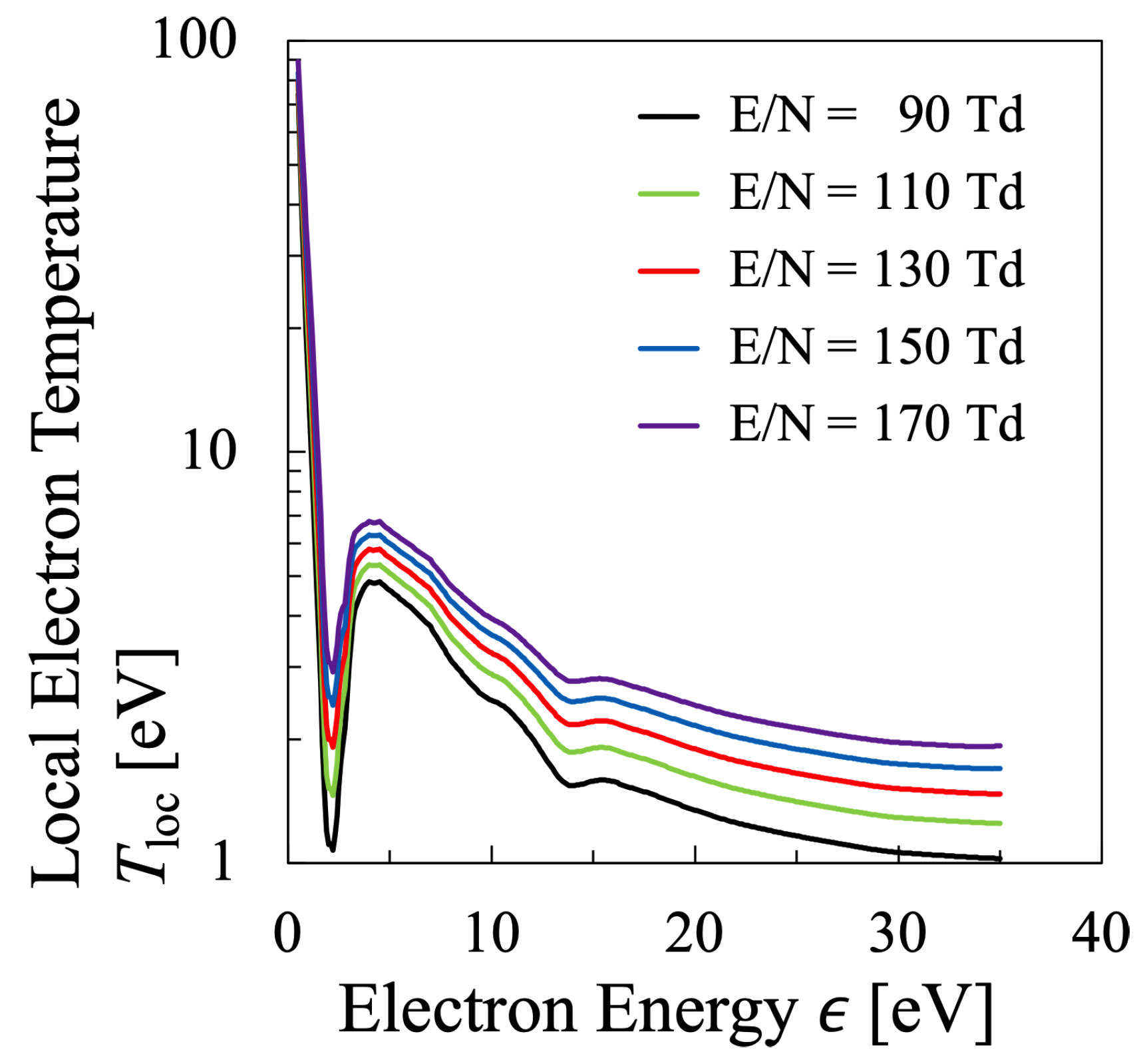
3.2. Nitrogen Plasma
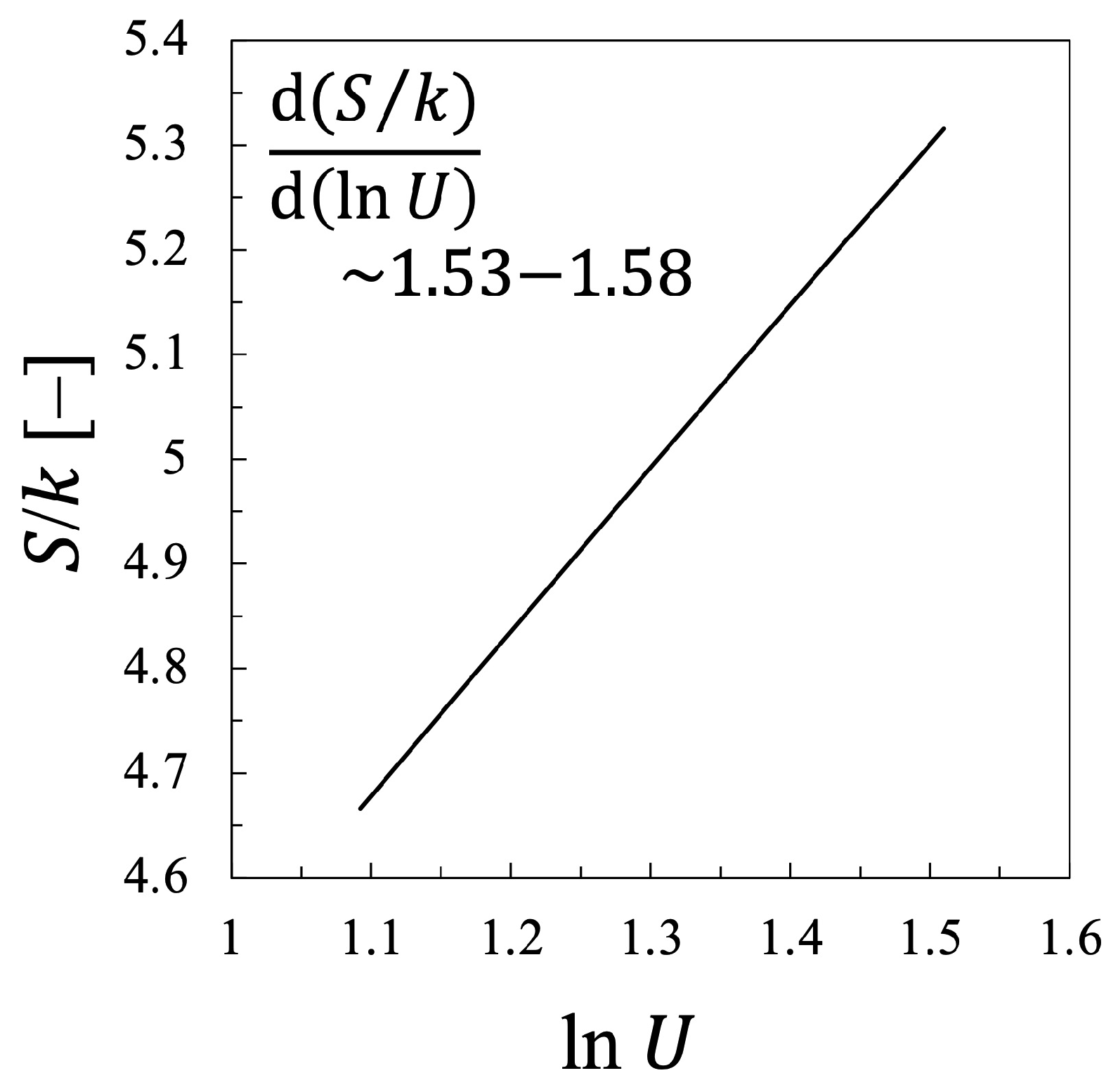
3.3. Mathematical Discussion on the Results of the Relation between S and from Alvarez et al.’s Theory
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Boulos, M.; Fauchais, P.; Pfender, E. Thermal Plasmas; Plenum Press: New York, NY, USA, 1994; Volume 1. [Google Scholar]
- Fridman, A. Plasma Chemistry; Cambridge: New York, NY, USA, 2008. [Google Scholar]
- Lieberman, M.A.; Lichtenberg, A.J. Principles of Plasma Discharges and Material Processing, 2nd ed.; Wiley: Hoboken, NJ, USA, 2005. [Google Scholar]
- Chabert, P.; Braithwaite, N. Physics of Radio-Frequency Plasmas; Cambridge: New York, NY, USA, 2022. [Google Scholar]
- d’Agostino, R.; Favia, P.; Kawai, Y.; Ikegami, H.; Saro, N.; Arefi-Khonsari, F. Advanced Plasma Technology; Wiley-VCH: Weinheim, Germany, 2008. [Google Scholar]
- Polak, L.S.; Lebedev, Y.A. Plasma Chemistry; Cambridge International: Cambridge, UK, 1998. [Google Scholar]
- Capitelli, M.; Ferreira, C.M.; Gordiets, B.F.; Osipov, A.I. Plasma Kinetics in Atmospheric Gases; Springer: Berlin, Germany, 2000. [Google Scholar]
- Loffhagen, D.; Sigeneger, F.; Winkler, R. Electron Kinetics in Weakly Ionized Plasmas, Ch. 2., Low Temperature Plasmas, 2nd ed.; Hippler, R., Kersten, H., Schmidt, M., Shoenbach, K.H., Eds.; Wiley: Weinheim, Germany, 2008; Volume 1. [Google Scholar]
- Capitelli, M.; Celiberto, R.; Colonna, G.; Esposito, F.; Gorse, C.; Hassouni, K.; Laricchiuta, A.; Longo, S. Fundamental Aspects of Plasma Chemical Physics, Kinetics; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Godyak, V.A.; Piejak, R.B. Abnormally low electron energy and heating-mode transition in a low-pressure argon rf discharge at 13.56 MHz. Phys. Rev. Lett. 1990, 65, 996–999. [Google Scholar] [CrossRef]
- Kimura, T.; Ohe, K. Electron energy distribution detection in symmetrically driven RF argon discharge. Jpn. J. Appl. Phys. 1993, 32, 3601–3605. [Google Scholar] [CrossRef]
- Abdel-Fattah, E.; Sugai, H. Influence of excitation frequency on the electron distribution function in capacitively coupled discharges in argon and helium. Jpn. J. Appl. Phys. 2003, 42, 6569–6577. [Google Scholar] [CrossRef]
- Mizuochi, J.; Sakamoto, T.; Matsuura, H.; Akatsuka, H. Evaluation of electron energy distribution function in microwave discharge plasmas by spectroscopic diagnostics with collisional radiative model. Jpn. J. Appl. Phys. 2010, 49, 036001. [Google Scholar] [CrossRef]
- Hagelaar, G.J.M.; Pitchford, L.C. Solving the Boltzmann equation to obtain electron transport coefficients and rate coefficients for fluid models. Plasma Sources Sci. Technol. 2005, 14, 722–733. [Google Scholar] [CrossRef]
- Alvarez, R.; Cotrino, J.; Palmero, A. On the kinetic and thermodynamic electron temperatures in non-thermal plasmas. Eur. Phys. Lett. 2014, 105, 15001. [Google Scholar] [CrossRef]
- Guerra, V.; Loureiro, J. Electron and heavy particle kinetics in a low-pressure nitrogen glow discharge. Plasma Sources Sci. Technol. 1997, 6, 361–372. [Google Scholar] [CrossRef]
- Guerra, V.; Sá, P.A.; Loureiro, J. Kinetic modeling of low-pressure nitrogen discharges and post-discharges. Eur. Phys. J. Appl. Phys. 2004, 28, 125–152. [Google Scholar] [CrossRef]
- Shakhatov, V.A.; Lebedev, Y.A. Kinetics of excitation of N2 (A ,vA), N2 (C 3Πu,vC), and N2 (B 3Πg,vB) in nitrogen discharge plasmas as studied by means of emission spectroscopy and computer simulation. High Energy Chem. 2008, 42, 170–204. [Google Scholar] [CrossRef]
- Gousset, G.; Ferreira, C.M.; Pinheiro, M.; Sá, P.A.; Touzeau, M.; Vialle, M.; Loureiro, J. Electron and heavy-particle kinetics in the low pressure oxygen positive column. J. Phys. D 1991, 24, 290–300. [Google Scholar] [CrossRef]
- Braginskiy, O.V.; Vasilieva, A.N.; Klopovskiy, K.S.; Kovalev, A.S.; Lopaev, D.V.; Proshina, O.V.; Rakhimova, T.V.; Rakhimov, A.T. Singlet oxygen generation in O2 flow excited by RF discharge: I. Homogeneous discharge mode: α-mode. J. Phys. D 2005, 38, 3609–3625. [Google Scholar] [CrossRef]
- Sakamoto, T.; Matsuura, H.; Akatsuka, H. Actinometry measurement of oxygen dissociation degree in a microwave discharge plasma and effect of electron energy distribution function. J. Adv. Oxid. Technol. 2007, 10, 247–252. [Google Scholar] [CrossRef]
- Ichikawa, Y.; Sakamoto, T.; Nezu, A.; Matsuura, H.; Akatsuka, H. Actinometry measurement of dissociation degrees of nitrogen and oxygen in N2-O2 microwave discharge plasma. Jpn. J. Appl. Phys. 2010, 49, 106101. [Google Scholar] [CrossRef]
- Konno, J.; Nezu, A.; Matsuura, H.; Akatsuka, H. Excitation kinetics of oxygen O(1D) state in low-pressure oxygen plasma and the effect of electron energy distribution function. J. Adv. Oxid. Technol. 2017, 20, 20170002. [Google Scholar] [CrossRef]
- Sakamoto, T.; Matsuura, H.; Akatsuka, H. Spectroscopic study on the vibrational populations of N2 C 3Π and B 3Π states in a microwave nitrogen discharge. J. Appl. Phys. 2007, 101, 023307. [Google Scholar] [CrossRef]
- Tan, H.; Nezu, A.; Akatsuka, H. Kinetic model and spectroscopic measurement of NO (A, B, C) states in low-pressure N2-O2 microwave discharge. Jpn. J. Appl. Phys. 2015, 54, 096103. [Google Scholar] [CrossRef]
- Akatsuka, H.; Shibata, T.; Nezu, A. Discussion on population kinetics and number densities of excited species of low-pressure discharge nitrogen plasma. IEEJ Trans. 2016, 11, S9–S18. [Google Scholar] [CrossRef]
- Mandl, F. Statistical Physics; Wiley: London, UK, 1971. [Google Scholar]
- Capitelli, M.; Colonna, G.; D’Angola, A. Fundamental Aspects of Plasma Chemical Physics, Thermodynamics; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Fujimoto, T. Plasma Spectroscopy; Oxford: Oxford, UK, 2004. [Google Scholar]
- Winkler, R.; Deutsch, H.; Wilhelm, J.; Wilke, C. Electron kinetics of weakly ionized HF plasmas. I. Direct treatment and Fourier expansion. Beitr. Plasmaphys. 1984, 24, 285–302. [Google Scholar] [CrossRef]
- Winkler, R.; Deutsch, H.; Wilhelm, J.; Wilke, C. Electron kinetics of weakly ionized HF plasmas. II. Decoupling in the Fourier hierarchy and simplified kinetics at higher frequencies. Beitr. Plasmaphys. 1984, 24, 303–316. [Google Scholar] [CrossRef]
- Gudmundsson, J.T. On the effect of the electron energy distribution on the plasma parameters of an argon discharge: A global (volume-averaged) model study. Plasma Sources Sci. Technol. 2001, 10, 76–81. [Google Scholar] [CrossRef]
- Boffard, J.B.; Jung, R.O.; Chun, C.L.; Wendt, A.E. Optical emission measurements of electron energy distributions in low-pressure argon inductively coupled plasmas. Plasma Sources Sci. Techlol. 2010, 19, 065001. [Google Scholar] [CrossRef]
- Henriques, J.; Tatarova, E.; Guerra, V.; Ferreira, C.M. Wave driven N2-Ar discharge. I. Self-consistent theoretical model. J. Appl. Phys. 2002, 91, 5622–5631. [Google Scholar] [CrossRef]
- Silva, A.F.; Morillo-Candás, A.S.; Tejero-del-Caz, A.; Alves, L.L.; Guaitella, O.; Guerra, V. A reaction mechanism for vibrationally-cold low-pressure CO2 plasmas. Plasma Sources Sci. Technol. 2020, 29, 125020. [Google Scholar] [CrossRef]
- Akatsuka, H. Progresses in experimental study of N2 plasma diagnostics by optical emission spectroscopy. In Chemical Kinetics; Patel, V., Ed.; IntechOpen: London, UK, 2012. [Google Scholar]
- Golant, V.E.; Zhilinsky, A.P.; Sakharov, I.E. Fundamentals of Plasma Physics; John Wiley and Sons: New York, NY, USA, 1980. [Google Scholar]
- Colonna, G.; D’Angola, A. Chapter 2 The two-term Boltzmann equation. In Plasma Modeling: Methods and Applications; IOP Publishing Ltd.: London, UK, 2016. [Google Scholar]
- Kashiwazaki, R.; Akatsuka, H. Effect of electron energy distribution function on spectroscopic characteristics of microwave discharge argon plasma. Jpn. J. Appl. Phys. 2002, 41, 5432–5441. [Google Scholar] [CrossRef]
- Phelps, A.V. Tabulations of Collision Cross Sections and Calculated Transport and Reaction Coefficients for Electron Collisions with O2; JILA Information Center Report No. 28; University of Colorado: Boulder, CO, USA, 1985. [Google Scholar]
- Yurova, I.Y.; Ivanov, V.E. 1989 Cross Sections for Scattering of Electrons by Atmospheric Gases; Nauka: Leningrad, Russia, 1989. (In Russian) [Google Scholar]
- Phelps, A.V. Nitrogen Electron Transport and Reaction Coefficients; JILA Information Center Report No. 26; University of Colorado: Boulder, CO, USA, 1985. [Google Scholar]
- Cosby, P.C. Electron-impact dissociation of nitrogen. J. Chem. Phys. 1993, 98, 9544–9553. [Google Scholar] [CrossRef]
- Kawakami, H.; Urabe, J.; Yukimura, K. Electron attachment coefficient in low E/N regions and a discussion of discharge instability in KrF laser. Trans. Inst. Elec. Electron. Jpn. 1991, 111, 212–220. (In Japanese) [Google Scholar] [CrossRef] [PubMed]
- Adkins, W.A.; Davidson, A.G. Ordinary Differential Equations; Springer: New York, NY, USA, 2012. [Google Scholar]
- Suyari, H. Mathematical structures derived from the q-multinomial coefficient in Tsallis statistics. Phys. A 2006, 368, 63–82. [Google Scholar] [CrossRef]
- Suyari, H. Tsallis entropy as a lower bound of average description length for the q-generalized code tree. In Proceedings of the 2007 IEEE International Symposium on Information Theory (2007IEEE-ISIT), Nice, France, 24–29 June 2007; pp. 901–905. [Google Scholar]
- Tsallis, C. What should a statistical mechanics satisfy to reflect nature? Phys. D Nonlinear Phenom. 2004, 193, 3–34. [Google Scholar] [CrossRef]
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Tsallis, C.; Levy, S.V.F.; Souza, A.M.C.; Maynard, R. Statistical-mechanical foundation of the ubiquity of levy distributions in nature. Phys. Rev. Lett. 1995, 75, 3589–3593. [Google Scholar] [CrossRef]
- Tsallis, C.; Anjos, J.C.; Borges, E.P. Fluxes of cosmic rays: A delicately balanced stationary state. Phys. Lett. A 2003, 310, 372–376. [Google Scholar] [CrossRef]

| Number | Electron Collision Reactions | References | |
|---|---|---|---|
| 1 | ⇄ | [7] | |
| 2 | ⇄ | [7] | |
| 3 | ⇄ | [20] | |
| 4 | → | [7] | |
| 5 | ⇄ | [40] | |
| 6 | ⇄ | [7,40] | |
| 7 | ⇄ | [20] | |
| 8 | ⇄ | [7,20] | |
| 9 | → | [7] | |
| 10 | ⇄ | [19] | |
| 11 | → | [3] | |
| 12 | → | [40] | |
| 13 | → | [7,40] | |
| 14 | ⇄ | [7] | |
| 15 | → | [40] | |
| Number | Atomic or Molecular Collision Reactions | References | |
|---|---|---|---|
| 16 | → | [7] | |
| 17 | → | [7] | |
| 18 | → | [7] | |
| 19 | ⇄ | [7] | |
| 20 | ⇄ | [7] | |
| 21 | ⇄ | [7] | |
| 22 | → | [7] | |
| 23 | → | [19] | |
| 24 | ⇄ | [7] | |
| 25 | → | [19] | |
| 26 | → | [7] | |
| 27 | → | [7] | |
| 28 | → | [3] | |
| 29 | → | [3] | |
| 30 | → | [3] | |
| Number | Electron Inelastic Collision Reactions | Reference | ||
|---|---|---|---|---|
| 31 | → | [40] | ||
| 32 | → | [7] | ||
| 33 | → | [7] | ||
| 34 | → | [41] | ||
| 35 | → | [40] | ||
| 36 | → | [40] | ||
| Reaction | Vibrational Collision Reactions of N | References | |
|---|---|---|---|
| e-V | ⇄ | [42] | |
| V-V | ⇄ | [7] | |
| V-T | ⇄ | [7] | |
| V-Diss. | → | [7] | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Akatsuka, H.; Tanaka, Y. Discussion on Electron Temperature of Gas-Discharge Plasma with Non-Maxwellian Electron Energy Distribution Function Based on Entropy and Statistical Physics. Entropy 2023, 25, 276. https://doi.org/10.3390/e25020276
Akatsuka H, Tanaka Y. Discussion on Electron Temperature of Gas-Discharge Plasma with Non-Maxwellian Electron Energy Distribution Function Based on Entropy and Statistical Physics. Entropy. 2023; 25(2):276. https://doi.org/10.3390/e25020276
Chicago/Turabian StyleAkatsuka, Hiroshi, and Yoshinori Tanaka. 2023. "Discussion on Electron Temperature of Gas-Discharge Plasma with Non-Maxwellian Electron Energy Distribution Function Based on Entropy and Statistical Physics" Entropy 25, no. 2: 276. https://doi.org/10.3390/e25020276
APA StyleAkatsuka, H., & Tanaka, Y. (2023). Discussion on Electron Temperature of Gas-Discharge Plasma with Non-Maxwellian Electron Energy Distribution Function Based on Entropy and Statistical Physics. Entropy, 25(2), 276. https://doi.org/10.3390/e25020276







