A Quantum-Classical Hybrid Solution for Deep Anomaly Detection
Abstract
1. Introduction
2. Related Work
2.1. Anomaly Detection
2.2. QML
3. A Quantum-Classical Hybrid Solution for Deep Anomaly Detection
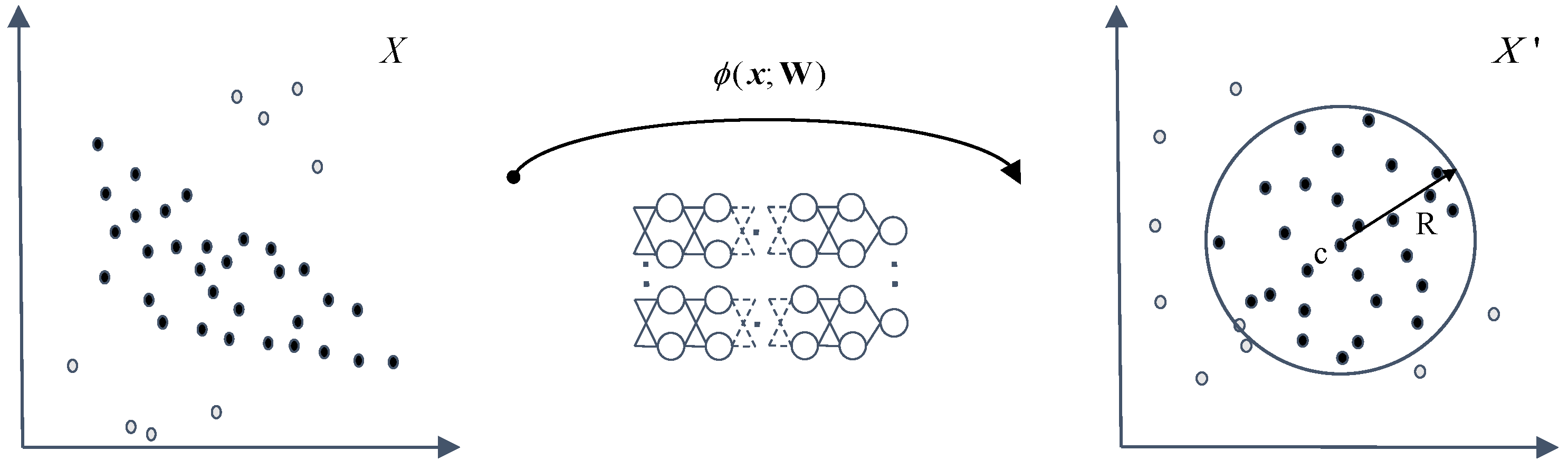
3.1. DSVDD
3.2. Quantum-Classical Hybrid Solution
3.2.1. Motivation
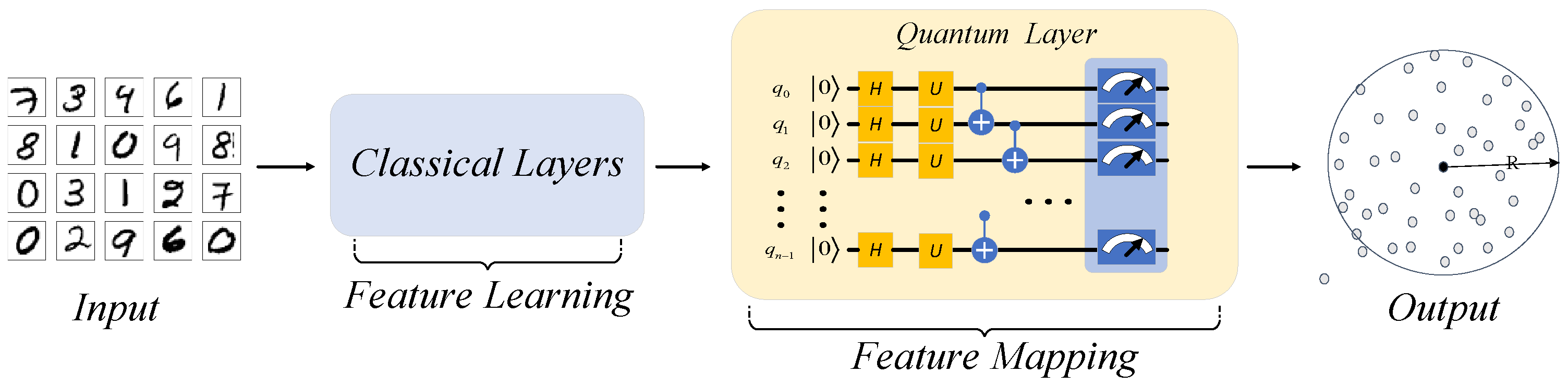
3.2.2. The Structure of QHDNN
3.2.3. Design of the Quantum Network Layer
4. Experiments
4.1. Settings of Experiments
4.2. Results and Discussion
4.2.1. Results
4.2.2. Discussion
4.3. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chandola, V.; Banerjee, A.; Kumar, V. Anomaly detection: A survey. Acm Comput. Surv. (Csur) 2009, 41, 1–58. [Google Scholar] [CrossRef]
- Mirowski, P.; Grimes, M.K.; Malinowski, M.; Hermann, K.M.; Anderson, K.; Teplyashin, D.; Simonyan, K.; Kavukcuoglu, K.; Zisserman, A.; Hadsell, R. Learning to Navigate in Cities Without a Map. arXiv 2018, arXiv:1804.00168. [Google Scholar]
- Lavin, A.; Ahmad, S. Evaluating real-time anomaly detection algorithms–the Numenta anomaly benchmark. In Proceedings of the 2015 IEEE 14th International Conference On Machine Learning and Applications (ICMLA), Miami, FL, USA, 9–11 December 2015; pp. 38–44. [Google Scholar]
- Garcia-Teodoro, P.; Diaz-Verdejo, J.; Maciá-Fernández, G.; Vázquez, E. Anomaly-based network intrusion detection: Techniques, systems and challenges. Comput. Secur. 2009, 28, 18–28. [Google Scholar] [CrossRef]
- Phua, C.; Lee, V.; Smith, K.; Gayler, R. A comprehensive survey of data mining-based fraud detection research. arXiv 2010, arXiv:1009.6119. [Google Scholar]
- Chen, J.; Qian, L.; Urakov, T.; Gu, W.; Liang, L. Adversarial robustness study of convolutional neural network for lumbar disk shape reconstruction from MR images. In Proceedings of the SPIE Image Processing 2021: Medical Imaging: Image Processing, San Diego, CA, USA, 14–18 February 2021; Volume 11596, pp. 306–318. [Google Scholar]
- Liang, L.; Ma, L.; Qian, L.; Chen, J. An algorithm for out-of-distribution attack to neural network encoder. arXiv 2020, arXiv:2009.08016. [Google Scholar]
- Schlegl, T.; Seeböck, P.; Waldstein, S.M.; Schmidt-Erfurth, U.; Langs, G. Unsupervised anomaly detection with generative adversarial networks to guide marker discovery. In Proceedings of the International Conference on Information Processing in Medical Imaging, Boone, NC, USA, 25–30 June 2017; pp. 146–157. [Google Scholar]
- Romero, J.; Olson, J.P.; Aspuru-Guzik, A. Quantum autoencoders for efficient compression of quantum data. Quantum Sci. Technol. 2017, 2, 045001. [Google Scholar] [CrossRef]
- Lamata, L.; Alvarez-Rodriguez, U.; Martín-Guerrero, J.D.; Sanz, M.; Solano, E. Quantum autoencoders via quantum adders with genetic algorithms. Quantum Sci. Technol. 2018, 4, 014007. [Google Scholar] [CrossRef]
- Ding, Y.; Lamata, L.; Sanz, M.; Chen, X.; Solano, E. Experimental implementation of a quantum autoencoder via quantum adders. Adv. Quantum Technol. 2019, 2, 1800065. [Google Scholar] [CrossRef]
- Kieferová, M.; Wiebe, N. Tomography and generative training with quantum Boltzmann machines. Phys. Rev. 2017, 96, 062327. [Google Scholar] [CrossRef]
- Jain, S.; Ziauddin, J.; Leonchyk, P.; Yenkanchi, S.; Geraci, J. Quantum and classical machine learning for the classification of non-small-cell lung cancer patients. Appl. Sci. 2020, 2, 1088 . [Google Scholar] [CrossRef]
- Dallaire-Demers, P.L.; Killoran, N. Quantum generative adversarial networks. Phys. Rev. 2018, 98, 012324. [Google Scholar] [CrossRef]
- Lloyd, S.; Weedbrook, C. Quantum Generative Adversarial Learning. Phys. Rev. Lett. 2018, 121, 040502.1–040502.5. [Google Scholar] [CrossRef] [PubMed]
- Romero, J.; Aspuru-Guzik, A. Variational quantum generators: Generative adversarial quantum machine learning for continuous distributions. Adv. Quantum Technol. 2021, 4, 2000003. [Google Scholar] [CrossRef]
- Zeng, J.; Wu, Y.; Liu, J.G.; Wang, L.; Hu, J. Learning and inference on generative adversarial quantum circuits. Phys. Rev. 2019, 99, 052306. [Google Scholar] [CrossRef]
- Rebentrost, P.; Mohseni, M.; Lloyd, S. Quantum support vector machine for big data classification. Phys. Rev. Lett. 2014, 113, 130503. [Google Scholar] [CrossRef]
- Mengoni, R.; Di Pierro, A. Kernel methods in quantum machine learning. Quantum Mach. Intell. 2019, 1, 65–71. [Google Scholar] [CrossRef]
- Huang, H.Y.; Broughton, M.; Mohseni, M.; Babbush, R.; Boixo, S.; Neven, H.; McClean, J.R. Power of data in quantum machine learning. Nat. Commun. 2021, 12, 1–9. [Google Scholar] [CrossRef]
- Ruff, L.; Vandermeulen, R.A.; Görnitz, N.; Deecke, L.; Kloft, M. Deep One-Class Classification. In Proceedings of the International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; pp. 4393–4402. [Google Scholar]
- Khan, S.S.; Madden, M.G. One-class classification: Taxonomy of study and review of techniques. Knowl. Eng. Rev. 2014, 29, 345–374. [Google Scholar] [CrossRef]
- Parzen, E. On estimation of a probability density function and mode. Ann. Math. Stat. 1962, 33, 1065–1076. [Google Scholar] [CrossRef]
- Schölkopf, B.; Platt, J.C.; Shawe-Taylor, J.; Smola, A.J.; Williamson, R.C. Estimating the support of a high-dimensional distribution. Neural Comput. 2001, 13, 1443–1471. [Google Scholar] [CrossRef]
- Tax, D.M.; Duin, R.P. Support vector data description. Mach. Learn. 2004, 54, 45–66. [Google Scholar] [CrossRef]
- Pekalska, E.; Tax, D.M.; Duin, R.P. One-class LP classifiers for dissimilarity representations. Adv. Neural Inf. Process. Syst. 2003, 15, 777–784. [Google Scholar]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Schmidhuber, J. Deep learning in neural networks: An overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef] [PubMed]
- Jinwon, A.; Sungzoon, C. Variational autoencoder based anomaly detection using reconstruction probability. Spec. Lect. 2015, 2, 1–18. [Google Scholar]
- Golan, I.; El-Yaniv, R. Deep anomaly detection using geometric transformations. Adv. Neural Inf. Process. Syst. 2018, 31, 9758–9769. [Google Scholar]
- Tack, J.; Mo, S.; Jeong, J.; Shin, J. Csi: Novelty detection via contrastive learning on distributionally shifted instances. Adv. Neural Inf. Process. Syst. 2020, 33, 11839–11852. [Google Scholar]
- Chen, H.; Wossnig, L.; Severini, S.; Neven, H.; Mohseni, M. Universal discriminative quantum neural networks. Quantum Mach. Intell. 2021, 3, 1–11. [Google Scholar] [CrossRef]
- Wilson, C.; Otterbach, J.; Tezak, N.; Smith, R.; Polloreno, A.; Karalekas, P.J.; Heidel, S.; Alam, M.S.; Crooks, G.; da Silva, M. Quantum kitchen sinks: An algorithm for machine learning on near-term quantum computers. arXiv 2018, arXiv:1806.08321. [Google Scholar]
- Skolik, A.; McClean, J.R.; Mohseni, M.; van der Smagt, P.; Leib, M. Layerwise learning for quantum neural networks. Quantum Mach. Intell. 2021, 3, 1–11. [Google Scholar] [CrossRef]
- Mari, A.; Bromley, T.R.; Izaac, J.; Schuld, M.; Killoran, N. Transfer learning in hybrid classical-quantum neural networks. Quantum 2020, 4, 340. [Google Scholar] [CrossRef]
- Park, G.; Huh, J.; Park, D.K. Variational quantum one-class classifier. arXiv 2022, arXiv:2210.02674. [Google Scholar] [CrossRef]
- Sakhnenko, A.; O’Meara, C.; Ghosh, K.J.; Mendl, C.B.; Cortiana, G.; Bernabé-Moreno, J. Hybrid classical-quantum autoencoder for anomaly detection. Quantum Mach. Intell. 2022, 4, 27. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Cong, I.; Choi, S.; Lukin, M.D. Quantum convolutional neural networks. Nat. Phys. 2019, 15, 1273–1278. [Google Scholar] [CrossRef]
- Farhi, E.; Neven, H. Classification with quantum neural networks on near term processors. arXiv 2018, arXiv:1802.06002. [Google Scholar]
- Killoran, N.; Bromley, T.R.; Arrazola, J.M.; Schuld, M.; Lloyd, S. Continuous-variable quantum neural networks. Phys. Rev. Res. 2019, 1, 033063. [Google Scholar] [CrossRef]
- McClean, J.R.; Romero, J.; Babbush, R.; Aspuru-Guzik, A. The theory of variational hybrid quantum-classical algorithms. New J. Phys. 2016, 18, 023023. [Google Scholar] [CrossRef]
- Li, W.; Deng, D.L. Recent advances for quantum classifiers. Sci. China Physics, Mech. Astron. 2022, 65, 220301. [Google Scholar] [CrossRef]
- Wierichs, D.; Izaac, J.; Wang, C.; Lin, C.Y.Y. General parameter-shift rules for quantum gradients. Quantum 2022, 6, 677. [Google Scholar] [CrossRef]
- Preskill, J. Quantum Computing in the NISQ era and beyond. Quantum 2018, 2, 79. [Google Scholar] [CrossRef]
- Shalev-Shwartz, S.; Shamir, O.; Shammah, S. Failures of gradient-based deep learning. In Proceedings of the International Conference on Machine Learning, PMLR, Sydney, Australia, 6–11 August 2017; pp. 3067–3075. [Google Scholar]
- Erfani, S.M.; Rajasegarar, S.; Karunasekera, S.; Leckie, C. High-dimensional and large-scale anomaly detection using a linear one-class SVM with deep learning. Pattern Recognit. 2016, 58, 121–134. [Google Scholar] [CrossRef]
- Sebastianelli, A.; Zaidenberg, D.A.; Spiller, D.; Le Saux, B.; Ullo, S.L. On circuit-based hybrid quantum neural networks for remote sensing imagery classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 2021, 15, 565–580. [Google Scholar] [CrossRef]
- Zeng, Y.; Wang, H.; He, J.; Huang, Q.; Chang, S. A Multi-Classification Hybrid Quantum Neural Network Using an All-Qubit Multi-Observable Measurement Strategy. Entropy 2022, 24, 394. [Google Scholar] [CrossRef] [PubMed]
- Smith, R.S.; Curtis, M.J.; Zeng, W.J. A practical quantum instruction set architecture. arXiv 2016, arXiv:1608.03355. [Google Scholar]



| Dataset | Network Type | Training Set Size | Qubit | Depth (D) | AUC | AUC* | |
|---|---|---|---|---|---|---|---|
| MNIST | DNN | 300 | 0 | 0 | 64 | 85.854% | 86.754% |
| QHDNN | 300 | 8 | 8 | 64 | 87.116% | 87.116% | |
| DNN | 300 | 0 | 0 | 256 | 86.273% | 86.588% | |
| QHDNN | 300 | 16 | 16 | 256 | 88.237% | 88.237% | |
| FashionMNIST | DNN | 300 | 0 | 0 | 64 | 86.032% | 86.725% |
| QHDNN | 300 | 8 | 8 | 64 | 87.591% | 88.132% | |
| DNN | 300 | 0 | 0 | 256 | 88.201% | 88.292% | |
| QHDNN | 300 | 16 | 16 | 256 | 88.186% | 89.414% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, M.; Huang, A.; Liu, Y.; Yi, X.; Wu, J.; Wang, S. A Quantum-Classical Hybrid Solution for Deep Anomaly Detection. Entropy 2023, 25, 427. https://doi.org/10.3390/e25030427
Wang M, Huang A, Liu Y, Yi X, Wu J, Wang S. A Quantum-Classical Hybrid Solution for Deep Anomaly Detection. Entropy. 2023; 25(3):427. https://doi.org/10.3390/e25030427
Chicago/Turabian StyleWang, Maida, Anqi Huang, Yong Liu, Xuming Yi, Junjie Wu, and Siqi Wang. 2023. "A Quantum-Classical Hybrid Solution for Deep Anomaly Detection" Entropy 25, no. 3: 427. https://doi.org/10.3390/e25030427
APA StyleWang, M., Huang, A., Liu, Y., Yi, X., Wu, J., & Wang, S. (2023). A Quantum-Classical Hybrid Solution for Deep Anomaly Detection. Entropy, 25(3), 427. https://doi.org/10.3390/e25030427






