Computing the Integrated Information of a Quantum Mechanism
Abstract
:1. Introduction
2. Theory
2.1. Classical Systems
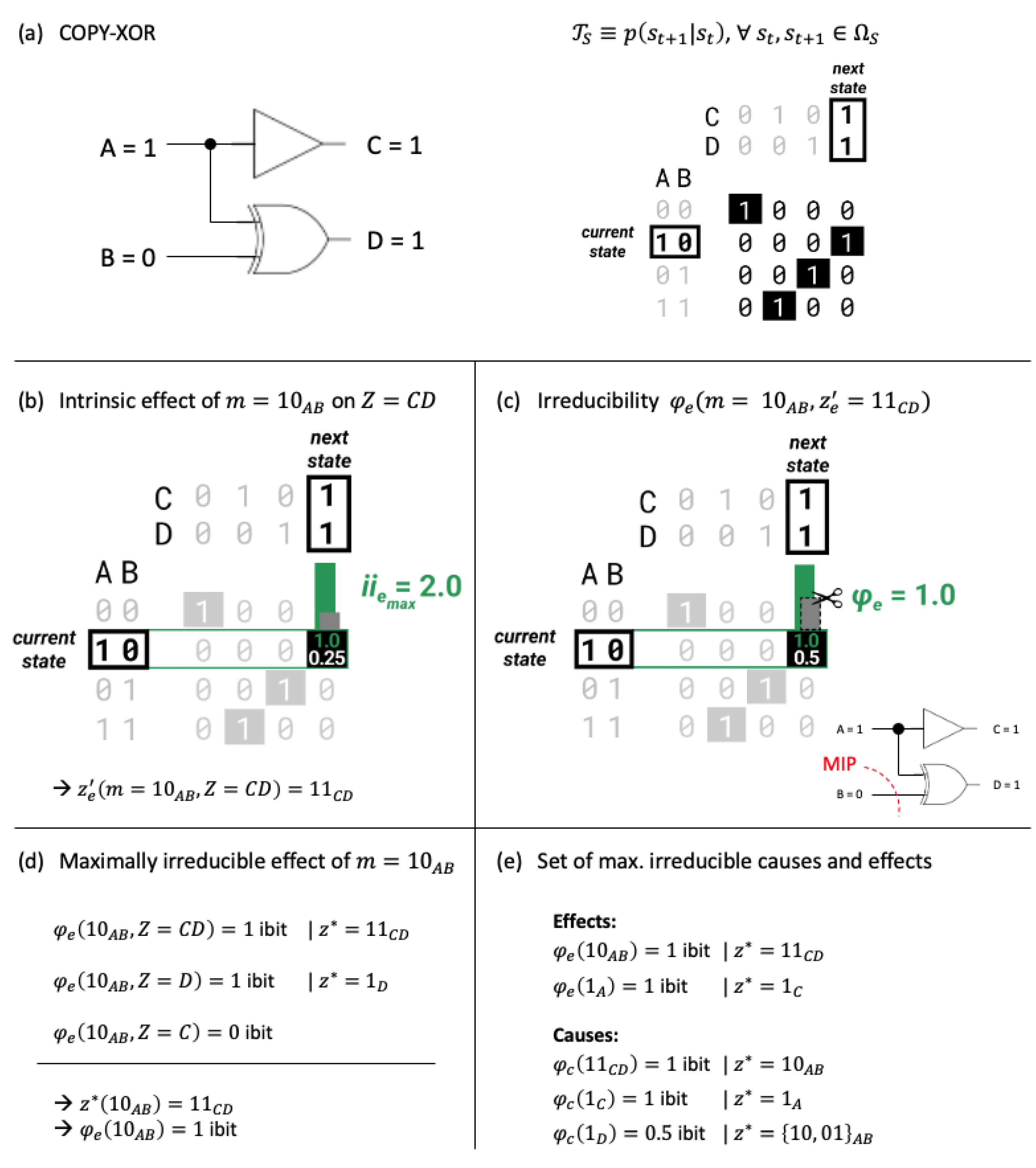
2.1.1. Cause and Effect Repertoires
2.1.2. Intrinsic Difference (ID)
2.1.3. Identifying Intrinsic Causes and Effects
2.1.4. Disintegrating Partitions
2.1.5. Mechanism Integrated Information
2.2. Quantum Systems
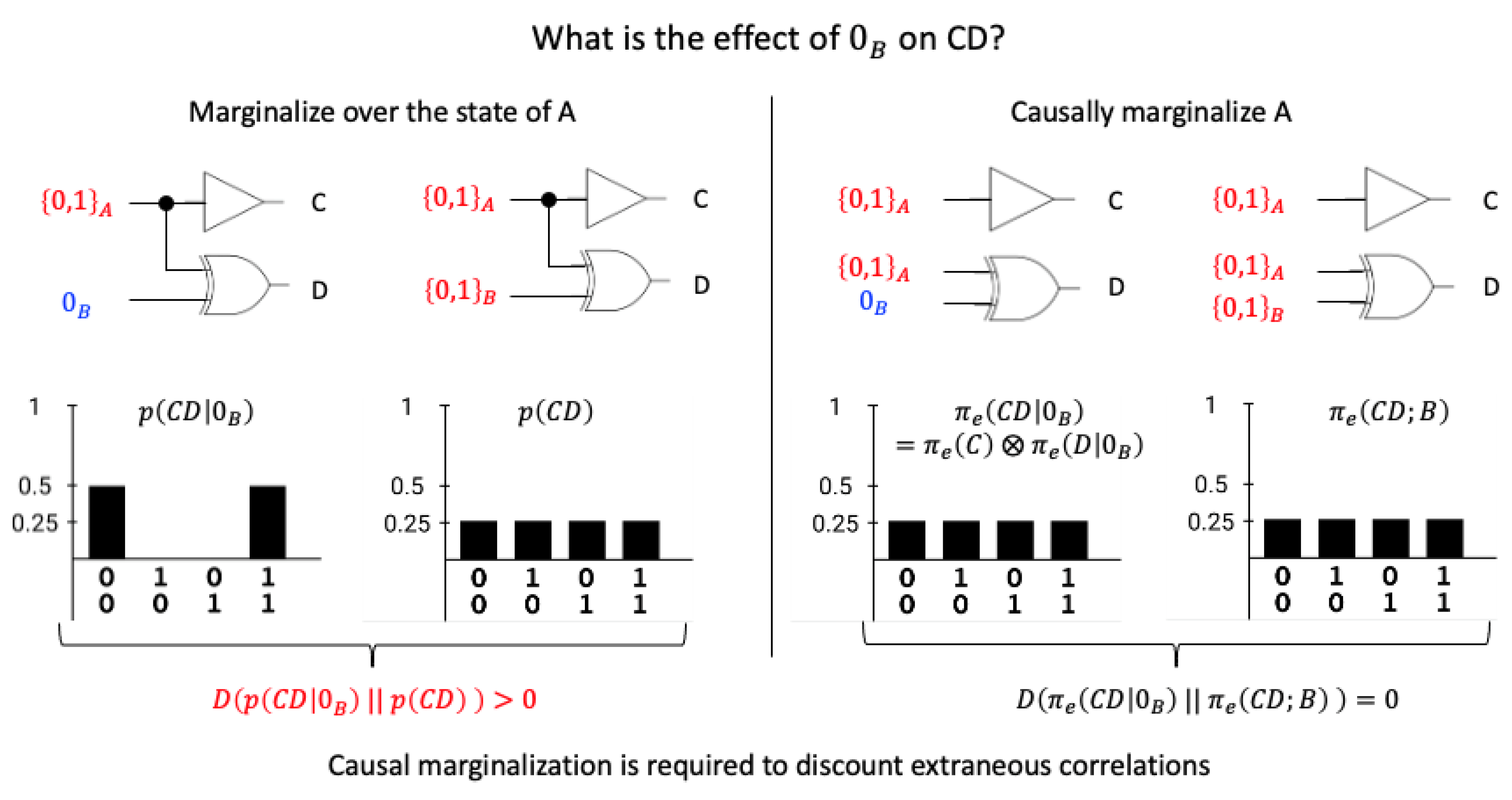
2.2.1. Quantum Cause and Effect Repertoires
- If corresponds to a pure state, the purview qubits are fully determined by the mechanism qubits. Thus, is not influenced by qubits outside of m. It follows that if the latter is pure. This is analogous to the classical case, where if is deterministic.
- Conceptually, entangled subsets are treated as indivisible units in the effect repertoire. If a purview is fully entangled, then .
- Extraneous classical correlations are successfully discounted, which means they will not contribute to the integrated information of a mechanism (Figure 3).
2.2.2. Quantum Intrinsic Information (QID)
2.2.3. Identifying Intrinsic Causes and Effects
2.2.4. Disintegrating Partitions
2.2.5. Quantum Mechanism Integrated Information
2.2.6. The Intrinsic Structure of a Quantum System
3. Results
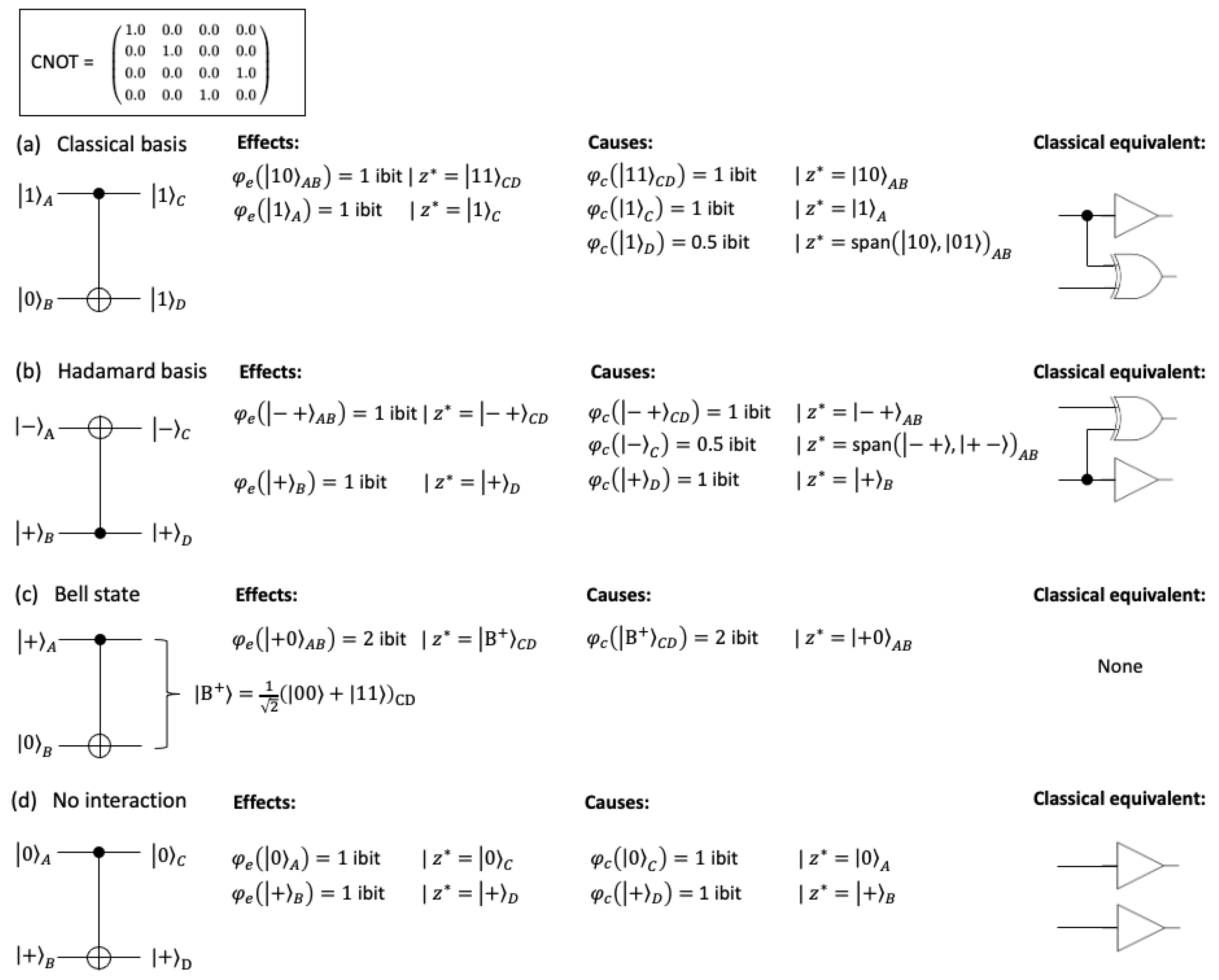
3.1. CNOT
3.1.1. Classical Case
3.1.2. Quantum Case
3.1.3. Mixed States and Extensions to Larger Systems
3.1.4. Intrinsic Structure Due to Entanglement
4. Discussion
4.1. Comparison with Previous Approaches
4.2. Measurement Dynamics
4.3. Formal Considerations and Limitations
4.4. From Micro to Macro?
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Oizumi, M.; Albantakis, L.; Tononi, G. From the Phenomenology to the Mechanisms of Consciousness: Integrated Information Theory 3.0. PLoS Comput. Biol. 2014, 10, e1003588. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tononi, G.; Boly, M.; Massimini, M.; Koch, C. Integrated information theory: From consciousness to its physical substrate. Nat. Rev. Neurosci. 2016, 17, 450–461. [Google Scholar] [CrossRef] [PubMed]
- Albantakis, L. Integrated information theory. In Beyond Neural Correlates of Consciousness; Overgaard, M., Mogensen, J., Kirkeby-Hinrup, A., Eds.; Routledge: Abingdon-on-Thames, UK, 2020; pp. 87–103. [Google Scholar] [CrossRef]
- Albantakis, L.; Barbosa, L.; Findlay, G.; Grasso, M.; Haun, A.M.; Marshall, W.; Mayner, W.G.; Zaeemzadeh, A.; Boly, M.; Juel, B.E.; et al. Integrated information theory (IIT) 4.0: Formulating the properties of phenomenal existence in physical terms. arXiv 2022. [Google Scholar] [CrossRef]
- Albantakis, L.; Tononi, G. Causal Composition: Structural Differences among Dynamically Equivalent Systems. Entropy 2019, 21, 989. [Google Scholar] [CrossRef] [Green Version]
- Barbosa, L.S.; Marshall, W.; Albantakis, L.; Tononi, G. Mechanism Integrated Information. Entropy 2021, 23, 362. [Google Scholar] [CrossRef]
- Grasso, M.; Albantakis, L.; Lang, J.P.; Tononi, G. Causal reductionism and causal structures. Nat. Neurosci. 2021, 24, 1348–1355. [Google Scholar] [CrossRef]
- Hoel, E.P.; Albantakis, L.; Tononi, G. Quantifying causal emergence shows that macro can beat micro. Proc. Natl. Acad. Sci. USA 2013, 110, 19790–19795. [Google Scholar] [CrossRef] [Green Version]
- Hoel, E.P.; Albantakis, L.; Marshall, W.; Tononi, G. Can the macro beat the micro? Integrated information across spatiotemporal scales. Neurosci. Conscious. 2016, 2016, niw012. [Google Scholar] [CrossRef] [Green Version]
- Marshall, W.; Albantakis, L.; Tononi, G. Black-boxing and cause-effect power. PLoS Comput. Biol. 2018, 14, e1006114. [Google Scholar] [CrossRef] [Green Version]
- Albantakis, L.; Massari, F.; Beheler-Amass, M.; Tononi, G. A Macro Agent and Its Actions. Synth. Libr. 2021, 439, 135–155. [Google Scholar] [CrossRef]
- Albantakis, L.; Tononi, G. The Intrinsic Cause-Effect Power of Discrete Dynamical Systems—From Elementary Cellular Automata to Adapting Animats. Entropy 2015, 17, 5472–5502. [Google Scholar] [CrossRef] [Green Version]
- Mayner, W.G.; Marshall, W.; Albantakis, L.; Findlay, G.; Marchman, R.; Tononi, G. PyPhi: A toolbox for integrated information theory. PLoS Comput. Biol. 2018, 14, e1006343. [Google Scholar] [CrossRef] [PubMed]
- Gomez, J.D.; Mayner, W.G.P.; Beheler-Amass, M.; Tononi, G.; Albantakis, L. Computing Integrated Information (Φ) in Discrete Dynamical Systems with Multi-Valued Elements. Entropy 2021, 23, 6. [Google Scholar] [CrossRef] [PubMed]
- Pearl, J. Causality: Models, Reasoning and Inference; Cambridge Univ Press: Cambridge, UK, 2000; Volume 29. [Google Scholar]
- Albantakis, L.; Marshall, W.; Hoel, E.; Tononi, G. What caused what? A quantitative account of actual causation using dynamical causal networks. Entropy 2019, 21, 459. [Google Scholar] [CrossRef] [Green Version]
- Barrett, A.B.; Mediano, P.A. The phi measure of integrated information is not well-defined for general physical systems. J. Conscious. Stud. 2019, 26, 11–20. [Google Scholar]
- Carroll, S. Consciousness and the Laws of Physics. J. Conscious. Stud. 2021, 28, 16–31. [Google Scholar] [CrossRef]
- Quantum causality. Nat. Phys. 2014, 10, 259–263. [CrossRef]
- D’Ariano, G.M. Causality re-established. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2018, 376, 20170313. [Google Scholar] [CrossRef] [Green Version]
- Tegmark, M. Consciousness as a state of matter. Chaos Solitons Fractals 2015, 76, 238–270. [Google Scholar] [CrossRef] [Green Version]
- Zanardi, P.; Tomka, M.; Venuti, L.C. Towards Quantum Integrated Information Theory. arXiv 2018, arXiv:1806.01421. [Google Scholar]
- Kleiner, J.; Tull, S. The Mathematical Structure of Integrated Information Theory. Front. Appl. Math. Stat. 2021, 6, 74. [Google Scholar] [CrossRef]
- Barbosa, L.S.; Marshall, W.; Streipert, S.; Albantakis, L.; Tononi, G. A measure for intrinsic information. Sci. Rep. 2020, 10, 18803. [Google Scholar] [CrossRef]
- Atmanspacher, H. Quantum Approaches to Consciousness. In The Stanford Encyclopedia of Philosophy, Summer 2020 ed.; Zalta, E.N., Ed.; Metaphysics Research Lab, Stanford University: Stanford, CA, USA, 2020. [Google Scholar]
- Prakash, C. On Invention of Structure in the World: Interfaces and Conscious Agents. Found. Sci. 2020, 25, 121–134. [Google Scholar] [CrossRef]
- Wigner, E.P. Remarks on the mind-body question. In Philosophical Reflections and Syntheses; Springer: Berlin/Heidelberg, Germany, 1995; pp. 247–260. [Google Scholar]
- Kremnizer, K.; Ranchin, A. Integrated Information-Induced Quantum Collapse. Found. Phys. 2015, 45, 889–899. [Google Scholar] [CrossRef] [Green Version]
- Chalmers, D.J.; McQueen, K.J. Consciousness and the Collapse of the Wave Function. arXiv 2021. [Google Scholar] [CrossRef]
- Penrose, R. The Emperor’s New Mind: Concerning Computers, Minds, and the Laws of Physics; Oxford University Press: Oxford, UK, 1999. [Google Scholar]
- Hameroff, S.; Penrose, R. Consciousness in the universe: A review of the ’Orch OR’ theory. Phys. Life Rev. 2014, 11, 39–78. [Google Scholar] [CrossRef] [Green Version]
- Tegmark, M. Importance of quantum decoherence in brain processes. Phys. Rev. E 2000, 61, 4194–4206. [Google Scholar] [CrossRef] [Green Version]
- Koch, C.; Hepp, K. Quantum mechanics in the brain. Nature 2006, 440, 611. [Google Scholar] [CrossRef]
- Hagan, S.; Hameroff, S.R.; Tuszyński, J.A. Quantum computation in brain microtubules: Decoherence and biological feasibility. Phys. Rev. E 2002, 65, 061901. [Google Scholar] [CrossRef] [Green Version]
- Vaziri, A.; Plenio, M.B. Quantum coherence in ion channels: Resonances, transport and verification. New J. Phys. 2010, 12, 085001. [Google Scholar] [CrossRef]
- Rourk, C.J. Indication of quantum mechanical electron transport in human substantia nigra tissue from conductive atomic force microscopy analysis. Biosystems 2019, 179, 30–38. [Google Scholar] [CrossRef] [Green Version]
- Atmanspacher, H.; Prentner, R. Desiderata for a Viable Account of Psychophysical Correlations. Mind Matter 2022, 20, 63–86. [Google Scholar]
- Janzing, D.; Balduzzi, D.; Grosse-Wentrup, M.; Schölkopf, B. Quantifying causal influences. Ann. Stat. 2013, 41, 2324–2358. [Google Scholar] [CrossRef]
- Ay, N.; Polani, D. Information Flows in Causal Networks. Adv. Complex Syst. 2008, 11, 17–41. [Google Scholar] [CrossRef] [Green Version]
- Marshall, W.; Grasso, M.; Mayner, W.G.P.; Zaeemzadeh, A.; Barbosa, L.S.; Chastain, E.; Findlay, G.; Sasai, S.; Albantakis, L.; Tononi, G. System Integrated Information. Entropy 2023, 25, 334. [Google Scholar] [CrossRef] [PubMed]
- Zaeemzadeh, A.; Tononi, G. Upper Bounds for Integrated Information. In preparation.
- Krohn, S.; Ostwald, D. Computing integrated information. Neurosci. Conscious. 2017, 2017, nix017. [Google Scholar] [CrossRef] [Green Version]
- Moon, K. Exclusion and Underdetermined Qualia. Entropy 2019, 21, 405. [Google Scholar] [CrossRef] [Green Version]
- Vedral, V. The role of relative entropy in quantum information theory. Rev. Mod. Phys. 2002, 74, 197. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Y.; Zhao, Q.; Yuan, X.; Ma, X. Detecting multipartite entanglement structure with minimal resources. Npj Quantum Inf. 2019, 5, 83. [Google Scholar] [CrossRef] [Green Version]
- Gühne, O.; Tóth, G. Entanglement detection. Phys. Rep. 2009, 474, 1–75. [Google Scholar] [CrossRef] [Green Version]
- Li, J.L.; Qiao, C.F. A Necessary and Sufficient Criterion for the Separability of Quantum State. Sci. Rep. 2018, 8, 1442. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Skorobagatko, G.A. Universal separability criterion for arbitrary density matrices from causal properties of separable and entangled quantum states. Sci. Rep. 2021, 11, 15866. [Google Scholar] [CrossRef] [PubMed]
- Peres, A. Separability Criterion for Density Matrices. Phys. Rev. Lett. 1996, 77, 1413. [Google Scholar] [CrossRef] [Green Version]
- Horodecki, M.; Horodecki, P.; Horodecki, R. Separability of mixed states: Necessary and sufficient conditions. Phys. Lett. A 1996, 223, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Bennett, C.H.; Di Vincenzo, D.P.; Mor, T.; Shor, P.W.; Smolin, J.A.; Terhal, B.M. Unextendible Product Bases and Bound Entanglement. Phys. Rev. Lett. 1999, 82, 5385. [Google Scholar] [CrossRef] [Green Version]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information: 10th Anniversary Edition, 10th ed.; Cambridge University Press: New York, NY, USA, 2011. [Google Scholar]
- Dur, W.; Vidal, G.; Cirac, J.I. Three qubits can be entangled in two inequivalent ways. Phys. Rev. A 2000, 62, 062314. [Google Scholar] [CrossRef] [Green Version]
- Haun, A.; Tononi, G. Why Does Space Feel the Way it Does? Towards a Principled Account of Spatial Experience. Entropy 2019, 21, 1160. [Google Scholar] [CrossRef] [Green Version]
- Mermin, N.D. Quantum Computer Science. An Introduction; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Schumacher, B.; Westmoreland, M.D. Isolation and Information Flow in Quantum Dynamics. Found. Phys. 2012, 42, 926–931. [Google Scholar] [CrossRef] [Green Version]
- Greenberger, D.M.; Horne, M.A.; Zeilinger, A. Going Beyond Bell’s Theorem. In Bell’s Theorem, Quantum Theory and Conceptions of the Universe; Springer: Dordrecht, The Netherlands, 1989; pp. 69–72. [Google Scholar] [CrossRef]
- Acín, A.; Bruß, D.; Lewenstein, M.; Sanpera, A. Classification of Mixed Three-Qubit States. Phys. Rev. Lett. 2001, 87, 040401. [Google Scholar] [CrossRef] [Green Version]
- Arkhipov, A. Non-Separability of Physical Systems as a Foundation of Consciousness. Entropy 2022, 24, 1539. [Google Scholar] [CrossRef]
- Schwindt, J.M. Nothing happens in the Universe of the Everett Interpretation. arXiv 2012. [Google Scholar] [CrossRef]
- Carroll, S.M.; Singh, A. Quantum mereology: Factorizing Hilbert space into subsystems with quasiclassical dynamics. Phys. Rev. A 2021, 103, 022213. [Google Scholar] [CrossRef]
- Everett, H., III. “ Relative state” formulation of quantum mechanics. Rev. Mod. Phys. 1957, 29, 454. [Google Scholar] [CrossRef] [Green Version]
- Seth, A. Being You: A New Science of Consciousness; Penguin: London, UK, 2021. [Google Scholar]
- Koch, C.; Massimini, M.; Boly, M.; Tononi, G. Neural correlates of consciousness: Progress and problems. Nat. Rev. Neurosci. 2016, 17, 307–321. [Google Scholar] [CrossRef]
- Durham, I. A Formal Model for Adaptive Free Choice in Complex Systems. Entropy 2020, 22, 568. [Google Scholar] [CrossRef] [PubMed]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Albantakis, L.; Prentner, R.; Durham, I. Computing the Integrated Information of a Quantum Mechanism. Entropy 2023, 25, 449. https://doi.org/10.3390/e25030449
Albantakis L, Prentner R, Durham I. Computing the Integrated Information of a Quantum Mechanism. Entropy. 2023; 25(3):449. https://doi.org/10.3390/e25030449
Chicago/Turabian StyleAlbantakis, Larissa, Robert Prentner, and Ian Durham. 2023. "Computing the Integrated Information of a Quantum Mechanism" Entropy 25, no. 3: 449. https://doi.org/10.3390/e25030449
APA StyleAlbantakis, L., Prentner, R., & Durham, I. (2023). Computing the Integrated Information of a Quantum Mechanism. Entropy, 25(3), 449. https://doi.org/10.3390/e25030449





