Interdiffusion in Refractory Metal System with a BCC Lattice: Ti/TiZrHfNbTaMo
Abstract
:1. Introduction
2. Materials and Methods
- (1)
- Obtaining HEA/Ti diffusion pairs by pre-welding the HEA samples along with titanium plates and quality control of the welded seams;
- (2)
- Diffusion annealing at different temperatures during the experiment time;
- (3)
- Diffusion penetration zone identification in the diffusion pair after annealing by a mechanical treatment aid using grinding abrasive paper and felt disks with a concentrated colloidal silicon suspension;
- (4)
- Interdiffusion zone profiling using EPMA;
- (5)
- Analytical processing of the obtained diffusion profiles, calculation of HEA diffusion characteristics by the Hall’s method, and discussion of the results obtained.
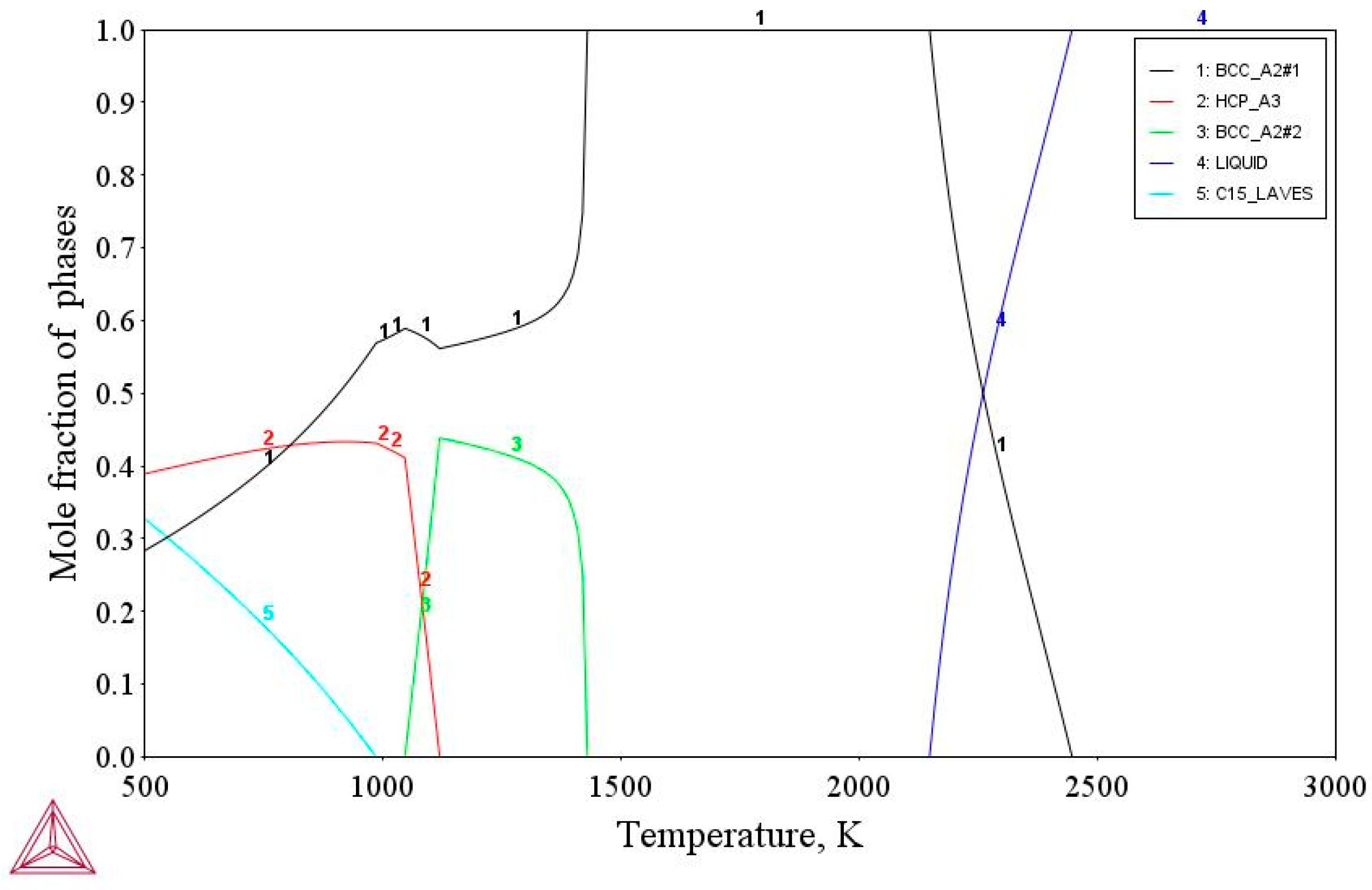
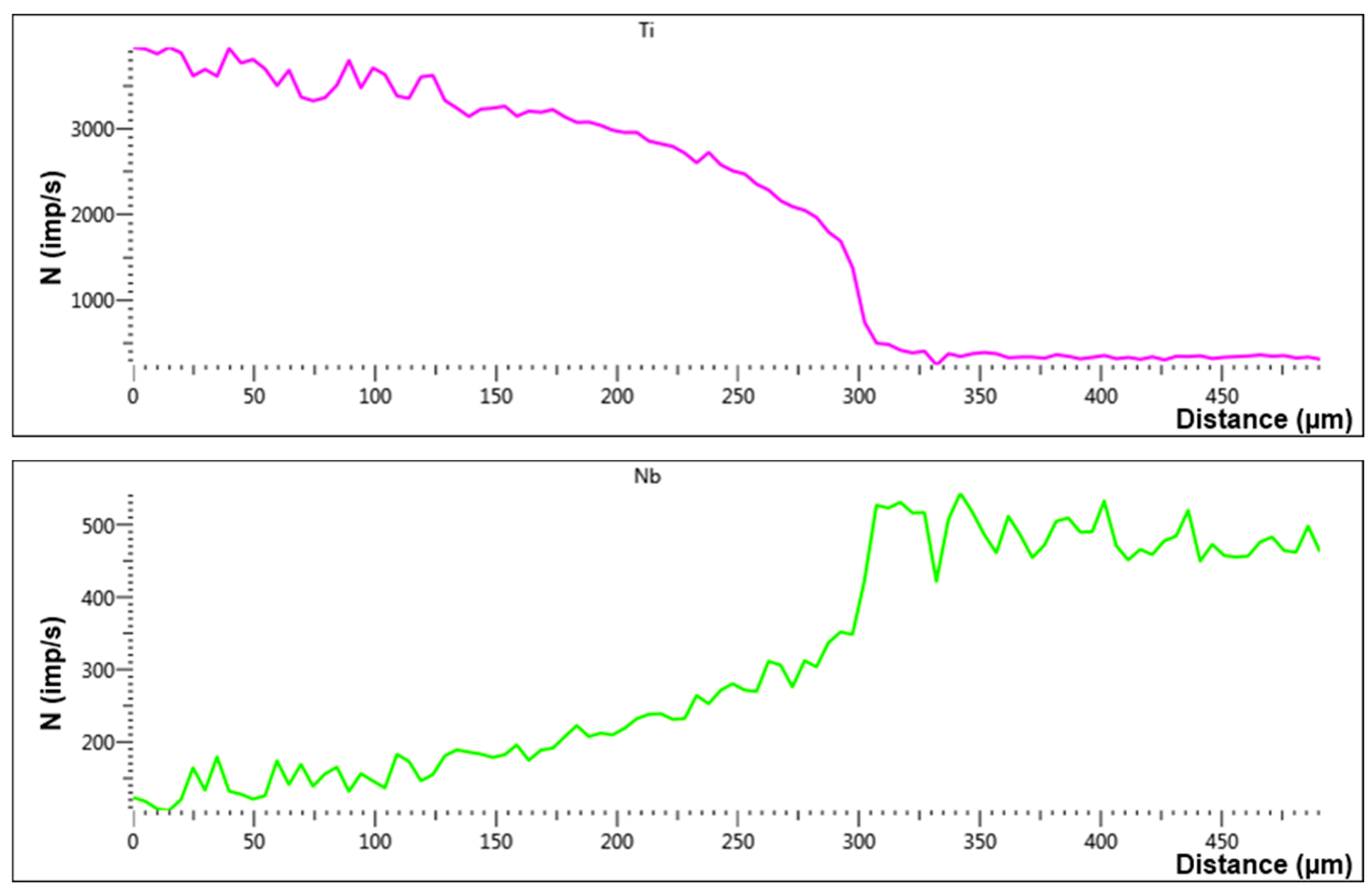
3. Experimental Results
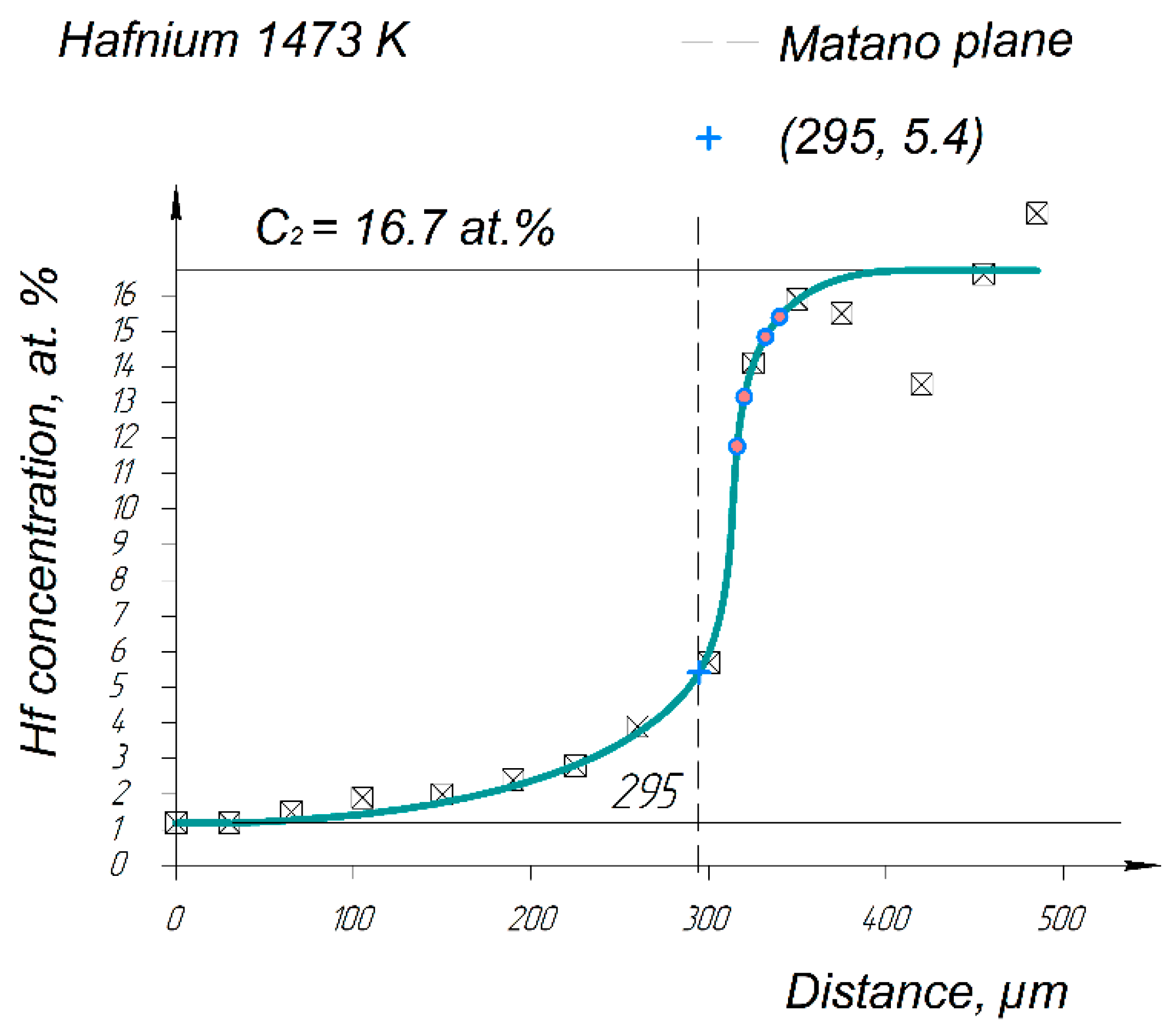
4. Calculation of Diffusion Parameters
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Diffusion Profiles of the Researched System Elements
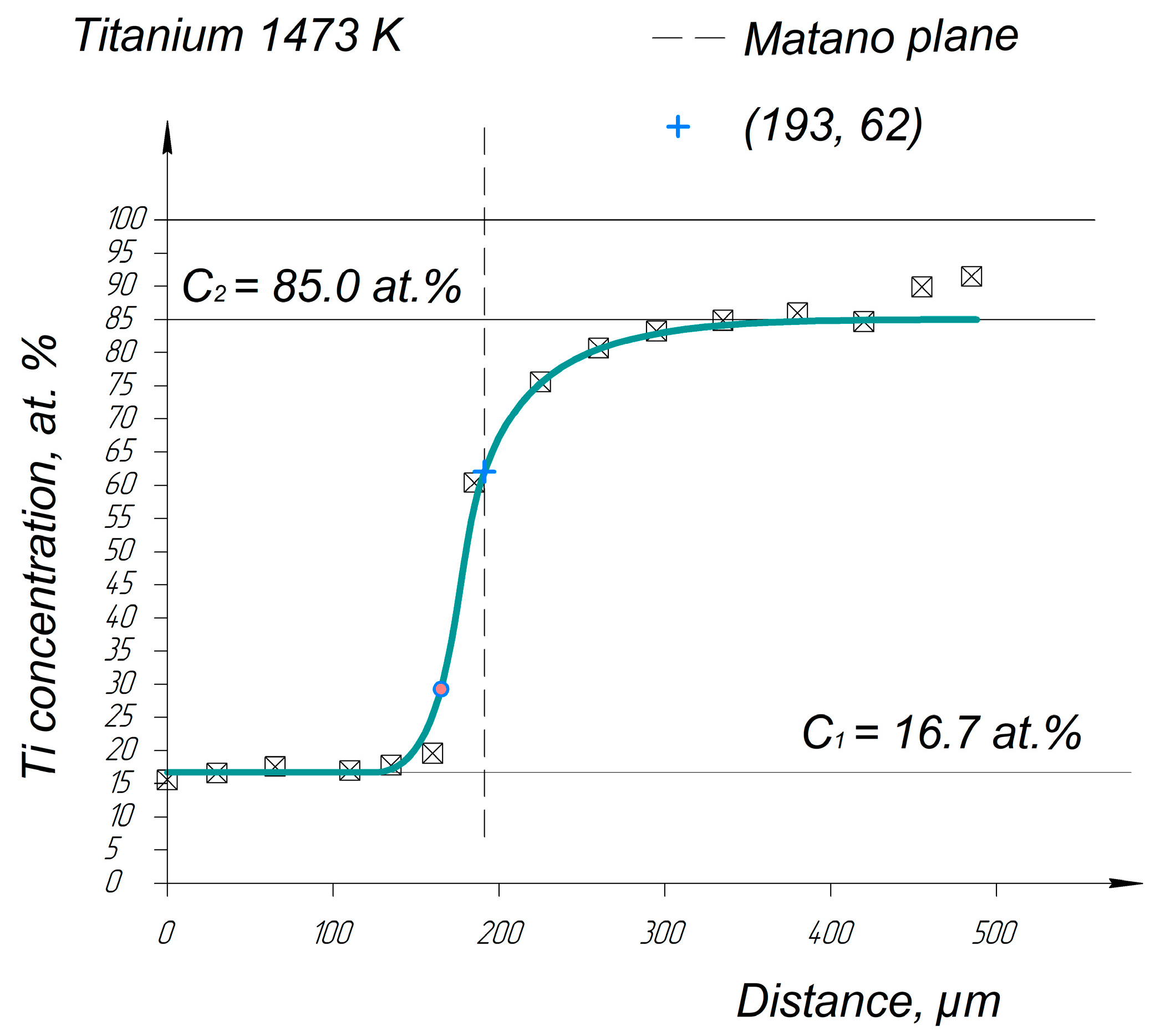
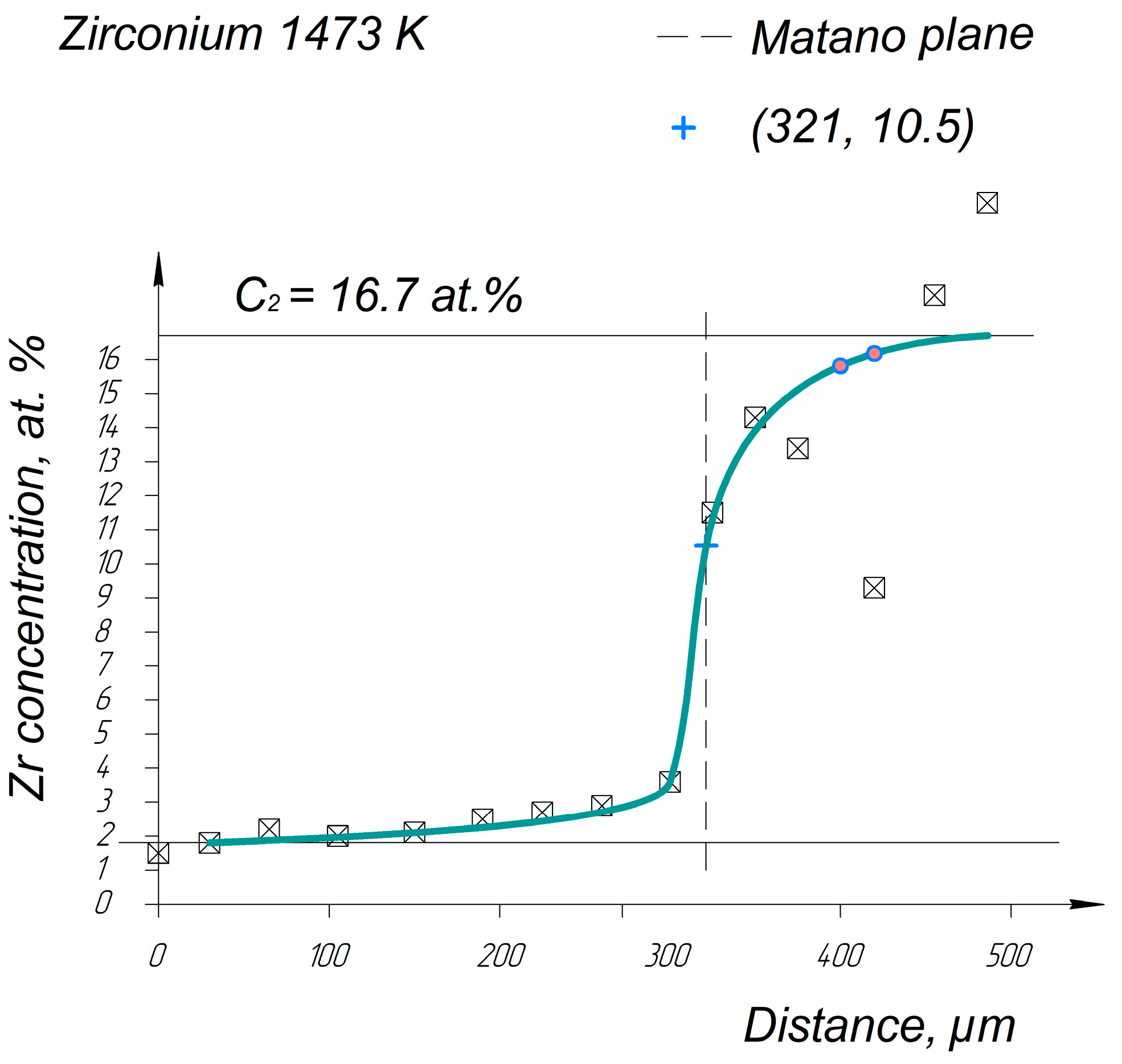


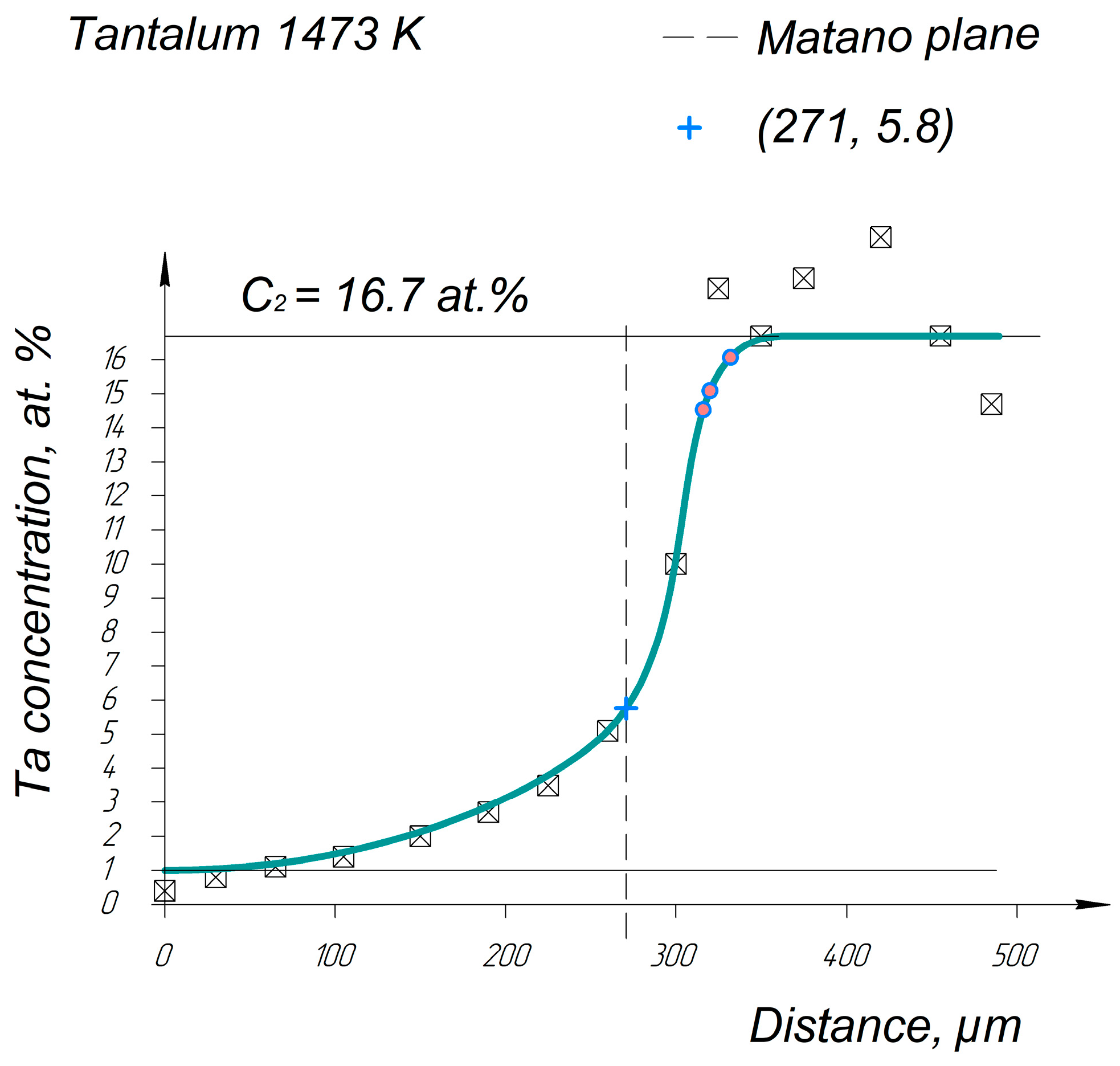
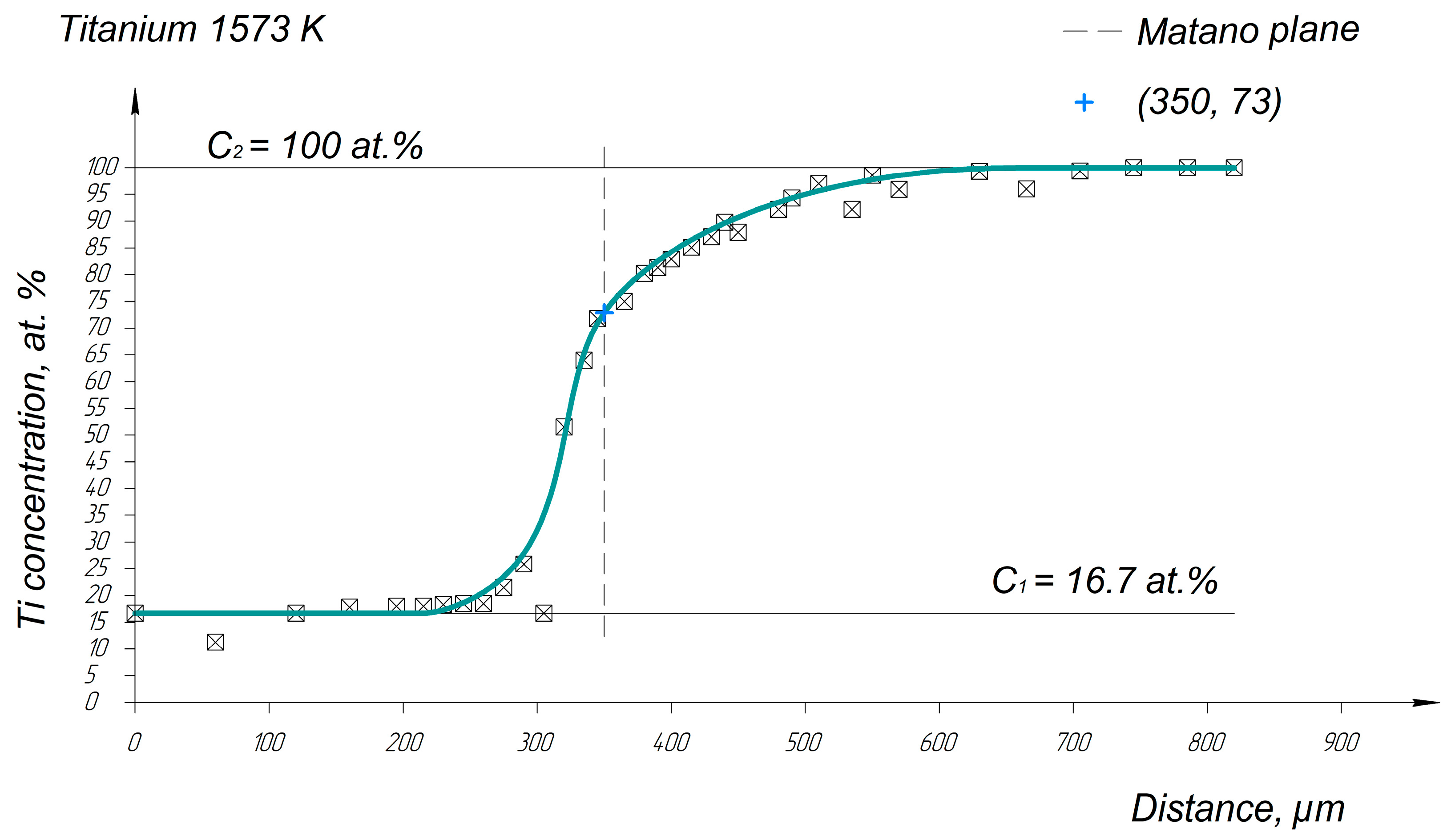
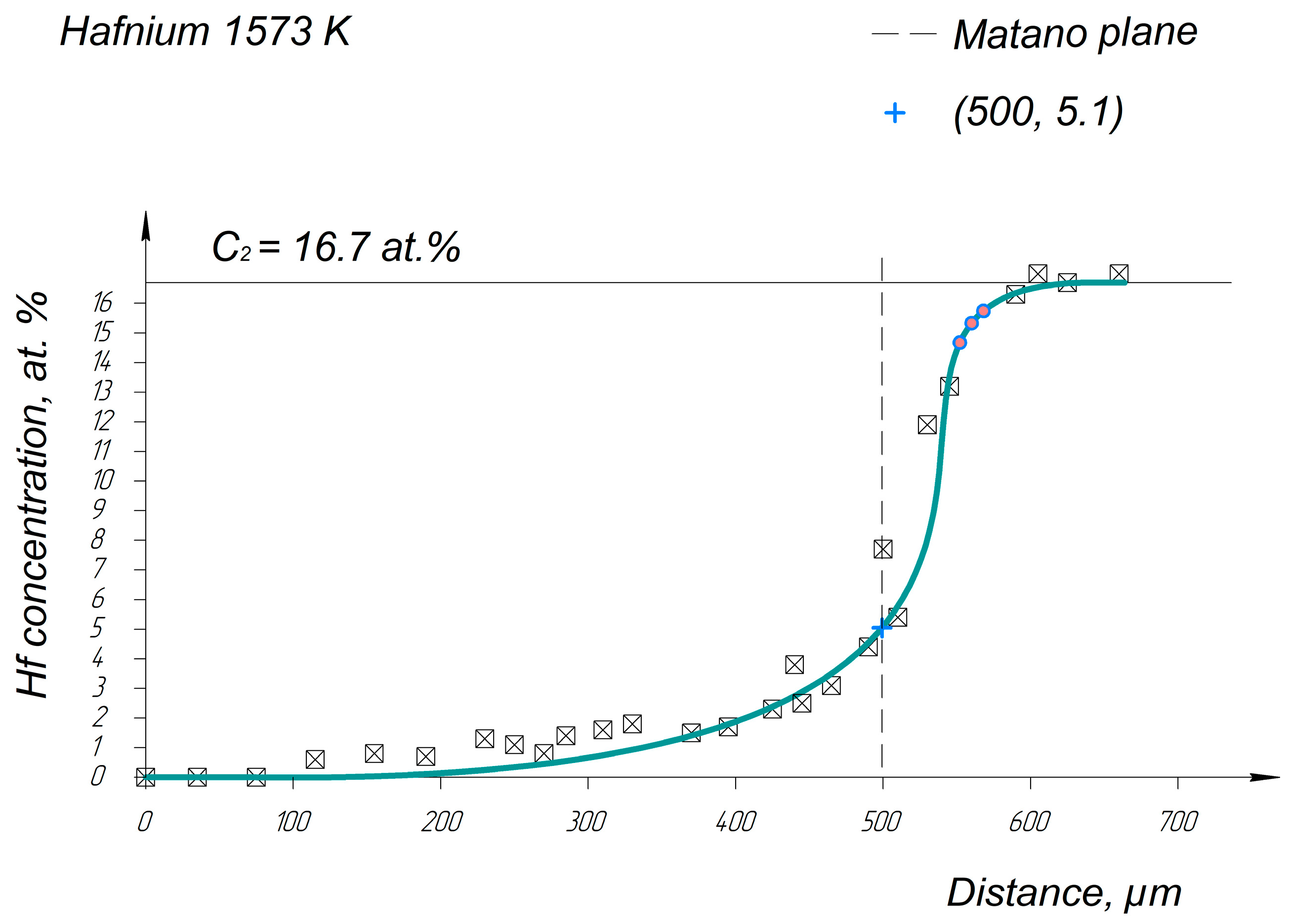


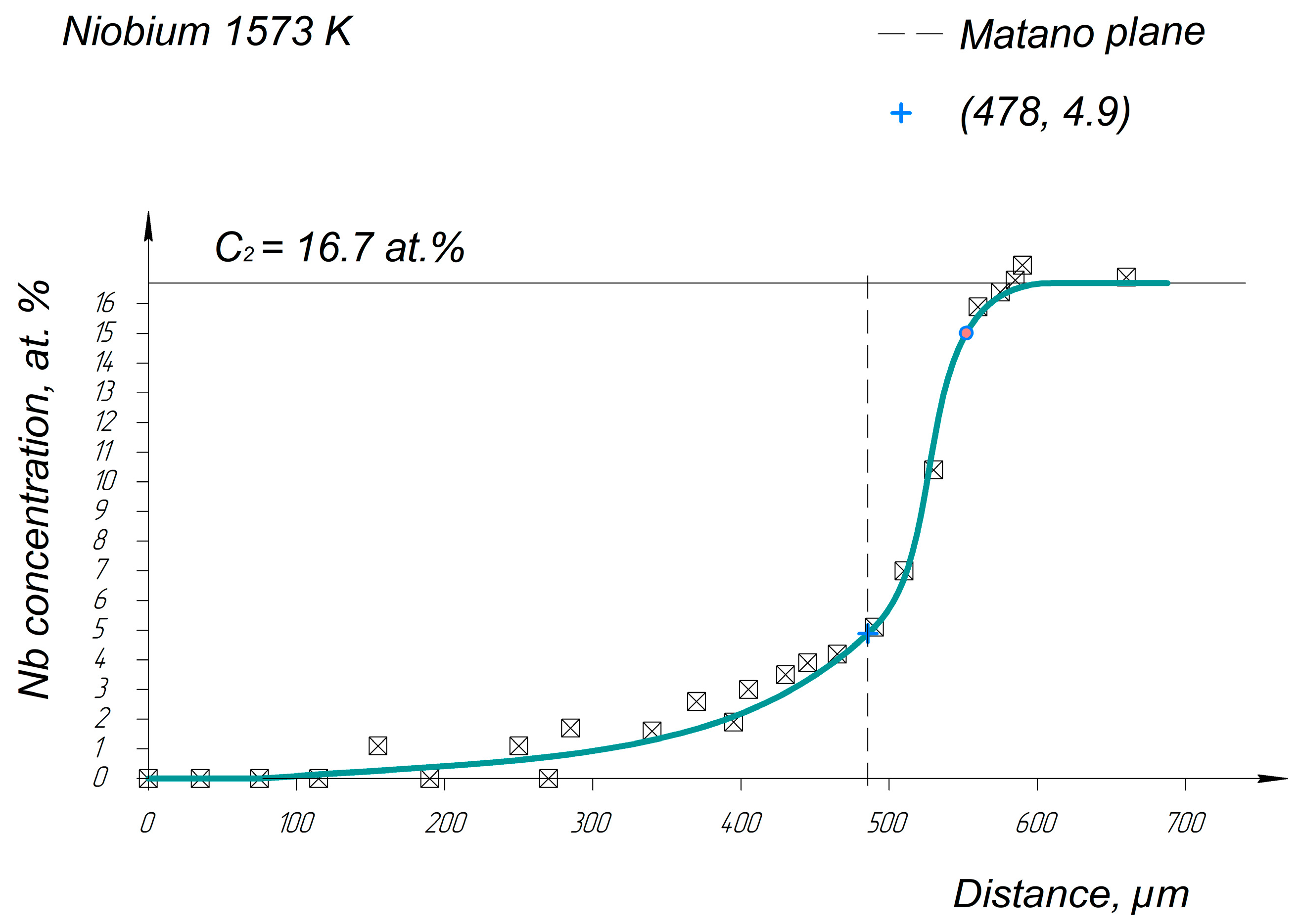
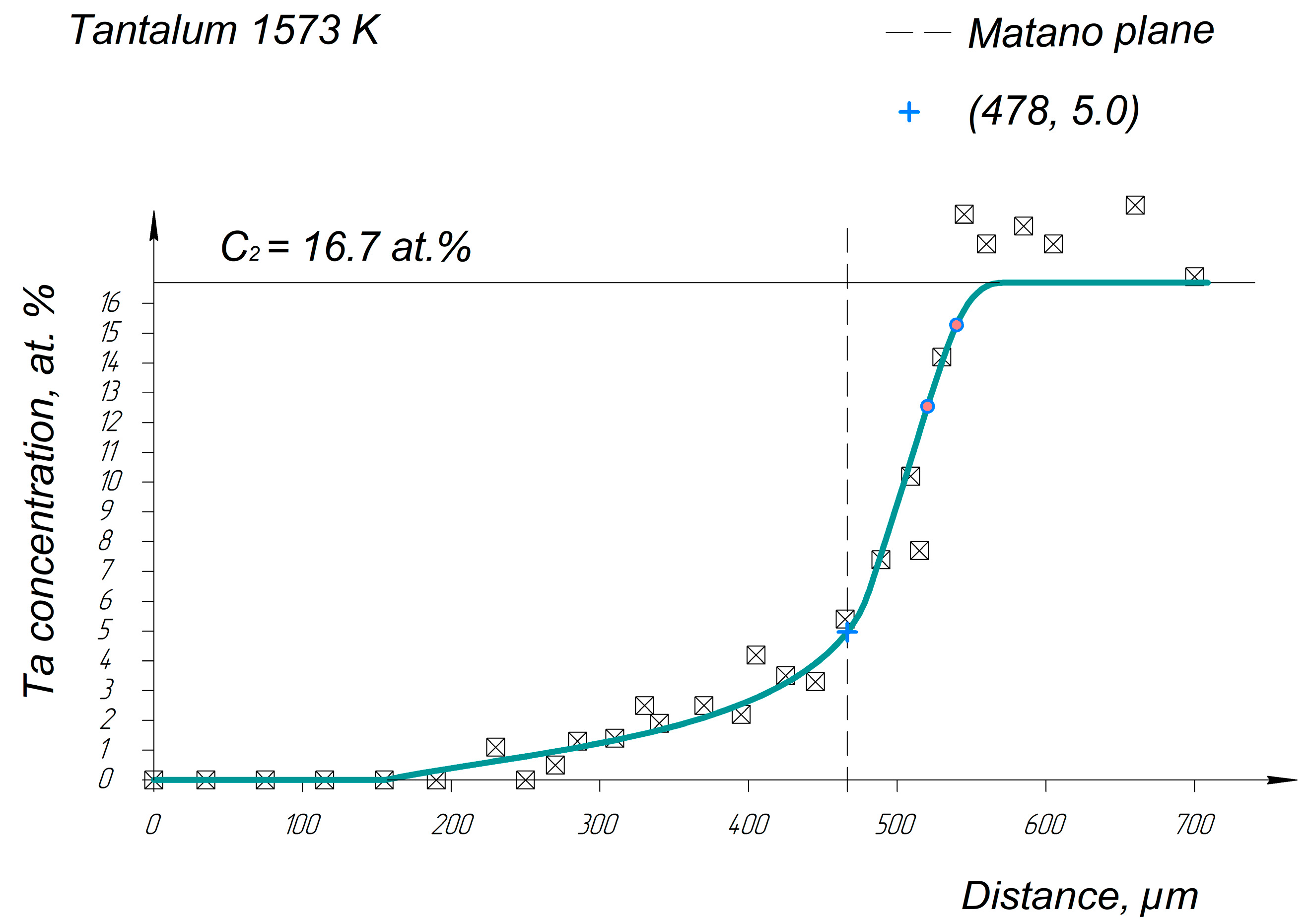
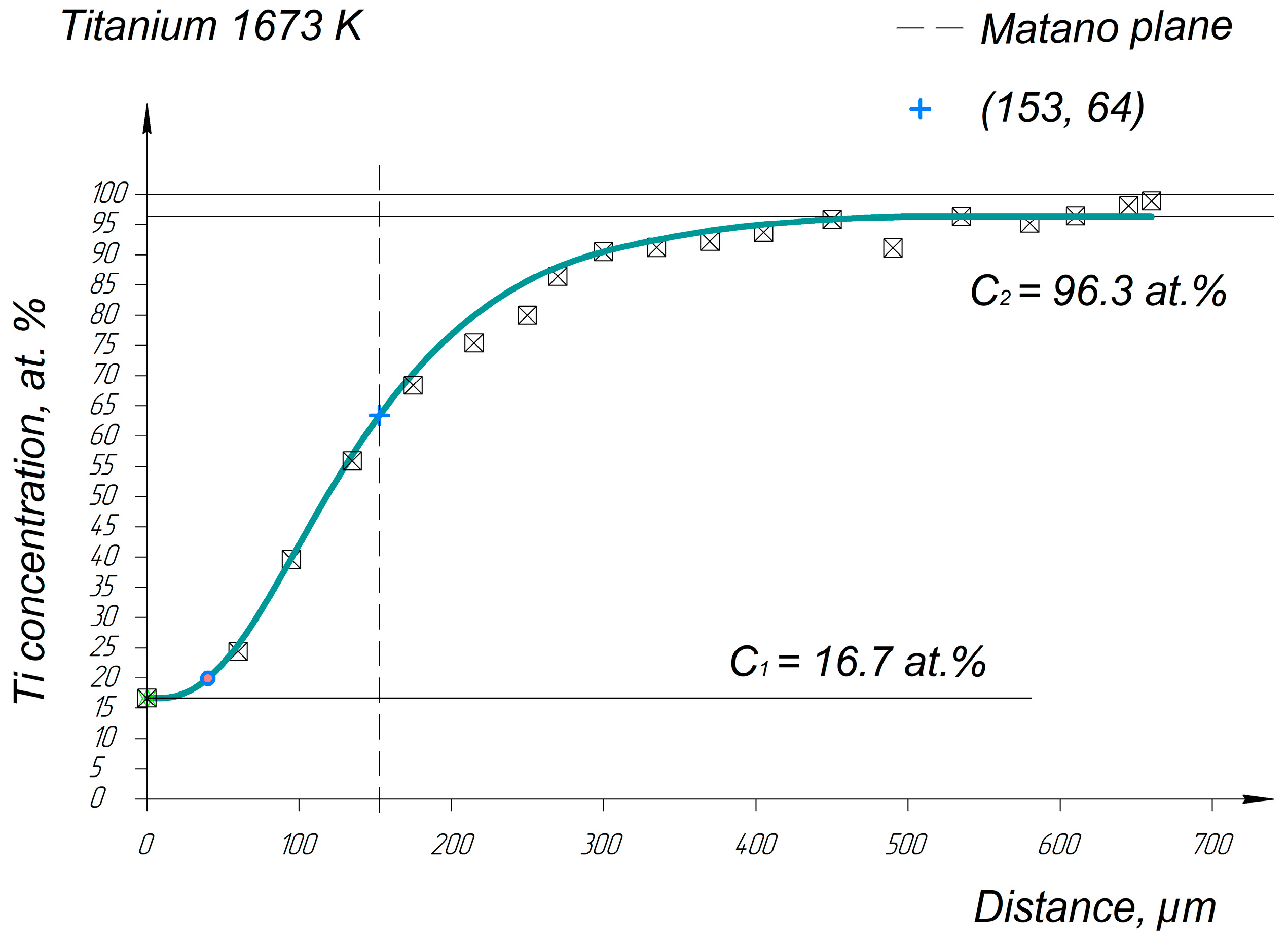
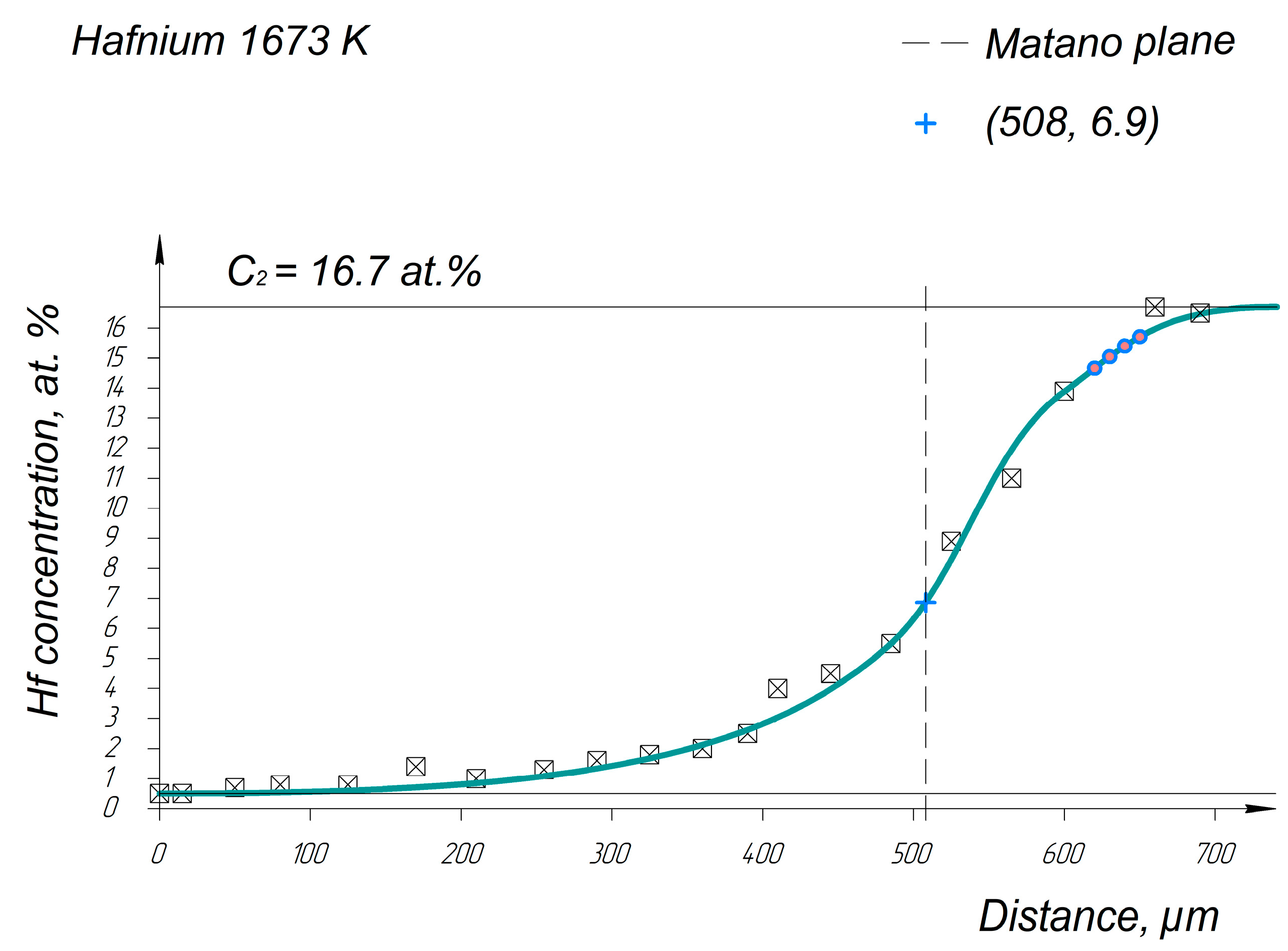

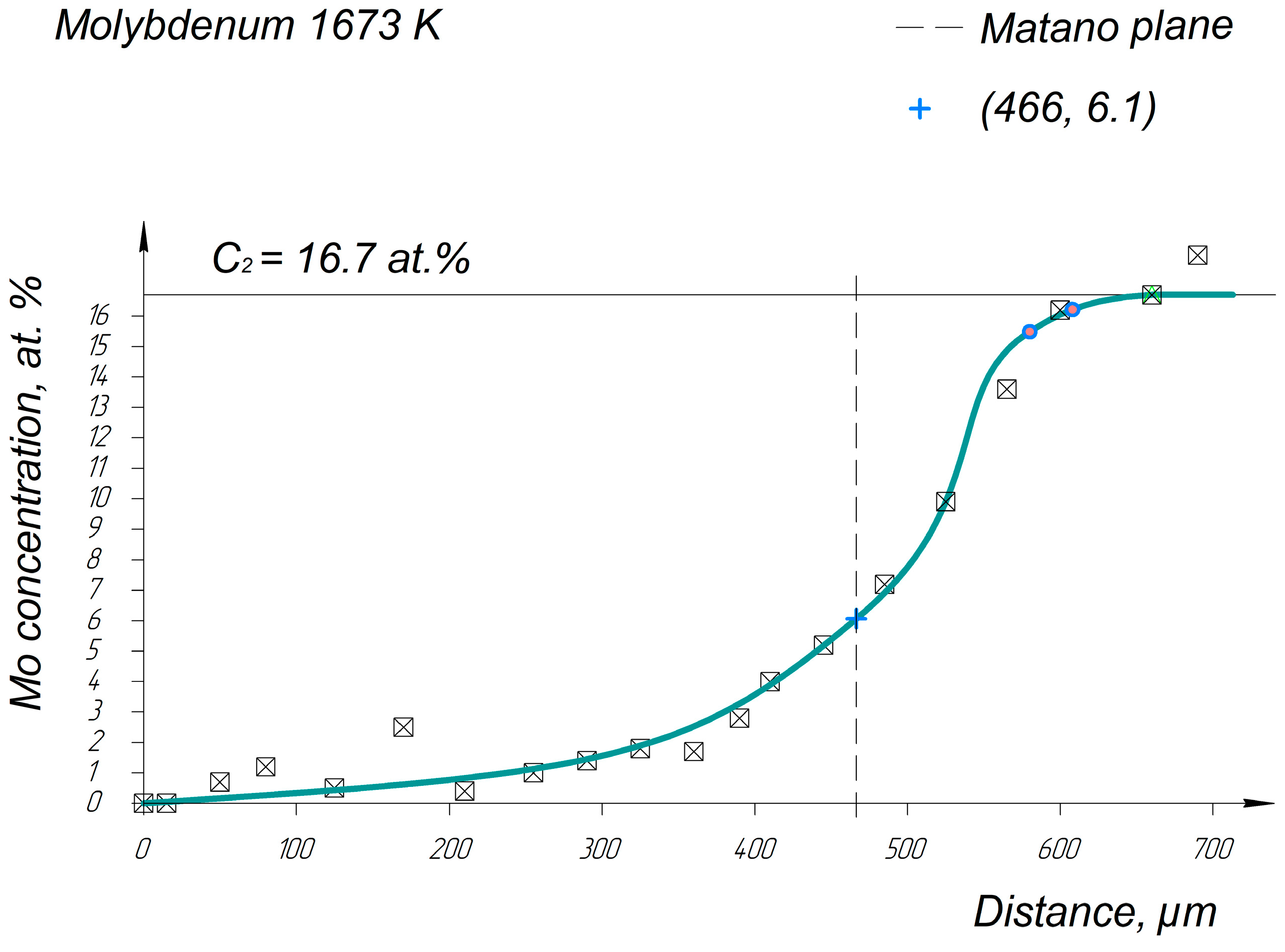

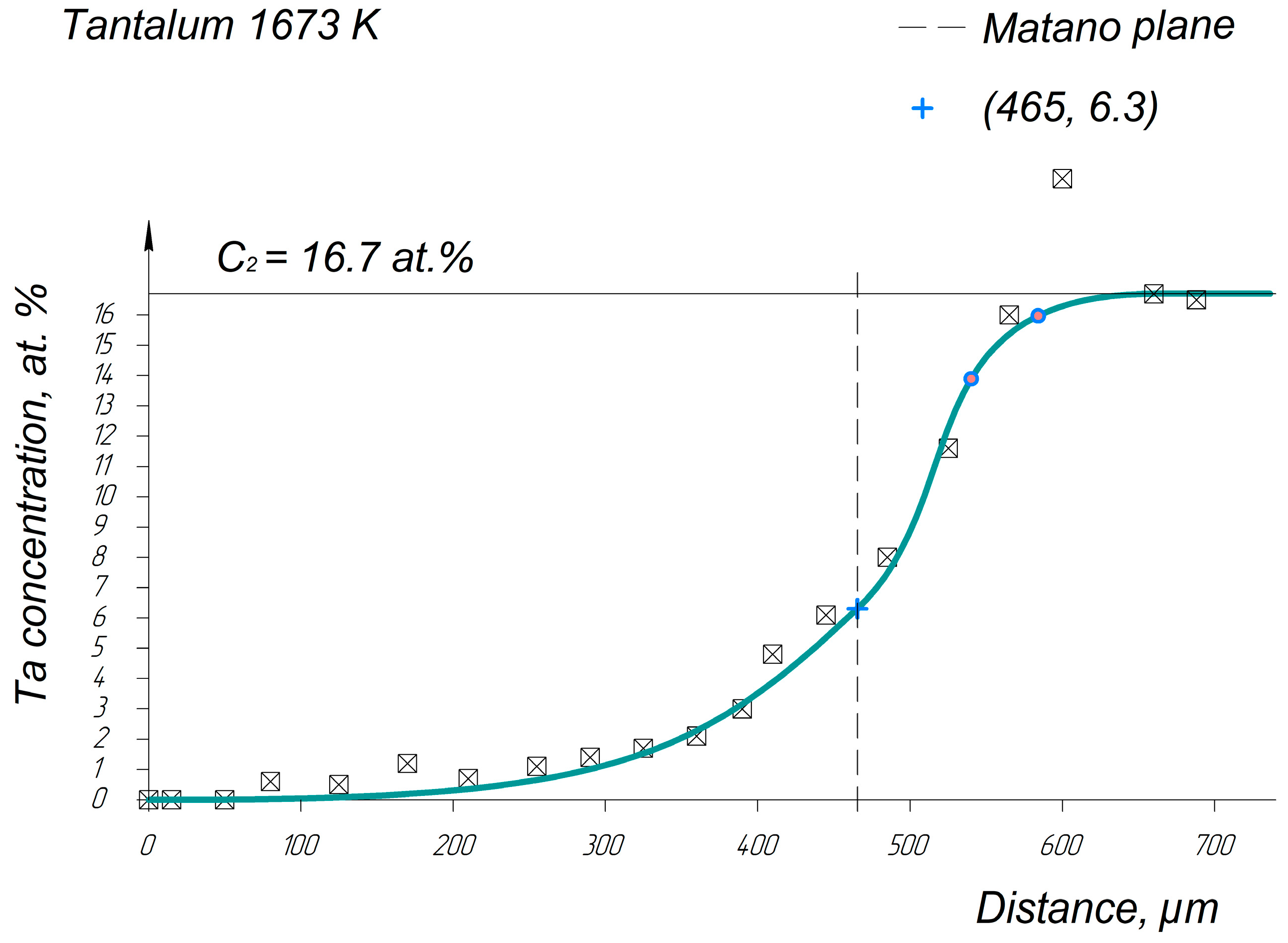
References
- Sims, C.T.; Stoloff, N.S.; Hagel, W.C. Superalloys II: High-Temperature Materials for Aerospace and Industrial Power, 2nd ed.; Wiley-Interscience: New York, NY, USA, 1987; p. 640. [Google Scholar]
- Kablov, E. Cast Blades of Gas Turbine Engines: Alloys, Technologies, Coatings; MISiS: Moscow, Russia, 2001; p. 632. (In Russian) [Google Scholar]
- Reed, R.C. The Superalloys. Fundamentals and Applications; Cambridge University Press: New York, NY, USA, 2006; p. 372. [Google Scholar]
- Yeh, J.-W.; Chen, S.K.; Lin, S.-J.; Gan, J.-Y.; Chin, T.-S.; Shun, T.-T.; Tsau, C.-H.; Chang, S.-Y. Nanostructured High-Entropy Alloys with Multiple Principal Elements: Novel Alloy Design Concepts and Outcomes. Adv. Eng. Mater. 2004, 6, 299–303. [Google Scholar] [CrossRef]
- Cantor, B. Multicomponent high-entropy Cantor alloys. Prog. Mater. Sci. 2021, 120, 100754. [Google Scholar] [CrossRef]
- Pickering, E.J.; Jones, N.G. High-entropy alloys: A critical assessment of their founding principles and future prospects. Int. Mater. Rev. 2016, 61, 183–202. [Google Scholar] [CrossRef] [Green Version]
- Miracle, D.B.; Senkov, O.N. A critical review of high entropy alloys and related concepts. Acta Mater. 2017, 122, 448–511. [Google Scholar] [CrossRef] [Green Version]
- Yeh, J.-W. Alloy design strategies and future trends in high-entropy alloys. JOM 2013, 65, 1759–1771. [Google Scholar] [CrossRef]
- Vaidya, M.; Pradeep, K.G.; Murty, B.S.; Wilde, G.; Divinski, S.V. Bulk tracer diffusion in CoCrFeNi and CoCrFeMnNi high entropy alloys. Acta Mater. 2018, 146, 211. [Google Scholar] [CrossRef]
- Dabrowa, J.; Zajusz, M.; Kucza, W.; Cieslak, G.; Berent, K.; Czeppe, T.; Kulik, T.; Danielewski, M. Demystifying the sluggish diffusion effect in high entropy alloys. J. Alloy. Compd. 2019, 783, 193–207. [Google Scholar] [CrossRef]
- Divinski, S.V.; Pokoev, A.; Esakkiraja, N.; Paul, A.A. Mystery of ’sluggish diffusion’ in high-entropy alloys: The truth or a myth? Diffus. Found. 2018, 17, 69–104. [Google Scholar] [CrossRef] [Green Version]
- Beke, D.L.; Erdélyi, G. On the Self- and Impurity Diffusion in High Entropy Alloys. Diffus. Found. 2018, 17, 105–114. [Google Scholar] [CrossRef]
- Savitskii, E.M.; Burkhanov, G.S. Physical Metallurgy of Refractory Metals and Alloys; Springer New York: New York, NY, USA, 1970; p. 288. [Google Scholar] [CrossRef]
- Razumovskii, I.M.; Beresnev, A.G.; Locacheva, A.I.; Gusakov, M.S.; Razumovsky, M.I. Physics and chemical factors of heat resistance of alloys based on many refractory metals: An introduction to the problem. Compos. Mater. Constr. 2022, 3, 25–35. [Google Scholar] [CrossRef]
- Portnoi, V.K.; Leonov, A.V.; Gusakov, M.S.; Logachev, I.A.; Fedotov, S.A. Preparation of high-temperature multicomponent alloys by mechanochemical synthesis from refractory elements. Inorg. Mater. 2019, 55, 195–199. [Google Scholar] [CrossRef]
- Razumovsky, M.I.; Khvan, A.V.; Bokstein, B.S. Kinetic and thermodynamic properties of alloy based on refractory metals (high-entropy alloy). In Proceedings of the 9-th International Conference with Elements of Scientific School for Young Scientists, Functional Nanomaterials and High-Purity Substances, Suzdal, Russia, 3–7 October 2022; pp. 191–193. (In Russian). [Google Scholar]
- Razumovsky, M.I.; Bokstein, B.S.; Rodin, A.O.; Logacheva, A.I. The welding of titanium and tantalum with powder alloys based on many refractory metals: Diffusion aspect. In Proceedings of the 15-th International Conference New Materials and Technologies: Powder Metallurgy, Composite Materials, Protective Coatings, Welding, Minsk, Belarus, 14–16 September 2022; pp. 709–715. (In Russian). [Google Scholar]
- Matano, C. On the relation between the diffusion-coefficients and concentrations of solid metals (the nickel-Copper system). Jpn. J. Phys. 1933, 8, 109–113. [Google Scholar]
- Hall, L.D. An analytical method of calculating variable diffusion coefficients. J. Chem. Phys. 1953, 21, 87–89. [Google Scholar] [CrossRef]
- Bokstein, B.S. Diffusion in Metals, 2nd ed.; Lenand: Moscow, Russia, 2019; p. 248. (In Russian) [Google Scholar]
- Adda, Y.; Phylibert, J. La Diffusion dans les Solides; Saclay & Paris: Paris, France, 1966; p. 1268. [Google Scholar]
- Herzig, C.H.R.; Divinski, S.; Mishin, Y. Bulk and Interface Boundary Diffusion in Group IV Hexagonal Close-Packed Metals and Alloys. Metall. Mater. Trans. A 2002, 33, 765–775. [Google Scholar] [CrossRef]
- Davis, B.E.; McMullen, W.D. Bulk self-diffusion of Hf181 in monocrystalline alpha hafnium—2.1% zirconium Self-diffusion dans la masse de Hf181 dans l'alliage hafnium-2,1% zirconium monocristallin volumen-selbstdiffusion von Hf181 in einkristallinem alpha-hafnium-2,1% Zirkon. Acta Metall. 1972, 20, 593–599. [Google Scholar] [CrossRef]
- Lundy, T.S.; Winslow, F.R.; Pawel, R.E.; McHargue, C.J. Diffusion of Nb-95 and Ta-182 in niobium (Columbium) Trans. Met. Soc. AIME 1965, 233, 1533–1539. [Google Scholar]
- Ablitzer, D. Diffusion of niobium, iron, cobalt, nickel and copper in niobium. Philos. Mag. 1977, 35, 1239–1256. [Google Scholar] [CrossRef]
- Einziger, R.E.; Mundy, J.N.; Hoff, H.A. Niobium self-diffusion. Philos. Rev. B 1978, 17, 440. [Google Scholar] [CrossRef]
- Neumann, G.; Tölle, V. Self-diffusion in body-centred cubic metals: Analysis of experimental data. Philos. Mag. A 1990, 61, 563–578. [Google Scholar] [CrossRef]
- Pawel, R.E.; Lundy, T.S. The diffusion of Nb95 and Ta182 in tantalum. J. Phys. Chem. Sol. 1965, 26, 937–942. [Google Scholar] [CrossRef]
- Maier, K.; Mehrer, H.; Rein, G. Self-diffusion in molybdenum. Int. J. Mater. Res. 1979, 70, 271–276. [Google Scholar] [CrossRef]
- Bronfin, M.B.; Bokshtein, S.Z.; Zhukhovitkii, A.A. Self-Diffusion in Molybdenum. Zavod. Lab. 1960, 26, 828–830. [Google Scholar]
- Borisov, E.V.; Gruzin, P.L.; Pavlinov, L.V.; Fedorov, G.B. Self-Diffusion of Molybdenum. Metall. Metalloved. 1959, 1, 213–218. [Google Scholar]
- Kidson, G.V.; McGurn, J. Self-diffusion in body-centered cubic zirconium. Can. J. Phys. 1961, 39, 1146. [Google Scholar] [CrossRef]
- Federer, J.I.; Lundy, T.S. Diffusion of Zr95 and Nb95 in b.c.c. (body-centered-cubic) zirconium. TMS-AIME 1963, 227, 592. [Google Scholar]
- Herzig, C.; Eckseler, H. On the anomalous self-diffusion in ß-zirconium: Temperature dependence of the isotope effect. Int. J. Mater. Res. 1979, 70, 215–223. [Google Scholar] [CrossRef]
- Köhler, U.; Herzig, C. On the anomalous self-diffusion in BCC titanium. Phys. Stat. Sol. 1987, 144, 243–251. [Google Scholar] [CrossRef]
- Murdock, J.F.; Lundy, T.S.; Stansbury, E.E. Diffusion of Ti44 and V48 in titanium. Acta Metall. 1964, 12, 1033. [Google Scholar] [CrossRef]
- Zhang, J.; Gadelmeier, C.; Sen, S.; Wang, R.; Zhang, X.; Zhong, Y.; Glatzel, U.; Grabowski, B.; Wilde, G.; Divinski, S.V. Zr diffusion in BCC refractory high entropy alloys: A case of ‘non-sluggish’ diffusion behavior. Acta Mater. 2022, 233, 117970. [Google Scholar] [CrossRef]
- American Society for Metals. Diffusion in Body-Centered Cubic Metals; American Society for Metals: Metals Park, OH, USA, 1965; p. 426. [Google Scholar]
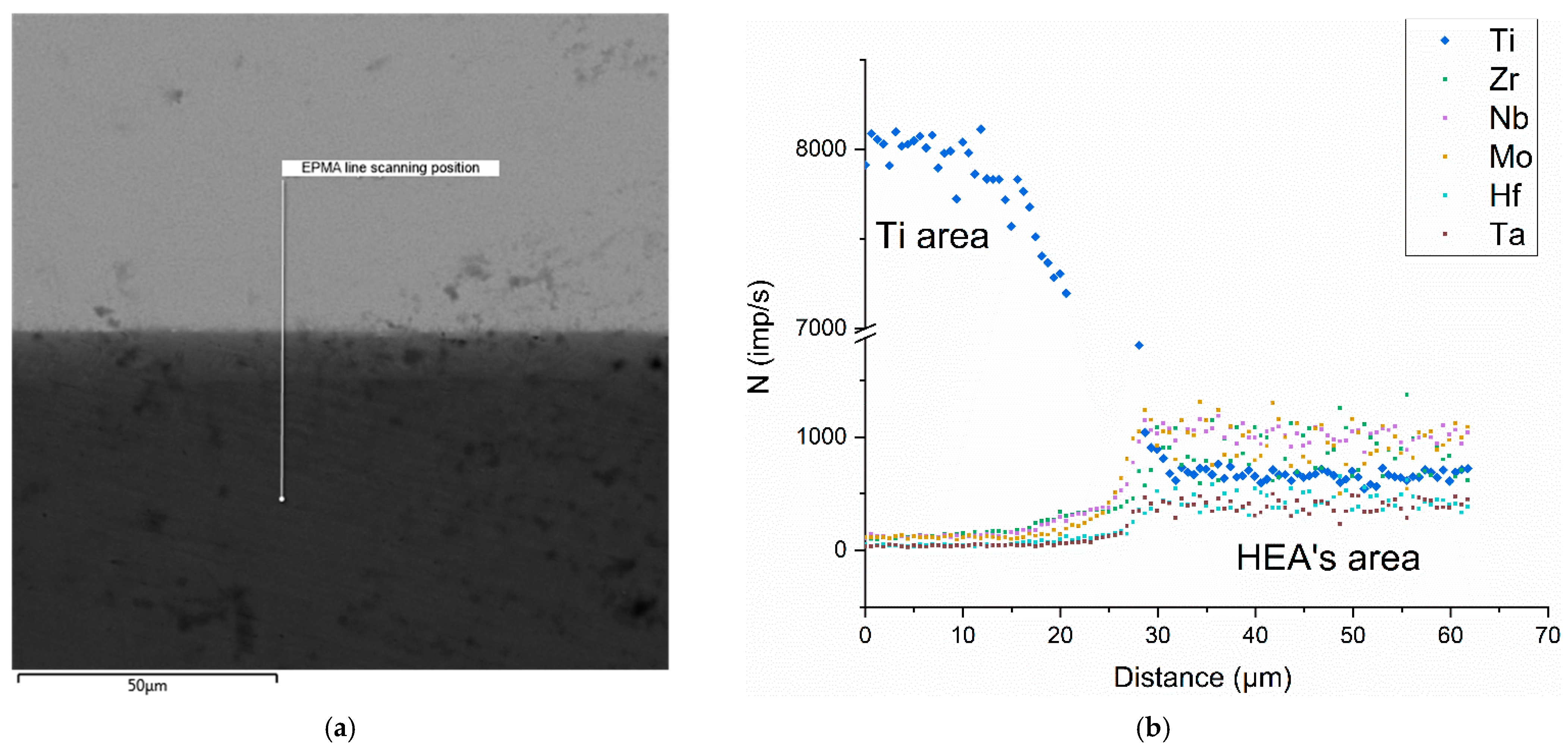


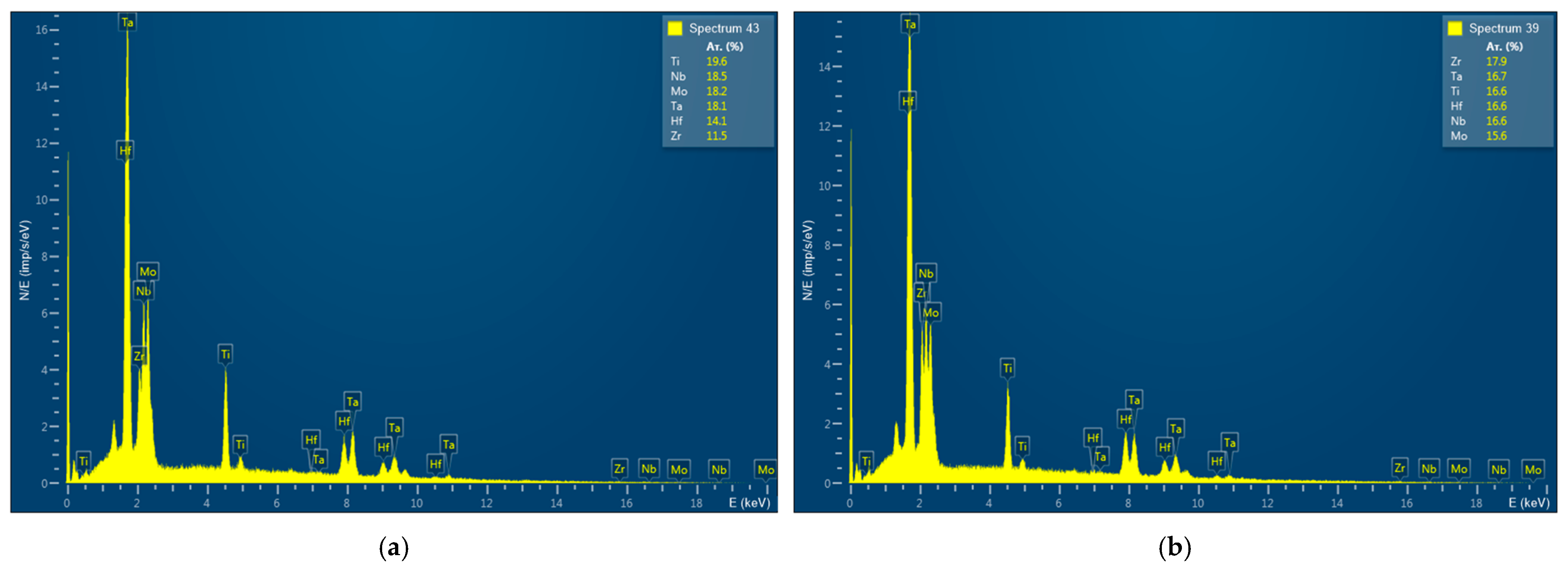

| Spectrum Number | Distance, µm | Ti | Zr | Hf | Mo | Ta | Nb |
|---|---|---|---|---|---|---|---|
| at.% | |||||||
| 38 | 0 | 15.6 | 20.6 | 18.3 | 14.7 | 14.7 | 14.7 |
| 39 | 35 | 16.6 | 17.9 | 16.6 | 15.6 | 16.7 | 16.6 |
| 40 | 70 | 17.6 | 9.3 | 13.5 | 19.7 | 19.6 | 19.4 |
| 41 | 105 | 17.0 | 13.4 | 15.5 | 18.4 | 18.4 | 17.3 |
| 42 | 140 | 17.8 | 14.3 | 15.9 | 17.3 | 16.7 | 18 |
| 43 | 175 | 19.6 | 11.5 | 14.1 | 18.2 | 18.1 | 18.5 |
| 44 | 210 | 60.4 | 3.6 | 5.7 | 9.8 | 10 | 8.4 |
| 45 | 245 | 75.6 | 2.9 | 3.9 | 5.2 | 5.1 | 4.6 |
| 46 | 280 | 80 | 2.7 | 2.7 | 3.5 | 3.5 | 3.3 |
| 47 | 315 | 83.3 | 2.5 | 2.4 | 2.8 | 2.7 | 3 |
| 48 | 350 | 85.5 | 2.1 | 2 | 2.1 | 2 | 2.3 |
| 49 | 385 | 87.5 | 2.1 | 1.9 | 1.6 | 1.4 | 1.7 |
| 50 | 420 | 87.3 | 2.2 | 1.5 | 1.6 | 1.1 | 1.7 |
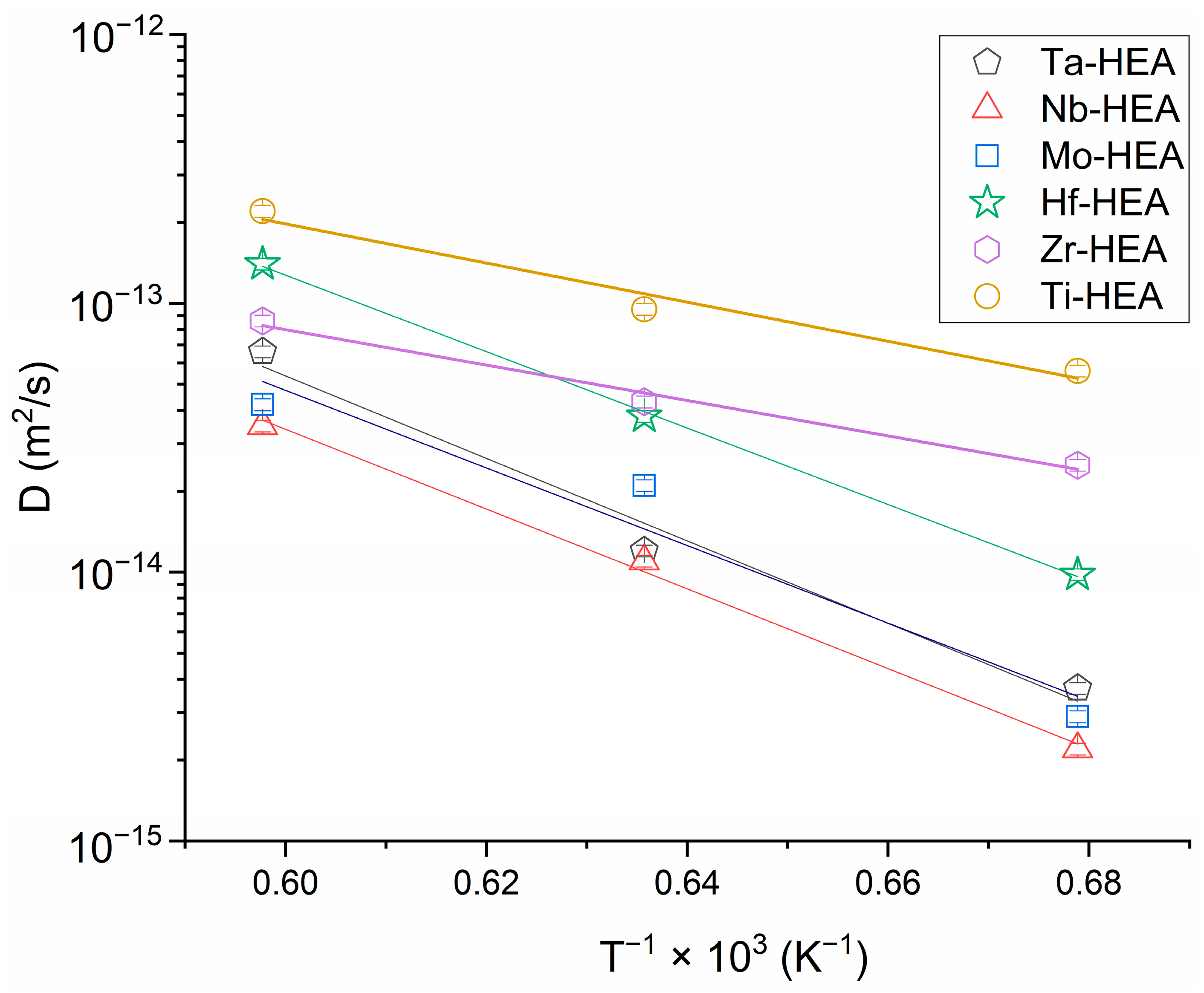
| Annealing Temperature/Diffusion Coefficient of the HEA’s Element | D (m2/s) | |||||
|---|---|---|---|---|---|---|
| Hf | Nb | Ta | Mo | Zr | Ti | |
| 1673 K | 1.4 × 10−13 | 3.5 × 10−14 | 6.6 × 10−14 | 4.2 × 10−14 | 8.6 × 10−14 | 2.2 × 10−13 |
| 1573 K | 3.8 × 10−14 | 1.1 × 10−14 | 1.2 × 10−14 | 2.1 × 10−14 | 4.3 × 10−14 | 9.5 × 10−14 |
| 1473 K | 9.8 × 10−15 | 2.2 × 10−15 | 3.7 × 10−15 | 2.9 × 10−15 | 2.5 × 10−14 | 5.6 × 10−14 |
| Diffusion Characteristics/HEA’s Element | Hf | Nb | Ta | Mo | Zr | Ti |
|---|---|---|---|---|---|---|
| Q (kJ/mol) | 272 | 284 | 294 | 276 | 126 | 139 |
| D0 (m2/s) | 4.3 × 10−5 | 2.710−5 | 8.7 × 10−5 | 2.1 × 10−5 | 7.1 × 10−10 | 4.6 × 10−9 |
| Element | Temperature Interval (K) | Qself (kJ/mol) | Literary Primary Source |
|---|---|---|---|
| Hf | 1173–1633 | 323.0 | [22] |
| 1437–1883 | 348.3 | [23] | |
| Nb | 1151–2668 | 402.0 | [24] |
| 1421–2509 | 397.3 | [25] | |
| 1354–2695 | 438.3 | [26] | |
| 1151–2695 | 503.0 | [27] | |
| Ta | 1523–2558 | 413.3 | [28] |
| 370.8 | [27] | ||
| Mo | 1360–2773 | 488.2 | [29] |
| 1973–2193 | 464.8 | [30] | |
| 2073–2448 | 481.5 | [31] | |
| Zr | 1441–1776 | 126.0 | [32] |
| 1174–2020 | 116.0 | [33] | |
| 1189–2000 | 184.4 | [34] | |
| 1174–2020 | 81.1 | [27] | |
| Ti | 1176–1893 | 328.3 | [35] |
| 1172–1813 | 130.6 | [36] | |
| 1172–1893 | 119.7 | [27] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Razumovsky, M.I.; Bokstein, B.S.; Rodin, A.O.; Khvan, A.V. Interdiffusion in Refractory Metal System with a BCC Lattice: Ti/TiZrHfNbTaMo. Entropy 2023, 25, 490. https://doi.org/10.3390/e25030490
Razumovsky MI, Bokstein BS, Rodin AO, Khvan AV. Interdiffusion in Refractory Metal System with a BCC Lattice: Ti/TiZrHfNbTaMo. Entropy. 2023; 25(3):490. https://doi.org/10.3390/e25030490
Chicago/Turabian StyleRazumovsky, Mikhail I., Boris S. Bokstein, Alexey O. Rodin, and Alexandra V. Khvan. 2023. "Interdiffusion in Refractory Metal System with a BCC Lattice: Ti/TiZrHfNbTaMo" Entropy 25, no. 3: 490. https://doi.org/10.3390/e25030490
APA StyleRazumovsky, M. I., Bokstein, B. S., Rodin, A. O., & Khvan, A. V. (2023). Interdiffusion in Refractory Metal System with a BCC Lattice: Ti/TiZrHfNbTaMo. Entropy, 25(3), 490. https://doi.org/10.3390/e25030490






