Holographic Dark Energy in Modified Barrow Cosmology
Abstract
:1. Introduction
2. HDE with the Hubble Horizon as the IR Cutoff
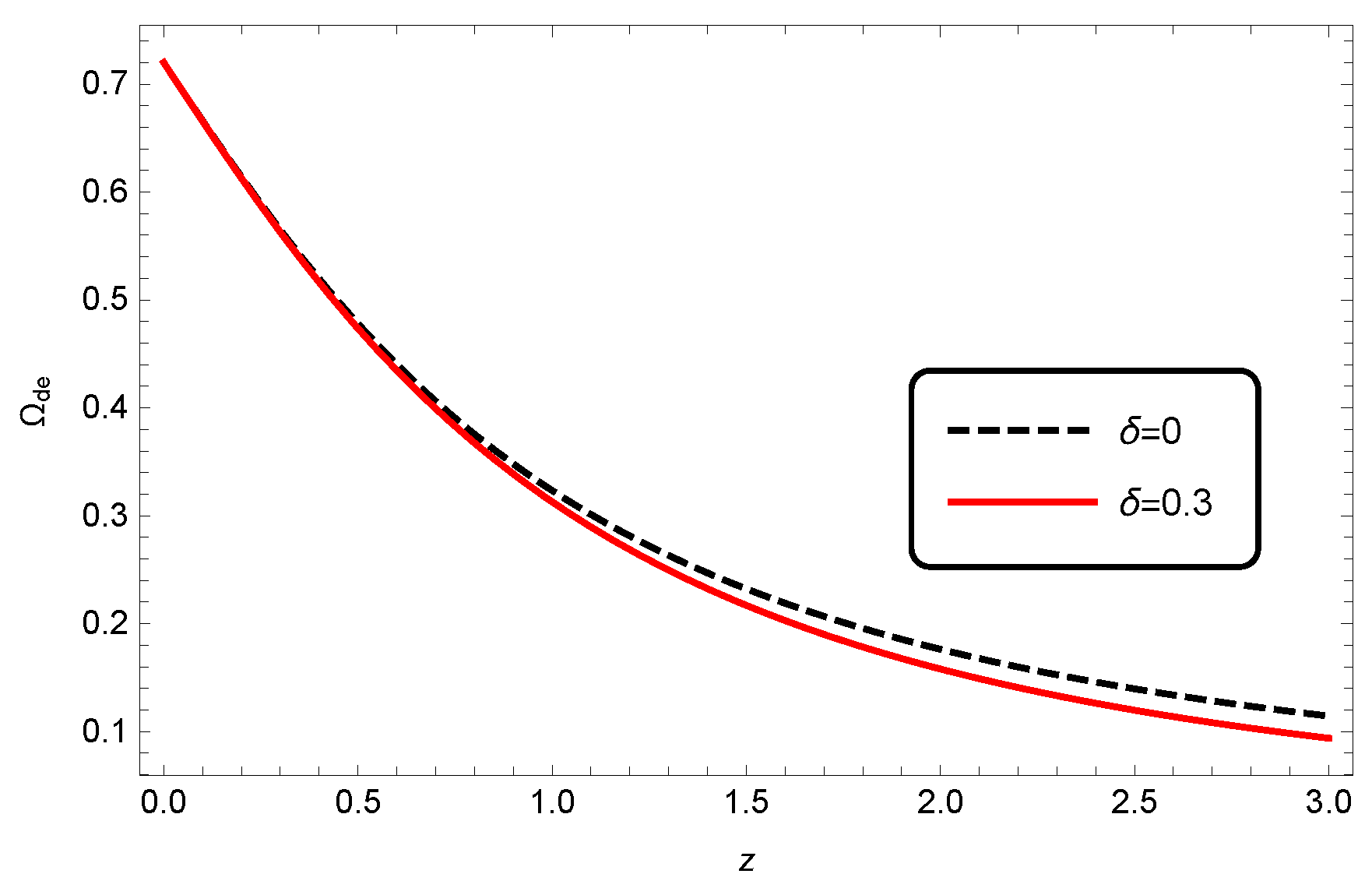
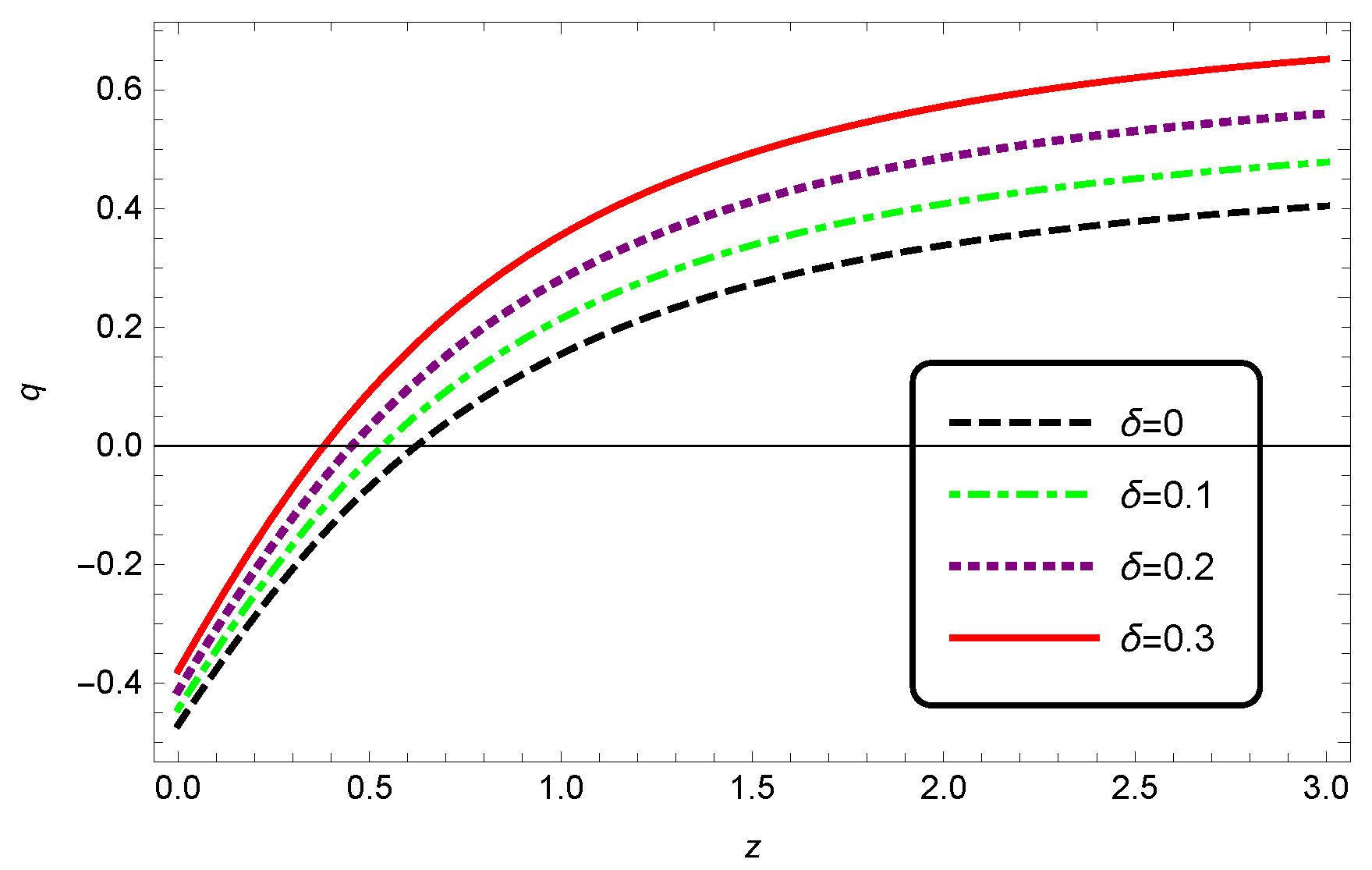
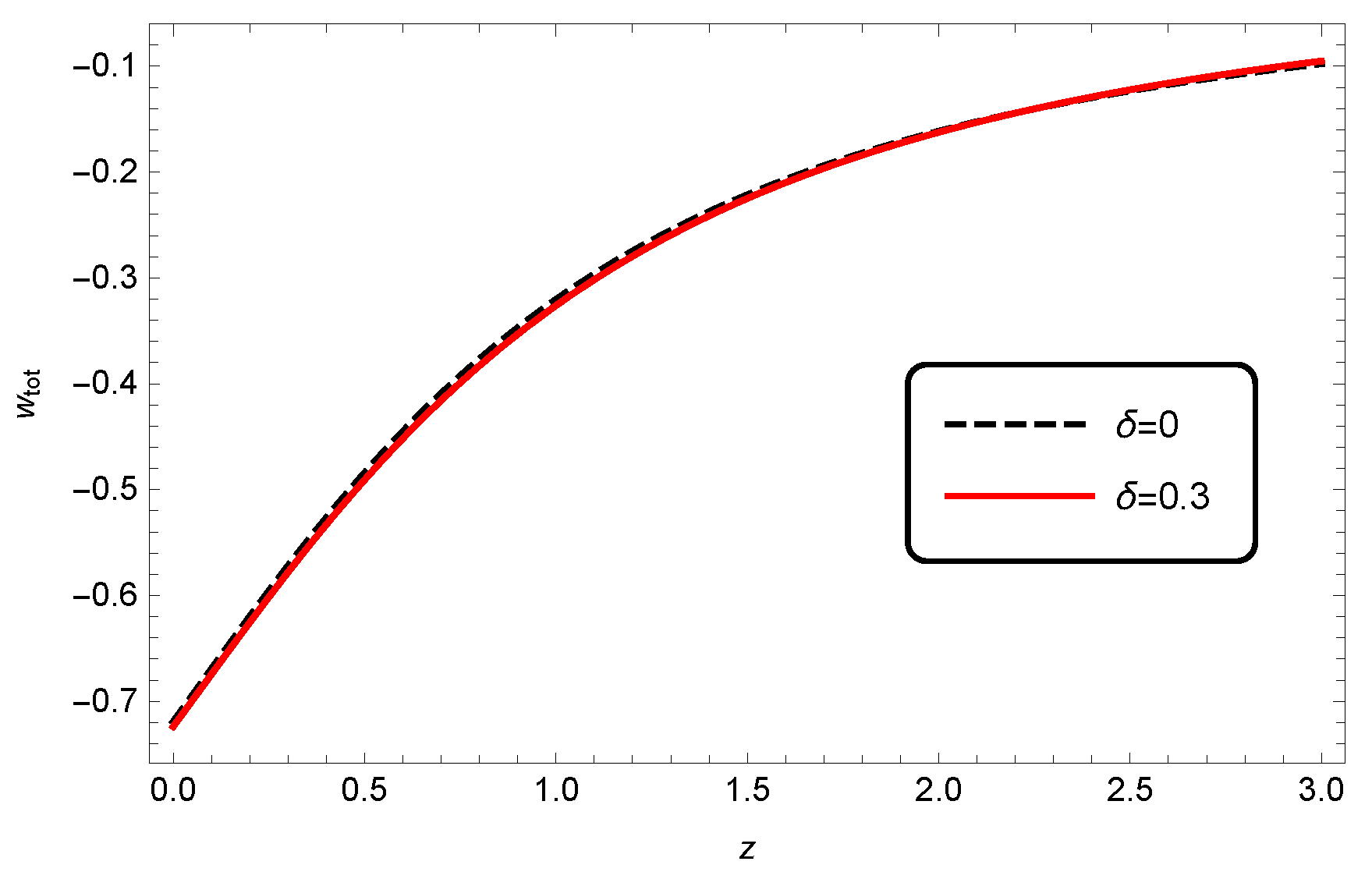
2.1. Non-Interacting Case
2.2. Interacting Case
3. HDE with the Future Event Horizon as the IR Cutoff
3.1. Non-Interacting Case
3.2. Interacting Case
4. Closing Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiattia, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational Evidence from Supernovae for an Accelerating Universe and a Cosmological Constant. Astron. J. 1998, 116, 1009. [Google Scholar] [CrossRef] [Green Version]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurements of Ω and Λ from 42 High-Redshift Supernovae. Astrophys. J. 1999, 517, 565. [Google Scholar] [CrossRef]
- Abbott, T.M.C.; Allam, S.; Andersen, P.; Angus, C.; Asorey, J.; Avelino, A.; Avila, S.; Bassett, B.A.; Bechtol, K.; Bernstein, G.M.; et al. First Cosmology Results using Type Ia Supernovae from the Dark Energy Survey: Constraints on Cosmological Parameters. Astrophys. J. Lett. 2019, 872, 30. [Google Scholar] [CrossRef]
- Copeland, E.J.; Sami, M.; Tsujikawa, S. Dynamics of dark energy. Int. J. Mod. Phys. D 2006, 15, 1753. [Google Scholar] [CrossRef] [Green Version]
- Lusso, E.; Piedipalumbo, E.; Risaliti, G.; Paolillo, M.; Bisogni, S.; Nardini, E.; Amati, L. Tension with the flat ΛCDM model from a high-redshift Hubble diagram of supernovae, quasars, and gamma-ray bursts. Astron. Astrophys. 2019, 628, L4. [Google Scholar] [CrossRef]
- Susskind, L. The World as a hologram. J. Math. Phys. 1995, 36, 6377. [Google Scholar] [CrossRef] [Green Version]
- Fischler, W.; Susskind, L. Holography and Cosmology. arXiv 1998, arXiv:9806039. [Google Scholar]
- Bousso, R. The Holographic principle. Rev. Mod. Phys. 2002, 74, 825. [Google Scholar] [CrossRef] [Green Version]
- Hsu, S.D.H. Entropy Bounds and Dark Energy. Phys. Lett. B 2004, 594, 13. [Google Scholar] [CrossRef] [Green Version]
- Bekenstein, J.D. Black Holes and Entropy. Phys. Rev. D 1973, 7, 2333. [Google Scholar] [CrossRef]
- Cohen, A.G.; Kaplan, D.B.; Nelson, A.E. Effective Field Theory, Black Holes, and the Cosmological Constant. Phys. Rev. Lett. 1999, 82, 4971. [Google Scholar] [CrossRef] [Green Version]
- Li, M. A Model of Holographic Dark Energy. Phys. Lett. B 2004, 603, 1. [Google Scholar] [CrossRef]
- Huang, Q.-G.; Li, M. The Holographic Dark Energy in a Non-flat Universe. JCAP 2004, 408, 13. [Google Scholar] [CrossRef]
- Wang, B.; Gong, Y.g.; Abdalla, E. Transition of the dark energy equation of state in an interacting holographic dark energy model. Phys. Lett. B 2005, 624, 141. [Google Scholar] [CrossRef] [Green Version]
- Pavon, D.; Zimdahl, W. Holographic dark energy and cosmic coincidence. Phys. Lett. B 2005, 628, 206. [Google Scholar] [CrossRef] [Green Version]
- Wang, B.; Lin, C.Y.; Abdalla, E. Constraints on the interacting holographic dark energy model. Phys. Lett. B 2006, 637, 357. [Google Scholar] [CrossRef] [Green Version]
- Setare, M.R. Interacting holographic dark energy model in non-flat Universe. Phys. Lett. B 2006, 642, 1. [Google Scholar] [CrossRef] [Green Version]
- Setare, M.R. The holographic dark energy in non-flat Brans-Dicke cosmology. Phys. Lett. B 2007, 644, 99. [Google Scholar] [CrossRef] [Green Version]
- Jamil, M.; Saridakis, E.N.; Setare, M.R. Holographic dark energy with varying gravitational constant. Phys. Lett. B 2009, 679, 172. [Google Scholar] [CrossRef] [Green Version]
- Sheykhi, A. Interacting holographic dark energy in Brans-Dicke theory. Phys. Lett. B 2009, 681, 205. [Google Scholar] [CrossRef] [Green Version]
- Sheykhi, A. Thermodynamics of interacting holographic dark energy with the apparent horizon as an IR cutoff. Class. Quantum Grav. 2010, 27, 025007. [Google Scholar] [CrossRef] [Green Version]
- Gong, Y.G.; Li, T.J. A modified holographic dark energy model with infrared infinite extra dimension(s). Phys. Lett. B 2010, 683, 241. [Google Scholar] [CrossRef] [Green Version]
- Sheykhi, A. Holographic scalar field models of dark energy. Phys. Rev. D 2011, 84, 107302. [Google Scholar] [CrossRef] [Green Version]
- Ghaffari, S.; Dehghani, M.H.; Sheykhi, A. Holographic dark energy in the DGP braneworld with GO cutoff. Phys. Rev. D 2014, 89, 123009. [Google Scholar] [CrossRef] [Green Version]
- Sheykhi, A.; Dehghani, M.H.; Ghaffari, S. New holographic dark energy model inspired by the DGP braneworld. IJMPD 2016, 25, 1650018. [Google Scholar] [CrossRef] [Green Version]
- Wang, B.; Abdalla, E.; Atrio-Barandela, F.; Pavon, D. Dark Matter and Dark Energy Interactions: Theoretical Challenges, Cosmological Implications and Observational Signatures. Rep. Prog. Phys. 2016, 79, 096901. [Google Scholar] [CrossRef] [Green Version]
- Wang, S.; Wang, Y.; Li, M. Holographic Dark Energy. Phys. Rep. 2017, 696, 1. [Google Scholar] [CrossRef] [Green Version]
- Kim, H.; Lee, J.W.; Lee, J. Causality Problem in a Holographic Dark Energy Model. Europhys. Lett. 2013, 102, 29001. [Google Scholar] [CrossRef] [Green Version]
- Barrow, J.D. The area of a rough black hole. Phys. Lett. B 2020, 808, 135643. [Google Scholar] [CrossRef]
- Saridakis, E.N. Barrow holographic dark energy. Phys. Rev. D 2020, 102, 123525. [Google Scholar] [CrossRef]
- Anagnostopoulos, F.K.; Basilakos, S.; Saridakis, E.N. Observational constraints on Barrow holographic dark energy. Eur. Phys. J. C 2020, 80, 826. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Faraoni, V. From nonextensive statistics and black hole entropy to the holographic dark universe. Phys. Rev. D 2022, 105, 044042. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Paul, T. Early and late universe holographic cosmology from a new generalized entropy. Phys. Lett. B 2022, 831, 137189. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Paul, T. Different Faces of Generalized Holographic Dark Energy. Symmetry 2021, 13, 928. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Paul, T. Barrow entropic dark energy: A member of generalized holographic dark energy family. Phys. Lett. B 2022, 825, 136844. [Google Scholar] [CrossRef]
- Saridakis, E.N.; Basilakos, S. The generalized second law of thermodynamics with Barrow entropy. arXiv 2021, arXiv:2005.08258. [Google Scholar] [CrossRef]
- Abreu, E.M.; Neto, J.A.; Barboza, E.M. Barrow’s black hole entropy and the equipartition theorem. Eur. Phys. Lett. 2020, 130, 40005. [Google Scholar] [CrossRef]
- Mamon, A.A.; Paliathanasis, A.; Saha, S. Dynamics of an Interacting Barrow Holographic Dark Energy Model and its Thermodynamic Implications. Eur. Phys. J. Plus 2021, 136, 134. [Google Scholar] [CrossRef]
- Abreu, E.M.C.; Neto, J.A. Barrow black hole corrected-entropy model and Tsallis nonextensivity. Phys. Lett. B 2020, 810, 135805. [Google Scholar] [CrossRef]
- Barrow, J.D.; Basilakos, S.S.; Saridakis, E.N. Big Bang Nucleosynthesis constraints on Barrow entropy. arXiv 2020, arXiv:2010.00986. [Google Scholar] [CrossRef]
- Srivastava, S.; Sharma, U.K. Barrow holographic dark energy with Hubble horizon as IR cutoff. Int. J. Geom. Methods Mod. Phys. 2021, 18, 2150014. [Google Scholar] [CrossRef]
- Das, B.; Pandey, B. A study of holographic dark energy models using configuration entropy. arXiv 2020, arXiv:2011.07337. [Google Scholar]
- Sharma, U.K.; Varshney, G.; Dubey, V.C. Barrow agegraphic dark energy. Int. J. Mod. Phys. D 2021, 30, 2150021. [Google Scholar] [CrossRef]
- Pradhan, A.; Dixit, A.; Bhardwaj, V.K. Barrow HDE model for Statefinder diagnostic in FLRW Universe. arXiv 2021, arXiv:2101.00176. [Google Scholar] [CrossRef]
- Jacobson, T. Thermodynamics of Spacetime: The Einstein Equation of State. Phys. Rev. Lett. 1995, 75, 1260. [Google Scholar] [CrossRef] [Green Version]
- Padmanabhan, T. Gravity and the Thermodynamics of Horizons. Phys. Rep. 2005, 406, 49. [Google Scholar] [CrossRef] [Green Version]
- Padmanabhan, T. Thermodynamical Aspects of Gravity: New insights. Rep. Prog. Phys. 2010, 73, 046901. [Google Scholar] [CrossRef] [Green Version]
- Paranjape, A.; Sarkar, S.; Padmanabhan, T. Thermodynamic route to Field equations in Lanczos-Lovelock Gravity. Phys. Rev. D 2006, 74, 104015. [Google Scholar] [CrossRef] [Green Version]
- Frolov, A.V.; Kofman, L. Inflation and de Sitter Thermodynamics. JCAP 2003, 305, 9. [Google Scholar] [CrossRef] [Green Version]
- Wang, B.; Abdalla, E.; Su, R.K. Relating Friedmann equation to Cardy formula in universes with cosmological constant. Phys. Lett. B 2001, 503, 394. [Google Scholar] [CrossRef] [Green Version]
- Verlinde, E. On the Origin of Gravity and the Laws of Newton. JHEP 2011, 1104, 029. [Google Scholar] [CrossRef] [Green Version]
- Cai, R.G.; Cao, L.M.; Ohta, N. Friedmann equations from entropic force. Phys. Rev. D 2010, 81, 061501. [Google Scholar] [CrossRef] [Green Version]
- Cai, R.G.; Cao, L.M.; Hu, Y.P. Corrected Entropy-Area Relation and Modified Friedmann Equations. JHEP 2008, 808, 090. [Google Scholar] [CrossRef] [Green Version]
- Sheykhi, A. Entropic corrections to Friedmann equations. Phys. Rev. D 2010, 81, 104011. [Google Scholar] [CrossRef] [Green Version]
- Sheykhi, A. Thermodynamics of apparent horizon and modified Friedmann equations. Eur. Phys. J. C 2010, 69, 265. [Google Scholar] [CrossRef] [Green Version]
- Sheykhi, A.; Hendi, S.H. Power-law entropic corrections to Newton law and Friedmann equations. Phys. Rev. D 2011, 84, 044023. [Google Scholar] [CrossRef] [Green Version]
- Nojiri, S.; Odintsov, S.D.; Saridakis, E.N. Modified cosmology from extended entropy with varying exponent. Eur. Phys. J. C 2019, 79, 242. [Google Scholar] [CrossRef]
- Abreu, E.M.; Neto, J.A.; Barboza, E.M., Jr.; Mendes, A.C.; Soares, B.B. On the equipartition theorem and black holes nongaussian entropies. Mod. Phys. Lett. A 2020, 35, 2050266. [Google Scholar] [CrossRef]
- Cai, R.G.; Kim, S.P. First Law of Thermodynamics and Friedmann Equations of Friedmann-Robertson-Walker Universe. JHEP 2005, 502, 50. [Google Scholar] [CrossRef] [Green Version]
- Akbar, M.; Cai, R.G. Thermodynamic behavior of the Friedmann equation at the apparent horizon of the FRW universe. Phys. Rev. D 2007, 75, 084003. [Google Scholar] [CrossRef] [Green Version]
- Sheykhi, A.; Wang, B.; Cai, R.G. Thermodynamical Properties of Apparent Horizon in Warped DGP Braneworld. Nucl. Phys. B 2007, 779, 1. [Google Scholar] [CrossRef] [Green Version]
- Sheykhi, A.; Wang, B.; Cai, R.G. Deep connection between thermodynamics and gravity in Gauss-Bonnet braneworlds. Phys. Rev. D 2007, 76, 023515. [Google Scholar] [CrossRef] [Green Version]
- Saridakis, E.N. Modified cosmology through spacetime thermodynamics and Barrow horizon entropy. JCAP 2020, 7, 031. [Google Scholar] [CrossRef]
- Sheykhi, A. Barrow entropy corrections to Firedmann equations. Phys. Rev. D 2021, 103, 123503. [Google Scholar] [CrossRef]
- Sheykhi, A. Modified cosmology throgh Barrow entropy. arXiv 2023, arXiv:2210.12525. [Google Scholar]








Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sheykhi, A.; Hamedan, M.S. Holographic Dark Energy in Modified Barrow Cosmology. Entropy 2023, 25, 569. https://doi.org/10.3390/e25040569
Sheykhi A, Hamedan MS. Holographic Dark Energy in Modified Barrow Cosmology. Entropy. 2023; 25(4):569. https://doi.org/10.3390/e25040569
Chicago/Turabian StyleSheykhi, Ahmad, and Maral Sahebi Hamedan. 2023. "Holographic Dark Energy in Modified Barrow Cosmology" Entropy 25, no. 4: 569. https://doi.org/10.3390/e25040569
APA StyleSheykhi, A., & Hamedan, M. S. (2023). Holographic Dark Energy in Modified Barrow Cosmology. Entropy, 25(4), 569. https://doi.org/10.3390/e25040569






