Federated Learning Based Fault Diagnosis Driven by Intra-Client Imbalance Degree
Abstract
:1. Introduction
- A federated learning framework driven by intra-client imbalance degree was designed in this paper to establish a federation strategy for the case where there is an imbalance mode mismatch between clients.
- The degree of intra-client imbalance was used to guide the design of the federation strategy related to cost-sensitivity. Using the imbalance data of the local client, an inter-class imbalance degree for each client was computed by the gain of a class-by-class model update on the federation model of the small balanced dataset.
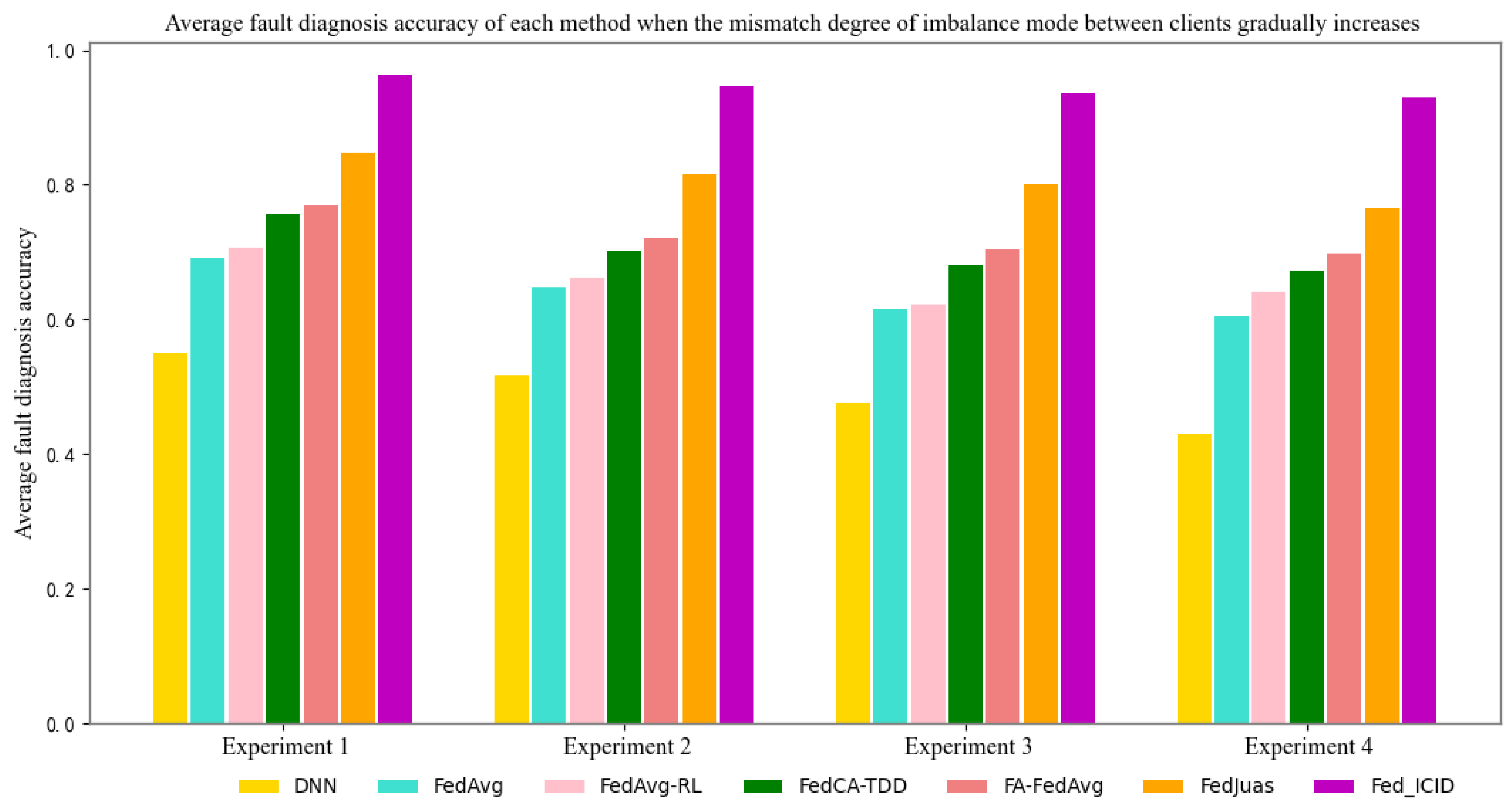
- In the case where there is a significant mismatch of imbalance mode between clients, the federated learning-based fault diagnosis proposed in this paper can well overcome the problem arisen by both intra-client imbalance and inter-client imbalance to ensure the accuracy of fault diagnosis for each client.
2. Related Theories
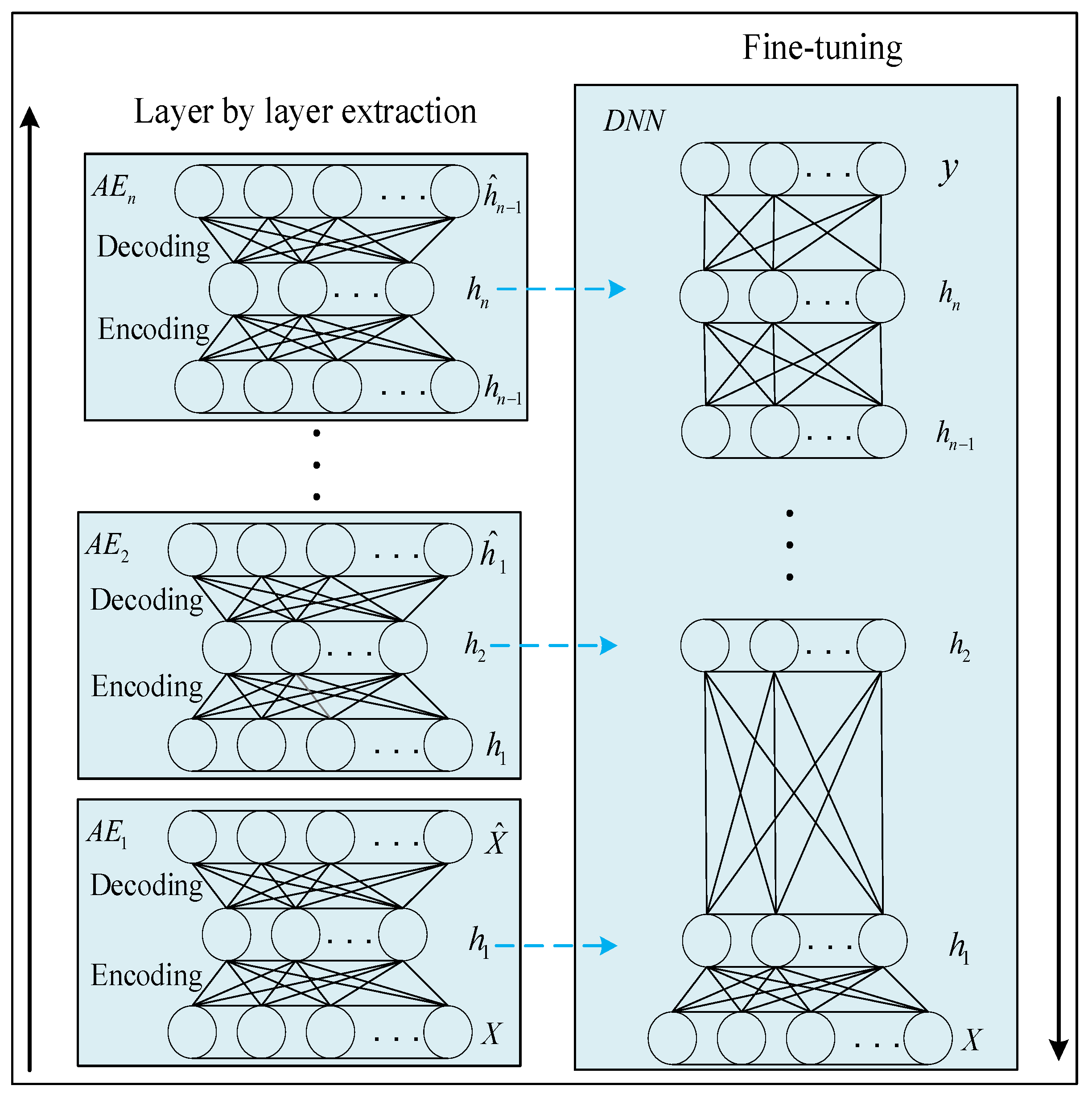
2.1. Deep Neural Network Based on Stack Autoencoder
2.2. Federated Learning
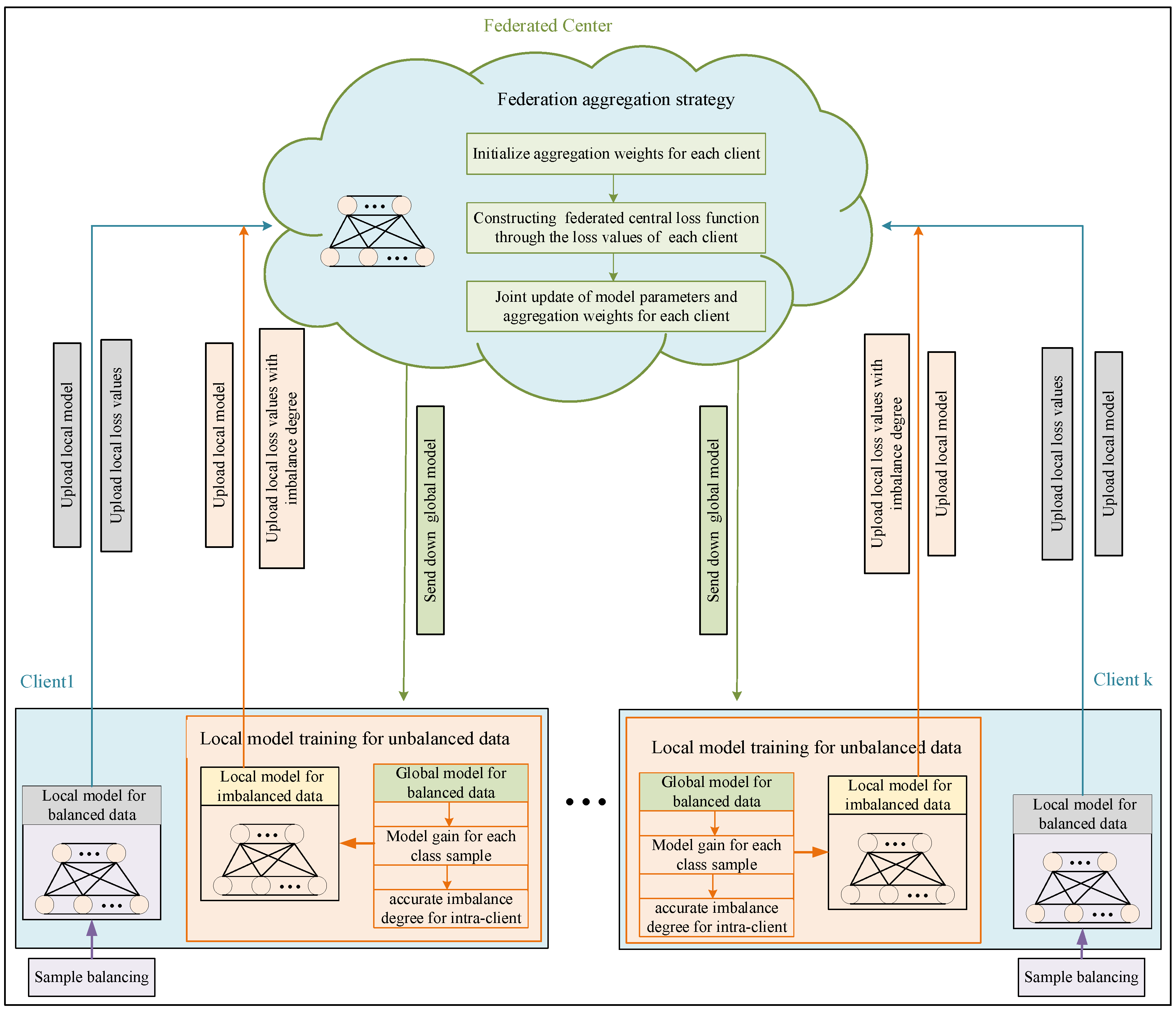
3. A Federated Learning Method Driven by Intra-Client Imbalance Degree
3.1. A Federated Learning Framework Driven by Intra-Client Imbalance Degree
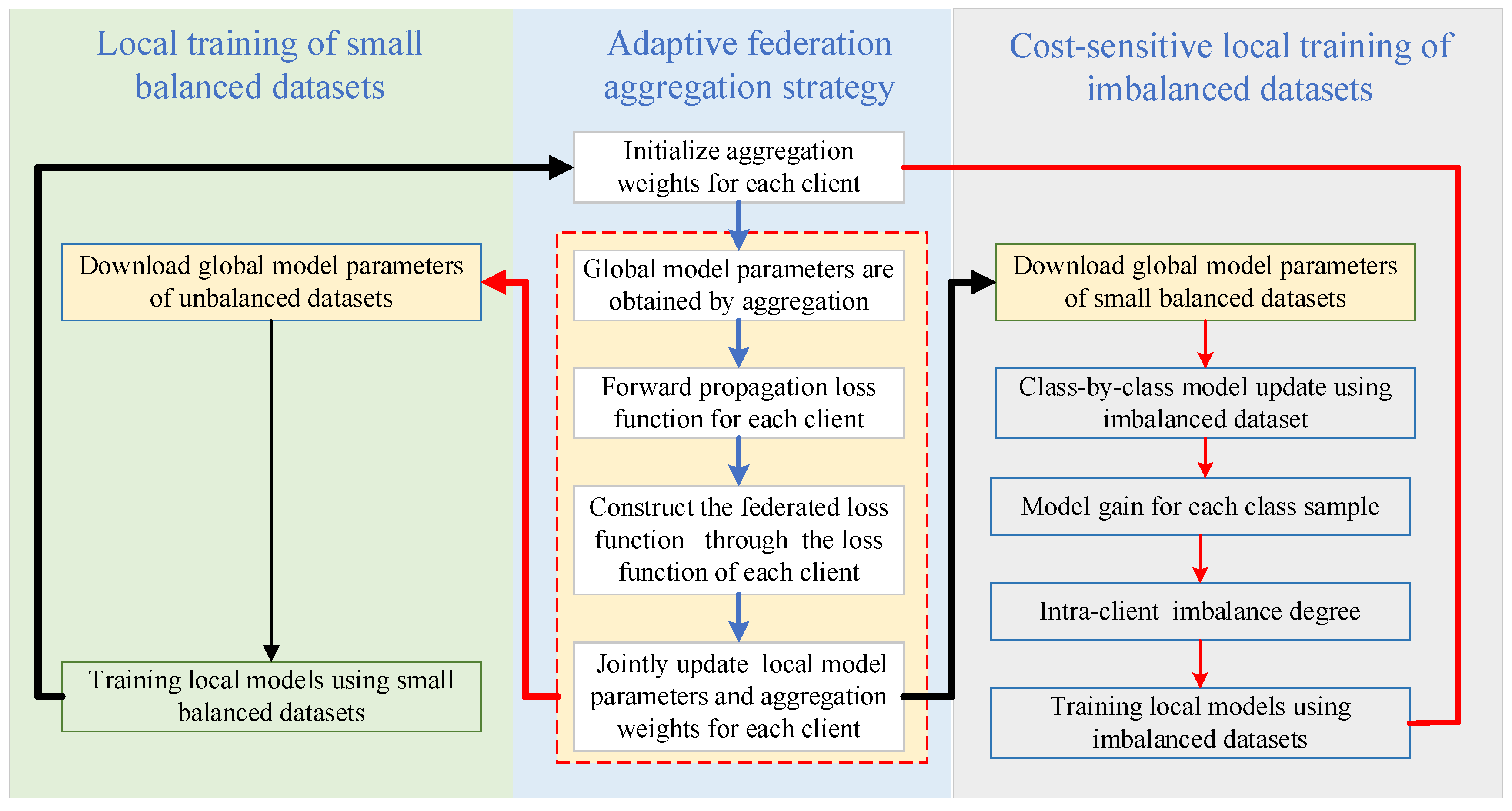
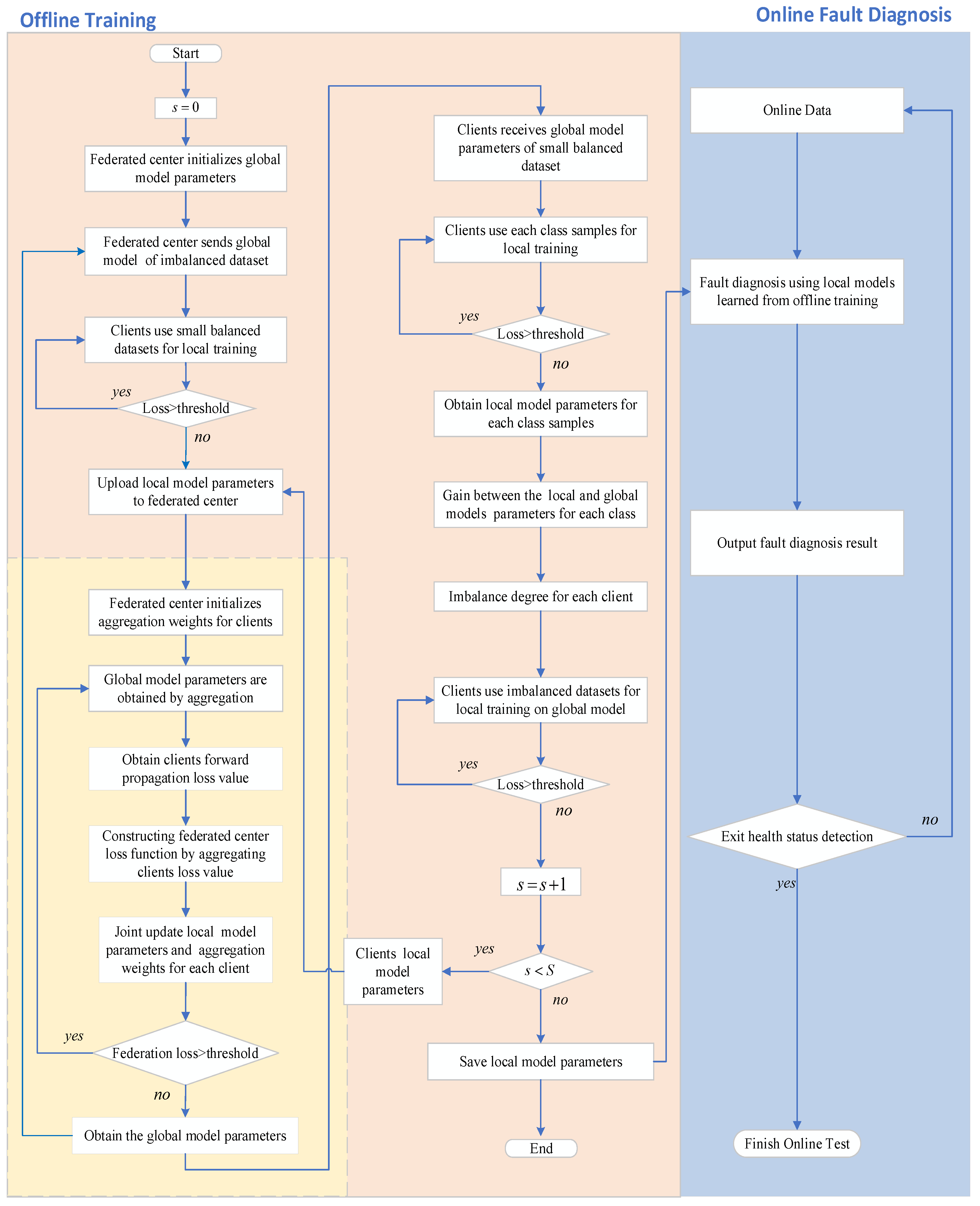
3.2. Detailed Steps for Fed_ICID Method
- Step 1:
- Define the training dataset for each client
- Step 2:
- Establish the federation model based on the small balanced dataset
- Step 3:
- Measure the intra-client imbalance degree by gain of the class-by-class model update of the federation model
- Step 4:
- Federation aggregation strategy driven by intra-client imbalance degree
4. Experiment and Analysis
4.1. Experimental Data Description
4.2. Experimental Design
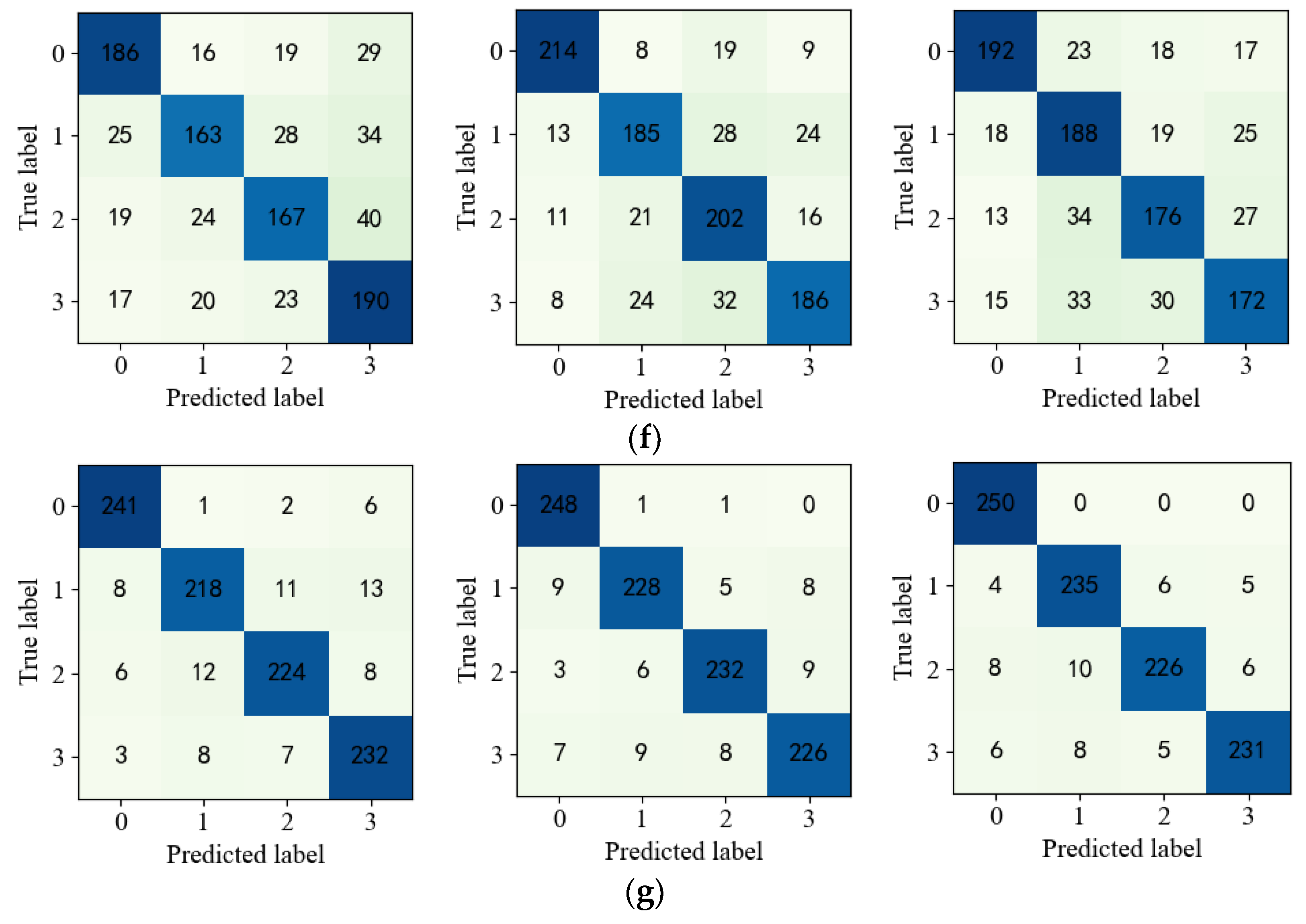
4.3. Analysis of Experimental Results
5. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Djelloul, I.; Sari, Z.; Sidibe, I.D.B. Fault diagnosis based on the quality effect of learning algorithm for manufacturing systems. Proc. Inst. Mech. Eng. Part I J. Syst. Control. Eng. 2019, 233, 801–814. [Google Scholar] [CrossRef]
- Quinde, I.R.; Sumba, J.C.; Ochoa, L.E.; Vallejo Guevara, A., Jr.; Morales-Menendez, R. Bearing Fault Diagnosis Based on Optimal Time-Frequency Representation Method. IFAC PapersOnLine 2019, 52, 194–199. [Google Scholar] [CrossRef]
- Wang, H.; Liu, Z.; Peng, D.; Yang, M.; Qin, Y. Feature-Level Attention-Guided Multitask CNN for Fault Diagnosis and Working Conditions Identification of Rolling Bearing. IEEE Trans. Neural Netw. Learn. Syst. 2021, 33, 4757–4769. [Google Scholar] [CrossRef] [PubMed]
- Zhou, F.N.; Zhang, Z.Q.; Chen, D.M. Bearing fault diagnosis based on DNN using multi-scale feature fusion. In Proceedings of the 2020 35th Youth Academic Annual Conference of Chinese Association of Automation (YAC), Zhanjiang, China, 16–18 October 2020; pp. 150–155. [Google Scholar]
- Zhou, F.N.; He, Y.F.; Han, H.T. Fault Diagnosis of Multi-source Heterogeneous Information Fusion Based on Deep Learning. In Proceedings of the 2019 IEEE 8th Data Driven Control and Learning Systems Conference (DDCLS), Dali, China, 24–27 May 2019; pp. 1295–1300. [Google Scholar]
- Zhou, F.; Zhang, Z.; Chen, D. Real-time fault diagnosis using deep fusion of features extracted by parallel long short-term memory with peephole and convolutional neural network. Proc. Inst. Mech. Eng. Part I J. Syst. Control. Eng. 2020, 235, 1873–1897. [Google Scholar] [CrossRef]
- Chang, C.-H. Deep and Shallow Architecture of Multilayer Neural Networks. IEEE Trans. Neural Netw. Learn. Syst. 2015, 26, 2477–2486. [Google Scholar] [CrossRef]
- Zhang, C.; Lim, P.; Qin, A.K.; Tan, K.C. Multiobjective Deep Belief Networks Ensemble for Remaining Useful Life Estimation in Prognostics. IEEE Trans. Neural Netw. Learn. Syst. 2017, 28, 2306–2318. [Google Scholar] [CrossRef]
- Chen, Z.; Li, C.; Sanchez, R.-V. Gearbox Fault Identification and Classification with Convolutional Neural Networks. Shock. Vib. 2015, 2015, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Guo, L.; Li, N.; Jia, F.; Lei, Y.; Lin, J. A recurrent neural network based health indicator for remaining useful life prediction of bearings. Neurocomputing 2017, 240, 98–109. [Google Scholar] [CrossRef]
- Jia, F.; Lei, Y.; Guo, L.; Lin, J.; Xing, S. A neural network constructed by deep learning technique and its application to intelligent fault diagnosis of machines. Neurocomputing 2018, 272, 619–628. [Google Scholar] [CrossRef]
- He, J.; Yin, L.; Liu, J.; Zhang, C.; Yang, H. A Fault Diagnosis Method for Unbalanced Data Based on a Deep Cost Sensitive Convolutional Neural Network. IFAC PapersOnLine 2022, 55, 43–48. [Google Scholar] [CrossRef]
- Zhou, F.; Yang, S.; Fujita, H.; Chen, D.; Wen, C. Deep learning fault diagnosis method based on global optimization GAN for unbalanced data. Knowl.-Based Syst. 2019, 187, 104837. [Google Scholar] [CrossRef]
- Le, H.L.; Landa-Silva, D.; Galar, M.; Garcia, S.; Triguero, I. EUSC: A clustering-based surrogate model to accelerate evolutionary undersampling in imbalanced classification. Appl. Soft Comput. 2020, 101, 107033. [Google Scholar] [CrossRef]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic Minority Over-sampling Technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Rendón, E.; Alejo, R.; Castorena, C.; Isidro-Ortega, F.J.; Granda-Gutiérrez, E.E. Data Sampling Methods to Deal with the Big Data Multi-Class Imbalance Problem. Appl. Sci. 2020, 10, 1276. [Google Scholar] [CrossRef] [Green Version]
- Zhu, X.; Ye, Y. Optimized Fault Diagnosis Algorithm under GAN and CNN Hybrid Model. Wirel. Commun. Mob. Comput. 2022, 2022, 1–9. [Google Scholar] [CrossRef]
- Zhao, W.D.; Zhang, S.D.; Wang, M. Software Defect Prediction Method Based on Cost-Sensitive Random Forest. In Proceedings of the Intelligent Information Processing XI: 12th IFIP TC 12 International Conference, IIP 2022, Qingdao, China, 27–30 May 2022; pp. 369–381. [Google Scholar]
- Gupta, R.; Alam, T. Survey on Federated-Learning Approaches in Distributed Environment. Wirel. Pers. Commun. 2022, 125, 1631–1652. [Google Scholar] [CrossRef]
- Liu, J.; Huang, J.; Zhou, Y.; Li, X.; Ji, S.; Xiong, H.; Dou, D. From distributed machine learning to federated learning: A survey. Knowl. Inf. Syst. 2022, 64, 885–917. [Google Scholar] [CrossRef]
- Hegedűs, I.; Danner, G.; Jelasity, M. Decentralized learning works: An empirical comparison of gossip learning and federated learning. J. Parallel Distrib. Comput. 2021, 148, 109–124. [Google Scholar] [CrossRef]
- Ma, X.; Zhu, J.; Lin, Z.; Chen, S.; Qin, Y. A state-of-the-art survey on solving non-IID data in Federated Learning. Futur. Gener. Comput. Syst. 2022, 135, 244–258. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, M.; Lai, L.Z.; Suda, N.; Civin, D.; Chandra, V. Federated Learning with Non-IID Data. arXiv 2018, arXiv:1806.00582. [Google Scholar] [CrossRef]
- Duan, M.; Liu, D.; Chen, X.; Liu, R.; Tan, Y.; Liang, L. Self-Balancing Federated Learning With Global Imbalanced Data in Mobile Systems. IEEE Trans. Parallel Distrib. Syst. 2020, 32, 59–71. [Google Scholar] [CrossRef]
- Xin, B.; Yang, W.; Geng, Y.; Chen, S.; Wang, S.; Huang, L. Private FL-GAN: Differential Privacy Synthetic Data Generation Based on Federated Learning. In Proceedings of the ICASSP 2020-2020 IEEE International Conference on Acoustics, Speech and Signal Processing, Barcelona, Spain, 4–8 May 2020; pp. 2927–2931. [Google Scholar] [CrossRef]
- McMahan, B.; Moore, E.; Ramage, D.; Hampson, S.; Arcas, B. Communication-efficient learning of deep networks from decentralized data. In Proceedings of the 20th International Conference on Artificial Intelligence and Statistics, Fort Lauderdale, FL, USA, 20–22 April 2017; pp. 1273–1282. [Google Scholar]
- Ma, Z.; Zhao, M.; Cai, X.; Jia, Z. Fast-convergent federated learning with class-weighted aggregation. J. Syst. Arch. 2021, 117, 102125. [Google Scholar] [CrossRef]
- Geng, D.; He, H.; Lan, X.; Liu, C. Bearing fault diagnosis based on improved federated learning algorithm. Computing 2021, 104, 1–19. [Google Scholar] [CrossRef]
- Xiao, J.H.; Du, C.H.; Duan, Z.J.; Guo, W. A novel server-side aggregation strategy for federated learning in non-IID situations. In Proceedings of the 2021 20th International Symposium on Parallel and Distributed Computing (ISPDC), Cluj-Napoca, Romania, 28–30 July 2021; pp. 17–24. [Google Scholar]
- Wang, L.X.; Xu, S.C.; Wang, X.; Zhu, Q. Addressing Class Imbalance in Federated Learning. In Proceedings of the AAAI Conference on Artificial Intelligence, A Virtual Conference, 2–9 February 2021; pp. 10165–10173. [Google Scholar] [CrossRef]
- Zeng, Y.; Wu, X.J.; Chen, J.L. Bearing Fault Diagnosis with Denoising Autoencoders in Few Labeled Sample Case. In Proceedings of the 2020 5th IEEE International Conference on Big Data Analytics (ICBDA), Xiamen, China, 8–11 May 2020; pp. 349–353. [Google Scholar]
- Hoang, D.-T.; Kang, H.-J. A survey on Deep Learning based bearing fault diagnosis. Neurocomputing 2018, 335, 327–335. [Google Scholar] [CrossRef]
- Huang, H.; Baddour, N. Bearing vibration data collected under time-varying rotational speed conditions. Data Brief 2018, 21, 1745–1749. [Google Scholar] [CrossRef]
- Case Western Reserve University Bearing Data Center Website. Available online: https://engineering.case.edu/bearingdatacenter (accessed on 20 September 2022).
- Smith, W.A.; Randall, R.B. Rolling element bearing diagnosis using the Case Western reserve university data: A benchmark study. Mech. Syst. Signal Process. 2015, 64, 100–131. [Google Scholar] [CrossRef]
- Hendriks, J.; Dumond, P.; Knox, D. Towards better benchmarking using the CWRU bearing fault dataset. Mech. Syst. Signal Process. 2021, 169, 108732. [Google Scholar] [CrossRef]


| Fault Type | Fault Diameter | Fault Label | Load (HP) | Speed (rpm) |
|---|---|---|---|---|
| Normal | 0 | 0 | 1 | 1772 |
| Inner race | 0.021 | 1 | 1 | 1772 |
| Outer race | 0.021 | 2 | 1 | 1772 |
| Ball | 0.021 | 3 | 1 | 1772 |
| Experiment | Intra-Client Imbalance Degree | Inter-Class Sample Size of Clients | Inter-Client Training Sample Size | Test Set Sample Size | Intra-Client Majority Classes/Minority Classes |
|---|---|---|---|---|---|
| Experiment 1 | 2:1 | 16/8/8/16 | 48/192/384 | 1000 | 03/12 |
| 64/32/64/32 | 02/13 | ||||
| 128/128/64/64 | 01/23 | ||||
| Experiment 2 | 5:1 | 20/4/4/20 | 48/192/384 | 1000 | 03/12 |
| 80/16/80/16 | 02/13 | ||||
| 160/160/32/32 | 01/23 | ||||
| Experiment 3 | 7:1 | 21/3/3/21 | 48/192/384 | 1000 | 03/12 |
| 84/12/84/12 | 02/13 | ||||
| 168/168/24/24 | 01/23 | ||||
| Experiment 4 | 23:1 | 23/1/1/23 | 48/192/384 | 1000 | 03/12 |
| 92/4/92/4 | 02/13 | ||||
| 184/184/8/8 | 01/23 |
| Model | Model Explanation |
|---|---|
| DNN | Traditional deep learning deep neural networks without federated learning |
| FedAvg [26] FedAvg-RL [30] | Traditional federal average aggregation strategy based on sample size Federated averaging method with local model ratio loss |
| FedCA-TDD [27] | Class-weighted aggregation strategy based on class sample size |
| FA-FedAvg [28] | Improved federated aggregation strategy based on model metrics F1-score |
| FedJuas | Federated strategy of joint update aggregation weights and model parameters proposed in this paper but without cost-sensitive learning |
| Fed_ICID | An inter-client federated learning method based on accurately measure the intra-client imbalance degree proposed in this paper |
| Model | Client 1 | Client 2 | Client 3 | Mean |
|---|---|---|---|---|
| DNN | 45.3% | 54.8% | 65.2% | 55.10% |
| FedAvg | 63.2% | 68.5% | 75.8% | 69.17% |
| FedAvg-RL | 65.6% | 66.9% | 79.7% | 70.73% |
| FedCA-TDD | 70.5% | 73.2% | 83.4% | 75.70% |
| FA-FedAvg | 72.4% | 75.6% | 82.8% | 76.93% |
| FedJuas | 83.7% | 84.3% | 86.5% | 84.83% |
| Fed_ICID | 95.5% | 96.7% | 96.9% | 96.37% |
| Model | Client 1 | Client 2 | Client 3 | Mean |
|---|---|---|---|---|
| DNN | 42.1% | 51.3% | 61.9% | 51.77% |
| FedAvg | 61.4% | 64.3% | 68.8% | 64.83% |
| FedAvg-RL | 58.7% | 63.7% | 75.9% | 66.10% |
| FedCA-TDD | 64.8% | 68.9% | 76.7% | 70.13% |
| FA-FedAvg | 67.3% | 69.3% | 79.5% | 72.03% |
| FedJuas | 79.8% | 81.4% | 83.7% | 81.63% |
| Fed_ICID | 93.8% | 94.2% | 95.7% | 94.57% |
| Model | Client 1 | Client 2 | Client 3 | Mean |
|---|---|---|---|---|
| DNN | 38.7% | 46.7% | 57.5% | 47.63% |
| FedAvg | 60.3% | 61.6% | 62.7% | 61.53% |
| FedAvg-RL | 57.1% | 63.3% | 66.5% | 62.30% |
| FedCA-TDD | 65.6% | 68.8% | 70.2% | 68.20% |
| FA-FedAvg | 69.2% | 69.6% | 72.5% | 70.43% |
| FedJuas | 80.6% | 81.3% | 78.3% | 80.07% |
| Fed_ICID | 92.2% | 94.5% | 93.9% | 93.53% |
| Model | Client 1 | Client 2 | Client 3 | Mean |
|---|---|---|---|---|
| DNN | 31.4% | 44.5% | 53.4% | 43.10% |
| FedAvg | 54.5% | 60.3% | 66.6% | 60.47% |
| FedAvg-RL | 59.2% | 67.8% | 65.4% | 64.13% |
| FedCA-TDD | 63.4% | 68.4% | 70.2% | 67.33% |
| FA-FedAvg | 65.7% | 70.6% | 72.8% | 69.70% |
| FedJuas | 70.6% | 78.7% | 80.3% | 76.53% |
| Fed_ICID | 91.5% | 93.4% | 94.2% | 93.03% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, F.; Yang, Y.; Wang, C.; Hu, X. Federated Learning Based Fault Diagnosis Driven by Intra-Client Imbalance Degree. Entropy 2023, 25, 606. https://doi.org/10.3390/e25040606
Zhou F, Yang Y, Wang C, Hu X. Federated Learning Based Fault Diagnosis Driven by Intra-Client Imbalance Degree. Entropy. 2023; 25(4):606. https://doi.org/10.3390/e25040606
Chicago/Turabian StyleZhou, Funa, Yi Yang, Chaoge Wang, and Xiong Hu. 2023. "Federated Learning Based Fault Diagnosis Driven by Intra-Client Imbalance Degree" Entropy 25, no. 4: 606. https://doi.org/10.3390/e25040606
APA StyleZhou, F., Yang, Y., Wang, C., & Hu, X. (2023). Federated Learning Based Fault Diagnosis Driven by Intra-Client Imbalance Degree. Entropy, 25(4), 606. https://doi.org/10.3390/e25040606







