Online/Offline MA-CP-ABE with Cryptographic Reverse Firewalls for IoT
Abstract
:1. Introduction
- (1)
- We propose a new MA-CP-ABE-CRF scheme, which not only avoids the crisis of single point of failure of single-authority ABE but also provides flexible access control for ciphertext data. In addition, four CRFs are used to re-randomize key parameters. This allows the MA-CP-ABE scheme to maintain functionality and resist ex-filtration even if it is compromised by unexpected attacks.
- (2)
- In order to make the scheme suitable for IoT, we have adopted online/offline key generation, online/offline encryption, and outsourcing decryption technologies to improve the computational efficiency of the scheme. These technologies are not only adopted by users and attribute authority but also by the four CRFs, which can significantly improve the efficiency of the scheme. Compared with other studies in terms of computational and storage overhead, our scheme has obvious advantages.
- (3)
- We have theoretically analyzed and proven the correctness and security of the OO-MA-CP-ABE-CRFs scheme, including CPA security, weak security reservation, and weak demonstration resistance. These security guarantees that devices in IOT are secure even when attacked by backdoors.
2. Related Work
2.1. Attribute-Based Encryption
2.2. Cryptographic Reverse Firewall
2.3. Online/Offline Cryptography
3. Preliminaries
3.1. Bilinear Groups
- (1)
- Bilinearity: For any and , it can calculate; .
- (2)
- Non-degeneracy: If is assumed, then is established;
- (3)
- Computability: For any , there exists an efficient algorithm to compute .
3.2. Linear Secret Sharing Schemes
- (1)
- The shares of each party constitute a vector over ;
- (2)
- There exists a share-generating matrix M with l rows and n columns for scheme . Furthermore, there exists a function that maps each row of the matrix M to an associated party. For example, each row of the matrix is closely related to , where . For column vector , we choose s from as the secret value that needs to be shared, and are randomly selected. represents a vector composed of l elements, and each element is the secret share generated by the scheme for s. The share belongs to party .
3.3. Cryptographic Reverse Firewall
3.4. System Model
3.5. Security Model
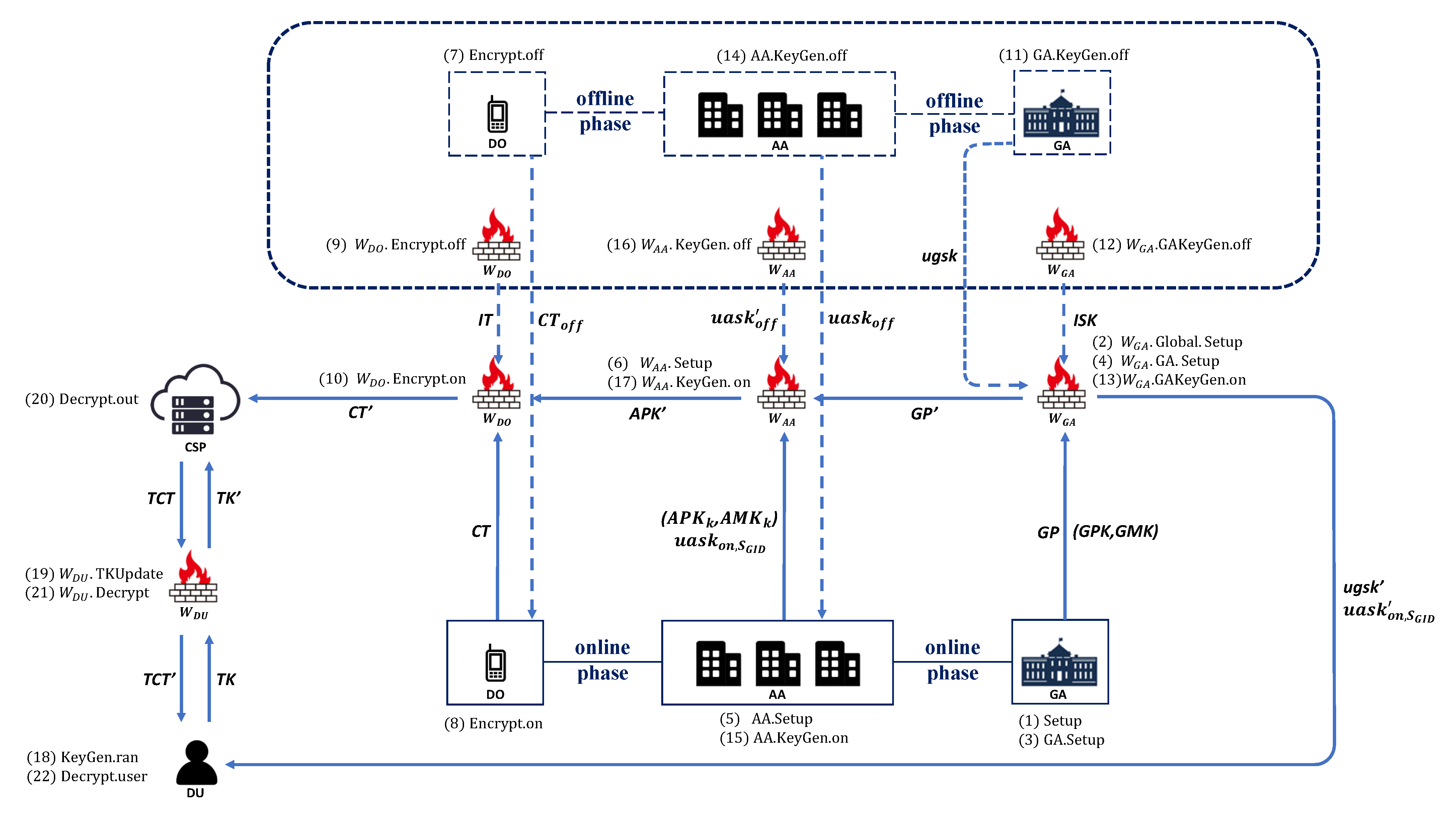
4. OO-MA-CP-ABE-CRFs
4.1. Basic Construction of OO-MA-CP-ABE Scheme
4.2. Construction of OO-MA-CP-ABE-CRFs
4.3. Security Analysis
5. Performance Evaluations
5.1. Property Comparison
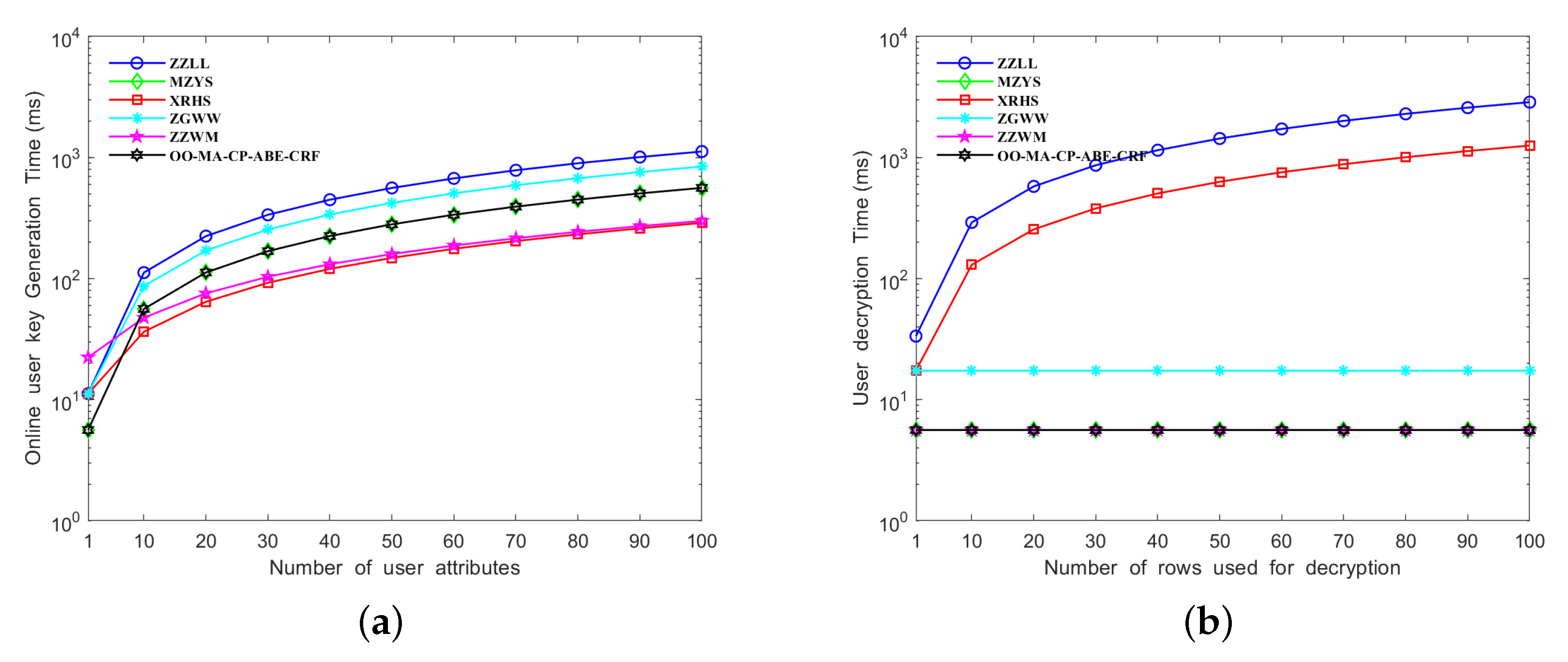
5.2. Performance Analysis
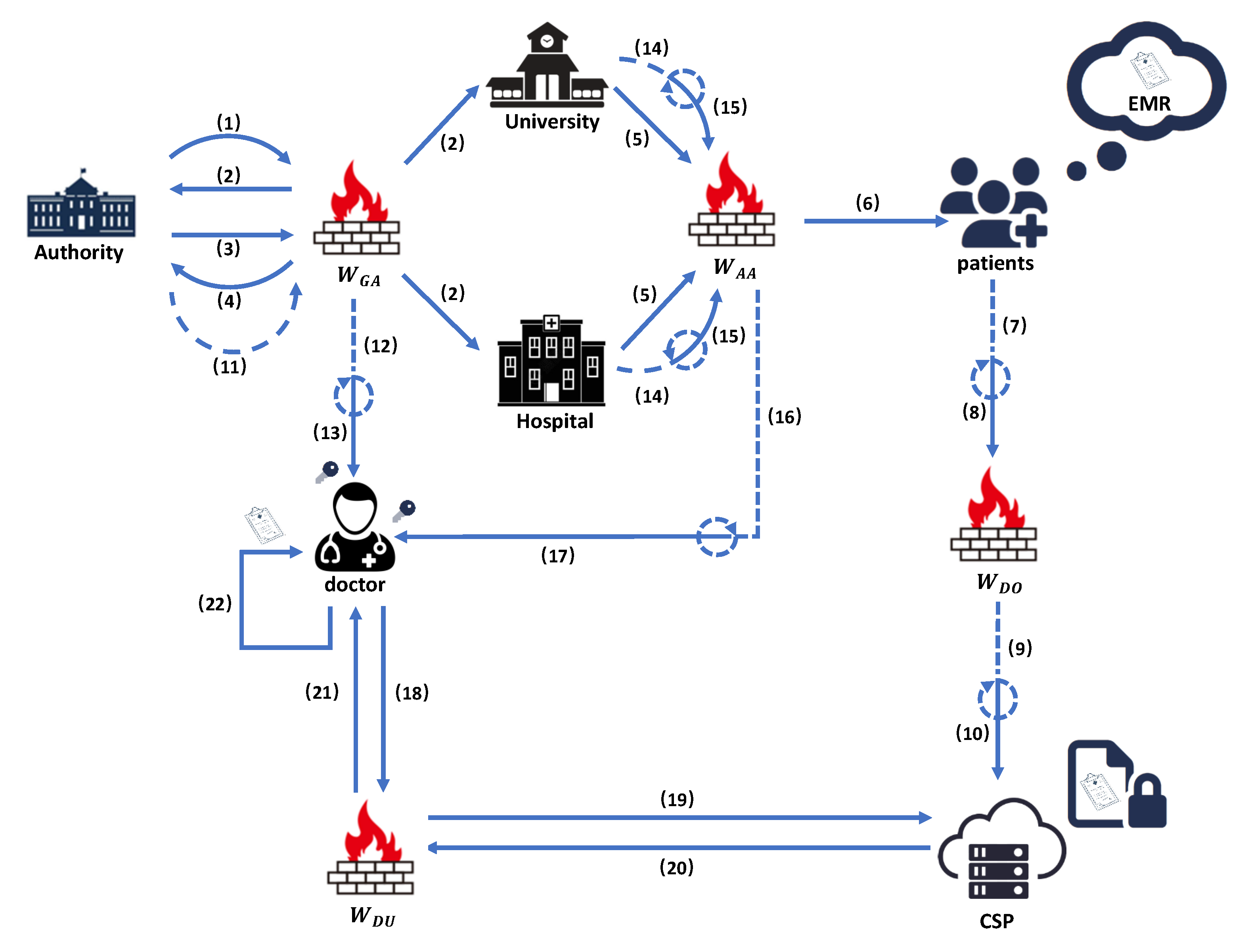
6. Real-World Application
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
References
- Le, T.; Hsu, C.; Chen, W. A hybrid blockchain-based log management scheme with nonrepudiation for smart grids. IEEE Trans. Ind. Inform. 2021, 18, 5771–5782. [Google Scholar] [CrossRef]
- Zhong, H.; Zhou, Y.; Zhang, Q.; Xu, Y.; Cui, J. An efficient and outsourcing-supported attribute-based access control scheme for edge-enabled smart healthcare. Future Gener. Comput. Syst. 2021, 115, 486–496. [Google Scholar] [CrossRef]
- Li, J.; Wang, S.; Li, Y.; Wang, H.; Wang, H.; Wang, H.; Chen, J.; You, Z. An efficient attribute-based encryption scheme with policy update and file update in cloud computing. IEEE Trans. Ind. Inform. 2019, 15, 6500–6509. [Google Scholar] [CrossRef]
- Chen, N.; Li, J.; Zhang, Y.; Guo, Y. Efficient CP-ABE scheme with shared decryption in cloud storage. IEEE Trans. Comput. 2020, 71, 175–184. [Google Scholar] [CrossRef]
- Li, J.; Yao, W.; Han, J.; Zhang, Y.; Shen, J. User collusion avoidance CP-ABE with efficient attribute revocation for cloud storage. IEEE Syst. J. 2017, 12, 1767–1777. [Google Scholar] [CrossRef]
- Ezhilarasi, T.P.; Sudheer, K.N.; Latchoumi, T.P.; Balayesu, N. A secure data sharing using IDSS CP-ABE in cloud storage. In Proceedings of the Advances in Industrial Automation and Smart Manufacturing, Kurnool, India, 26–27 July 2019; Springer: Singapore, 2021; pp. 1073–1085. [Google Scholar]
- Chaudhary, C.K.; Sarma, R.; Barbhuiya, F.A. RMA-CPABE: A multi-authority CPABE scheme with reduced ciphertext size for IoT devices. Future Gener. Comput. Syst. 2023, 138, 226–242. [Google Scholar] [CrossRef]
- Zhong, H.; Zhu, W.; Xu, Y.; Cui, J. Multi-authority attribute-based encryption access control scheme with policy hidden for cloud storage. Soft Comput. 2018, 22, 243–251. [Google Scholar] [CrossRef]
- Das, S.; Namasudra, S. Multi-Authority CP-ABE-Based Access Control Model for IoT-Enabled Healthcare Infrastructure. IEEE Trans. Ind. Inform. 2023, 19, 821–829. [Google Scholar] [CrossRef]
- Ball, J.; Borger, J.; Greenwald, G. Revealed: How US and UK spy agencies defeat internet privacy and security. Know Your Neighborhood 2013, 6, 1–10. [Google Scholar]
- Perlroth, N.; Larson, J.; Shane, S. NSA Able to Foil Basic Safeguards of Privacy on Web. The New York Times, 5 September 2013; pp. 1–8. [Google Scholar]
- Greenwald, G. No Place to Hide: Edward Snowden, the NSA, and the US Surveillance State; Macmillan: New York, NY, USA, 2014. [Google Scholar]
- Mironov, I.; Stephens-Davidowitz, N. Cryptographic reverse firewalls. In Proceedings of the Annual International Conference on the Theory and Applications of Cryptographic Techniques, Sofia, Bulgaria, 26–30 April 2015; Springer: Berlin/ Heidelberg, Germany, 2015; pp. 657–686. [Google Scholar]
- Miao, Y.; Tong, Q.; Choo, K.K.R.; Liu, X.; Deng, R.H.; Li, H. Secure online/offline data sharing framework for cloud-assisted industrial Internet of Things. IEEE Internet Things J. 2019, 6, 8681–8691. [Google Scholar] [CrossRef]
- Sahai, A.; Waters, B. Fuzzy identity-based encryption. In Proceedings of the Annual international conference on the theory and applications of cryptographic techniques, Aarhus, Denmark, 22–26 May 2005; Springer: Berlin/ Heidelberg, Germany, 2005; pp. 457–473. [Google Scholar]
- Goyal, V.; Pandey, O.; Sahai, A.; Waters, B. Attribute-based encryption for fine-grained access control of encrypted data. In Proceedings of the 13th ACM Conference on Computer and Communications Security, Lexandria, VA, USA, 30 October–3 November 2006; pp. 89–98. [Google Scholar]
- Bethencourt, J.; Sahai, A.; Waters, B. Ciphertext-policy attribute-based encryption. In Proceedings of the 2007 IEEE Symposium on Security and Privacy (SP’07), Berkeley, CA, USA, 20–23 May 2007; pp. 321–334. [Google Scholar]
- Chase, M. Multi-authority attribute based encryption. In Proceedings of the Theory of Cryptography Conference, Amsterdam, The Netherlands, 21–24 February 2007; Springer: Berlin/Heidelberg, Germany, 2007; pp. 515–534. [Google Scholar]
- Chase, M.; Chow, S.S.M. Improving privacy and security in multi-authority attribute-based encryption. In Proceedings of the 16th ACM Conference on Computer and Communications Security, Chicago, IL, USA, 9–13 November 2009; pp. 121–130. [Google Scholar]
- Lin, H.; Cao, Z.; Liang, X.; Shao, J. Secure threshold multi authority attribute based encryption without a central authority. Inf. Sci. 2010, 180, 2618–2632. [Google Scholar] [CrossRef]
- Qian, H.; Li, J.; Zhang, Y.; Han, J. Privacy-preserving personal health record using multi-authority attribute-based encryption with revocation. Int. J. Inf. Secur. 2015, 14, 487–497. [Google Scholar] [CrossRef]
- Zhou, Y.; Guan, Y.; Zhang, Z.; Li, F. Cryptographic reverse firewalls for identity-based encryption. In Proceedings of the International Conference on Frontiers in Cyber Security, Xi’an, China, 15–17 November 2019; Springer: Singapore, 2019; pp. 36–52. [Google Scholar]
- Chen, R.; Mu, Y.; Yang, G.; Susilo, W.; Guo, F.; Zhang, M. Cryptographic reverse firewall via malleable smooth projective hash functions. In Proceedings of the International Conference on the Theory and Application of Cryptology and Information Security, Hanoi, Vietnam, 4–8 December 2016; Springer: Berlin/Heidelberg, Germany, 2016; pp. 844–876. [Google Scholar]
- Zhou, Y.; Guo, J.; Li, F. Certificateless public key encryption with cryptographic reverse firewalls. J. Syst. Archit. 2020, 109, 101754. [Google Scholar] [CrossRef]
- Zhou, Y.; Hu, Z.; Li, F. Searchable public-key encryption with cryptographic reverse firewalls for cloud storage. IEEE Trans. Cloud Comput. 2021, 11, 383–396. [Google Scholar] [CrossRef]
- Ma, H.; Zhang, R.; Yang, G.; Song, Z.; Sun, S.; Xiao, Y. Concessive online/offline attribute based encryption with cryptographic reverse firewalls—Secure and efficient fine-grained access control on corrupted machines. In Proceedings of the European Symposium on Research in Computer Security, Barcelona, Spain, 3–7 September 2018; Springer: Cham, Switzerland, 2018; pp. 507–526. [Google Scholar]
- Hong, B.; Chen, J.; Zhang, K.; Qian, H. Multi-authority non-monotonic KP-ABE with cryptographic reverse firewall. IEEE Access 2019, 7, 159002–159012. [Google Scholar] [CrossRef]
- Khan, S.; Zareei, M.; Khan, S.; Alanazi, F.; Alam, M.; Waheed, A. OO-ABMS: Online/Offline-Aided Attribute-Based Multi-Keyword Search. IEEE Access 2021, 9, 114392–114406. [Google Scholar] [CrossRef]
- Ali, M.; Sadeghi, M.R.; Liu, X.; Miao, Y.; Vasilakos, A.V. Verifiable online/offline multi-keyword search for cloud-assisted Industrial Internet of Things. J. Inf. Secur. Appl. 2022, 65, 103101. [Google Scholar] [CrossRef]
- Zhang, L.; Su, J.; Mu, Y. Outsourcing attributed-based ranked searchable encryption with revocation for cloud storage. IEEE Access 2020, 8, 104344–104356. [Google Scholar] [CrossRef]
- Shao, J.; Zhu, Y.; Ji, Q. Privacy-preserving online/offline and outsourced multi-authority attribute-based encryption. In Proceedings of the 2017 IEEE/ACIS 16th International Conference on Computer and Information Science (ICIS), Wuhan, China, 24–26 May 2017; pp. 285–291. [Google Scholar]
- Zhang, Y.; Zheng, D.; Li, Q.; Li, J.; Li, H. Online/offline unbounded multi-authority attribute-based encryption for data sharing in mobile cloud computing. Secur. Commun. Netw. 2016, 9, 3688–3702. [Google Scholar] [CrossRef]
- Green, M.; Hohenberger, S.; Waters, B. Outsourcing the decryption of abe ciphertexts. USENIX Secur. Symp. 2011, 3, 8–12. [Google Scholar]
- Xie, M.; Ruan, Y.; Hong, H.; Shao, J. A CP-ABE scheme based on multi-authority in hybrid clouds for mobile devices. Future Gener. Comput. Syst. 2021, 121, 114–122. [Google Scholar] [CrossRef]
- Zhang, J.; Gong, Q.; Wei, Z.; Wang, X.; Yan, X.; Zhang, X. Efficient Multi-Authority Attribute-Based Encryption with Policy Hiding and Updating. In Proceedings of the 2022 IEEE 10th International Conference on Computer Science and Network Technology (ICCSNT), Dalian, China, 22–23 October 2022; pp. 34–38. [Google Scholar]
- Zhang, L.; Zhao, C.; Wu, Q.; Mu, Y.; Rezaeibagha, F. A traceable and revocable multi-authority access control scheme with privacy preserving for mHealth. J. Syst. Archit. 2022, 130, 102654. [Google Scholar] [CrossRef]
- Datta, P.; Dutta, R.; Mukhopadhyay, S. Fully secure online/offline predicate and attribute-based encryption. In Proceedings of the International Conference on Information Security Practice and Experience, Beijing, China, 5–8 May 2015; Springer: Cham, Switzerland, 2015; pp. 331–345. [Google Scholar]

| Schemes | Multi-Authority | Online/Offline Key Generation | Online/Offline Encryption | CRF |
|---|---|---|---|---|
| [26] | × | ✓ | ✓ | ✓ |
| [37] | × | × | ✓ | × |
| [32] | ✓ | ✓ | ✓ | × |
| [34] | ✓ | × | × | × |
| [35] | ✓ | × | × | × |
| [36] | ✓ | × | ✓ | × |
| Proposed | ✓ | ✓ | ✓ | ✓ |
| Schemes | System Setup | Online User Key Generation | Online User Encryption | User Decryption |
|---|---|---|---|---|
| [32] | ||||
| [26] | ||||
| [34] | ||||
| [35] | ||||
| [36] | ||||
| Proposed |
| Schemes | Public Parameters | Ciphertext | User Decryption Key |
|---|---|---|---|
| [32] | |||
| [26] | |||
| [34] | |||
| [35] | |||
| [36] | |||
| Proposed |
| Operation | Time Cost |
|---|---|
| bilinear pairing operation | 2.05 ms |
| exponentiation in | 2.80 ms |
| multiplication in | 2.82 ms |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Fan, Y.; Bian, X.; Yuan, Q. Online/Offline MA-CP-ABE with Cryptographic Reverse Firewalls for IoT. Entropy 2023, 25, 616. https://doi.org/10.3390/e25040616
Li J, Fan Y, Bian X, Yuan Q. Online/Offline MA-CP-ABE with Cryptographic Reverse Firewalls for IoT. Entropy. 2023; 25(4):616. https://doi.org/10.3390/e25040616
Chicago/Turabian StyleLi, Juyan, Ye Fan, Xuefen Bian, and Qi Yuan. 2023. "Online/Offline MA-CP-ABE with Cryptographic Reverse Firewalls for IoT" Entropy 25, no. 4: 616. https://doi.org/10.3390/e25040616
APA StyleLi, J., Fan, Y., Bian, X., & Yuan, Q. (2023). Online/Offline MA-CP-ABE with Cryptographic Reverse Firewalls for IoT. Entropy, 25(4), 616. https://doi.org/10.3390/e25040616








