Performance Comparison of Different Flat Plate Solar Collectors by Means of the Entropy Generation Rate Using Computational Fluid Dynamics
Abstract
:1. Introduction
2. Geometries and Mathematical Model
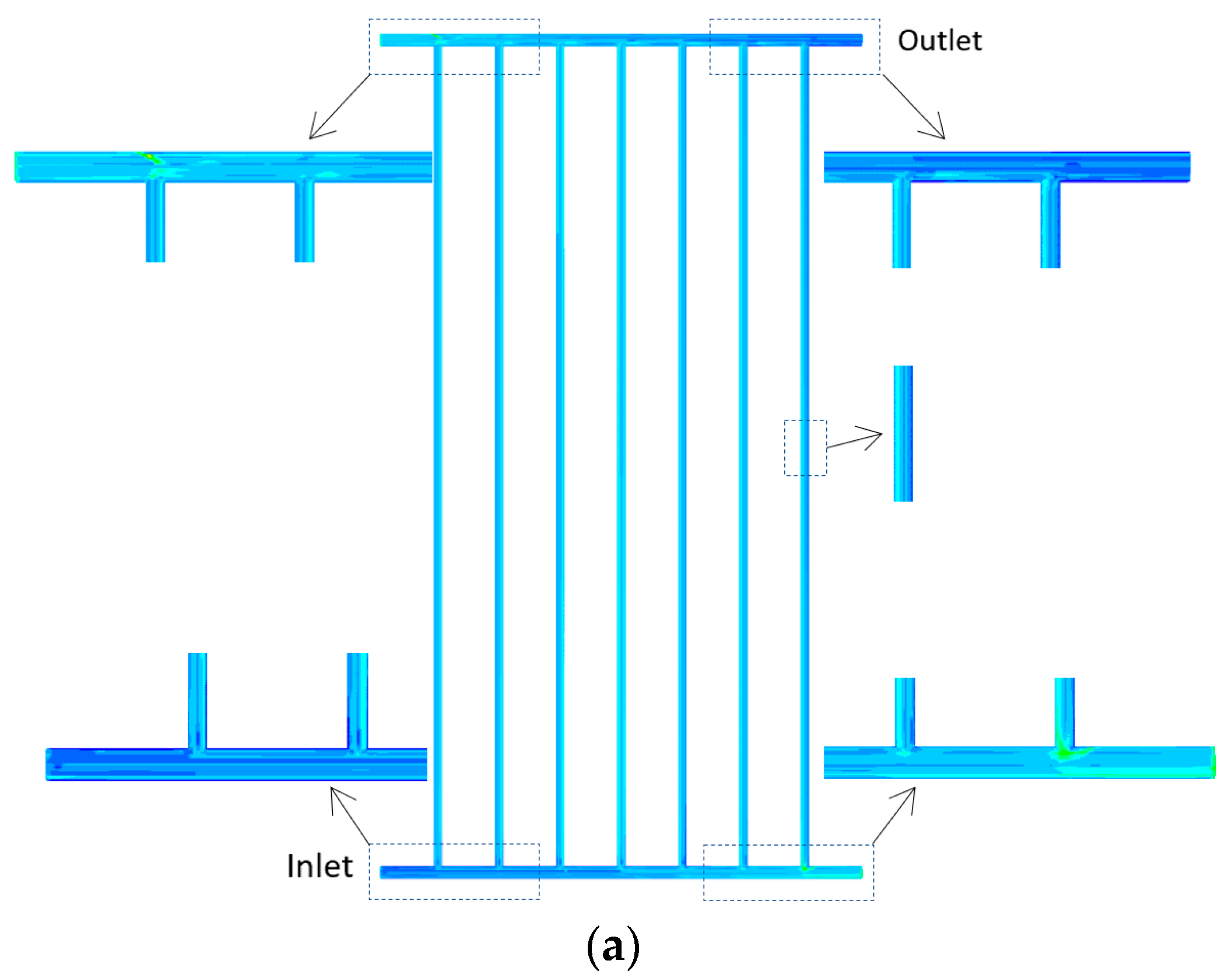
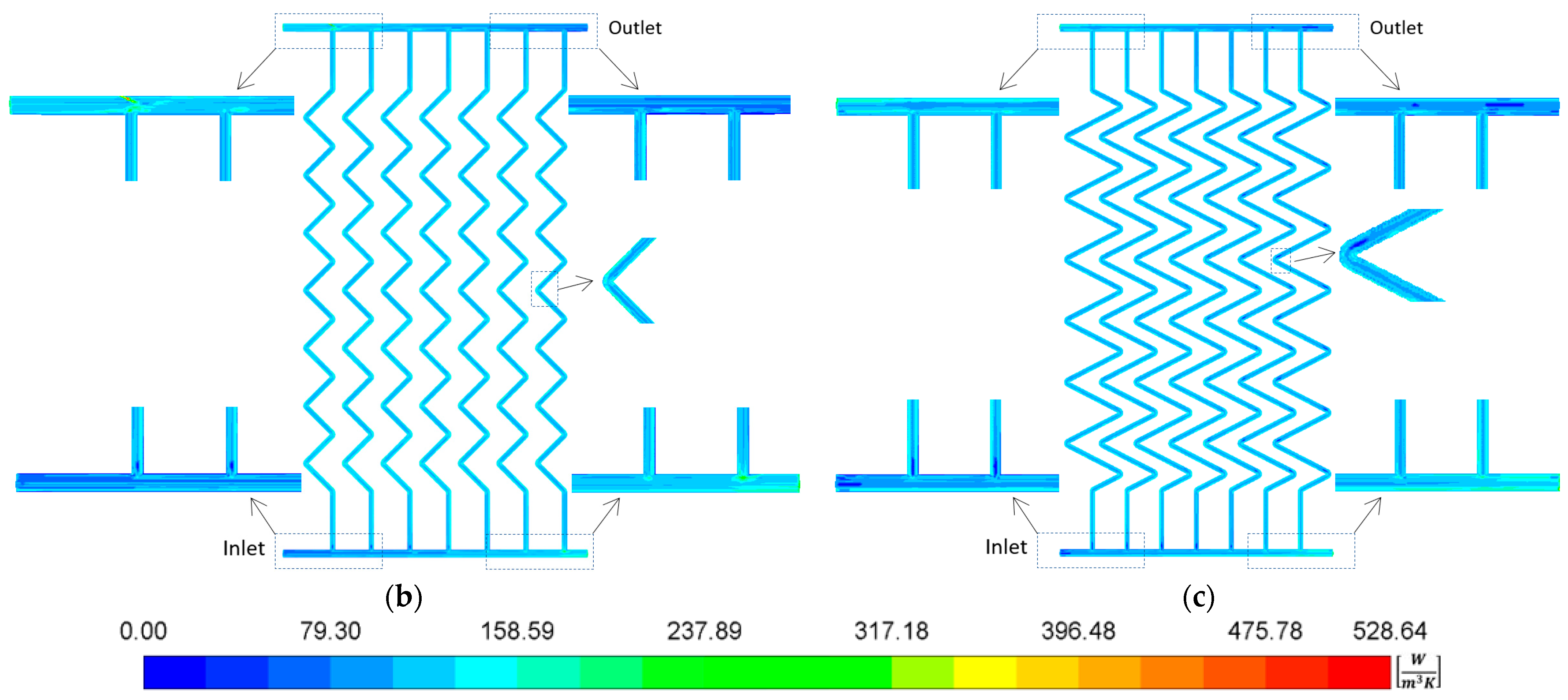
2.1. Configurations of the Geometries of the Solar Collectors
2.2. Equations Used in the Model
2.3. Computing the Irreversibilities Using the Entropy Generation Rate
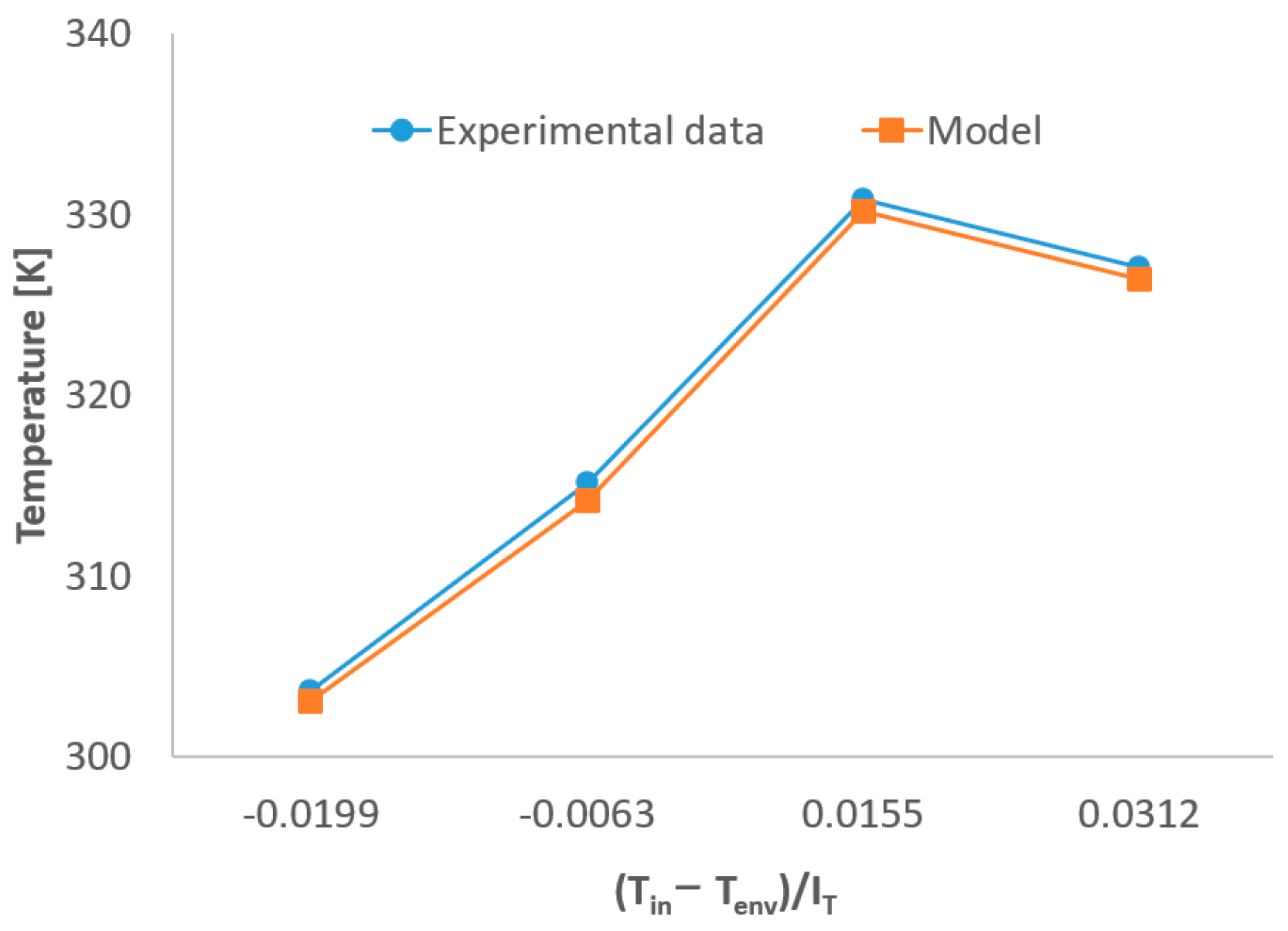
2.4. Boundary Conditions of the Model
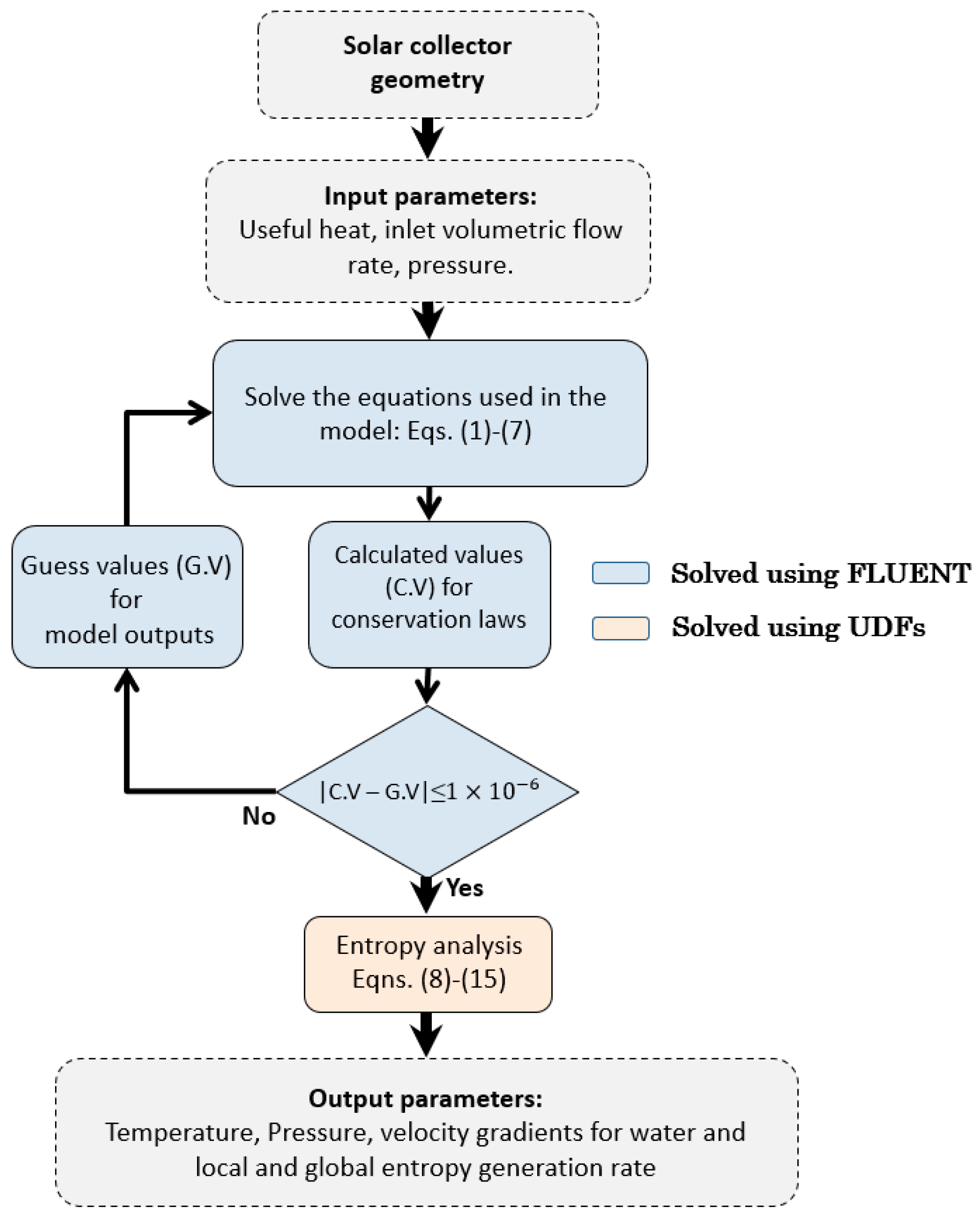
2.5. Numerical Approach
3. Results
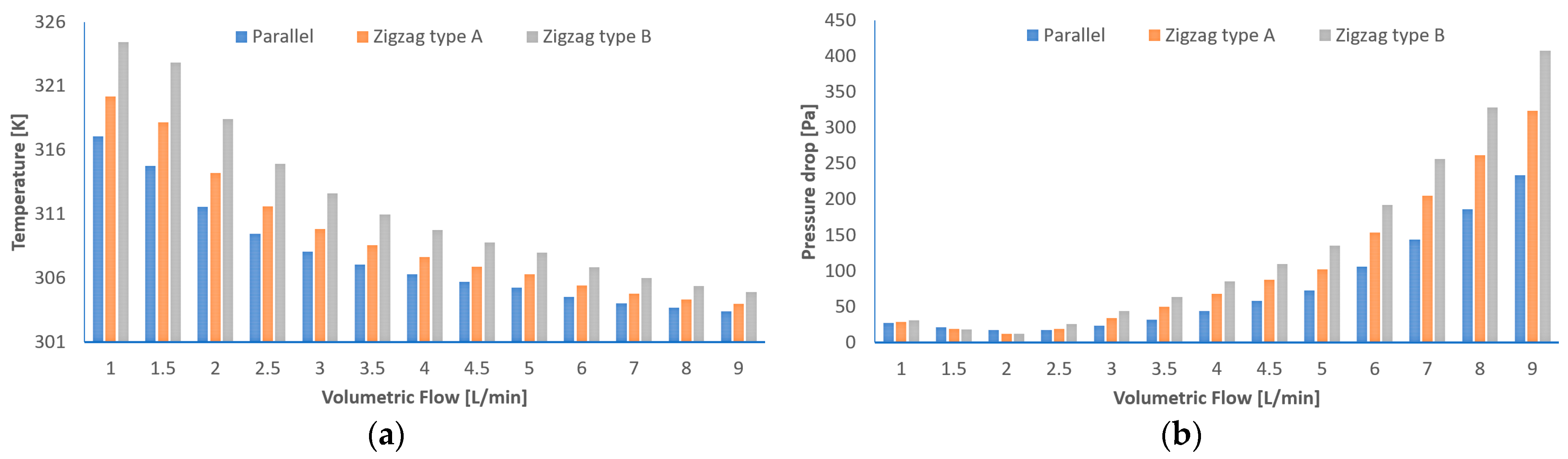
3.1. Thermal Performance Comparison of the FPCs: Variable Volumetric Flow Rates
3.2. Performance Comparison of the FPCs at 3.0 L/min
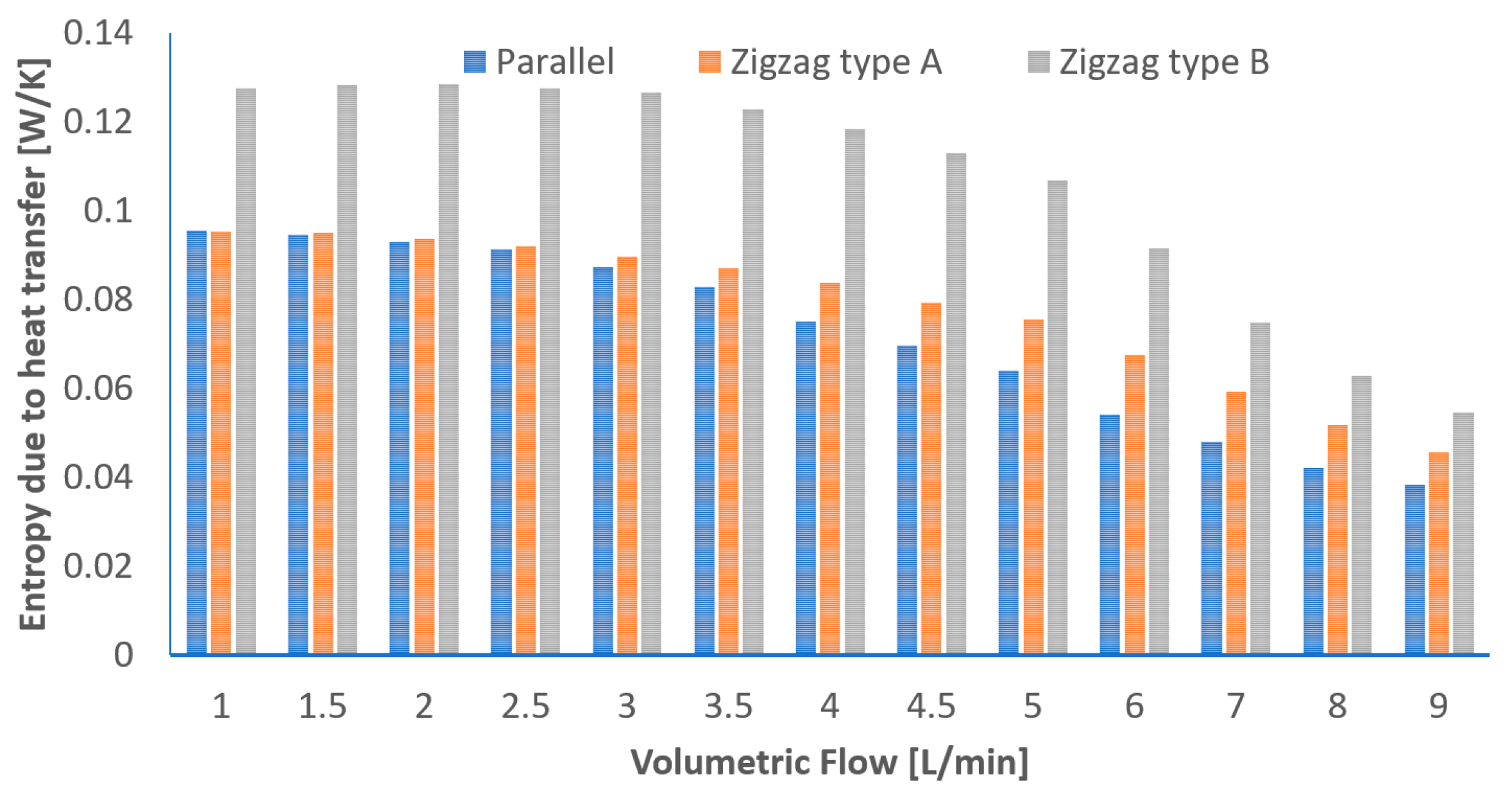
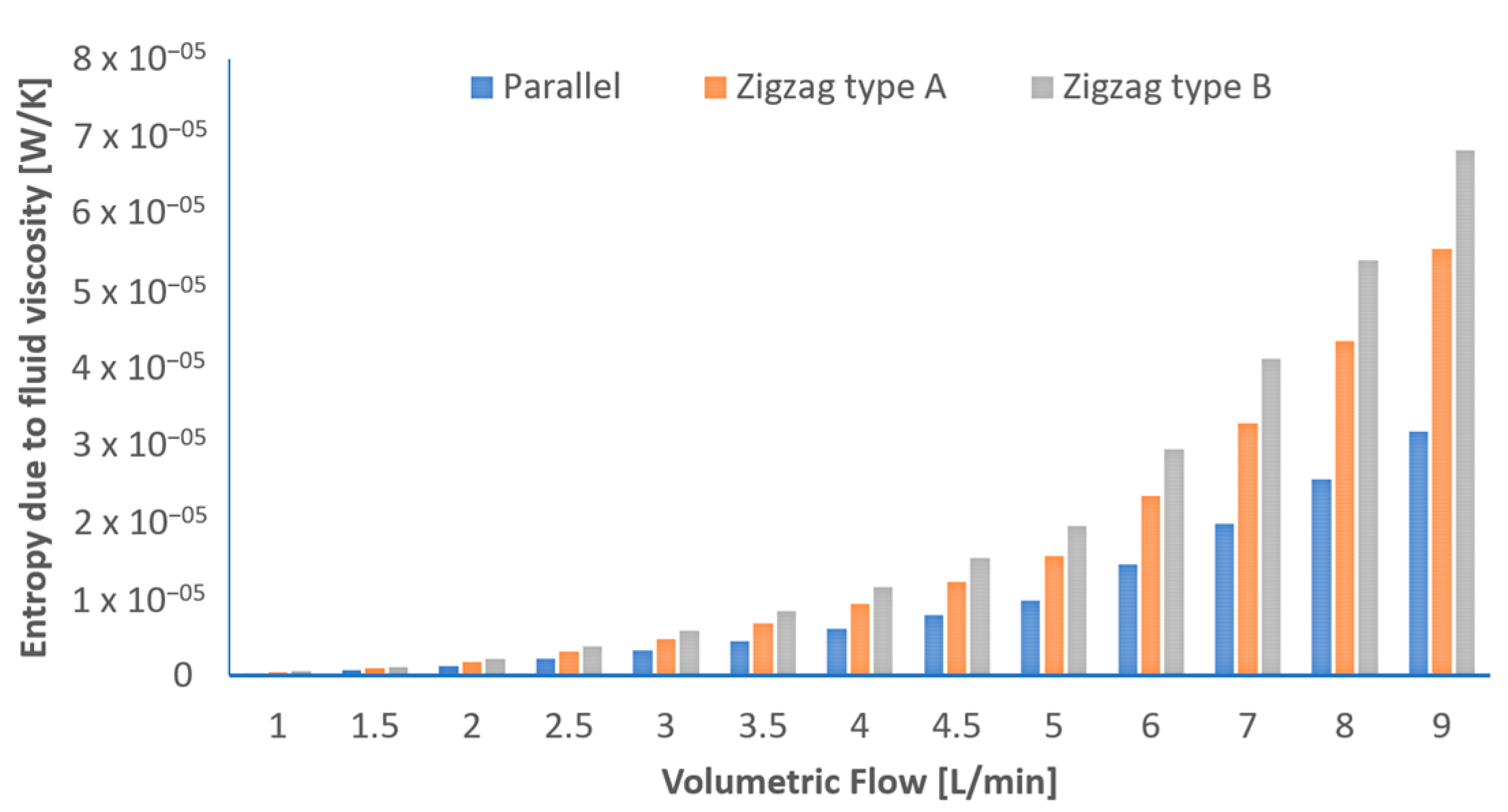
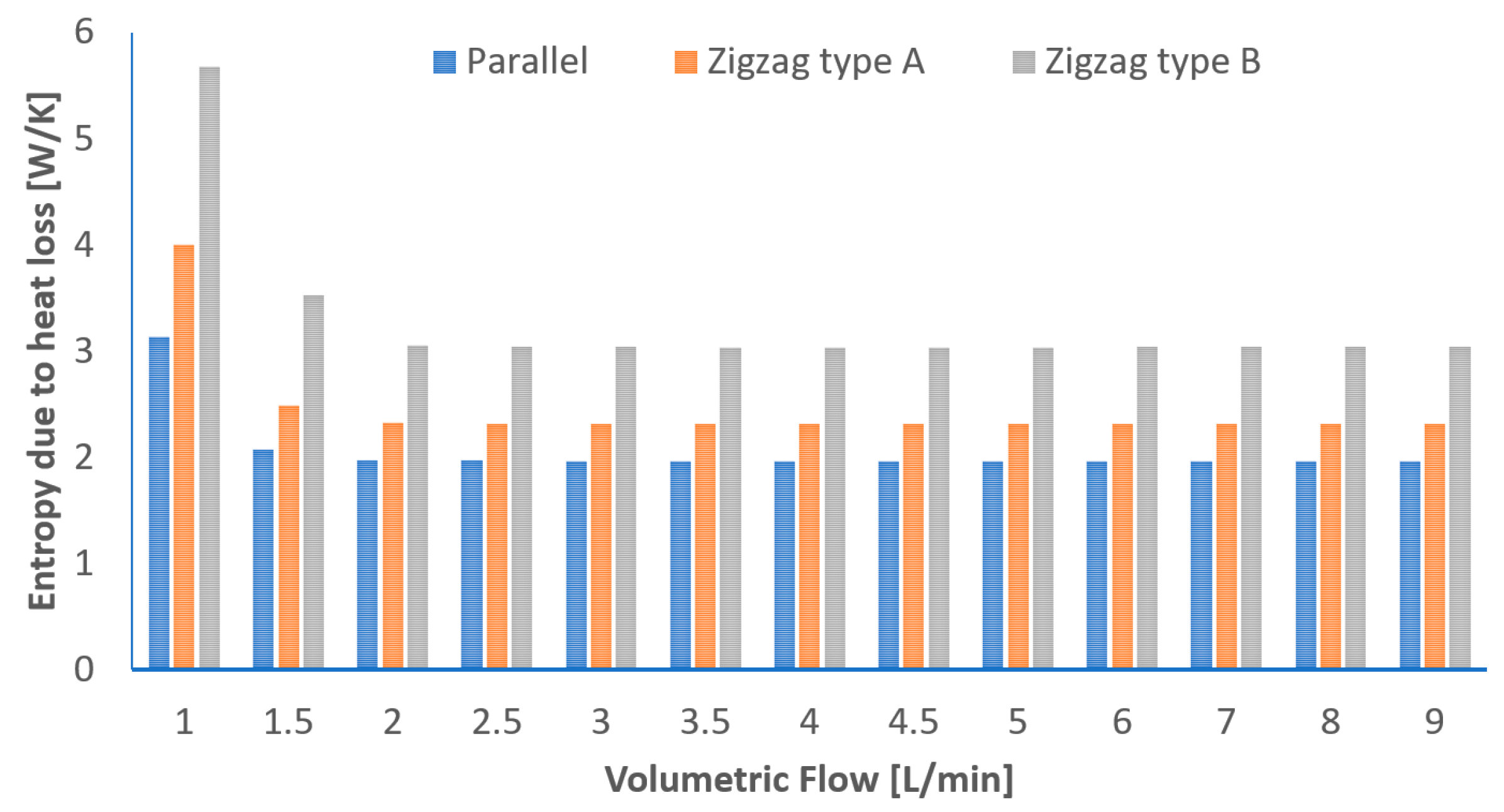
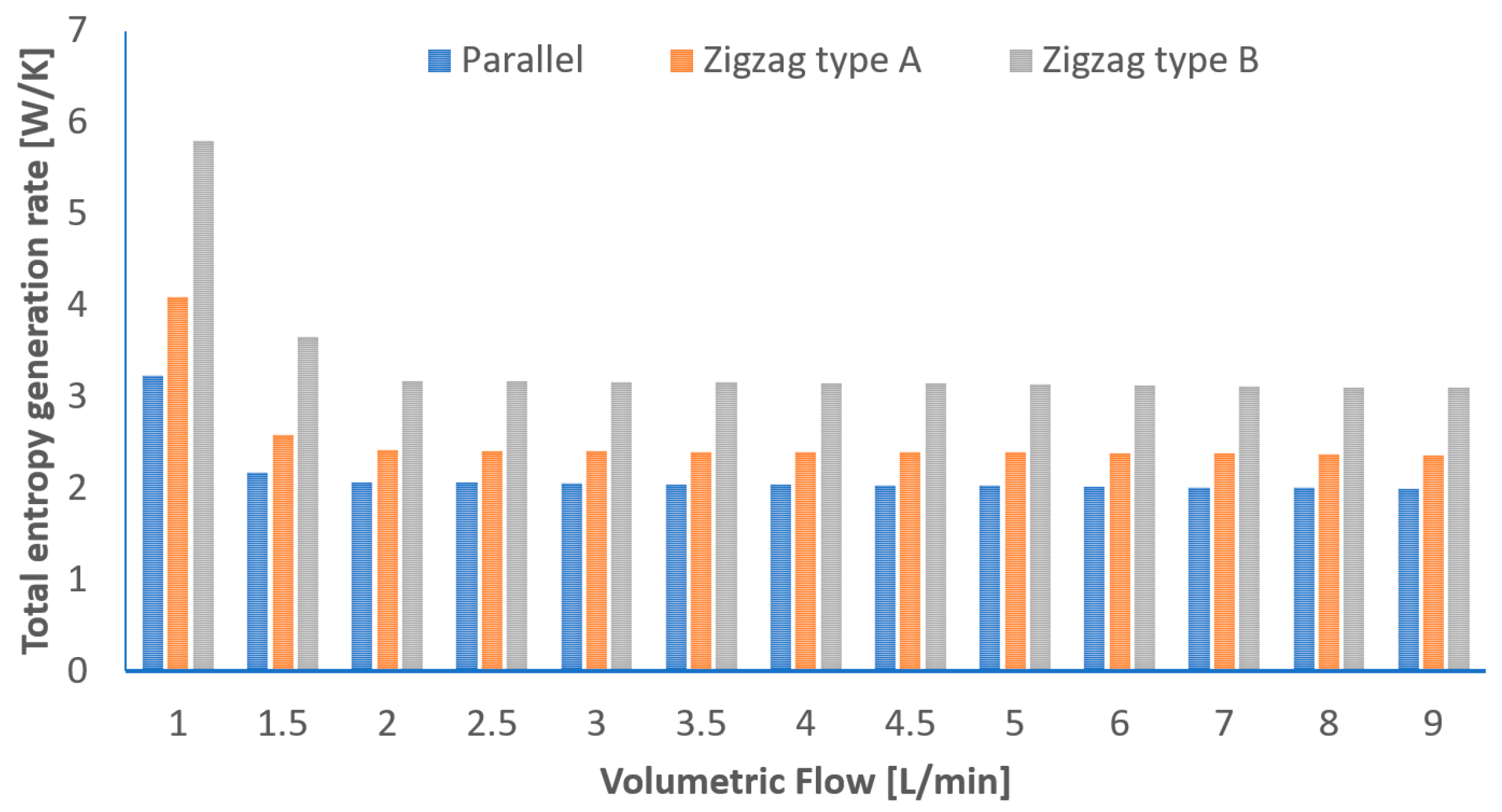
3.3. Entropy Generation Analysis
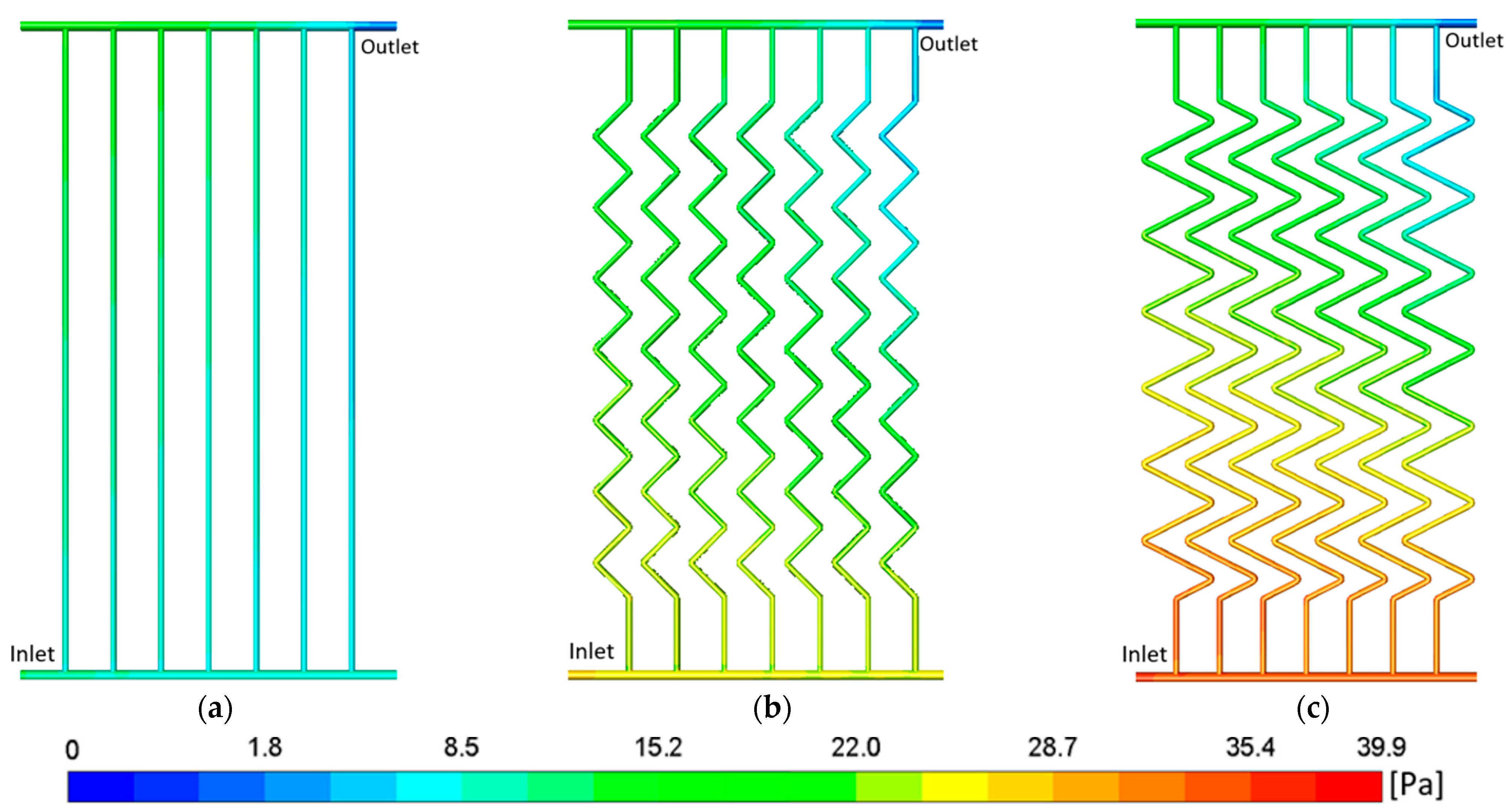
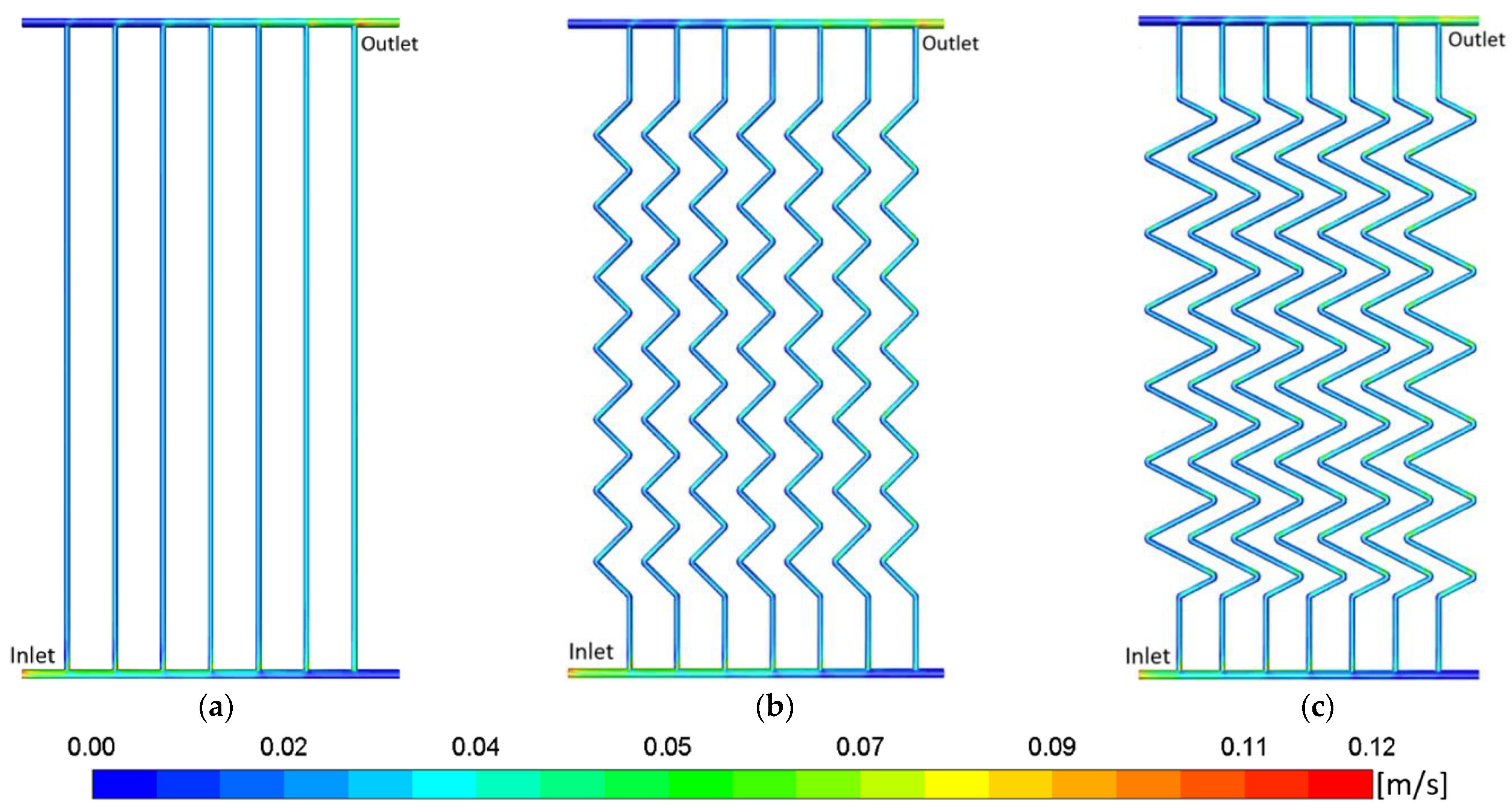
3.4. Maps of the Local Entropy Generation Rates inside the Tubes of the FPCs at 3.0 L/min
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ahmadia, A.; Ehyaei, M.A.; Doustgani, A.; El, A.M.; Hmida, A.; Jamalif, D.H.; Kumarg, R.; Li, Z.X.; Razmjoo, A. Recent residential applications of low-temperature solar collector. J. Clean. Prod. 2021, 279, 123549. [Google Scholar] [CrossRef]
- Chow, T.T.; Dong, Z.; Chan, L.S.; Fong, K.F.; Bai, Y. Performance evaluation of evacuated tube solar domestic hot water systems in Hong Kong. Energy Build. 2011, 43, 3467–3474. [Google Scholar] [CrossRef]
- Bhatia, S.C. Solar thermal energy, chapter 4. In Advanced Renewable Energy Systems, 1st ed.; Taylor & Francis Group: New York, NY, USA, 2014; pp. 94–143. [Google Scholar] [CrossRef]
- Tang, R.; Cheng, Y.; Wu, M.; Li, Z.; Yu, Y. Experimental and modeling studies on thermosiphon domestic solar water heaters with flat-plate collectors at clear nights. Energy Convers. Manag. 2010, 51, 2548–2556. [Google Scholar] [CrossRef]
- Elsheikh, A.H.; Sharshir, S.W.; Mostafa, M.E.; Essa, F.A.; Ali, M.K. Applications of nanofluids in solar energy: A review of recent advances. Renew. Sustain. Energy Rev. 2018, 82, 3483–3502. [Google Scholar] [CrossRef]
- Olfian, H.; Ajarostaghi, S.S.; Ebrahimnataj, M. Development on evacuated tube solar collectors: A review of the last decade results of using nanofluids. Sol. Energy 2020, 211, 265–282. [Google Scholar] [CrossRef]
- Ashour, A.F.; Ahmed, E.A.; Mohsen, A.T. Numerical investigation on the thermal performance of a flat plate solar collector using ZnO & CuO water nanofluids under Egyptian weathering conditions. Energy 2022, 240, 122743. [Google Scholar] [CrossRef]
- Cao, Y.; Ayed, H.; Hashemian, M.; Issakhov, A.; Jarad, F.; Makatar, W. Inducing swirl flow inside the pipes of flat-plate solar collector by using multiple nozzles for enhancing thermal performance. Renew. Energy 2021, 180, 1344–1357. [Google Scholar] [CrossRef]
- Vengadesan, E.; Senthil, R. Experimental study on the thermal performance of a flat plate solar water collector with a bifunctional flow insert. Sustain. Energy Technol. Assess. 2022, 50, 101829. [Google Scholar] [CrossRef]
- Wang, D.; Mo, Z.; Liu, Y.; Ren, Y.; Fan, J. Thermal performance analysis of large-scale flat plate solar collectors and regional applicability in China. Energy 2022, 238, 121931. [Google Scholar] [CrossRef]
- Azad, E. Experimental analysis of thermal performance of solar collectors with different numbers of heat pipes versus a flow-through solar collector. Renew. Sustain. Energy Rev. 2018, 82, 4320–4325. [Google Scholar] [CrossRef]
- Alwan, N.T.; Shcheklein, S.E.; Ali, O.M. Experimental analysis of thermal performance for flat plate solar water collector in the climate conditions of Yekaterinburg, Russia. Mater. Today Proc. 2021, 42, 2076–2083. [Google Scholar] [CrossRef]
- Hashim, W.M.; Shomran, A.T.; Jurmut, H.A.; Gaaz, T.S.; Kadhum, A.A.H.; Al-Amiery, A.A. Case study on solar water heating for flat plate collector. Case Stud. Therm. Eng. 2018, 12, 666–671. [Google Scholar] [CrossRef]
- Wei, L.; Yuan, D.; Tang, D.; Wu, B. A study on a flat-plate type of solar heat collector with an integrated heat pipe. Sol. Energy 2013, 97, 19–25. [Google Scholar] [CrossRef]
- Kargarsharifabad, H.; Behshad, S.M.; Taeibi, R.M.; Abbaspour, M. Exergy Analysis of a Flat Plate Solar Collector in Combination with Heat Pipe. Int. J. Environ. Res. 2014, 8, 39–48. [Google Scholar] [CrossRef]
- Mansour, M.K. Thermal analysis of novel minichannel-based solar flat-plate collector. Energy 2013, 60, 333–343. [Google Scholar] [CrossRef]
- Robles, A.; Duong, V.; Martin, A.J.; Guadarrama, J.L.; Diaz, G. Aluminum minichannel solar water heater performance under year-round weather conditions. Sol. Energy 2014, 110, 356–364. [Google Scholar] [CrossRef]
- Deng, Y.; Zhao, Y.; Wang, W.; Quan, Z.; Wang, L.; Yu, D. Experimental investigation of performance for the novelflat platesolar collector with micro-channel heat pipe array (MHPA-FPC). Appl. Therm. Eng. 2013, 54, 440–449. [Google Scholar] [CrossRef]
- Azad, E. Assessment of three types of heat pipe solar collectors. Renew. Sustain. Energy Rev. 2012, 16, 2833–2838. [Google Scholar] [CrossRef]
- Dovic, D.; Andrassy, M. Numerically assisted analysis of flat and corrugated plate solar collectors thermal performances. Sol. Energy 2012, 86, 2416–2431. [Google Scholar] [CrossRef]
- García, A.; Herrero-Martin, R.; Solano, J.P.; Pérez-García, J. The role of insert devices on enhancing heat transfer in a flat-plate solar water collector. Appl. Therm. Eng. 2018, 132, 479–489. [Google Scholar] [CrossRef]
- Gunjo, D.G.; Mahanta, P.; Robi, P.S. Exergy and energy analysis of a novel type solar collector under steady state condition: Experimental and CFD analysis. Renew. Energy 2017, 114, 655–669. [Google Scholar] [CrossRef]
- Alim, M.A.; Abdin, Z.; Saidur, R.; Hepbasli, A.; Khairul, M.A.; Rahim, N.A. Analyses of entropy generation and pressure drop for a conventional flat plate solar collector using different types of metal oxide nanofluids. Energy Build. 2013, 66, 289–296. [Google Scholar] [CrossRef]
- Jilani, J.; Thomas, C. Effect of thermo-geometric parameters on entropy generation in absorber plate fin of a solar flat plate collector. Energy 2014, 70, 35–42. [Google Scholar] [CrossRef]
- Jouybari, H.J.; Saedodin, S.; Zamzamian, A.; Nimvari, M.E. Experimental investigation of thermal performance and entropy generation of a flat-plate solar collector filled with porous media. Appl. Therm. Eng. 2017, 127, 1506–1517. [Google Scholar] [CrossRef]
- Alklaibi, A.M.; Sundar, L.S.; Sousa, A.C.M. Experimental analysis of exergy efficiency and entropy generation of diamond/water nanofluids flow in a thermosyphon flat plate solar collector. Int. Commun. Heat Mass Transf. 2019, 120, 105057. [Google Scholar] [CrossRef]
- Launder, B.; Spalding, D. Lectures in Mathematical Models of Turbulence, 1st ed.; Academic Press: London, UK, 1972. [Google Scholar]
- Takashima, T.; Tanaka, T.; Doi, T.; Kamoshida, J.; Tani, T.; Horigome, T. New proposal for photovoltaic-thermal solar energy utilization method. Sol. Energy 1994, 52, 241–245. [Google Scholar] [CrossRef]
- Li, Z.; Chen, C.; Luo, H.; Zhang, Y.; Xue, Y. All-glass vacuum tube collector heat transfer model used in forced-circulation solar water heating system. Sol. Energy 2010, 84, 1413–1421. [Google Scholar] [CrossRef]
- Budihardjo, I.; Morrison, G.L. Performance of a water-in-glass evacuated tube solar water heater. Sol. Energy 2009, 83, 49–56. [Google Scholar] [CrossRef]
- Zambolin, E.; Del, C.D. Experimental analysis of thermal performance of flat plate and evacuated tube solar collectors in stationary standard and daily conditions. Sol. Energy 2010, 84, 1382–1396. [Google Scholar] [CrossRef]
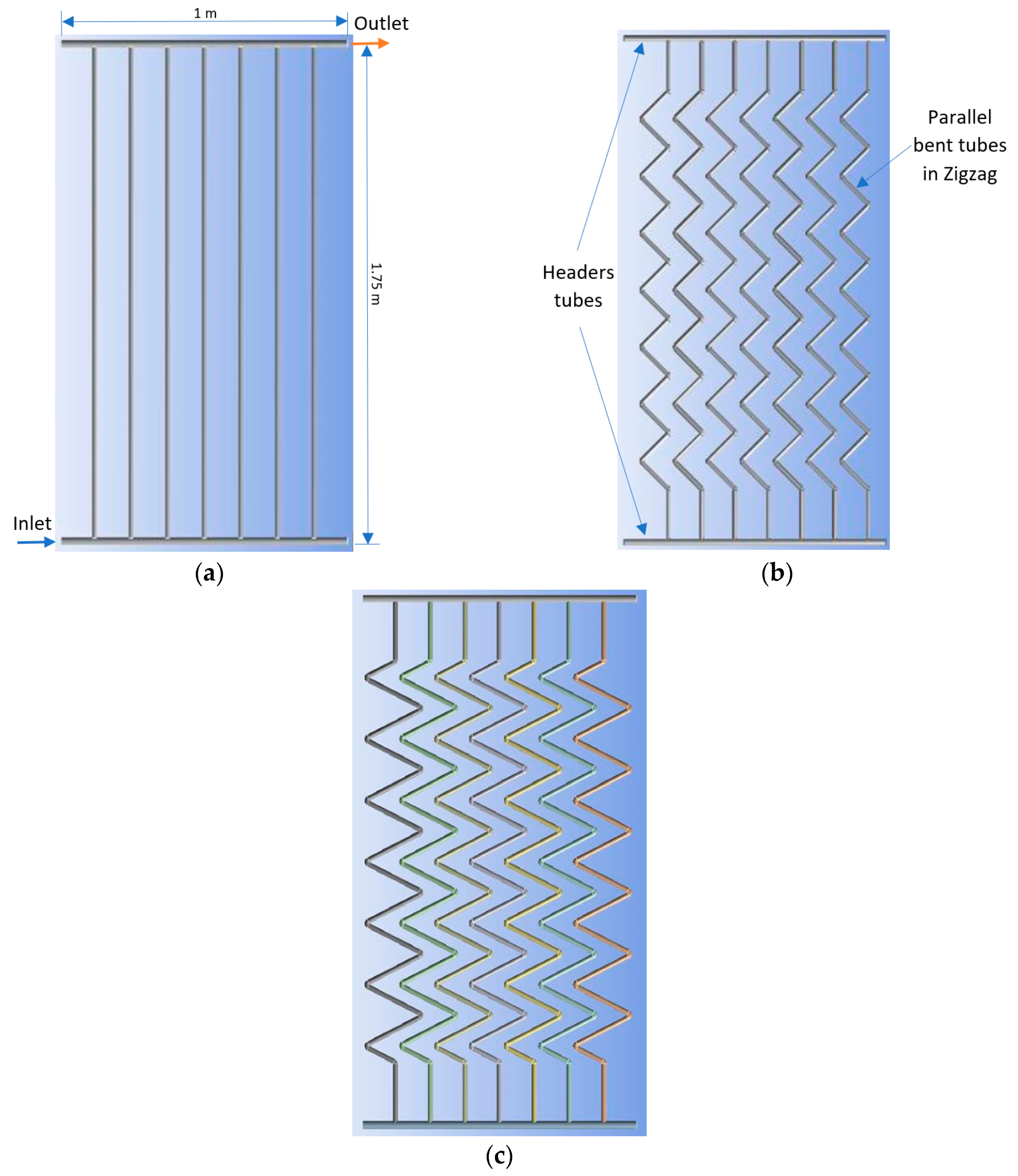

| Description | Specification |
|---|---|
| Number of tubes, [-] | 7 |
| External diameter, [m] | 0.0254 |
| Internal diameter, [m] | 0.025 |
| Width of the FPC, [m] | 1 |
| Length of the FPC, [m] | 1.75 |
| Area of the FPC, [m2] | 1.75 |
| Horizontal inclination of the FPC, [°] | 21 |
| Density, [kg∙m−3] | Boussinesq, Equation (7) |
| Thermal expansion coefficient, [K−1] | 0.000206 |
| Specific heat, [J∙kg−1∙K−1] | 4182 |
| Thermal conductivity, [W/m∙K] | 0.6 |
| Viscosity, kg∙m−1∙s−1 | 001003 |
| Number of Elements | Average Temperature [K] | Variation between the Previous Value of Average Temperature [K] | Convergence Time [Hour] |
|---|---|---|---|
| 30,253 | 306.50 | - | 0.58 |
| 82,341 | 307.22 | 0.72 | 1.5 |
| 278,864 | 307.71 | 0.49 | 5.5 |
| 649,887 | 308.07 | 0.36 | 8.2 |
| 1,734,153 | 308.06 | 0.01 | 17.5 |
| Number of Elements | Average Temperature [K] | Variation between the Previous Value of Average Temperature [K] | Convergence Time [Hour] |
|---|---|---|---|
| 516,833 | 308.90 | - | 7.5 |
| 1,260,857 | 309.85 | 0.95 | 13.8 |
| 2,501,458 | 309.81 | 0.04 | 22.6 |
| Number of Elements | Average Temperature [K] | Variation between the Previous Value of Average Temperature [K] | Convergence Time [Hour] |
|---|---|---|---|
| 405,458 | 310.50 | - | 6.7 |
| 906,544 | 311.84 | 1.34 | 11.0 |
| 1,923,992 | 312.63 | 0.79 | 21.2 |
| 4,589,410 | 312.52 | 0.11 | 39.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ramírez-Minguela, J.J.; Rangel-Hernández, V.H.; Alfaro-Ayala, J.A.; Elizalde-Blancas, F.; Ruiz-Camacho, B.; López-Núñez, O.A.; Alvarado-Rodríguez, C.E. Performance Comparison of Different Flat Plate Solar Collectors by Means of the Entropy Generation Rate Using Computational Fluid Dynamics. Entropy 2023, 25, 621. https://doi.org/10.3390/e25040621
Ramírez-Minguela JJ, Rangel-Hernández VH, Alfaro-Ayala JA, Elizalde-Blancas F, Ruiz-Camacho B, López-Núñez OA, Alvarado-Rodríguez CE. Performance Comparison of Different Flat Plate Solar Collectors by Means of the Entropy Generation Rate Using Computational Fluid Dynamics. Entropy. 2023; 25(4):621. https://doi.org/10.3390/e25040621
Chicago/Turabian StyleRamírez-Minguela, J. J., V. H. Rangel-Hernández, J. A. Alfaro-Ayala, F. Elizalde-Blancas, B. Ruiz-Camacho, O. A. López-Núñez, and C. E. Alvarado-Rodríguez. 2023. "Performance Comparison of Different Flat Plate Solar Collectors by Means of the Entropy Generation Rate Using Computational Fluid Dynamics" Entropy 25, no. 4: 621. https://doi.org/10.3390/e25040621





