An Adaptive Model Filtering Algorithm Based on Grubbs Test in Federated Learning
Abstract
:1. Introduction
2. Related Work
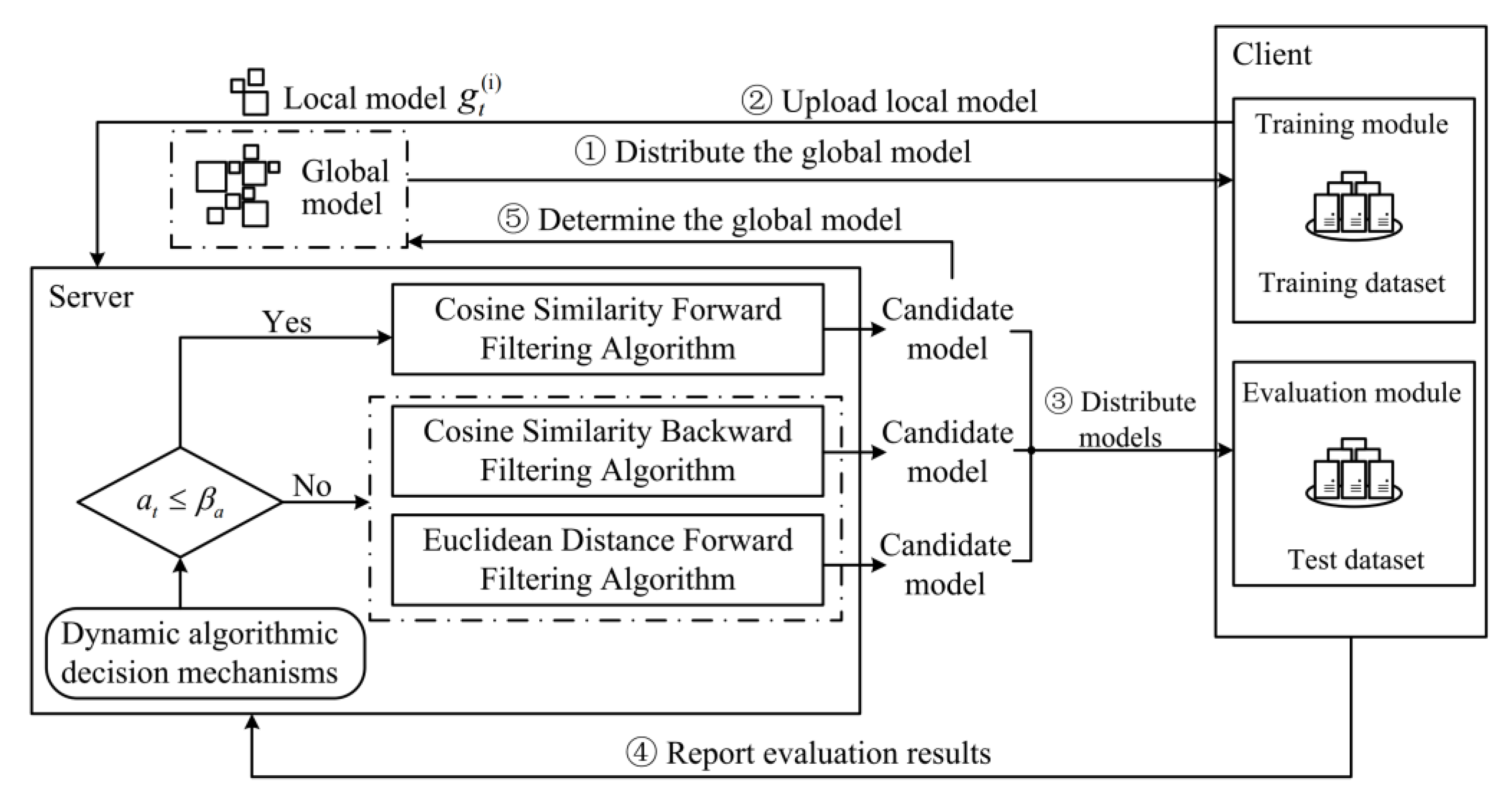
3. Design of FedGaf
3.1. Adaptive Filtering Algorithm Based on Grubbs Test
3.1.1. Cosine Similarity Forward Filtering
3.1.2. Cosine Similarity Backward Filtering
3.1.3. Euclidean Distance Forward Filtering
3.1.4. Model Weighted Aggregation
3.2. Dynamic Algorithmic Decision Mechanism
4. Performance Evaluation
4.1. Experimental Setup
4.2. Defending Label-Flipping Attack
4.3. Defending Sign-Flipping Attack
4.4. Defending Random-Label Attack
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mothukuri, V.; Parizi, R.M.; Pouriyeh, S.; Huang, Y.; Dehghantanha, A.; Srivastava, G. A survey on security and privacy of federated learning. Future Gener. Comput. Syst. 2021, 115, 619–640. [Google Scholar] [CrossRef]
- Aledhari, M.; Razzak, R.; Parizi, R.M.; Saeed, F. Federated learning: A survey on enabling technologies, protocols, and applications. IEEE Access 2020, 8, 140699–140725. [Google Scholar] [CrossRef] [PubMed]
- Duan, M.; Liu, D.; Chen, X.; Liu, R.; Tan, Y.; Liang, L. Self-balancing federated learning with global imbalanced data in mobile systems. IEEE Trans. Parallel Distrib. Syst. 2020, 32, 59–71. [Google Scholar] [CrossRef]
- Li, T.; Sahu, A.K.; Talwalkar, A.; Smith, V. Federated learning: Challenges, methods, and future directions. IEEE Signal Process. Mag. 2020, 37, 50–60. [Google Scholar] [CrossRef]
- Shayan, M.; Fung, C.; Yoon, C.J.M.; Beschastnikh, I. Biscotti: A blockchain system for private and secure federated learning. IEEE Trans. Parallel Distrib. Syst. 2020, 32, 1513–1525. [Google Scholar] [CrossRef]
- Cao, D.; Chang, S.; Lin, Z.; Liu, G.; Sun, D. Understanding distributed poisoning attack in federated learning. In Proceedings of the 2019 IEEE 25th International Conference on Parallel and Distributed Systems (ICPADS), Tianjin, China, 4–6 December 2019; pp. 233–239. [Google Scholar]
- Tolpegin, V.; Truex, S.; Gursoy, M.E.; Liu, L. Data poisoning attacks against federated learning systems. In Proceedings of the Computer Security–ESORICS 2020: 25th European Symposium on Research in Computer Security, ESORICS 2020, Guildford, UK, 14–18 September 2020; Springer International Publishing: Cham, Switzerland, 2020; pp. 480–501. [Google Scholar]
- Fung, C.; Yoon, C.J.M.; Beschastnikh, I. The Limitations of Federated Learning in Sybil Settings. In Proceedings of the 23rd International Symposium on Research in Attacks, Intrusions and Defenses, Virtual, 14–16 October 2020; 2020; pp. 301–316. [Google Scholar]
- Li, L.; Xu, W.; Chen, T.; Giannakis, B.; Ling, Q. RSA: Byzantine-robust stochastic aggregation methods for distributed learning from heterogeneous datasets. In Proceedings of the AAAI Conference on Artificial Intelligence, Hawaii, HI, USA, 27 January–1 February 2019; Volume 33, pp. 1544–1551. [Google Scholar]
- Fang, M.; Cao, X.; Jia, J.; Gong, N. Local model poisoning attacks to byzantine-robust federated learning. In Proceedings of the 29th USENIX Conference on Security Symposium, Boston, MA, USA, 12–14 August 2020; pp. 1623–1640. [Google Scholar]
- Blanchard, P.; El Mhamdi, E.M.; Guerraoui, R.; Stainer, J. Machine learning with adversaries: Byzantine tolerant gradient descent. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar]
- Yin, D.; Chen, Y.; Kannan, R.; Bartlett, P. Byzantine-robust distributed learning: Towards optimal statistical rates. In PMLR, Proceedings of the International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; Microtome Publishing: Brookline, MA, USA, 2018; pp. 5650–5659. [Google Scholar]
- Li, X.; Huang, K.; Yang, W.; Wang, S.; Zhang, Z. On the convergence of fedavg on non-iid data. arXiv 2019, arXiv:1907.02189. [Google Scholar]
- McMahan, B.; Moore, E.; Ramage, D.; Hampson, S.; Aguera y Arcas, B. Communication-efficient learning of deep networks from decentralized data. In PMLR, Proceedings of the Artificial Intelligence and Statistics, Ft. Lauderdale, FL, USA, 20–22 April 2017; Microtome Publishing: Brookline, MA, USA, 2017; pp. 1273–1282. [Google Scholar]
- Lyu, L.; Yu, H.; Yang, Q. Threats to federated learning: A survey. arXiv 2020, arXiv:2003.02133. [Google Scholar]
- Lamport, L.; Shostak, R.; Pease, M. The Byzantine generals problem. In Concurrency: The Works of Leslie Lamport; ACM Books: New York, NY, USA, 2019; pp. 203–226. [Google Scholar]
- Bagdasaryan, E.; Veit, A.; Hua, Y.; Estrin, D.; Shmatikov, V. How to backdoor federated learning. In PMLR, Proceedings of the International Conference on Artificial Intelligence and Statistics, Online, 26–28 August 2020; Microtome Publishing: Brookline, MA, USA, 2020; pp. 2938–2948. [Google Scholar]
- Kairouz, P.; McMahan, H.B.; Avent, B.; Bellet, A.; Bennis, M.; Bhagoji, A.N.; Bonawitz, K.; Charles, Z.; Cormode, G.; Cummings, R.; et al. Advances and open problems in federated learning. Found. Trends Mach. Learn. 2021, 14, 1–210. [Google Scholar] [CrossRef]
- Chen, L.; Wang, H.; Charles, Z.; Papailiopoulos, D. Draco: Byzantine-resilient distributed training via redundant gradients. In PMLR, Proceedings of the International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; Microtome Publishing: Brookline, MA, USA, 2018; pp. 903–912. [Google Scholar]
- Cao, X.; Jia, J.; Gong, N.Z. Provably secure federated learning against malicious clients. In Proceedings of the AAAI conference on artificial intelligence, Vancouver, BC, Canada, 2–9 February 2021; Volume 35, pp. 6885–6893. [Google Scholar]
- Kang, J.; Xiong, Z.; Niyato, D.; Xie, S.; Zhang, J. Incentive mechanism for reliable federated learning: A joint optimization approach to combining reputation and contract theory. IEEE Internet Things J. 2019, 6, 10700–10714. [Google Scholar] [CrossRef]
- Fung, C.; Yoon, C.J.M.; Beschastnikh, I. Mitigating sybils in federated learning poisoning. arXiv 2018, arXiv:1808.04866. [Google Scholar]
- Li, M.; Wang, Q.; Zhang, W. Blockchain-Based Distributed Machine Learning Towards Statistical Challenges. In Proceedings of the International Conference on Blockchain and Trustworthy Systems, Dali, China, 6–7 August 2020; Springer: Singapore, 2020; pp. 549–564. [Google Scholar]
- Bonawitz, K.; Eichner, H.; Grieskamp, W.; Huba, D.; Ingerman, A.; Ivanov, V.; Kiddon, C.; Konečný, J.; Mazzocchi, S.; McMahan, B.; et al. Towards federated learning at scale: System design. Proc. Mach. Learn. Syst. 2019, 1, 374–388. [Google Scholar]
- Zhai, K.; Ren, Q.; Wang, J.; Yan, C. Byzantine-robust federated learning via credibility assessment on non-IID data. arXiv 2021, arXiv:2109.02396. [Google Scholar] [CrossRef] [PubMed]
- Jain, R.B. A recursive version of Grubbs’ test for detecting multiple outliers in environmental and chemical data. Clin. Biochem. 2010, 43, 1030–1033. [Google Scholar] [CrossRef]














| Symbol | Description | Setting |
|---|---|---|
| Communication rounds | 75 | |
| Local batch-size | 10 | |
| Local training epochs | 5 | |
| Number of clients | 100 | |
| Percentage of clients participating in training | 0.1 | |
| Dirichlet distribution parameter | 1.0 | |
| Proportion of malicious clients | 0.33 or 0.49 | |
| Strict filtering coefficient | 1.1–1.3 | |
| Strategy conversion threshold | 0.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, W.; Pan, B.; Hou, Y.; Li, X.; Xia, Y. An Adaptive Model Filtering Algorithm Based on Grubbs Test in Federated Learning. Entropy 2023, 25, 715. https://doi.org/10.3390/e25050715
Yao W, Pan B, Hou Y, Li X, Xia Y. An Adaptive Model Filtering Algorithm Based on Grubbs Test in Federated Learning. Entropy. 2023; 25(5):715. https://doi.org/10.3390/e25050715
Chicago/Turabian StyleYao, Wenbin, Bangli Pan, Yingying Hou, Xiaoyong Li, and Yamei Xia. 2023. "An Adaptive Model Filtering Algorithm Based on Grubbs Test in Federated Learning" Entropy 25, no. 5: 715. https://doi.org/10.3390/e25050715
APA StyleYao, W., Pan, B., Hou, Y., Li, X., & Xia, Y. (2023). An Adaptive Model Filtering Algorithm Based on Grubbs Test in Federated Learning. Entropy, 25(5), 715. https://doi.org/10.3390/e25050715









