On the Possibility of Reproducing Utsu’s Law for Earthquakes with a Spring-Block SOC Model
Abstract
:1. Introduction
2. Methodology
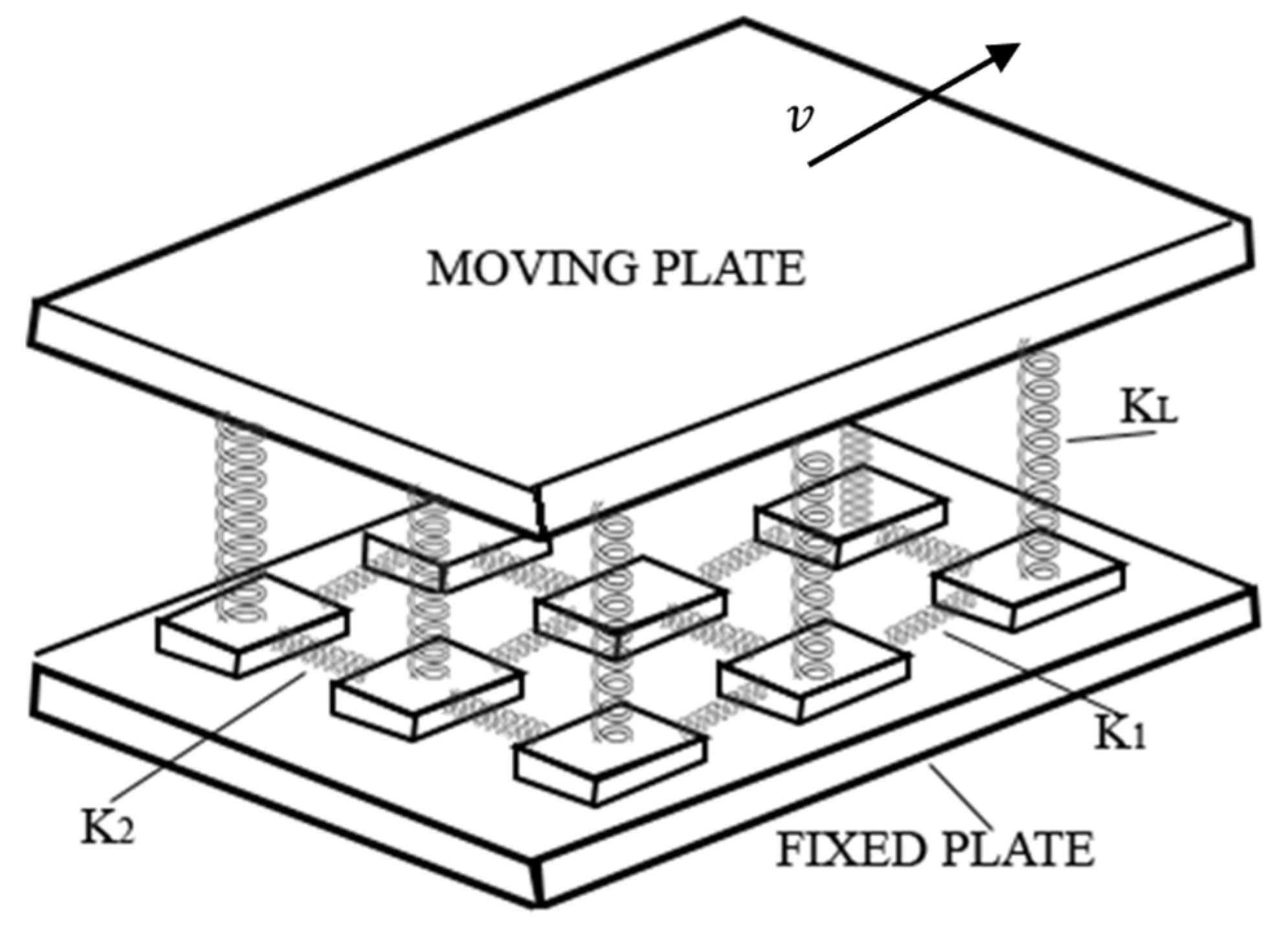
2.1. The Olami-Feder-Christensen Model
- The lattice sites are initialized with random values between zero and a force threshold
- The block with the largest force, is located, and the difference between and is added to all sites. This causes a global perturbation.
- For all sites where , the force is redistributed among the neighbors of according to the following rule: , the forces of the neighboring blocks of the relaxed cell are increased by , and is reduced to zero.
- Step 3 is repeated until the earthquake has fully evolved.
- Once a state of rest is reached, the process returns to step 2, and synthetic earthquakes are observed until the desired number of events is reached.
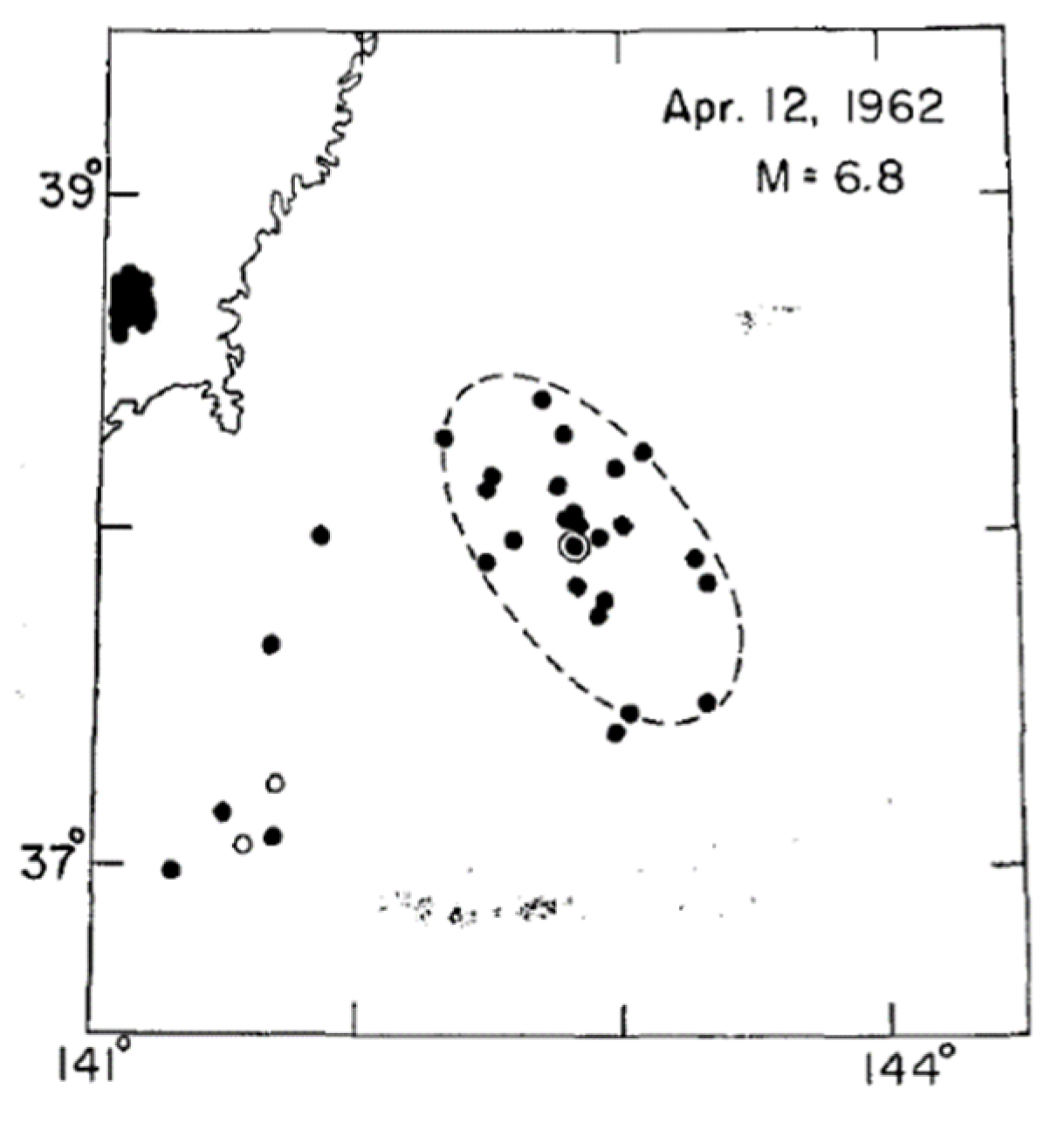
2.2. Utsu’s Law
2.3. Aftershocks in the OFC Model
3. Results
3.1. Utsu’s Law Simulations
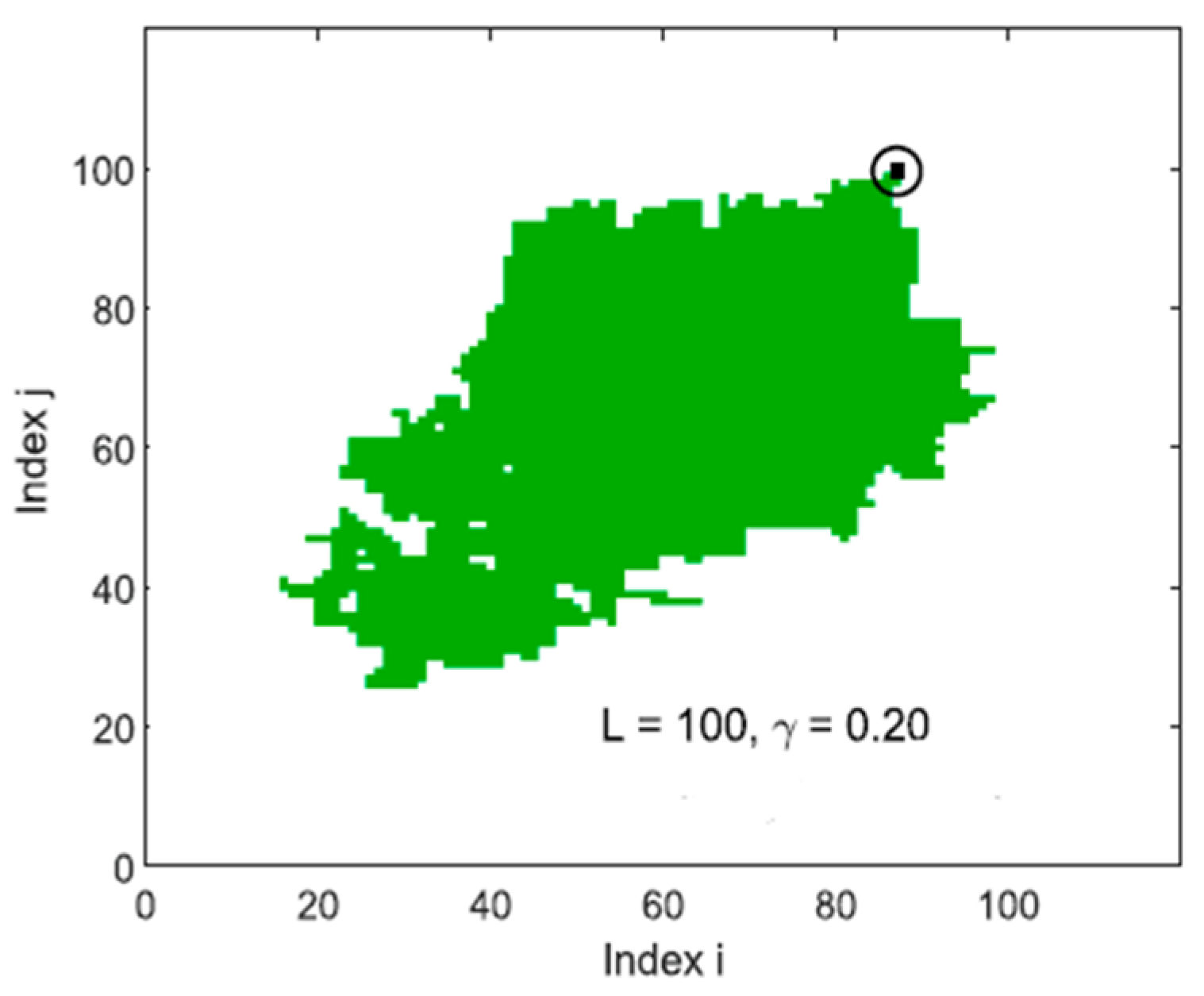
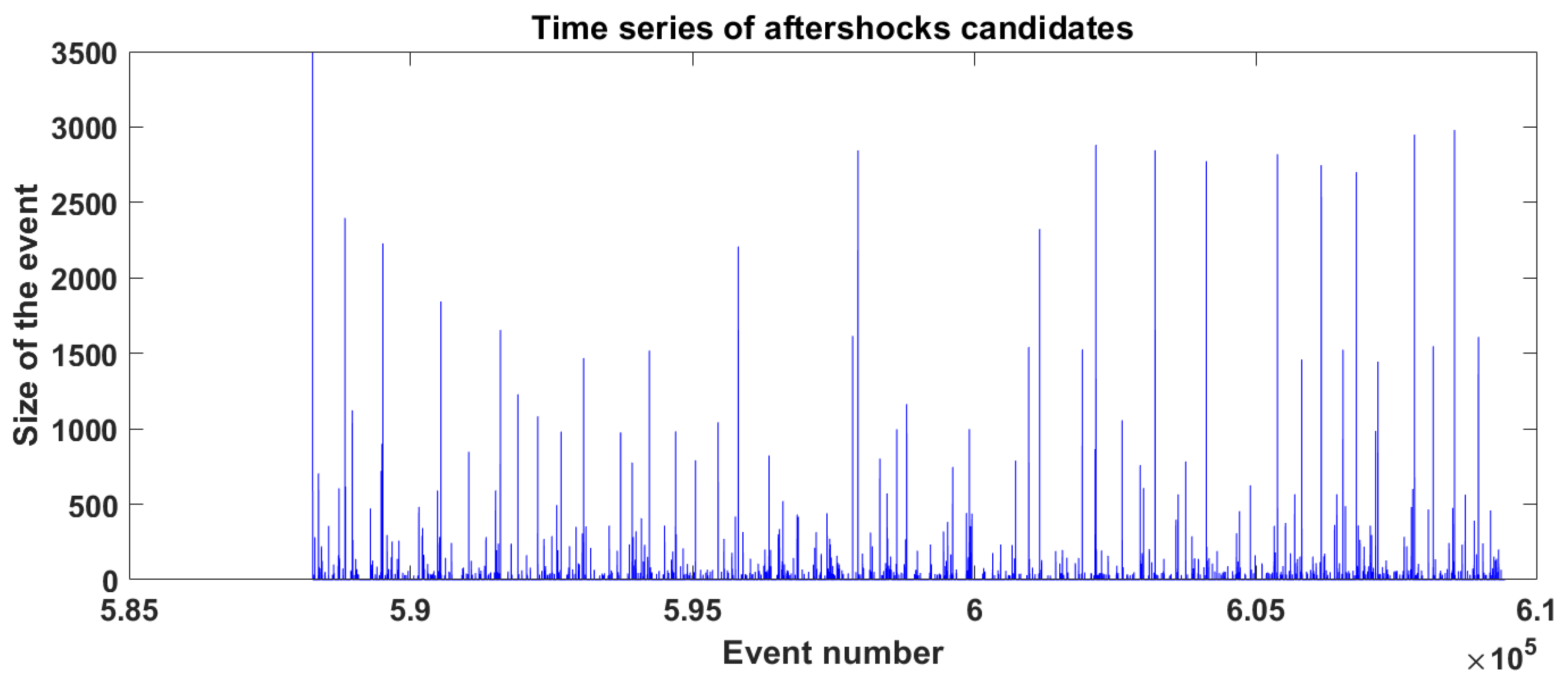
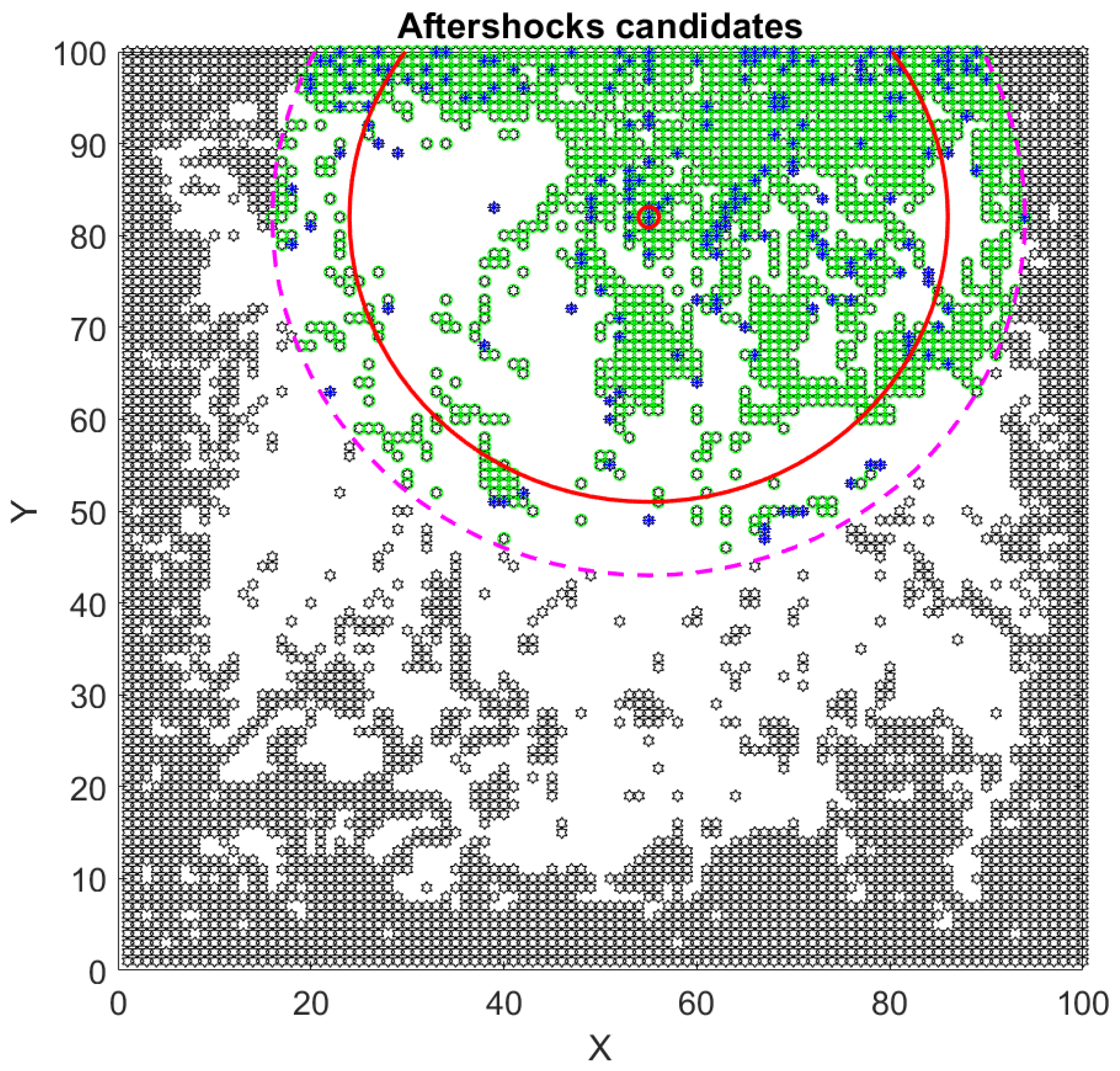
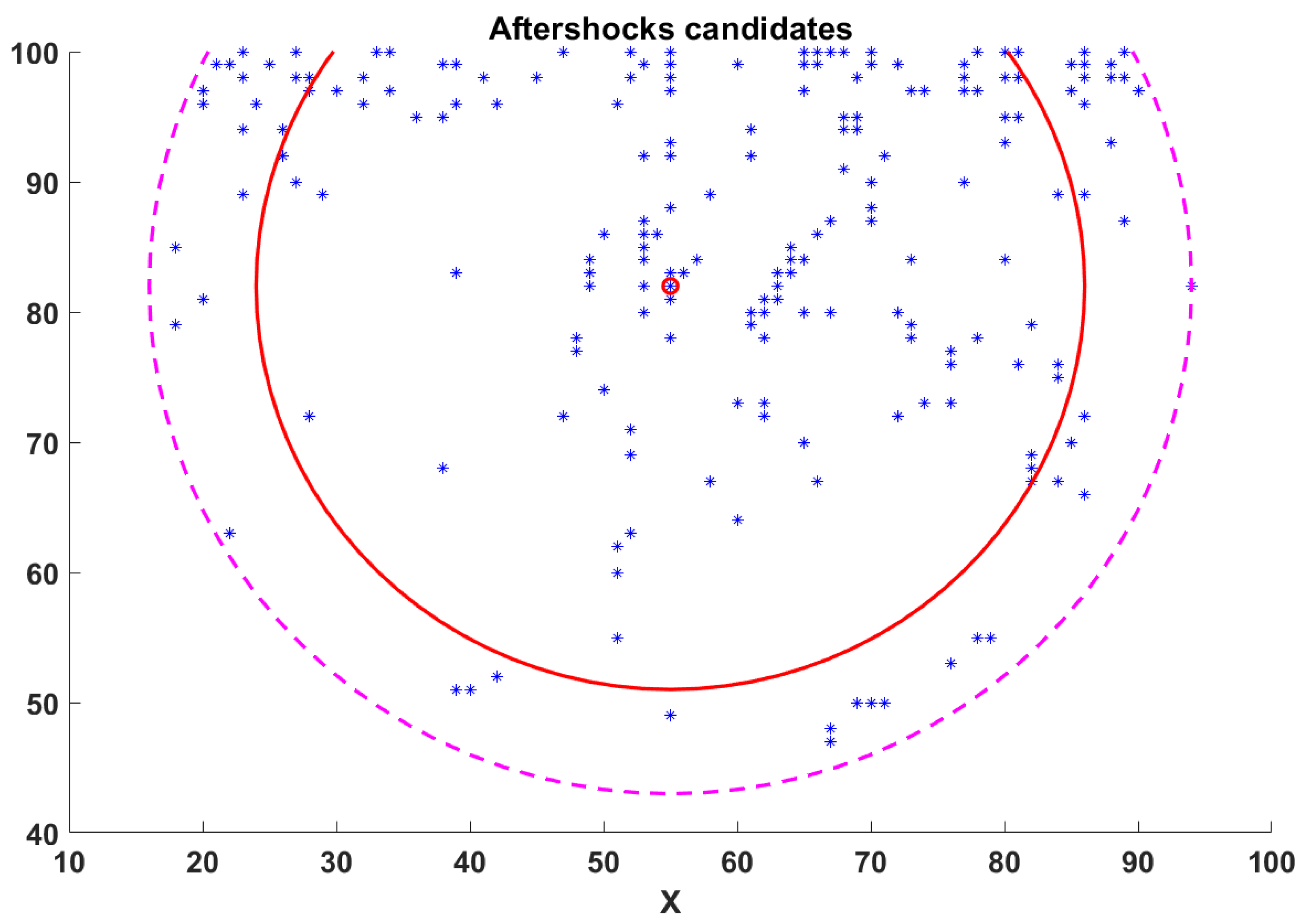
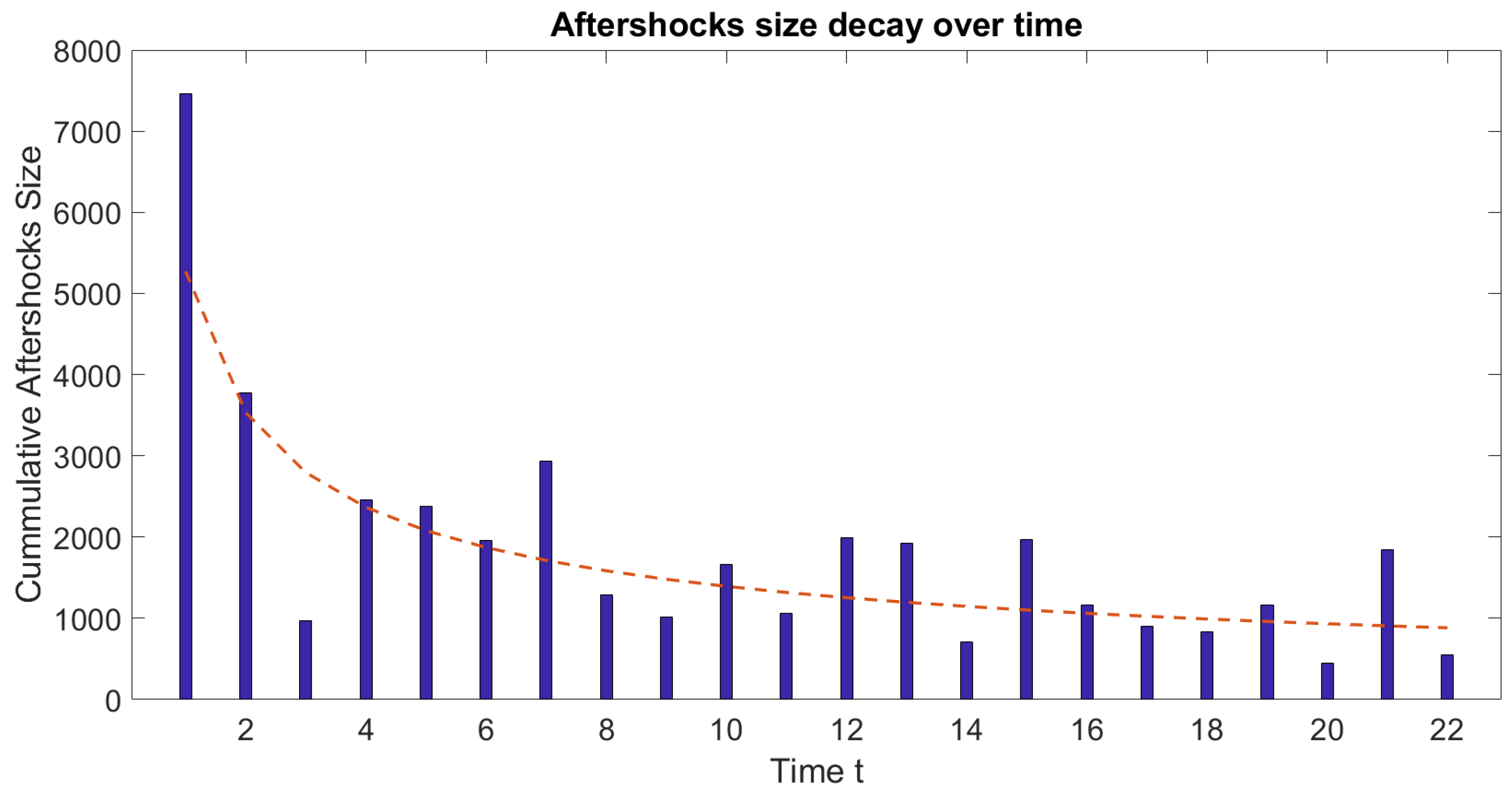
3.2. Aftershocks and Utsu’s Law in a Spring-Block Model
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Utsu, T. A statistical study on the occurrence of aftershocks. Geophys. Mag. 1961, 30, 521–605. [Google Scholar]
- Utsu, T. Aftershocks and Earthquake Statistics (1): Some Parameters Which Characterize an Aftershock Sequence and Their Interrelations. J. Fac. Sci. Hokkaido Univ. Ser. 7 Geophys. 1970, 3, 129–195. [Google Scholar]
- Olami, Z.; Feder, H.; Christensen, K. Self-Organized Criticality in a Continuous, Nonconservative Cellular Automaton Modeling Earthquakes. Phys. Rev. Lett. 1992, 68, 1244–1247. [Google Scholar] [CrossRef] [PubMed]
- Bak, P.; Tang, C.; Wiesenfeld, K. Self-organized criticality: An explanation of the 1/f noise. Phys. Rev. Lett. 1987, 59, 381. [Google Scholar] [CrossRef]
- Bak, P.; Tang, C.; Wiesenfeld, K. Self-organized criticality. Phys. Rev. A 1988, 38, 364. [Google Scholar] [CrossRef] [PubMed]
- Bak, P.; Tang, C. Earthquakes as a Self-Organized Critical Phenomenon. J. Geophys. Res. 1989, B94, 15635. [Google Scholar] [CrossRef]
- Bak, P. How Nature Works; Springer Science: New York, NY, USA, 1996. [Google Scholar]
- Watkins, N.W.; Pruessner, G.; Chapman, S.C.; Crosby, N.B.; Jensen, H.J. 25 Years of Self-organized Criticality: Concepts and Controversies. Space Sci. Rev. 2016, 198, 3–44. [Google Scholar] [CrossRef]
- Gutenberg, B.; Richter, C.F. Frequency of earthquakes in California. Bull. Seismol. Soc. Am. 1944, 34, 185–188. [Google Scholar] [CrossRef]
- Hergarten, S.; Neugebauer, H.J. Foreshocks and aftershocks in the Olami-Feder-Christensen Model. Phys. Rev. Lett. 2002, 88, 238501. [Google Scholar] [CrossRef]
- Omori, F. On the aftershocks of earthquakes. J. Coll. Sci. Imp. Univ. Tokyo 1894, 7, 111–200. [Google Scholar]
- Sornette, D.; Ouillon, G. Multifractal Scaling of Thermally Activated Rupture Processes. Phys. Rev. Lett. 2005, 94, 038501. [Google Scholar] [CrossRef] [PubMed]
- Davidsen, J.; Gu, C.; Baiesi, M. Generalized Omori–Utsu law for aftershock sequences in southern California. Geoph. J. Int. 2015, 201, 965–978. [Google Scholar] [CrossRef]
- Guglielmi, A.V. Interpretation of the Omori law. Izv. Phys. Solid Earth 2016, 52, 785–786. [Google Scholar] [CrossRef]
- Guglielmi, A.V.; Zavyalov, A.D. The Omori Law: The 150-Year Birthday Jubilee of Fusakichi Omori. J. Volcanolog. Seismol. 2018, 12, 353–358. [Google Scholar] [CrossRef]
- Baranov, S.; Narteau, C.; Shebalin, P. Modeling and Prediction of Aftershock Activity. Surv. Geophys. 2022, 43, 437–481. [Google Scholar] [CrossRef]
- Wang, J.-H. On the correlation of observed Gutenberg-Richter’s b value and Omori’s p value for aftershocks. Bull. Seismol. Soc. Am. 1994, 84, 2008–2011. [Google Scholar] [CrossRef]
- Helmstetter, A.; Sornette, D. Subcritical and supercritical regimes in epidemic models of earthquake aftershocks. J. Geophys. Res. Solid Earth 2002, 107, ESE-10. [Google Scholar] [CrossRef]
- Guo, Z.; Ogata, Y. Statistical relations between the parameters of aftershocks in time, space, and magnitude. J. Geophys. Res. Solid Earth 1997, 102, 2857–2873. [Google Scholar] [CrossRef]
- Zaccagnino, D.; Telesca, L.; Doglioni, C. Scaling properties of seismicity and faulting. Earth Planet. Sci. Lett. 2022, 584, 117511. [Google Scholar] [CrossRef]
- Perez Oregon, J.; Muñoz Diosdado, A.; Rudolf-Navarro, A.H.; Angulo-Brown, F. A simple model to relate the elastic ratio gamma of a critically self-organized spring-block model with the age of a lithospheric downgoing plate in a subduction zone. Entropy 2020, 7, 868. [Google Scholar] [CrossRef]
- Perez Oregon, J. On some Little-Known Properties of the Gutenberg-Richter Relationship for the Frequency of Earthquakes. Ph.D. Thesis, Instituto Politécnico Nacional, ESFM, Mexico City, Mexico, 2018. [Google Scholar]
- Perez-Oregon, J.; Muñoz-Diosdado, A.; Rudolf-Navarro, A.H.; Angulo-Brown, F. Some Common Features Between a Spring-Block Self-Organized Critical Model, Stick–Slip Experiments with Sandpapers and Actual Seismicity. Pure Appl. Geophys. 2020, 177, 889–903. [Google Scholar] [CrossRef]
- Perez-Oregon, J.; Muñoz-Diosdado, A.; Rudolf-Navarro, A.H.; Guzman-Saenz, A.; Angulo-Brown, F. On the possible correlation between the Gutenberg-Richter parameters of the frequency-magnitude relationship. J. Seism. 2018, 22, 1025–1035. [Google Scholar] [CrossRef]
- Salinas-Martínez, A.; Aguilar-Molina, A.M.; Pérez-Oregon, J.; Angulo-Brown, F.; Muñoz-Diosdado, A. Review and Update on Some Connections between a Spring-Block SOC Model and Actual Seismicity in the Case of Subduction Zones. Entropy 2022, 24, 435. [Google Scholar] [CrossRef] [PubMed]
- Muñoz-Diosdado, A.; Angulo-Brown, F. Patterns of synthetic seismicity and recurrence times in a spring-block earthquake model. Rev. Mex. Fís. 1999, 45, 393–400. [Google Scholar]
- Muñoz-Diosdado, A.; Rudolf-Navarro, A.H.; Angulo-Brown, F. Simulation and properties of a non-homogeneous spring-block earthquake model with asperities. Acta Geophys. 2012, 60, 740–757. [Google Scholar] [CrossRef]
- Muñoz Diosdado, A.; Rudolf-Navarro, A.H.; Angulo Brown, F. A qualitative comparison between some synthetic and empirical scaling properties in seismicity. Rev. Mex. Fís. S 2012, 58, 96–103. [Google Scholar]
- Ruff, L.; Kanamori, H. Seismicity and the subduction process. Phys. Earth Planet. Inter. 1980, 23, 240–252. [Google Scholar] [CrossRef]
- Utsu, T.; Seki, A. Relation between the area of aftershock region and the energy of the main shock. J. Seism. Soc. Jap. 1955, 7, 233–240. [Google Scholar]
- Goto, K. On the relation between the distribution of aftershocks and the magnitude. J. Seism. Soc. Jap. 1962, 15, 116–121. [Google Scholar]
- Bath, M.; Buda, S.I. Earthquake volume, fault plane area, seismic energy, strain, deformation, and related quantities. Ann. Geofis. 1964, 17, 363–368. [Google Scholar]
- Purcaru, G. Some problems of the Vrancea earthquakes and their aftershocks. St. Cerc. Geol. Geofiz. Geogr. Ser. Geofiz. 1966, 4, 87–99. [Google Scholar]
- Pelletier, J.D. GeoComplexity and the Physics of Earthquakes; Rundle, J.B., Turcotte, D.L., Klein, W., Eds.; American Geophysical Union: Washington, DC, USA, 2000; pp. 27–42. [Google Scholar]
- Hainzl, S.; Zöller, G.; Kurths, J. Similar power laws for fore- and aftershock sequences in a spring-block model for earthquakes. J. Geophys. Res. 1999, 104, 7243. [Google Scholar] [CrossRef]
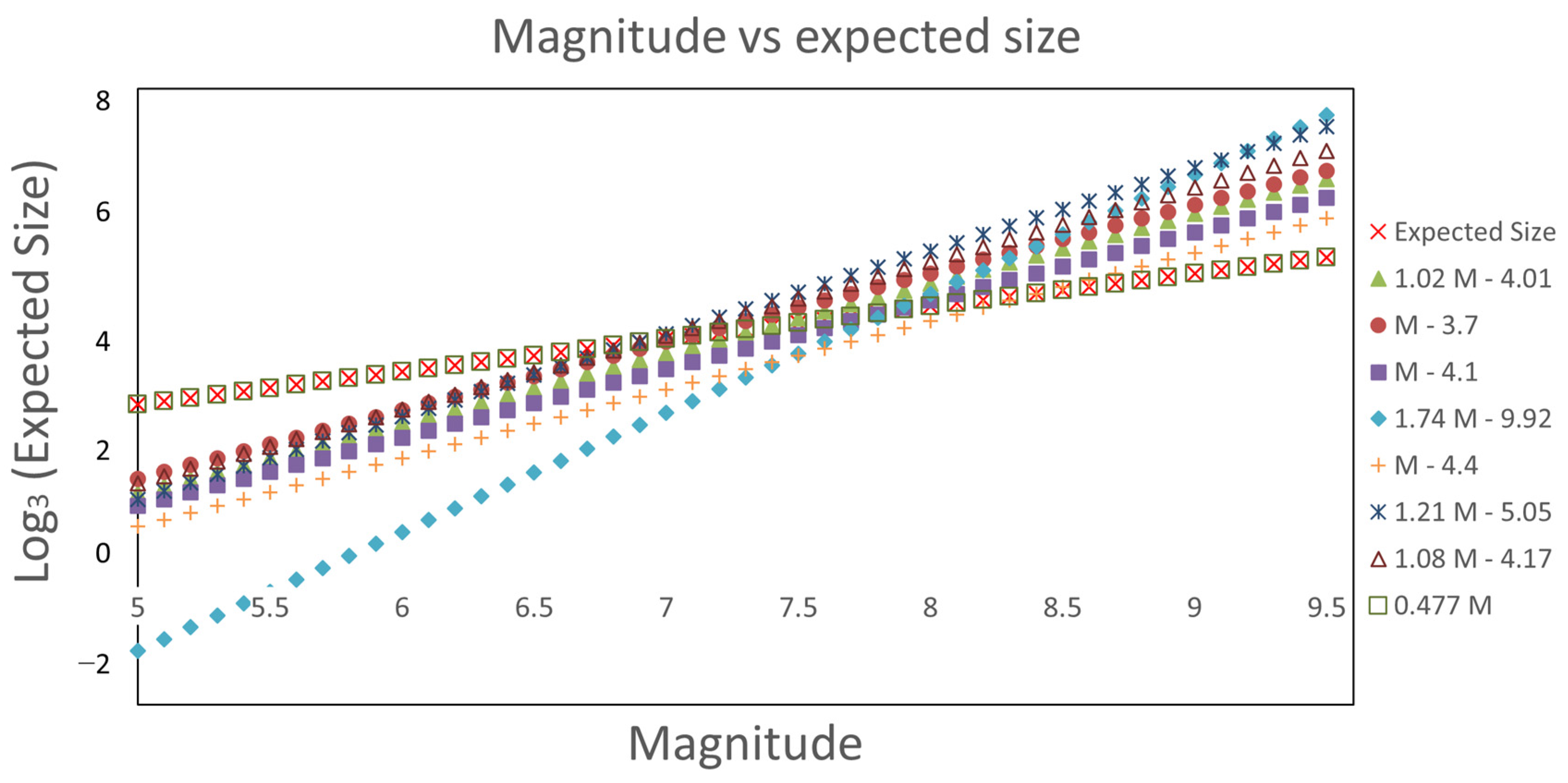


| Subduction Seismic Region | M | Expected Size | Equation (8) | Equation (9) | Equation (10) | Equation (11) | Equation (12) | Equation (13) | Equation (14) | Equation (16) |
|---|---|---|---|---|---|---|---|---|---|---|
| Caribbean | 7.5 | 3788 | 4365 | 6310 | 2512 | 1349 | 1259 | 10,593 | 8511 | 3780 |
| Marianas | 7.5 | 3788 | 4365 | 6310 | 2512 | 1349 | 1259 | 10,593 | 8511 | 3780 |
| Scotia arc | 7.6 | 4228 | 5521 | 7943 | 3162 | 2014 | 1585 | 13,996 | 10,914 | 4219 |
| S. Java | 7.7 | 4719 | 6982 | 10,000 | 3981 | 3006 | 1995 | 18,493 | 13,996 | 4709 |
| New Zealand | 7.8 | 5267 | 8831 | 12,589 | 5012 | 4487 | 2512 | 24,434 | 17,947 | 5255 |
| Patagonia | 7.8 | 5267 | 8831 | 12,589 | 5012 | 4487 | 2512 | 24,434 | 17,947 | 5255 |
| Vanatu (New Hebrides) | 7.9 | 5878 | 11,169 | 15,849 | 6310 | 6699 | 3162 | 32,285 | 23,014 | 5865 |
| Izu Bonin | 7.9 | 5878 | 11,169 | 15849 | 6310 | 6699 | 3162 | 32,285 | 23,014 | 5865 |
| Kermadec | 7.9 | 5878 | 11,169 | 15,849 | 6310 | 6699 | 3162 | 32,285 | 23,014 | 5865 |
| México-Oaxaca | 7.9 | 5878 | 11,169 | 15,849 | 6310 | 6699 | 3162 | 32,285 | 23,014 | 5865 |
| México-Guerrero | 7.9 | 5878 | 11,169 | 15,849 | 6310 | 6699 | 3162 | 32,285 | 23,014 | 5865 |
| Ryukyus | 8 | 6,561 | 14,125 | 19,953 | 7943 | 10,000 | 3981 | 42,658 | 29,512 | 6546 |
| Tonga | 8.1 | 7323 | 17,865 | 25,119 | 10,000 | 14,928 | 5012 | 56,364 | 37,844 | 7306 |
| Peru | 8.1 | 7323 | 17,865 | 25,119 | 10,000 | 14,928 | 5012 | 56,364 | 37,844 | 7306 |
| Central America | 8.1 | 7323 | 17,865 | 25,119 | 10,000 | 14,928 | 5012 | 56,364 | 37,844 | 7306 |
| Mexico-Michoacán | 8.1 | 7323 | 17,865 | 25,119 | 10,000 | 14,928 | 5012 | 56,364 | 37,844 | 7306 |
| W. Alaska | 8.2 | 8173 | 22,594 | 31,623 | 12,589 | 22,284 | 6310 | 74,473 | 48,529 | 8155 |
| México- Jalisco | 8.2 | 8173 | 22,594 | 31,623 | 12,589 | 22,284 | 6310 | 74,473 | 48,529 | 8155 |
| Sumba Island | 8.3 | 9122 | 28,576 | 39,811 | 15,849 | 33,266 | 7943 | 98,401 | 62,230 | 9101 |
| Kuriles | 8.5 | 11,364 | 45,709 | 63,096 | 25,119 | 74,131 | 12,589 | 171,791 | 102,329 | 11,337 |
| West Aleutians | 8.6 | 12,684 | 57,810 | 79,433 | 31,623 | 110,662 | 15,849 | 226,986 | 131,220 | 12,653 |
| Komandorski | 8.7 | 14,156 | 73,114 | 100,000 | 39,811 | 165,196 | 19,953 | 299,916 | 168,267 | 14,122 |
| Central Chile | 8.8 | 15,800 | 92,470 | 125,893 | 50,119 | 246,604 | 25,119 | 396,278 | 215,774 | 15,762 |
| Colombia-Ecuador | 8.8 | 15,800 | 92,470 | 125,893 | 50,119 | 246,604 | 25,119 | 396,278 | 215,774 | 15,762 |
| Kamchatka | 9 | 19,683 | 147,911 | 199,526 | 79,433 | 549,541 | 39,811 | 691,831 | 354,813 | 19,634 |
| NE Japan | 9.1 | 21,969 | 187,068 | 251,189 | 100,000 | 820,352 | 50,119 | 914,113 | 454,988 | 21,913 |
| Sumatra-Andaman | 9.2 | 24,520 | 236,592 | 316,228 | 125,893 | 1,224,616 | 63,096 | 1,207,814 | 583,445 | 24,457 |
| East Alaska | 9.2 | 24,520 | 236,592 | 316,228 | 125,893 | 1,224,616 | 63,096 | 1,207,814 | 583,445 | 24,457 |
| South Chile | 9.5 | 34,092 | 478,630 | 630,957 | 251,189 | 4,073,803 | 125,893 | 2,786,121 | 1,230,269 | 34,002 |
| Subduction Seismic Region | M | Synthetic Size | Equation (8) | Equation (9) | Equation (10) | Equation (11) | Equation (12) | Equation (13) | Equation (14) | Equation (16) |
|---|---|---|---|---|---|---|---|---|---|---|
| Caribbean | 6.8 | 1832 | 924 | 1376 | 548 | 95 | 275 | 1678 | 1644 | 1829 |
| Marianas | 7.2 | 2738 | 2181 | 3195 | 1272 | 413 | 638 | 4650 | 4082 | 2732 |
| Scotia arc | 7.2 | 2786 | 2263 | 3314 | 1319 | 440 | 661 | 4860 | 4246 | 2780 |
| Vanatu (New Hebrides) | 7.6 | 4187 | 5407 | 7783 | 3099 | 1944 | 1553 | 13,655 | 10,677 | 4178 |
| Izu Bonin | 7.6 | 4216 | 5488 | 7897 | 3144 | 1993 | 1576 | 13,896 | 10,845 | 4207 |
| S. Java | 7.7 | 4561 | 6493 | 9312 | 3707 | 2655 | 1858 | 16,964 | 12,959 | 4551 |
| Kermadec | 7.7 | 4598 | 6606 | 9471 | 3770 | 2735 | 1890 | 17,315 | 13,198 | 4588 |
| New Zealand | 7.7 | 4610 | 6643 | 9523 | 3791 | 2761 | 1900 | 17,430 | 13,276 | 4600 |
| Sumba Island | 7.8 | 5175 | 8505 | 12,134 | 4831 | 4209 | 2421 | 23,369 | 17,247 | 5164 |
| Patagonia | 8.0 | 6298 | 12,942 | 18,313 | 7291 | 8614 | 3654 | 38,454 | 26,902 | 6284 |
| Tonga | 8.1 | 7099 | 16,718 | 23,536 | 9370 | 13,330 | 4696 | 52,096 | 35,276 | 7083 |
| NE Japan | 8.2 | 7959 | 21,347 | 29,910 | 11,908 | 20,227 | 5968 | 69,622 | 45,697 | 7941 |
| Kuriles | 8.2 | 8405 | 23,986 | 33,531 | 13,349 | 24,677 | 6690 | 79,946 | 51,700 | 8386 |
| Ryukyus | 8.3 | 9043 | 28,047 | 39,088 | 15,561 | 32,223 | 7799 | 96,245 | 61,012 | 9022 |
| Kamchatka | 8 | 9994 | 34,732 | 48,202 | 19,190 | 46,402 | 9618 | 124,025 | 76,509 | 9971 |
| W. Alaska | 8.4 | 10,054 | 35,179 | 48,811 | 19,432 | 47,426 | 9739 | 125,923 | 77,553 | 10,030 |
| Komandorski | 8.4 | 10,124 | 35,705 | 49,526 | 19,717 | 48,641 | 9882 | 128,158 | 78,780 | 10,100 |
| Sumatra-Andaman | 8.4 | 10,283 | 36,914 | 51,170 | 20,371 | 51,486 | 10,210 | 133,324 | 81,609 | 10,259 |
| West Aleutians | 8.4 | 10,352 | 37,446 | 51,892 | 20,659 | 52,757 | 10,354 | 135,604 | 82,853 | 10,328 |
| Peru | 8.4 | 10,572 | 39,168 | 54,231 | 21,590 | 56,962 | 10,820 | 143,033 | 86,893 | 10,547 |
| East Alaska | 8.6 | 13,084 | 61,781 | 84,779 | 33,751 | 123,944 | 16,916 | 245,601 | 140,784 | 13,053 |
| Central America | 8.7 | 14,301 | 74,719 | 102,152 | 40,667 | 171,431 | 20,382 | 307,743 | 172,181 | 14,266 |
| Central Chile | 8.8 | 15,020 | 82,980 | 113,213 | 45,071 | 205,012 | 22,589 | 348,509 | 192,401 | 14,983 |
| México-Oaxaca | 8.9 | 18,605 | 131,131 | 177,309 | 70,588 | 447,499 | 35,378 | 599,742 | 312,341 | 18,559 |
| México-Guerrero | 9.1 | 21,842 | 184,770 | 248,163 | 98,795 | 803,235 | 49,515 | 900,807 | 449,072 | 21,787 |
| Mexico-Michoacán | 9.3 | 26,583 | 281,198 | 374,578 | 149,122 | 1,644,232 | 74,738 | 1,482,470 | 700,528 | 26,514 |
| Colombia-Ecuador | 9 | 28,450 | 325,111 | 431,843 | 171,920 | 2,106,040 | 86,164 | 1,760,938 | 816,868 | 28,376 |
| México-Jalisco | 9.4 | 29,780 | 358,469 | 475,240 | 189,197 | 2,487,879 | 94,823 | 1,977,267 | 905,871 | 29,702 |
| South Chile | 9.6 | 36,428 | 551,485 | 724,982 | 288,621 | 5,187,635 | 144,653 | 3,296,066 | 1,429,399 | 36,331 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salinas-Martínez, A.; Perez-Oregon, J.; Aguilar-Molina, A.M.; Muñoz-Diosdado, A.; Angulo-Brown, F. On the Possibility of Reproducing Utsu’s Law for Earthquakes with a Spring-Block SOC Model. Entropy 2023, 25, 816. https://doi.org/10.3390/e25050816
Salinas-Martínez A, Perez-Oregon J, Aguilar-Molina AM, Muñoz-Diosdado A, Angulo-Brown F. On the Possibility of Reproducing Utsu’s Law for Earthquakes with a Spring-Block SOC Model. Entropy. 2023; 25(5):816. https://doi.org/10.3390/e25050816
Chicago/Turabian StyleSalinas-Martínez, Alfredo, Jennifer Perez-Oregon, Ana María Aguilar-Molina, Alejandro Muñoz-Diosdado, and Fernando Angulo-Brown. 2023. "On the Possibility of Reproducing Utsu’s Law for Earthquakes with a Spring-Block SOC Model" Entropy 25, no. 5: 816. https://doi.org/10.3390/e25050816






