Transformer-Based Detection for Highly Mobile Coded OFDM Systems
Abstract
:1. Introduction
- A Transformer-based detection algorithm is proposed for the coded OFDM system. Although DL-based detectors do not outperform the conventional detector in the uncoded OFDM system, they have better performance in the coded OFDM system.
- In our coded OFDM system, the LDPC codes are performed, and the soft information is required by the decoder. Thus, we propose the soft demapping algorithm based on Transformer.
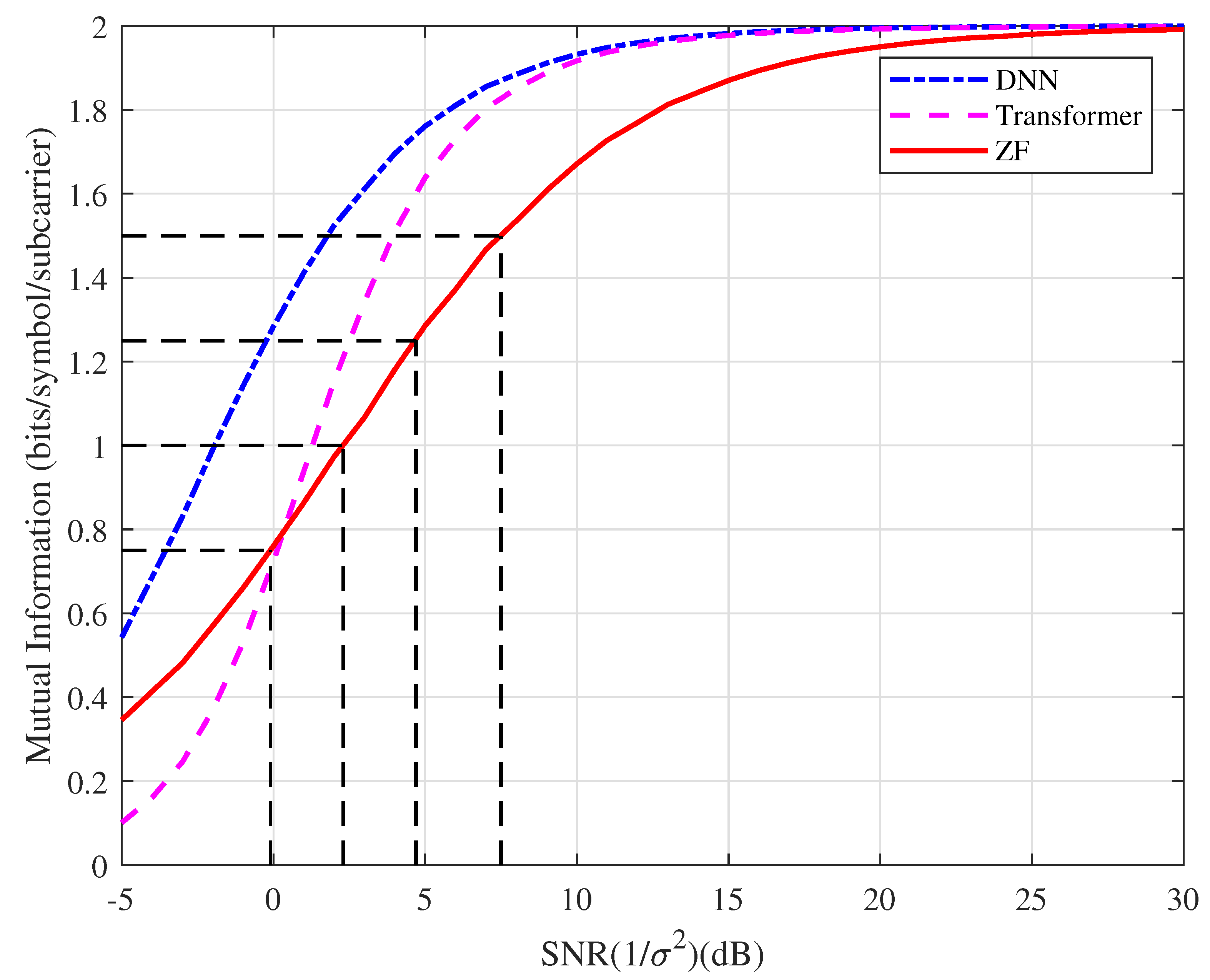
- In the OFDM system, it is difficult to compute the mutual information based on the optimal detector. Thus, we can compute the mutual information with a suboptimal detector, which can be regarded as the soft information quality (SIQ) [24,25]. We compute the SIQ with the assistance of the Transformer network.
2. System Model
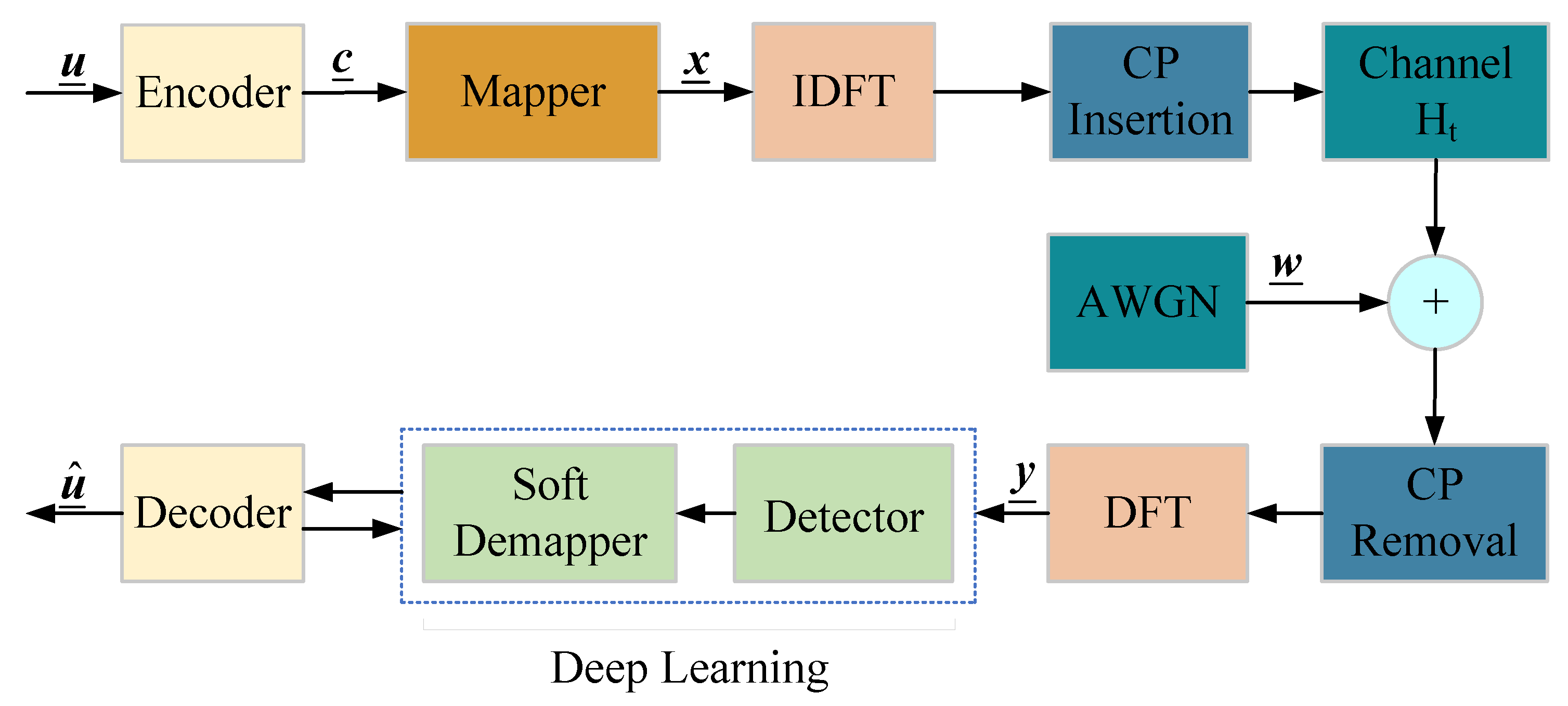
2.1. The Coded OFDM System Model
2.2. The Channel Model
2.3. The Classical Signal Detection and Demapping Algorithm
2.4. Rate Allocation
3. The Detection and Soft Demapping Algorithm with Deep Learning
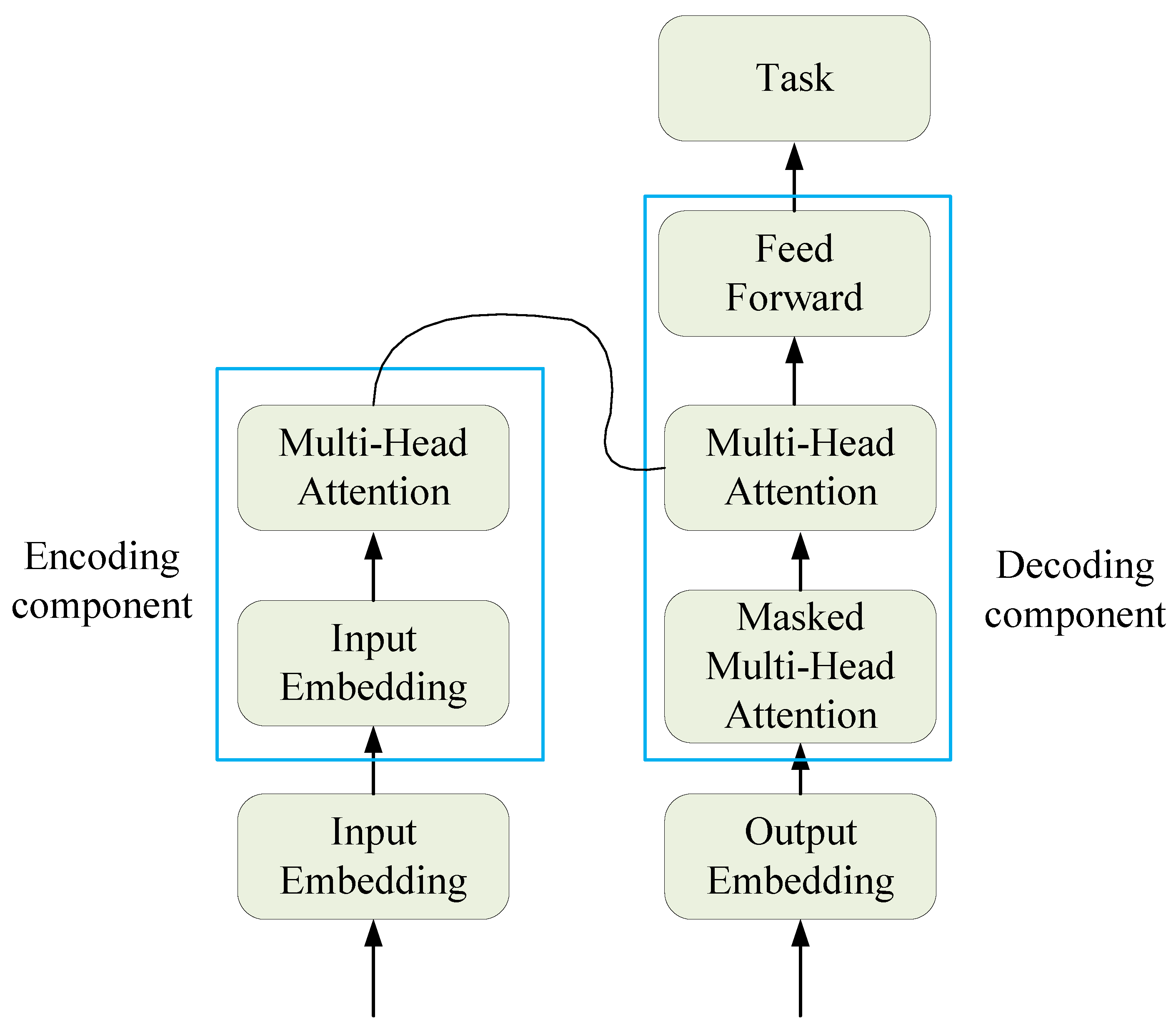
3.1. Transformer
3.2. Experimental Method with Transformer
3.3. Model Training
3.4. DNN Detection Algorithm
4. Experimental Results
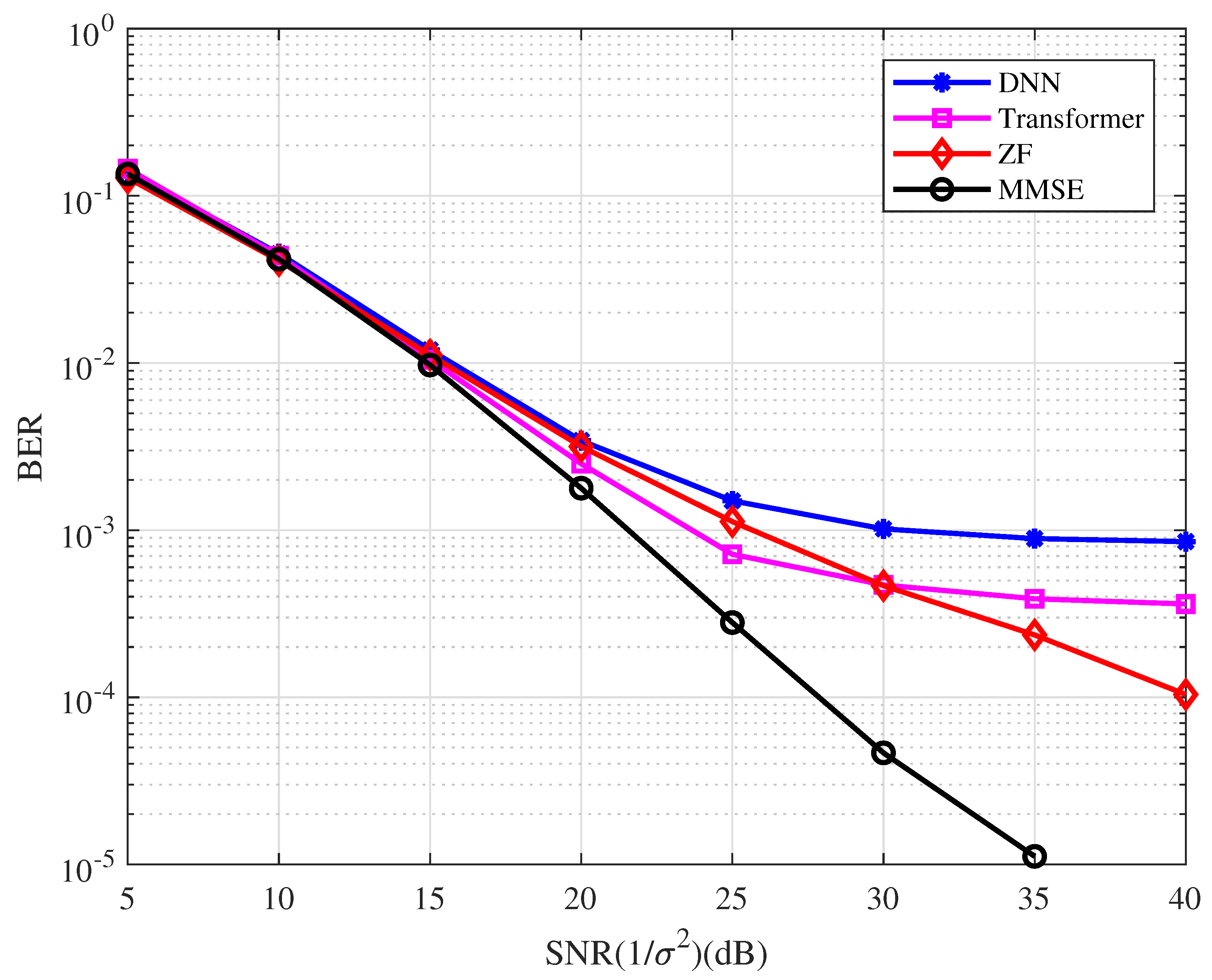
- The BER performance of the uncoded OFDM system with the conventional detectors is better than that with the DL detectors in the high SNR region.
- The MMSE detector performs better than the ZF detector, while the Transformer-based detector performs better than the DNN-based detector.

- At the BER of , the BER performance with the ZF detector is approximately 6.2 dB away from the Shannon limit.
- The BER performance corresponding to the Transformer detector has an approximately 2.0 dB gain compared with the DNN detector.
- The Transformer-based system performs better than the ZF system in the high SNR region.
- The ZF detector has better performance than the MMSE detector in the coded OFDM system.
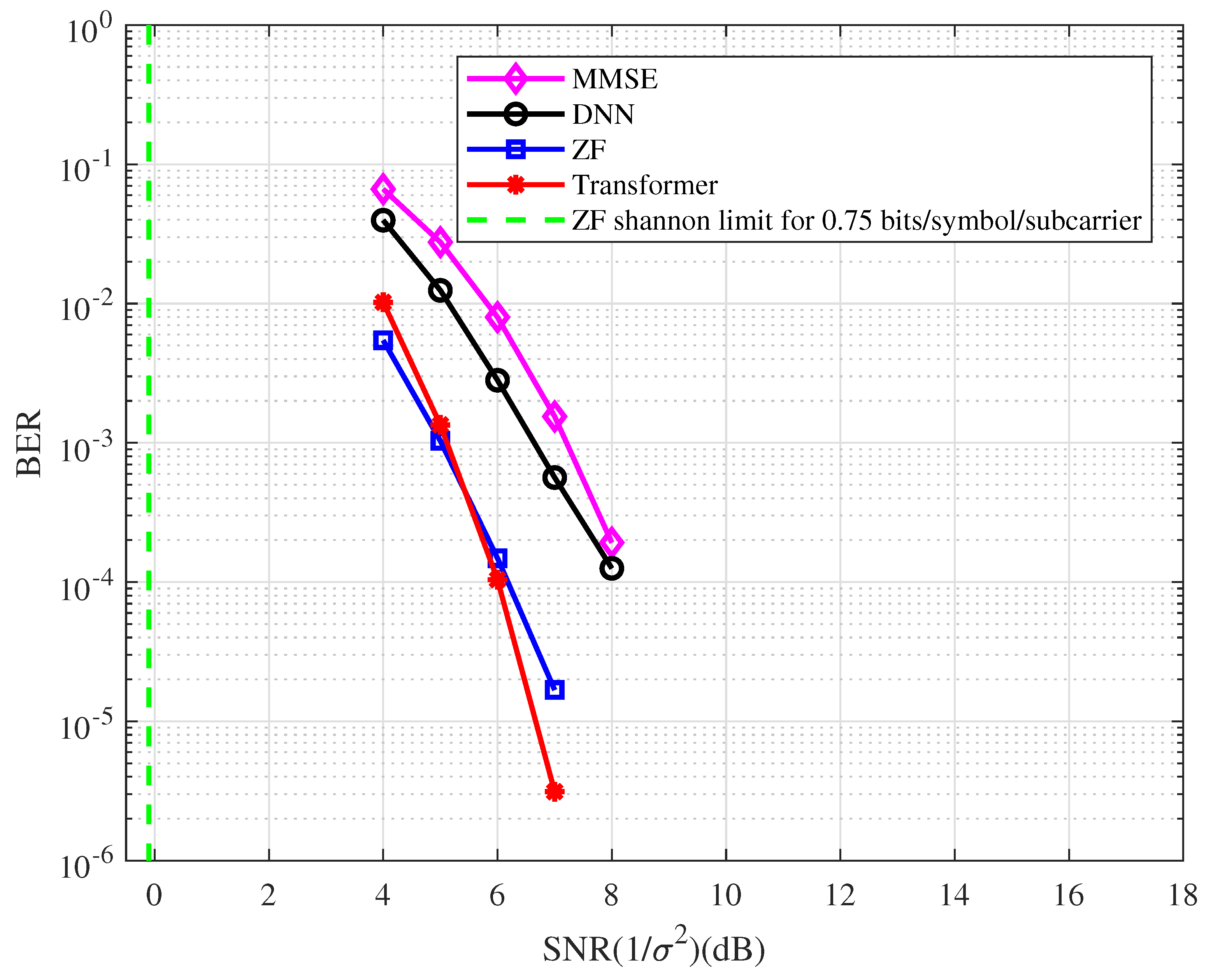
- At the BER of , the BER performance with the ZF detector is approximately 6.0 dB away from the Shannon limit.
- At the BER of , the BER performance corresponding to the Transformer detector has an approximately 0.4 dB, 1.4 dB, and 2.0 dB gain compared with the ZF, DNN, and MMSE detectors, respectively.
- The BER performance with the ZF detector has an approximately 1.6 dB gain compared with the MMSE detector in the coded OFDM system.
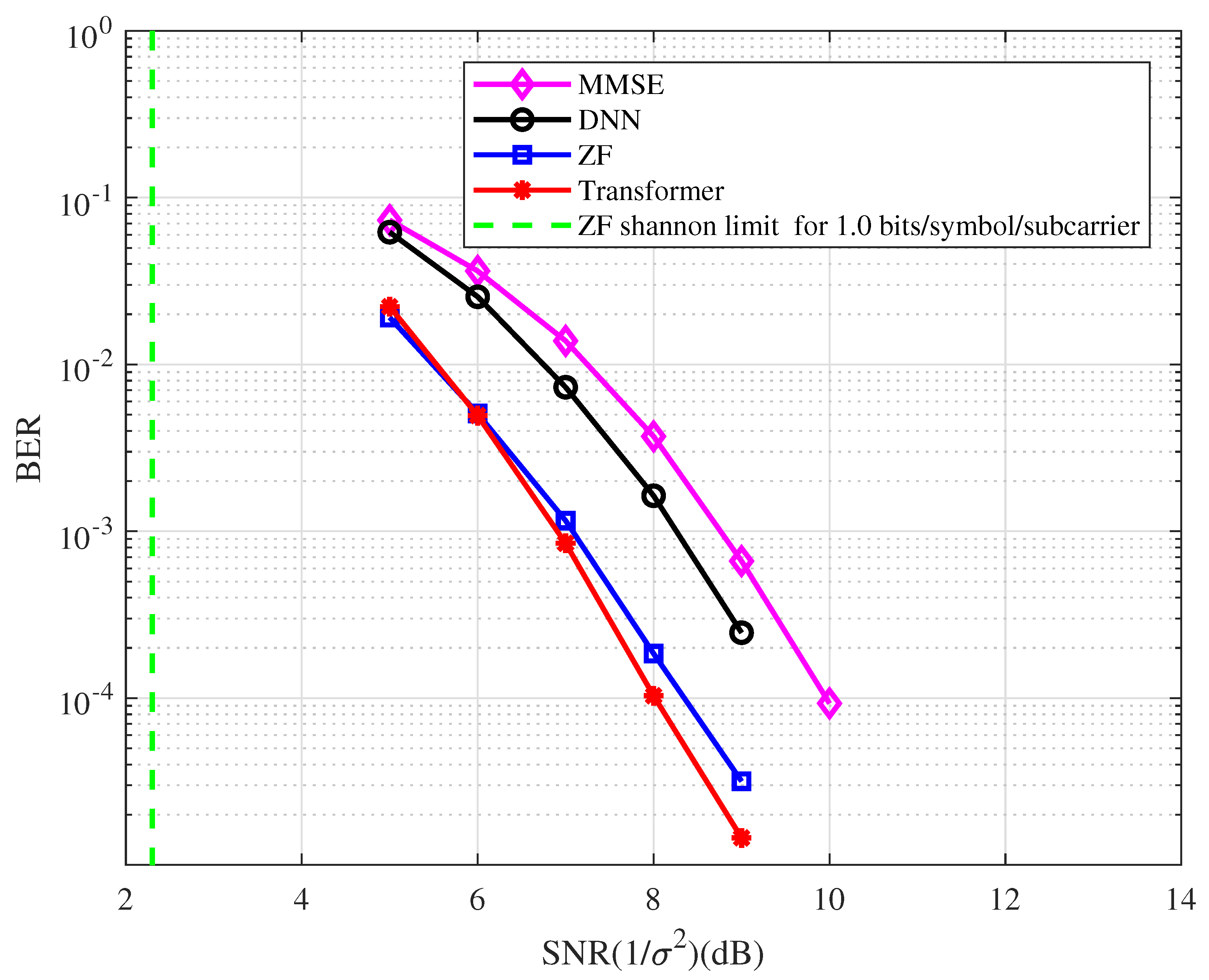
- At the BER of , the BER performance with the ZF detector is approximately 6.0 dB away from the Shannon limit.
- The Transformer-based system performs better than the ZF system in the high SNR region.
- At the BER of , the BER performance corresponding to the Transformer detector has an approximately 1.0 dB and 1.4 dB gain compared with the DNN and MMSE detectors, respectively.
- The BER performance with the ZF detector has an approximately 1.1 dB gain compared with the MMSE detector in the coded OFDM system.
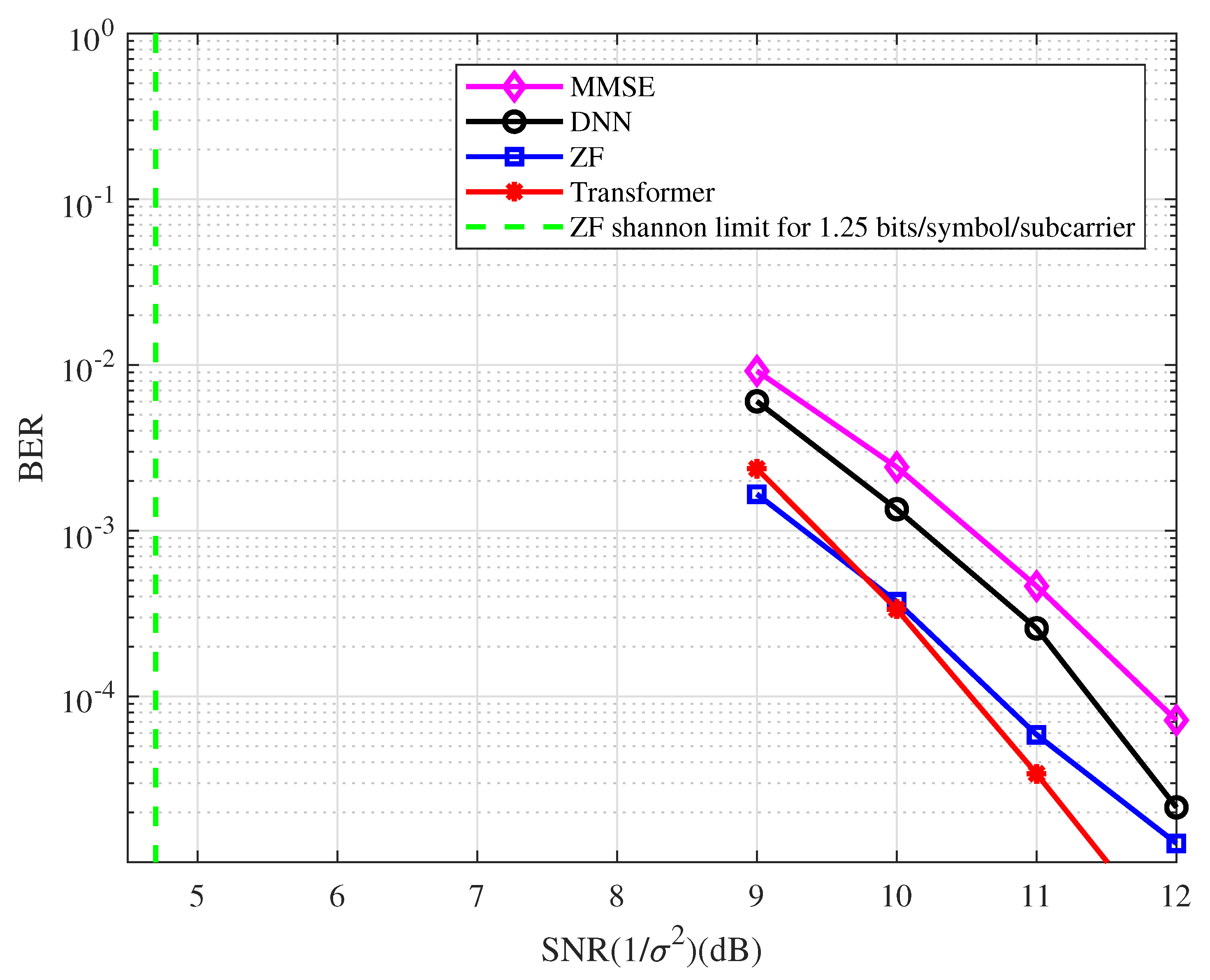
- At the BER of , the BER performance with the ZF detector is approximately 7.0 dB away from the Shannon limit.
- The DL-based system performs better than the ZF system in the high SNR region.
- At the BER of , the BER performance corresponding to the Transformer detector has an approximately 0.8 dB gain compared with the MMSE detector.

- As with the uncoded system, the MMSE detector performs better than the ZF detector.
- The DL-based systems perform no better than the ZF and MMSE systems and have an error floor in the high SNR region. This implies that the proposed network is more suitable for the decoding algorithm based on the factor graph.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| BCJR | Bahl–Cocke–Jelinek–Raviv |
| BER | bit error rate |
| BMST | block Markov superposition transmission |
| BP | belief propagation |
| CC | convolutional codes |
| CSI | channel state information |
| CP | cyclic prefix |
| DFT | discrete Fourier transform |
| DL | deep learning |
| DNN | deep neural network |
| GD | gradient descent |
| ICI | intercarrier interference |
| IDFT | inverse discrete Fourier transform |
| IFFT | inverse fast Fourier transform |
| LDPC | low-density parity check |
| ML | maximum likelihood |
| MMSE | minimum mean square error |
| OFDM | orthogonal frequency division multiplexing |
| OFDM-IM | OFDM with index modulation |
| PDP | power-delay profile |
| PEG | progressive edge growth |
| SIQ | soft information quality |
| SNR | signal-to-noise ratio |
| SPA | sum product algorithm |
| ZF | zero forcing |
References
- Ma, X.; Liang, C.; Huang, K.; Zhuang, Q. Block Markov superposition transmission: Construction of big convolutional codes from short codes. IEEE Trans. Inf. Theory 2015, 61, 3150–3163. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, Y.; Ma, X. Block Markov superposition transmission for high-speed railway wireless communication systems. In Proceedings of the 2015 International Workshop on High Mobility Wireless Communications (HMWC), Xi’an, China, 21–23 October 2015; pp. 61–65. [Google Scholar]
- Ma, P.; Ren, J.; Sun, G.; Zhao, H.; Jia, X.; Yan, Y.; Zabalza, J. Multiscale Superpixelwise Prophet Model for Noise-Robust Feature Extraction in Hyperspectral Images. IEEE Trans. Geosci. Remote. Sens. 2023, 61, 1–12. [Google Scholar] [CrossRef]
- Chen, R.; Huang, H.; Yu, Y.; Ren, J.; Wang, P.; Zhao, H.; Lu, X. Rapid Detection of Multi-QR Codes Based on Multistage Stepwise Discrimination and A Compressed MobileNet. IEEE Internet Things J. 2023, 1. [Google Scholar] [CrossRef]
- Li, Y.; Ren, J.; Yan, Y.; Liu, Q.; Ma, P.; Petrovski, A.; Sun, H. CBANet: An End-to-end Cross Band 2-D Attention Network for Hyperspectral Change Detection in Remote Sensing. IEEE Trans. Geosci. Remote. Sens. 2023, 1. [Google Scholar] [CrossRef]
- Xie, G.; Ren, J.; Marshall, S.; Zhao, H.; Li, R.; Chen, R. Self-attention enhanced deep residual network for spatial image steganalysis. Digit. Signal Process. 2023, 139, 104063. [Google Scholar] [CrossRef]
- Mao, Q.; Hu, F.; Hao, Q. Deep learning for intelligent wireless networks: A comprehensive survey. IEEE Commun. Surv. Tutor. 2018, 20, 2595–2621. [Google Scholar] [CrossRef]
- O’shea, T.; Hoydis, J. An introduction to deep learning for the physical layer. IEEE Trans. Cogn. Commun. Netw. 2017, 3, 563–575. [Google Scholar] [CrossRef]
- Wang, T.; Wen, C.K.; Wang, H.; Gao, F.; Jiang, T.; Jin, S. Deep learning for wireless physical layer: Opportunities and challenges. China Commun. 2017, 14, 92–111. [Google Scholar] [CrossRef]
- Qin, Z.; Ye, H.; Li, G.Y.; Juang, B.H.F. Deep learning in physical layer communications. IEEE Wirel. Commun. 2019, 26, 93–99. [Google Scholar] [CrossRef]
- Ye, H.; Li, G.Y.; Juang, B.H. Power of deep learning for channel estimation and signal detection in OFDM systems. IEEE Wirel. Commun. Lett. 2018, 7, 114–117. [Google Scholar] [CrossRef]
- Gao, X.; Jin, S.; Wen, C.K.; Li, G.Y. ComNet: Combination of deep learning and expert knowledge in OFDM receivers. IEEE Commun. Lett. 2018, 22, 2627–2630. [Google Scholar] [CrossRef]
- Jiang, P.; Wang, T.; Han, B.; Gao, X.; Zhang, J.; Wen, C.K.; Jin, S.; Li, G.Y. AI-aided online adaptive OFDM receiver: Design and experimental results. IEEE Trans. Wirel. Commun. 2021, 20, 7655–7668. [Google Scholar] [CrossRef]
- Van Luong, T.; Ko, Y.; Vien, N.A.; Nguyen, D.H.; Matthaiou, M. Deep learning-based detector for OFDM-IM. IEEE Wirel. Commun. Lett. 2019, 8, 1159–1162. [Google Scholar] [CrossRef]
- Zhang, D.; Wang, S.; Niu, K.; Dai, J.; Wang, S.; Yuan, Y. Transformer-based detector for OFDM with index modulation. IEEE Commun. Lett. 2022, 26, 1313–1317. [Google Scholar] [CrossRef]
- Li, Y.; Chen, Z.; Wang, Y.; Yang, C.; Ai, B.; Wu, Y.C. Heterogeneous Transformer: A Scale Adaptable Neural Network Architecture for Device Activity Detection. IEEE Trans. Wirel. Commun. 2023, 22, 3432–3446. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is all you need. In Proceedings of the 31st International Conference on Neural Information Processing Systems, NIPS’17, Red Hook, NY, USA, 4 December 2017; pp. 6000–6010. [Google Scholar]
- Carion, N.; Massa, F.; Synnaeve, G.; Usunier, N.; Kirillov, A.; Zagoruyko, S. End-to-end object detection with transformers. In Computer Vision–ECCV 2020, Proceedings of the 16th European Conference, Proceedings, Part I 16, Glasgow, UK, 23–28 August 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 213–229. [Google Scholar]
- Li, Y.; Chen, Z.; Liu, G.; Wu, Y.C.; Wong, K.K. Learning to Construct Nested Polar Codes: An Attention-Based Set-to-Element Model. IEEE Commun. Lett. 2021, 25, 3898–3902. [Google Scholar] [CrossRef]
- Gruber, T.; Cammerer, S.; Hoydis, J.; ten Brink, S. On deep learning-based channel decoding. In Proceedings of the 2017 51st Annual Conference on Information Sciences and Systems (CISS), IEEE, Baltimore, MD, USA, 22–24 March 2017; pp. 1–6. [Google Scholar]
- Xu, W.; Wu, Z.; Ueng, Y.L.; You, X.; Zhang, C. Improved polar decoder based on deep learning. In Proceedings of the 2017 IEEE International Workshop on Signal Processing Systems (SiPS), IEEE, Lorient, France, 3–5 October 2017; pp. 1–6. [Google Scholar]
- Liang, F.; Shen, C.; Wu, F. An iterative BP-CNN architecture for channel decoding. IEEE J. Sel. Top. Signal Process. 2018, 12, 144–159. [Google Scholar] [CrossRef]
- Bi, S.; Wang, Q.; Chen, Z.; Sun, J.; Ma, X. Deep learning-based decoding of block Markov superposition transmission. In Proceedings of the 2019 11th International Conference on Wireless Communications and Signal Processing (WCSP), Xi’an, China, 23–25 October 2019; pp. 1–5. [Google Scholar]
- Kavčić, A.; Ma, X.; Mitzenmacher, M. Binary intersymbol interference channels: Gallager codes, density evolution, and code performance bounds. IEEE Trans. Inf. Theory 2003, 49, 1636–1652. [Google Scholar] [CrossRef]
- Asadi, M.; Huang, X.; Kavcic, A.; Santhanam, N.P. Optimal detector for multilevel NAND flash memory channels with intercell interference. IEEE J. Sel. Areas Commun. 2014, 32, 825–835. [Google Scholar] [CrossRef]
- Zheng, Y.R.; Xiao, C. Simulation models with correct statistical properties for Rayleigh fading channels. IEEE Trans. Commun. 2003, 51, 920–928. [Google Scholar] [CrossRef]


| Parameter | Value |
|---|---|
| Subcarriers N | 64 |
| Subcarrier Spacing | 15 KHz |
| Carrier Frequency | 2 GHz |
| Multipaths | 9 |
| CP Length | 8 |
| Relative Speed | 360 km/h |
| Speed of Light | m/s |
| Modulation Mapper | QPSK |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Zhou, W.; Tong, Z.; Zeng, X.; Zhan, J.; Li, J.; Chen, R. Transformer-Based Detection for Highly Mobile Coded OFDM Systems. Entropy 2023, 25, 852. https://doi.org/10.3390/e25060852
Wang L, Zhou W, Tong Z, Zeng X, Zhan J, Li J, Chen R. Transformer-Based Detection for Highly Mobile Coded OFDM Systems. Entropy. 2023; 25(6):852. https://doi.org/10.3390/e25060852
Chicago/Turabian StyleWang, Leijun, Wenbo Zhou, Zian Tong, Xianxian Zeng, Jin Zhan, Jiawen Li, and Rongjun Chen. 2023. "Transformer-Based Detection for Highly Mobile Coded OFDM Systems" Entropy 25, no. 6: 852. https://doi.org/10.3390/e25060852
APA StyleWang, L., Zhou, W., Tong, Z., Zeng, X., Zhan, J., Li, J., & Chen, R. (2023). Transformer-Based Detection for Highly Mobile Coded OFDM Systems. Entropy, 25(6), 852. https://doi.org/10.3390/e25060852









