Optimum k-Nearest Neighbors for Heading Synchronization on a Swarm of UAVs under a Time-Evolving Communication Network
Abstract
:1. Introduction
- Cohesion, which means that the members of the group should stay together. This is achieved if the elements try to reduce the distance between them.
- Separation, the distance between elements should be enough to ensure that collisions between flockmates do not occur.
- Alignment, the members of the group have to match their speed vectors. This, has two requirements, they have to maintain similar linear velocity to stay in the flock, and the elements need to synchronize their orientation, in order to follow the same direction of the group.
2. Preliminaries
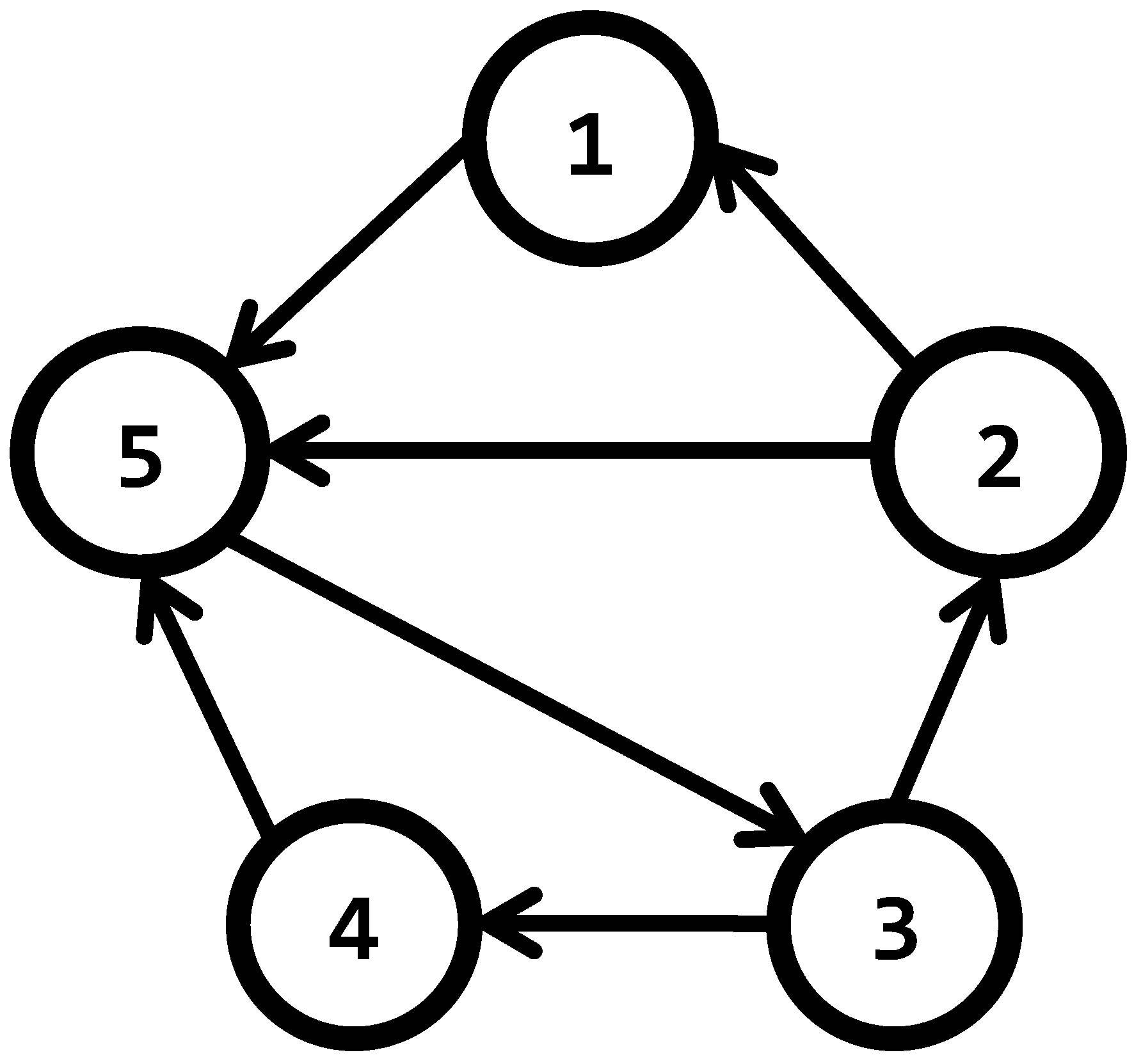
Graph Theory
3. Heading Synchronization
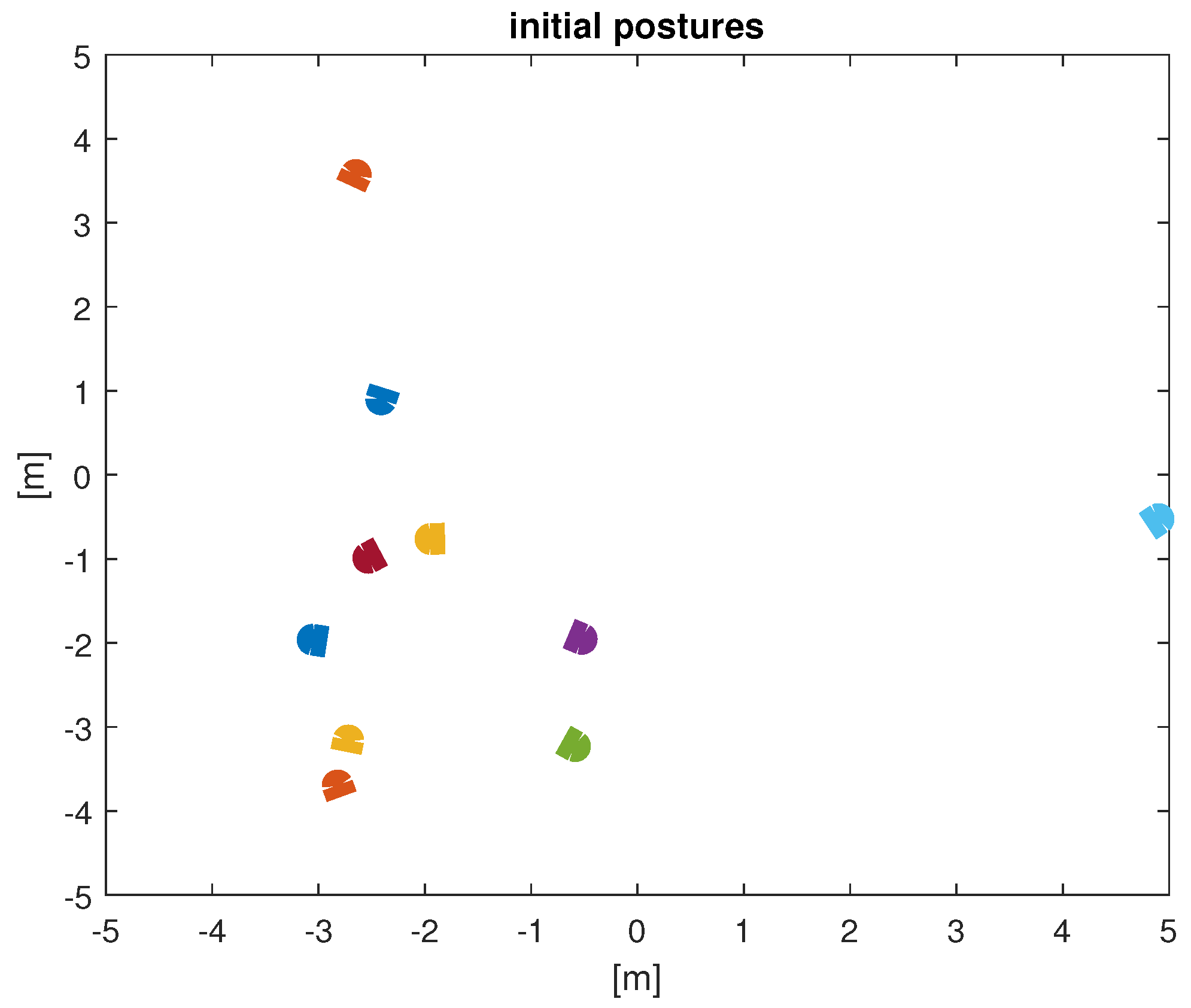
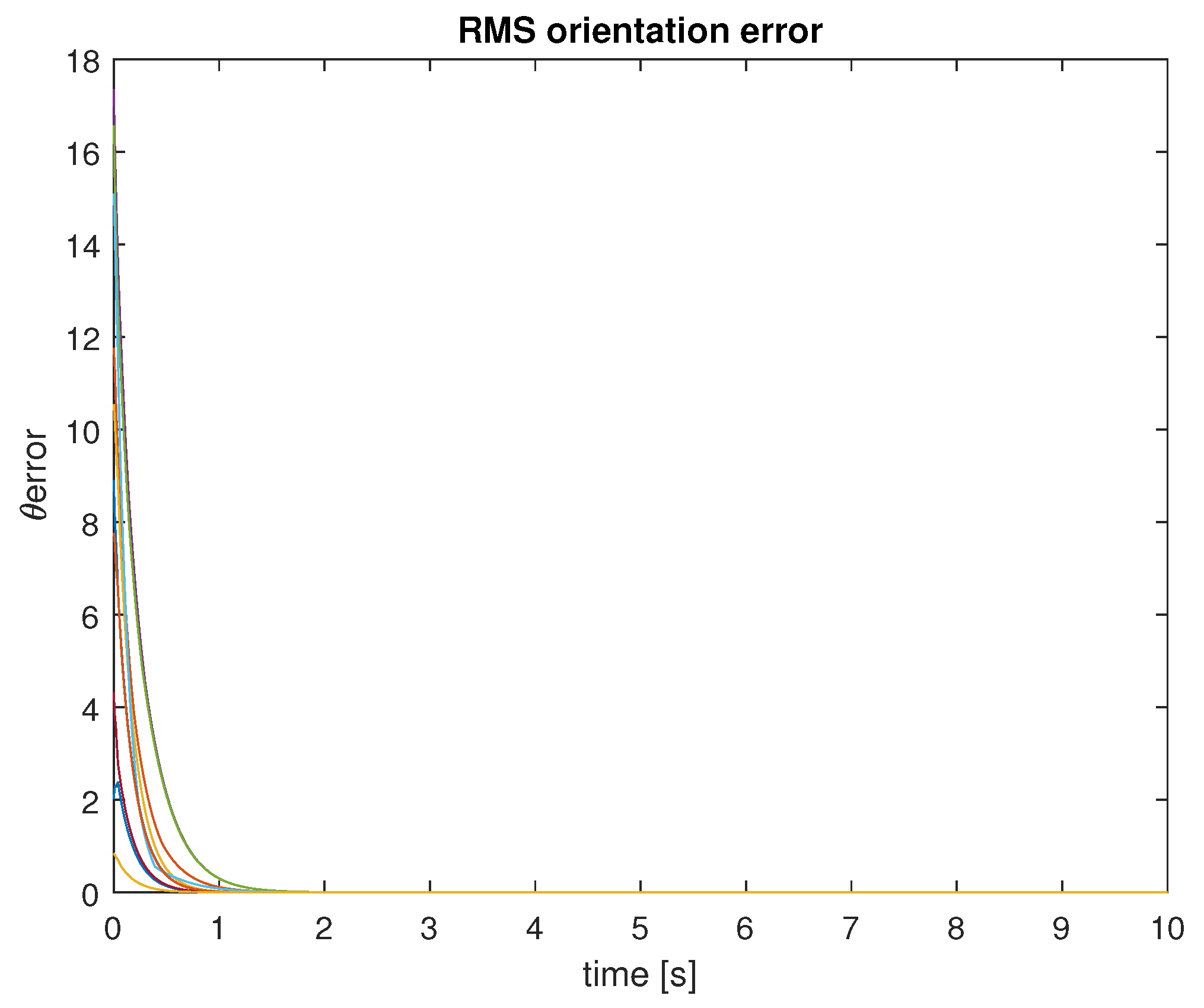
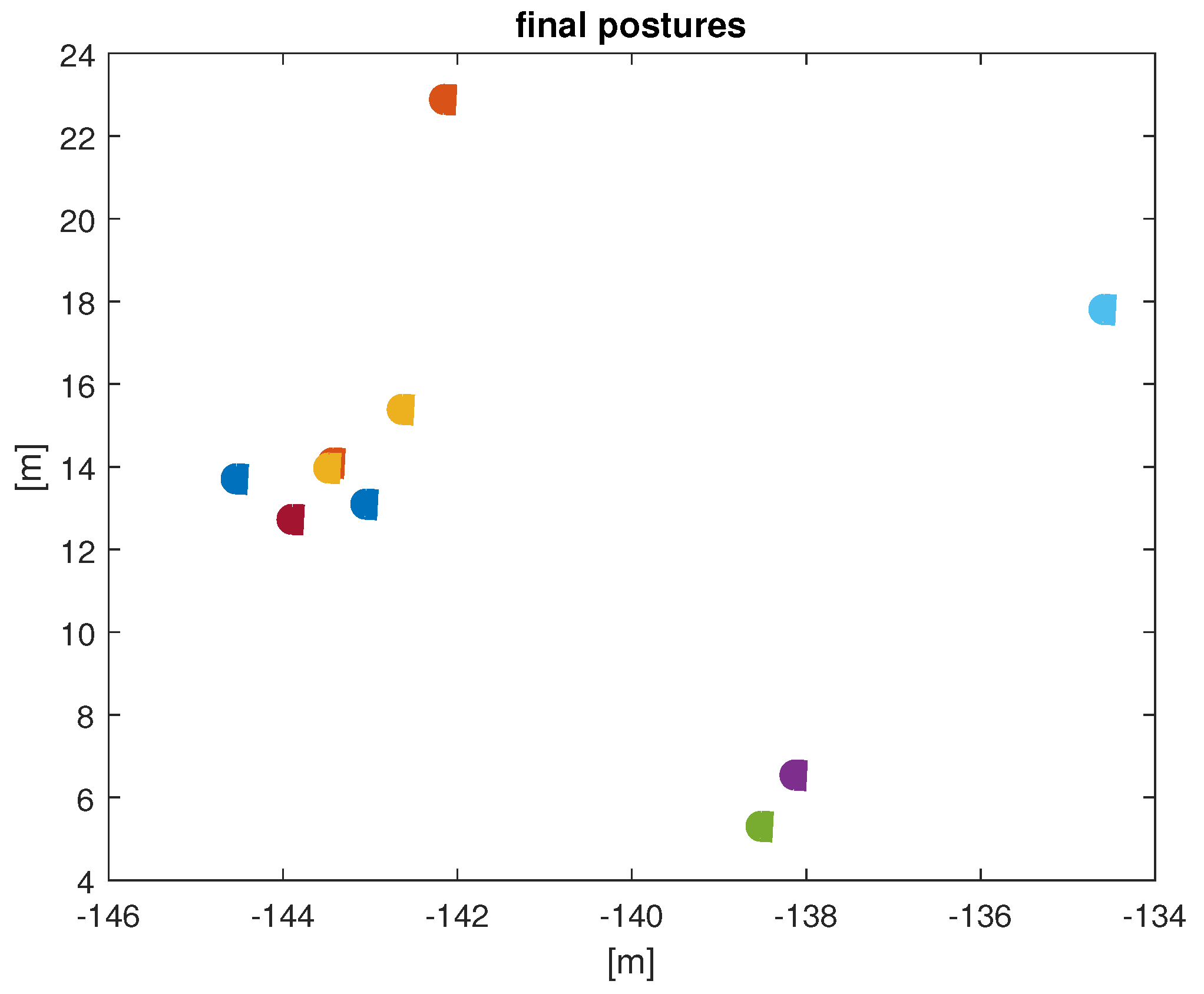
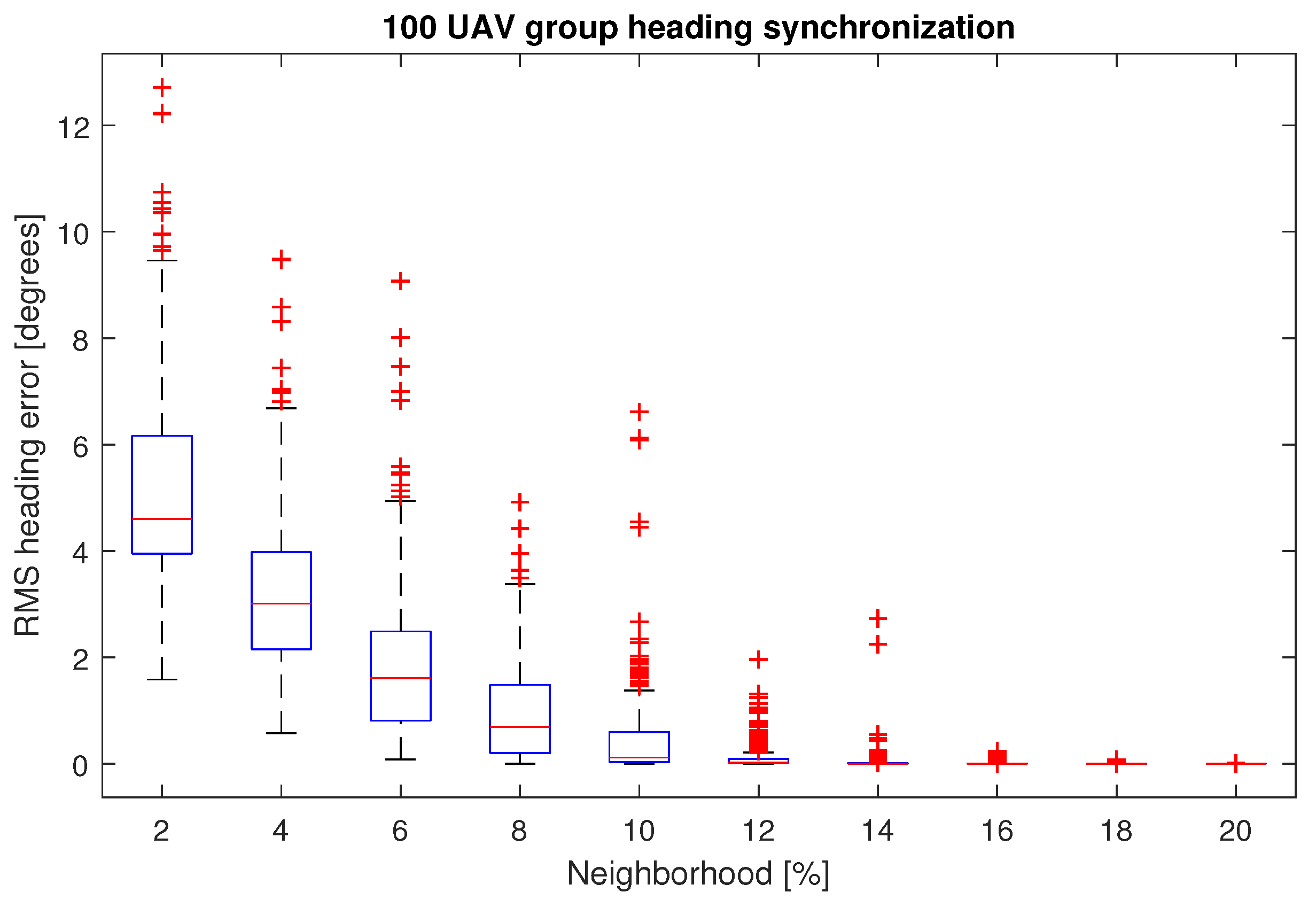
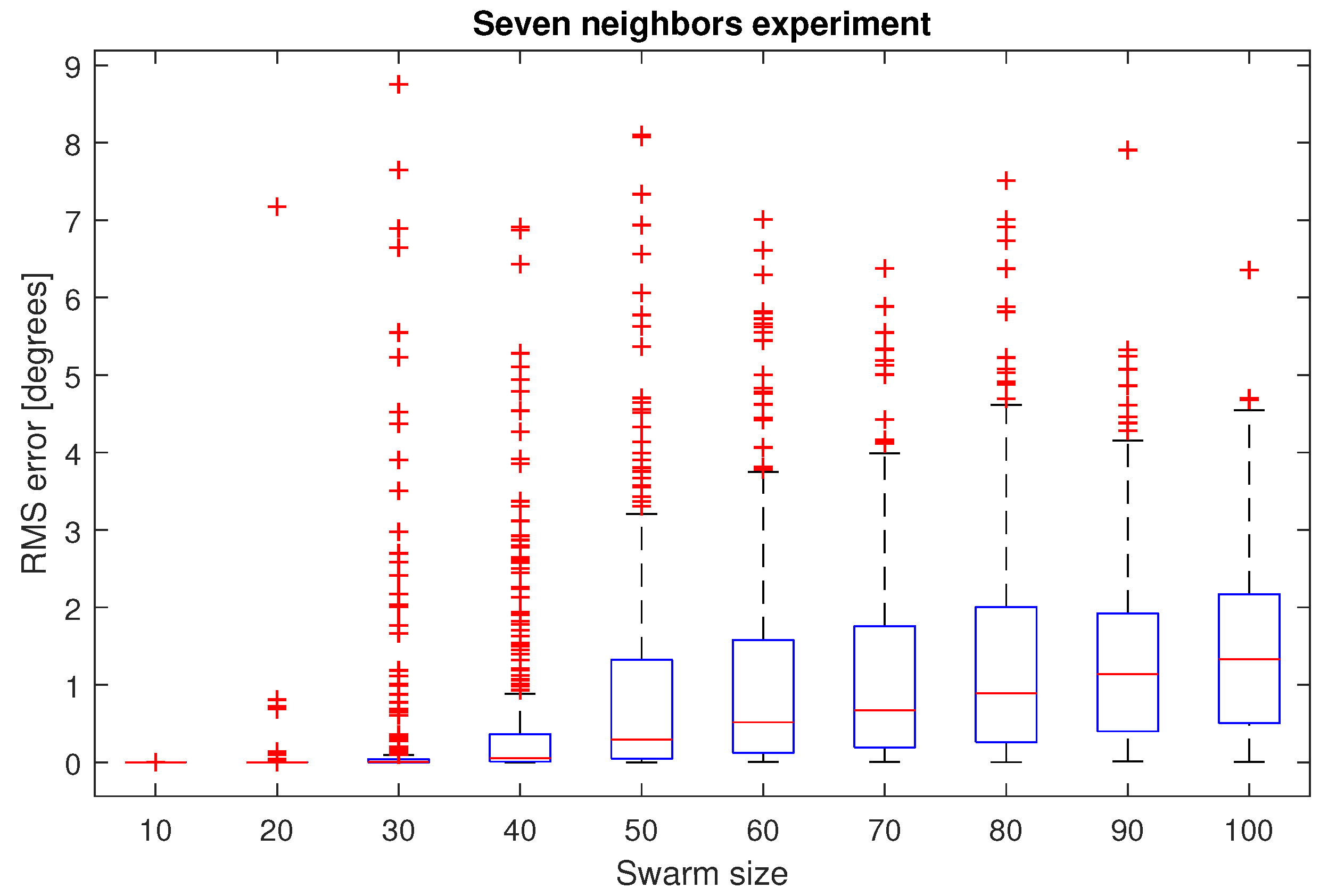
4. Optimum k-NN Neighborhood Size for a Group of UAVs
5. Discussion
6. Conclusions
- There exists a bulk of literature on consensus, that relies on the simple P-like consensus algorithm, some of them combining it with another control technique to improve it benefits. This algorithm is efficient only if the communication graph is connected, or at least contains a spanning tree.
- A simple asymptotic P-like controller, was successfully employed to achieve heading synchronization on a group of up to 100 UAVs.
- For the different scenarios, the statistical evidence shows that seven neighbors were enough to cope with the problem, as observed in nature with flocks of European starlings.
- A small neighborhood, combined with a simple heading synchronization based on graph theory, is recommended to be employed with simple UAVs, especially for the swarm robotics community.
- Further analysis on the communication scheme should be made to implement this solution.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kim, J.; Kim, S.; Ju, C.; Son, H.I. Unmanned aerial vehicles in agriculture: A review of perspective of platform, control, and applications. IEEE Access 2019, 7, 105100–105115. [Google Scholar] [CrossRef]
- Skorobogatov, G.; Barrado, C.; Salamí, E. Multiple UAV systems: A survey. Unmanned Syst. 2020, 8, 149–169. [Google Scholar] [CrossRef]
- Zhou, G.; Bao, X.; Ye, S.; Wang, H.; Yan, H. Selection of optimal building facade texture images from UAV-based multiple oblique image flows. IEEE Trans. Geosci. Remote Sens. 2020, 59, 1534–1552. [Google Scholar] [CrossRef]
- Cao, B.; Li, M.; Liu, X.; Zhao, J.; Cao, W.; Lv, Z. Many-objective deployment optimization for a drone-assisted camera network. IEEE Trans. Netw. Sci. Eng. 2021, 8, 2756–2764. [Google Scholar] [CrossRef]
- Yang, Z.; Yu, X.; Dedman, S.; Rosso, M.; Zhu, J.; Yang, J.; Xia, Y.; Tian, Y.; Zhang, G.; Wang, J. UAV remote sensing applications in marine monitoring: Knowledge visualization and review. Sci. Total Environ. 2022, 838, 155939. [Google Scholar] [CrossRef] [PubMed]
- Hosseini, N.; Jamal, H.; Haque, J.; Magesacher, T.; Matolak, D.W. UAV command and control, navigation and surveillance: A review of potential 5G and satellite systems. In Proceedings of the 2019 IEEE Aerospace Conference, Big Sky, MT, USA, 2–9 March 2019; IEEE: New York, NY, USA, 2019; pp. 1–10. [Google Scholar]
- Li, B.; Li, Q.; Zeng, Y.; Rong, Y.; Zhang, R. 3D trajectory optimization for energy-efficient UAV communication: A control design perspective. IEEE Trans. Wirel. Commun. 2021, 21, 4579–4593. [Google Scholar] [CrossRef]
- Outay, F.; Mengash, H.A.; Adnan, M. Applications of unmanned aerial vehicle (UAV) in road safety, traffic and highway infrastructure management: Recent advances and challenges. Transp. Res. Part A Policy Pract. 2020, 141, 116–129. [Google Scholar] [CrossRef]
- Muchiri, G.; Kimathi, S. A review of applications and potential applications of UAV. In Proceedings of the Sustainable Research and Innovation Conference, New York City, NY, USA, 21–22 September 2016; pp. 280–283. [Google Scholar]
- Lu, S.; Wang, X.; Wang, L.; Jia, L.; Shao, M.; Yu, Y. Distributed event-trigger model predictive control for stochastic disturbance systems. In Proceedings of the 2022 IEEE 17th Conference on Industrial Electronics and Applications (ICIEA), Chengdu, China, 16–19 December 2022; pp. 138–143. [Google Scholar] [CrossRef]
- Liang, Y.; Dong, Q.; Zhao, Y. Adaptive leader–follower formation control for swarms of unmanned aerial vehicles with motion constraints and unknown disturbances. Chin. J. Aeronaut. 2020, 33, 2972–2988. [Google Scholar] [CrossRef]
- Misra, S.; Deb, P.K.; Saini, K. Dynamic leader selection in a master-slave architecture-based micro UAV swarm. In Proceedings of the 2021 IEEE Global Communications Conference (GLOBECOM), Madrid, Spain, 7–11 December 2021; IEEE: New York, NY, USA, 2021; pp. 1–6. [Google Scholar]
- Liu, L.; Zhang, S.; Zhang, L.; Pan, G.; Yu, J. Multi-UUV Maneuvering Counter-Game for Dynamic Target Scenario Based on Fractional-Order Recurrent Neural Network. IEEE Trans. Cybern. 2022, 1–14. [Google Scholar] [CrossRef]
- Brambilla, M.; Ferrante, E.; Birattari, M.; Dorigo, M. Swarm robotics: A review from the swarm engineering perspective. Swarm Intell. 2013, 7, 1–41. [Google Scholar] [CrossRef]
- Duan, H.b.; Zhang, X.y.; Wu, J.; Ma, G.j. Max-min adaptive ant colony optimization approach to multi-UAVs coordinated trajectory replanning in dynamic and uncertain environments. J. Bionic Eng. 2009, 6, 161–173. [Google Scholar] [CrossRef]
- Perez-Carabaza, S.; Besada-Portas, E.; Lopez-Orozco, J.A.; Jesus, M. Ant colony optimization for multi-UAV minimum time search in uncertain domains. Appl. Soft Comput. 2018, 62, 789–806. [Google Scholar] [CrossRef]
- Gao, S.; Wu, J.; Ai, J. Multi-UAV reconnaissance task allocation for heterogeneous targets using grouping ant colony optimization algorithm. Soft Comput. 2021, 25, 7155–7167. [Google Scholar] [CrossRef]
- Duan, H.; Luo, Q.; Shi, Y.; Ma, G. ?Hybrid particle swarm optimization and genetic algorithm for multi-UAV formation reconfiguration. IEEE Comput. Intell. Mag. 2013, 8, 16–27. [Google Scholar] [CrossRef]
- Ghamry, K.A.; Kamel, M.A.; Zhang, Y. Multiple UAVs in forest fire fighting mission using particle swarm optimization. In Proceedings of the 2017 International conference on unmanned aircraft systems (ICUAS), Miami, FL USA, 13–16 June 2017; IEEE: New York, NY, USA, 2017; pp. 1404–1409. [Google Scholar]
- Shao, S.; Peng, Y.; He, C.; Du, Y. Efficient path planning for UAV formation via comprehensively improved particle swarm optimization. ISA Trans. 2020, 97, 415–430. [Google Scholar] [CrossRef]
- Harrou, F.; Khaldi, B.; Sun, Y.; Cherif, F. An efficient statistical strategy to monitor a robot swarm. IEEE Sens. J. 2019, 20, 2214–2223. [Google Scholar] [CrossRef]
- Lee, J.M.; Cho, S.H.; Calvo, R.A. A fast algorithm for simulation of flocking behavior. In Proceedings of the 2009 International IEEE Consumer Electronics Society’s Games Innovations Conference, London, UK, 25–28 August 2009; IEEE: New York, NY, USA, 2009; pp. 186–190. [Google Scholar]
- Lee, J.M.; Cho, H.K. A simple heuristic to find efficiently k-nearest neighbors in flocking behaviors. In Proceedings of the 6th WSEAS International Conference on Computer Engineering and Applications, and Proceedings of the 2012 American Conference on Applied Mathematics, Harvard, MA, USA, 25–27 January 2012; pp. 60–64. [Google Scholar]
- Lizzio, F.F.; Capello, E.; Guglieri, G. A Review of Consensus-based Multi-agent UAV Implementations. J. Intell. Robot. Syst. 2022, 106, 43. [Google Scholar] [CrossRef]
- Ren, W.; Beard, R.W.; McLain, T.W. Coordination variables and consensus building in multiple vehicle systems. In Proceedings of the Cooperative Control: A Post-Workshop Volume 2003 Block Island Workshop on Cooperative Control; Springer: Berlin/Heidelberg, Germany, 2005; pp. 171–188. [Google Scholar]
- Ren, W. Consensus strategies for cooperative control of vehicle formations. IET Control Theory Appl. 2007, 1, 505–512. [Google Scholar] [CrossRef]
- Yan, M.d.; Zhu, X.; Zhang, X.x.; Qu, Y.h. Consensus-based three-dimensionalmulti-UAV formation control strategy with high precision. Front. Inf. Technol. Electron. Eng. 2017, 18, 968–977. [Google Scholar] [CrossRef]
- Muslimov, T.Z.; Munasypov, R.A. Multi-UAV cooperative target tracking via consensus-based guidance vector fields and fuzzy MRAC. Aircr. Eng. Aerosp. Technol. 2021, 93, 1204–1212. [Google Scholar] [CrossRef]
- Wang, N.; Dai, J.; Ying, J. UAV formation obstacle avoidance control algorithm based on improved artificial potential field and consensus. Int. J. Aeronaut. Space Sci. 2021, 22, 1413–1427. [Google Scholar] [CrossRef]
- Martínez-Clark, R.; Cruz-Hernández, C.; Pliego-Jimenez, J.; Arellano-Delgado, A. Control algorithms for the emergence of self-organized behaviours in swarms of differential-traction wheeled mobile robots. Int. J. Adv. Robot. Syst. 2018, 15, 1729881418806435. [Google Scholar] [CrossRef]
- Reynolds, C.W. Flocks, herds and schools: A distributed behavioral model. In Proceedings of the 14th Annual Conference on Computer Graphics and Interactive Techniques, Anaheim, CA, USA, 27–31 July 1987; pp. 25–34. [Google Scholar]
- Muslimov, T.Z.; Munasypov, R.A. Consensus-based cooperative control of parallel fixed-wing UAV formations via adaptive backstepping. Aerosp. Sci. Technol. 2021, 109, 106416. [Google Scholar] [CrossRef]
- Dai, F.; Chen, M.; Wei, X.; Wang, H. Swarm intelligence-inspired autonomous flocking control in UAV networks. IEEE Access 2019, 7, 61786–61796. [Google Scholar] [CrossRef]
- He, T.; Wang, L. Neural network-based velocity-controllable UAV flocking. Aeronaut. J. 2023, 127, 289–304. [Google Scholar] [CrossRef]
- Luo, Q.; Duan, H. Distributed UAV flocking control based on homing pigeon hierarchical strategies. Aerosp. Sci. Technol. 2017, 70, 257–264. [Google Scholar] [CrossRef]
- Vicsek, T.; Czirók, A.; Ben-Jacob, E.; Cohen, I.; Shochet, O. Novel type of phase transition in a system of self-driven particles. Phys. Rev. Lett. 1995, 75, 1226. [Google Scholar] [CrossRef]
- Li, Q.; Jiang, Z.P. Two decentralized heading consensus algorithms for nonlinear multi-agent systems. Asian J. Control 2008, 10, 187–200. [Google Scholar] [CrossRef]
- Bardhan, R.; Ghose, D. Differential games guidance for heading angle consensus among unmanned aerial vehicles. J. Guid. Control Dyn. 2019, 42, 2568–2575. [Google Scholar] [CrossRef]
- Jin, J.; Ramirez, J.P.; Wee, S.; Lee, D.; Kim, Y.; Gans, N. A switched-system approach to formation control and heading consensus for multi-robot systems. Intell. Serv. Robot. 2018, 11, 207–224. [Google Scholar] [CrossRef]
- Bouabdallah, S.; Siegwart, R. Full control of a quadrotor. In Proceedings of the 2007 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Diego, CA, USA, 29 October–2 November 2007; IEEE: New York, NY, USA, 2007; pp. 153–158. [Google Scholar]
- Azar, A.T.; Serrano, F.E.; Kamal, N.A.; Koubaa, A. Robust kinematic control of unmanned aerial vehicles with non-holonomic constraints. In Proceedings of the International Conference on Advanced Intelligent Systems and Informatics 2020, Cairo, Egypt, 19–21 October 2020; Springer: Berlin/Heidelberg, Germany, 2021; pp. 839–850. [Google Scholar]
- Hu, J.; Sun, X.; He, L. Time-varying formation tracking for multiple UAVs with nonholonomic constraints and input quantization via adaptive backstepping control. Int. J. Aeronaut. Space Sci. 2019, 20, 710–721. [Google Scholar] [CrossRef]
- Wang, X.F. Complex networks: Topology, dynamics and synchronization. Int. J. Bifurc. Chaos 2002, 12, 885–916. [Google Scholar] [CrossRef]
- Wang, X.F.; Chen, G. Synchronization in small-world dynamical networks. Int. J. Bifurc. Chaos 2002, 12, 187–192. [Google Scholar] [CrossRef]
- Bialek, W.; Cavagna, A.; Giardina, I.; Mora, T.; Silvestri, E.; Viale, M.; Walczak, A.M. Statistical mechanics for natural flocks of birds. Proc. Natl. Acad. Sci. USA 2012, 109, 4786–4791. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martínez-Clark, R.; Pliego-Jimenez, J.; Flores-Resendiz, J.F.; Avilés-Velázquez, D. Optimum k-Nearest Neighbors for Heading Synchronization on a Swarm of UAVs under a Time-Evolving Communication Network. Entropy 2023, 25, 853. https://doi.org/10.3390/e25060853
Martínez-Clark R, Pliego-Jimenez J, Flores-Resendiz JF, Avilés-Velázquez D. Optimum k-Nearest Neighbors for Heading Synchronization on a Swarm of UAVs under a Time-Evolving Communication Network. Entropy. 2023; 25(6):853. https://doi.org/10.3390/e25060853
Chicago/Turabian StyleMartínez-Clark, Rigoberto, Javier Pliego-Jimenez, Juan Francisco Flores-Resendiz, and David Avilés-Velázquez. 2023. "Optimum k-Nearest Neighbors for Heading Synchronization on a Swarm of UAVs under a Time-Evolving Communication Network" Entropy 25, no. 6: 853. https://doi.org/10.3390/e25060853
APA StyleMartínez-Clark, R., Pliego-Jimenez, J., Flores-Resendiz, J. F., & Avilés-Velázquez, D. (2023). Optimum k-Nearest Neighbors for Heading Synchronization on a Swarm of UAVs under a Time-Evolving Communication Network. Entropy, 25(6), 853. https://doi.org/10.3390/e25060853





