Quantifying Information of Dynamical Biochemical Reaction Networks
Abstract
1. Introduction
2. Method of Information Geometry
3. Model and Analysis
3.1. Linear Biochemical Reaction Network
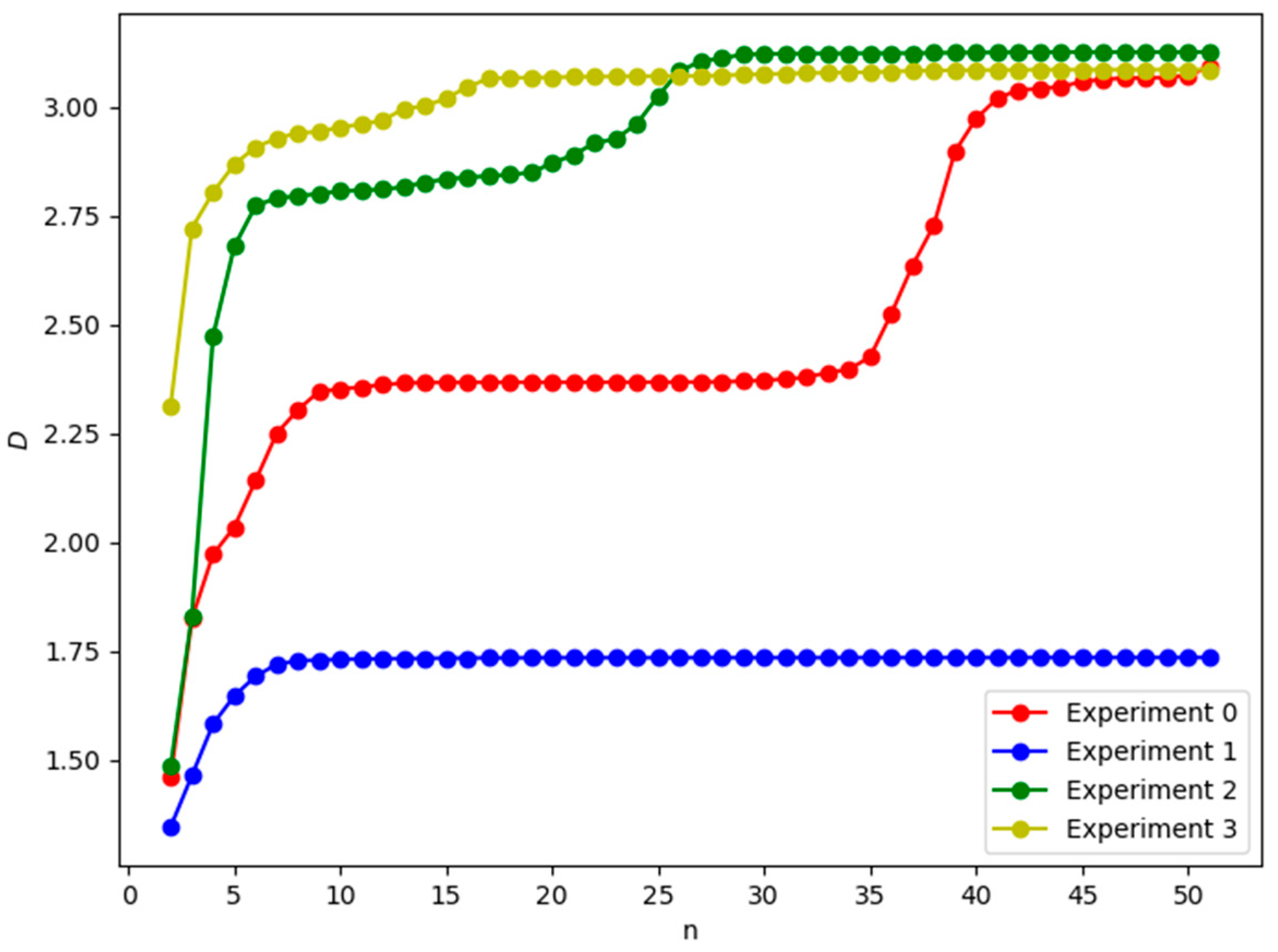
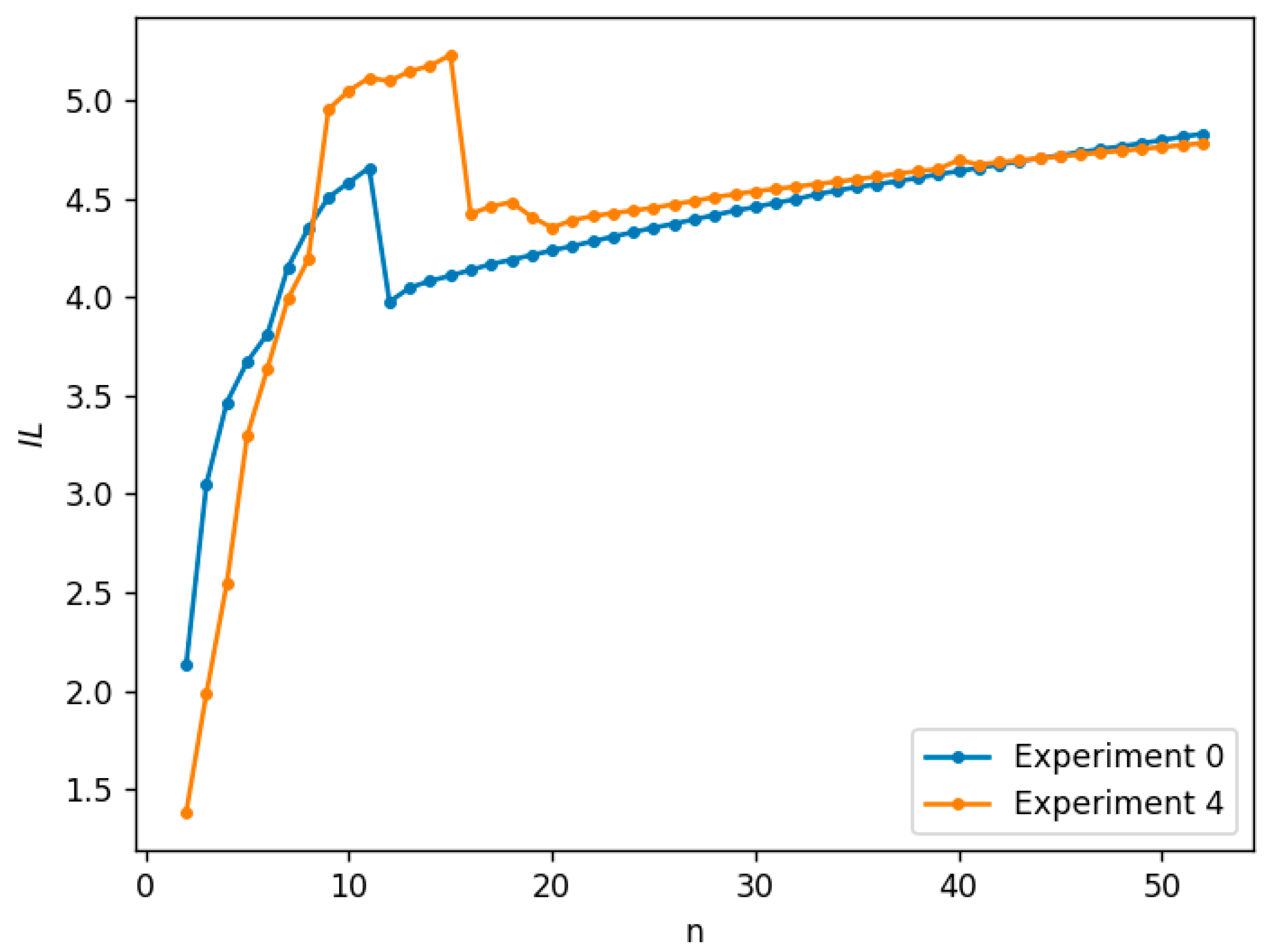
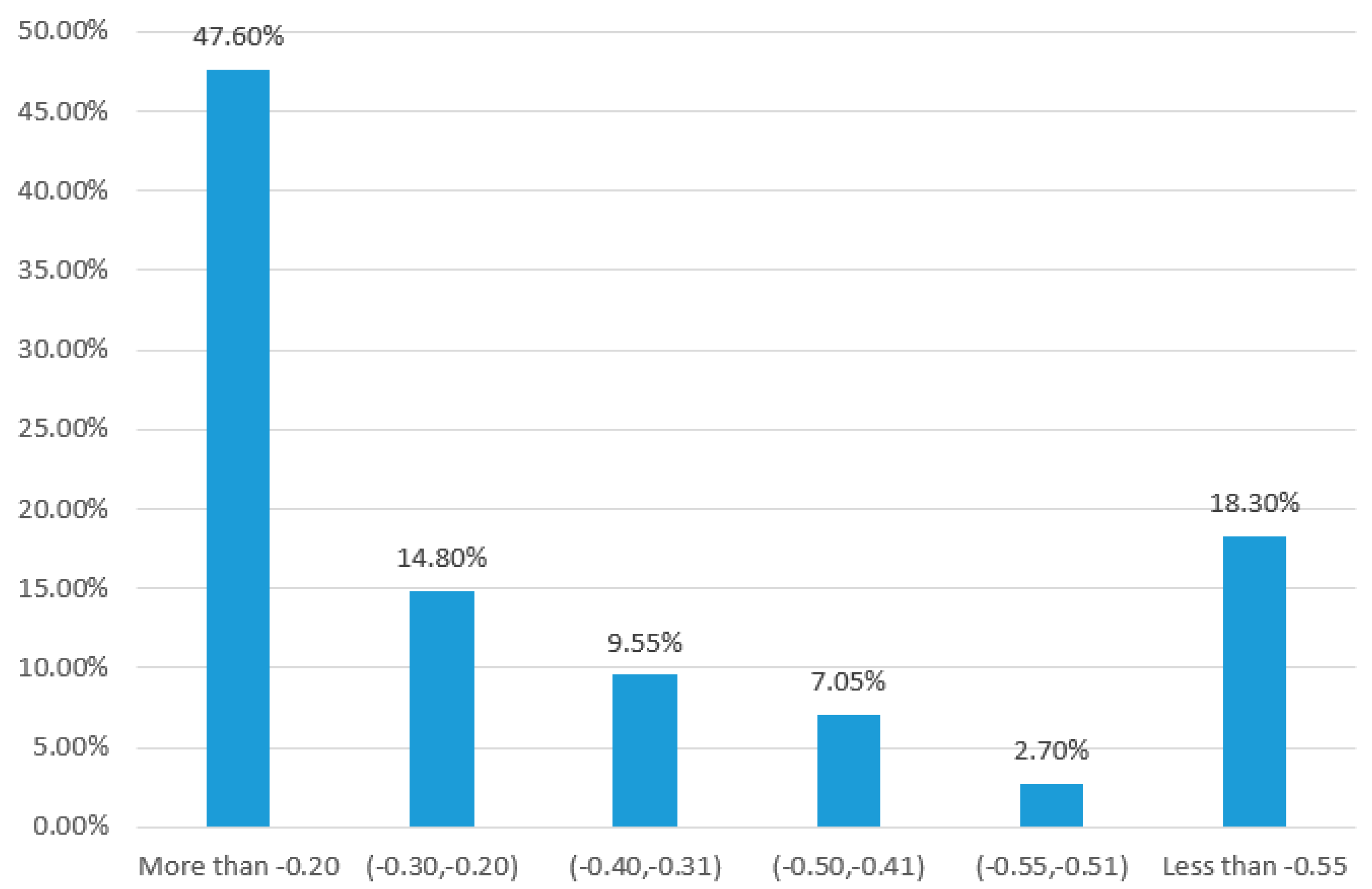
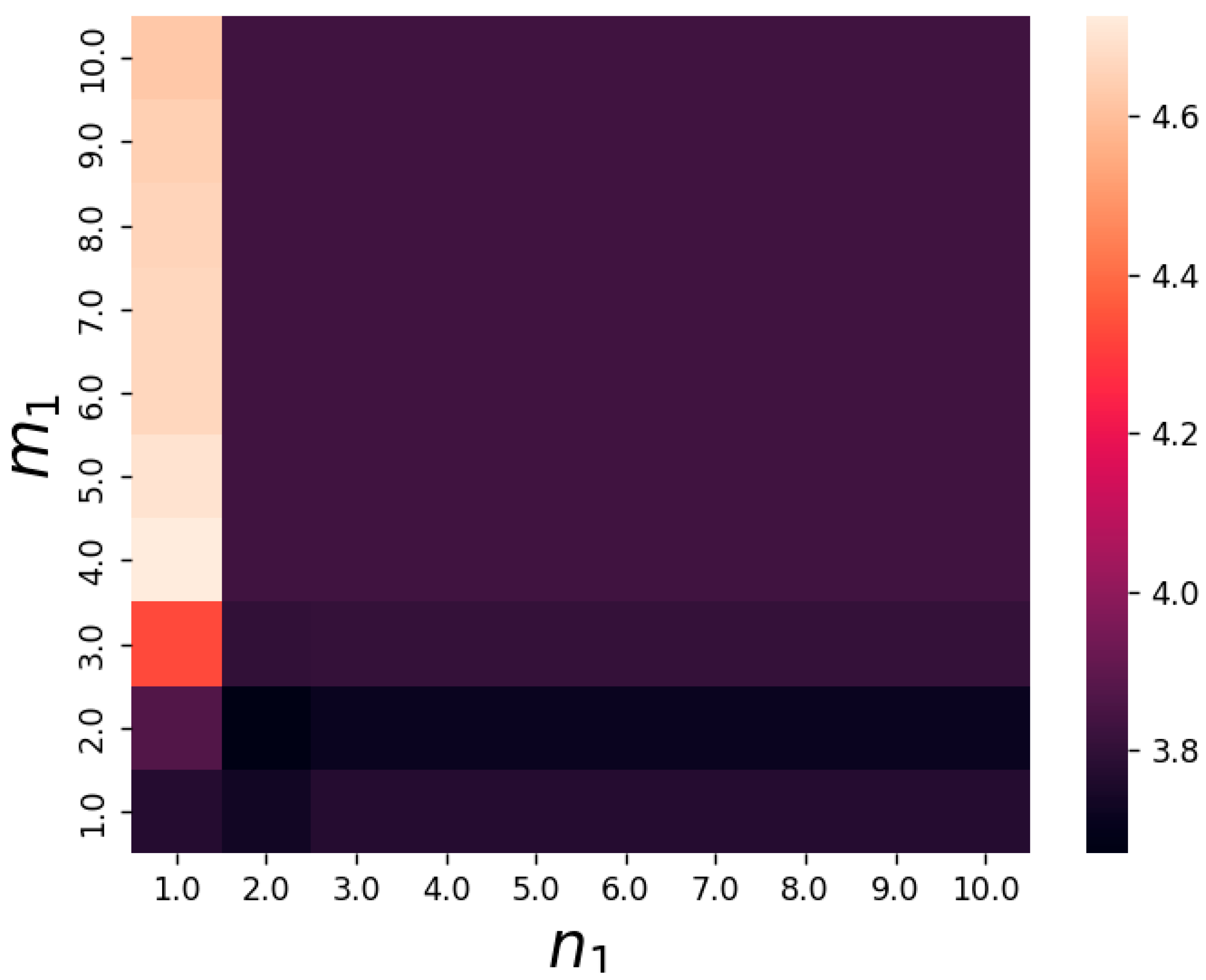
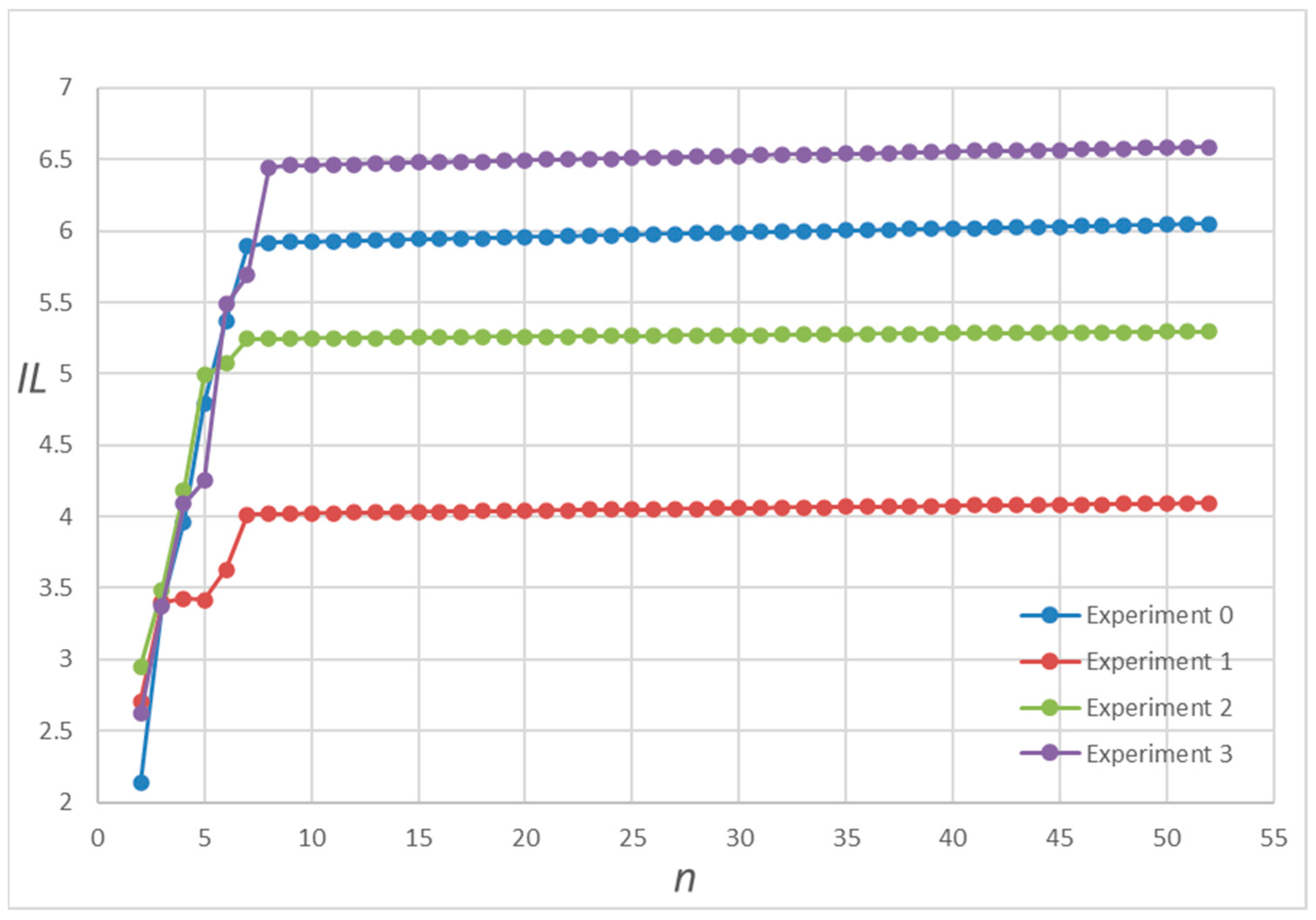
3.2. Numerical Simulations and Results
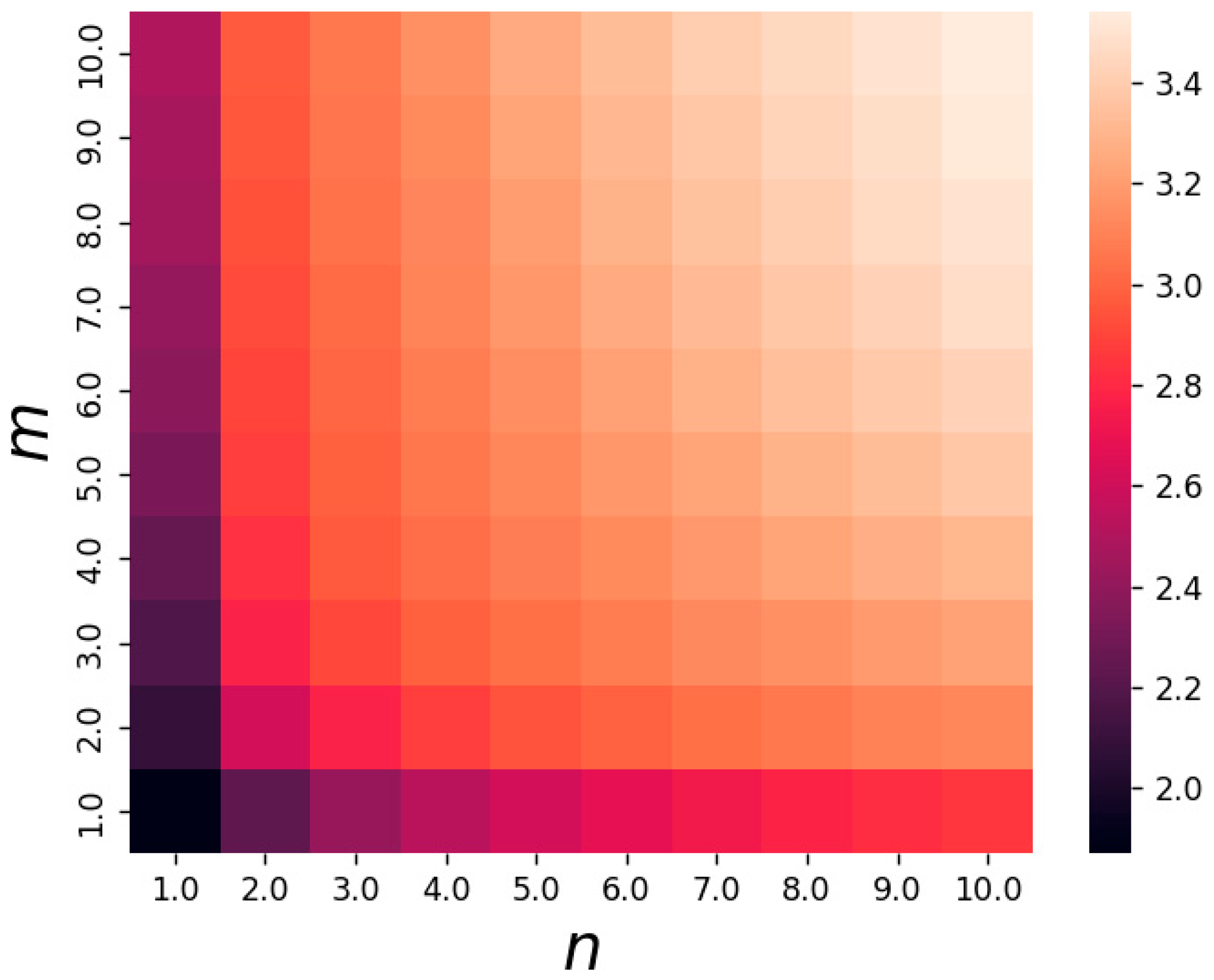
3.3. Nonlinear Biochemical Reaction Network
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Exp | E0 | E1 | E2 | E3 | E4 | Exp | E0 | E1 | E2 | E3 | E4 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Rate | Rate | ||||||||||||
| k1 | 0.594 | 0.475 | 0.824 | 0.986 | 0.147 | k−1 | 0.744 | 0.748 | 0.981 | 0.190 | 0.304 | ||
| k2 | 0.642 | 0.100 | 0.757 | 0.742 | 0.343 | k−2 | 0.590 | 0.372 | 0.751 | 0.229 | 0.554 | ||
| k3 | 0.481 | 0.232 | 0.927 | 0.677 | 0.637 | k−3 | 0.681 | 0.183 | 0.119 | 0.916 | 0.573 | ||
| k4 | 0.494 | 0.268 | 0.720 | 0.626 | 0.767 | k−4 | 0.903 | 0.411 | 0.489 | 0.420 | 0.115 | ||
| k5 | 0.967 | 0.457 | 0.976 | 0.529 | 0.952 | k−5 | 0.445 | 0.585 | 0.888 | 0.497 | 0.522 | ||
| k6 | 0.813 | 0.477 | 0.277 | 0.690 | 0.701 | k−6 | 0.576 | 0.717 | 0.937 | 0.947 | 0.410 | ||
| k7 | 0.611 | 0.284 | 0.134 | 0.805 | 0.424 | k−7 | 0.933 | 0.890 | 0.548 | 0.992 | 0.894 | ||
| k8 | 0.164 | 0.125 | 0.208 | 0.141 | 0.753 | k−8 | 0.178 | 0.703 | 0.142 | 0.687 | 0.600 | ||
| k9 | 0.118 | 0.476 | 0.534 | 0.744 | 0.125 | k−9 | 0.849 | 0.603 | 0.515 | 0.136 | 0.346 | ||
| k10 | 0.800 | 0.226 | 0.375 | 0.393 | 0.748 | k−10 | 0.883 | 0.278 | 0.951 | 0.726 | 0.914 | ||
| k11 | 0.981 | 0.821 | 0.566 | 0.478 | 0.611 | k−11 | 0.819 | 0.971 | 0.565 | 0.242 | 0.260 | ||
| k12 | 0.515 | 0.382 | 0.771 | 0.987 | 0.208 | k−12 | 0.802 | 0.723 | 0.287 | 0.255 | 0.752 | ||
| k13 | 0.206 | 0.889 | 0.847 | 0.178 | 0.324 | k−13 | 0.676 | 0.905 | 0.388 | 0.519 | 0.716 | ||
| k14 | 0.229 | 0.177 | 0.423 | 0.684 | 0.792 | k−14 | 0.950 | 0.135 | 0.641 | 0.198 | 0.643 | ||
| k15 | 0.570 | 0.253 | 0.586 | 0.932 | 0.913 | k−15 | 0.473 | 0.890 | 0.863 | 0.338 | 0.255 | ||
| k16 | 0.338 | 0.189 | 0.535 | 0.225 | 0.217 | k−16 | 0.797 | 0.479 | 0.711 | 0.162 | 0.819 | ||
| k17 | 0.511 | 0.962 | 0.844 | 0.166 | 0.266 | k−17 | 0.612 | 0.580 | 0.882 | 0.923 | 0.742 | ||
| k18 | 0.117 | 0.723 | 0.873 | 0.109 | 0.960 | k−18 | 0.656 | 0.384 | 0.461 | 0.735 | 0.848 | ||
| k19 | 0.651 | 0.718 | 0.999 | 0.354 | 0.528 | k−19 | 0.655 | 0.851 | 0.220 | 0.134 | 0.986 | ||
| k20 | 0.949 | 0.116 | 0.988 | 0.586 | 0.973 | k−20 | 0.714 | 0.775 | 0.847 | 0.753 | 0.319 | ||
| k21 | 0.424 | 0.990 | 0.463 | 0.717 | 0.273 | k−21 | 0.493 | 0.773 | 0.253 | 0.746 | 0.575 | ||
| k22 | 0.728 | 0.352 | 0.227 | 0.682 | 0.178 | k−22 | 0.154 | 0.810 | 0.514 | 0.903 | 0.507 | ||
| k23 | 0.700 | 0.193 | 0.722 | 0.589 | 0.156 | k−23 | 0.704 | 0.503 | 0.137 | 0.735 | 0.333 | ||
| k24 | 0.289 | 0.918 | 0.919 | 0.242 | 0.603 | k−24 | 0.216 | 0.364 | 0.198 | 0.422 | 0.470 | ||
| k25 | 0.384 | 0.359 | 0.558 | 0.751 | 0.786 | k−25 | 0.427 | 0.217 | 0.112 | 0.250 | 0.260 | ||
| k26 | 0.613 | 0.117 | 0.764 | 0.551 | 0.873 | k−26 | 0.495 | 0.711 | 0.363 | 0.697 | 0.952 | ||
| k27 | 0.990 | 0.290 | 0.334 | 0.821 | 0.590 | k−27 | 0.192 | 0.339 | 0.338 | 0.325 | 0.469 | ||
| k28 | 0.288 | 0.542 | 0.920 | 0.900 | 0.491 | k−28 | 0.245 | 0.148 | 0.383 | 0.662 | 0.962 | ||
| k29 | 0.688 | 0.617 | 0.291 | 0.877 | 0.895 | k−29 | 0.328 | 0.232 | 0.642 | 0.871 | 0.562 | ||
| k30 | 0.520 | 0.630 | 0.228 | 0.989 | 0.137 | k−30 | 0.320 | 0.730 | 0.689 | 0.878 | 0.917 | ||
| k31 | 0.243 | 0.192 | 0.533 | 0.286 | 0.841 | k−31 | 0.199 | 0.473 | 0.570 | 0.432 | 0.786 | ||
| k32 | 0.691 | 0.725 | 0.456 | 0.477 | 0.724 | k−32 | 0.224 | 0.473 | 0.968 | 0.483 | 0.188 | ||
| k33 | 0.277 | 0.145 | 0.316 | 0.738 | 0.658 | k−33 | 0.432 | 0.582 | 0.417 | 0.647 | 0.954 | ||
| k34 | 0.839 | 0.697 | 0.656 | 0.375 | 0.505 | k−34 | 0.187 | 0.563 | 0.536 | 0.582 | 0.388 | ||
| k35 | 0.854 | 0.950 | 0.579 | 0.988 | 0.598 | k−35 | 0.186 | 0.628 | 0.731 | 0.328 | 0.351 | ||
| k36 | 0.979 | 0.913 | 0.792 | 0.146 | 0.591 | k−36 | 0.522 | 0.224 | 0.788 | 0.200 | 0.426 | ||
| k37 | 0.979 | 0.225 | 0.921 | 0.364 | 0.460 | k−37 | 0.644 | 0.827 | 0.418 | 0.328 | 0.612 | ||
| k38 | 0.765 | 0.458 | 0.363 | 0.351 | 0.145 | k−38 | 0.135 | 0.249 | 0.190 | 0.779 | 0.735 | ||
| k39 | 0.355 | 0.935 | 0.306 | 0.726 | 0.756 | k−39 | 0.208 | 0.413 | 0.407 | 0.862 | 0.120 | ||
| k40 | 0.367 | 0.776 | 0.501 | 0.711 | 0.587 | k−40 | 0.207 | 0.753 | 0.444 | 0.948 | 0.844 | ||
| k41 | 0.386 | 0.895 | 0.492 | 0.525 | 0.694 | k−41 | 0.473 | 0.661 | 0.409 | 0.514 | 0.497 | ||
| k42 | 0.158 | 0.776 | 0.438 | 0.731 | 0.331 | k−42 | 0.723 | 0.414 | 0.683 | 0.873 | 0.569 | ||
| k43 | 0.610 | 0.343 | 0.241 | 0.207 | 0.468 | k−43 | 0.339 | 0.906 | 0.745 | 0.840 | 0.970 | ||
| k44 | 0.571 | 0.485 | 0.273 | 0.430 | 0.993 | k−44 | 0.185 | 0.968 | 0.957 | 0.585 | 0.863 | ||
| k45 | 0.618 | 0.697 | 0.369 | 0.160 | 0.421 | k−45 | 0.936 | 0.660 | 0.813 | 0.158 | 0.571 | ||
| k46 | 0.387 | 0.203 | 0.484 | 0.343 | 0.456 | k−46 | 0.701 | 0.955 | 0.808 | 0.982 | 0.170 | ||
| k47 | 0.219 | 0.505 | 0.401 | 0.147 | 0.984 | k−47 | 0.745 | 0.621 | 0.222 | 0.879 | 0.417 | ||
| k48 | 0.360 | 0.467 | 0.851 | 0.315 | 0.309 | k−48 | 0.265 | 0.313 | 0.899 | 0.581 | 0.661 | ||
| k49 | 0.628 | 0.913 | 0.488 | 0.328 | 0.709 | k−49 | 0.118 | 0.616 | 0.265 | 0.324 | 0.798 | ||
| k50 | 0.846 | 0.103 | 0.849 | 0.243 | 0.676 | k−50 | 0.104 | 0.655 | 0.610 | 0.491 | 0.228 | ||
| k51 | 0.710 | 0.394 | 0.969 | 0.119 | 0.230 | k−51 | 0.343 | 0.574 | 0.986 | 0.722 | 0.170 | ||
| k52 | 0.762 | 0.897 | 0.667 | 0.181 | 0.415 | k−52 | 0.966 | 0.422 | 0.982 | 0.767 | 0.383 | ||
| Exp | E0 | E1 | E2 | E3 | Exp | E0 | E1 | E2 | E3 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| n | n | ||||||||||
| 1 | 1 | 1 | 1 | 1 | 27 | 1 | 9 | 4 | 9 | ||
| 2 | 1 | 9 | 5 | 2 | 28 | 3 | 9 | 1 | 8 | ||
| 3 | 4 | 6 | 9 | 3 | 29 | 4 | 4 | 4 | 9 | ||
| 4 | 4 | 1 | 3 | 4 | 30 | 9 | 9 | 3 | 7 | ||
| 5 | 8 | 1 | 7 | 1 | 31 | 2 | 8 | 2 | 7 | ||
| 6 | 4 | 2 | 2 | 9 | 32 | 4 | 4 | 2 | 8 | ||
| 7 | 6 | 8 | 6 | 2 | 33 | 4 | 7 | 9 | 2 | ||
| 8 | 3 | 7 | 5 | 8 | 34 | 4 | 6 | 4 | 9 | ||
| 9 | 5 | 3 | 5 | 8 | 35 | 8 | 2 | 9 | 5 | ||
| 10 | 8 | 5 | 3 | 2 | 36 | 1 | 4 | 3 | 1 | ||
| 11 | 7 | 6 | 3 | 8 | 37 | 2 | 5 | 1 | 1 | ||
| 12 | 9 | 3 | 8 | 3 | 38 | 1 | 9 | 1 | 6 | ||
| 13 | 9 | 5 | 3 | 3 | 39 | 5 | 2 | 3 | 3 | ||
| 14 | 2 | 3 | 2 | 6 | 40 | 8 | 5 | 9 | 3 | ||
| 15 | 7 | 5 | 7 | 2 | 41 | 4 | 1 | 8 | 9 | ||
| 16 | 8 | 8 | 1 | 1 | 42 | 3 | 4 | 6 | 6 | ||
| 17 | 8 | 8 | 5 | 4 | 43 | 8 | 3 | 8 | 9 | ||
| 18 | 9 | 2 | 5 | 5 | 44 | 3 | 1 | 3 | 5 | ||
| 19 | 2 | 8 | 1 | 4 | 45 | 1 | 5 | 2 | 8 | ||
| 20 | 6 | 1 | 5 | 4 | 46 | 1 | 3 | 8 | 8 | ||
| 21 | 9 | 7 | 5 | 5 | 47 | 5 | 8 | 5 | 4 | ||
| 22 | 5 | 8 | 9 | 2 | 48 | 6 | 8 | 6 | 3 | ||
| 23 | 4 | 7 | 9 | 1 | 49 | 6 | 9 | 2 | 9 | ||
| 24 | 1 | 2 | 2 | 1 | 50 | 7 | 7 | 2 | 7 | ||
| 25 | 4 | 1 | 6 | 3 | 51 | 9 | 4 | 3 | 4 | ||
| 26 | 6 | 2 | 9 | 5 | 52 | 5 | 8 | 9 | 4 | ||
References
- Upadhyay, A.; Moss-Taylor, L.; Kim, M.J.; Ghosh, A.C.; O’Connor, M.B. TGF-β Family Signaling in Drosophila. Cold Spring Harb. Perspect. Biol. 2017, 9, a022152. [Google Scholar] [CrossRef] [PubMed]
- Barkai, N.; Shilo, B.Z. Robust generation and decoding of morphogen gradients. Cold Spring Harb. Perspect. Biol. 2009, 1, a001990. [Google Scholar] [CrossRef] [PubMed]
- Wartlick, O.; Kicheva, A.; González-Gaitán, M. Morphogen gradient formation. Cold Spring Harb. Perspect. Biol. 2009, 1, a001255. [Google Scholar] [CrossRef] [PubMed]
- Porcher, A.; Dostatni, N. The bicoid morphogen system. Curr. Biol. 2010, 20, R249–R254. [Google Scholar] [CrossRef]
- Demirkıran, G.; Kalaycı Demir, G.; Güzeliş, C. Two-dimensional polynomial type canonical relaxation oscillator model for p53 dynamics. IET Syst. Biol. 2018, 12, 138–147. [Google Scholar] [CrossRef]
- Cruz-Rodríguez, L.; Figueroa-Morales, N.; Mulet, R. On the role of intrinsic noise on the response of the p53-Mdm2 module. J. Stat. Mech. Theory Exp. 2015, 2015, P09015. [Google Scholar] [CrossRef]
- Zhang, X.P.; Liu, F.; Wang, W. Two-phase dynamics of p53 in the DNA damage response. Proc. Natl. Acad. Sci. USA 2011, 108, 8990. [Google Scholar] [CrossRef]
- Zhang, X.P.; Liu, F.; Cheng, Z.; Wang, W. Cell fate decision mediated by p53 pulses. Proc. Natl. Acad. Sci. USA 2009, 106, 12245–12250. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, L.; Zhou, T. Analytical Distribution and Tunability of Noise in a Model of Promoter Progress. Biophys. J. 2012, 102, 1247–1257. [Google Scholar] [CrossRef]
- Zhang, J.; Zhou, T. Promoter-mediated Transcriptional Dynamics. Biophys. J. 2014, 106, 479–488. [Google Scholar] [CrossRef]
- Kumar, N.; Kulkarni, R.V. Constraining the complexity of promoter dynamics using fluctuations in gene expression. Phys. Biol. 2019, 17, 015001. [Google Scholar] [CrossRef] [PubMed]
- Thattai, M.; van Oudenaarden, A. Intrinsic Noise in Gene Regulatory Networks. Proc. Natl. Acad. Sci. USA 2001, 98, 8614–8619. [Google Scholar] [CrossRef] [PubMed]
- Zarubin, T.; Han, J. Activation and signaling of the p38 MAP kinase pathway. Cell Res. 2005, 15, 11–18. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.C.; Kumar, S.; Griswold, D.E.; Underwood, D.C.; Votta, B.J.; Adams, J.L. Inhibition of p38 MAP kinase as a therapeutic strategy. Immunopharmacology 2000, 47, 185–201. [Google Scholar] [CrossRef] [PubMed]
- Ono, K.; Han, J. The p38 signal transduction pathway activation and function. Cell. Signal. 2000, 12, 1–13. [Google Scholar] [CrossRef]
- Weston, C.R.; Davis, R.J. The JNK signal transduction pathway. Curr. Opin. Cell Biol. 2007, 19, 142–149. [Google Scholar] [CrossRef]
- Dhanasekaran, D.N.; Reddy, E.P. JNK signaling in apoptosis. Oncogene 2008, 27, 6245–6251. [Google Scholar] [CrossRef]
- Song, M.S.; Salmena, L.; Pandolfi, P.P. The functions and regulation of the PTEN tumour suppressor. Nat. Rev. Mol. Cell Biol. 2012, 13, 283–296. [Google Scholar] [CrossRef]
- Chu, E.C.; Tarnawski, A.S. PTEN regulatory functions in tumor suppression and cell biology. Med. Sci. Monit. Int. Med. J. Exp. Clin. Res. 2004, 10, RA235–RA241. [Google Scholar]
- Tamura, M.; Gu, J.; Matsumoto, K.; Aota, S.-I.; Parsons, R.; Yamada, K.M. Inhibition of cell migration, spreading, and focal adhesions by tumor suppressor PTEN. Science 1998, 280, 1614–1617. [Google Scholar] [CrossRef]
- Fruman, D.A.; Chiu, H.; Hopkins, B.D.; Bagrodia, S.; Cantley, L.C.; Abraham, R.T. The PI3K pathway in human disease. Cell 2017, 170, 605–635. [Google Scholar] [CrossRef]
- Assinder, S.J.; Dong, Q.; Kovacevic, Z.; Richardson, D.R. The TGF-β, PI3K/Akt and PTEN pathways: Established and proposed biochemical integration in prostate cancer. Biochem. J. 2009, 417, 411–421. [Google Scholar]
- Kim, K.M.; Lee, Y.J. Amiloride augments TRAIL-induced apoptotic death by inhibiting phosphorylation of kinases and phosphatases associated with the P13K-Akt pathway. Oncogene 2005, 24, 355–366. [Google Scholar] [CrossRef]
- Kreisberg, J.I.; Malik, S.N.; Prihoda, T.J.; Bedolla, R.G.; Troyer, D.A.; Kreisberg, S.; Ghosh, P.M. Phosphorylation of Akt (Ser473) is an excellent predictor of poor clinical outcome in prostate cancer. Cancer Res. 2004, 64, 5232–5236. [Google Scholar] [CrossRef]
- Litchfield, D.W. Protein kinase CK2: Structure, regulation and role in cellular decisions of life and death. Biochem. J. 2003, 369, 1–15. [Google Scholar] [CrossRef]
- You, L.; Shi, J.; Shen, L.; Li, L.; Fang, C.; Yu, C.; Cheng, W.; Feng, Y.; Zhang, Y. Structural basis for transcription antitermination at bacterial intrinsic terminator. Nat. Commun. 2019, 10, 3048. [Google Scholar] [CrossRef]
- Bhalla, U.S.; Iyengar, R. Emergent properties of networks of biological signaling pathways. Science 1999, 283, 381–387. [Google Scholar] [CrossRef]
- Weng, G.; Bhalla, U.S.; Iyengar, R. Complexity in biological signaling systems. Science 1999, 284, 92–96. [Google Scholar] [CrossRef]
- Kolch, W.; Halasz, M.; Granovskaya, M.; Kholodenko, B.N. The dynamic control of signal transduction networks in cancer cells. Nat. Rev. Cancer 2015, 15, 515–527. [Google Scholar] [CrossRef]
- Cheong, R.; Rhee, A.; Wang, C.J.; Nemenman, I.; Levchenko, A. Information transduction capacity of noisy biochemical signaling networks. Science 2011, 334, 354–358. [Google Scholar] [CrossRef]
- Kholodenko, B.N. Cell-signalling dynamics in time and space. Nat. Rev. Mol. Cell Biol. 2006, 7, 165–176. [Google Scholar] [CrossRef] [PubMed]
- Purvis, J.E.; Lahav, G. Encoding and decoding cellular information through signaling dynamics. Cell 2013, 152, 945–956. [Google Scholar] [CrossRef] [PubMed]
- Kim, E. Information geometry, fluctuations, non-equilibrium thermodynamics, and geodesics in complex systems. Entropy 2021, 23, 1393. [Google Scholar] [CrossRef] [PubMed]
- Ito, S. Stochastic Thermodynamic Interpretation of Information Geometry. Phys. Rev. Lett. 2018, 121, 030605. [Google Scholar] [CrossRef]
- Zhang, Z.; Guan, S.; Shi, H. Information geometry in the population dynamics of bacteria. J. Stat. Mech. Theory Exp. 2020, 2020, 073501. [Google Scholar] [CrossRef]
- Yin, H.; Li, Q.; Wen, X. Formation of morphogen gradient based on information geometry. Int. J. Mod. Phys. B 2022, 36, 2250143. [Google Scholar] [CrossRef]
- Beelman, C.A.; Parker, R. Degradation of mRNA in eukaryotes. Cell 1995, 81, 179–183. [Google Scholar] [CrossRef]
- Schoenfelder, S.; Fraser, P. Long-range enhancer–promoter contacts in gene expression control. Nat. Rev. Genet. 2019, 20, 437–455. [Google Scholar] [CrossRef]
- Cover, T.M. Elements of Information Theory; John Wiley & Sons: Hoboken, NJ, USA, 1999. [Google Scholar]
- Braunstein, S.L.; Caves, C.M. Statistical distance and the geometry of quantum states. Phys. Rev. Lett. 1994, 72, 3439. [Google Scholar] [CrossRef]
- Wootters, W.K. Statistical distance and Hilbert space. Phys. Rev. D 1981, 23, 357. [Google Scholar] [CrossRef]
- Kim, E. Investigating information geometry in classical and quantum systems through information length. Entropy 2018, 20, 574. [Google Scholar] [CrossRef]
- Kim, E.; Lewis, P. Information length in quantum systems. J. Stat. Mech. Theory Exp. 2018, 2018, 043106. [Google Scholar] [CrossRef]
- Amari, S.; Nagaoka, H. Methods of Information Geometry; American Mathematical Society: Providence, RI, USA, 2000. [Google Scholar]
- Filatova, T.; Popović, N.; Grima, R. Modulation of nuclear and cytoplasmic mRNA fluctuations by time-dependent stimuli: Analytical distributions. Math. Biosci. 2022, 347, 108828. [Google Scholar] [CrossRef]
- Li, R.; Turaga, P.; Srivastava, A.; Chellappa, R. Differential geometric representations and algorithms for some pattern recognition and computer vision problems. Pattern Recognit. Lett. 2014, 43, 3–16. [Google Scholar] [CrossRef]
- Zhang, Z.; Sun, H.; Zhong, F. Natural gradient-projection algorithm for distribution control. Optim. Control. Appl. Methods 2009, 30, 495–504. [Google Scholar] [CrossRef]
- Duan, X.; Sun, H.; Peng, L.; Zhao, X. A natural gradient descent algorithm for the solution of discrete algebraic Lyapunov equations based on the geodesic distance. Appl. Math. Comput. 2013, 219, 9899–9905. [Google Scholar] [CrossRef]
- Amari, S.; Kurata, K.; Nagaoka, H. Information geometry of Boltzmann machines. IEEE Trans. Neural Netw. 1992, 3, 260–271. [Google Scholar] [CrossRef]
- Yang, Z.; Laaksonen, J. Principal whitened gradient for information geometry. Neural Netw. 2008, 21, 232–240. [Google Scholar] [CrossRef]
- Desjardins, G.; Pascanu, R.; Courville, A.; Bengio, Y. Metric-free natural gradient for joint-training of boltzmann machines. arXiv 2013, arXiv:1301.3545. [Google Scholar]
- Sun, K.; Nielsen, F. Relative natural gradient for learning large complex models. arXiv 2016, arXiv:1606.06069. [Google Scholar]
- Berezhkovskii, A.M.; Coppey, M.; Shvartsman, S.Y. Signaling gradients in cascades of two-state reaction-diffusion systems. Proc. Natl. Acad. Sci. USA 2009, 106, 1087–1092. [Google Scholar] [CrossRef] [PubMed]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, Z.; Su, Y.-H.; Yin, H. Quantifying Information of Dynamical Biochemical Reaction Networks. Entropy 2023, 25, 887. https://doi.org/10.3390/e25060887
Jiang Z, Su Y-H, Yin H. Quantifying Information of Dynamical Biochemical Reaction Networks. Entropy. 2023; 25(6):887. https://doi.org/10.3390/e25060887
Chicago/Turabian StyleJiang, Zhiyuan, You-Hui Su, and Hongwei Yin. 2023. "Quantifying Information of Dynamical Biochemical Reaction Networks" Entropy 25, no. 6: 887. https://doi.org/10.3390/e25060887
APA StyleJiang, Z., Su, Y.-H., & Yin, H. (2023). Quantifying Information of Dynamical Biochemical Reaction Networks. Entropy, 25(6), 887. https://doi.org/10.3390/e25060887






