Threshold Cascade Dynamics in Coevolving Networks
Abstract
1. Introduction
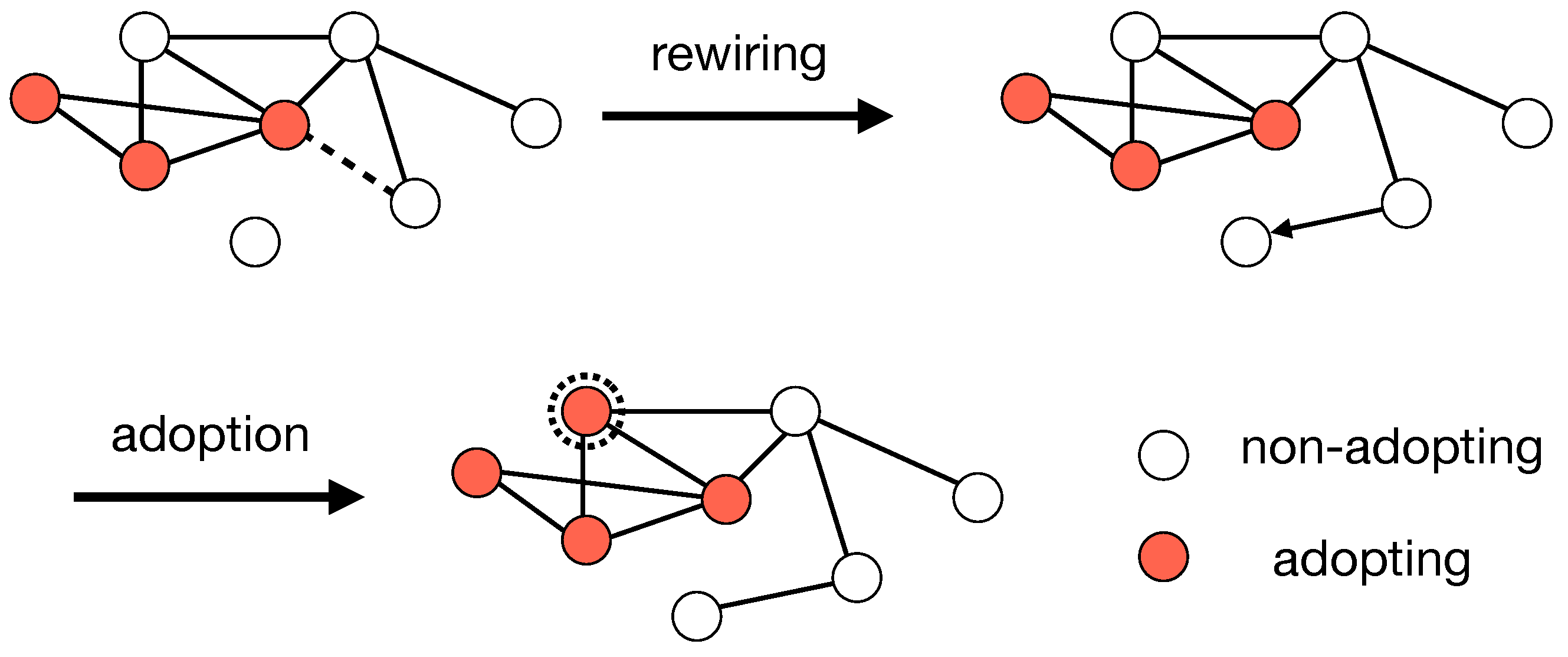
2. Model
3. Results
3.1. On a Static Network
3.2. Segregation of Adopting Nodes via Link Rewiring
3.3. Phase Diagram for Global Cascades
3.4. Non-Monotonicity in the Size of the Global Cascade
3.5. Structure of Rewired Networks
3.6. Mean-Field Approximations
4. Summary and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Granovetter, M. Threshold models of collective behavior. Am. J. Soc. 1978, 83, 1420–1443. [Google Scholar] [CrossRef]
- Watts, D.J. A simple model of global cascades on random networks. Proc. Natl. Acad. Sci. USA 2002, 99, 5766. [Google Scholar] [CrossRef]
- Centola, D.; Macy, M. Complex Contagions and the Weakness of Long Ties. SSRN Electron. J. 2007, 113, 702. [Google Scholar] [CrossRef]
- Centola, D. How Behavior Spreads: The Science of Complex Contagions How Behavior Spreads: The Science of Complex Contagions; Princeton University Press: Princeton, NJ, USA, 2018. [Google Scholar]
- Battiston, F.; Amico, E.; Barrat, A.; Bianconi, G.; de Arruda, G.F.; Franceschiello, B.; Iacopini, I.; Kéfi, S.; Latora, V.; Moreno, Y.; et al. The physics of higher-order interactions in complex systems. Nat. Phys. 2021, 17, 1093–1098. [Google Scholar] [CrossRef]
- Centola, D. The Spread of Behavior in an Online Social Network Experiment. Science 2010, 329, 5996. [Google Scholar] [CrossRef]
- Levine, J.M.; Bascompte, J.; Adler, P.B.; Allesina, S. Beyond pairwise mechanisms of species coexistence in complex communities. Nature 2017, 546, 56–64. [Google Scholar] [CrossRef]
- Hébert-Dufresne, L.; Scarpino, S.V.; Young, J.-G. Macroscopic patterns of interacting contagions are indistinguishable from social reinforcement. Nat. Phys. 2020, 16, 426–431. [Google Scholar] [CrossRef]
- Schelling, T. Hockey helmets, concealed weapons, and daylight saving: A study of binary choices with externalities. Confl. Resolut. 1973, 17, 381–428. [Google Scholar] [CrossRef]
- Gleeson, J.P.; Cahalane, D.J. Seed size strongly affects cascades on random networks. Phys. Rev. E 2007, 75, 056103. [Google Scholar] [CrossRef]
- Karsai, M.; Iñiguez, G.; Kaski, K.; Kertész, J. Complex contagion process in spreading of online innovation. J. R. Soc. Interface 2014, 11, 20140694. [Google Scholar] [CrossRef]
- Nematzadeh, A.; Ferrara, E.; Flammini, A.; Ahn, Y.-Y. Optimal Network Modularity for Information Diffusion. Phys. Rev. Lett. 2014, 113, 088701. [Google Scholar] [CrossRef]
- Auer, S.; Heitzig, J.; Kornek, U.; Schöll, E.; Kurths, J. The Dynamics of Coalition Formation on Complex Networks. Sci. Rep. 2015, 5, 13386. [Google Scholar] [CrossRef]
- Kook, J.; Choi, J.; Min, B. Double transitions and hysteresis in heterogeneous contagion processes. Phys. Rev. E 2021, 104, 044306. [Google Scholar] [CrossRef]
- Pastor-Satorras, R.; Castellano, C.; Van Mieghem, P.; Vespignani, A. Epidemic processes in complex networks. Rev. Mod. Phys. 2015, 87, 925–979. [Google Scholar] [CrossRef]
- Friedman, N.; Ito, S.; Brinkman, B.A.; Shimono, M.; DeVille, R.L.; Dahmen, K.A.; Beggs, J.M.; Butler, T.C. Universal Critical Dynamics in High Resolution Neuronal Avalanche Data. Phys. Rev. Lett. 2012, 108, 208102. [Google Scholar] [CrossRef]
- Lee, K.-M.; Yang, J.-S.; Kim, G.; Lee, J.; Goh, K.-I.; Kim, I.-M. Impact of the Topology of Global Macroeconomic Network on the Spreading of Economic Crises. PLoS ONE 2011, 6, e18443. [Google Scholar] [CrossRef]
- Motter, A.E.; Lai, Y.-C. Cascade-based attacks on complex networks. Phys. Rev. E 2002, 66, 065102. [Google Scholar] [CrossRef]
- Hackett, A.; Melnik, S.; Gleeson, J. Cascades on a class of clustered random networks. Phys. Rev. E 2011, 83, 056107. [Google Scholar] [CrossRef]
- Lee, K.-M.; Brummitt, C.D.; Goh, K.-I. Threshold cascades with response heterogeneity in multiplex networks. Phys. Rev. E 2014, 90, 062816. [Google Scholar] [CrossRef]
- Min, B.; Miguel, M.S. Competition and dual users in complex contagion processes. Sci. Rep. 2018, 8, 14580. [Google Scholar] [CrossRef]
- Abella, D.; Miguel, M.S.; Ramasco, J.J. Aging in binary-state models: The Threshold model for complex contagion. Phys. Rev. E 2023, 107, 024101. [Google Scholar] [CrossRef]
- Lee, K.-M.; Lee, S.; Min, B.; Goh, K.-I. Threshold cascade dynamics on signed random networks. Chaos Solitons Fractals 2023, 168, 113118. [Google Scholar] [CrossRef]
- Diaz-Diaz, F.; Miguel, M.S.; Meloni, S. Echo chambers and information transmission biases in homophilic and heterophilic networks. Sci. Rep. 2022, 12, 9350. [Google Scholar] [CrossRef]
- Czaplicka, A.; Toral, R.; Miguel, M.S. Competition of simple and complex adoption on interdependent networks. Phys. Rev. E 2016, 94, 062301. [Google Scholar] [CrossRef]
- Min, B.; Miguel, M.S. Competing contagion processes: Complex contagion triggered by simple contagion. Sci. Rep. 2018, 8, 10422. [Google Scholar] [CrossRef]
- Holme, P.; Saramaki, J. Temporal Networks; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Gross, T.; Sayama, H. Adaptive Networks: Theory, Models and Applications; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Gross, T.; Blasius, B. Adaptive coevolutionary networks: A review. J. R. Soc. Interface 2007, 5, 259–271. [Google Scholar] [CrossRef]
- Funk, S.; Gilad, E.; Watkins, C.; Jansen, V.A.A. The spread of awareness and its impact on epidemic outbreaks. Proc. Natl. Acad. Sci. USA 2009, 106, 6872–6877. [Google Scholar] [CrossRef]
- Holme, P.; Newman, M.E.J. Nonequilibrium phase transition in the coevolution of networks and opinions. Phys. Rev. E 2006, 74, 056108. [Google Scholar] [CrossRef]
- Vazquez, F.; Eguíluz, V.M.; Miguel, M.S. Generic Absorbing Transition in Coevolution Dynamics. Phys. Rev. Lett. 2008, 100, 108702. [Google Scholar] [CrossRef]
- Yi, S.D.; Baek, S.K.; Zhu, C.-P.; Kim, B.J. Phase transition in a coevolving network of conformist and constrarian voters. Phys. Rev. E 2013, 87, 012806. [Google Scholar] [CrossRef]
- Diakonova, M.; Miguel, M.S.; Eguíluz, V.M. Absorbing and shattered fragmentation transitions in multilayer coevolution. Phys. Rev. E 2014, 89, 062818. [Google Scholar] [CrossRef]
- Diakonova, M.; Eguíluz, V.M.; Miguel, M.S. Noise in coevolving networks. Phys. Rev. E 2015, 92, 032803. [Google Scholar] [CrossRef]
- Min, B.; Miguel, M.S. Fragmentation transitions in a coevolving nonlinear voter model. Sci. Rep. 2017, 7, 12864. [Google Scholar] [CrossRef]
- Raducha, T.; Min, B.; Miguel, M.S. Coevolving nonlinear voter model with triadic closure. EPL 2018, 124, 30001. [Google Scholar] [CrossRef]
- Min, B.; Miguel, M.S. Multilayer coevolution dynamics of the nonlinear voter model. New J. Phys. 2019, 21, 035004. [Google Scholar] [CrossRef]
- Raducha, T.; Wilinski, M.; Gubiec, T.; Stanley, H.E. Statistical mechanics of a coevolving spin system. Phys. Rev. E 2018, 98, 030301. [Google Scholar] [CrossRef]
- Mandrà, S.; Fortunato, S.; Castellano, C. Coevolution of Glauber-like Ising dynamics and topology. Phys. Rev. E 2009, 80, 056105. [Google Scholar] [CrossRef] [PubMed]
- Fu, F.; Wang, L. Coevolutionary dynamics of opinions and networks: From diversity to uniformity. Phys. Rev. E 2008, 78, 016104. [Google Scholar] [CrossRef]
- Su, J.; Liu, B.; Li, Q.; Ma, H. Coevolution of Opinions and Directed Adaptive Networks in a Social Group. J. Artif. Soc. Soc. Simul. 2014, 17, 4. [Google Scholar] [CrossRef]
- Gross, T.; D’lima, C.J.D.; Blasius, B. Epidemic Dynamics on an Adaptive Network. Phys. Rev. Lett. 2006, 96, 208701. [Google Scholar] [CrossRef] [PubMed]
- Marceau, V.; Noël, P.-A.; Hébert-Dufresne, L.; Allard, A.; Dubé, L.J. Adaptive networks: Coevolution of disease and topology. Phys. Rev. E 2010, 82, 036116. [Google Scholar] [CrossRef] [PubMed]
- Shaw, L.B.; Schwartz, I.B. Fluctuating epidemics on adaptive networks. Phys. Rev. E 2008, 77, 066101. [Google Scholar] [CrossRef] [PubMed]
- Vazquez, F.; Gonzalez-Avella, J.C.; Eguiluz, V.M.; San Miguel, M. Time scale competition leading to fragmentation and recombination transitions in the co-evolution of network and states. Phys. Rev. E 2007, 76, 046120. [Google Scholar] [CrossRef] [PubMed]
- Centola, D.; González-Avella, J.C.; Eguíluz, V.M.; Miguel, M.S. Homophily, Cultural Drift, and the Co-Evolution of Cultural Groups. J. Confl. Resolut. 2007, 51, 905–929. [Google Scholar] [CrossRef]
- Casado, M.A.G.; Sánchez, A.; Miguel, M.S. Network coevolution drives segregation and enhances Pareto optimal equilibrium selection in coordination games. Sci. Rep. 2023, 13, 2866. [Google Scholar] [CrossRef]
- Coelho, F.C.; Codeco, C.T. Dynamic modeling of vaccinating behavior as a function of individual beliefs. PLoS Comput. Biol. 2009, 5, e1000425. [Google Scholar] [CrossRef]
- Granell, C.; Gómez, S.; Arenas, A. Dynamical Interplay between Awareness and Epidemic Spreading in Multiplex Networks. Phys. Rev. Lett. 2013, 111, 128701. [Google Scholar] [CrossRef]
- Pires, M.A.; Oestereich, A.L.; Crokidakis, N.; Queirós, S.M.D. Antivax movement and epidemic spreading in the era of social networks: Nonmonotonic effects, bistability, and network segregation. Phys. Rev. E 2021, 104, 034302. [Google Scholar] [CrossRef]
- Fang, F.; Ma, J.; Li, Y. The coevolution of the spread of a disease and competing opinions in multiplex networks. Chaos Solitons Fractals 2023, 170, 113376. [Google Scholar] [CrossRef]
- Lambiotte, R.; González-Avella, J.C. On co-evolution and the importance of initial conditions. Physics A 2010, 390, 392–397. [Google Scholar] [CrossRef]
- Karimi, F.; Holme, P. Threshold model of cascades in empirical temporal networks. Physics A 2013, 392, 3476–3483. [Google Scholar] [CrossRef]
- Rosenthal, S.B.; Twomey, C.R.; Hartnett, A.T.; Wu, H.S.; Couzin, I.D. Revealing the hidden networks of interaction in mobile animal groups allows prediction of complex behavioral contagion. Proc. Natl. Acad. Sci. USA 2015, 112, 4690–4695. [Google Scholar] [CrossRef] [PubMed]
- Karsai, M.; Iñiguez, G.; Kikas, R.; Kaski, K.; Kertész, J. Local cascades induced global contagion: How heterogeneous thresholds, exogenous effects, and unconcerned behaviour govern online adoption spreading. Sci. Rep. 2016, 6, 27178. [Google Scholar] [CrossRef] [PubMed]
- Mønsted, B.; Sapieżyński, P.; Ferrara, E.; Lehmann, S. Evidence of complex contagion of information in social media: An experiment using Twitter bots. PLoS ONE 2017, 12, e0184148. [Google Scholar] [CrossRef] [PubMed]
- Unicomb, S.; Iñiguez, G.; Karsai, M. Threshold driven contagion on weighted networks. Sci. Rep. 2018, 8, 1–10. [Google Scholar] [CrossRef]
- Guibeault, D.; Centola, D. Topological measures for identifying and predicting the spread of complex contagions. Nat. Commun. 2021, 12, 4430. [Google Scholar] [CrossRef]
- Aral, S.; Nicolaides, C. Exercise contagion in a global social network. Nat. Commun. 2017, 8, 14753. [Google Scholar] [CrossRef]
- McPherson, M.; Smith-Lovin, L.; Cook, J.M. Birds of a Feather: Homophily in Social Networks. Annu. Rev. Sociol. 2001, 27, 415–444. [Google Scholar] [CrossRef]
- Lee, E.; Karimi, F.; Wagner, C.; Jo, H.-H.; Strohmaier, M.; Galesic, M. Homophily and minority-group size explain perception biases in social networks. Nat. Hum. Behav. 2019, 3, 1078–1087. [Google Scholar] [CrossRef] [PubMed]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Min, B.; San Miguel, M. Threshold Cascade Dynamics in Coevolving Networks. Entropy 2023, 25, 929. https://doi.org/10.3390/e25060929
Min B, San Miguel M. Threshold Cascade Dynamics in Coevolving Networks. Entropy. 2023; 25(6):929. https://doi.org/10.3390/e25060929
Chicago/Turabian StyleMin, Byungjoon, and Maxi San Miguel. 2023. "Threshold Cascade Dynamics in Coevolving Networks" Entropy 25, no. 6: 929. https://doi.org/10.3390/e25060929
APA StyleMin, B., & San Miguel, M. (2023). Threshold Cascade Dynamics in Coevolving Networks. Entropy, 25(6), 929. https://doi.org/10.3390/e25060929






