A New Thermodynamic Model to Approximate Properties of Subcritical Liquids
Abstract
1. Introduction
2. Materials and Methods
2.1. Development of the Model
2.1.1. Caloric Equations
2.1.2. Constant Pressure Specific Thermal Capacity
2.1.3. Entropy Equations
2.2. Calculation of Properties According to the Model
2.2.1. Specific Enthalpy
2.2.2. Specific Internal Energy
2.2.3. Specific Entropy
2.3. Applications of the Model
- For the approximation of compressed liquid property values when saturation values are known.
- For the calculation of the specific internal energy , specific enthalpy and specific entropy of any incompressible system with data of specific volume and specific thermal capacity at a reference pressure as a function of temperature.
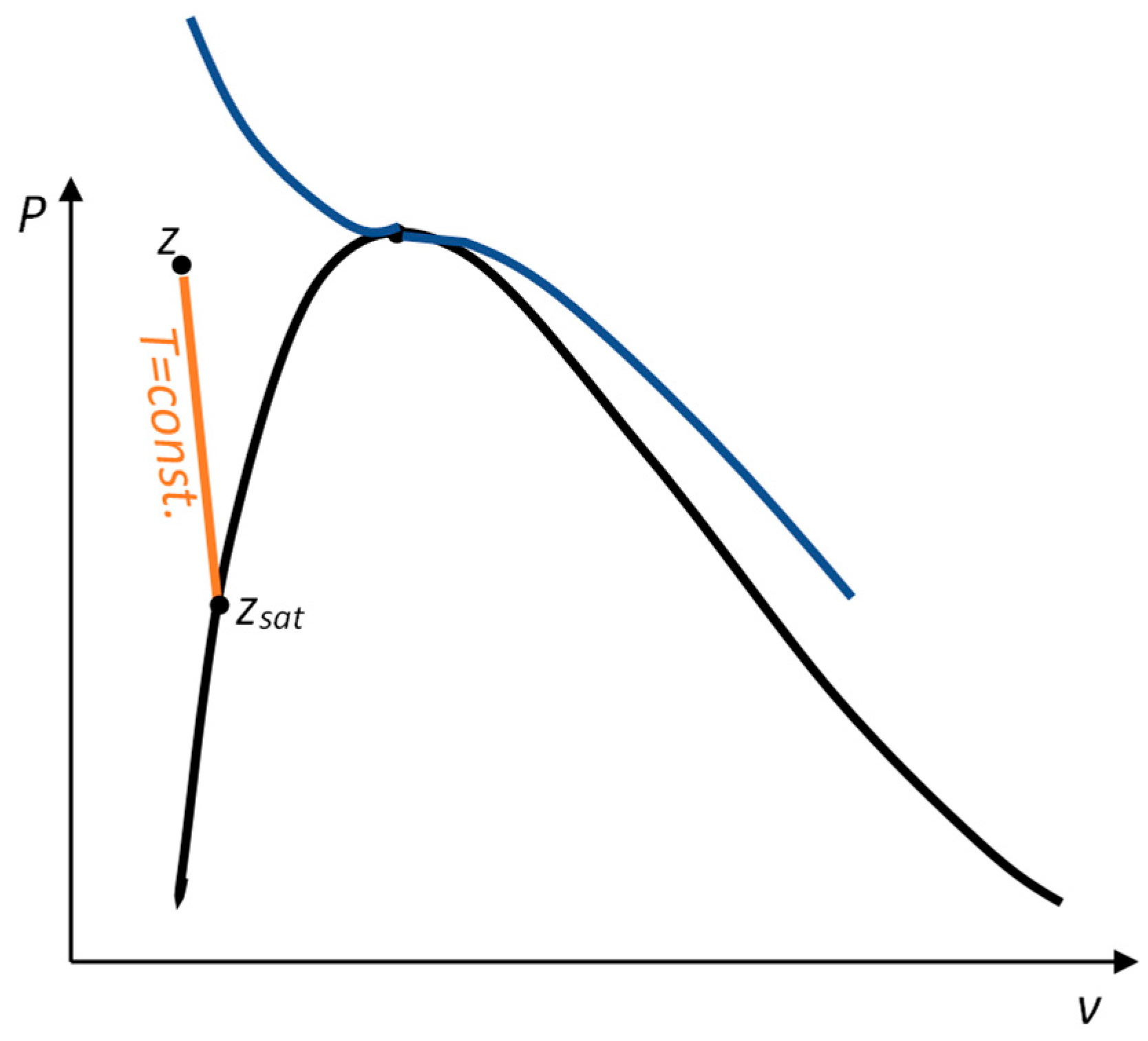
2.3.1. Approximation of Compressed Liquid Properties from Saturation
2.3.2. Calculation of of an Incompressible System
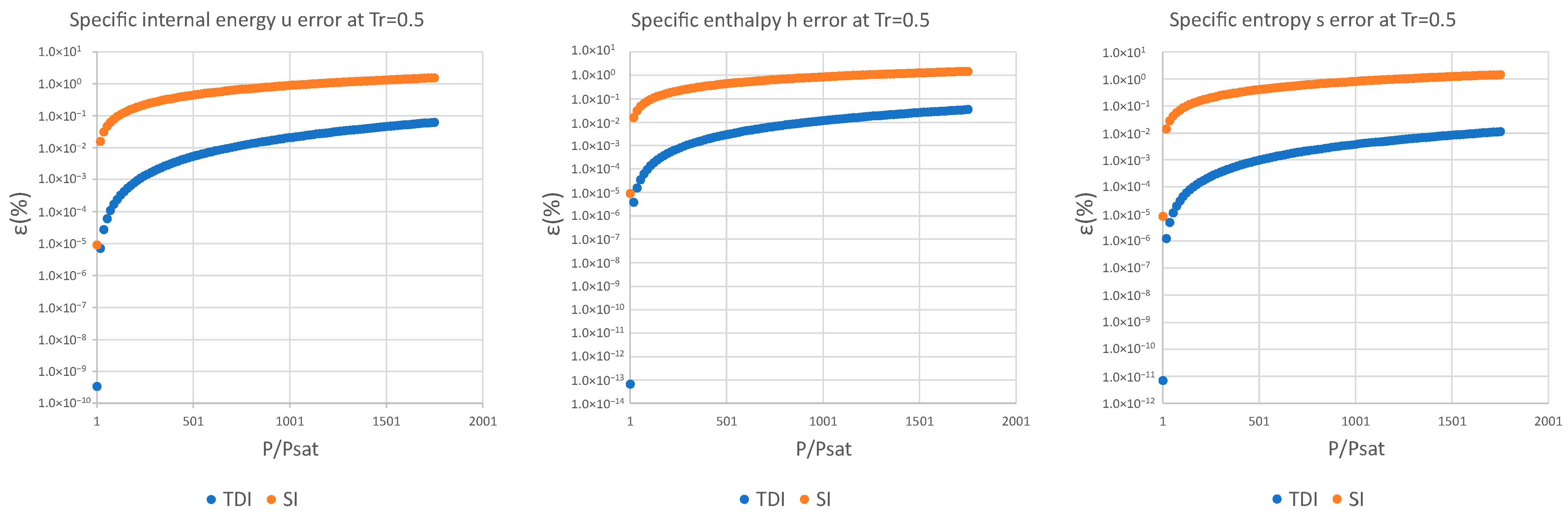
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A
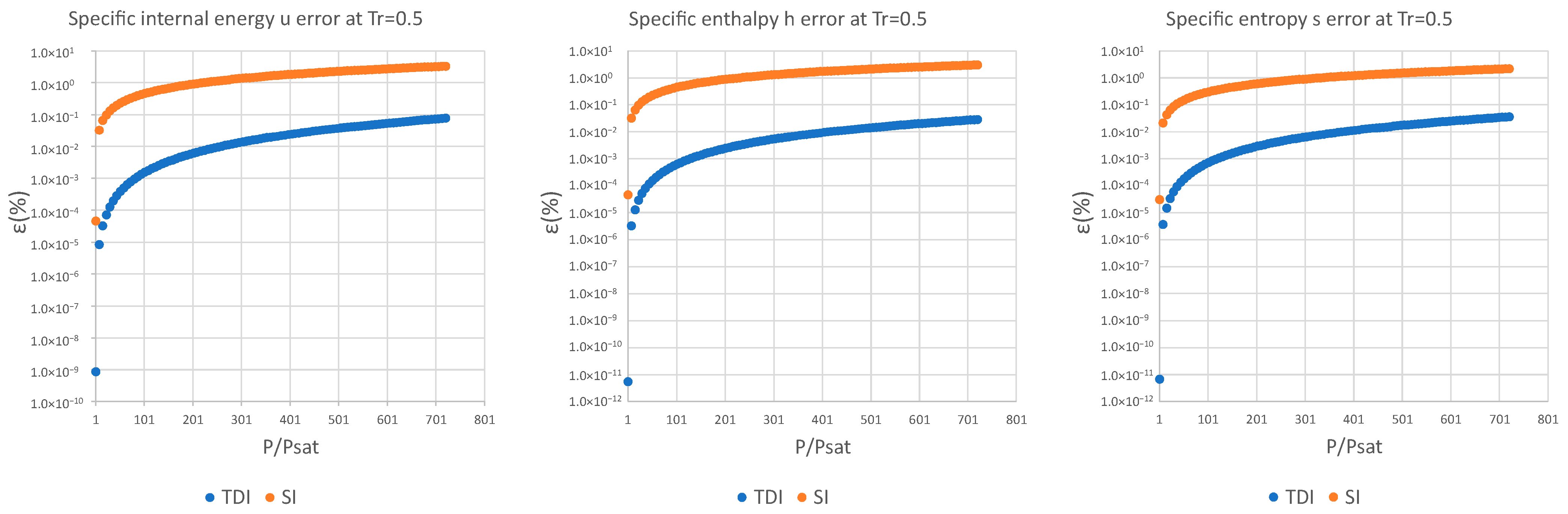
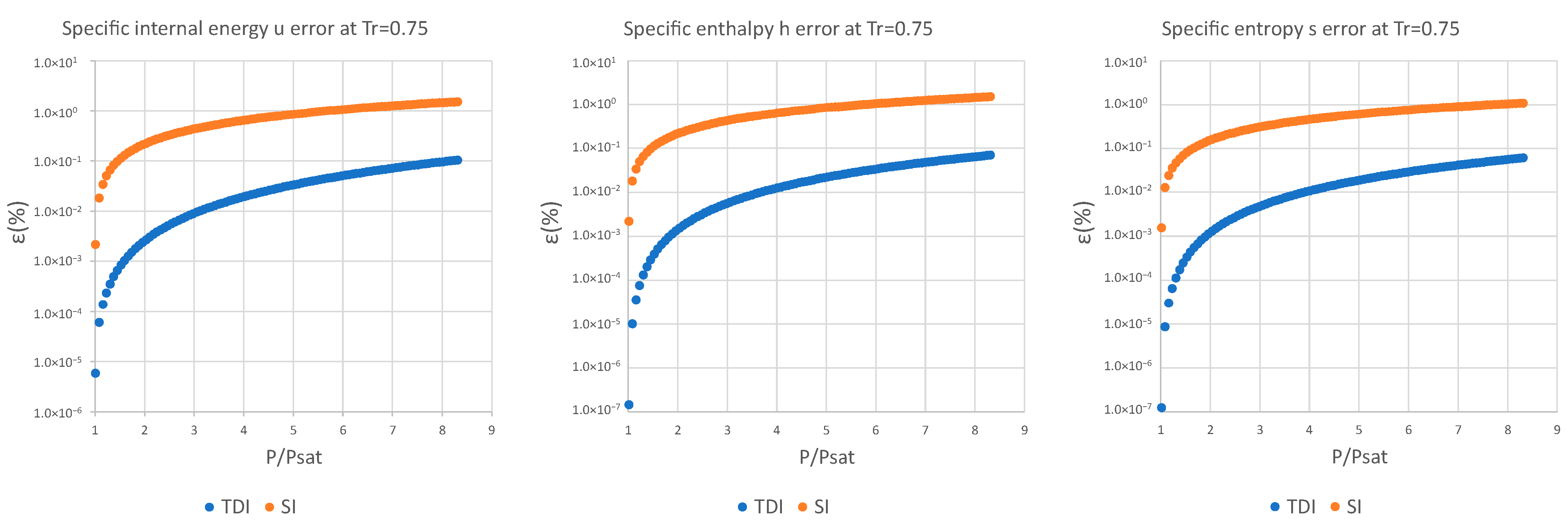
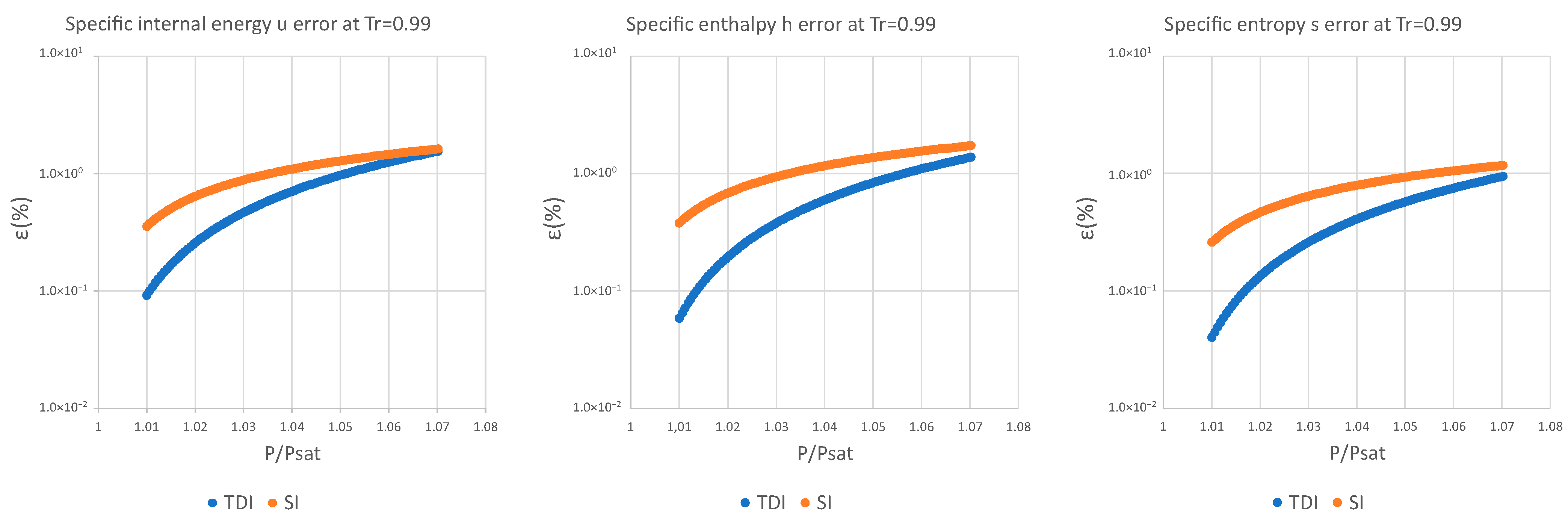
| (%) | (%) | (%) | (%) | (%) | (%) | |
|---|---|---|---|---|---|---|
| 0.3 | 1.94 × 10−13 | 1.25 × 10−12 | 3.48 × 10−13 | 1.14 × 10−2 | 1.90 × 10−3 | 9.48 × 10−3 |
| 0.5 | 8.82 × 10−10 | 5.63 × 10−12 | 6.96 × 10−12 | 7.72 × 10−2 | 2.87 × 10−2 | 3.67 × 10−2 |
| 0.6 | 5.68 × 10−8 | 6.56 × 10−10 | 6.91 × 10−10 | 6.06 × 10−2 | 3.09 × 10−2 | 3.42 × 10−2 |
| 0.75 | 5.84 × 10−6 | 1.47 × 10−7 | 1.25 × 10−7 | 1.04 × 10−1 | 6.98 × 10−2 | 6.12 × 10−2 |
| 0.9 | 3.60 × 10−4 | 3.00 × 10−5 | 2.19 × 10−5 | 3.13 × 10−1 | 2.51 × 10−1 | 1.85 × 10−1 |
| 0.99 | 9.14 × 10−2 | 5.83 × 10−2 | 4.02 × 10−2 | 1.55 × 100 | 1.38 × 100 | 9.48 × 10−1 |

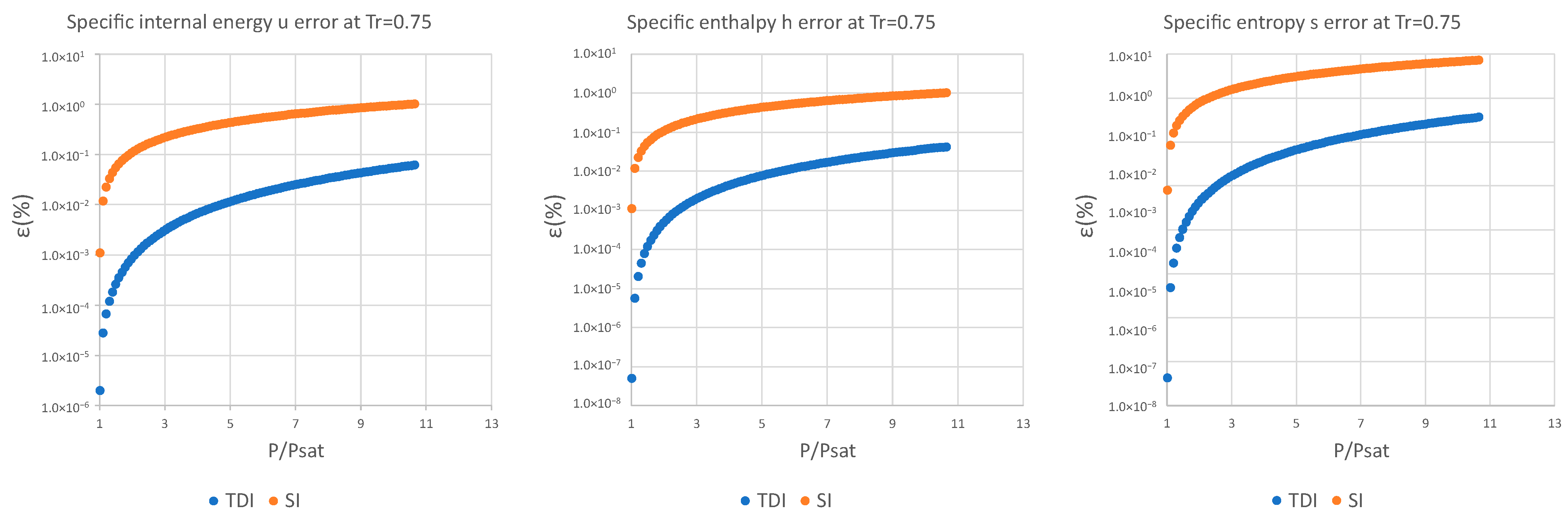
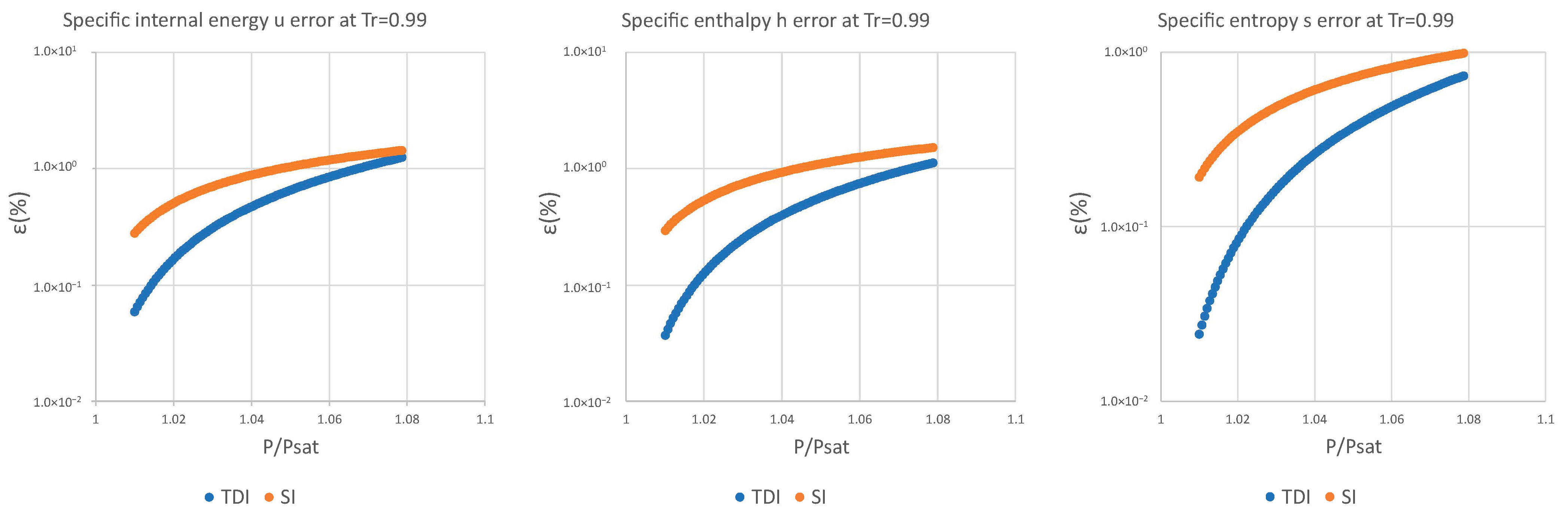
| (%) | (%) | (%) | (%) | (%) | (%) | |
|---|---|---|---|---|---|---|
| 0.5 | 3.10 × 10−11 | 6.33 × 10−14 | 1.94 × 10−13 | 1.82 × 10−2 | 7.56 × 10−3 | 1.21 × 10−2 |
| 0.6 | 7.61 × 10−9 | 9.06 × 10−11 | 1.04 × 10−10 | 2.55 × 10−2 | 1.36 × 10−2 | 1.61 × 10−2 |
| 0.75 | 1.98 × 10−6 | 5.04 × 10−8 | 4.33 × 10−8 | 6.13 × 10−2 | 4.22 × 10−2 | 3.70 × 10−2 |
| 0.9 | 1.99 × 10−4 | 1.62 × 10−5 | 1.14 × 10−5 | 2.28 × 10−1 | 1.85 × 10−1 | 1.32 × 10−1 |
| 0.99 | 5.89 × 10−2 | 3.70 × 10−2 | 2.43 × 10−2 | 1.25 × 100 | 1.12 × 100 | 7.35 × 10−1 |
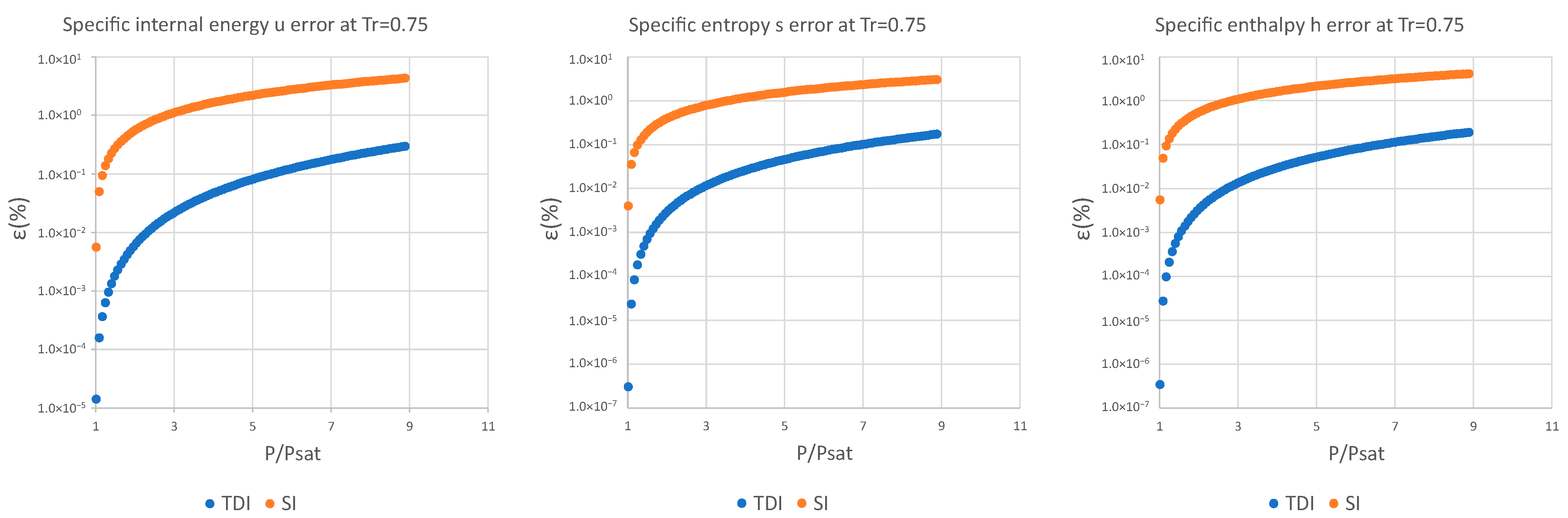

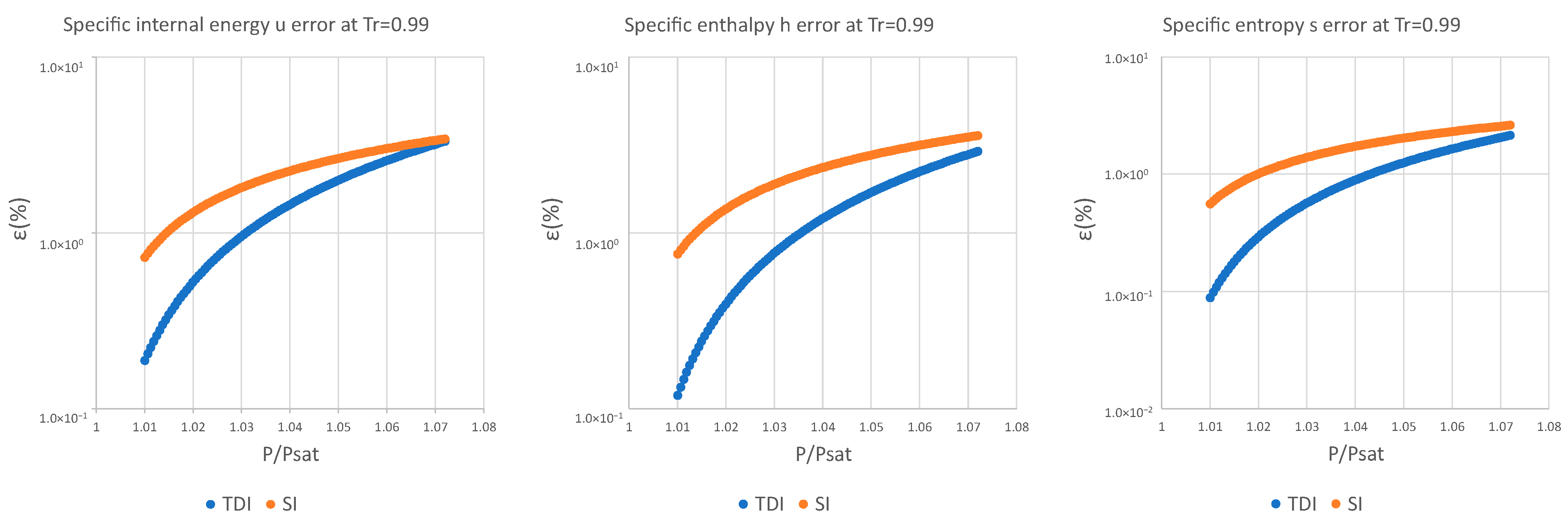
| (%) | (%) | (%) | (%) | (%) | (%) | |
|---|---|---|---|---|---|---|
| 0.75 | 1.41 × 10−5 | 3.48 × 10−7 | 3.04 × 10−7 | 2.97 × 10−1 | 1.92 × 10−1 | 1.75 × 10−1 |
| 0.8 | 5.07 × 10−5 | 1.70 × 10−6 | 1.42 × 10−6 | 3.62 × 10−1 | 2.52 × 10−1 | 2.19 × 10−1 |
| 0.85 | 1.86 × 10−4 | 9.23 × 10−6 | 7.40 × 10−6 | 4.89 × 10−1 | 3.63 × 10−1 | 3.00 × 10−1 |
| 0.9 | 7.83 × 10−4 | 6.50 × 10−5 | 5.01 × 10−5 | 7.35 × 10−1 | 5.77 × 10−1 | 4.53 × 10−1 |
| 0.95 | 5.11 × 10−3 | 9.14 × 10−4 | 6.85 × 10−4 | 1.29 × 100 | 1.07 × 100 | 8.06 × 10−1 |
| 0.99 | 1.88 × 10−1 | 1.19 × 10−1 | 8.86 × 10−2 | 3.31 × 100 | 2.91 × 100 | 2.15 × 100 |
References
- Boukelia, T.E.; Mecibah, M.S.; Kumar, B.N.; Reddy, K.S. Investigation of solar parabolic trough power plants with and without integrated TES (thermal energy storage) and FBS (fuel backup system) using thermic oil and solar salt. Energy 2015, 88, 292–303. [Google Scholar] [CrossRef]
- Bruch, A.; Fourmigué, J.F.; Couturier, R. Experimental and numerical investigation of a pilot-scale thermal oil packed bed thermal storage system for CSP power plant. Sol. Energy 2014, 105, 116–125. [Google Scholar] [CrossRef]
- Liu, M.; Tay, N.S.; Bell, S.; Belusko, M.; Jacob, R.; Will, G.; Saman, W.; Bruno, F. Review on concentrating solar power plants and new developments in high temperature thermal energy storage technologies. Renew. Sustain. Energy Rev. 2016, 53, 1411–1432. [Google Scholar] [CrossRef]
- Kuravi, S.; Trahan, J.; Goswami, D.Y.; Rahman, M.M.; Stefanakos, E.K. Thermal energy storage technologies and systems for concentrating solar power plants. Prog. Energy Combust. Sci. 2013, 39, 285–319. [Google Scholar] [CrossRef]
- Moran, M.J.; Shapiro, H.N. Fundamentals of Engineering Thermodynamics; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Wark, K.; Richards, D.E. Termodynamics; Mc. Graw Hill: New York, NY, USA, 1998. [Google Scholar]
- Çengel, Y.A.; Boles, M.A. Termodynamics: An Engineering Approach; Mc. Graw Hill: New York, NY, USA, 2014. [Google Scholar]
- Spencer, C.F.; Danner, R.P. Improved Equation for Prediction of Saturated Liquid Density. J. Chem. Eng. Data 1972, 17, 236–241. [Google Scholar] [CrossRef]
- Péneloux, A.; Rauzy, E.; Fréze, R. A Consistent Correction for Redlich-Kwong-Soave Volumes. Fluid Phase Equilibria 1982, 8, 7–23. [Google Scholar] [CrossRef]
- Sangi, R.; Martínez Martín, P.; Müller, D. Thermoeconomic analysis of a building heating system. Energy 2016, 111, 351–363. [Google Scholar] [CrossRef]
- Kostic, M.M. Analysis of enthalpy approximation for compressed liquid water. J. Heat Transf. 2006, 128, 421–426. [Google Scholar] [CrossRef]
- Karimi, A.; Tan, I. A New Approach in Approximating Thermodynamics Properties in Compressed Liquid Region. In Proceedings of the ASME 2008 International Mechanical Engineering Congress and Exposition, Boston, MA, USA, 31 October–6 November 2008; pp. 481–492. [Google Scholar] [CrossRef]
- Bell, I.H.; Wronski, J.; Quoilin, S.; Lemort, V. Pure and Pseudo-pure Fluid Thermophysical Property Evaluation and the Open-Source Thermophysical Property Library CoolProp. Ind. Eng. Chem. Res. 2014, 53, 2498–2508. [Google Scholar] [CrossRef] [PubMed]
- Coolprop. Available online: http://www.coolprop.org/fluid_properties/Incompressibles.html#equations (accessed on 22 June 2023).



| … | … | … |
| (%) | (%) | (%) | (%) | (%) | (%) | |
|---|---|---|---|---|---|---|
| 0.45 | 9.98 × 10−11 | 2.11 × 10−13 | 6.32 × 10−11 | 2.42 × 10−3 | 2.24 × 10−1 | 1.38 × 10−1 |
| 0.5 | 3.46 × 10−10 | 6.90 × 10−14 | 7.02 × 10−12 | 6.26 × 10−2 | 3.50 × 10−2 | 1.15 × 10−2 |
| 0.6 | 3.33 × 10−8 | 1.63 × 10−10 | 2.72 × 10−10 | 7.79 × 10−2 | 2.34 × 10−2 | 4.33 × 10−2 |
| 0.75 | 5.23 × 10−6 | 1.09 × 10−7 | 1.03 × 10−7 | 1.52 × 10−1 | 9.65 × 10−2 | 9.42 × 10−2 |
| 0.9 | 4.26 × 10−4 | 3.41 × 10−5 | 2.59 × 10−5 | 5.05 × 10−1 | 4.05 × 10−1 | 3.12 × 10−1 |
| 0.99 | 1.31 × 10−1 | 8.45 × 10−2 | 6.04 × 10−2 | 2.76 × 100 | 2.48 × 100 | 1.77 × 100 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sánchez-Orgaz, S.; Varela, F.; Rodríguez, J.; González, C. A New Thermodynamic Model to Approximate Properties of Subcritical Liquids. Entropy 2023, 25, 1002. https://doi.org/10.3390/e25071002
Sánchez-Orgaz S, Varela F, Rodríguez J, González C. A New Thermodynamic Model to Approximate Properties of Subcritical Liquids. Entropy. 2023; 25(7):1002. https://doi.org/10.3390/e25071002
Chicago/Turabian StyleSánchez-Orgaz, Susana, Fernando Varela, Javier Rodríguez, and Celina González. 2023. "A New Thermodynamic Model to Approximate Properties of Subcritical Liquids" Entropy 25, no. 7: 1002. https://doi.org/10.3390/e25071002
APA StyleSánchez-Orgaz, S., Varela, F., Rodríguez, J., & González, C. (2023). A New Thermodynamic Model to Approximate Properties of Subcritical Liquids. Entropy, 25(7), 1002. https://doi.org/10.3390/e25071002







