Ergodic Measure and Potential Control of Anomalous Diffusion
Abstract
1. Introduction
2. Ergodic Convergence Properties
2.1. Finite-Time Scale Function
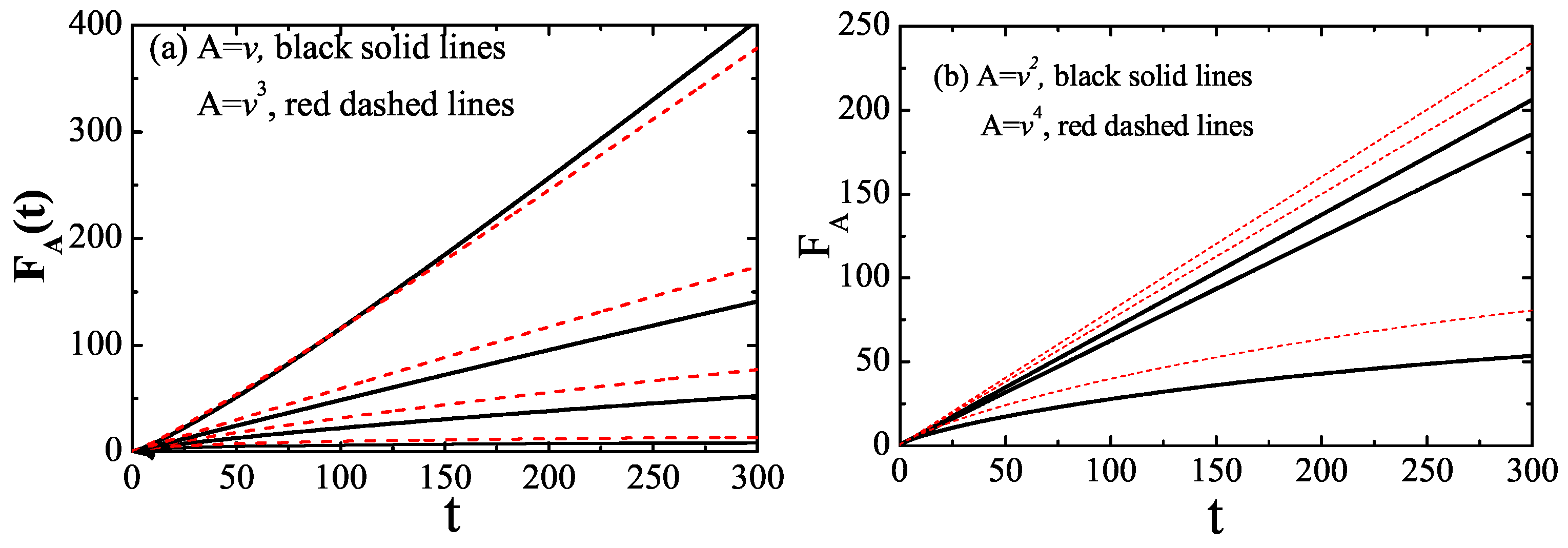
2.2. Normal Diffusive Case
2.3. Non-Ohmic Memory Case
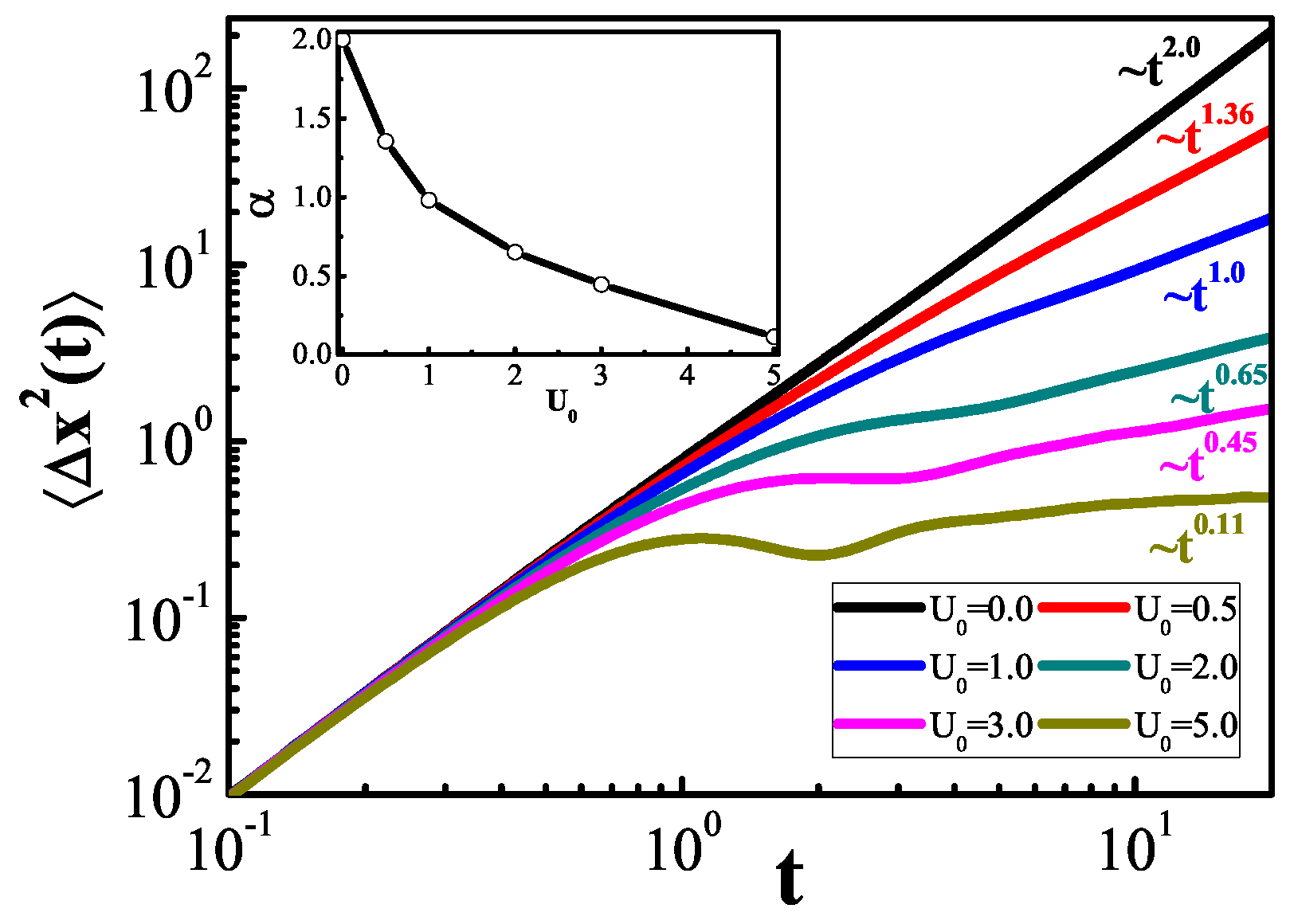
3. Anomalous Diffusion in Logarithmic Potential
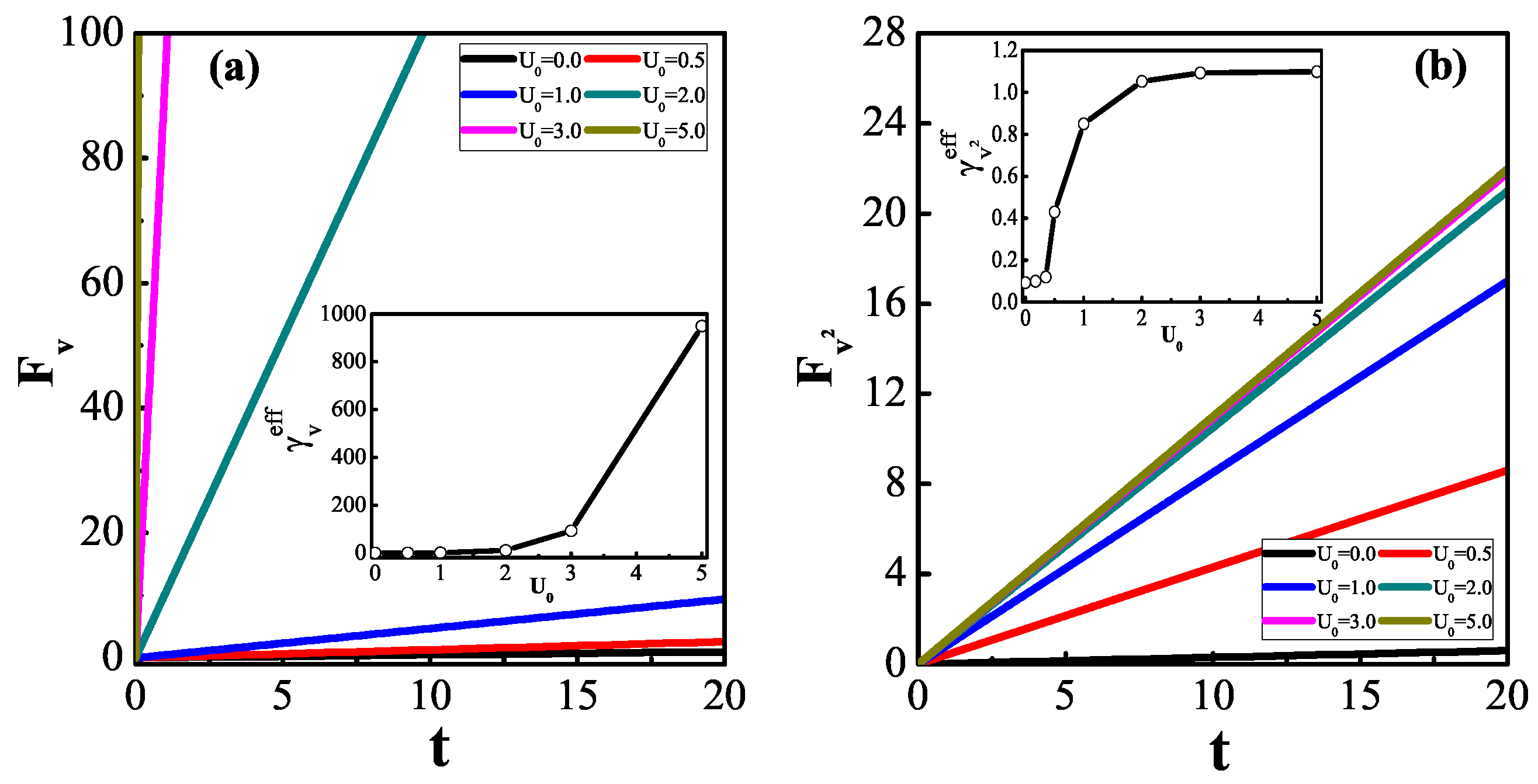
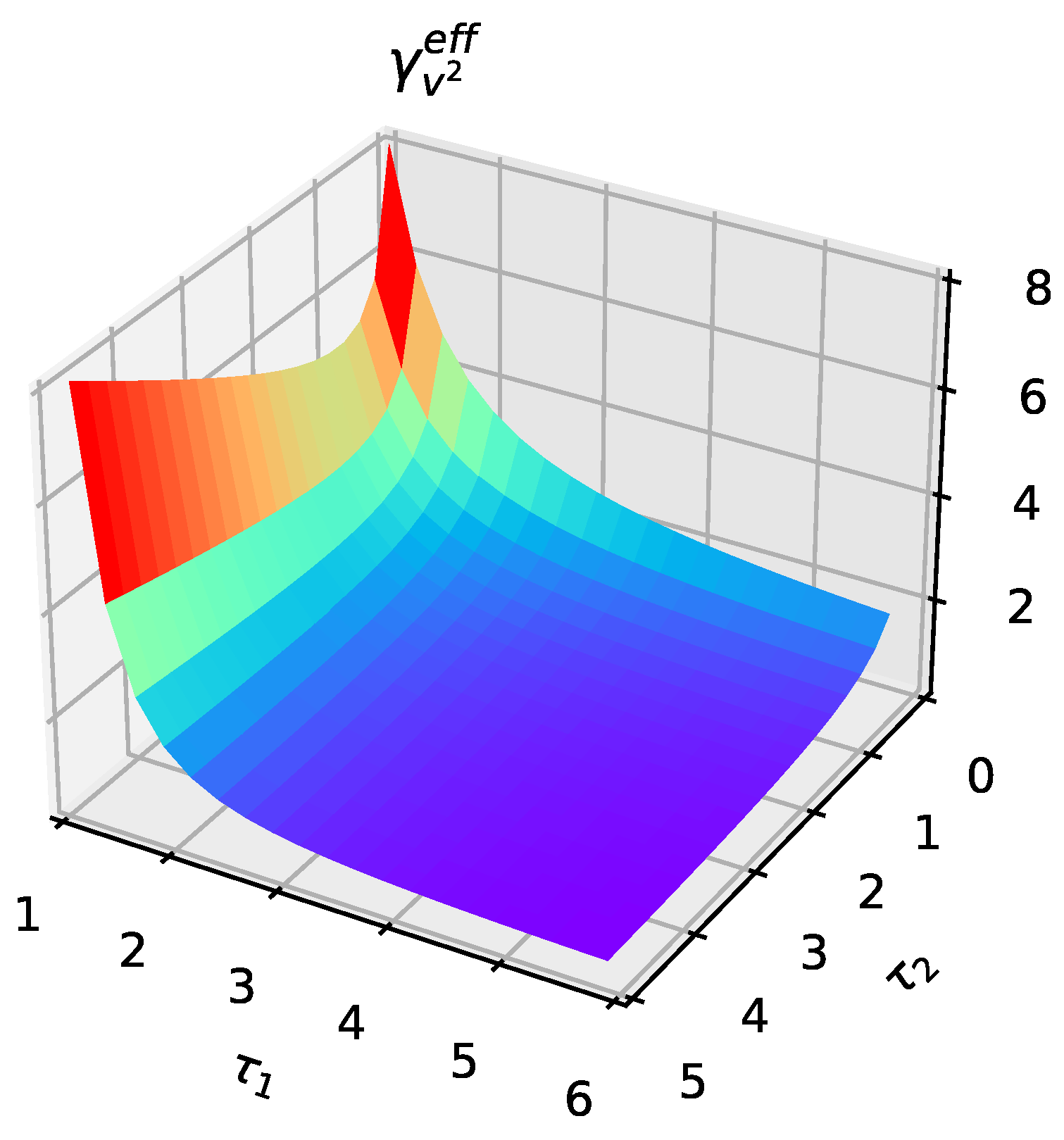
4. Ergodic Measurement
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Metzler, R.; Klafter, J. The random walk’s guide to anomalous diffusion: A fractional dynamics approach. Phys. Rep. 2000, 339, 1. [Google Scholar] [CrossRef]
- Marchesoni, F.; Taloni, A. Subdiffusion and Long-Time Anticorrelation in a Stochastic Single File. Phys. Rev. Lett. 2006, 97, 106101. [Google Scholar] [CrossRef] [PubMed]
- Bao, J.D. Generalization of the Kubo relation for confined motion and ergodicity breakdown. Phys. Rev. E 2020, 101, 062131. [Google Scholar] [CrossRef] [PubMed]
- Spiechowicz, J.; Marchenko, I.G.; Hänggi, P.; Łuczka, J. Diffusion Coefficient of a Brownian Particle in Equilibrium and Nonequilibrium: Einstein Model and Beyond. Entropy 2023, 25, 42. [Google Scholar] [CrossRef]
- Spiechowicz, J.; Łuczka, J. Diffusion in a biased washboard potential revisited. Phys. Rev. E 2020, 101, 032123. [Google Scholar] [CrossRef]
- Spiechowicz, J.; Łuczka, J. Conundrum of weak-noise limit for diffusion in a tilted periodic potential. Phys. Rev. E 2021, 104, 034104. [Google Scholar] [CrossRef]
- Hänggi, P.; Talkner, P.; Borkovec, M. Reaction Rate Theory: Fifty Years After Kramers. Rev. Mod. Phys. 1990, 62, 251. [Google Scholar] [CrossRef]
- Kneller, G.R. Communication: A scaling approach to anomalous diffusion. J. Chem. Phys. 2014, 141, 041105. [Google Scholar] [CrossRef]
- Stachura, S.; Kneller, G.R. Communication: Probing anomalous diffusion in frequency space. J. Chem. Phys. 2015, 143, 191103. [Google Scholar] [CrossRef]
- Bouchaud, J.P.; Georges, A.; Doussal, P. Le Towards a scaling theory of finite-time properties in dynamical systems. Europhys. Lett. 1998, 5, 119. [Google Scholar] [CrossRef]
- Thirumalai, D.; Mountain, R.D. Ergodic convergence properties of supercooled liquids and glasses. Phys. Rev. A 1990, 42, 4574. [Google Scholar] [CrossRef]
- Thirumalai, D.; Mountain, R.D. Activated dynamics, loss of ergodicity, and transport in supercoold liquids. Phys. Rev. E 1993, 47, 479. [Google Scholar] [CrossRef]
- Sagnella, D.E.; Straub, J.E.; Thirumalai, D. Time scales and pathways for kinetic energy relaxation in solvated proteins: Application to Carbonmonoxy myoglobin. J. Chem. Phys. 2000, 113, 7702. [Google Scholar] [CrossRef]
- Lapas, L.C.; Morgado, R.; Vainstein, M.H.; Rubi, J.M.; Oliveira, F.A. Khinchin Theorem and Anomalous Diffusion. Phys. Rev. Lett. 2008, 101, 230602. [Google Scholar] [CrossRef] [PubMed]
- Weron, A.; Magdziarz, M. Generalization of the Khinchin Theorem to Lévy Flights. Phys. Rev. Lett. 2010, 105, 260603. [Google Scholar] [CrossRef]
- Burov, S.; Metzler, R.; Barkai, E. Aging and nonergodicity beyond the Khinchin theorem. Proc. Natl. Acad. Sci. USA 2010, 107, 13228. [Google Scholar] [CrossRef] [PubMed]
- Barkai, E.; Radons, G.; Akimoto, T. Transitions in the Ergodicity of Subrecoil-Laser-Cooled Gases. Phys. Rev. Lett. 2021, 127, 140605. [Google Scholar] [CrossRef]
- Aghion, E.; Kessler, D.A.; Barkai, E. From Non-Normalizable Boltzmann-Gibbs Statistics to Infinite-Ergodic Theory. Phys. Rev. Lett. 2019, 122, 010601. [Google Scholar] [CrossRef]
- Lutz, E. Power-Law Tail Distribution and Nonergodicity. Phys. Rev. Lett. 2004, 93, 190602. [Google Scholar] [CrossRef]
- Jack, R.L. Ergodicity and large deviations in physical systems with stochastic dynamics. Eur. Phys. J. B 2020, 93, 74. [Google Scholar] [CrossRef]
- He, Y.; Burov, S.; Metzler, R.; Barkai, E. Random Time-Scale Invariant Diffusion and Transport Coefficients. Phys. Rev. Lett. 2008, 101, 058101. [Google Scholar] [CrossRef] [PubMed]
- Akimoto, T.; Barkai, E.; Saito, K. Universal Fluctuations of Single-Particle Diffusivity in a Quenched Environment. Phys. Rev. Lett. 2016, 117, 180602. [Google Scholar] [CrossRef] [PubMed]
- Bao, J.D.; Zhuo, Y.Z.; Oliveira, F.A.; Hänggi, P. Intermediate dynamics between Newton and Langevin. Phys. Rev. E 2006, 74, 061111. [Google Scholar] [CrossRef] [PubMed]
- Porrà, J.M.; Wang, K.-G.; Masoliver, J. Generalized Langevin equations: Anomalous diffusion and probability distributions. Phys. Rev. E 1996, 53, 5872. [Google Scholar] [CrossRef] [PubMed]
- Weiss, U. Quantum Dissipative Systems, 3rd ed.; World Scientific: Singapore, 2008. [Google Scholar]
- Pottier, N.; Mauger, A. Aging effects in free quantum Brownian motion. Physica A 2000, 282, 77. [Google Scholar] [CrossRef][Green Version]
- Pottier, N. Aging properties of an anomalously diffusion particle. Physica A 2003, 317, 371. [Google Scholar] [CrossRef]
- Deng, W.H.; Barkai, E. Eorodic properties of fractional Brownian-Langevin motion. Phys. Rev. E 2009, 79, 011112. [Google Scholar] [CrossRef] [PubMed]
- Lubelski, A.; Sokolov, I.M.; Klafter, J. Nonergodicity Minics Inhonmogeneity in single particle tracking. Phys. Rev. Lett. 2008, 100, 250602. [Google Scholar] [CrossRef] [PubMed]
- Bao, J.D.; Zhuo, Y.Z. Ballistic Diffusion Induced by a Thermal Brodband Noise. Phys. Rev. Lett. 2003, 91, 138104. [Google Scholar] [CrossRef]
- Siegle, P.; Goychuk, I.; Hänggi, P. Origin of Hyperdiffusion in Generalized Brownian Motion. Phys. Rev. Lett. 2010, 105, 100602. [Google Scholar] [CrossRef]
- Siegle, P.; Goychuk, I.; Talkner, P.; Hänggi, P. Markovian embedding of non-Markovian superdiffusion. Phys. Rev. E 2010, 81, 011136. [Google Scholar] [CrossRef] [PubMed]
- Kessler, D.A.; Barkai, E. Infinite-Covariant Density for Diffusion in Logarithmic Potentials and Optical Lattices. Phys. Rev. Lett. 2010, 105, 120602. [Google Scholar] [CrossRef] [PubMed]
- Campisi, M.; Zhan, F.; Talkner, P.; Hänggi, P. Logarithmic oscillators: Ideal Hamiltonian thermostats. Phys. Rev. Lett. 2012, 108, 250601. [Google Scholar] [CrossRef]
- Campisi, M.; Hänggi, P. Thermostated Hamiltonian dynamics with log oscillators. J. Phys. Chem. B 2013, 117, 12829. [Google Scholar] [CrossRef]
- Korosec, C.S.; Sivak, D.A.; Forde, N.R. Apparent superballistic dynamics in one-dimensional random walks with biased detachment. Phys. Rev. Res. 2020, 2, 033520. [Google Scholar] [CrossRef]
- Defaveri, L.; Anteneodo, C.; Kessler, D.A.; Barkai, E. Regularized Boltzmann-Gibbs statistics for a Brownian particle in a nonconfining field. Phys. Rev. Res. 2020, 2, 043088. [Google Scholar] [CrossRef]
- Bao, J.D.; Wang, X.R.; Liu, W.M. Ergodic time scale and transitive dynamics in single-particle tracking. Phys. Rev. E 2021, 103, 032136. [Google Scholar] [CrossRef]
- Bao, J.D. Time-dependent fractional diffusion and friction functions for anomalous diffusion. Front. Phys. 2021, 9, 567161. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wen, B.; Li, M.-G.; Liu, J.; Bao, J.-D. Ergodic Measure and Potential Control of Anomalous Diffusion. Entropy 2023, 25, 1012. https://doi.org/10.3390/e25071012
Wen B, Li M-G, Liu J, Bao J-D. Ergodic Measure and Potential Control of Anomalous Diffusion. Entropy. 2023; 25(7):1012. https://doi.org/10.3390/e25071012
Chicago/Turabian StyleWen, Bao, Ming-Gen Li, Jian Liu, and Jing-Dong Bao. 2023. "Ergodic Measure and Potential Control of Anomalous Diffusion" Entropy 25, no. 7: 1012. https://doi.org/10.3390/e25071012
APA StyleWen, B., Li, M.-G., Liu, J., & Bao, J.-D. (2023). Ergodic Measure and Potential Control of Anomalous Diffusion. Entropy, 25(7), 1012. https://doi.org/10.3390/e25071012





