Feature Fusion Based on Graph Convolution Network for Modulation Classification in Underwater Communication
Abstract
1. Introduction
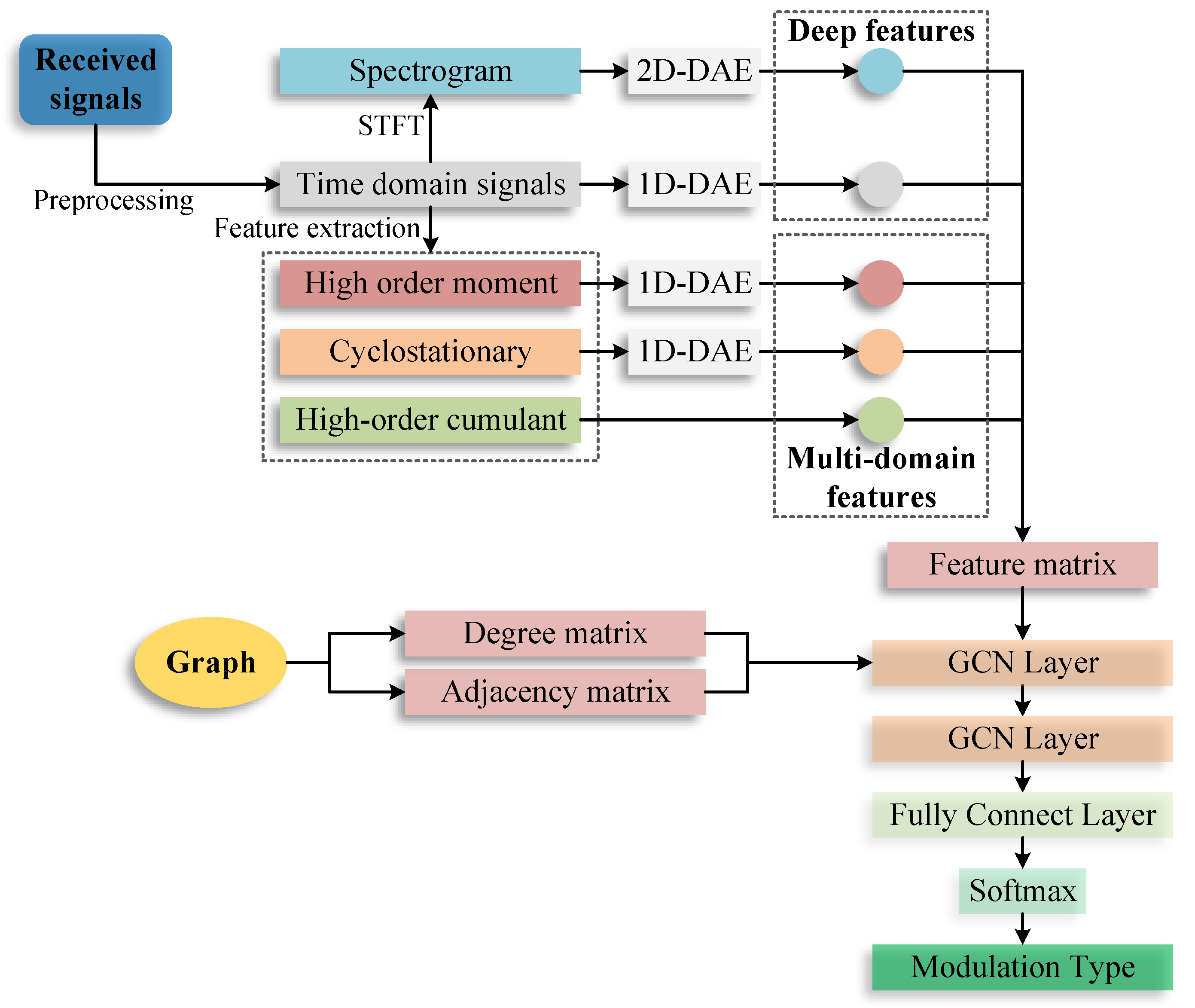
- We adopted GCN to AMC to improve the stability and robustness of AMC in underwater communication scenarios. GCN was used to fuse the multi-domain features and deep features of the received signals.
- To take the relationships between multi-domain features and deep features into account, we built a graph of the multi-domain features and deep features using their properties.
- The performance of the proposed method was validated using the simulated dataset in different underwater acoustic channels and a real-world dataset.
2. Materials and Methods
2.1. Multi-Domain Features
2.1.1. High-Order Cumulant
2.1.2. Cyclostationary Statistics
2.1.3. High Order Moment
2.2. The Proposed AMC Method
2.2.1. Graph Convolution Network
2.2.2. Features Fusion Based on GCN
- (a)
- Build graph for the features.
- (b)
- Extract features for each node.
- (c)
- Construct the input of GCN.
- (d)
- Feature fusion and modulation classification.
3. Experiments and Discussion
- (1)
- We analyzed the influence of the different features.
- (2)
- We analyzed the influence of the edges inside HOC.
- (3)
- We compared the performance of the proposed method with other AMC methods.
- (4)
- The performance of the proposed method was verified using real-world underwater acoustic communication signals.
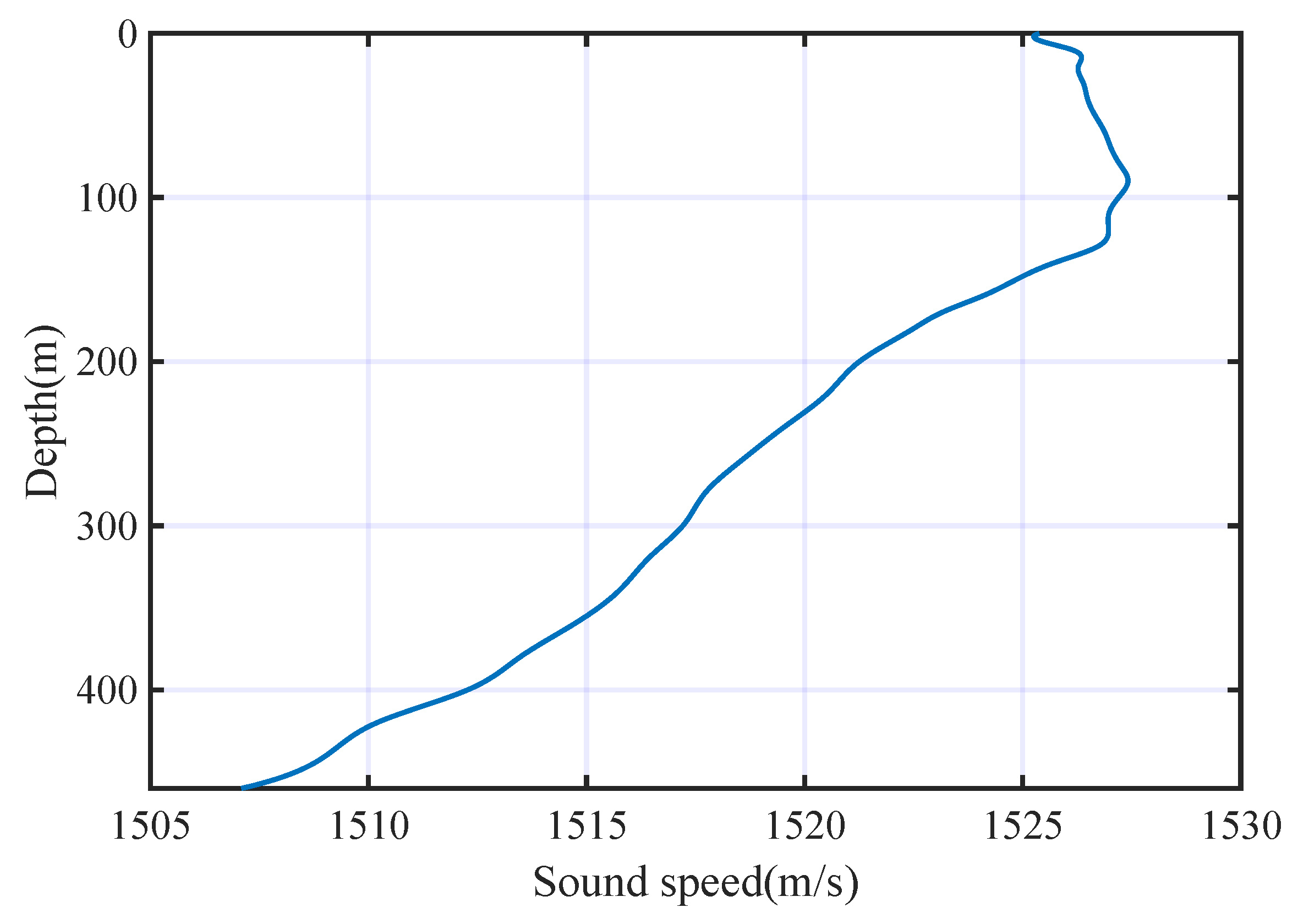
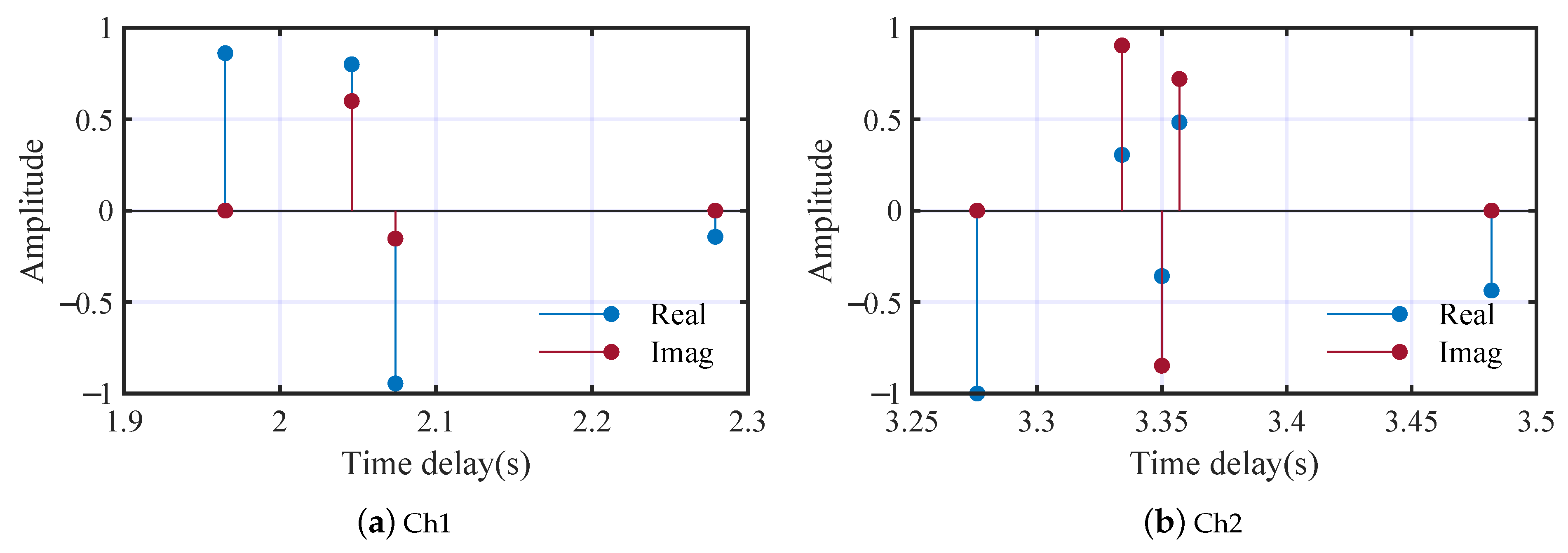
3.1. Dataset and Parameters
Signals Generation
3.2. Experiment Results Analysis
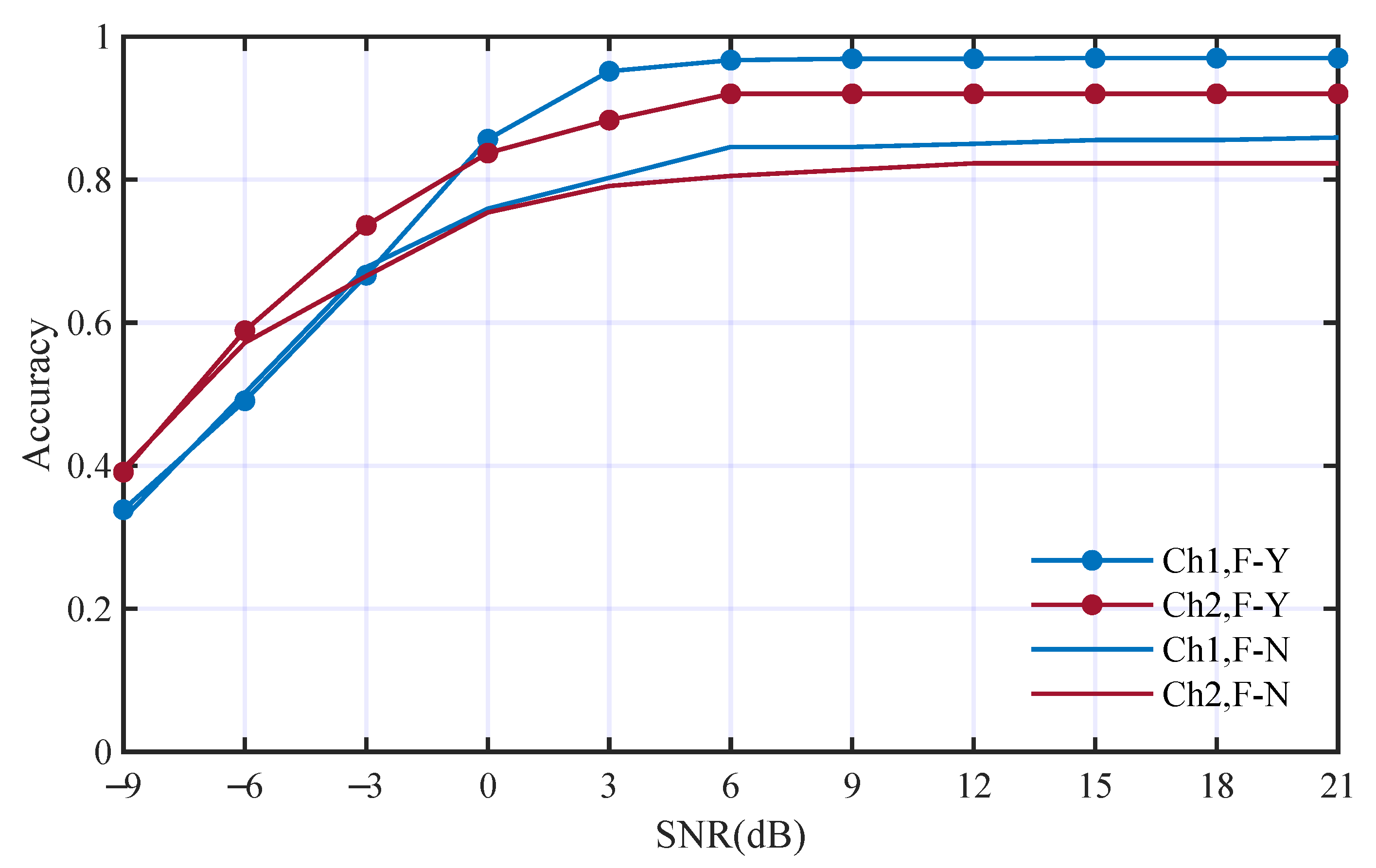
3.2.1. The Analysis of the Influence of the Different Features
- (a)
- Baseline performance.
- (b)
- Deep feature of time domain.
- (c)
- Deep features of STFT.
- (d)
- HOC features.
- (e)
- CS features.
- (f)
- HOM features.
3.2.2. The Analysis of the Influence of the Edges Inside HOC
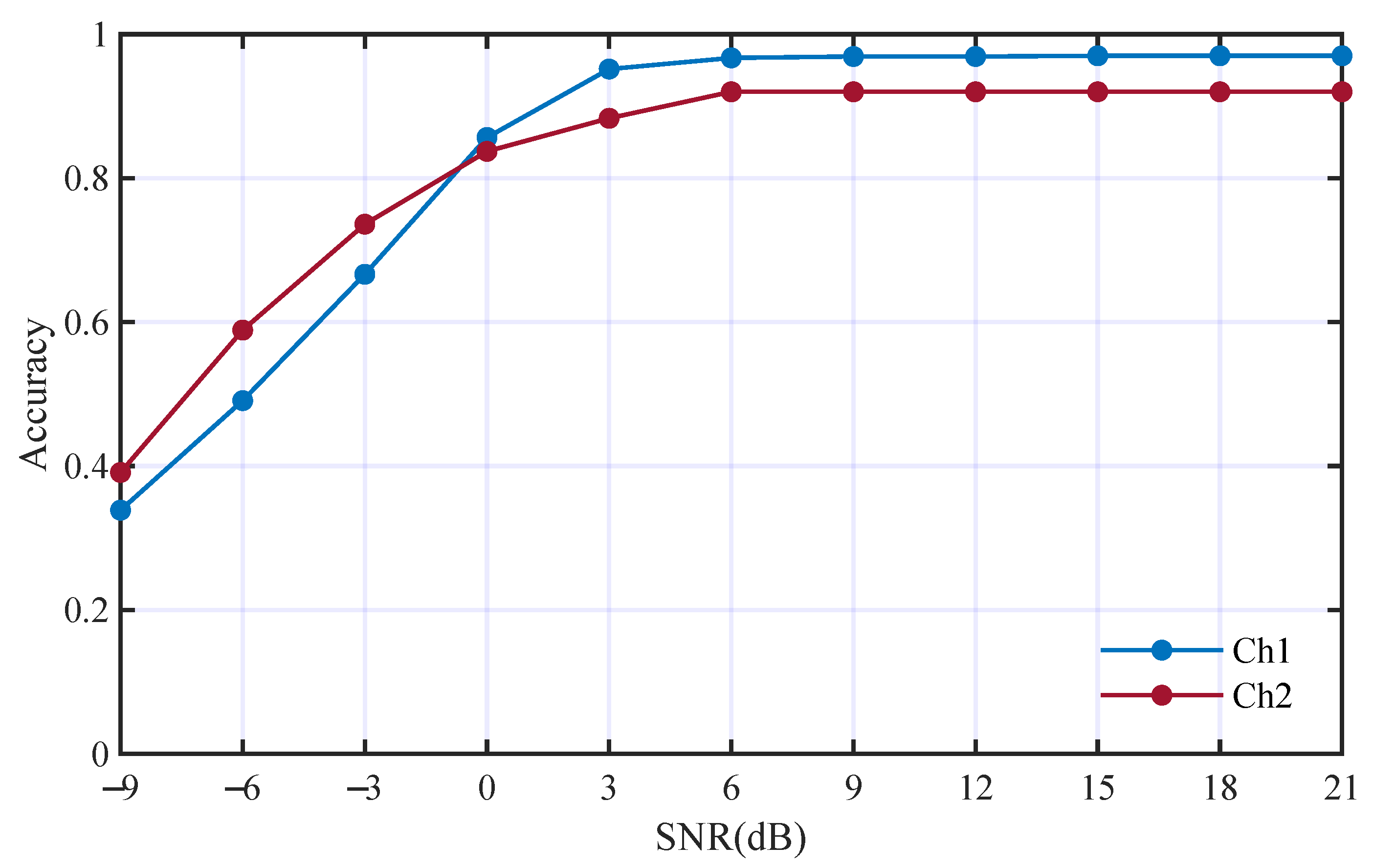
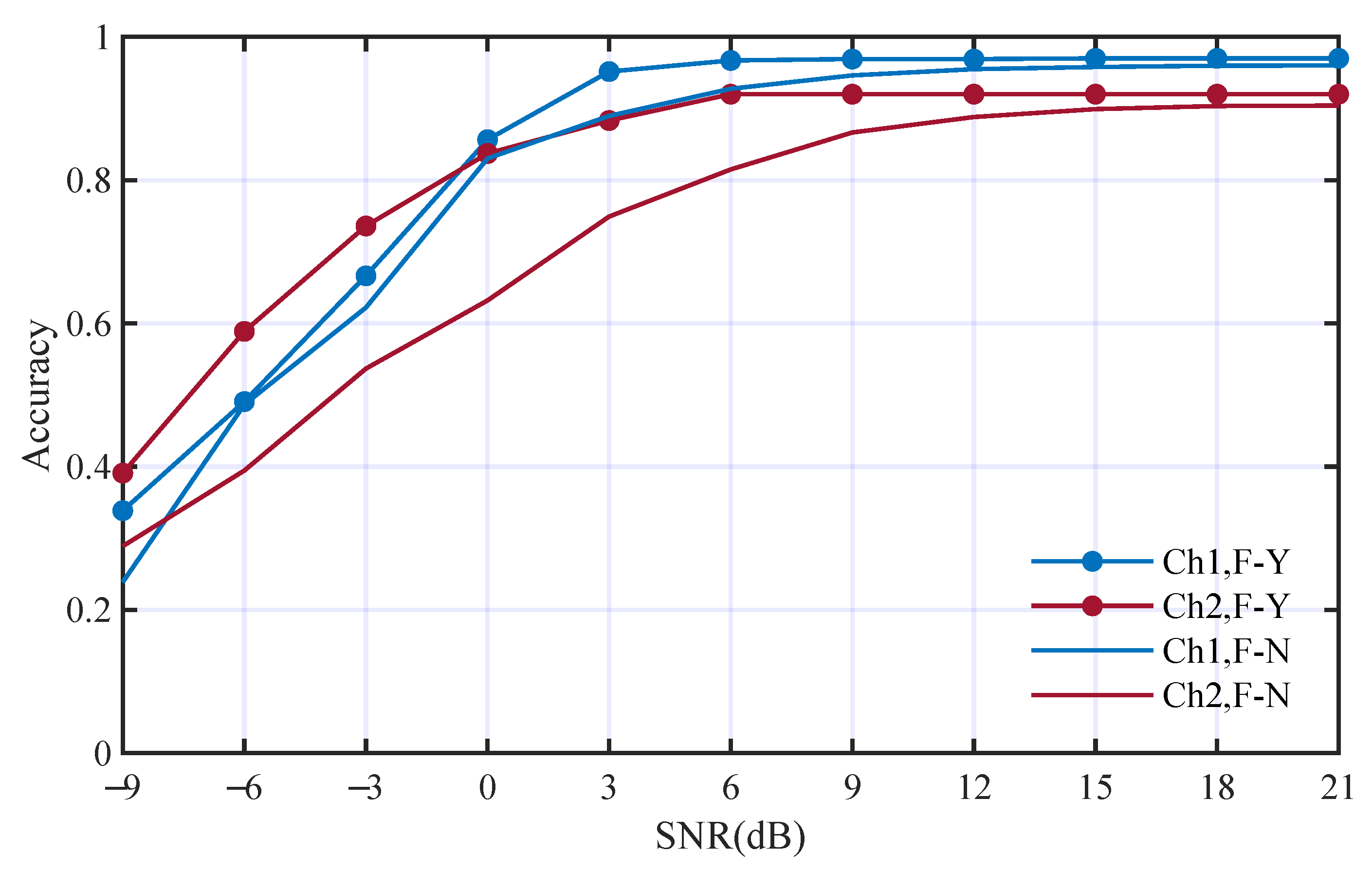
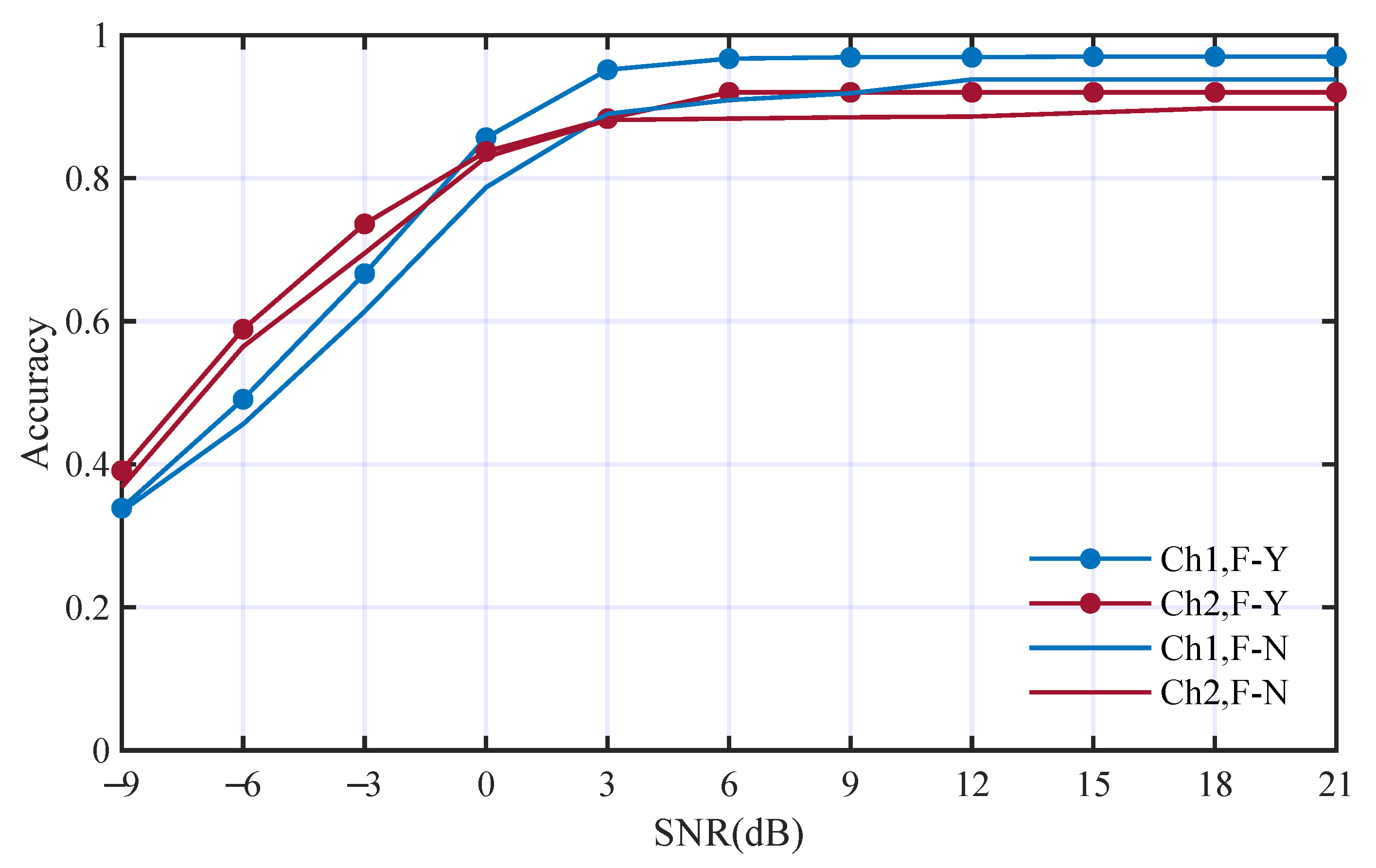
3.2.3. Comparison with Other State-of-the-Art AMC Methods
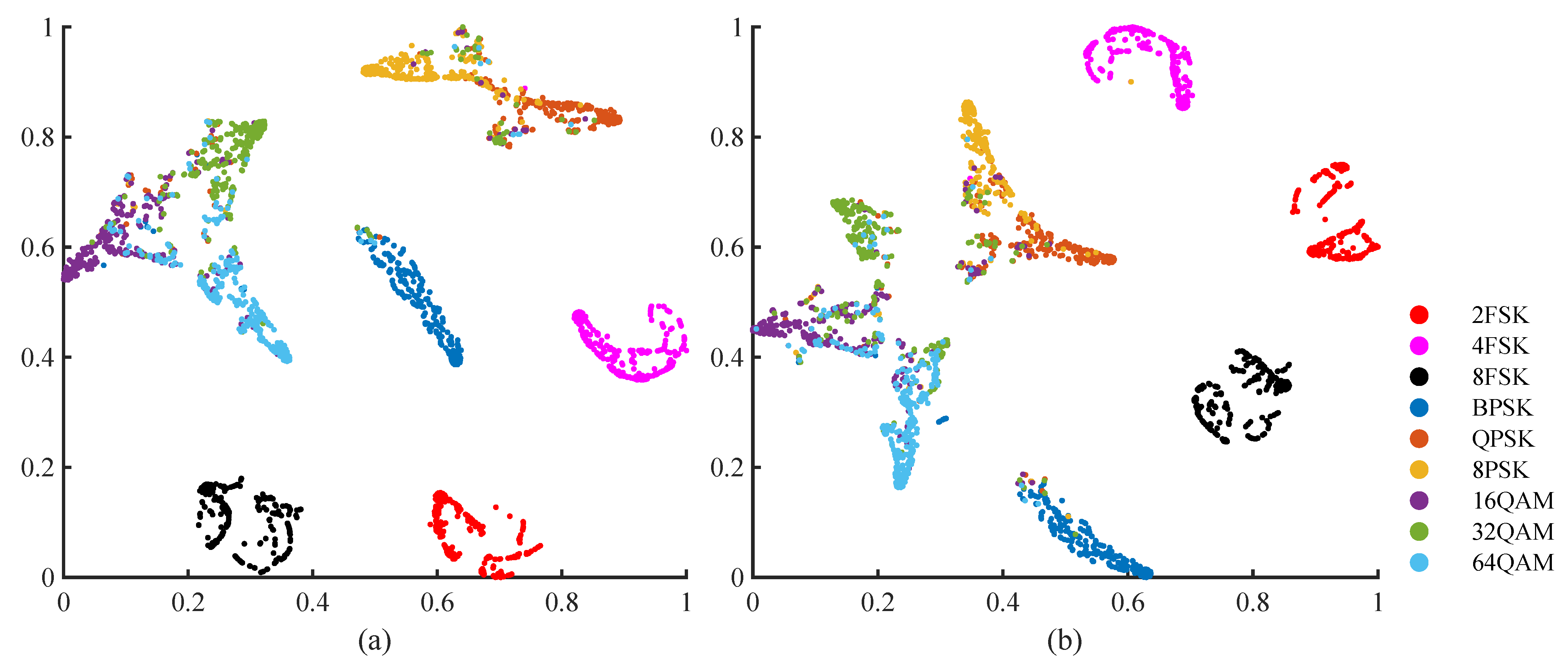
3.2.4. Performance Analysis Using Real-World Dataset
3.2.5. Computational Cost Analysis
4. Conclusions
- (1)
- To improve the stability and robustness of AMC in underwater scenarios, a new feature fusion method based on a graph convolution network was proposed to fuse the multi-domain features and deep features of underwater acoustic communication signals. The feature extraction methods and deep learning methods were effectively integrated into the constructed feature fusion framework.
- (2)
- A graph was built for the multi-domain features and deep features based on their properties. The proposed feature fusion method can make full use of the relationships among these features. The experiments have shown that making use of the relationships can improve the AMC performance.
- (3)
- The comparative experiments indicate that the feature fusion method based on GCN can significantly improve the AMC performance in underwater scenarios and achieve excellent classification performance in different simulated and real-world underwater acoustic channels.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AMC | Automatic modulation classification |
| GCN | Graph convolution network |
| HOC | High-order cumulant |
| CS | Cyclostationary statistics |
| DNN | Deep neural networks |
| CNN | Convolution neural network |
| GAN | Generative adversarial networks |
| RNN | Recurrent neural network |
| LSTM | Long short term memory |
| GRU | Gate recurrent unit |
| HOM | high order moment |
| SCD | Spectral correlation density |
| SCF | Spectral coherence function |
| STFT | Short-time Fourier transform |
| WGN | white Gaussian noise |
| FSK | Frequency shift keying |
| PSK | Phase shift keying |
| QAM | Quadrature amplitude modulation |
| DCN | Deep complex networks |
References
- Yao, X.H.; Yang, H.H.; Sheng, M.P. Automatic Modulation Classification for Underwater Acoustic Communication Signals Based on Deep Complex Networks. Entropy 2023, 25, 318. [Google Scholar] [CrossRef] [PubMed]
- Azzouz, E.E.; Nandi, A.K. Automatic identification of digital modulation types. Signal Process. 1995, 47, 55–69. [Google Scholar] [CrossRef]
- Vanhoy, G.; Asadi, H.; Volos, H.; Bose, T. Multi-receiver modulation classification for non-cooperative scenarios based on higher-order cumulants. Analog. Integr. Circuits Signal Process. 2021, 106, 1–7. [Google Scholar] [CrossRef]
- Wenxuan, C.; Yuan, J.; Lin, Z.; Yang, Z. A New Modulation Recognition Method Based on Wavelet Transform and High-order Cumulants. J. Phys. Conf. Ser. 2021, 1738, 12025. [Google Scholar] [CrossRef]
- Fang, T.; Wang, Q.; Zhang, L.; Liu, S. Modulation Mode Recognition Method of Non-Cooperative Underwater Acoustic Communication Signal Based on Spectral Peak Feature Extraction and Random Forest. Remote Sens. 2022, 14, 1603. [Google Scholar] [CrossRef]
- Jeong, S.; Lee, U.; Kim, S.C. Spectrogram-Based Automatic Modulation Recognition Using Convolutional Neural Network. In Proceedings of the 10th International Conference on Ubiquitous and Future Networks, ICUFN 2018, IEEE Computer Society, Prague, Czech Republic, 3–6 July 2018; Volume 2018, pp. 843–845. [Google Scholar] [CrossRef]
- Fan, H.; Yang, Z.; Cao, Z. Automatic Recognition for common used modulations in satellite communication. J. China Inst. Commun. 2004, 25, 140–149. [Google Scholar] [CrossRef]
- Sanderson, J.; Li, X.; Liu, Z.; Wu, Z. Hierarchical Blind Modulation Classification for Underwater Acoustic Communication Signal via Cyclostationary and Maximal Likelihood Analysis. In Proceedings of the Military Communications Conference, Milcom 2013, San Diego, CA, USA, 18–20 November 2013; Institute of Electrical and Electronics Engineers Inc.: San Diego, CA, USA, 2013; pp. 29–34. [Google Scholar] [CrossRef]
- Wu, Z.; Yang, T.C.; Liu, Z.; Chakarvarthy, V. Modulation detection of underwater acoustic communication signals through cyclostationary analysis. In Proceedings of the Military Communications Conference, 2012-Milcom, Orlando, FL, USA, 29 October–1 November 2012; Institute of Electrical and Electronics Engineers Inc.: Orlando, FL, USA, 2012; pp. 1–6. [Google Scholar] [CrossRef]
- Like, E.; Chakravarthy, V.; Ratazzi, P.; Wu, Z. Signal Classification in Fading Channels Using Cyclic Spectral Analysis. EURASIP J. Wirel. Comm. Netw. 2009, 2009, 879812. [Google Scholar] [CrossRef]
- Chen, J.; Kuo, Y.H.; Li, J.D.; Ma, Y.B. Modulation Identification of Digital Signals with Wavelet Transform. J. Electron. Inf. Technol. 2006, 28, 2026–2029. [Google Scholar]
- Li, Y.; Tang, B.; Geng, B.; Jiao, S. Fractional Order Fuzzy Dispersion Entropy and Its Application in Bearing Fault Diagnosis. Fractal Fract. 2022, 6, 544. [Google Scholar] [CrossRef]
- Li, Y.; Tang, B.; Jiao, S. SO-slope entropy coupled with SVMD: A novel adaptive feature extraction method for ship-radiated noise. Ocean. Eng. 2023, 280, 114677. [Google Scholar] [CrossRef]
- Lippmann, R.P. Pattern classification using neural networks. IEEE Commun. Mag. 1989, 27, 47–50. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Safavian, S.R.; Landgrebe, D. A survey of decision tree classifier methodology. IEEE Trans. Syst. Man Cybern. 1991, 21, 660–674. [Google Scholar] [CrossRef]
- Zhao, Z.; Wang, S.; Zhang, W.; Xie, Y. A novel Automatic Modulation Classification method based on Stockwell-transform and energy entropy for underwater acoustic signals. In Proceedings of the IEEE International Conference on Signal Processing, Communications and Computing, Hong Kong, China, 5–8 August 2016; Institute of Electrical and Electronics Engineers Inc.: New York, NY, USA, 2016. [Google Scholar] [CrossRef]
- Ge, Y.; Zhang, X.; Zhou, Q. Modulation Recognition of Underwater Acoustic Communication Signals Based on Joint Feature Extraction. In Proceedings of the 2019 IEEE International Conference on Signal, Information and Data Processing (ICSIDP), Chongqing, China, 11–13 December 2019; pp. 1–4. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. In Proceedings of the International Conference on Neural Information Processing Systems, Neural Information Processing Systems Foundation, Lake Tahoe, Nevada, USA, 3–6 December 2012; Volume 5, pp. 1097–1105. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition, IEEE Computer Society, Las Vegas, NV, USA, 27–30 June 2016; Volume 2016, pp. 770–778. [Google Scholar] [CrossRef]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going Deeper with Convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2015, IEEE Computer Society, Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. In Proceedings of the International Conference on Learning Representations 2015, International Conference on Learning Representations, ICLR, Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Goodfellow, I.J.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative Adversarial Networks. In Proceedings of the 28th Annual Conference on Neural Information Processing Systems 2014, NIPS 2014, Neural Information Processing Systems Foundation, Montreal, QC, Canada, 8–13 December 2014; Volume 3, pp. 2672–2680. [Google Scholar]
- Arjovsky, M.; Shah, A.; Bengio, Y. Unitary Evolution Recurrent Neural Networks. In Proceedings of the 33rd International Conference on Machine Learning. JMLR.org, New York, NY, USA, 20–22 June 2016; Volume 48, pp. 1120–1128. [Google Scholar] [CrossRef]
- Danihelka, I.; Wayne, G.; Uria, B.; Kalchbrenner, N.; Graves, A. Associative Long Short-Term Memory. In Proceedings of the 33rd International Conference on Machine Learning, New York, NY, USA, 20–22 June 2016; Volume 48, pp. 1986–1994. [Google Scholar] [CrossRef]
- Cho, K.; Merrienboer, B.V.; Bahdanau, D.; Bengio, Y. On the Properties of Neural Machine Translation: Encoder-Decoder Approaches. Comput. Sci. 2014, 103–111. [Google Scholar] [CrossRef]
- Zhang, H.; Zhou, F.; Wu, Q.; Wu, W.; Hu, R.Q. A Novel Automatic Modulation Classification Scheme Based on Multi-Scale Networks. IEEE Trans. Cogn. Commun. Netw. 2022, 8, 97–110. [Google Scholar] [CrossRef]
- Zhou, Q.; Zhang, R.H.; Mu, J.S.; Zhang, H.M.; Zhang, F.P.; Jing, X.J. AMCRN: Few-Shot Learning for Automatic Modulation Classification. IEEE Commun. Lett. 2022, 26, 542–546. [Google Scholar] [CrossRef]
- Yao, X.; Yang, H.; Li, Y. Modulation Identification of Underwater Acoustic Communications Signals Based on Generative Adversarial Networks. In Proceedings of the OCEANS 2019—Marseille, Marseille, France, 17–20 June 2019; Institute of Electrical and Electronics Engineers Inc.: New York, NY, USA, 2019; pp. 1–6. [Google Scholar] [CrossRef]
- O’Shea, T.J.; Roy, T.; Clancy, T.C. Over-the-Air Deep Learning Based Radio Signal Classification. IEEE J. Sel. Top. Signal Process. 2018, 12, 168–179. [Google Scholar] [CrossRef]
- Wang, M.; Fan, Y.; Fang, S.; Cui, T.; Cheng, D. A Joint Automatic Modulation Classification Scheme in Spatial Cognitive Communication. Sensors 2022, 22, 6500. [Google Scholar] [CrossRef]
- Yu, X.; Li, L.; Yin, J.; Shao, M.; Han, X. Modulation Pattern Recognition of Non-cooperative Underwater Acoustic Communication Signals Based on LSTM Network. In Proceedings of the 2019 IEEE International Conference on Signal, Information and Data Processing (ICSIDP), Chongqing, China, 11–13 December 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Jiang, N.; Wang, B. Modulation Recognition of Underwater Acoustic Communication Signals Based on Data Transfer. In Proceedings of the 2019 IEEE 8th Joint International Information Technology and Artificial Intelligence Conference (ITAIC), Chongqing, China, 24–26 May 2019; pp. 243–246. [Google Scholar] [CrossRef]
- Lida, D.; Shilian, W.; Wei, Z. Modulation Classification of Underwater Acoustic Communication Signals Based on Deep Learning. In Proceedings of the 2018 OCEANS-MTS/IEEE Kobe Techno-Oceans, OCEANS-Kobe 2018, Kobe, Japan, 28–31 May 2018; Institute of Electrical and Electronics Engineers Inc.: New York, NY, USA, 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Scarselli, F.; Gori, M.; Tsoi, A.C.; Hagenbuchner, M.; Monfardini, G. The Graph Neural Network Model. IEEE Trans. Neural Netw. 2009, 20, 61–80. [Google Scholar] [CrossRef]
- Long, Y.; Wu, J.Y.; Lu, B.; Jin, Y.; Unberath, M.; Liu, Y.H.; Heng, P.A.; Dou, Q. Relational Graph Learning on Visual and Kinematics Embeddings for Accurate Gesture Recognition in Robotic Surgery. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; pp. 13346–13353. [Google Scholar] [CrossRef]
- Kipf, T.; Welling, M. Semi-Supervised Classification with Graph Convolutional Networks. In Proceedings of the International Conference on Learning Representations, Toulon, France, 24–26 April 2017. [Google Scholar] [CrossRef]
- Xuan, Q.; Zhou, J.; Qiu, K.; Chen, Z.; Xu, D.; Zheng, S.; Yang, X. AvgNet: Adaptive Visibility Graph Neural Network and Its Application in Modulation Classification. IEEE Trans. Netw. Sci. Eng. 2022, 9, 1516–1526. [Google Scholar] [CrossRef]
- Gao, Y.Q.; Chen, J.A. Recognition of Digital Modulation Signals Based on High Order Cumulants. Wirel. Commun. Technol. 2006, 1, 26–29. [Google Scholar]
- Wu, Z.; Yang, T.C. Blind cyclostationary carrier frequency and symbol rate estimation for underwater acoustic communication. In Proceedings of the 2012 IEEE International Conference on Communications (ICC), Ottawa, ON, Canada, 10–15 June 2012; pp. 3482–3486. [Google Scholar] [CrossRef]
- Reichert, J. Automatic classification of communication signals using higher order statistics. In Proceedings of the 1992 IEEE International Conference on Acoustics, Speech, and Signal Processing, San Francisco, CA, USA, 23–26 March 1992; Volume 5, pp. 221–224. [Google Scholar] [CrossRef]
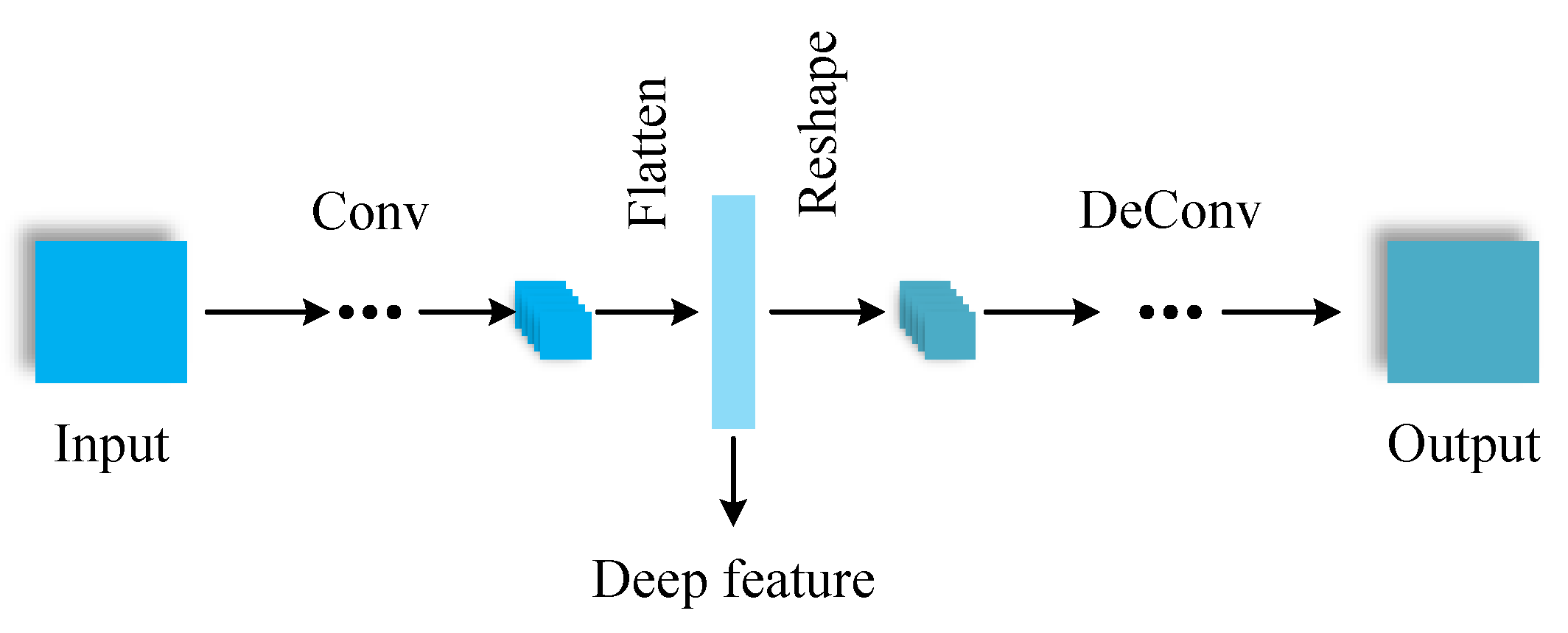
- Vincent, P.; Larochelle, H.; Bengio, Y.; Manzagol, P.A. Extracting and composing robust features with denoising autoencoders. In Proceedings of the 25th International Conference on Machine Learning, ICML 2008, Association for Computing Machinery (ACM), Helsinki, Finland, 5–9 July 2008; pp. 1096–1103. [Google Scholar] [CrossRef]
- van der Maaten, L.; Hinton, G. Viualizing data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- Yao, X.; Yang, H.; Li, Y. Modulation recognition of underwater acoustic communication signals based on convolutional neural networks. Unmanned Syst. Technol. 2018, 1, 68–74. [Google Scholar]
- Szegedy, C.; Vanhoucke, V.; Ioffe, S.; Shlens, J.; Wojna, Z. Rethinking the Inception Architecture for Computer Vision. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 2818–2826. [Google Scholar] [CrossRef]
- Wu, P.; Sun, B.; Su, S.; Wei, J.; Wen, X. Automatic Modulation Classification Based on Deep Learning for Software-Defined Radio. Math. Probl. Eng. 2020, 2020, 1–13. [Google Scholar] [CrossRef]
- Qi, P.; Zhou, X.; Zheng, S.; Li, Z. Automatic Modulation Classification Based on Deep Residual Networks With Multimodal Information. IEEE Trans. Cogn. Commun. Netw. 2021, 7, 21–33. [Google Scholar] [CrossRef]
- Karahan, S.N.; Kalaycioğlu, A. Deep Learning Based Automatic Modulation Classification With Long-Short Term Memory Networks. In Proceedings of the 2020 28th Signal Processing and Communications Applications Conference (SIU), Gaziantep, Turkey, 5–7 October 2020; pp. 1–4. [Google Scholar] [CrossRef]
- Hamza, M.A.; Hassine, S.B.; Larabi-Marie-Sainte, S.; Nour, M.K.; Al-Wesabi, F.N.; Motwakel, A.; Hilal, A.M.; Al Duhayyim, M. Optimal Bidirectional LSTM for Modulation Signal Classification in Communication Systems. Cmc-Comput. Mater. Contin. 2022, 72, 3055–3071. [Google Scholar] [CrossRef]
- Liu, X.; Li, C.J.; Jin, C.T.; Leong, P.H.W. Wireless Signal Representation Techniques for Automatic Modulation Classification. IEEE Access 2022, 10, 84166–84187. [Google Scholar] [CrossRef]
- Chen, J.; Kuo, Y.; Li, J.; Fu, F.; Ma, Y. Digital modulation identification by wavelet analysis. In Proceedings of the Sixth International Conference on Computational Intelligence and Multimedia Applications (ICCIMA’05), Las Vegas, NV, USA, 16–18 August 2005; pp. 29–34. [Google Scholar] [CrossRef]







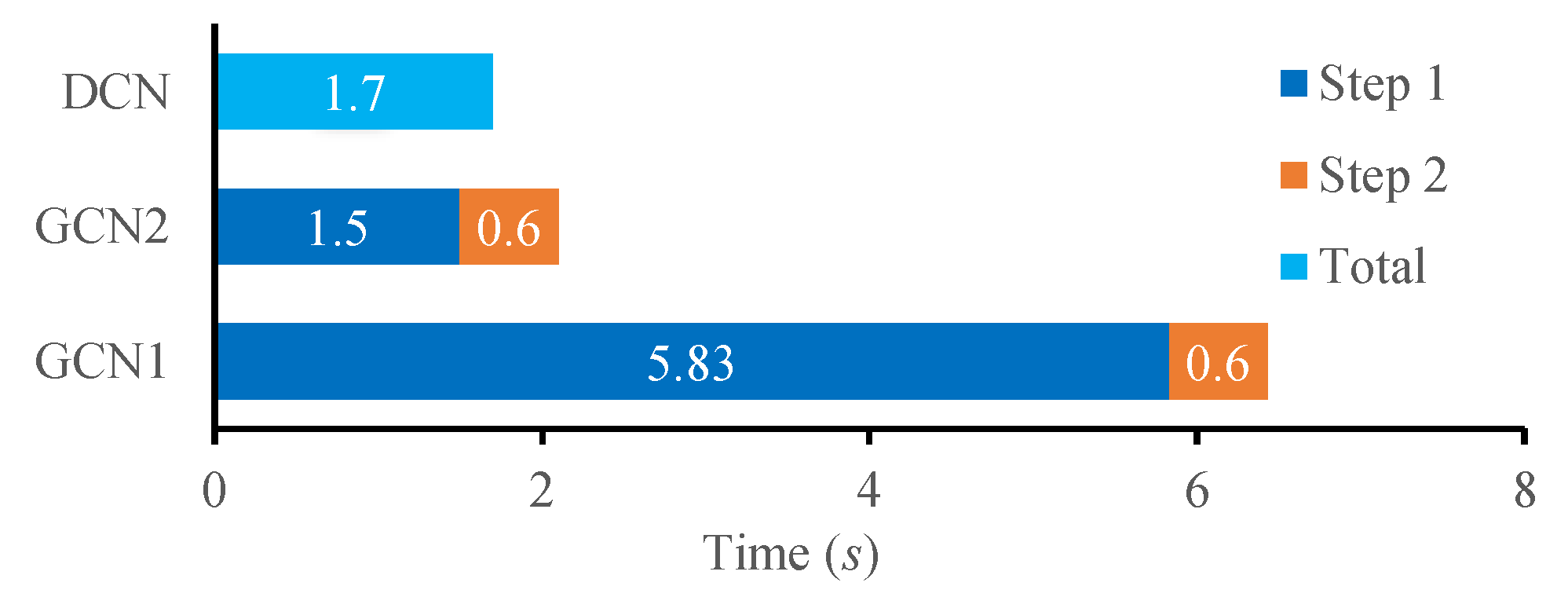
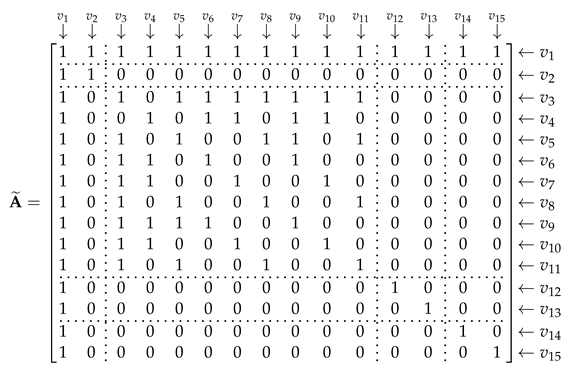
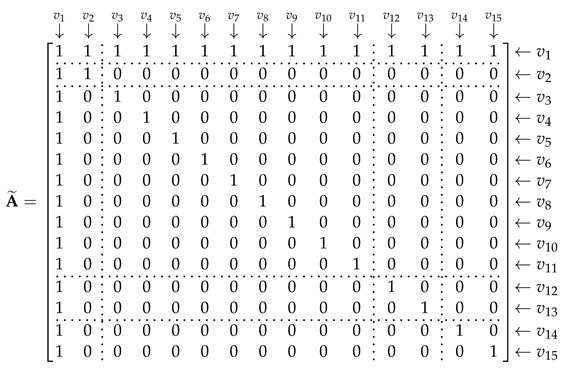
| - | |||||||||
| ∘ | - | ||||||||
| • | ∘ | - | |||||||
| • | • | ∘ | - | ||||||
| • | • | ∘ | ∘ | - | |||||
| • | ∘ | • | ∘ | ∘ | - | ||||
| • | • | • | • | ∘ | ∘ | - | |||
| • | • | ∘ | ∘ | • | ∘ | ∘ | - | ||
| • | ∘ | • | ∘ | ∘ | • | ∘ | ∘ | - |
| Node | Feature | Node | Feature | Node | Feature |
|---|---|---|---|---|---|
| Modulation Type | Sampling Rate (kHz) | Carrier Frequency Offset (Hz) | Symbol Rate (Baud) | Roll off Value | SNR (dB) |
|---|---|---|---|---|---|
| FSK | 12k | 300 | 100∼200 | - | −9∼21 |
| PSK | 12k | 300 | 800∼1200 | 0.1∼0.4 | −9∼21 |
| QAM | 12k | 300 | 800∼1200 | 0.1∼0.4 | −9∼21 |
| AMC Accuracy | |||
|---|---|---|---|
| Feature Sets | Ch1 | Ch2 | Average |
| All features | 82.9% | 81.4% | 82.2% |
| Without time domain | 59.3% | 50.8% | 55.1% |
| Without STFT | 79.7% | 71.6% | 75.7% |
| Without HOC | 74.3% | 73.5% | 73.9% |
| Without CS | 78.7% | 78.9% | 78.8% |
| Without HOM | 79.2% | 78.1% | 78.7% |
| AMC Accuracy | |||
|---|---|---|---|
| Features Set | Ch1 | Ch2 | Average |
| With HOC edges | 82.9% | 81.4% | 82.3% |
| Without HOC edges | 79.5% | 78.4% | 79.0% |
| 82.9% | 81.4% | 82.2% | 74.5% | 73.4% | 74.0% | ||
| 69.3% | 76.0% | 72.7% | 78.8% | 77.5% | 78.2% | ||
| 68.5% | 70.4% | 69.5% | 59.7% | 69.6% | 64.7% | ||
| 73.2% | 69.2% | 71.2% | 60.6% | 63.6% | 62.1% | ||
| 74.9% | 78.1% | 76.5% | 61.7% | 65.3% | 63.5% | ||
| 68.4% | 69.0% | 69.7% |
| Accuracy | 84% | 80% | 77% | 71% | 67% | 73% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, X.; Yang, H.; Sheng, M. Feature Fusion Based on Graph Convolution Network for Modulation Classification in Underwater Communication. Entropy 2023, 25, 1096. https://doi.org/10.3390/e25071096
Yao X, Yang H, Sheng M. Feature Fusion Based on Graph Convolution Network for Modulation Classification in Underwater Communication. Entropy. 2023; 25(7):1096. https://doi.org/10.3390/e25071096
Chicago/Turabian StyleYao, Xiaohui, Honghui Yang, and Meiping Sheng. 2023. "Feature Fusion Based on Graph Convolution Network for Modulation Classification in Underwater Communication" Entropy 25, no. 7: 1096. https://doi.org/10.3390/e25071096
APA StyleYao, X., Yang, H., & Sheng, M. (2023). Feature Fusion Based on Graph Convolution Network for Modulation Classification in Underwater Communication. Entropy, 25(7), 1096. https://doi.org/10.3390/e25071096






