Multiparameter Estimation with Two-Qubit Probes in Noisy Channels
Abstract
:1. Introduction
2. Preliminaries
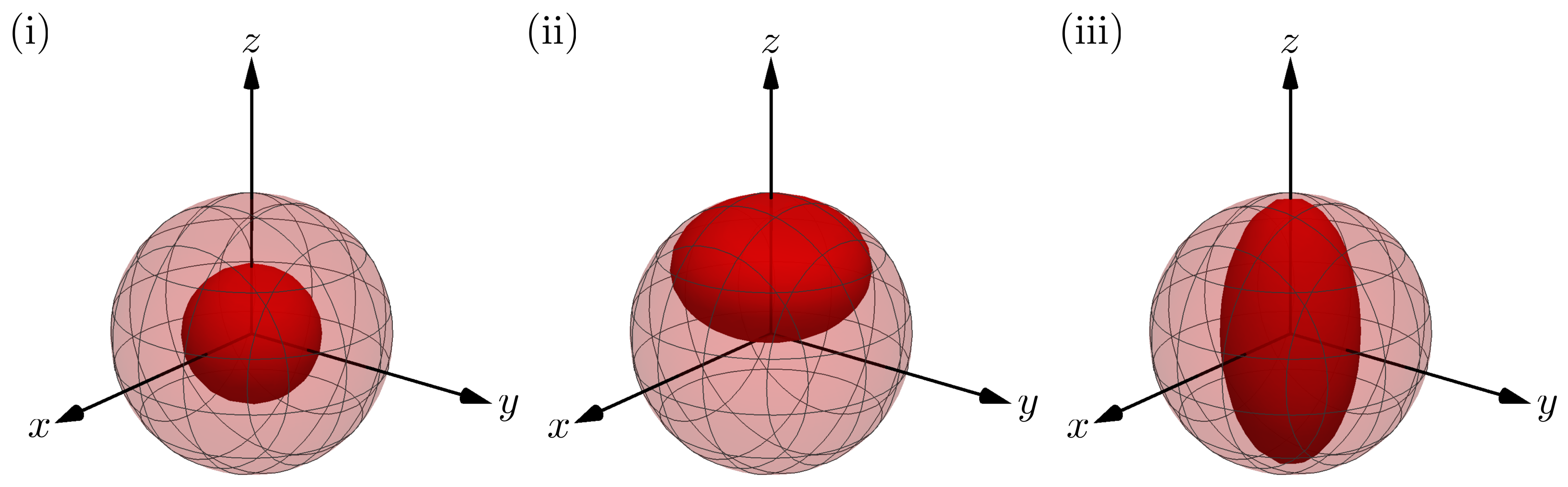
2.1. Parameter Estimation and Quantum Fisher Information
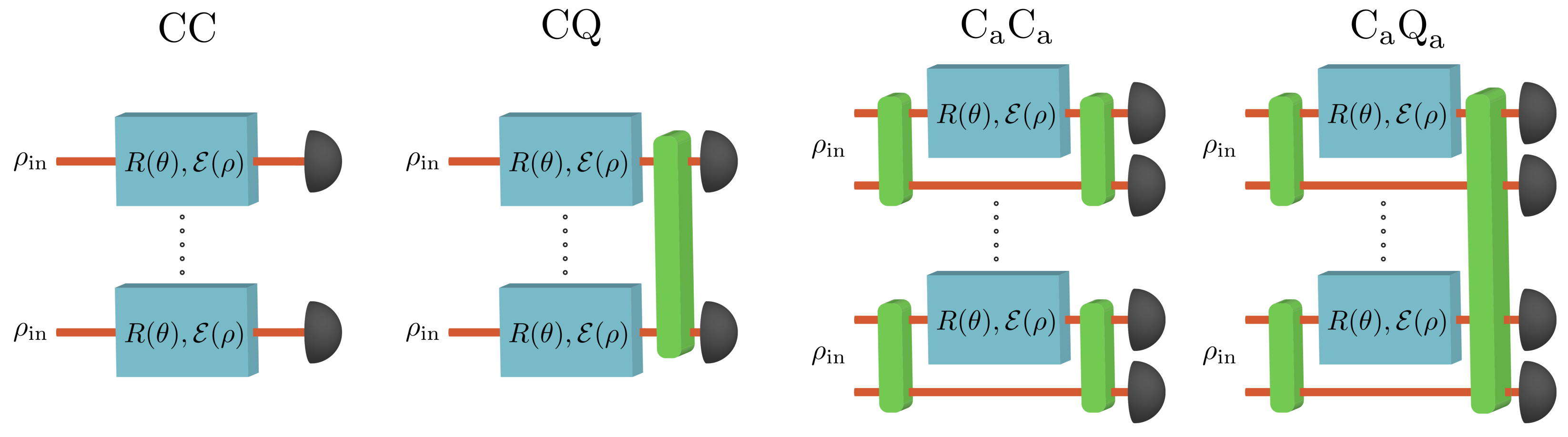
2.2. Holevo and Nagaoka–Hayashi Bounds
2.3. Quantum Channels
3. Results
3.1. Decoherence Channel
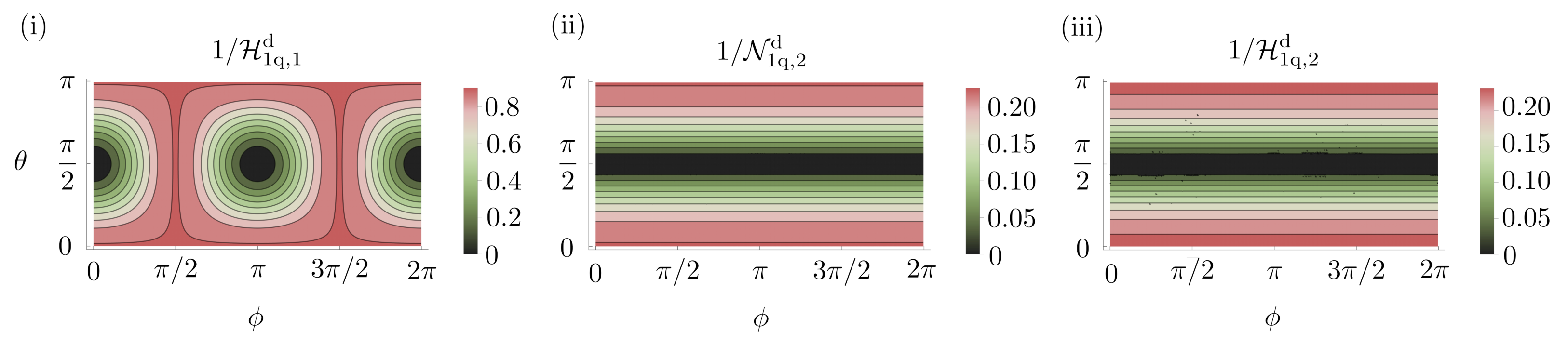
3.1.1. Single-Qubit Probe
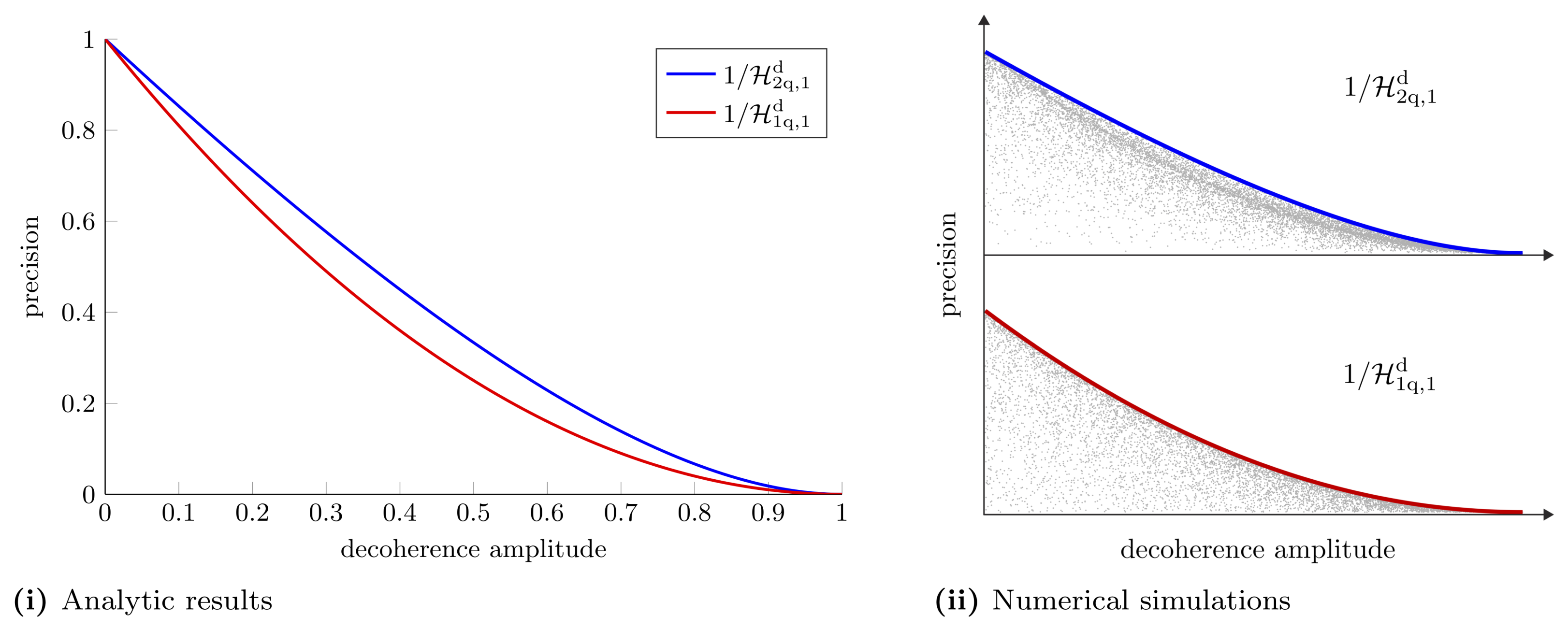
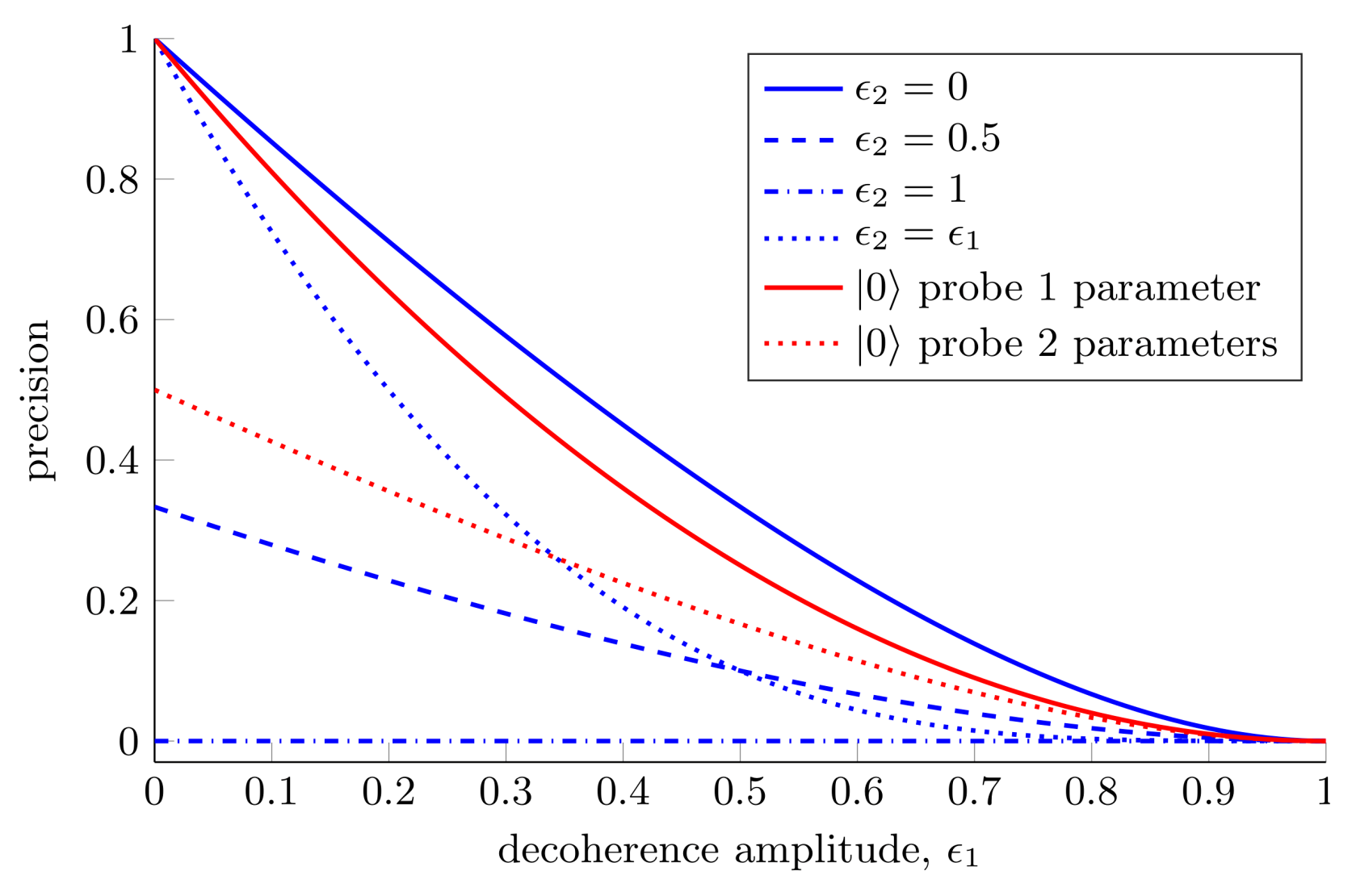
3.1.2. Two-Qubit Probe
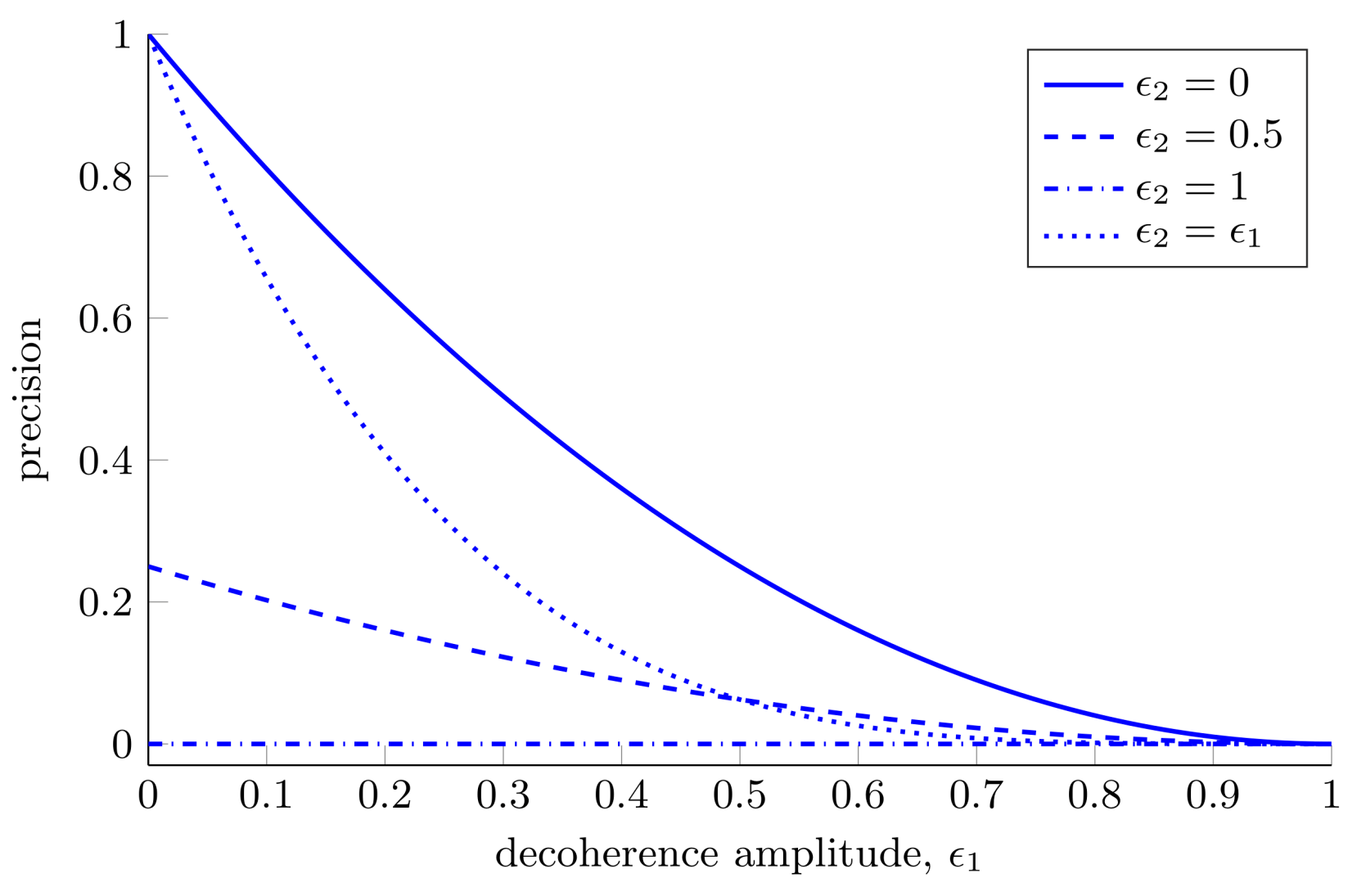
3.1.3. Decoherence of Both Qubits
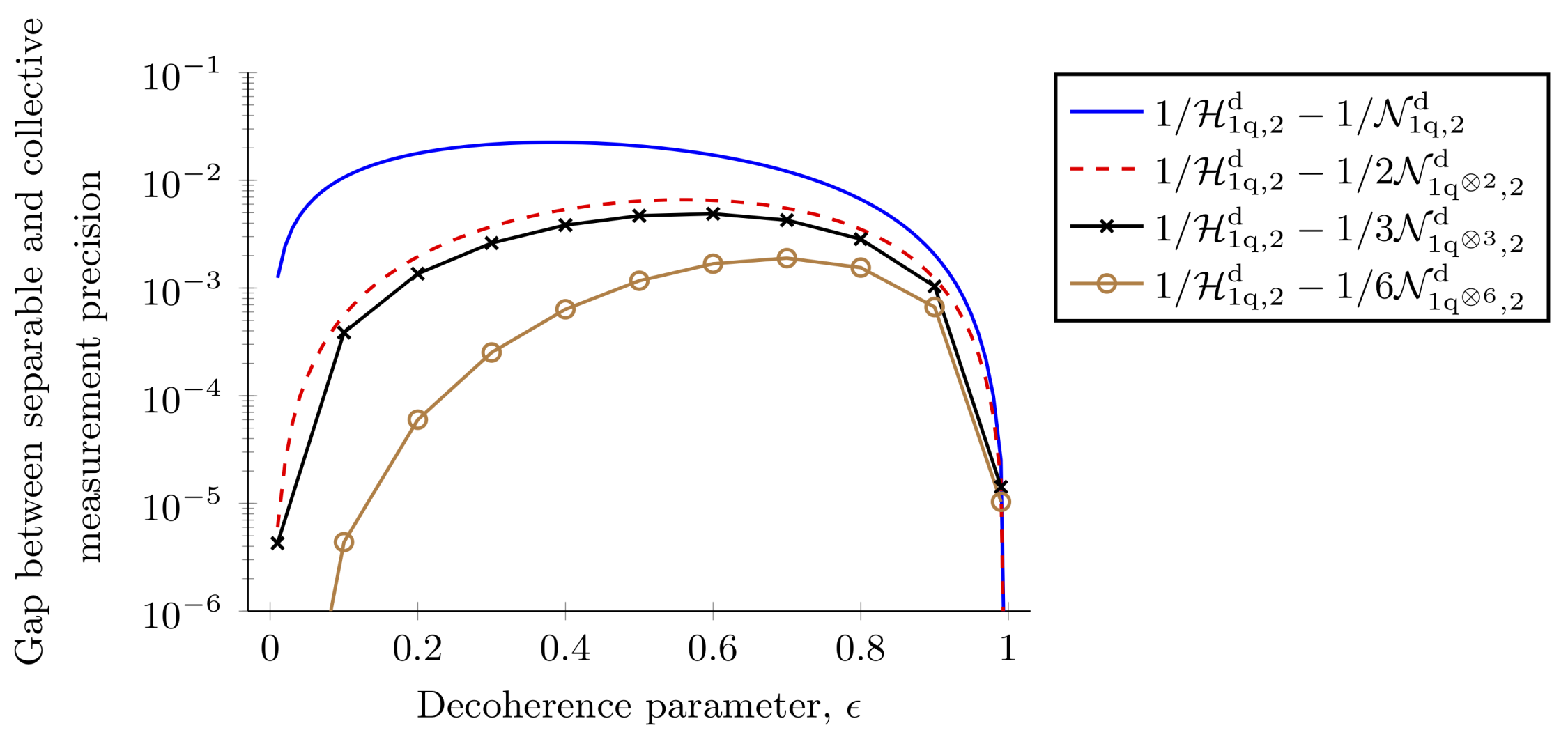
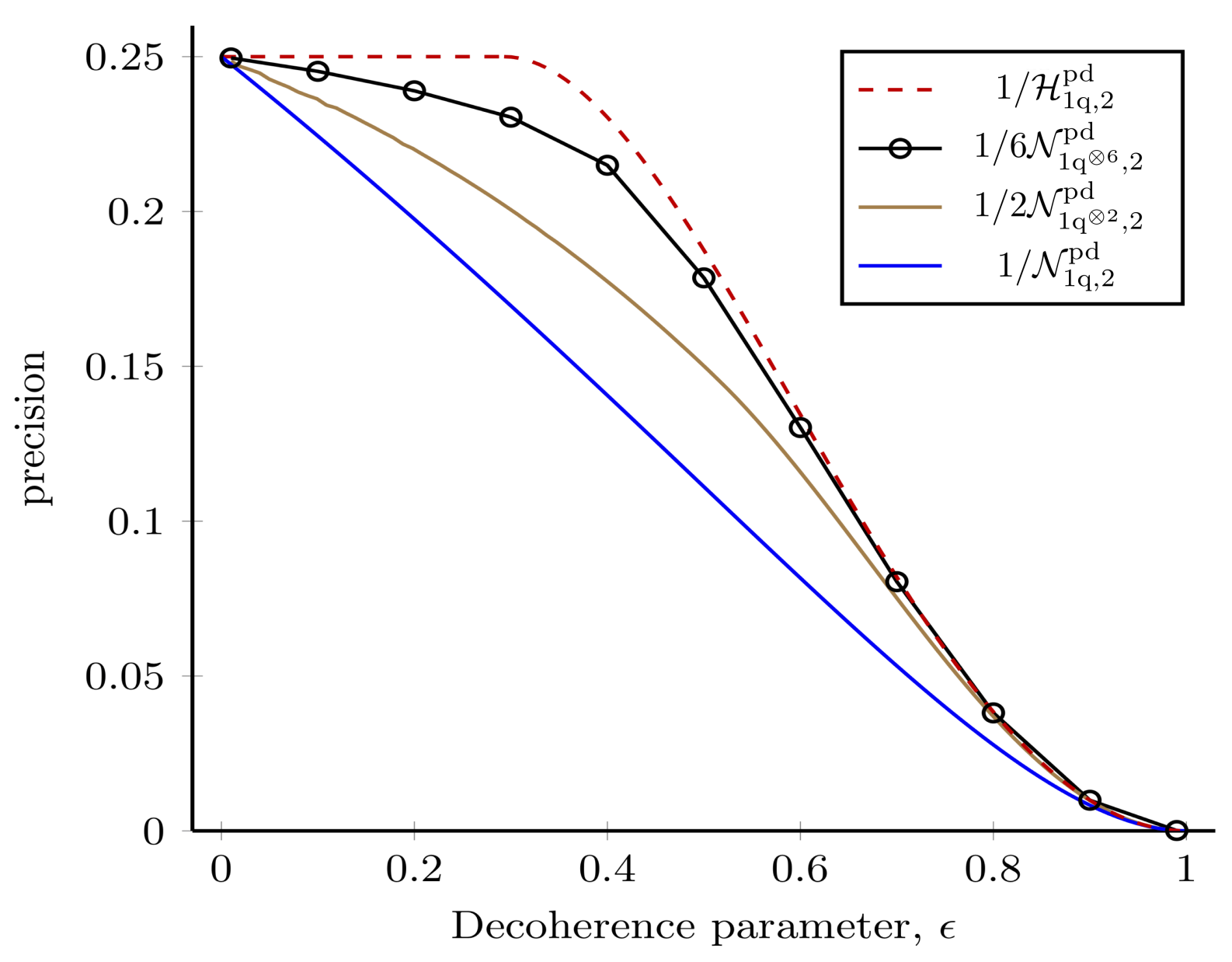
3.1.4. Collective Measurements on Multiple Copies of the State
3.2. Amplitude Damping Channel
3.2.1. Single-Qubit Probe
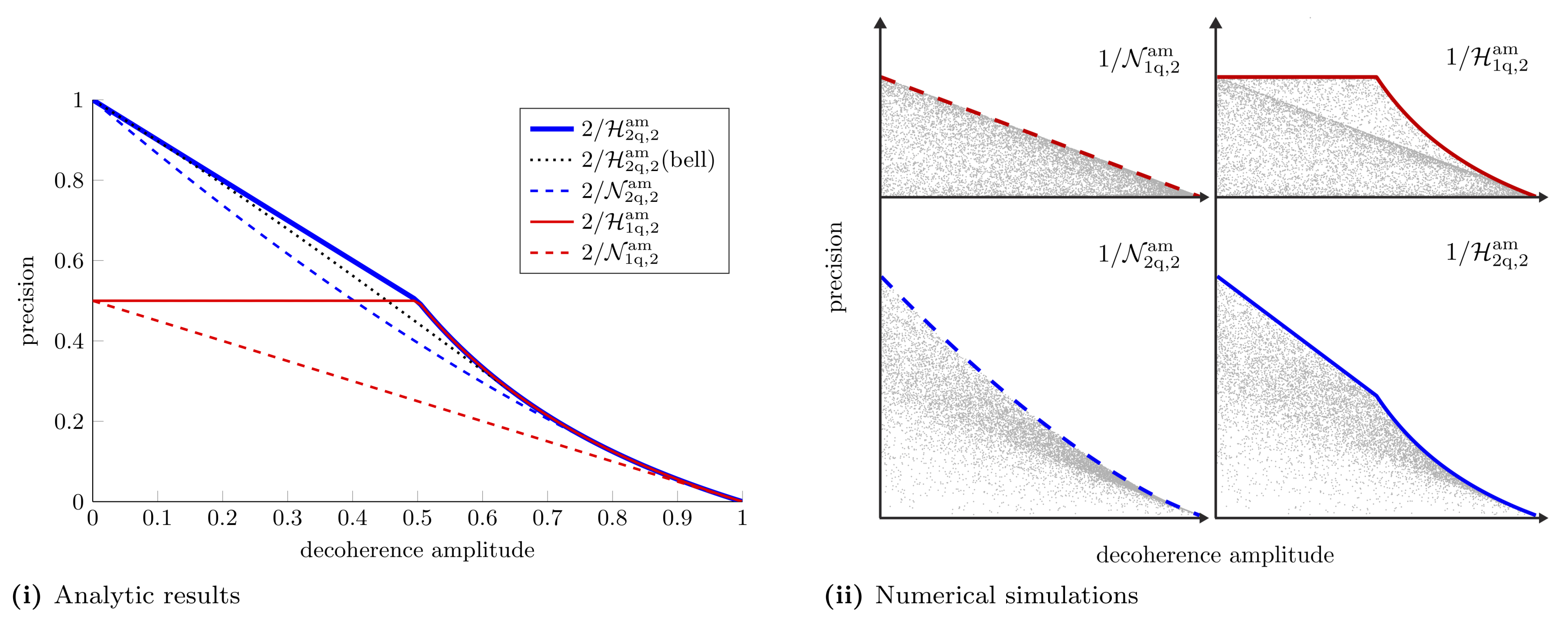
3.2.2. Two-Qubit Probe
3.2.3. Decoherence of Both Qubits
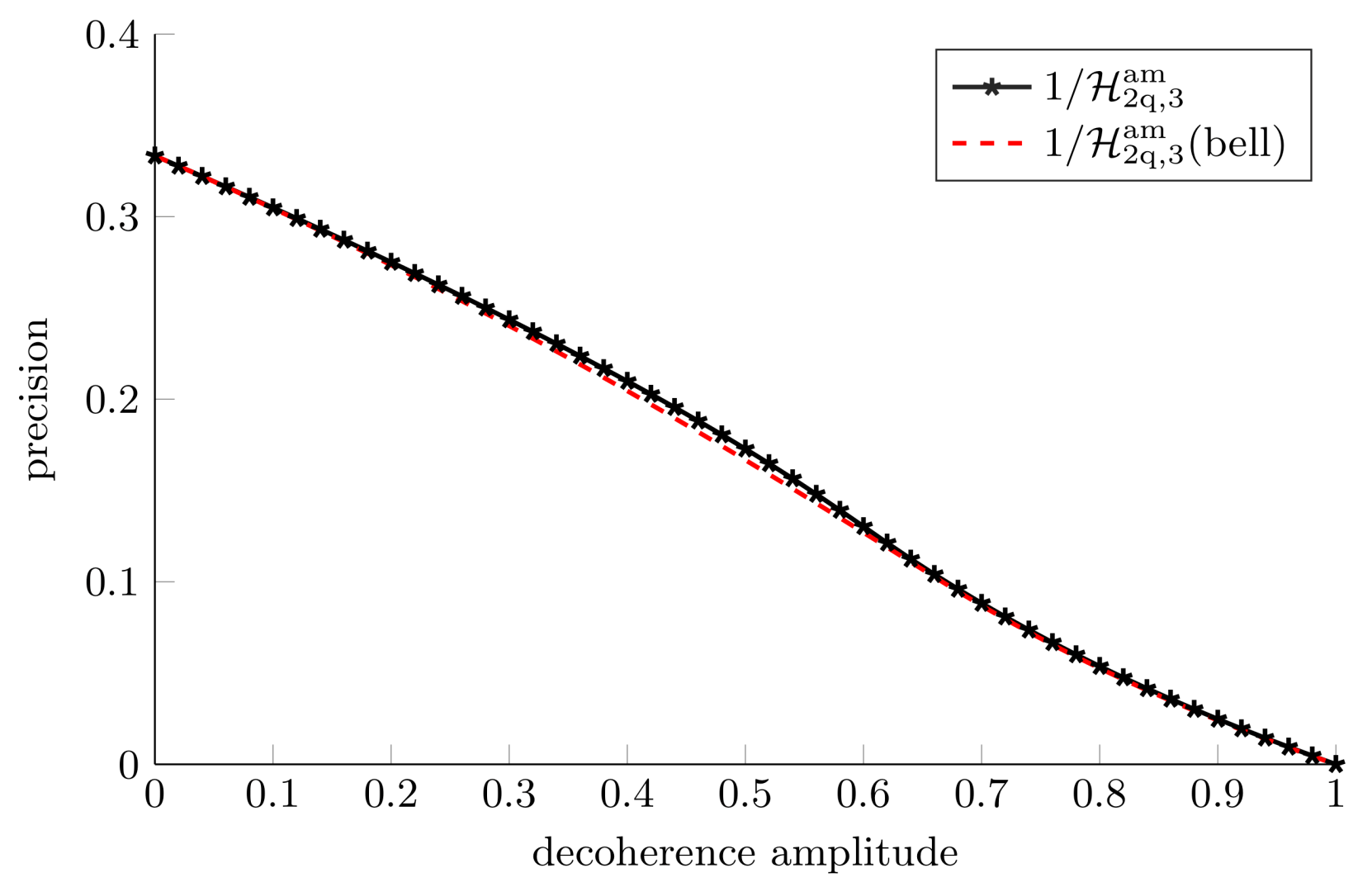
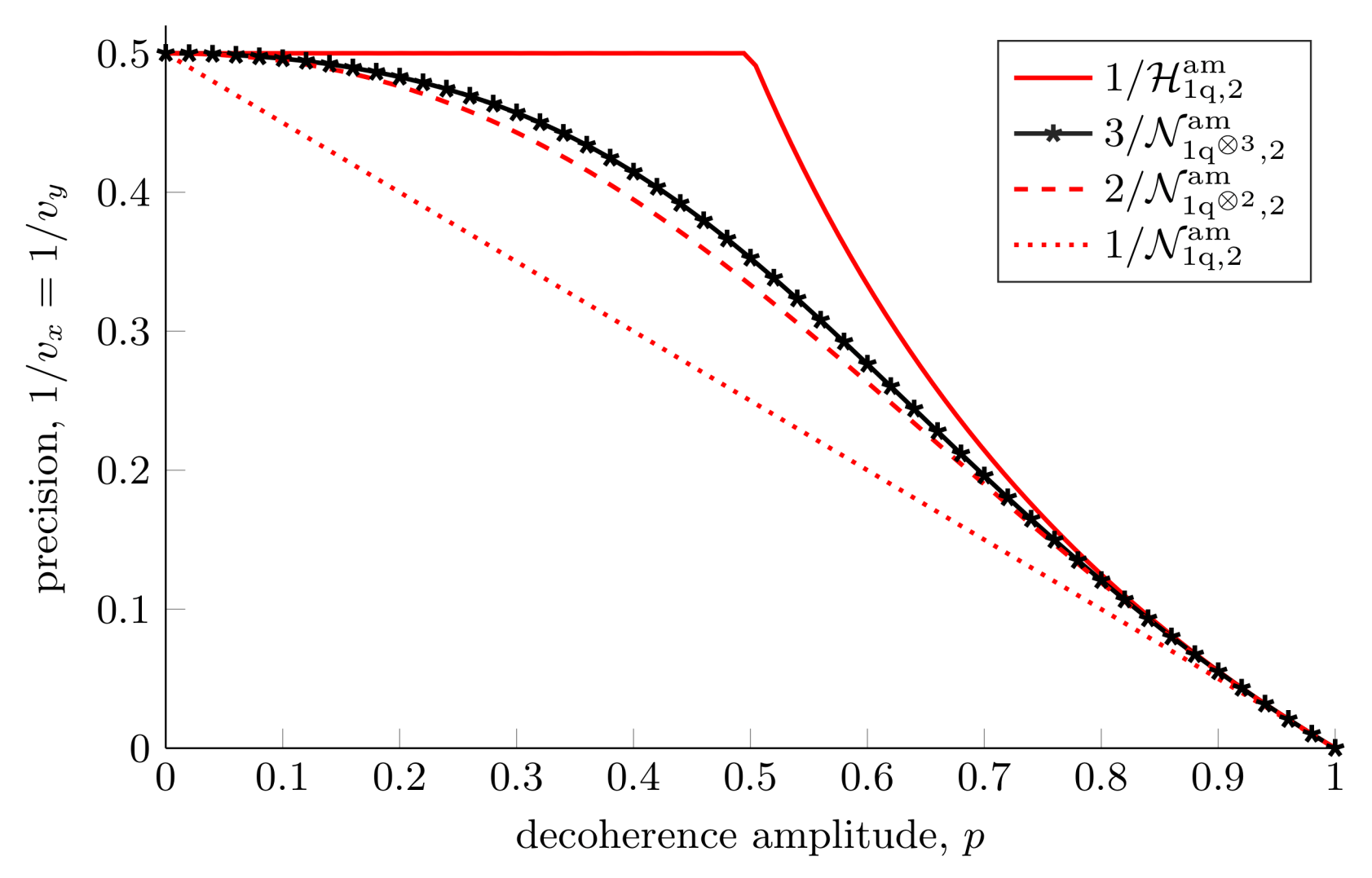
3.2.4. Collective Measurements on Multiple Copies of the State
3.3. Phase Damping Channel
3.3.1. Single-Qubit Probe
3.3.2. Two-Qubit Probe
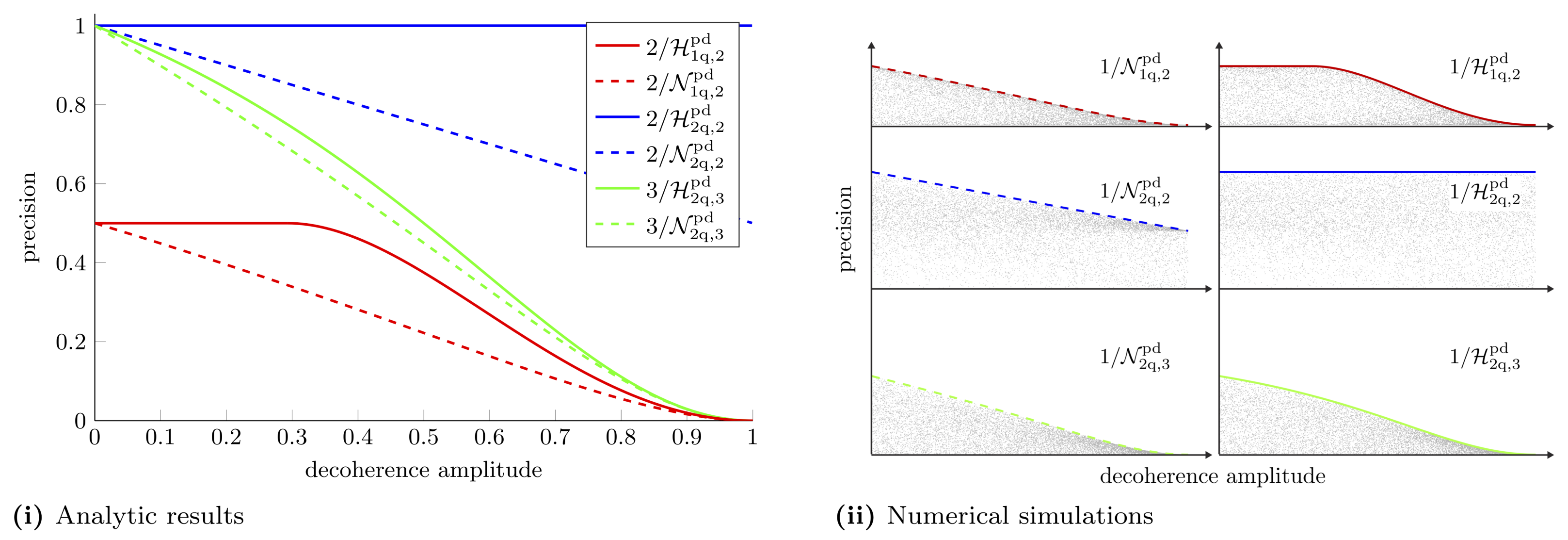
3.3.3. Decoherence of Both Qubits
3.3.4. Collective Measurements on Many Copies of the State
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Computing the SLD Bound for Single Parameter Estimation in the Decoherence Channel
Appendix B. Explicit Construction of Xx Matrix for Single Parameter Estimation in the Decoherence Channel
Appendix C. Measurement Scheme Attaining the Nagaoka Bound for Single Qubit Probes Subject to the Decoherence Channel
Appendix D. Measurement Saturating the Nagaoka Bound for Estimating Two Parameters with a Two-Qubit Probe Subject to the Decoherence Channel
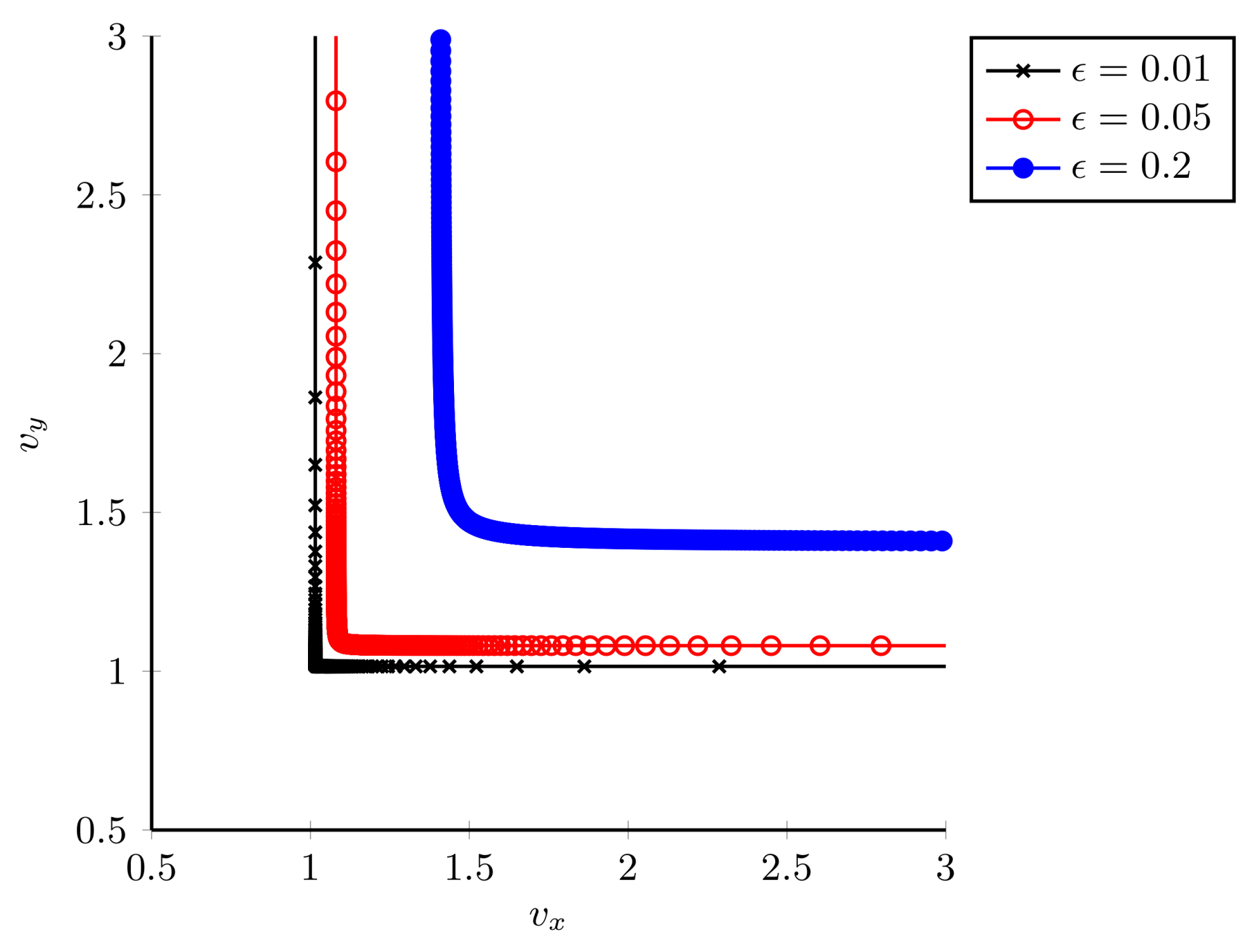
Appendix E. Measurement Scheme Required to Saturate the NHB for Estimating Three Parameters with the Optimal Two-Qubit Probe in the Decoherence Channel
Appendix F. Measurement Saturating the Nagaoka Bound for Estimating Two Parameters with Two Copies of a Single Qubit Probe Subject to the Decoherence Channel
Appendix G. POVM’s Attaining the Nagaoka Bound for Single Qubit Probes Subject to the Amplitude Damping Channel
Appendix H. Optimal Estimator for Estimating Two Parameters in the Amplitude Damping Channel with Two Copies of the Single-Qubit Probe
Appendix I. Explicit Construction of the Optimal Estimator for Estimating a Single Parameter in the Phase Damping Channel with a Single Qubit Probe
Appendix J. Explicit Construction of the Optimal Estimator for Estimating Two Parameters in the Phase Damping Channel with a Single Qubit Probe
Appendix K. Measurement Scheme Which Saturates the NHB for Estimating Three Parameters in the Phase Damping Channel with a Two-Qubit Probe
References
- Robertson, H.P. The uncertainty principle. Phys. Rev. 1929, 34, 163. [Google Scholar] [CrossRef]
- Arthurs, E.; Kelly, J. BSTJ briefs: On the simultaneous measurement of a pair of conjugate observables. Bell Syst. Tech. J. 1965, 44, 725–729. [Google Scholar] [CrossRef]
- Heisenberg, W. Über quantentheoretische Umdeutung kinematischer und mechanischer Beziehungen. In Original Scientific Papers Wissenschaftliche Originalarbeiten; Springer: Berlin/Heidelberg, Germany, 1985; pp. 382–396. [Google Scholar]
- Caves, C.M. Quantum-mechanical noise in an interferometer. Phys. Rev. D 1981, 23, 1693. [Google Scholar] [CrossRef]
- Barnett, S.M.; Fabre, C.; Maître, A. Ultimate quantum limits for resolution of beam displacements. Eur. Phys. J. D-At. Mol. Opt. Plasma Phys. 2003, 22, 513–519. [Google Scholar] [CrossRef]
- Dorner, U.; Demkowicz-Dobrzański, R.; Smith, B.; Lundeen, J.; Wasilewski, W.; Banaszek, K.; Walmsley, I. Optimal quantum phase estimation. Phys. Rev. Lett. 2009, 102, 040403. [Google Scholar] [CrossRef] [Green Version]
- Demkowicz-Dobrzański, R.; Dorner, U.; Smith, B.; Lundeen, J.; Wasilewski, W.; Banaszek, K.; Walmsley, I. Quantum phase estimation with lossy interferometers. Phys. Rev. A 2009, 80, 013825. [Google Scholar] [CrossRef] [Green Version]
- Zhuang, Q.; Zhang, Z.; Shapiro, J.H. Distributed quantum sensing using continuous-variable multipartite entanglement. Phys. Rev. A 2018, 97, 032329. [Google Scholar] [CrossRef] [Green Version]
- Ge, W.; Jacobs, K.; Eldredge, Z.; Gorshkov, A.V.; Foss-Feig, M. Distributed quantum metrology with linear networks and separable inputs. Phys. Rev. Lett. 2018, 121, 043604. [Google Scholar] [CrossRef] [Green Version]
- Conlon, L.O.; Michel, T.; Guccione, G.; McKenzie, K.; Assad, S.M.; Lam, P.K. Enhancing the precision limits of interferometric satellite geodesy missions. Npj Microgravity 2022, 8, 21. [Google Scholar] [CrossRef] [PubMed]
- Tsang, M.; Nair, R.; Lu, X.M. Quantum theory of superresolution for two incoherent optical point sources. Phys. Rev. X 2016, 6, 031033. [Google Scholar] [CrossRef] [Green Version]
- Tsang, M. Resolving starlight: A quantum perspective. Contemp. Phys. 2019, 60, 279–298. [Google Scholar] [CrossRef] [Green Version]
- Giovannetti, V.; Lloyd, S.; Maccone, L. Quantum-enhanced positioning and clock synchronization. Nature 2001, 412, 417. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lamine, B.; Fabre, C.; Treps, N. Quantum improvement of time transfer between remote clocks. Phys. Rev. Lett. 2008, 101, 123601. [Google Scholar] [CrossRef] [Green Version]
- Brady, A.J.; Gao, C.; Harnik, R.; Liu, Z.; Zhang, Z.; Zhuang, Q. Entangled sensor-networks for dark-matter searches. PRX Quantum 2022, 3, 030333. [Google Scholar] [CrossRef]
- Marchese, M.M.; Belenchia, A.; Paternostro, M. Optomechanics-based quantum estimation theory for collapse models. Entropy 2023, 25, 500. [Google Scholar] [CrossRef]
- Shi, H.; Zhuang, Q. Ultimate precision limit of noise sensing and dark matter search. Npj Quantum Inf. 2023, 9, 27. [Google Scholar] [CrossRef]
- Higgins, B.L.; Berry, D.W.; Bartlett, S.D.; Wiseman, H.M.; Pryde, G.J. Entanglement-free Heisenberg-limited phase estimation. Nature 2007, 450, 393–396. [Google Scholar] [CrossRef] [Green Version]
- Kacprowicz, M.; Demkowicz-Dobrzański, R.; Wasilewski, W.; Banaszek, K.; Walmsley, I. Experimental quantum-enhanced estimation of a lossy phase shift. Nat. Photonics 2010, 4, 357. [Google Scholar] [CrossRef]
- Yonezawa, H.; Nakane, D.; Wheatley, T.A.; Iwasawa, K.; Takeda, S.; Arao, H.; Ohki, K.; Tsumura, K.; Berry, D.W.; Ralph, T.C.; et al. Quantum-enhanced optical-phase tracking. Science 2012, 337, 1514–1517. [Google Scholar] [CrossRef] [Green Version]
- Girolami, D.; Souza, A.M.; Giovannetti, V.; Tufarelli, T.; Filgueiras, J.G.; Sarthour, R.S.; Soares-Pinto, D.O.; Oliveira, I.S.; Adesso, G. Quantum discord determines the interferometric power of quantum states. Phys. Rev. Lett. 2014, 112, 210401. [Google Scholar] [CrossRef] [Green Version]
- Strobel, H.; Muessel, W.; Linnemann, D.; Zibold, T.; Hume, D.B.; Pezzè, L.; Smerzi, A.; Oberthaler, M.K. Fisher information and entanglement of non-Gaussian spin states. Science 2014, 345, 424–427. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Slussarenko, S.; Weston, M.M.; Chrzanowski, H.M.; Shalm, L.K.; Verma, V.B.; Nam, S.W.; Pryde, G.J. Unconditional violation of the shot-noise limit in photonic quantum metrology. Nat. Photonics 2017, 11, 700–703. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Zheng, K.; Liu, F.; Zhao, W.; Tang, L.; Yonezawa, H.; Zhang, L.; Zhang, Y.; Xiao, M. Quantum-limited fiber-optic phase tracking beyond π range. Opt. Express 2019, 27, 2327–2334. [Google Scholar] [CrossRef]
- McCormick, K.C.; Keller, J.; Burd, S.C.; Wineland, D.J.; Wilson, A.C.; Leibfried, D. Quantum-enhanced sensing of a single-ion mechanical oscillator. Nature 2019, 572, 86–90. [Google Scholar] [CrossRef]
- Wang, W.; Wu, Y.; Ma, Y.; Cai, W.; Hu, L.; Mu, X.; Xu, Y.; Chen, Z.J.; Wang, H.; Song, Y.; et al. Heisenberg-limited single-mode quantum metrology in a superconducting circuit. Nat. Commun. 2019, 10, 4382. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Aasi, J.; Abadie, J.; Abbott, B.; Abbott, R.; Abbott, T.; Abernathy, M.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.; et al. Enhanced sensitivity of the LIGO gravitational wave detector by using squeezed states of light. Nat. Photonics 2013, 7, 613–619. [Google Scholar] [CrossRef] [Green Version]
- Guo, X.; Breum, C.R.; Borregaard, J.; Izumi, S.; Larsen, M.V.; Gehring, T.; Christandl, M.; Neergaard-Nielsen, J.S.; Andersen, U.L. Distributed quantum sensing in a continuous-variable entangled network. Nat. Phys. 2020, 16, 281–284. [Google Scholar] [CrossRef] [Green Version]
- Liu, L.Z.; Zhang, Y.Z.; Li, Z.D.; Zhang, R.; Yin, X.F.; Fei, Y.Y.; Li, L.; Liu, N.L.; Xu, F.; Chen, Y.A.; et al. Distributed quantum phase estimation with entangled photons. Nat. Photonics 2021, 15, 137–142. [Google Scholar] [CrossRef]
- Backes, K.M.; Palken, D.A.; Kenany, S.A.; Brubaker, B.M.; Cahn, S.; Droster, A.; Hilton, G.C.; Ghosh, S.; Jackson, H.; Lamoreaux, S.K.; et al. A quantum enhanced search for dark matter axions. Nature 2021, 590, 238–242. [Google Scholar] [CrossRef]
- Casacio, C.A.; Madsen, L.S.; Terrasson, A.; Waleed, M.; Barnscheidt, K.; Hage, B.; Taylor, M.A.; Bowen, W.P. Quantum-enhanced nonlinear microscopy. Nature 2021, 594, 201–206. [Google Scholar] [CrossRef]
- Marciniak, C.D.; Feldker, T.; Pogorelov, I.; Kaubruegger, R.; Vasilyev, D.V.; van Bijnen, R.; Schindler, P.; Zoller, P.; Blatt, R.; Monz, T. Optimal metrology with programmable quantum sensors. Nature 2022, 603, 604–609. [Google Scholar] [CrossRef]
- Malia, B.K.; Wu, Y.; Martínez-Rincón, J.; Kasevich, M.A. Distributed quantum sensing with mode-entangled spin-squeezed atomic states. Nature 2022, 612, 661–665. [Google Scholar] [CrossRef] [PubMed]
- Nielsen, J.A.H.; Neergaard-Nielsen, J.S.; Gehring, T.; Andersen, U.L. Deterministic Quantum Phase Estimation beyond N00N States. Phys. Rev. Lett. 2023, 130, 123603. [Google Scholar] [CrossRef]
- Baumgratz, T.; Datta, A. Quantum enhanced estimation of a multidimensional field. Phys. Rev. Lett. 2016, 116, 030801. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hou, Z.; Zhang, Z.; Xiang, G.Y.; Li, C.F.; Guo, G.C.; Chen, H.; Liu, L.; Yuan, H. Minimal tradeoff and ultimate precision limit of multiparameter quantum magnetometry under the parallel scheme. Phys. Rev. Lett. 2020, 125, 020501. [Google Scholar] [CrossRef] [PubMed]
- Montenegro, V.; Jones, G.S.; Bose, S.; Bayat, A. Sequential measurements for quantum-enhanced magnetometry in spin chain probes. Phys. Rev. Lett. 2022, 129, 120503. [Google Scholar] [CrossRef]
- Kaubruegger, R.; Shankar, A.; Vasilyev, D.V.; Zoller, P. Optimal and Variational Multi-Parameter Quantum Metrology and Vector Field Sensing. arXiv 2023, arXiv:2302.07785. [Google Scholar]
- Spagnolo, N.; Aparo, L.; Vitelli, C.; Crespi, A.; Ramponi, R.; Osellame, R.; Mataloni, P.; Sciarrino, F. Quantum interferometry with three-dimensional geometry. Sci. Rep. 2012, 2, 862. [Google Scholar] [CrossRef] [Green Version]
- Humphreys, P.C.; Barbieri, M.; Datta, A.; Walmsley, I.A. Quantum enhanced multiple phase estimation. Phys. Rev. Lett. 2013, 111, 070403. [Google Scholar] [CrossRef] [Green Version]
- Yue, J.D.; Zhang, Y.R.; Fan, H. Quantum-enhanced metrology for multiple phase estimation with noise. Sci. Rep. 2014, 4, 5933. [Google Scholar] [CrossRef] [Green Version]
- Gagatsos, C.N.; Branford, D.; Datta, A. Gaussian systems for quantum-enhanced multiple phase estimation. Phys. Rev. A 2016, 94, 042342. [Google Scholar] [CrossRef] [Green Version]
- Ciampini, M.A.; Spagnolo, N.; Vitelli, C.; Pezzè, L.; Smerzi, A.; Sciarrino, F. Quantum-enhanced multiparameter estimation in multiarm interferometers. Sci. Rep. 2016, 6, 28881. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pezzè, L.; Ciampini, M.A.; Spagnolo, N.; Humphreys, P.C.; Datta, A.; Walmsley, I.A.; Barbieri, M.; Sciarrino, F.; Smerzi, A. Optimal measurements for simultaneous quantum estimation of multiple phases. Phys. Rev. Lett. 2017, 119, 130504. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Chan, K.W.C. Quantum multiparameter estimation with generalized balanced multimode NOON-like states. Phys. Rev. A 2017, 95, 032321. [Google Scholar] [CrossRef] [Green Version]
- Crowley, P.J.; Datta, A.; Barbieri, M.; Walmsley, I.A. Tradeoff in simultaneous quantum-limited phase and loss estimation in interferometry. Phys. Rev. A 2014, 89, 023845. [Google Scholar] [CrossRef] [Green Version]
- Szczykulska, M.; Baumgratz, T.; Datta, A. Reaching for the quantum limits in the simultaneous estimation of phase and phase diffusion. Quantum Sci. Technol. 2017, 2, 044004. [Google Scholar] [CrossRef] [Green Version]
- Cimini, V.; Gianani, I.; Ruggiero, L.; Gasperi, T.; Sbroscia, M.; Roccia, E.; Tofani, D.; Bruni, F.; Ricci, M.A.; Barbieri, M. Quantum sensing for dynamical tracking of chemical processes. Phys. Rev. A 2019, 99, 053817. [Google Scholar] [CrossRef] [Green Version]
- Chrostowski, A.; Demkowicz-Dobrzański, R.; Jarzyna, M.; Banaszek, K. On super-resolution imaging as a multiparameter estimation problem. Int. J. Quantum Inf. 2017, 15, 1740005. [Google Scholar] [CrossRef] [Green Version]
- Řehaček, J.; Hradil, Z.; Stoklasa, B.; Paúr, M.; Grover, J.; Krzic, A.; Sánchez-Soto, L. Multiparameter quantum metrology of incoherent point sources: Towards realistic superresolution. Phys. Rev. A 2017, 96, 062107. [Google Scholar] [CrossRef] [Green Version]
- Chiribella, G.; D’Ariano, G.; Sacchi, M. Joint estimation of real squeezing and displacement. J. Phys. A Math. Gen. 2006, 39, 2127. [Google Scholar] [CrossRef] [Green Version]
- Monras, A.; Illuminati, F. Measurement of damping and temperature: Precision bounds in Gaussian dissipative channels. Phys. Rev. A 2011, 83, 012315. [Google Scholar] [CrossRef] [Green Version]
- Genoni, M.; Paris, M.; Adesso, G.; Nha, H.; Knight, P.; Kim, M. Optimal estimation of joint parameters in phase space. Phys. Rev. A 2013, 87, 012107. [Google Scholar] [CrossRef] [Green Version]
- Gao, Y.; Lee, H. Bounds on quantum multiple-parameter estimation with Gaussian state. Eur. Phys. J. D 2014, 68, 347. [Google Scholar] [CrossRef] [Green Version]
- Bradshaw, M.; Assad, S.M.; Lam, P.K. A tight Cramér–Rao bound for joint parameter estimation with a pure two-mode squeezed probe. Phys. Lett. A 2017, 381, 2598–2607. [Google Scholar] [CrossRef] [Green Version]
- Bradshaw, M.; Lam, P.K.; Assad, S.M. Ultimate precision of joint quadrature parameter estimation with a Gaussian probe. Phys. Rev. A 2018, 97, 012106. [Google Scholar] [CrossRef] [Green Version]
- Assad, S.M.; Li, J.; Liu, Y.; Zhao, N.; Zhao, W.; Lam, P.K.; Ou, Z.; Li, X. Accessible precisions for estimating two conjugate parameters using Gaussian probes. Phys. Rev. Res. 2020, 2, 023182. [Google Scholar] [CrossRef]
- Park, K.; Oh, C.; Filip, R.; Marek, P. Optimal estimation of conjugate shifts in position and momentum by classically correlated probes and measurements. Phys. Rev. Appl. 2022, 18, 014060. [Google Scholar] [CrossRef]
- Steinlechner, S.; Bauchrowitz, J.; Meinders, M.; Müller-Ebhardt, H.; Danzmann, K.; Schnabel, R. Quantum-dense metrology. Nat. Photonics 2013, 7, 626–630. [Google Scholar] [CrossRef] [Green Version]
- Vidrighin, M.D.; Donati, G.; Genoni, M.G.; Jin, X.M.; Kolthammer, W.S.; Kim, M.; Datta, A.; Barbieri, M.; Walmsley, I.A. Joint estimation of phase and phase diffusion for quantum metrology. Nat. Commun. 2014, 5, 3532. [Google Scholar] [CrossRef] [Green Version]
- Hou, Z.; Zhu, H.; Xiang, G.Y.; Li, C.F.; Guo, G.C. Achieving quantum precision limit in adaptive qubit state tomography. Npj Quantum Inf. 2016, 2, 16001. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Li, J.; Cui, L.; Huo, N.; Assad, S.M.; Li, X.; Ou, Z. Loss-tolerant quantum dense metrology with SU(1, 1) interferometer. Opt. Express 2018, 26, 27705–27715. [Google Scholar] [CrossRef] [PubMed]
- Li, B.; Conlon, L.O.; Lam, P.K.; Assad, S.M. Optimal Single Qubit Tomography: Realization of Locally Optimal Measurements on a Quantum Computer. arXiv 2023, arXiv:2302.05140. [Google Scholar]
- Vaneph, C.; Tufarelli, T.; Genoni, M.G. Quantum estimation of a two-phase spin rotation. Quantum Meas. Quantum Metrol. 2013, 1, 12–20. [Google Scholar] [CrossRef]
- Suzuki, J. Parameter estimation of qubit states with unknown phase parameter. Int. J. Quantum Inf. 2015, 13, 1450044. [Google Scholar] [CrossRef] [Green Version]
- Suzuki, J. Explicit formula for the Holevo bound for two-parameter qubit-state estimation problem. J. Math. Phys. 2016, 57, 042201. [Google Scholar] [CrossRef]
- Szczykulska, M.; Baumgratz, T.; Datta, A. Multi-parameter quantum metrology. Adv. Phys. X 2016, 1, 621–639. [Google Scholar] [CrossRef] [Green Version]
- Proctor, T.J.; Knott, P.A.; Dunningham, J.A. Multiparameter estimation in networked quantum sensors. Phys. Rev. Lett. 2018, 120, 080501. [Google Scholar] [CrossRef] [Green Version]
- Gessner, M.; Pezzè, L.; Smerzi, A. Sensitivity bounds for multiparameter quantum metrology. Phys. Rev. Lett. 2018, 121, 130503. [Google Scholar] [CrossRef] [Green Version]
- Tsang, M.; Albarelli, F.; Datta, A. Quantum Semiparametric Estimation. Phys. Rev. X 2020, 10, 031023. [Google Scholar] [CrossRef]
- Carollo, A.; Spagnolo, B.; Dubkov, A.A.; Valenti, D. On quantumness in multi-parameter quantum estimation. J. Stat. Mech. Theory Exp. 2019, 2019, 094010. [Google Scholar] [CrossRef] [Green Version]
- Demkowicz-Dobrzański, R.; Górecki, W.; Guţă, M. Multi-parameter estimation beyond quantum Fisher information. J. Phys. A Math. Theor. 2020, in press. [Google Scholar] [CrossRef]
- Razavian, S.; Paris, M.G.; Genoni, M.G. On the quantumness of multiparameter estimation problems for qubit systems. Entropy 2020, 22, 1197. [Google Scholar] [CrossRef]
- Gessner, M.; Smerzi, A.; Pezzè, L. Multiparameter squeezing for optimal quantum enhancements in sensor networks. Nat. Commun. 2020, 11, 3817. [Google Scholar] [CrossRef] [PubMed]
- Lu, X.M.; Wang, X. Incorporating Heisenberg’s uncertainty principle into quantum multiparameter estimation. Phys. Rev. Lett. 2021, 126, 120503. [Google Scholar] [CrossRef] [PubMed]
- Gebhart, V.; Smerzi, A.; Pezzè, L. Bayesian quantum multiphase estimation algorithm. Phys. Rev. Appl. 2021, 16, 014035. [Google Scholar] [CrossRef]
- Albarelli, F.; Demkowicz-Dobrzański, R. Probe incompatibility in multiparameter noisy quantum metrology. Phys. Rev. X 2022, 12, 011039. [Google Scholar] [CrossRef]
- Huang, Z.; Lupo, C.; Kok, P. Quantum-limited estimation of range and velocity. PRX Quantum 2021, 2, 030303. [Google Scholar] [CrossRef]
- Gianani, I.; Albarelli, F.; Verna, A.; Cimini, V.; Demkowicz-Dobrzanski, R.; Barbieri, M. Kramers–Kronig relations and precision limits in quantum phase estimation. Optica 2021, 8, 1642–1645. [Google Scholar] [CrossRef]
- Hanamura, F.; Asavanant, W.; Fukui, K.; Konno, S.; Furusawa, A. Estimation of Gaussian random displacement using non-Gaussian states. Phys. Rev. A 2021, 104, 062601. [Google Scholar] [CrossRef]
- Di Fresco, G.; Spagnolo, B.; Valenti, D.; Carollo, A. Multiparameter quantum critical metrology. SciPost Phys. 2022, 13, 077. [Google Scholar] [CrossRef]
- Hosseiny, S.M.; Jahromi, H.R.; Radgohar, R.; Amniat-Talab, M. Estimating energy levels of a three-level atom in single and multi-parameter metrological schemes. Phys. Scr. 2022, 97, 125402. [Google Scholar] [CrossRef]
- Fadel, M.; Yadin, B.; Mao, Y.; Byrnes, T.; Gessner, M. Multiparameter quantum metrology and mode entanglement with spatially split nonclassical spin states. arXiv 2022, arXiv:2201.11081. [Google Scholar]
- Len, Y.L. Multiparameter estimation for qubit states with collective measurements: A case study. New J. Phys. 2022, 24, 033037. [Google Scholar] [CrossRef]
- Xie, D.; Xu, C.; Wang, A.M. Quantum thermometry in diffraction-limited systems. Phys. Rev. A 2022, 106, 052407. [Google Scholar] [CrossRef]
- Liu, J.; Yuan, H.; Lu, X.M.; Wang, X. Quantum Fisher information matrix and multiparameter estimation. J. Phys. A Math. Theor. 2019, 53, 023001. [Google Scholar] [CrossRef]
- Albarelli, F.; Barbieri, M.; Genoni, M.G.; Gianani, I. A perspective on multiparameter quantum metrology: From theoretical tools to applications in quantum imaging. Phys. Lett. A 2020, 384, 126311. [Google Scholar] [CrossRef] [Green Version]
- Sidhu, J.S.; Kok, P. Geometric perspective on quantum parameter estimation. AVS Quantum Sci. 2020, 2, 014701. [Google Scholar] [CrossRef] [Green Version]
- Polino, E.; Valeri, M.; Spagnolo, N.; Sciarrino, F. Photonic quantum metrology. AVS Quantum Sci. 2020, 2, 024703. [Google Scholar] [CrossRef]
- Bennett, C.H.; Shor, P.W. Quantum information theory. IEEE Trans. Inf. Theory 1998, 44, 2724–2742. [Google Scholar] [CrossRef] [Green Version]
- Giovannetti, V.; Lloyd, S.; Maccone, L. Quantum metrology. Phys. Rev. Lett. 2006, 96, 010401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Matsumoto, K. A new approach to the Cramér-Rao-type bound of the pure-state model. J. Phys. A Math. Gen. 2002, 35, 3111–3123. [Google Scholar] [CrossRef] [Green Version]
- Helstrom, C.W. Minimum mean-squared error of estimates in quantum statistics. Phys. Lett. A 1967, 25, 101–102. [Google Scholar] [CrossRef]
- Helstrom, C.W. The minimum variance of estimates in quantum signal detection. IEEE Trans. Inf. Theory 1968, 14, 234–242. [Google Scholar] [CrossRef]
- Yuen, H.; Lax, M. Multiple-parameter quantum estimation and measurement of nonselfadjoint observables. IEEE Trans. Inf. Theory 1973, 19, 740–750. [Google Scholar] [CrossRef]
- Holevo, A.S. Probabilistic and Statistical Aspects of Quantum Theory; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011; Volume 1. [Google Scholar]
- Holevo, A.S. Statistical decision theory for quantum systems. J. Multivar. Anal. 1973, 3, 337–394. [Google Scholar] [CrossRef] [Green Version]
- Kahn, J.; Guţă, M. Local asymptotic normality for finite dimensional quantum systems. Commun. Math. Phys. 2009, 289, 597–652. [Google Scholar] [CrossRef] [Green Version]
- Yamagata, K.; Fujiwara, A.; Gill, R.D. Quantum local asymptotic normality based on a new quantum likelihood ratio. Ann. Stat. 2013, 41, 2197–2217. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.; Chiribella, G.; Hayashi, M. Attaining the ultimate precision limit in quantum state estimation. Commun. Math. Phys. 2019, 368, 223–293. [Google Scholar] [CrossRef] [Green Version]
- Yu, M.; Liu, Y.; Yang, P.; Gong, M.; Cao, Q.; Zhang, S.; Liu, H.; Heyl, M.; Ozawa, T.; Goldman, N.; et al. Quantum Fisher information measurement and verification of the quantum Cramér–Rao bound in a solid-state qubit. Npj Quantum Inf. 2022, 8, 56. [Google Scholar] [CrossRef]
- Li, C.; Chen, M.; Cappellaro, P. A geometric perspective: Experimental evaluation of the quantum Cramer-Rao bound. arXiv 2022, arXiv:2204.13777. [Google Scholar]
- Conlon, L.O.; Suzuki, J.; Lam, P.K.; Assad, S.M. The gap persistence theorem for quantum multiparameter estimation. arXiv 2022, arXiv:2208.07386. [Google Scholar]
- Nagaoka, H. A new approach to Cramér–Rao bounds for quantum state estimation. In Asymptotic Theory of Quantum Statistical Inference: Selected Papers; World Scientific: Singapore, 2005; pp. 100–112. [Google Scholar]
- Hayashi, M. A linear programming approach to attainable Cramer-Rao type bounds. In Asymptotic Theory of Quantum Statistical Inference: Selected Papers; World Scientific: Singapore, 1997; pp. 150–161. [Google Scholar]
- Conlon, L.O.; Suzuki, J.; Lam, P.K.; Assad, S.M. Efficient computation of the Nagaoka–Hayashi bound for multiparameter estimation with separable measurements. Npj Quantum Inf. 2021, 7, 110. [Google Scholar] [CrossRef]
- Nagaoka, H. A generalization of the simultaneous diagonalization of Hermitian matrices and its relation to quantum estimation theory. In Asymptotic Theory of Quantum Statistical Inference: Selected Papers; World Scientific: Singapore, 2005; pp. 133–149. [Google Scholar]
- Hayashi, M.; Ouyang, Y. Tight Cramér-Rao type bounds for multiparameter quantum metrology through conic programming. arXiv 2022, arXiv:2209.05218. [Google Scholar]
- Roccia, E.; Gianani, I.; Mancino, L.; Sbroscia, M.; Somma, F.; Genoni, M.G.; Barbieri, M. Entangling measurements for multiparameter estimation with two qubits. Quantum Sci. Technol. 2017, 3, 01LT01. [Google Scholar] [CrossRef] [Green Version]
- Hou, Z.; Tang, J.F.; Shang, J.; Zhu, H.; Li, J.; Yuan, Y.; Wu, K.D.; Xiang, G.Y.; Li, C.F.; Guo, G.C. Deterministic realization of collective measurements via photonic quantum walks. Nat. Commun. 2018, 9, 1414. [Google Scholar] [CrossRef]
- Parniak, M.; Borówka, S.; Boroszko, K.; Wasilewski, W.; Banaszek, K.; Demkowicz-Dobrzański, R. Beating the Rayleigh limit using two-photon interference. Phys. Rev. Lett. 2018, 121, 250503. [Google Scholar] [CrossRef] [Green Version]
- Wu, K.D.; Yuan, Y.; Xiang, G.Y.; Li, C.F.; Guo, G.C.; Perarnau-Llobet, M. Experimentally reducing the quantum measurement back action in work distributions by a collective measurement. Sci. Adv. 2019, 5, eaav4944. [Google Scholar] [CrossRef] [Green Version]
- Wu, K.D.; Bäumer, E.; Tang, J.F.; Hovhannisyan, K.V.; Perarnau-Llobet, M.; Xiang, G.Y.; Li, C.F.; Guo, G.C. Minimizing backaction through entangled measurements. Phys. Rev. Lett. 2020, 125, 210401. [Google Scholar] [CrossRef]
- Yuan, Y.; Hou, Z.; Tang, J.F.; Streltsov, A.; Xiang, G.Y.; Li, C.F.; Guo, G.C. Direct estimation of quantum coherence by collective measurements. Npj Quantum Inf. 2020, 6, 46. [Google Scholar] [CrossRef]
- Conlon, L.O.; Vogl, T.; Marciniak, C.D.; Pogorelov, I.; Yung, S.K.; Eilenberger, F.; Berry, D.W.; Santana, F.S.; Blatt, R.; Monz, T.; et al. Approaching optimal entangling collective measurements on quantum computing platforms. Nat. Phys. 2023, 19, 351–357. [Google Scholar] [CrossRef]
- Conlon, L.O.; Eilenberger, F.; Lam, P.K.; Assad, S.M. Discriminating qubit states with entangling collective measurements. arXiv 2023, arXiv:2302.08882. [Google Scholar]
- Martínez, D.; Gómez, E.S.; Cariñe, J.; Pereira, L.; Delgado, A.; Walborn, S.P.; Tavakoli, A.; Lima, G. Certification of a non-projective qudit measurement using multiport beamsplitters. Nat. Phys. 2023, 19, 190–195. [Google Scholar] [CrossRef]
- Albarelli, F.; Friel, J.F.; Datta, A. Evaluating the Holevo Cramér-Rao Bound for Multiparameter Quantum Metrology. Phys. Rev. Lett. 2019, 123, 200503. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sidhu, J.S.; Ouyang, Y.; Campbell, E.T.; Kok, P. Tight Bounds on the Simultaneous Estimation of Incompatible Parameters. Phys. Rev. X 2021, 11, 011028. [Google Scholar] [CrossRef]
- Genoni, M.G.; Olivares, S.; Paris, M.G. Optical phase estimation in the presence of phase diffusion. Phys. Rev. Lett. 2011, 106, 153603. [Google Scholar] [CrossRef] [PubMed]
- Datta, A.; Zhang, L.; Thomas-Peter, N.; Dorner, U.; Smith, B.J.; Walmsley, I.A. Quantum metrology with imperfect states and detectors. Phys. Rev. A 2011, 83, 063836. [Google Scholar] [CrossRef] [Green Version]
- Ragy, S.; Jarzyna, M.; Demkowicz-Dobrzański, R. Compatibility in multiparameter quantum metrology. Phys. Rev. A 2016, 94, 052108. [Google Scholar] [CrossRef] [Green Version]
- Kull, I.; Guérin, P.A.; Verstraete, F. Uncertainty and trade-offs in quantum multiparameter estimation. J. Phys. A Math. Theor. 2020, 53, 244001. [Google Scholar] [CrossRef] [Green Version]
- Ballester, M.A. Optimal estimation of SU (d) using exact and approximate 2-designs. arXiv 2005, arXiv:quant-ph/0507073. [Google Scholar]
- Imai, H.; Fujiwara, A. Geometry of optimal estimation scheme for SU (D) channels. J. Phys. A Math. Theor. 2007, 40, 4391. [Google Scholar] [CrossRef]
- Napolitano, M.; Koschorreck, M.; Dubost, B.; Behbood, N.; Sewell, R.; Mitchell, M.W. Interaction-based quantum metrology showing scaling beyond the Heisenberg limit. Nature 2011, 471, 486–489. [Google Scholar] [CrossRef] [Green Version]
- Hayashi, M.; Liu, Z.W.; Yuan, H. Global Heisenberg scaling in noisy and practical phase estimation. Quantum Sci. Technol. 2022, 7, 025030. [Google Scholar] [CrossRef]
- Pinel, O.; Jian, P.; Treps, N.; Fabre, C.; Braun, D. Quantum parameter estimation using general single-mode Gaussian states. Phys. Rev. A 2013, 88, 040102. [Google Scholar] [CrossRef] [Green Version]
- Holevo, A. Noncommutative analogues of the Cramér-Rao inequality in the quantum measurement theory. In Proceedings of the Third Japan—USSR Symposium on Probability Theory; Springer: Berlin/Heidelberg, Germany, 1976; pp. 194–222. [Google Scholar]
- Gill, R.D.; Massar, S. State estimation for large ensembles. Phys. Rev. A 2000, 61, 042312. [Google Scholar] [CrossRef] [Green Version]
- Suzuki, J. Information Geometrical Characterization of Quantum Statistical Models in Quantum Estimation Theory. Entropy 2019, 21, 703. [Google Scholar] [CrossRef]
- Kraus, K. States, Effects and Operations: Fundamental Notions of Quantum Theory; Springer: Berlin/Heidelberg, Germany, 1983. [Google Scholar]
- Serafini, A. Quantum Continuous Variables: A Primer of Theoretical Methods; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Suzuki, J. Nuisance parameter problem in quantum estimation theory: Tradeoff relation and qubit examples. J. Phys. A Math. Theor. 2020, 53, 264001. [Google Scholar] [CrossRef]
- Suzuki, J.; Yang, Y.; Hayashi, M. Quantum state estimation with nuisance parameters. J. Phys. A Math. Theor. 2020, in press. [Google Scholar] [CrossRef]
- Ozaydin, F. Phase damping destroys quantum Fisher information of W states. Phys. Lett. A 2014, 378, 3161–3164. [Google Scholar] [CrossRef] [Green Version]
- Ma, J.; Huang, Y.X.; Wang, X.; Sun, C. Quantum Fisher information of the Greenberger-Horne-Zeilinger state in decoherence channels. Phys. Rev. A 2011, 84, 022302. [Google Scholar] [CrossRef] [Green Version]
- Huelga, S.F.; Macchiavello, C.; Pellizzari, T.; Ekert, A.K.; Plenio, M.B.; Cirac, J.I. Improvement of frequency standards with quantum entanglement. Phys. Rev. Lett. 1997, 79, 3865. [Google Scholar] [CrossRef] [Green Version]
- Myatt, C.J.; King, B.E.; Turchette, Q.A.; Sackett, C.A.; Kielpinski, D.; Itano, W.M.; Monroe, C.; Wineland, D.J. Decoherence of quantum superpositions through coupling to engineered reservoirs. Nature 2000, 403, 269–273. [Google Scholar] [CrossRef]
- Turchette, Q.; Myatt, C.; King, B.; Sackett, C.; Kielpinski, D.; Itano, W.; Monroe, C.; Wineland, D. Decoherence and decay of motional quantum states of a trapped atom coupled to engineered reservoirs. Phys. Rev. A 2000, 62, 053807. [Google Scholar] [CrossRef]
- Nielsen, M.A.; Chuang, I. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Fujiwara, A. Estimation of SU (2) operation and dense coding: An information geometric approach. Phys. Rev. A 2001, 65, 012316. [Google Scholar] [CrossRef] [Green Version]
- Demkowicz-Dobrzański, R.; Kołodyński, J.; Guţă, M. The elusive Heisenberg limit in quantum-enhanced metrology. Nat. Commun. 2012, 3, 1063. [Google Scholar] [CrossRef] [Green Version]
- Hayashi, M.; Matsumoto, K. Asymptotic performance of optimal state estimation in qubit system. J. Math. Phys. 2008, 49, 102101. [Google Scholar] [CrossRef]
- Friel, J.; Palittapongarnpim, P.; Albarelli, F.; Datta, A. Attainability of the Holevo-Cramér-Rao bound for two-qubit 3D magnetometry. arXiv 2020, arXiv:2008.01502. [Google Scholar]
- Hayashi, M. Quantum Information Theory; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Šafránek, D. Discontinuities of the quantum Fisher information and the Bures metric. Phys. Rev. A 2017, 95, 052320. [Google Scholar] [CrossRef] [Green Version]
- Šafránek, D. Simple expression for the quantum Fisher information matrix. Phys. Rev. A 2018, 97, 042322. [Google Scholar] [CrossRef] [Green Version]
- Seveso, L.; Albarelli, F.; Genoni, M.G.; Paris, M.G. On the discontinuity of the quantum Fisher information for quantum statistical models with parameter dependent rank. J. Phys. A Math. Theor. 2019, 53, 02LT01. [Google Scholar] [CrossRef] [Green Version]
- Rezakhani, A.; Hassani, M.; Alipour, S. Continuity of the quantum Fisher information. Phys. Rev. A 2019, 100, 032317. [Google Scholar] [CrossRef] [Green Version]
- Goldberg, A.Z.; Romero, J.L.; Sanz, Á.S.; Sánchez-Soto, L.L. Taming singularities of the quantum Fisher information. Int. J. Quantum Inf. 2021, 19, 2140004. [Google Scholar] [CrossRef]
- Ye, Y.; Lu, X.M. Quantum Cramér-Rao bound for quantum statistical models with parameter-dependent rank. Phys. Rev. A 2022, 106, 022429. [Google Scholar] [CrossRef]
- Suzuki, J. Bayesian Nagaoka-Hayashi Bound for Multiparameter Quantum-State Estimation Problem. arXiv 2023, arXiv:2302.14223. [Google Scholar]
- Rubio, J.; Dunningham, J. Bayesian multiparameter quantum metrology with limited data. Phys. Rev. A 2020, 101, 032114. [Google Scholar] [CrossRef] [Green Version]
- Thearle, O.; Assad, S.M.; Symul, T. Estimation of output-channel noise for continuous-variable quantum key distribution. Phys. Rev. A 2016, 93, 042343. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.; Yin, Z.Q.; Wang, S.; Chen, W.; Guo, G.C.; Han, Z.F. Measurement-device-independent quantum key distribution robust against environmental disturbances. Optica 2017, 4, 1016–1023. [Google Scholar] [CrossRef]
- Wang, S.; Yin, Z.Q.; He, D.Y.; Chen, W.; Wang, R.Q.; Ye, P.; Zhou, Y.; Fan-Yuan, G.J.; Wang, F.X.; Chen, W.; et al. Twin-field quantum key distribution over 830-km fibre. Nat. Photonics 2022, 16, 154–161. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Conlon, L.O.; Lam, P.K.; Assad, S.M. Multiparameter Estimation with Two-Qubit Probes in Noisy Channels. Entropy 2023, 25, 1122. https://doi.org/10.3390/e25081122
Conlon LO, Lam PK, Assad SM. Multiparameter Estimation with Two-Qubit Probes in Noisy Channels. Entropy. 2023; 25(8):1122. https://doi.org/10.3390/e25081122
Chicago/Turabian StyleConlon, Lorcán O., Ping Koy Lam, and Syed M. Assad. 2023. "Multiparameter Estimation with Two-Qubit Probes in Noisy Channels" Entropy 25, no. 8: 1122. https://doi.org/10.3390/e25081122
APA StyleConlon, L. O., Lam, P. K., & Assad, S. M. (2023). Multiparameter Estimation with Two-Qubit Probes in Noisy Channels. Entropy, 25(8), 1122. https://doi.org/10.3390/e25081122





