The Kaniadakis Distribution for the Analysis of Income and Wealth Data
Abstract
1. Introduction
2. The -Generalized Model for Income Distribution
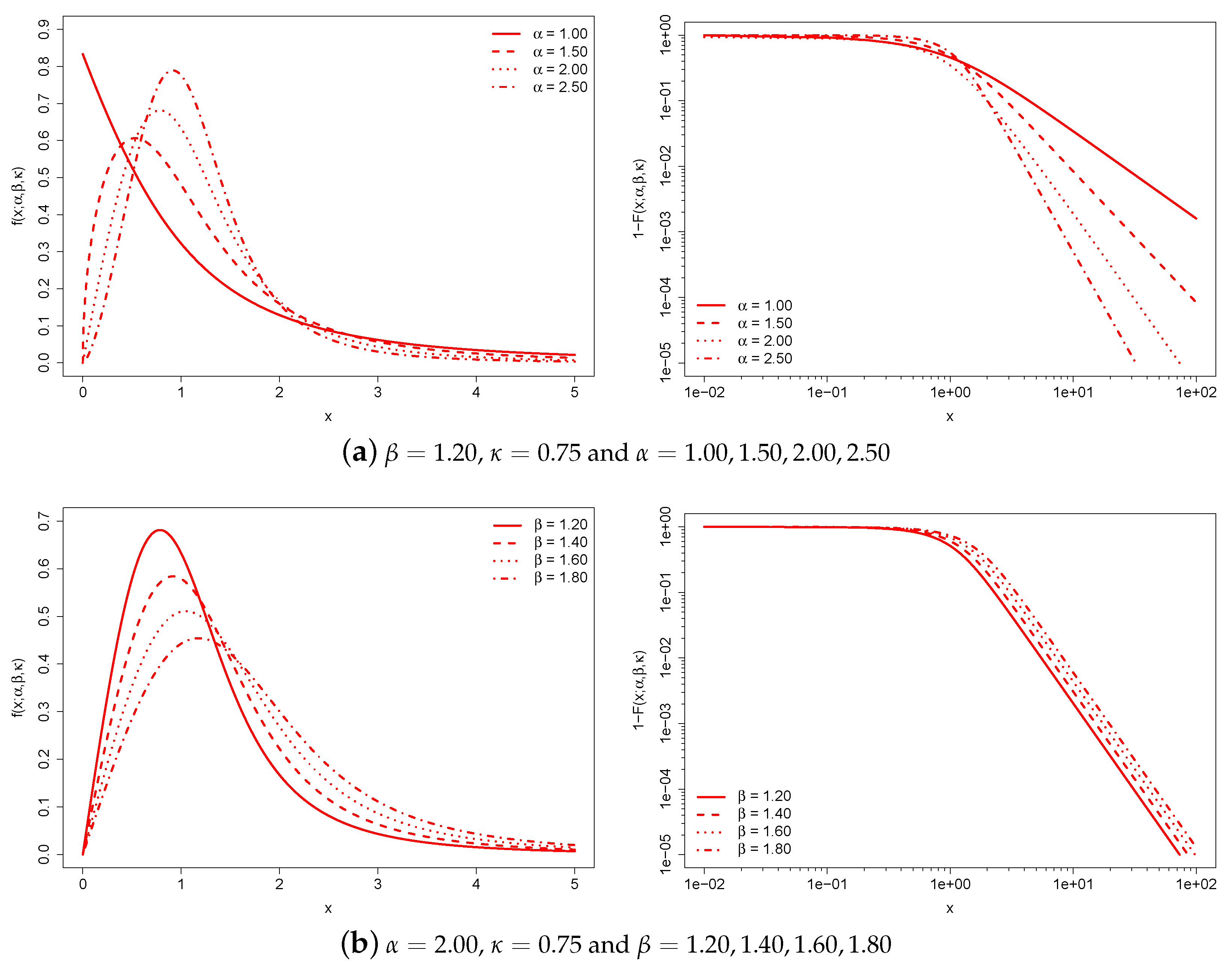
2.1. Definitions and Basic Properties
2.2. Measuring Income Inequality Using the -Generalized Distribution
2.3. Estimation
3. Application to the Income Distribution in Greece
3.1. Description of the Income Data
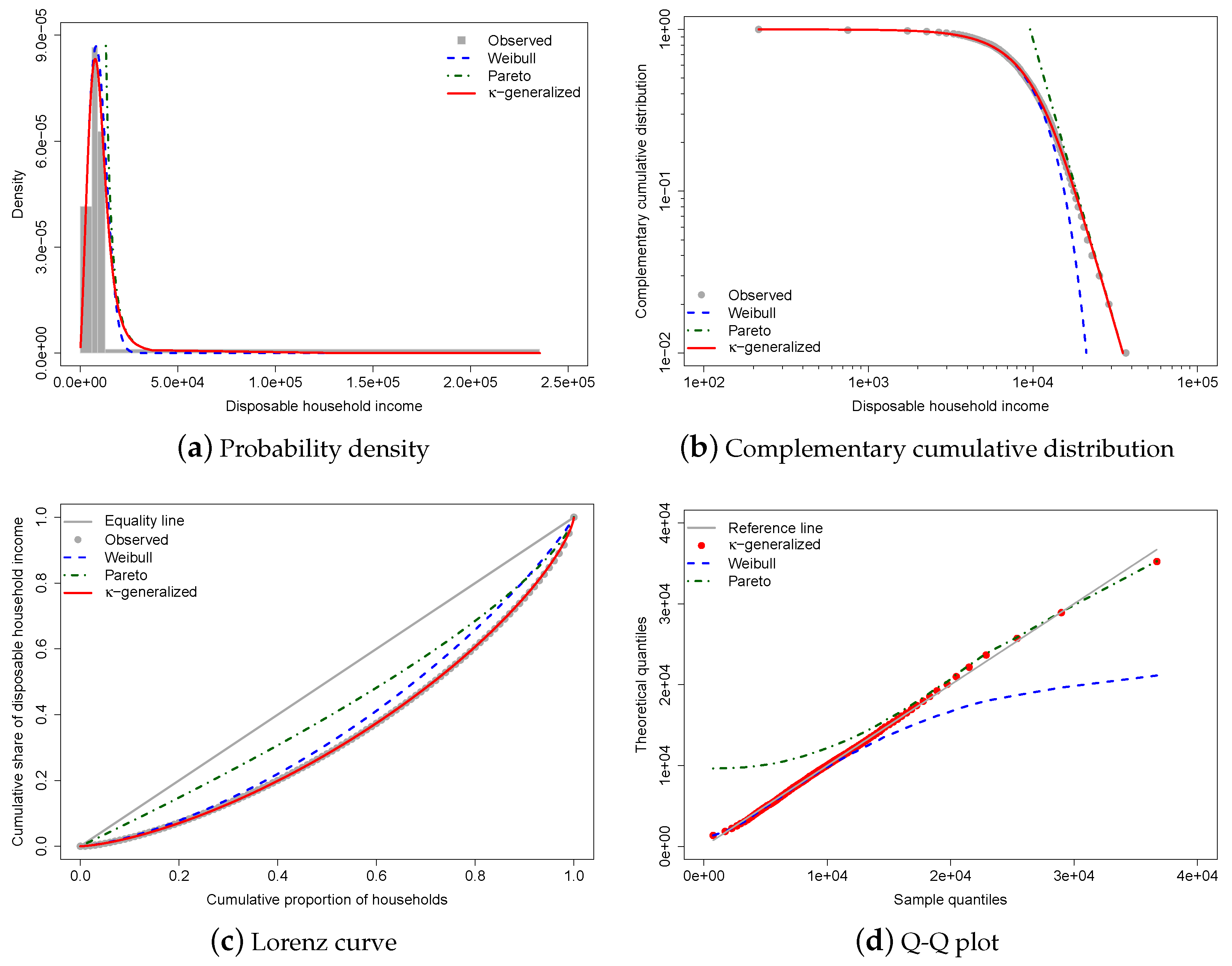
3.2. Results of Fitting
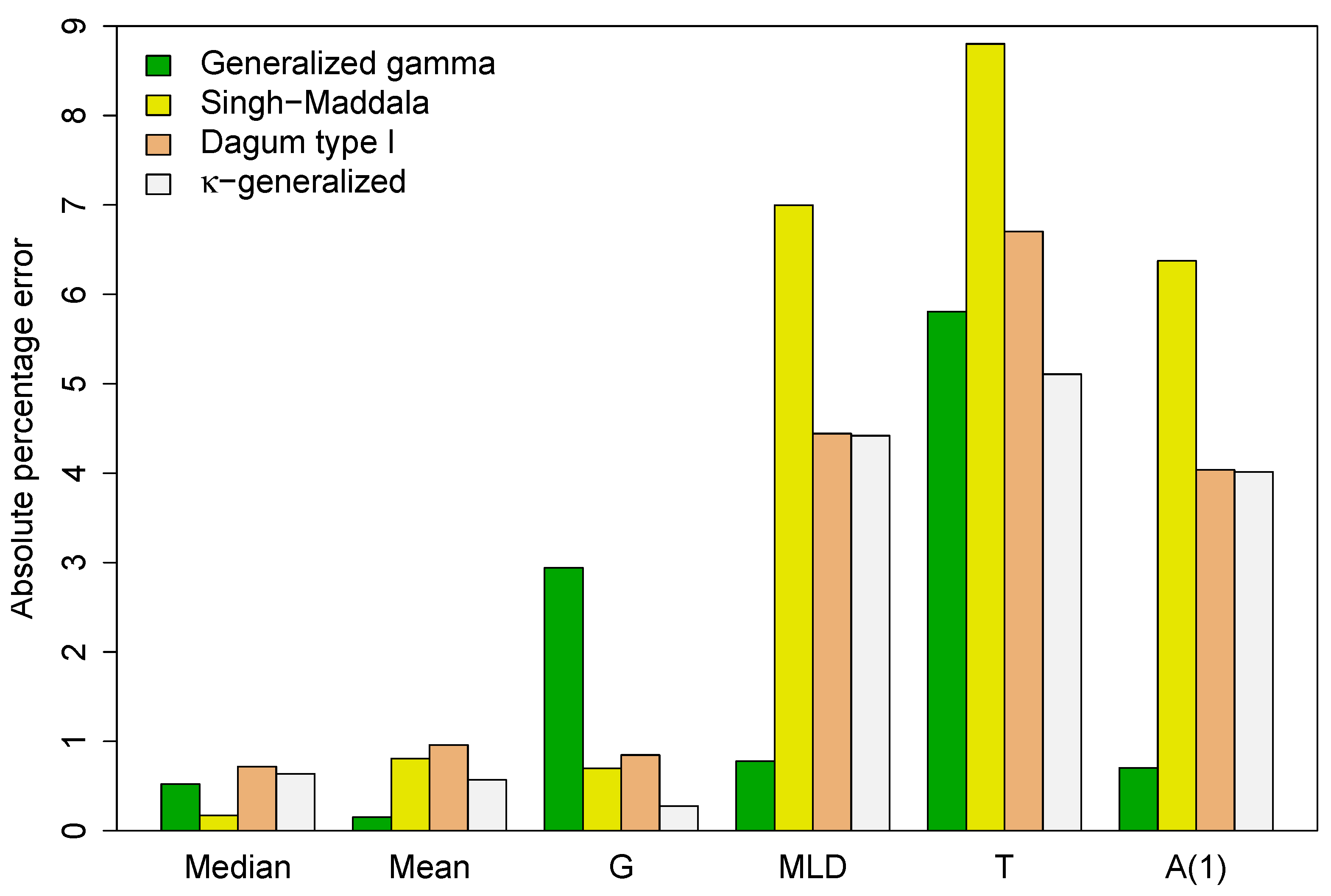
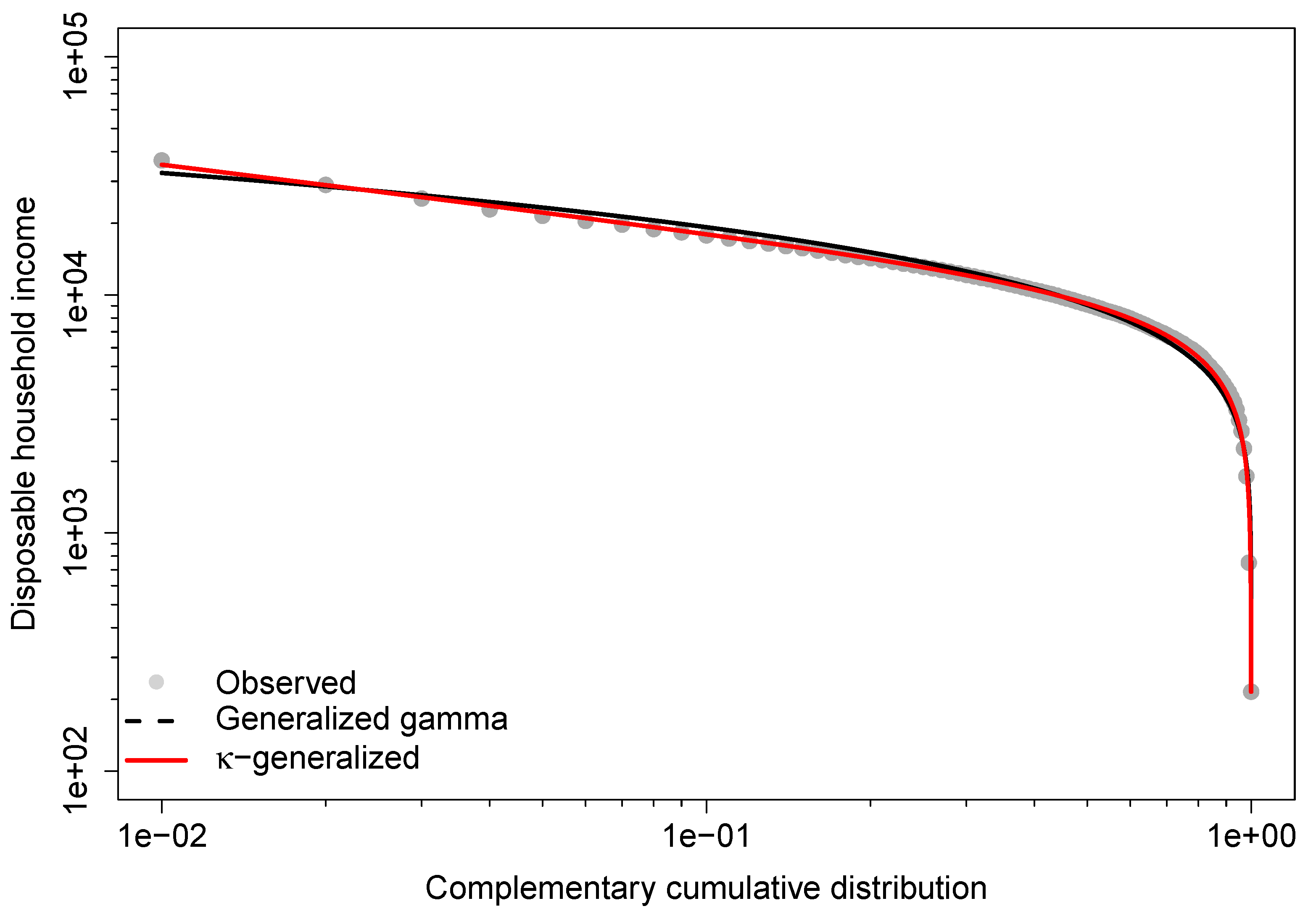
3.3. Comparisons of Alternative Distributions
4. Applications of -Generalized Models to Income and Wealth Data
5. Concluding Remarks
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chatterjee, A.; Yarlagadda, S.; Chakrabarti, B.K. Econophysics of Wealth Distributions; Springer: Milano, Italia, 2005. [Google Scholar]
- Yakovenko, V.M. Econophysics, statistical mechanics approach to. In Encyclopedia of Complexity and Systems Science; Meyers, R.A., Ed.; Springer: New York, NY, USA, 2009; pp. 2800–2826. [Google Scholar]
- Yakovenko, V.M.; Rosser, J.B. Colloquium: Statistical mechanics money, wealth, income. Rev. Mod. Phys. 2009, 81, 1703–1725. [Google Scholar] [CrossRef]
- Chakrabarti, B.K.; Chakraborti, A.; Chakravarty, S.R.; Chatterjee, A. Econophysics of Income and Wealth Distributions; Cambridge University Press: New York, NY, USA, 2013. [Google Scholar]
- Milanovic, B. The Haves and the Have-Nots: A Brief and Idiosyncratic History of Global Inequality; Basic Books: New York, NY, USA, 2011. [Google Scholar]
- Stiglitz, J.E. The Price of Inequality: How Today’s Divided Society Endangers Our Future; W. W. Norton & Company: New York, NY, USA, 2012. [Google Scholar]
- Piketty, T. Capital in the Twenty-First Century; The Belknap Press of Harvard University Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Atkinson, A.B. Inequality: What Can Be Done? Harvard University Press: Cambridge, MA, USA, 2015. [Google Scholar]
- Stiglitz, J.E. The Great Divide: Unequal Societies and What We Can Do about Them; W. W. Norton & Company: New York, NY, USA, 2015. [Google Scholar]
- Pareto, V. La legge della domanda. G. Degli Econ. 1895, 10, 59–68. [Google Scholar]
- Pareto, V. La courbe de la répartition de la richesse. In Recueil Publié par la Faculté de Droit à l’Occasion de l’Exposition Nationale Suisse; Viret-Genton, C., Ed.; Université de Lausanne: Lausanne, Switerland, 1896; pp. 373–387. [Google Scholar]
- Pareto, V. Cours d’Économie Politique; Macmillan: London, UK, 1897. [Google Scholar]
- Pareto, V. Aggiunta allo studio della curva delle entrate. G. Degli Econ. 1897, 14, 15–26. [Google Scholar]
- Montroll, E.W.; Shlesinger, M.F. On 1/f noise and other distributions with long tails. Proc. Natl. Acad. Sci. USA 1982, 79, 3380–3383. [Google Scholar] [CrossRef] [PubMed]
- Montroll, E.W.; Shlesinger, M.F. Maximum entropy formalism, fractals, scaling phenomena, and 1/f noise: A tale of tails. J. Stat. Phys. 1983, 32, 209–230. [Google Scholar] [CrossRef]
- Drăgulescu, A.; Yakovenko, V.M. Evidence for the exponential distribution of income in the USA. Eur. Phys. J. B 2001, 20, 585–589. [Google Scholar] [CrossRef]
- Drăgulescu, A.; Yakovenko, V.M. Exponential and power-law probability distributions of wealth and income in the United Kingdom and the United States. Phys. A Stat. Mech. Its Appl. 2001, 299, 213–221. [Google Scholar] [CrossRef]
- Souma, W. Universal structure of the personal income distribution. Fractals 2001, 9, 463–470. [Google Scholar] [CrossRef]
- Clementi, F.; Gallegati, M. Power law tails in the Italian personal income distribution. Phys. A Stat. Mech. Its Appl. 2005, 350, 427–438. [Google Scholar] [CrossRef][Green Version]
- Clementi, F.; Gallegati, M. Pareto’s law of income distribution: Evidence for Germany, the United Kingdom, and the United States. In Econophysics of Wealth Distributions; Chatterjee, A., Yarlagadda, S., Chakrabarti, B.K., Eds.; Springer: Milan, Italy, 2005; pp. 3–14. [Google Scholar]
- Silva, A.C.; Yakovenko, V.M. Temporal evolution of the “thermal” and “superthermal” income classes in the USA during 1983–2001. Europhys. Lett. 2005, 69, 304–310. [Google Scholar] [CrossRef]
- Nirei, M.; Souma, W. A two factor model of income distribution dynamics. Rev. Income Wealth 2007, 53, 440–459. [Google Scholar] [CrossRef]
- Gibrat, R. Les Inégalités économiques. Applications: Aux Inégalités des Richesses, à la Concentration des Entreprises, aux Population des Villes, aux Statistiques des Familles, etc., d’une loi Nouvelle: La loi de l’Effet Proportionnel; Librairie du Recueil Sirey: Paris, France, 1931. [Google Scholar]
- Salem, A.B.Z.; Mount, T.D. A convenient descriptive model of income distribution: The gamma density. Econometrica 1974, 42, 1115–1127. [Google Scholar] [CrossRef]
- Aitchison, J.; Brown, J.A.C. On criteria for descriptions of income distribuition. Metroeconomica 1954, 6, 88–107. [Google Scholar] [CrossRef]
- Aitchison, J.; Brown, J.A.C. The Lognormal Distribution with Special Reference to Its Use in Economics; Cambridge University Press: New York, NY, USA, 1957. [Google Scholar]
- McDonald, J.B.; Ransom, M.R. Functional forms, estimation techniques and the distribution of income. Econometrica 1979, 47, 1513–1525. [Google Scholar] [CrossRef]
- Majumder, A.; Chakravarty, S.R. Distribution of personal income: Development of a new model and its application to U. S. income aata. J. Appl. Econom. 1990, 5, 189–196. [Google Scholar] [CrossRef]
- Atoda, N.; Suruga, T.; Tachibanaki, T. Statistical inference of functional forms for income distribution. Econ. Stud. Q. 1988, 39, 14–40. [Google Scholar]
- Esteban, J.M. Income-share elasticity and the size distribution of income. Int. Econ. Rev. 1986, 27, 439–444. [Google Scholar] [CrossRef]
- Kloek, T.; van Dijk, H.K. Efficient estimation of income distribution parameters. J. Econom. 1978, 8, 61–74. [Google Scholar] [CrossRef]
- Taillie, C. Lorenz ordering within the generalized gamma family of income distributions. In Statistical Distributions in Scientific Work; Taillie, C., Patil, G.P., Baldessari, B.A., Eds.; D. Reidel Publishing Company: Dordrecht, The Netherlands, 1981; Volume 6, pp. 181–192. [Google Scholar]
- Singh, S.K.; Maddala, G.S. A function for size distribution of incomes. Econometrica 1976, 44, 963–970. [Google Scholar] [CrossRef]
- Dagum, C. A new model of personal income distribution: Specification and estimation. Econ. Appliquée 1977, 30, 413–436. [Google Scholar]
- McDonald, J.B. Some generalized functions for the size distribution of income. Econometrica 1984, 52, 647–665. [Google Scholar] [CrossRef]
- Reed, W.J.; Jorgensen, M. The double Pareto-lognormal distribution—A new parametric model for size distributions. Commun. Stat.-Theory Methods 2004, 33, 1733–1753. [Google Scholar] [CrossRef]
- McDonald, J.B.; Xu, Y.J. A generalization of the beta distribution with applications. J. Econom. 1995, 66, 133–152. [Google Scholar] [CrossRef]
- Reed, W.J. Brownian-Laplace motion and its use in financial modelling. Commun. Stat. Theory Methods 2007, 36, 473–484. [Google Scholar] [CrossRef][Green Version]
- McDonald, J.B.; Ransom, M.R. The generalized beta distribution as a model for the distribution of income: Estimation of related measures of Inequality. In Modeling Income Distributions and Lorenz Curves; Chotikapanich, D., Ed.; Springer: New York, NY, USA, 2008; pp. 147–166. [Google Scholar]
- Reed, W.J.; Wu, F. New four- and five-parameter models for income distributions. In Modeling Income Distributions and Lorenz Curves; Chotikapanich, D., Ed.; Springer: New York, NY, USA, 2008; pp. 211–223. [Google Scholar]
- Kaniadakis, G. Non-linear kinetics underlying generalized statistics. Phys. A Stat. Mech. Its Appl. 2001, 296, 405–425. [Google Scholar] [CrossRef]
- Kaniadakis, G. Statistical mechanics in the context of special relativity. Phys. Rev. E 2002, 66, 056125. [Google Scholar] [CrossRef] [PubMed]
- Kaniadakis, G. Statistical mechanics in the context of special relativity. II. Phys. Rev. E 2005, 72, 036108. [Google Scholar] [CrossRef] [PubMed]
- Kaniadakis, G. Maximum entropy principle and power-law tailed distributions. Eur. Phys. J. B 2009, 70, 3–13. [Google Scholar] [CrossRef]
- Kaniadakis, G. Relativistic entropy and related Boltzmann kinetics. Eur. Phys. J. A 2009, 40, 275–287. [Google Scholar] [CrossRef]
- Kaniadakis, G. Theoretical foundations and mathematical formalism of the power-law tailed statistical distributions. Entropy 2013, 15, 3983–4010. [Google Scholar] [CrossRef]
- Clementi, F.; Gallegati, M.; Kaniadakis, G. κ-generalized statistics in personal income distribution. Eur. Phys. J. B 2007, 57, 187–193. [Google Scholar] [CrossRef]
- Rajaonarison, D.; Bolduc, D.; Jayet, H. The K-deformed multinomial logit model. Econ. Lett. 2005, 86, 13–20. [Google Scholar] [CrossRef]
- Rajaonarison, D. Deterministic heterogeneity in tastes and product differentiation in the K-logit model. Econ. Lett. 2008, 100, 396–398. [Google Scholar] [CrossRef]
- Trivellato, B. Replication and shortfall risk in a binomial model with transaction costs. Math. Methods Oper. Res. 2009, 69, 1–26. [Google Scholar] [CrossRef]
- Imparato, D.; Trivellato, B. Geometry of extended exponential models. In Algebraic and Geometric Methods in Statistics; Gibilisco, P., Riccomagno, E., Pistone, G., Wynn, H.P., Eds.; Cambridge University Press: Cambridge, UK, 2009; pp. 307–326. [Google Scholar]
- Trivellato, B. The minimal κ-entropy martingale measure. Int. J. Theor. Appl. Financ. 2012, 15, 1250038. [Google Scholar] [CrossRef]
- Trivellato, B. Deformed exponentials and applications to finance. Entropy 2013, 15, 3471–3489. [Google Scholar] [CrossRef]
- Moretto, E.; Pasquali, S.; Trivellato, B. Option pricing under deformed Gaussian distributions. Phys. A Stat. Mech. Appl. 2016, 446, 246–263. [Google Scholar] [CrossRef]
- Moretto, E.; Pasquali, S.; Trivellato, B. A non-Gaussian option pricing model based on Kaniadakis exponential deformation. Eur. Phys. J. B 2017, 90, 179. [Google Scholar] [CrossRef]
- Clementi, F.; Di Matteo, T.; Gallegati, M.; Kaniadakis, G. The κ-generalized distribution: A new descriptive model for the size distribution of incomes. Phys. A Stat. Mech. Appl. 2008, 387, 3201–3208. [Google Scholar] [CrossRef]
- Clementi, F.; Gallegati, M.; Kaniadakis, G. A κ-generalized statistical mechanics approach to income analysis. J. Stat. Mech. Theory Exp. 2009, 2009, P02037. [Google Scholar] [CrossRef]
- Clementi, F.; Gallegati, M.; Kaniadakis, G. A model of personal income distribution with application to Italian data. Empir. Econ. 2010, 39, 559–591. [Google Scholar] [CrossRef]
- Clementi, F.; Gallegati, M.; Kaniadakis, G. A new model of income distribution: The κ-generalized distribution. J. Econ. 2012, 105, 63–91. [Google Scholar] [CrossRef]
- Clementi, F.; Gallegati, M. The Distribution of Income and Wealth: Parametric Modeling with the κ-Generalized Family; Springer International Publishing AG: Cham, Switerland, 2016. [Google Scholar]
- Clementi, F.; Gallegati, M.; Kaniadakis, G.; Landini, S. κ-generalized models of income and wealth distributions: A survey. Eur. Phys. J. Spec. Top. 2016, 225, 1959–1984. [Google Scholar] [CrossRef]
- Clementi, F.; Gallegati, M. New economic windows on income and wealth: The κ-generalized family of distributions. J. Soc. Econ. Stat. 2017, 6, 1–15. [Google Scholar]
- Landini, S. Mathematics of strange quantities: Why are κ-generalized models a good fit to income and wealth distributions? An explanation. In The Distribution of Income and Wealth: Parametric Modeling with the κ-Generalized Family; Clementi, F., Gallegati, M., Eds.; Springer International Publishing AG: Cham, Switerland, 2016; pp. 93–132. [Google Scholar]
- Bartels, C.P.A.; van Metelen, H. Alternative Probability Density Functions of Income: A Comparison of the Longnormal-, Gamma- and Weibull-Distribution with Dutch Data; Research Memorandum 29; Department of Quantitative Studies, Faculty of Economics, Vrije Universiteit: Amsterdam, The Netherlands, 1975. [Google Scholar]
- Bartels, C.P.A. Economic Aspects of Regional Welfare: Income Distribution and Unemployment; Martinus Nijhoff: Leiden, The Netherlands, 1977. [Google Scholar]
- Espinguet, P.; Terraza, M. Essai d’extrapolation des distributions de salaires français. Econ. Appliquée 1983, 36, 535–561. [Google Scholar]
- Bordley, R.F.; McDonald, J.B.; Mantrala, A. Something new, something old: Parametric models for the size distribution of income. J. Income Distrib. 1996, 6, 91–103. [Google Scholar] [CrossRef]
- Brachmann, K.; Stich, A.; Trede, M. Evaluating parametric income distribution models. Allg. Stat. Arch. 1996, 80, 285–298. [Google Scholar]
- Tachibanaki, T.; Suruga, T.; Atoda, N. Estimations of income distribution parameters for individual observations by maximum likelihood method. J. Jpn. Stat. Soc. 1997, 27, 191–203. [Google Scholar] [CrossRef][Green Version]
- Mandelbrot, B. The Pareto-Lévy law and the distribution of income. Int. Econ. Rev. 1960, 1, 79–106. [Google Scholar] [CrossRef]
- Kakwani, N. Income Inequality and Poverty: Methods of Estimation and Policy Applications; Oxford University Press: New York, NY, USA, 1980. [Google Scholar]
- Lorenz, M.O. Methods of measuring the concentration of wealth. Publ. Am. Stat. Assoc. 1905, 9, 209–219. [Google Scholar]
- Gastwirth, J.L. A general definition of the Lorenz curve. Econometrica 1971, 39, 1037–1039. [Google Scholar] [CrossRef]
- Okamoto, M. Extension of the κ-Generalized Distribution: New Four-Parameter Models for the Size Distribution of Income and Consumption; Working Paper 600; LIS Cross-National Data Center: Luxembourg, 2013; Available online: https://www.lisdatacenter.org/wps/liswps/600.pdf (accessed on 26 June 2023).
- Gini, C. Sulla misura della concentrazione e della variabilità dei caratteri. Atti Del R. Ist. Veneto Di Sci. Lett. Ed Arti 1914, 73, 1201–1248. [Google Scholar]
- Arnold, B.C.; Laguna, L. On Generalized Pareto Distributions with Applications to Income Data; Iowa State University Press: Ames, IA, USA, 1977. [Google Scholar]
- Kleiber, C.; Kotz, S. Statistical Size Distributions in Economics and Actuarial Sciences; John Wiley & Sons: New York, NY, USA, 2003. [Google Scholar]
- Allison, P.D. Measures of inequality. Am. Sociol. Rev. 1978, 43, 865–880. [Google Scholar] [CrossRef]
- Cowell, F.A. Generalized entropy and the measurement of distributional change. Eur. Econ. Rev. 1980, 13, 147–159. [Google Scholar] [CrossRef]
- Cowell, F.A. On the structure of additive inequality measures. Rev. Econ. Stud. 1980, 47, 521–531. [Google Scholar] [CrossRef]
- Shorrocks, A.F. The class of additively decomposable inequality measures. Econometrica 1980, 48, 613–625. [Google Scholar] [CrossRef]
- Cowell, F.A.; Kuga, K. Additivity and the entropy concept: An axiomatic approach to inequality measurement. J. Econ. Theory 1981, 25, 131–143. [Google Scholar] [CrossRef]
- Cowell, F.A.; Kuga, K. Inequality measurement: An axiomatic approach. Eur. Econ. Rev. 1981, 15, 287–305. [Google Scholar] [CrossRef]
- Theil, H. Economics and Information Theory; North-Holland: Amsterdam, The Netherlands, 1967. [Google Scholar]
- Sarabia, J.M.; Jordá, V.; Remuzgo, L. The Theil indices in parametric families of income distributions—A short review. Rev. Income Wealth 2017, 63, 867–880. [Google Scholar] [CrossRef]
- Atkinson, A.B. On the measurement of inequality. J. Econ. Theory 1970, 2, 244–263. [Google Scholar] [CrossRef]
- Jenkins, S.P. Distributionally-sensitive inequality indices and the GB2 income distribution. Rev. Income Wealth 2009, 55, 392–398. [Google Scholar] [CrossRef]
- Cowell, F.A. Measuring Inequality; Oxford University Press: New York, NY, USA, 2011. [Google Scholar]
- Kleiber, C. The existence of population inequality measures. Econ. Lett. 1997, 57, 39–44. [Google Scholar] [CrossRef]
- Rao, C. Linear Statistical Inference and Its Applications; John Wiley & Sons: New York, NY, USA, 1973. [Google Scholar]
- Ghosh, J.K. Higher Order Asymptotics; Institute of Mathematical Statistics and American Statistical Association: Hayward, CA, USA, 1994. [Google Scholar]
- Araar, A.; Duclos, J.Y. User Manual for Stata Package DASP: Version 3.0; PEP, World Bank, UNDP and Université Laval, 2022. Available online: http://dasp.ecn.ulaval.ca/dasp3/manual/DASP_MANUAL_V303.pdf (accessed on 26 June 2023).
- Stacy, E.W. A generalization of the gamma distribution. Ann. Math. Stat. 1962, 33, 1187–1192. [Google Scholar] [CrossRef]
- Chotikapanich, D.; Griffiths, W.; Hajargasht, G.; Karunarathne, W.; Rao, D. Using the GB2 income distribution. Econometrics 2018, 6, 21. [Google Scholar] [CrossRef]
- Jordá, V.; Alonso, J.M. New estimates on educational attainment using a continuous approach (1970–2010). World Dev. 2017, 90, 281–293. [Google Scholar] [CrossRef]
- Fellman, J. Estimation of Gini coefficients using Lorenz curves. J. Stat. Econom. Methods 2012, 1, 31–38. [Google Scholar]
- Takayasu, H. Fractals in Physical Science; Manchester University Press: Manchester, UK, 1991. [Google Scholar]
- Okamoto, M. Evaluation of the goodness of fit of new statistical size distributions with consideration of accurate income inequality estimation. Econ. Bull. 2012, 32, 2969–2982. [Google Scholar]
- Vallejos, A.; Ormazábal, I.; Borotto, F.A.; Astudillo, H.F. A new κ-deformed parametric model for the size distribution of wealth. Phys. Stat. Mech. Appl. 2019, 514, 819–829. [Google Scholar] [CrossRef]
- Clementi, F.; Gallegati, M.; Kaniadakis, G. A generalized statistical model for the size distribution of wealth. J. Stat. Mech. Theory Exp. 2012, 2012, P12006. [Google Scholar] [CrossRef]
- StataCorp. Stata Statistical Software: Release 17; StataCorp: College Station, TX, USA, 2021; Available online: https://www.stata.com/ (accessed on 26 June 2023).
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2023; Available online: https://www.R-project.org/ (accessed on 26 June 2023).


| Statistic | Observed | Predicted | ||
|---|---|---|---|---|
| Value | LB a | UB b | ||
| Median | 9123 | 8983 | 9264 | 9181 |
| Mean | 10,548 | 10,292 | 10,805 | 10,488 |
| G | 0.323 | 0.312 | 0.334 | 0.322 |
| 0.179 | 0.169 | 0.189 | 0.172 | |
| Model | Parameters | Goodness-of-Fit Criteria | |||||||
|---|---|---|---|---|---|---|---|---|---|
| () | () | , , | |||||||
| GG | 0.684 | 829 | 5.475 | 2.325 | 2.047 | 0.939 | 0.812 | ||
| (0.018) | (115) | (0.270) | |||||||
| SM | 2.441 | 12,531 | 1.835 | 0.716 | 0.574 | 0.319 | 0.187 | ||
| (0.021) | (219) | (0.053) | |||||||
| D | 3.705 | 11,705 | 0.560 | 0.539 | 0.437 | 0.281 | 0.211 | ||
| (0.041) | (104) | (0.011) | |||||||
| -gen | 2.233 | 10,667 | 0.630 | 0.530 | 0.418 | 0.188 | 0.139 | ||
| (0.017) | (46) | (0.014) | |||||||
| Statistic a | Observed | Predicted d | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Value | LB b | UB c | GG | SM | D | -gen | |||
| Median | 9123 | 8983 | 9264 | 9076 | 9108 | 9189 | 9181 | ||
| Mean | 10,548 | 10,292 | 10,805 | 10,532 | 10,463 | 10,447 | 10,488 | ||
| G | 0.323 | 0.312 | 0.334 | 0.333 | 0.321 | 0.320 | 0.322 | ||
| 0.197 | 0.185 | 0.209 | 0.196 | 0.183 | 0.188 | 0.188 | |||
| T | 0.191 | 0.175 | 0.207 | 0.180 | 0.174 | 0.178 | 0.181 | ||
| 0.179 | 0.169 | 0.189 | 0.178 | 0.168 | 0.172 | 0.172 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Clementi, F. The Kaniadakis Distribution for the Analysis of Income and Wealth Data. Entropy 2023, 25, 1141. https://doi.org/10.3390/e25081141
Clementi F. The Kaniadakis Distribution for the Analysis of Income and Wealth Data. Entropy. 2023; 25(8):1141. https://doi.org/10.3390/e25081141
Chicago/Turabian StyleClementi, Fabio. 2023. "The Kaniadakis Distribution for the Analysis of Income and Wealth Data" Entropy 25, no. 8: 1141. https://doi.org/10.3390/e25081141
APA StyleClementi, F. (2023). The Kaniadakis Distribution for the Analysis of Income and Wealth Data. Entropy, 25(8), 1141. https://doi.org/10.3390/e25081141








