Coherences in the Dynamics of Physical Systems from a Multifractal Perspective of Motion
Abstract
1. Introduction
2. Correspondences between Multifractal Schrödinger Equation and Dumped Oscillator through a Special Ansatz
3. Conclusions
- i.
- An analogy between the multifractal Schrödinger equation and the dumped oscillator equation through a special ansatz is established;
- ii.
- Using a Ricatti-type gauge, Stoler-type coherences in the dynamics of physical systems are highlighted;
- iii.
- This Ricatti-type gauge was assimilated to a calibration process of the difference between the kinetic and the potential energy of a Lagrangian, specified as a perfect square in generic coordinates.
Author Contributions
Funding
Conflicts of Interest
Appendix A
Appendix B
Appendix C
References
- Nottale, L. Scale Relativity and Fractal Space-Time: A New Approach to Unifying Relativity and Quantum Mechanics; Imperial College Press: London, UK, 2011. [Google Scholar]
- Merches, I.; Agop, M. Differentiability and Fractality in Dynamics of Physical Systems; World Scientific: Hackensack, NJ, USA, 2016. [Google Scholar]
- Agop, M.; Paun, V.P. On the new perspectives of fractal theory. In Fundaments and Applications; Romanian Academy Publishing House: Bucharest, Romania, 2017. [Google Scholar]
- Mandelbrot, B.B. Fractal and Chaos; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Cristescu, C.P. Nonlinear dynamics and chaos. In Theoretical Fundaments and Applications; Romanian Academy Publishing House: Bucharest, Romania, 2008. [Google Scholar]
- Farhi, E.; Khoze, V.V.; Singleton, R., Jr. Minkowski space non-Abelian classical solutions with noninteger winding number change. Phys. Rev. D 1993, 47, 5551. [Google Scholar] [CrossRef] [PubMed]
- Taraboanta, I.; Stoleriu, S.; Nica, I.; Georgescu, A.; Gamen, A.C.; Maftei, G.A.; Andrian, S. Roughness variation of a nanohybrid composite resin submitted to acid and abrasive challenges. Int. J. Med. Dent. 2020, 24, 182–187. [Google Scholar]
- Iovan, G.; Stoleriu, S.; Nica, I.; Solomon, S.; Munteanu, A.; Andrian, S. Surface characteristics of restorative composite resins after polishing with profine lamineer tips. Mater. Plast. 2016, 53, 755–758. [Google Scholar]
- Tofan, N.; Andrian, S.; Nica, I.; Stoleriu, S.; Topoliceanu, C.; Chelariu, R.; Bolat, M.; Pancu, G. The Assessment of Erosive Potential of Some Acid Beverages on Indirect—Restorative Materials. Rev. Chim. 2016, 67, 1144–1149. [Google Scholar]
- Pancu, G.; Iovan, G.; Ghiorghe, A.; Topoliceanu, C.; Nica, I.; Tofan, N.; Stoleriu, S.; Sandu, A.V.; Andrian, S. The assessment of biological parameters and remineralisation potential of saliva in pregnancy. Rev. Chim. 2015, 66, 2051–2056. [Google Scholar]
- Stoleriu, S.; Iovan, G.; Pancu, G.; Nica, I.; Andrian, S. Study concerning the influence of the finishing and polishing systems on the surface state of various types of composite resins. Rom. J. Oral Rehabil. 2013, 5, 78–83. [Google Scholar]
- Mazilu, N.; Agop, M.; Gatu, I.; Iacob, D.D.; Ghizdovăt, V. From Kepler problem to skyrmions. Mod. Phys. Lett. B 2016, 30, 1650153. [Google Scholar] [CrossRef]
- Dittrich, W.; Reuter, M. Classical, and Quantum Dynamics; Springer: New York, NY, USA, 2017. [Google Scholar]
- Zelikin, M.I. Control Theory and Optimization, Encyclopaedia of Mathematical Sciences; Springer: Berlin/Heidelberg, Germany, 2000; Volume 86. [Google Scholar]
- Denman, H.H. Time Translation Invariance for Certain Dissipative Classical Systems. Am. J. Phys. 1968, 36, 516. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifschitz, E.M. Mécanique, Mir Editions, Moscou Larmor, J. (1900): Aether and Matter; Cambridge University Press: Cambridge, UK, 1966. [Google Scholar]
- Carinena, J.F.; Ramos, A. Integrability of the Riccati equation from a group-theoretical viewpoint. Int. J. Mod. Phys. A 1999, 14, 1935–1951. [Google Scholar] [CrossRef]
- Stoler, D. Equivalence Classes of Minimum Uncertainty Packets. Phys. Rev. 1970, D1, 3217. [Google Scholar] [CrossRef]
- Stoler, D. Generalized Coherent States. Phys. Rev. 1971, D4, 2309. [Google Scholar] [CrossRef]
- Skyrme, T.H.R. The Origins of Skyrmions. Int. J. Mod. Phys. 1988, A3, 2745–2751. [Google Scholar] [CrossRef]
- Skyrme, T.H.R. Selected Papers, with Comentary; Brown, G.E., Ed.; World Scientific Series in 20th Century Physics; World Scientific: Singapore, 1994; Volume 3. [Google Scholar]
- Slobodeanu, R. On the Geometrized Skyrme and Faddeev Models. arXiv 2009, arXiv:0809.4864v5. [Google Scholar] [CrossRef]
- Misner, C.W. Harmonic Maps as Models for Physical Theories. Phys. Rev. D 1978, 18, 4510–4524. [Google Scholar] [CrossRef]
- Skyrme, T.H.R. A Non-Linear Field Theory. Proc. R. Soc. Lond. 1961, A260, 127–138. [Google Scholar]
- Atiyah, M.F.; Sutcliffe, P. Skyrmions, Instantons, Mass and Curvature. Phy. Lett. D 2004, 605, 106–114. [Google Scholar] [CrossRef]
- Rogers, C.; Schief, W.K. Bäcklund and Darboux Transformations; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Canfora, F.; Maeda, H. Hedgehog ansatz and its generalization for self-gravitating Skyrmions. Phys. Rev. D 2013, 87, 084049. [Google Scholar] [CrossRef]
- Niederer, U. The Maximal Kinematical Invariance Group of the Free Schrödinger Equation. Helv. Phys. Acta 1972, 45, 802–810. [Google Scholar]
- De Alfaro, V.; Fubini, S.; Furlan, G. Conformal Invariance in Quantum Mechanics. Nuovo Cimento A 1976, 34, 569–611. [Google Scholar] [CrossRef]

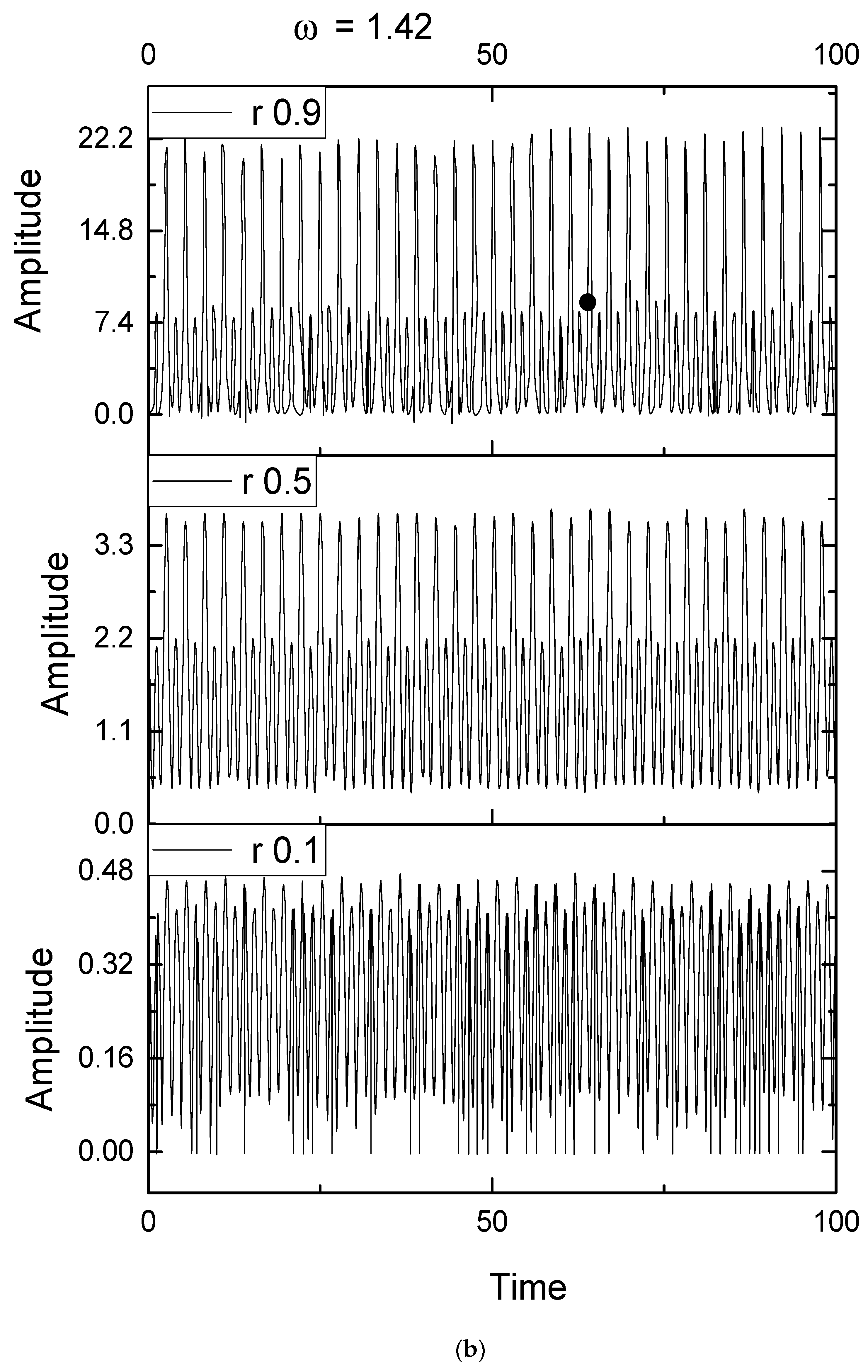
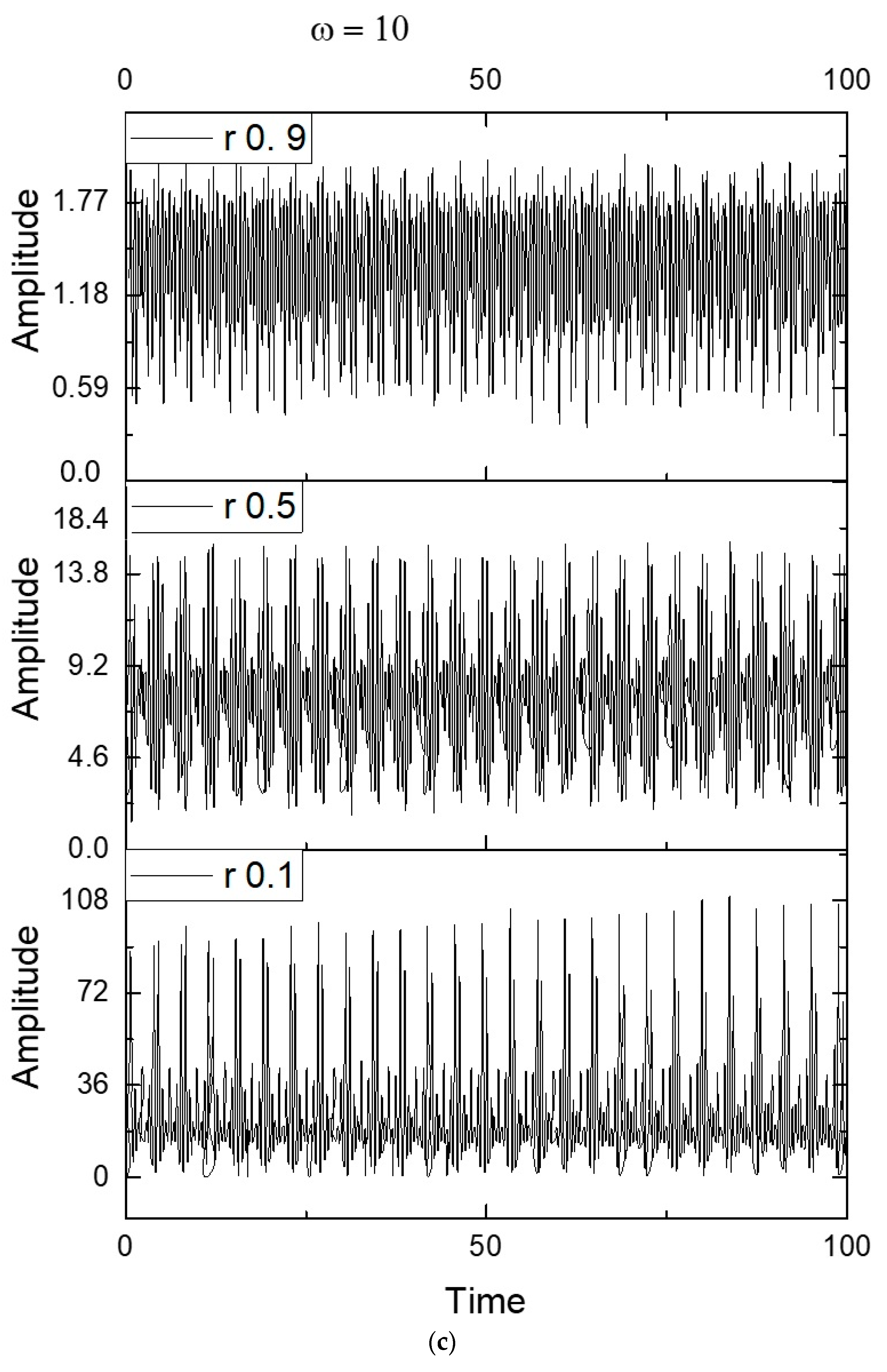
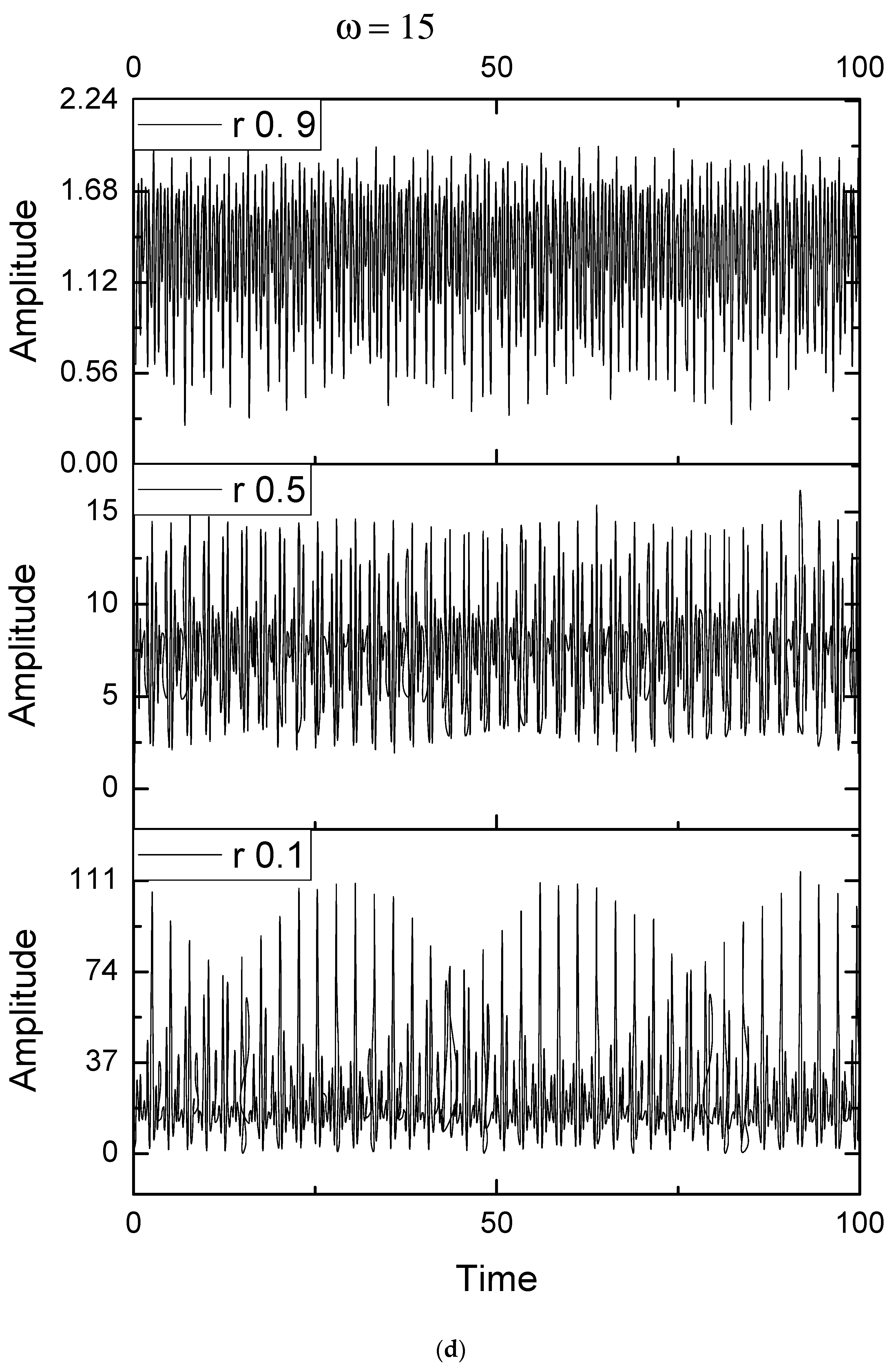
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vasincu, D.; Bruma, A.B.; Rusu, O.; Rusu, C.M.; Ghizdovat, V.; Agop, M. Coherences in the Dynamics of Physical Systems from a Multifractal Perspective of Motion. Entropy 2023, 25, 1143. https://doi.org/10.3390/e25081143
Vasincu D, Bruma AB, Rusu O, Rusu CM, Ghizdovat V, Agop M. Coherences in the Dynamics of Physical Systems from a Multifractal Perspective of Motion. Entropy. 2023; 25(8):1143. https://doi.org/10.3390/e25081143
Chicago/Turabian StyleVasincu, Decebal, Andreea Bianca Bruma, Oana Rusu, Cristina Marcela Rusu, Vlad Ghizdovat, and Maricel Agop. 2023. "Coherences in the Dynamics of Physical Systems from a Multifractal Perspective of Motion" Entropy 25, no. 8: 1143. https://doi.org/10.3390/e25081143
APA StyleVasincu, D., Bruma, A. B., Rusu, O., Rusu, C. M., Ghizdovat, V., & Agop, M. (2023). Coherences in the Dynamics of Physical Systems from a Multifractal Perspective of Motion. Entropy, 25(8), 1143. https://doi.org/10.3390/e25081143






