Superimposed Perfect Binary Array-Aided Channel Estimation for OTFS Systems
Abstract
1. Introduction
- (i)
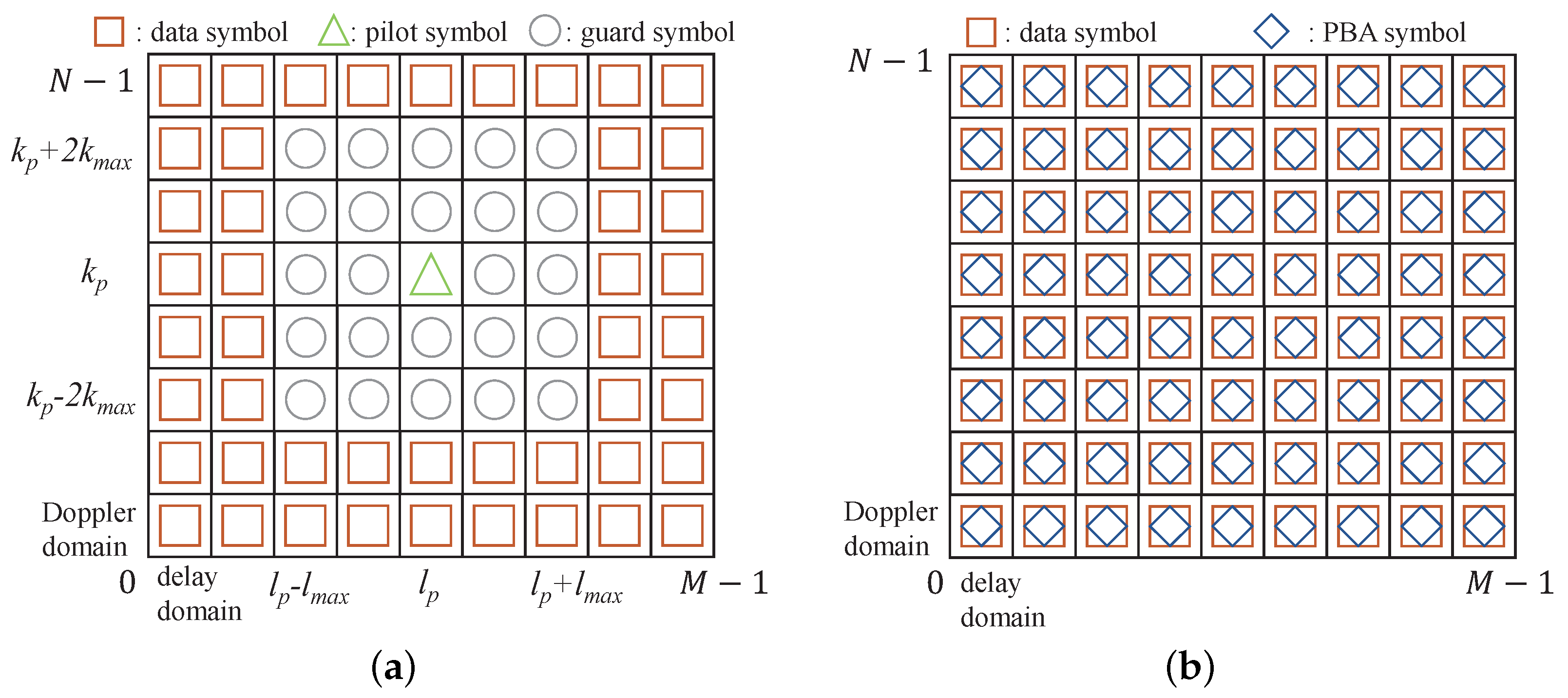
- In the proposed SPBA method, the whole OTFS frame is used for data transmission, while a perfect binary array (PBA) that plays the role of the pilot is superimposed on data symbols in the DD domain, resulting in higher SE when compared to that of the EP scheme in [11]. Furthermore, in contrast to similar work in [17], the SPBA method can estimate delay-Doppler taps and complex path gains in the same superimposed frame, which means the additional non-superimposed EP frame is no longer required. As a result, the SPBA method has better adaptability to rapidly delay-Doppler varying channels.
- (ii)
- A channel estimator for the SPBA framework is proposed. At the receiver side, local PBAs with different circular shifts in the DD domain are correlated with the received signal. By utilizing the perfect autocorrelation of PBA [19,20,21], we can find the propagation paths and determine the delay-Doppler taps together with the complex path gains by comparing the correlation values to a threshold. Hence, channel estimation is performed through a linear search for the correlation peak. The proposed channel estimator can achieve high estimation accuracy with a significant SE improvement.
- (iii)
- The SPBA’s optimal power ratio is calculated by deriving the signal-to-interference-plus-noise ratio (SINR) and maximizing it. We validate that the adoption of the optimal power ratio will further improve SE and bit error rate (BER) performance of the SPBA method.
2. System Model
3. Superimposed Perfect Binary Array-Aided OTFS Channel Estimator
3.1. Proposed Channel Estimator
| Algorithm 1 Superimposed Perfect Binary Array-Aided OTFS Channel Estimation Method |
| Input: Received symbol matrix , PBA , maximum delay , maximum Doppler shift , threshold Output: Channel estimates 1: Initialize: path number 2: for to do 3: for to do 4: Generate the local PBA via (11); 5: Compute the correlation value via (12); 6: if then 7: Update ; 8: , , ; 9: end if 10: end for 11: end for |
3.2. Design of the PBA
- (i)
- Suppose that and are PBA and QPBA, respectively. A new PBA can be constructed as follows:where denotes the -th element of , and .
- (ii)
- Suppose that and are QPBA and DQPBA, respectively. A new QPBA can be constructed as follows:where denotes the -th element of , and .
- (iii)
- Suppose that is a QPBA and that , where the operator outputs the greatest common divisor of N and M. A new DQPBA can be constructed as follows:where denotes the -th element of , and .
- (iv)
- Suppose that and are PBA and DQPBA, respectively. Then, and are the new PBA and DQPBA, respectively, where the superscript denotes the transpose of the matrix.
3.3. Rectangular Pulse Conditions
3.4. Minimum Mean Square Error Estimator
4. Spectral Efficiency and Optimal Power Ratio
4.1. Spectrum Efficiency Analysis
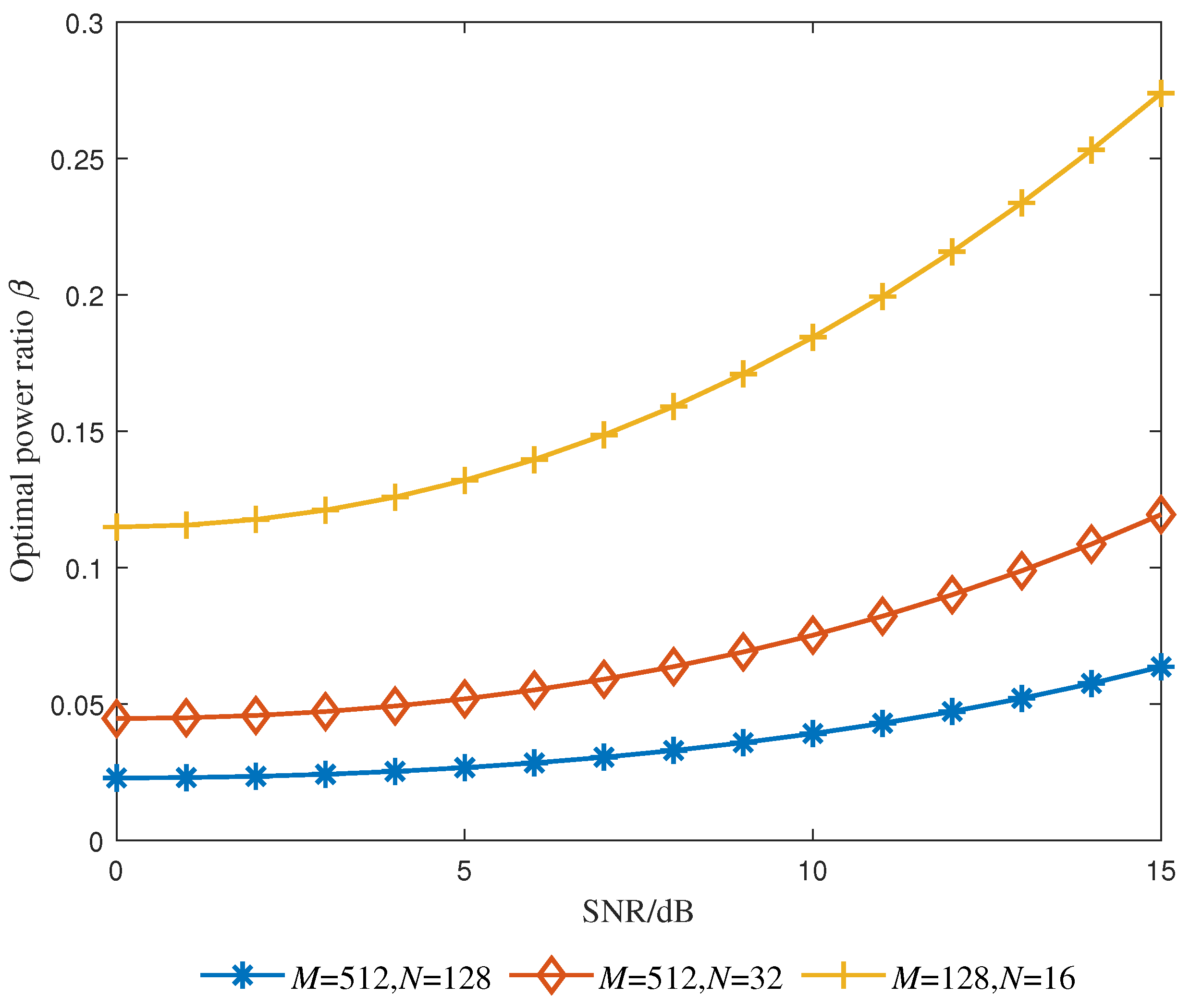
4.2. Optimal Power Ratio
5. Simulation Results
5.1. Optimal Power Ratio and SE Performance
5.2. Channel Estimation Performance
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Feng, Y.; Zhang, W.; Ge, Y.; Stüber, G.L. Channel Time-Variation Suppression With Optimized Receive Beamforming for High-Mobility OFDM Downlink Transmissions. IEEE Trans. Commun. 2021, 70, 1183–1196. [Google Scholar] [CrossRef]
- Zhang, C.; Shi, J.; Zhang, Z.; Liu, Y.; Hu, X. FRFT-Based Interference Suppression for OFDM Systems in IoT Environment. IEEE Commun. Lett. 2019, 23, 2068–2072. [Google Scholar] [CrossRef]
- Tang, T.; Zou, X.; Li, P.; Pan, W.; Luo, B.; Yan, L. Proposal and Demonstration of Subcarrier Index Modulation OFDM for RoF System With Enhanced Spectral Efficiency. J. Lightwave Technol. 2018, 36, 4501–4506. [Google Scholar] [CrossRef]
- Hadani, R.; Rakib, S.; Tsatsanis, M.; Monk, A.; Goldsmith, A.J.; Molisch, A.F.; Calderbank, R. Orthogonal Time Frequency Space Modulation. In Proceedings of the 2017 IEEE Wireless Communications and Networking Conference (WCNC), San Francisco, CA, USA, 19–22 March 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Hadani, R.; Rakib, S.; Molisch, A.F.; Ibars, C.; Monk, A.; Tsatsanis, M.; Delfeld, J.; Goldsmith, A.; Calderbank, R. Orthogonal Time Frequency Space (OTFS) modulation for millimeter-wave communications systems. In Proceedings of the 2017 IEEE MTT-S International Microwave Symposium (IMS), Honololu, HI, USA, 4–9 June 2017; pp. 681–683. [Google Scholar] [CrossRef]
- Wei, Z.; Yuan, W.; Li, S.; Yuan, J.; Bharatula, G.; Hadani, R.; Hanzo, L. Orthogonal Time-Frequency Space Modulation: A Promising Next-Generation Waveform. IEEE Wirel. Commun. 2021, 28, 136–144. [Google Scholar] [CrossRef]
- Murali, K.R.; Chockalingam, A. On OTFS Modulation for High-Doppler Fading Channels. In Proceedings of the 2018 Information Theory and Applications Workshop (ITA), San Diego, CA, USA, 11–16 February 2018; pp. 1–10. [Google Scholar] [CrossRef]
- Wei, Z.; Yuan, W.; Li, S.; Yuan, J.; Ng, D.W.K. Transmitter and Receiver Window Designs for Orthogonal Time-Frequency Space Modulation. IEEE Trans. Commun. 2021, 69, 2207–2223. [Google Scholar] [CrossRef]
- Qu, H.; Liu, G.; Zhang, L.; Wen, S.; Imran, M.A. Low-Complexity Symbol Detection and Interference Cancellation for OTFS System. IEEE Trans. Commun. 2021, 69, 1524–1537. [Google Scholar] [CrossRef]
- Farhang, A.; RezazadehReyhani, A.; Doyle, L.E.; Farhang-Boroujeny, B. Low Complexity Modem Structure for OFDM-Based Orthogonal Time Frequency Space Modulation. IEEE Wirel. Commun. Lett. 2018, 7, 344–347. [Google Scholar] [CrossRef]
- Raviteja, P.; Phan, K.T.; Hong, Y.; Viterbo, E. Interference Cancellation and Iterative Detection for Orthogonal Time Frequency Space Modulation. IEEE Trans. Wirel. Commun. 2018, 17, 6501–6515. [Google Scholar] [CrossRef]
- Kollengode, R.M.; Chockalingam, A. MIMO-OTFS in High-Doppler Fading Channels: Signal Detection and Channel Estimation. In Proceedings of the 2018 IEEE Global Communications Conference (GLOBECOM), Abu Dhabi, United Arab Emirates, 9–13 December 2018; pp. 206–212. [Google Scholar] [CrossRef]
- Raviteja, P.; Phan, K.T.; Hong, Y. Embedded Pilot-Aided Channel Estimation for OTFS in Delay–Doppler Channels. IEEE Trans. Veh. Technol. 2019, 68, 4906–4917. [Google Scholar] [CrossRef]
- Wang, S.; Guo, J.; Wang, X.; Yuan, W.; Fei, Z. Pilot Design and Optimization for OTFS Modulation. IEEE Wirel. Commun. Lett. 2021, 10, 1742–1746. [Google Scholar] [CrossRef]
- Zhao, L.; Gao, W.; Guo, W. Sparse Bayesian Learning of Delay-Doppler Channel for OTFS System. IEEE Commun. Lett. 2020, 24, 2766–2769. [Google Scholar] [CrossRef]
- Reddy, C.S.; Priya, P.; Sen, D.; Singhal, C. Spectral Efficient Modem Design with OTFS Modulation for Vehicular-IoT System. IEEE Internet Things J. 2023, 10, 2444–2458. [Google Scholar] [CrossRef]
- Mishra, H.B.; Singh, P.; Prasad, A.K.; Budhiraja, R. OTFS Channel Estimation and Data Detection Designs With Superimposed Pilots. IEEE Trans. Wirel. Commun. 2022, 21, 2258–2274. [Google Scholar] [CrossRef]
- Yuan, W.; Li, S.; Wei, Z.; Yuan, J.; Ng, D.W.K. Data-Aided Channel Estimation for OTFS Systems With a Superimposed Pilot and Data Transmission Scheme. IEEE Wirel. Commun. Lett. 2021, 10, 1954–1958. [Google Scholar] [CrossRef]
- Lüke, H.D.; Bömer, L.; Antweiler, M. Perfect binary arrays. Signal Process. 1989, 17, 69–80. [Google Scholar] [CrossRef]
- Jedwab, J. Generalized perfect arrays and Menon difference sets. Des. Codes Cryptogr. 1992, 2, 19–68. [Google Scholar] [CrossRef]
- Jedwab, J.; Mitchell, C.; Piper, F.; Wild, P. Perfect binary arrays and difference sets. Discrete Math. 1994, 125, 241–254. [Google Scholar] [CrossRef]
- TS 36.104. Evolved Universal Terrestrial Radio Access. Base Station Radio Transmission and Reception Release 16. Available online: https://www.3gpp.org/ftp/Specs/archive/36_series/36.104 (accessed on 18 June 2023).



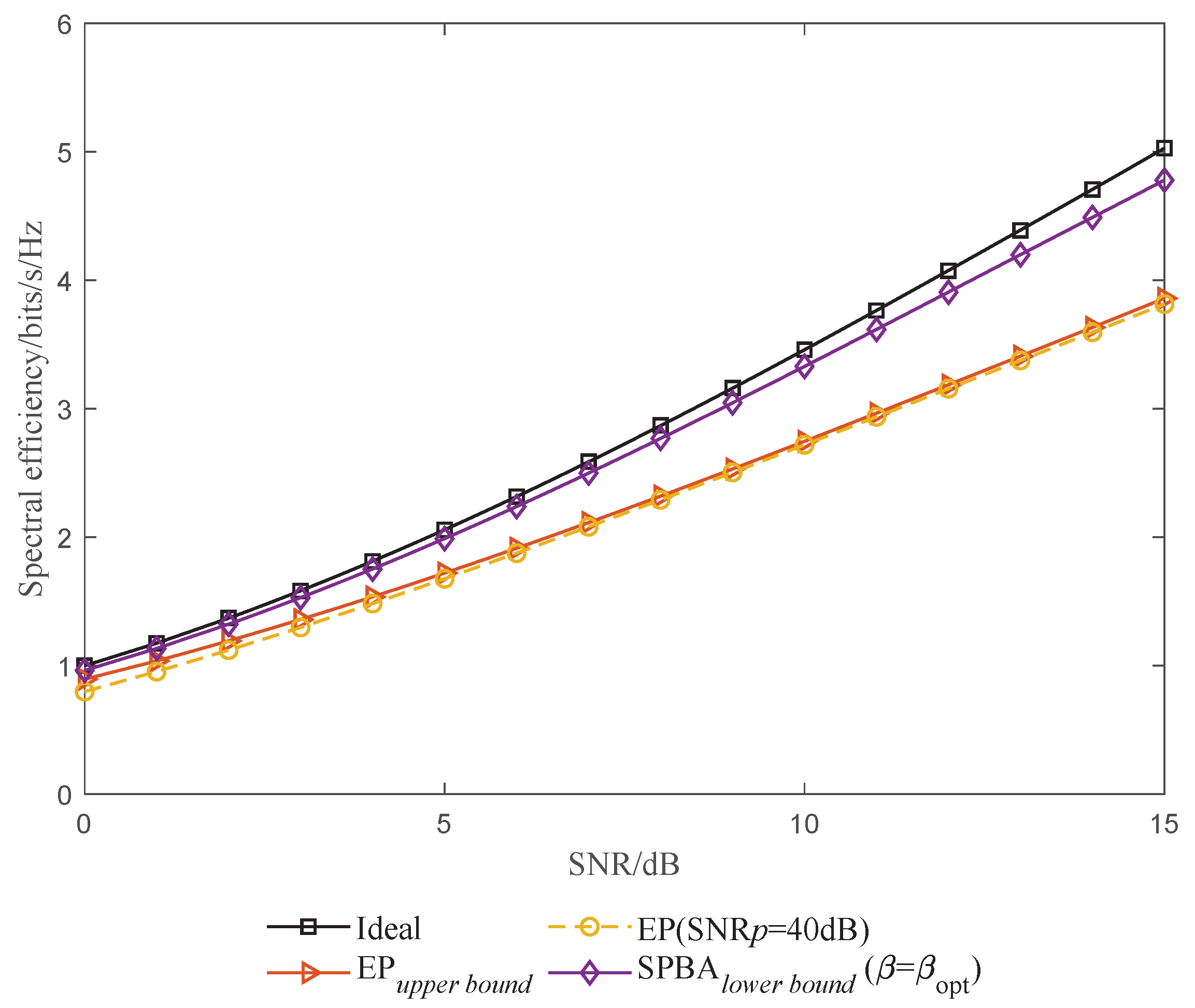


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, Z.; Kong, H.; Wu, Z.; Wei, J. Superimposed Perfect Binary Array-Aided Channel Estimation for OTFS Systems. Entropy 2023, 25, 1163. https://doi.org/10.3390/e25081163
Tang Z, Kong H, Wu Z, Wei J. Superimposed Perfect Binary Array-Aided Channel Estimation for OTFS Systems. Entropy. 2023; 25(8):1163. https://doi.org/10.3390/e25081163
Chicago/Turabian StyleTang, Zuping, Hengyou Kong, Ziyu Wu, and Jiaolong Wei. 2023. "Superimposed Perfect Binary Array-Aided Channel Estimation for OTFS Systems" Entropy 25, no. 8: 1163. https://doi.org/10.3390/e25081163
APA StyleTang, Z., Kong, H., Wu, Z., & Wei, J. (2023). Superimposed Perfect Binary Array-Aided Channel Estimation for OTFS Systems. Entropy, 25(8), 1163. https://doi.org/10.3390/e25081163








