Geometric Insights into the Multivariate Gaussian Distribution and Its Entropy and Mutual Information
Abstract
:1. Introduction
2. Geometry of the Gaussian Distribution
2.1. Standard Parametric Representation of an Ellipse
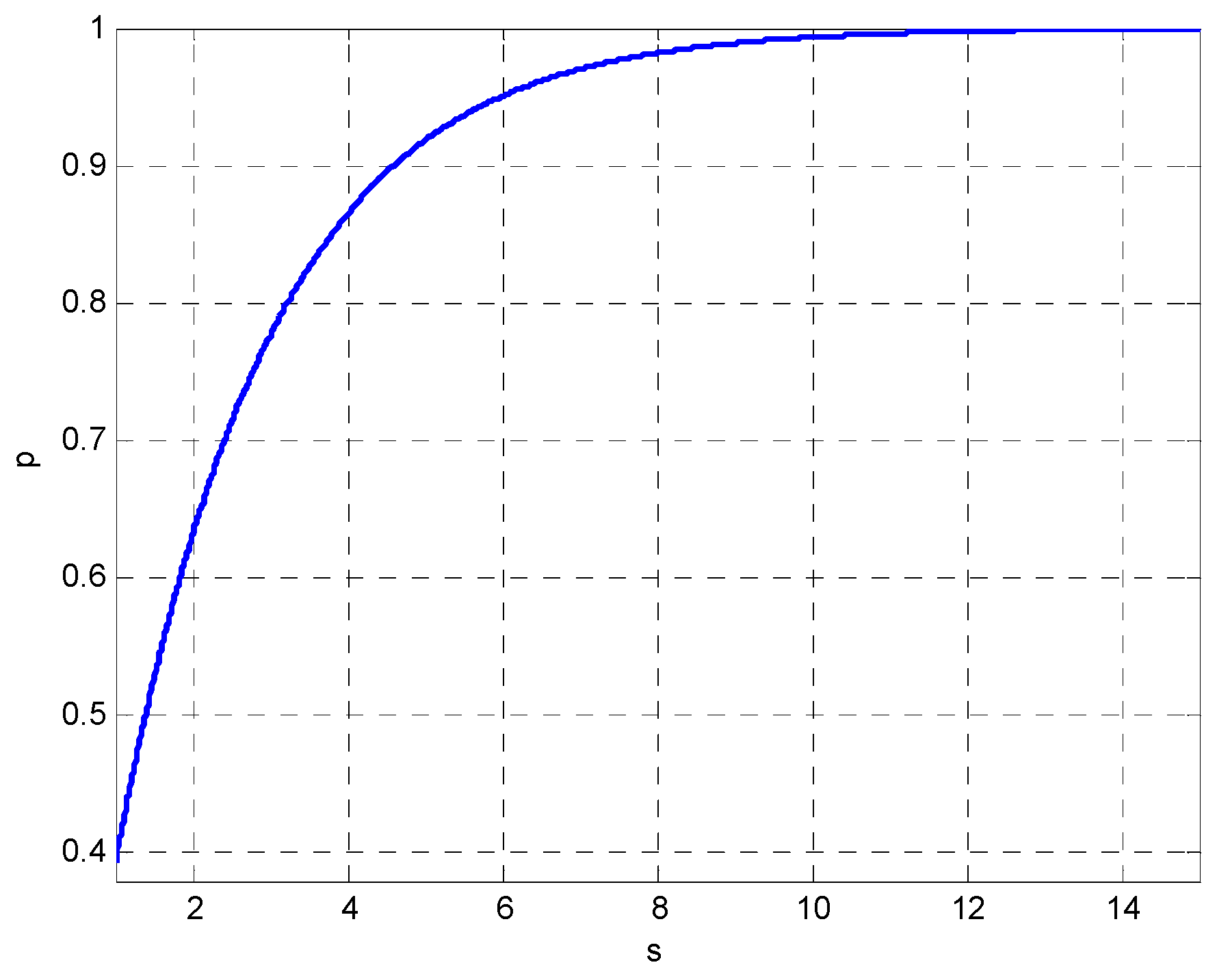
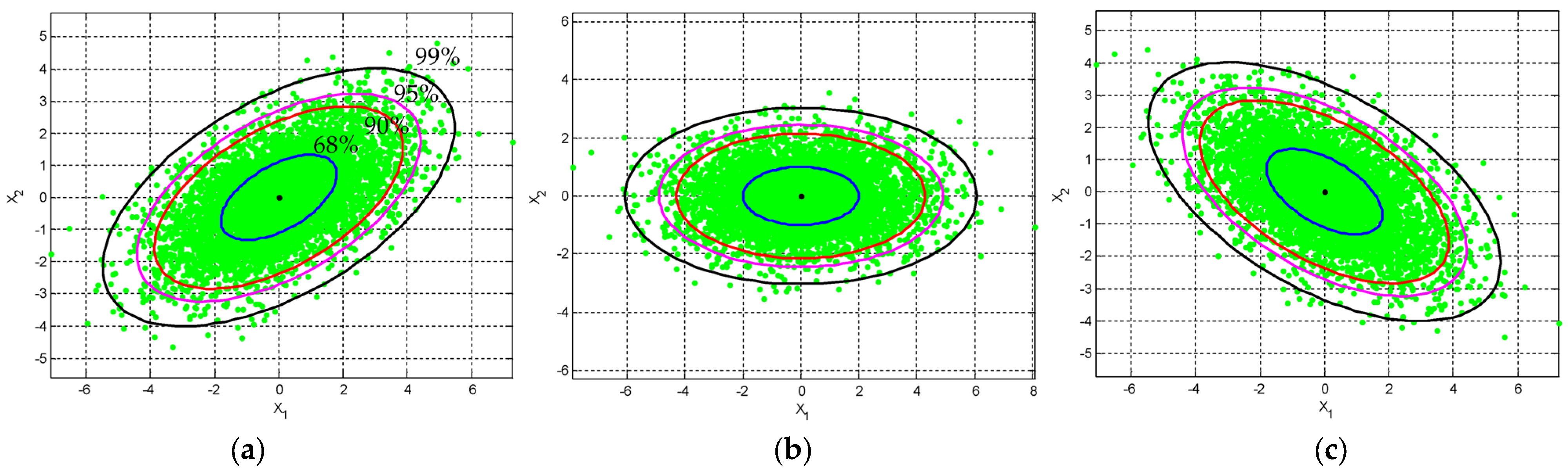
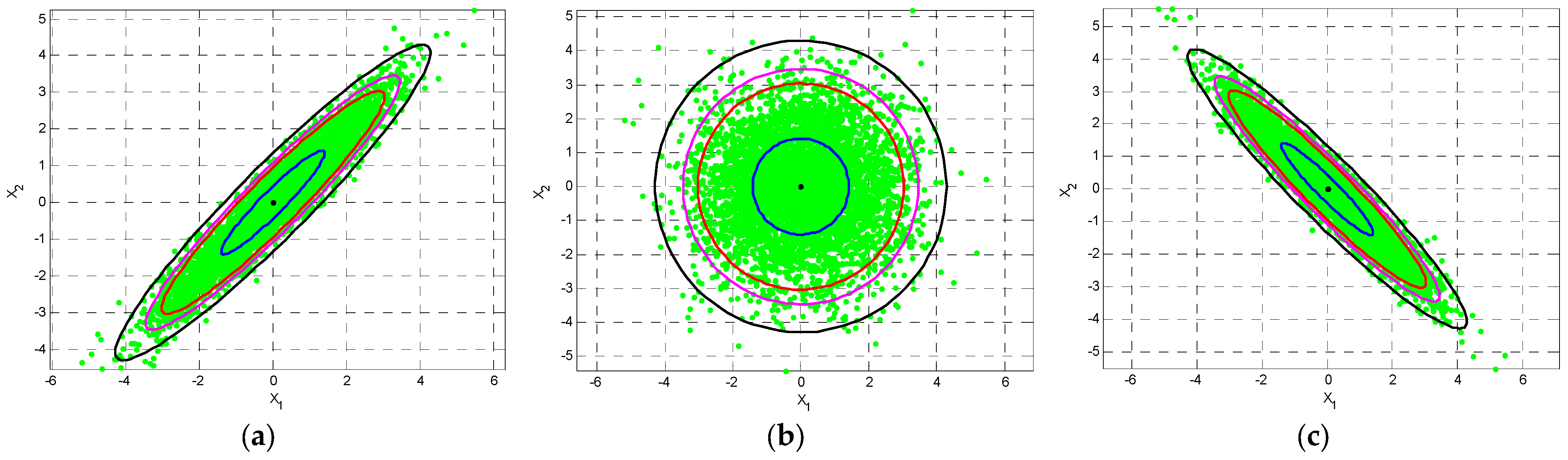
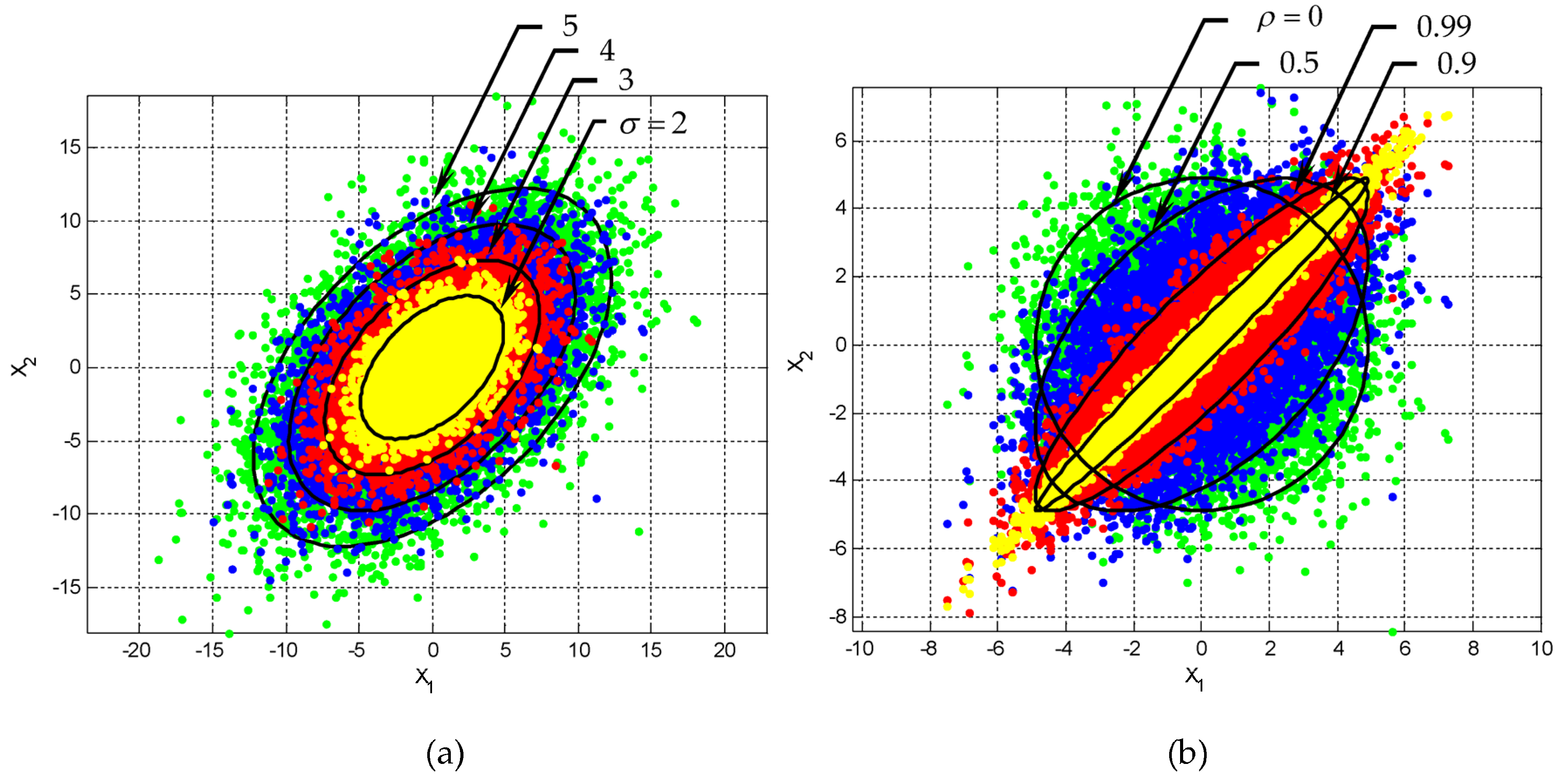
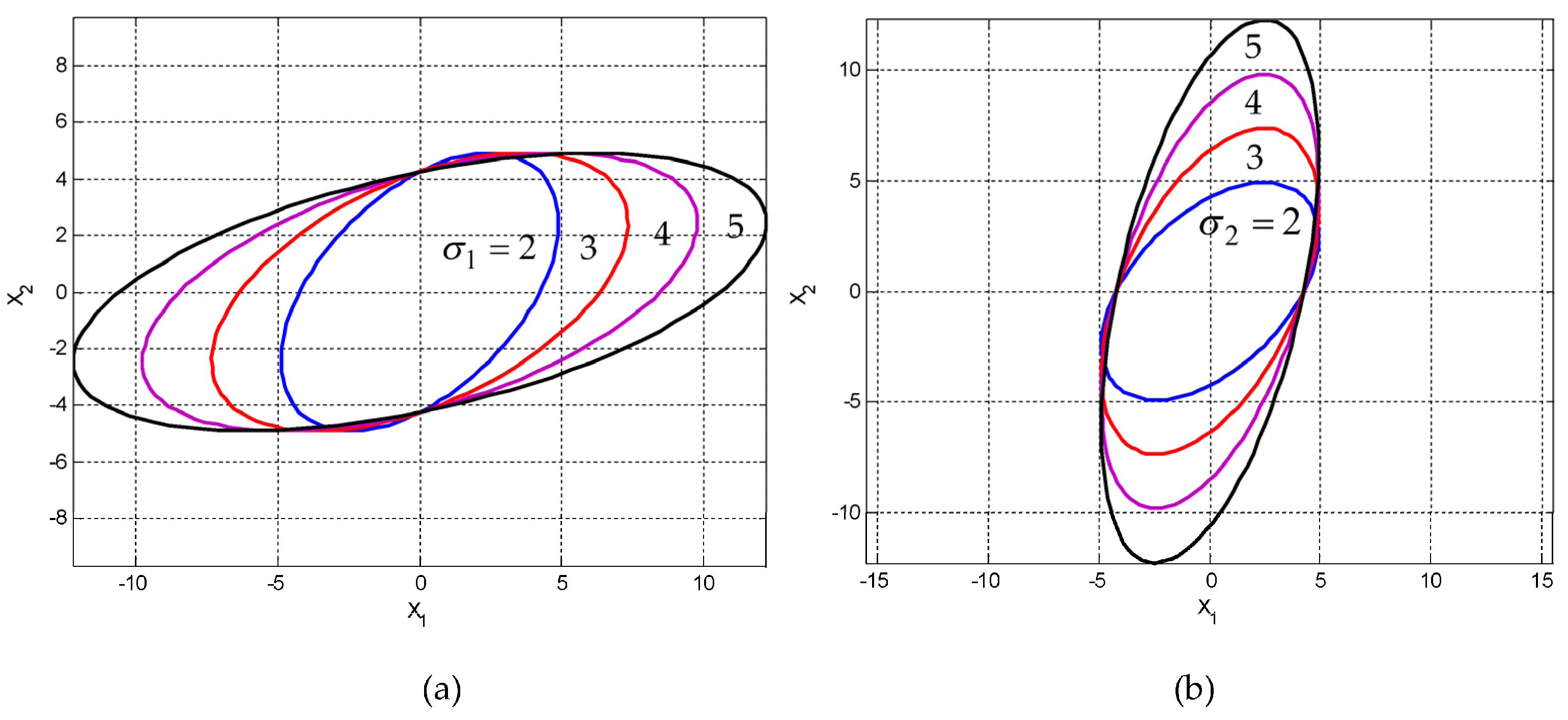
2.2. The Confidence Ellipse
- ▪
- It accounts for the fact that the variances in each direction are different;
- ▪
- It accounts for the covariance between variables;
- ▪
- It reduces to the familiar Euclidean distance for uncorrelated variables with unit variance.
2.3. Similarity Transform
- Scaling
- 2.
- Rotation
- 3.
- Translation
2.4. Simulation with a Given Variance-Covariance Matrix
3. Continuous Entropy/Differential Entropy
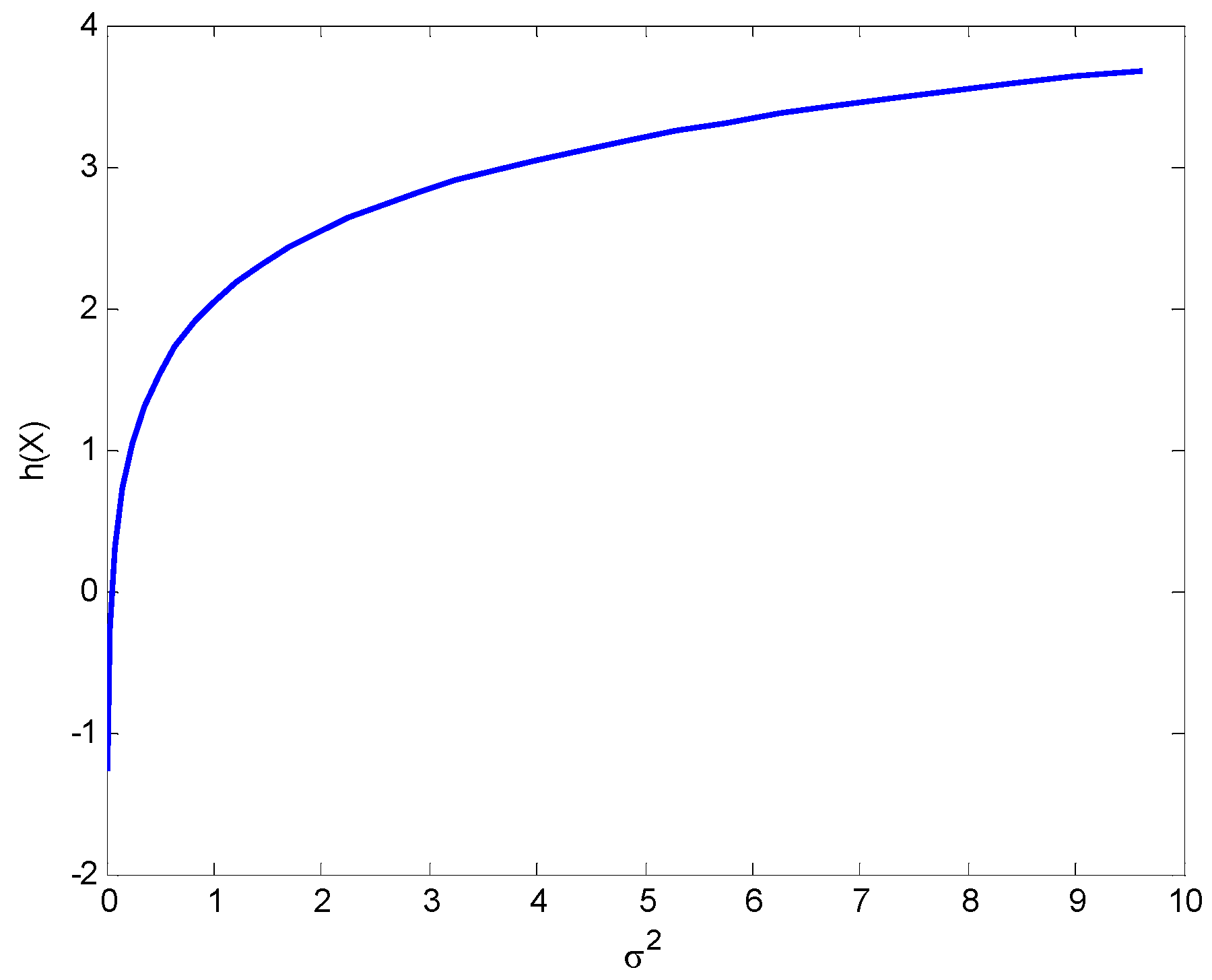
3.1. Entropy of a Univariate Gaussian Distribution
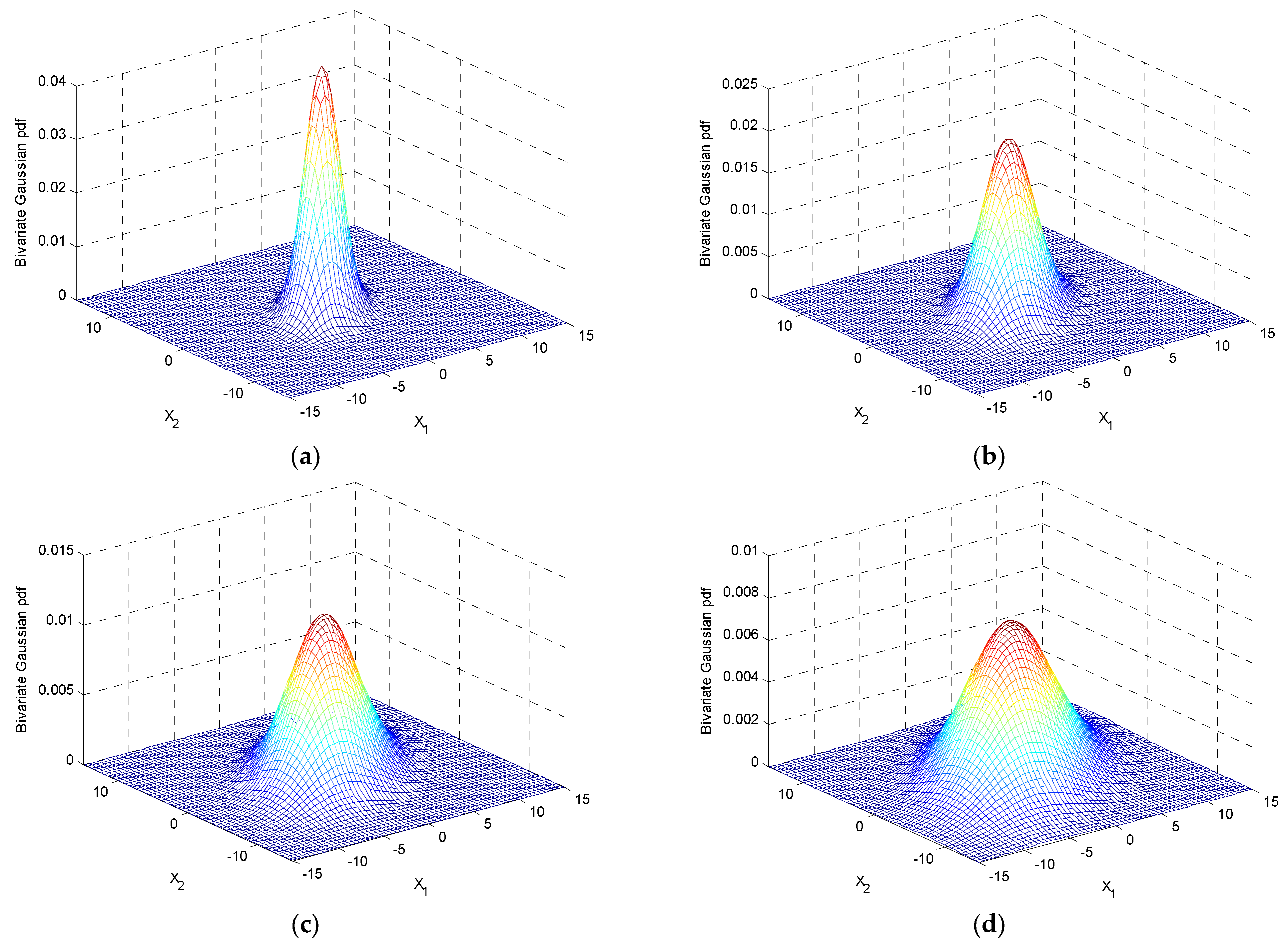
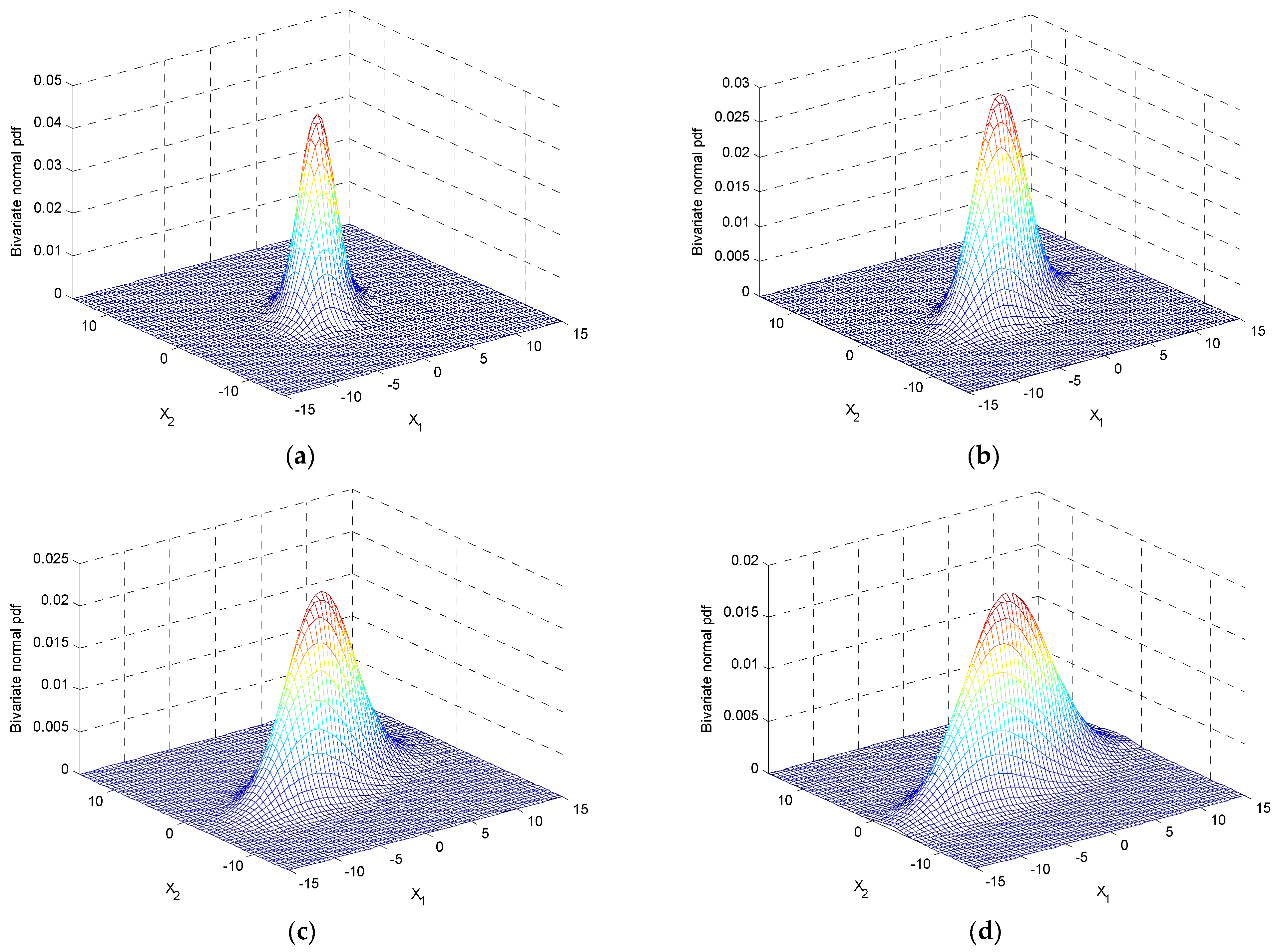
3.2. Entropy of a Multivariate Gaussian Distribution
3.3. The Differential Entropy in the Transformed Frame
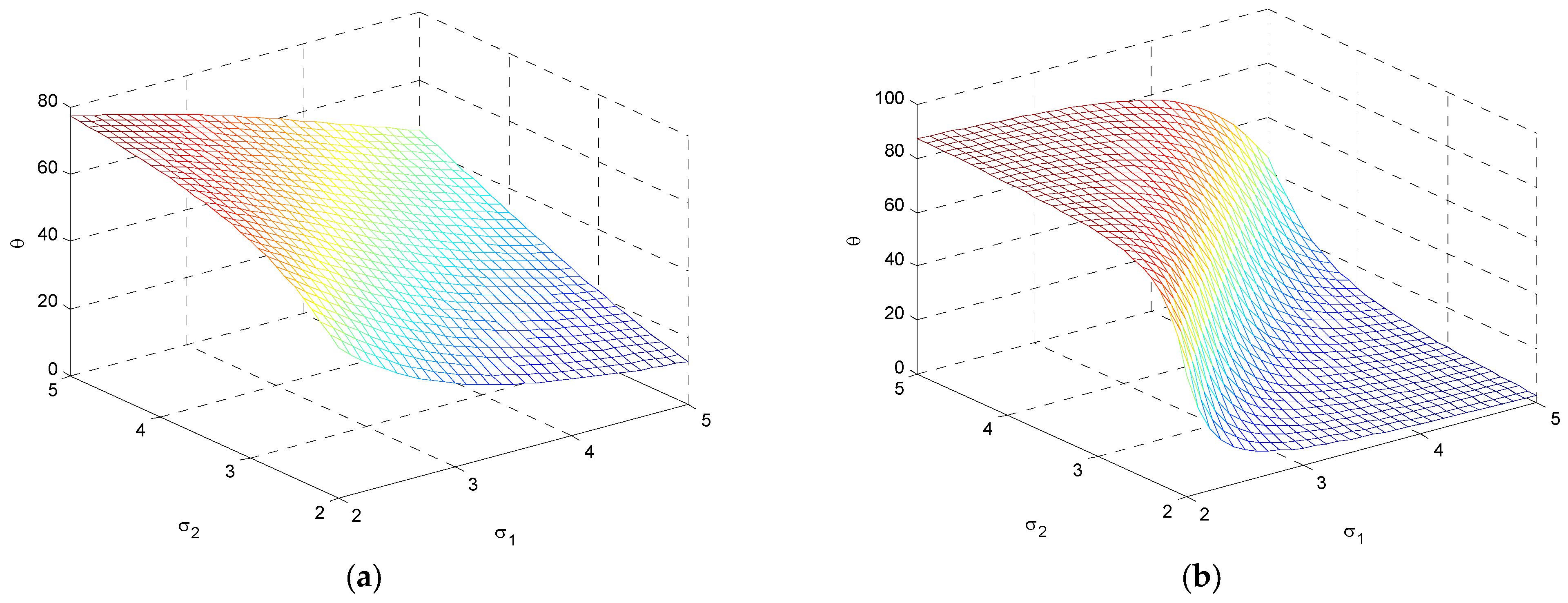
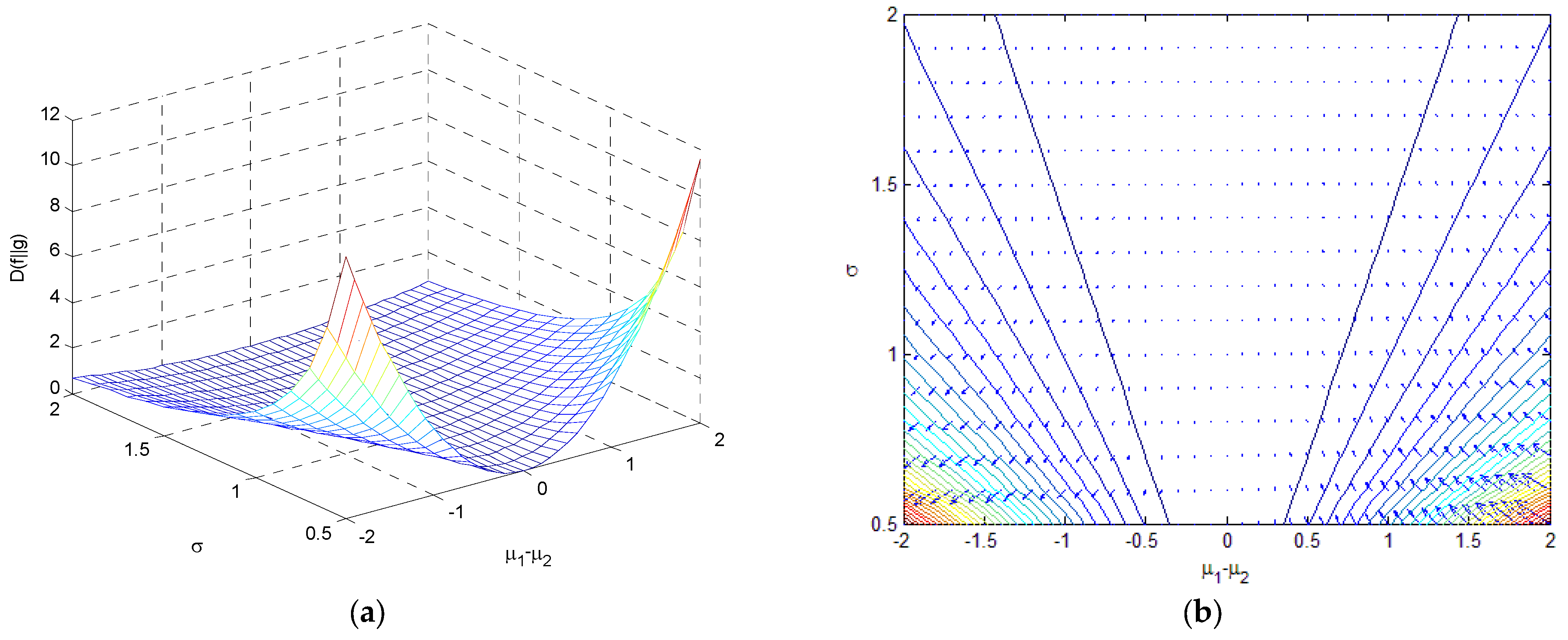
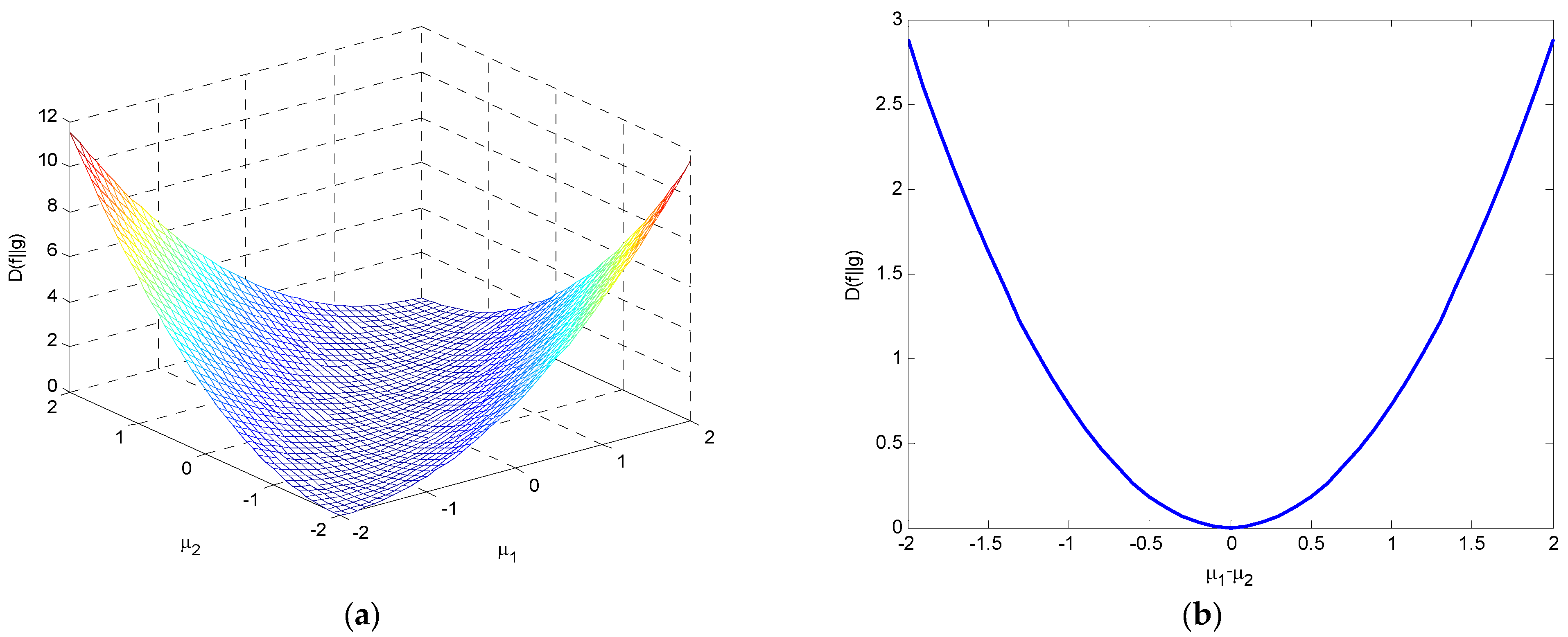
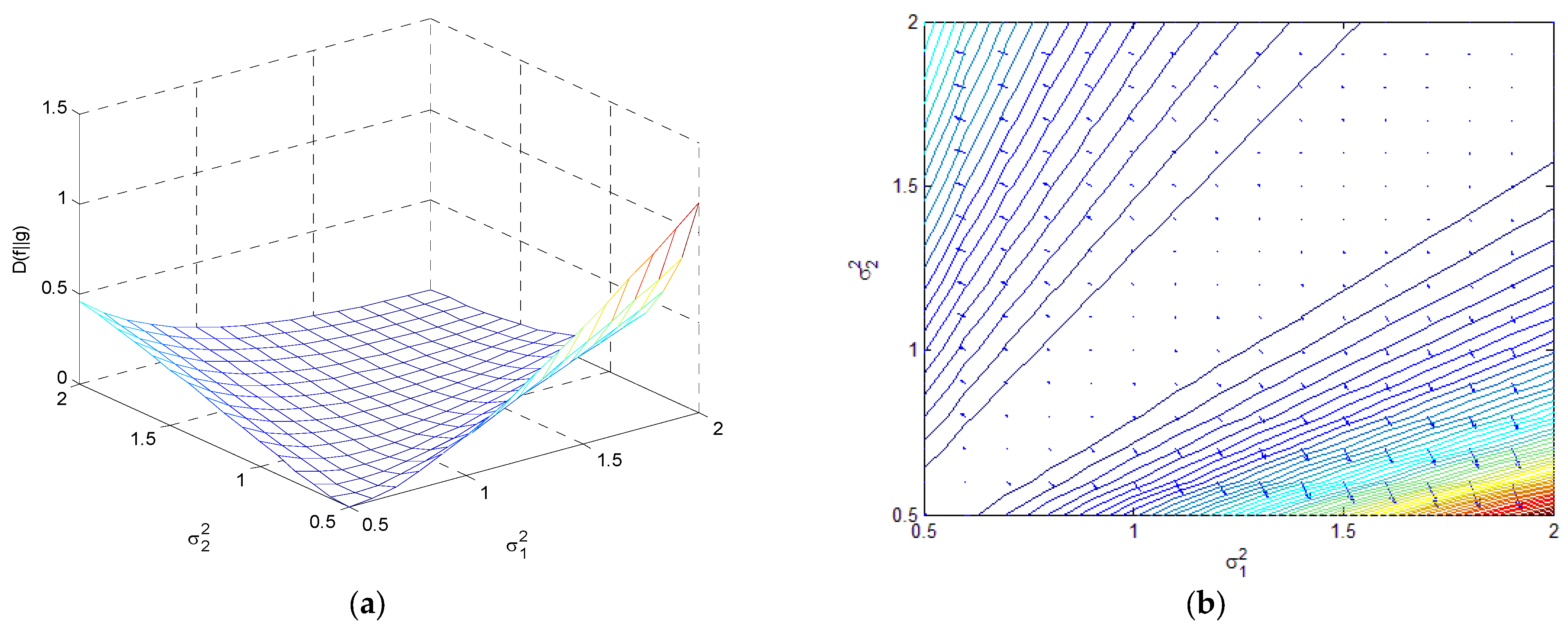
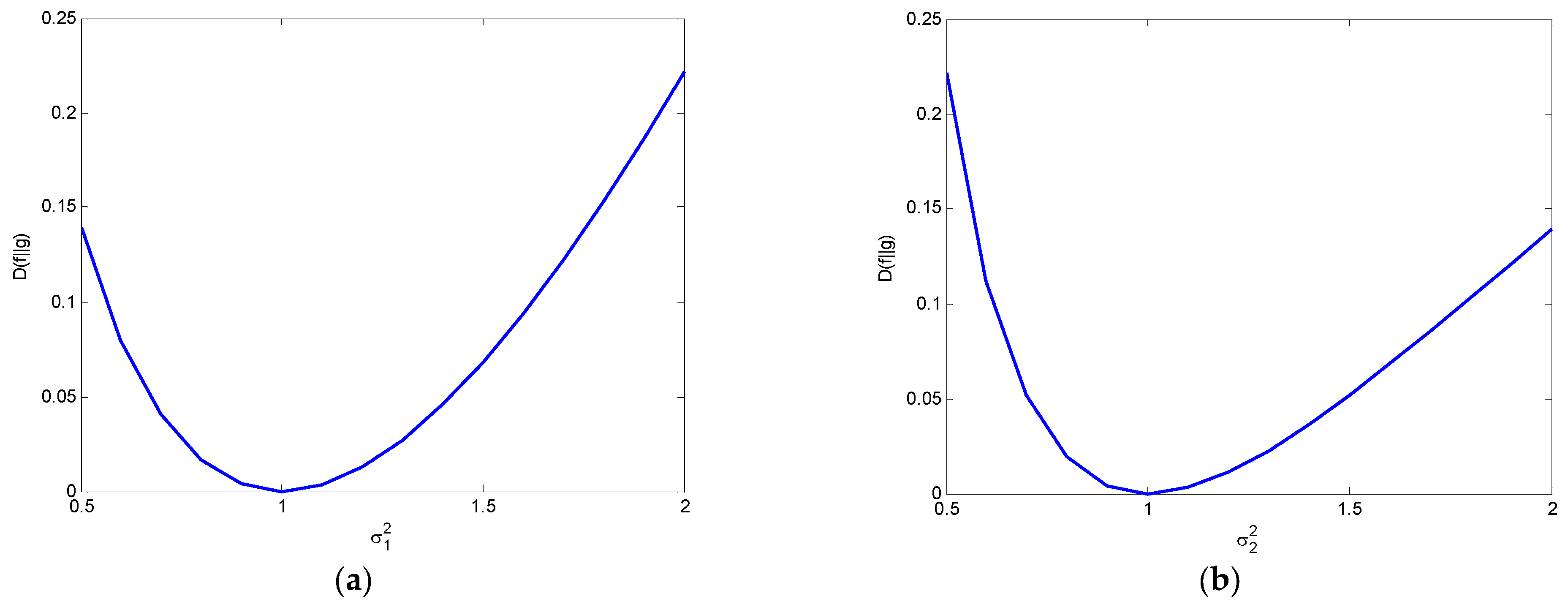
4. Relative Entropy (Kullback–Leibler Divergence)
- –
- If , , it is a function of concave upward.
- –
- If , , it is a function of concave upward.
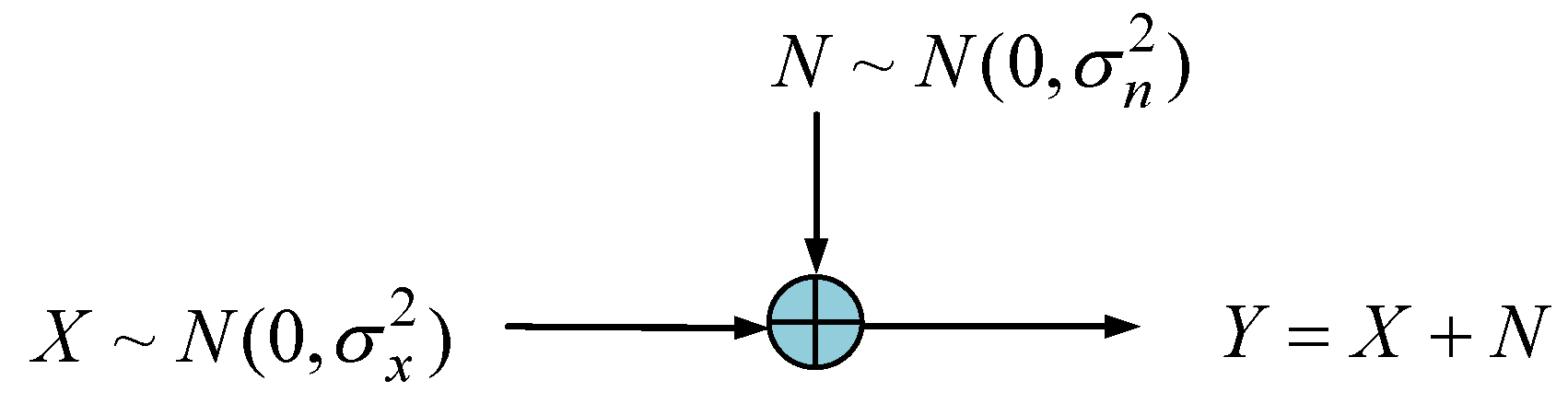
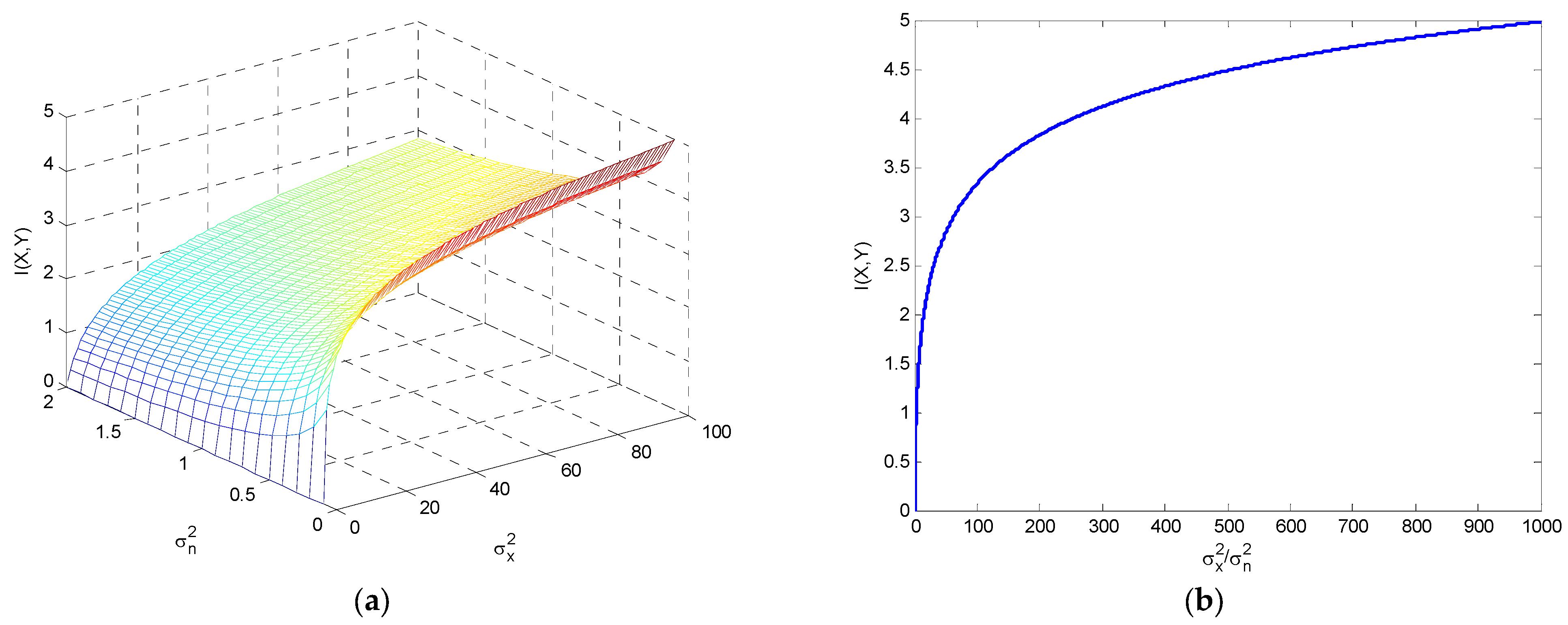
5. Mutual Information
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Derivation of the Differential Entropy for the Univariate Gaussian Distribution
Appendix B. Derivation of the Differential Entropy for the Multivariate Gaussian Distribution
Appendix C. Evaluation of Expectations of the Mahalanobis Distance
Appendix D. Derivation of the Differential Entropy in the Transformed Frame
Appendix E. Derivation of the Kullback–Leibler Divergence between Two Normal Distributions
References
- Verdú, S. On channel capacity per unit cost. IEEE Trans. Inf. Theory 1990, 36, 1019–1030. [Google Scholar] [CrossRef] [Green Version]
- Lapidoth, A.; Shamai, S. Fading channels: How perfect need perfect side information be? IEEE Trans. Inf. Theory 2002, 48, 1118–1134. [Google Scholar] [CrossRef]
- Verdú, S. Spectral efficiency in the wideband regime. IEEE Trans. Inf. Theory 2002, 48, 1319–1343. [Google Scholar] [CrossRef] [Green Version]
- Prelov, V.; Verdú, S. Second-order asymptotics of mutual information. IEEE Trans. Inf. Theory 2004, 50, 1567–1580. [Google Scholar] [CrossRef]
- Kailath, T. A general likelihood-ratio formula for random signals in Gaussian noise. IEEE Trans. Inf. Theory 1969, IT-15, 350–361. [Google Scholar] [CrossRef]
- Kailath, T. A note on least squares estimates from likelihood ratios. Inf. Control 1968, 13, 534–540. [Google Scholar] [CrossRef] [Green Version]
- Kailath, T. A further note on a general likelihood formula for random signals in Gaussian noise. IEEE Trans. Inf. Theory 1970, IT-16, 393–396. [Google Scholar] [CrossRef]
- Jaffer, A.G.; Gupta, S.C. On relations between detection and estimation of discrete time processes. Inf. Control 1972, 20, 46–54. [Google Scholar] [CrossRef] [Green Version]
- Duncan, T.E. On the calculation of mutual information. SIAM J. Appl. Math. 1970, 19, 215–220. [Google Scholar] [CrossRef] [Green Version]
- Kadota, T.T.; Zakai, M.; Ziv, J. Mutual information of the white Gaussian channel with and without feedback. IEEE Trans. Inf. Theory 1971, 17, 368–371. [Google Scholar] [CrossRef]
- Amari, S.I. Information Geometry and Its Applications; Springer: Berlin/Heidelberg, Germany, 2016; Volume 194. [Google Scholar]
- Schneidman, E.; Still, S.; Berry, M.J.; Bialek, W. Network information and connected correlations. Phys. Rev. Lett. 2003, 91, 238701. [Google Scholar] [CrossRef] [Green Version]
- Timme, N.; Alford, W.; Flecker, B.; Beggs, J.M. Synergy, redundancy, and multivariate information measures: An experimentalist’s perspective. J. Comput. Neurosci. 2014, 36, 119–140. [Google Scholar] [CrossRef]
- Ahmed, N.A.; Gokhale, D.V. Entropy expressions and their estimators for multivariate distributions. IEEE Trans. Inform. Theory 1989, 35, 688–692. [Google Scholar] [CrossRef]
- Misra, N.; Singh, H.; Demchuk, E. Estimation of the entropy of a multivariate normal distribution. J. Multivar. Anal. 2005, 92, 324–342. [Google Scholar] [CrossRef] [Green Version]
- Arellano-Valle, R.B.; Contreras-Reyes, J.E.; Genton, M.G. Shannon entropy and mutual information for multivariate skew-elliptical distributions. Scand. J. Stat. 2013, 40, 42–62. [Google Scholar] [CrossRef]
- Liang, K.C.; Wang, X. Gene regulatory network reconstruction using conditional mutual information. EURASIP J. Bioinform. Syst. Biol. 2008, 2008, 253894. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Novais, R.G.; Wanke, P.; Antunes, J.; Tan, Y. Portfolio optimization with a mean-entropy-mutual information model. Entropy 2022, 24, 369. [Google Scholar] [CrossRef]
- Verdú, S. Error exponents and α-mutual information. Entropy 2021, 23, 199. [Google Scholar] [CrossRef] [PubMed]
- Panzeri, S.; Magri, C.; Logothetis, N.K. On the use of information theory for the analysis of the relationship between neural and imaging signals. Magn. Reson. Imaging 2008, 26, 1015–1025. [Google Scholar] [CrossRef]
- Katz, Y.; Tunstrøm, K.; Ioannou, C.C.; Huepe, C.; Couzin, I.D. Inferring the structure and dynamics of interactions in schooling fish. Proc. Natl. Acad. Sci. USA 2011, 108, 18720–18725. [Google Scholar] [CrossRef] [PubMed]
- Cutsuridis, V.; Hussain, A.; Taylor, J.G. (Eds.) Perception-Action Cycle: Models, Architectures, and Hardware; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Ay, N.; Bernigau, H.; Der, R.; Prokopenko, M. Information-driven self-organization: The dynamical system approach to autonomous robot behavior. Theory Biosci. 2012, 131, 161–179. [Google Scholar] [CrossRef] [PubMed]
- Rosas, F.; Ntranos, V.; Ellison, C.J.; Pollin, S.; Verhelst, M. Understanding interdependency through complex information sharing. Entropy 2016, 18, 38. [Google Scholar] [CrossRef] [Green Version]
- Ince, R.A. The Partial Entropy Decomposition: Decomposing multivariate entropy and mutual information via pointwise common surprisal. arXiv 2017, arXiv:1702.01591. [Google Scholar]
- Harder, M.; Salge, C.; Polani, D. Bivariate measure of redundant information. Phys. Rev. E 2013, 87, 012130. [Google Scholar] [CrossRef] [Green Version]
- Rauh, J.; Banerjee, P.K.; Olbrich, E.; Jost, J.; Bertschinger, N. On extractable shared information. Entropy 2017, 19, 328. [Google Scholar] [CrossRef] [Green Version]
- Ince, R.A. Measuring multivariate redundant information with pointwise common change in surprisal. Entropy 2017, 19, 318. [Google Scholar] [CrossRef] [Green Version]
- Perrone, P.; Ay, N. Hierarchical quantification of synergy in channels. Front. Robot. AI 2016, 2, 35. [Google Scholar] [CrossRef] [Green Version]
- Bertschinger, N.; Rauh, J.; Olbrich, E.; Jost, J.; Ay, N. Quantifying unique information. Entropy 2014, 16, 2161–2183. [Google Scholar] [CrossRef] [Green Version]
- Chicharro, D.; Panzeri, S. Synergy and redundancy in dual decompositions of mutual information gain and information loss. Entropy 2017, 19, 71. [Google Scholar] [CrossRef] [Green Version]
- Michalowicz, J.V.; Nichols, J.M.; Bucholtz, F. Calculation of differential entropy for a mixed Gaussian distribution. Entropy 2008, 10, 200. [Google Scholar] [CrossRef] [Green Version]
- Benish, W.A. A review of the application of information theory to clinical diagnostic testing. Entropy 2020, 22, 97. [Google Scholar] [CrossRef] [Green Version]
- Cadirci, M.S.; Evans, D.; Leonenko, N.; Makogin, V. Entropy-based test for generalised Gaussian distributions. Comput. Stat. Data Anal. 2022, 173, 107502. [Google Scholar] [CrossRef]
- Goethe, M.; Fita, I.; Rubi, J.M. Testing the mutual information expansion of entropy with multivariate Gaussian distributions. J. Chem. Phys. 2017, 147, 224102. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jwo, D.-J.; Cho, T.-S.; Biswal, A. Geometric Insights into the Multivariate Gaussian Distribution and Its Entropy and Mutual Information. Entropy 2023, 25, 1177. https://doi.org/10.3390/e25081177
Jwo D-J, Cho T-S, Biswal A. Geometric Insights into the Multivariate Gaussian Distribution and Its Entropy and Mutual Information. Entropy. 2023; 25(8):1177. https://doi.org/10.3390/e25081177
Chicago/Turabian StyleJwo, Dah-Jing, Ta-Shun Cho, and Amita Biswal. 2023. "Geometric Insights into the Multivariate Gaussian Distribution and Its Entropy and Mutual Information" Entropy 25, no. 8: 1177. https://doi.org/10.3390/e25081177
APA StyleJwo, D.-J., Cho, T.-S., & Biswal, A. (2023). Geometric Insights into the Multivariate Gaussian Distribution and Its Entropy and Mutual Information. Entropy, 25(8), 1177. https://doi.org/10.3390/e25081177






