A Novel Complex-Valued Gaussian Measurement Matrix for Image Compressed Sensing
Abstract
:1. Introduction
1.1. Related Work
1.2. Contributions
- We constructed a complex-valued Gaussian matrix as the measurement matrix using two real-valued Gaussian matrices. The results illustrate that the reconstructed image quality is superior when using the complex-valued matrix compared to the real-valued measurement matrix.
- To enhance the performance of compressed sensing reconstruction, we performed Gram–Schmidt orthogonalization on the two real-valued matrices that make up the complex-valued Gaussian matrix. Based on our experiments, this orthogonalized measurement matrix can significantly enhance the reconstructed image quality.
- We applied a sparsification operation to the proposed complex-valued measurement matrix to save storage space and reduce the calculation amount during image compression. Our analysis indicates that this sparsification operation effectively reduces the calculation amount required and computational complexity.
2. Concepts and Theoretical Basis
2.1. Compressed Sensing
2.2. Gaussian Random Matrix
2.3. Gram–Schmidt Orthogonalization
- (1)
- Orthogonalization
- (2)
- Unitization
3. Compressed Sensing Scheme
3.1. Design of Measurement Matrix
| Algorithm 1: Generate the real part of complex-valued measurement matrix |
| Input: The size of measurement matrix |
| Output: The real part of the complex-valued measurement matrix |
| 1 Begin |
| 2 Initialize a Gaussian random matrix Mtx |
| 3 Initialize an all-zero matrix Mtx_orth |
| 4 Mtx_orth(:, 1) = Mtx(:, 1) |
| 5 for i = 2 to n do |
| 6 for j = 1 to i − 1 do |
| 7 Mtx_orth(:, i) = Mtx_orth(:, i) − dot(Mtx(:, i), Mtx_orth(:, j))/ dot(Mtx_orth(:, j), Mtx_orth(:, j)) * Mtx_orth(:, j) |
| 8 end |
| 9 Mtx_orth(:, i) = Mtx_orth(:, i) + Mtx(:, i); |
| 10 end |
| 11 end |
3.2. Compressed Sensing with Complex-Valued Measurement Matrix
- Step 1: Image sparsification. Use Discrete Cosine Transform (DCT) to make the image sparse.
- Step 2: Construct the measurement matrix. Two Gaussian matrices are orthogonalized via Gram–Schmidt orthogonalization, respectively. Then, one is used as the real part of the measurement matrix, and the other is used as the imaginary part.
- Step 3: Image compression. Apply the measurement matrix to compress the image.
- Step 4: Image reconstruction. Use the SL0 algorithm to reconstruct the sparse signal of the original image in the DCT domain.
- Step 5: Inverse sparsification. Use inverse sparsification operation to obtain the original image from the sparse signal in the DCT domain.
4. Experimental Analysis
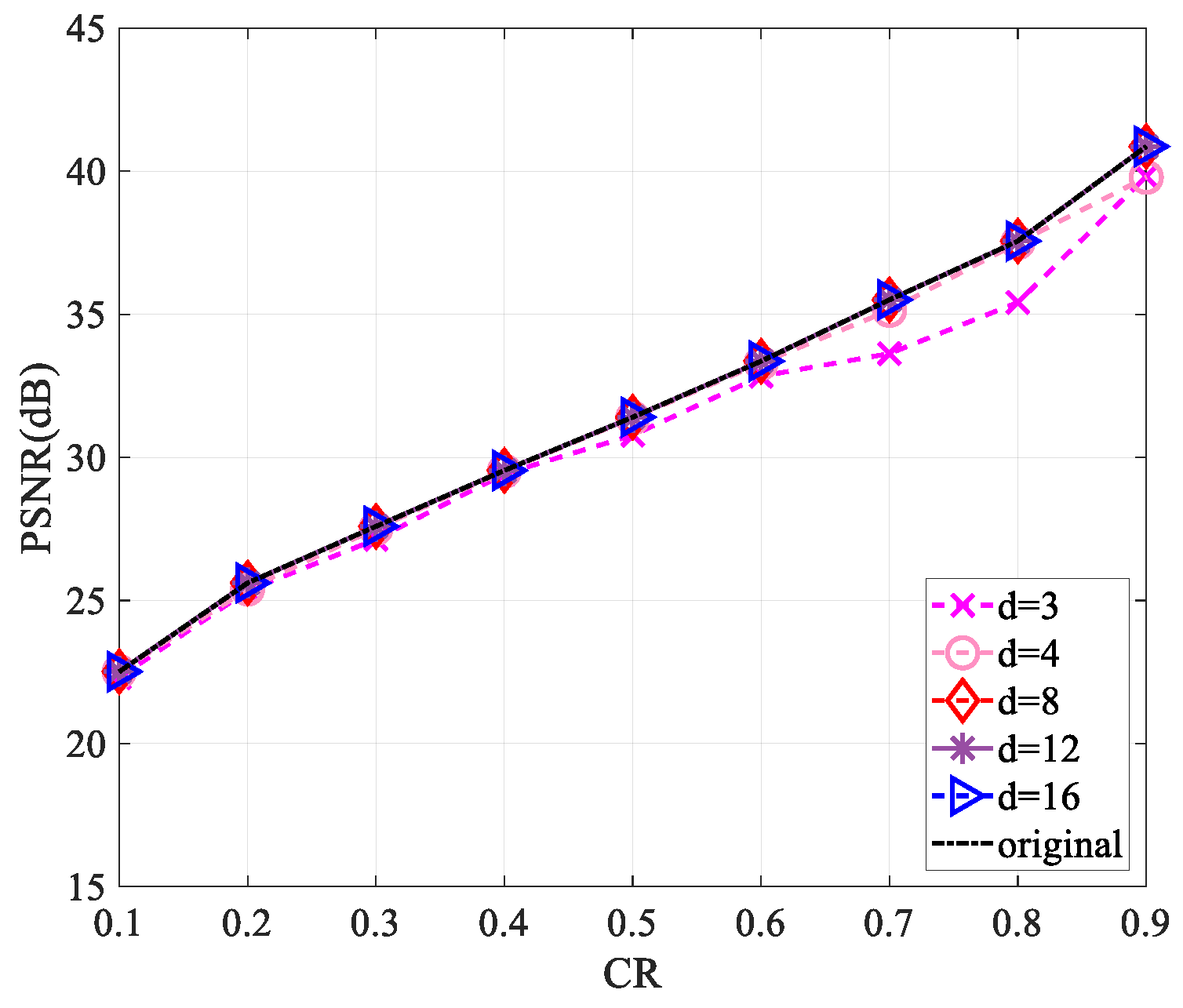
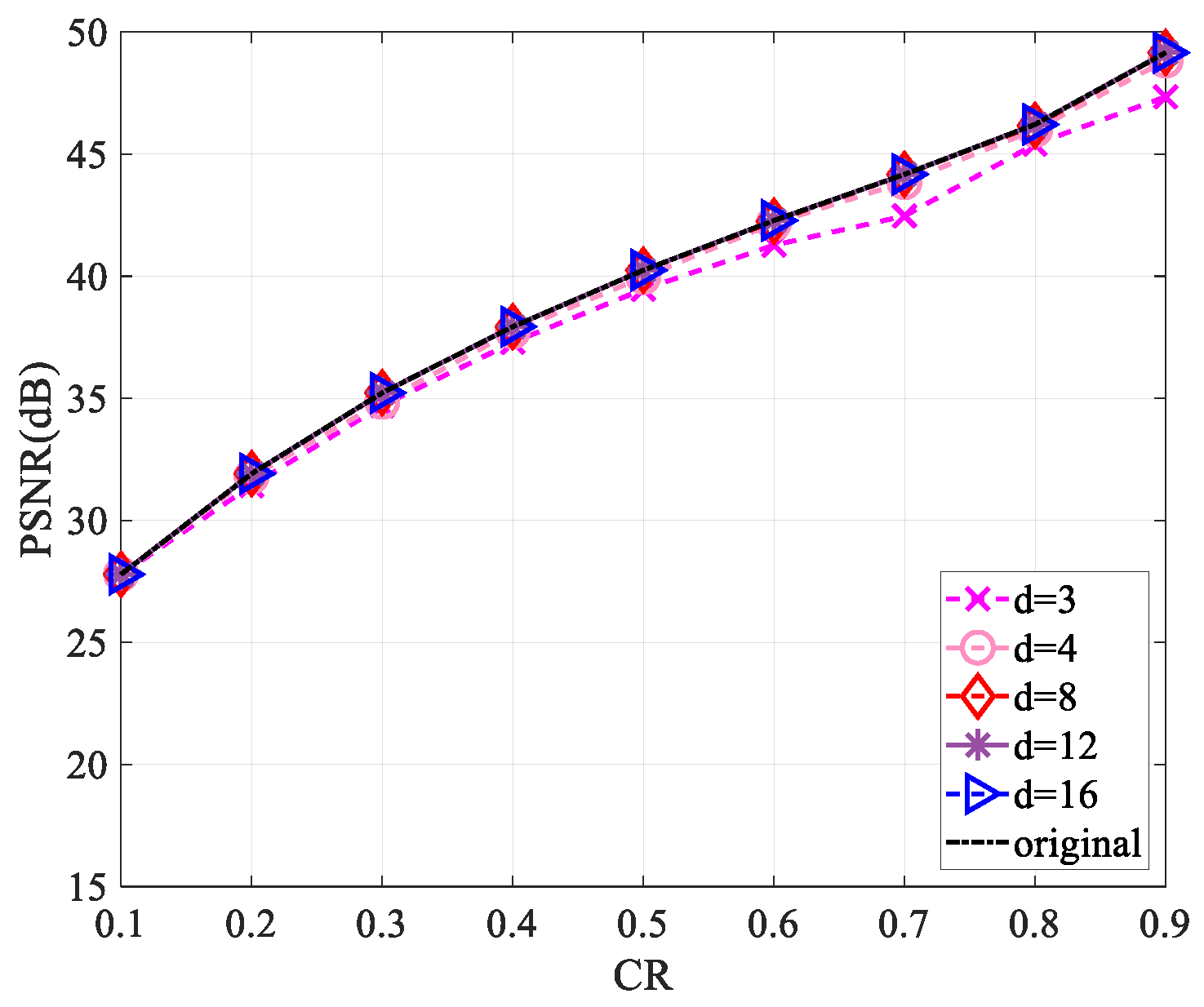
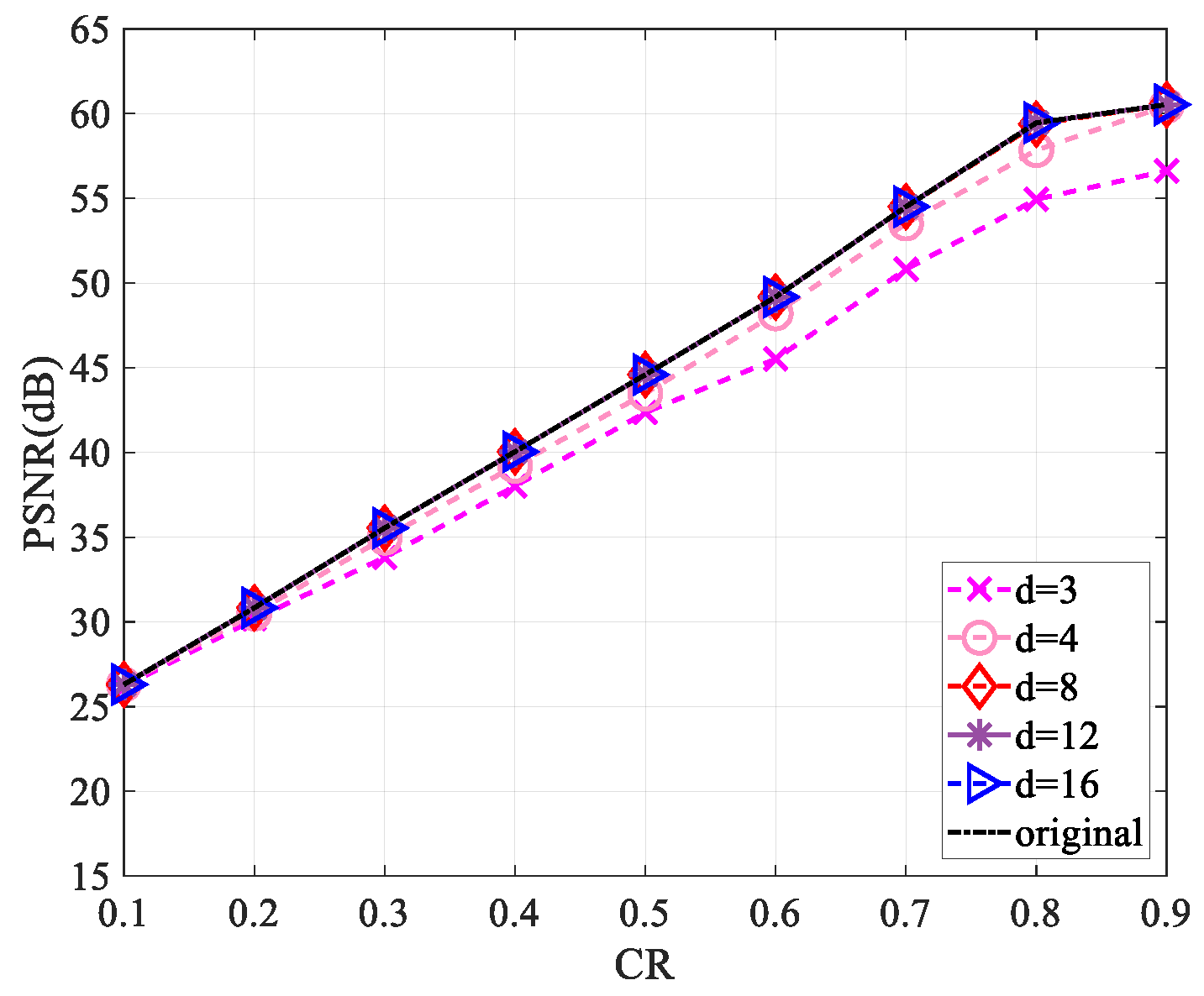
4.1. Peak Signal-to-Noise Ratio Analysis
4.2. Structural Similarity Analysis
4.3. Comparison of Different Algorithms
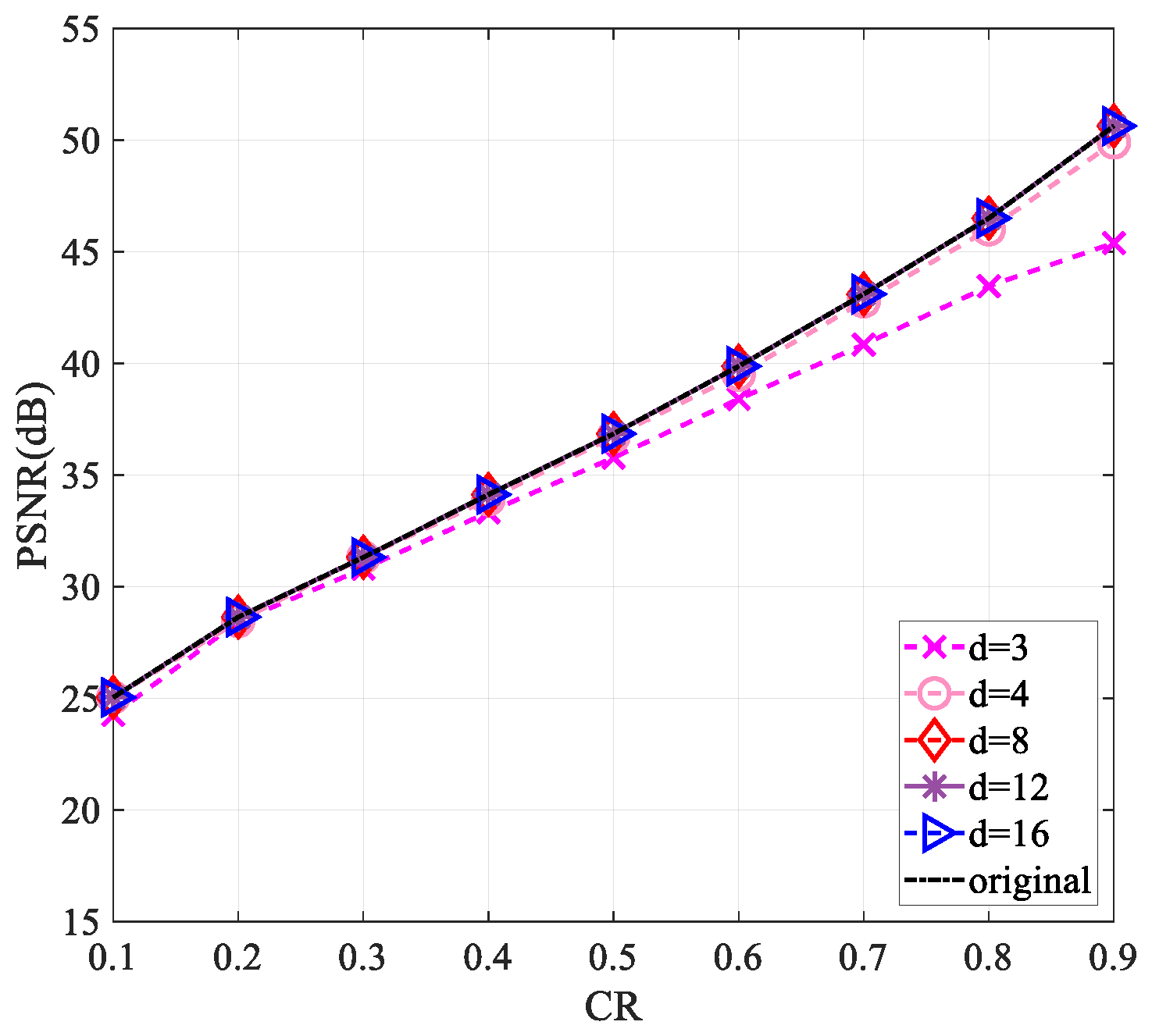
4.4. Sparsity Analysis of the Measurement Matrix
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Donoho, D.L. Compressed sensing. IEEE Trans. Inform. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Al-Hayani, B.; Ilhan, H. Efficient cooperative image transmission in one-way multi-hop sensor network. Int. J. Electr. Eng. Educ. 2020, 57, 321–339. [Google Scholar] [CrossRef]
- Li, L.; Fang, Y.; Liu, L.; Peng, H.; Kurths, J.; Yang, Y. Overview of Compressed Sensing: Sensing Model, Reconstruction Algorithm, and Its Applications. Appl. Sci. 2020, 10, 5909. [Google Scholar] [CrossRef]
- Qie, Y.; Hao, C.; Song, P. Wireless Transmission Method for Large Data Based on Hierarchical Compressed Sensing and Sparse Decomposition. Sensors 2020, 20, 7146. [Google Scholar] [CrossRef] [PubMed]
- Chakraborty, P.; Tharini, C. An Efficient Parallel Block Compressive Sensing Scheme for Medical Signals and Image Compression. Wirel. Pers. Commun 2022, 123, 2959–2970. [Google Scholar] [CrossRef]
- Wang, H.; Wu, Y.; Xie, H. Secure and Efficient Image Transmission Scheme for Smart Cities Using Sparse Signal Transformation and Parallel Compressive Sensing. Math. Probl. Eng. 2021, 2021, 5598009. [Google Scholar] [CrossRef]
- Belyaev, E. An Efficient Compressive Sensed Video Codec with Inter-Frame Decoding and Low-Complexity Intra-Frame Encoding. Sensors 2023, 23, 1368. [Google Scholar] [CrossRef]
- Belyaev, E.; Codreanu, M.; Juntti, M.; Egiazarian, K. Compressive sensed video recovery via iterative thresholding with random transforms. IET Image Process. 2020, 14, 1187–1199. [Google Scholar] [CrossRef]
- Tsaig, Y.; Donoho, D.L. Extensions of compressed sensing. Signal Process. 2006, 86, 549–571. [Google Scholar] [CrossRef]
- Zhang, G.; Jiao, S.; Xu, X.; Wang, L. Compressed sensing and reconstruction with bernoulli matrices. In Proceedings of the 2010 IEEE International Conference on Information and Automation, Harbin, China, 20–23 June 2010. [Google Scholar]
- Zhou, N.; Zhang, A.; Wu, J.; Pei, D.; Yang, Y. Novel hybrid image compression–encryption algorithm based on compressive sensing. Optik 2014, 125, 5075–5080. [Google Scholar] [CrossRef]
- Yu, L.; Barbot, J.P.; Zheng, G.; Sun, H. Compressive Sensing with Chaotic Sequence. IEEE Signal Process. Lett. 2010, 17, 731–734. [Google Scholar] [CrossRef]
- Gan, H.; Li, Z.; Li, J.; Wang, X.; Cheng, Z. Compressive sensing using chaotic sequence based on Chebyshev map. Nonlinear Dynam 2014, 78, 2429–2438. [Google Scholar] [CrossRef]
- Arjoune, Y.; Hu, W.C.; Kaabouch, N. Chebyshev Vandermonde-like Measurement Matrix Based Compressive Spectrum Sensing. In Proceedings of the 2019 IEEE International Conference on Electro Information Technology (EIT), Brookings, SD, USA, 20–22 May 2019. [Google Scholar]
- Bajwa, W.U.; Haupt, J.D.; Raz, G.M.; Wright, S.J.; Nowak, R.D. Toeplitz-Structured Compressed Sensing Matrices. In Proceedings of the 2007 IEEE/SP 14th Workshop on Statistical Signal Processing, Madison, WI, USA, 26–29 August 2007. [Google Scholar]
- Wang, J.; Xu, Z.; Wang, Z.; Xu, S.; Jiang, J. Rapid compressed sensing reconstruction: A semi-tensor product approach. Inf. Sci. 2020, 512, 693–707. [Google Scholar] [CrossRef]
- Li, X.; Ling, Y. Research on the construction algorithm of measurement matrix based on mixed chaotic. Microelectron. Comput. 2021, 38, 23–30. [Google Scholar]
- Xue, L.; Wang, Y.; Wang, Z. Secure image block compressive sensing using complex Hadamard measurement matrix and bit-level XOR. IET Inf. Secur. 2022, 16, 417–431. [Google Scholar] [CrossRef]
- Xue, L.; Qiu, W.; Wang, Y.; Wang, Z. An Image-Based Quantized Compressive Sensing Scheme Using Zadoff–Chu Measurement Matrix. Sensors 2023, 23, 1016. [Google Scholar] [CrossRef] [PubMed]
- Tropp, J.A.; Gilbert, A.C. Signal Recovery From Random Measurements Via Orthogonal Matching Pursuit. IEEE Trans. Inform. Theory 2007, 53, 4655–4666. [Google Scholar] [CrossRef]
- Do, T.T.; Gan, L.; Nguyen, N.; Tran, T.D. Sparsity adaptive matching pursuit algorithm for practical compressed sensing. In Proceedings of the 2008 42nd Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 26–29 October 2008. [Google Scholar]
- Mohimani, H.; Babaie-Zadeh, M.; Jutten, C. A Fast Approach for Overcomplete Sparse Decomposition Based on Smoothed ℓ0 Norm. IEEE Trans. Signal Process. 2009, 57, 289–301. [Google Scholar] [CrossRef]
- Beck, A.; Teboulle, M. A Fast Iterative Shrinkage-Thresholding Algorithm for Linear Inverse Problems. SIAM J. Imaging Sci. 2009, 2, 183–202. [Google Scholar] [CrossRef]
- Candès, E.J.; Romberg, J.K.; Tao, T. Stable Signal Recovery from Incomplete and Inaccurate Measurements. Commun. Pure Appl. Math. A J. Issued Courant Inst. Math. Sci. 2006, 8, 1207–1223. [Google Scholar] [CrossRef]
- Cai, G. A Note and Application of the Schmidt Orthogonalization. J. Anqing Teach. Coll. (Nat. Sci. Ed.) 2015, 21, 106–108. [Google Scholar] [CrossRef]
- Wei, C. Research on Construction and Optimization of Measurement Matrix in Compressed Sensing. Master’s Thesis, Nanjing University of Posts and Telecommunications, Nanjing, China, 2016. [Google Scholar]
- Aung, A.; Ng, B.P.; Rahardja, S. Sequency-Ordered Complex Hadamard Transform: Properties, Computational Complexity and Applications. IEEE Trans. Signal Process. 2008, 56, 3562–3571. [Google Scholar] [CrossRef]
- Mahdaoui, A.E.; Ouahabi, A.; Moulay, M.S. Image Denoising Using a Compressive Sensing Approach Based on Regularization Constraints. Sensors 2022, 22, 2199. [Google Scholar] [CrossRef]
- Chen, Z.; Huang, C.; Lin, S. A new sparse representation framework for compressed sensing MRI. Knowl.-Based Syst. 2020, 188, 104969. [Google Scholar] [CrossRef]
- Gilbert, A.; Indyk, P. Sparse Recovery Using Sparse Matrices. Proc. IEEE 2010, 98, 937–947. [Google Scholar] [CrossRef]


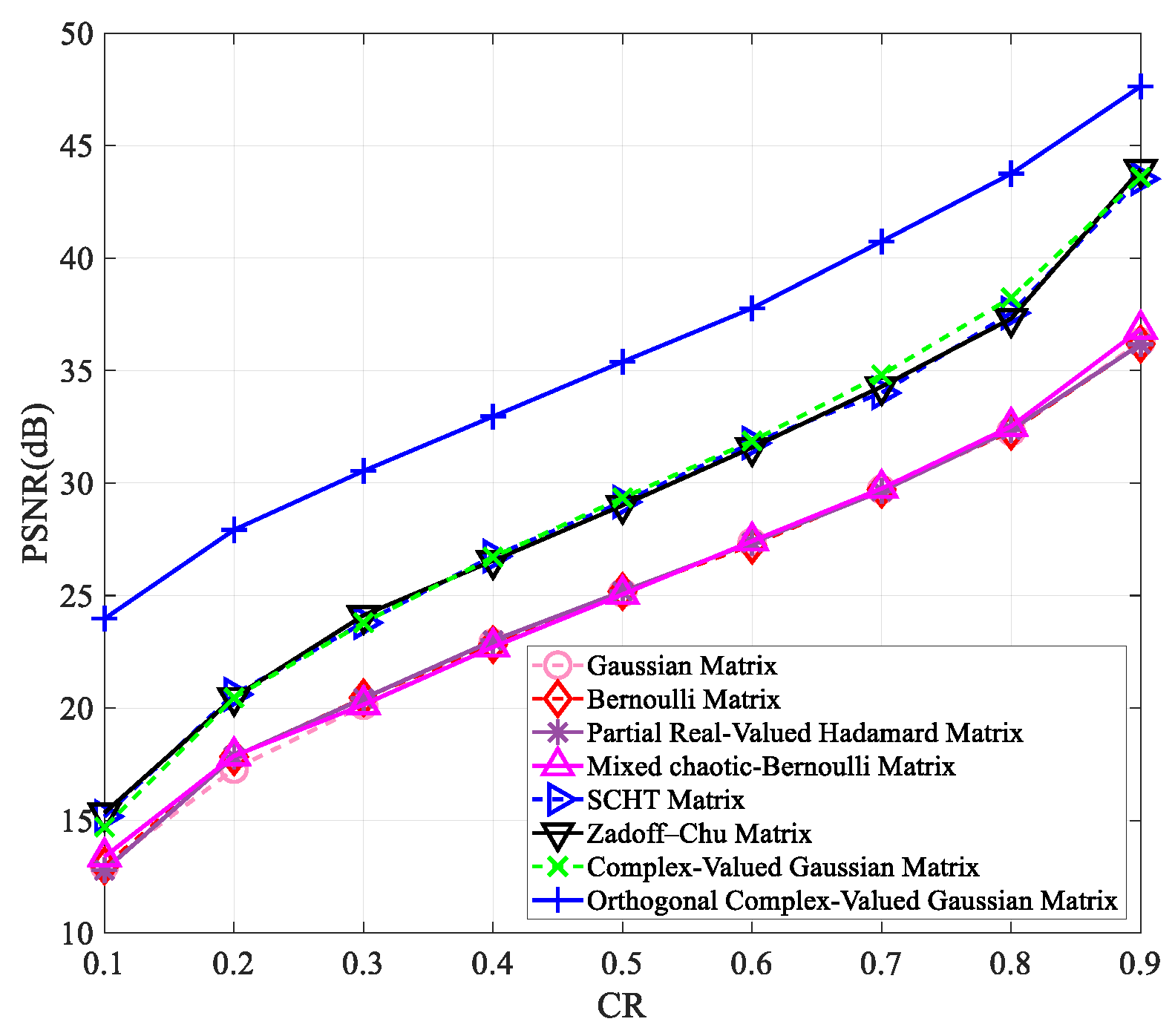
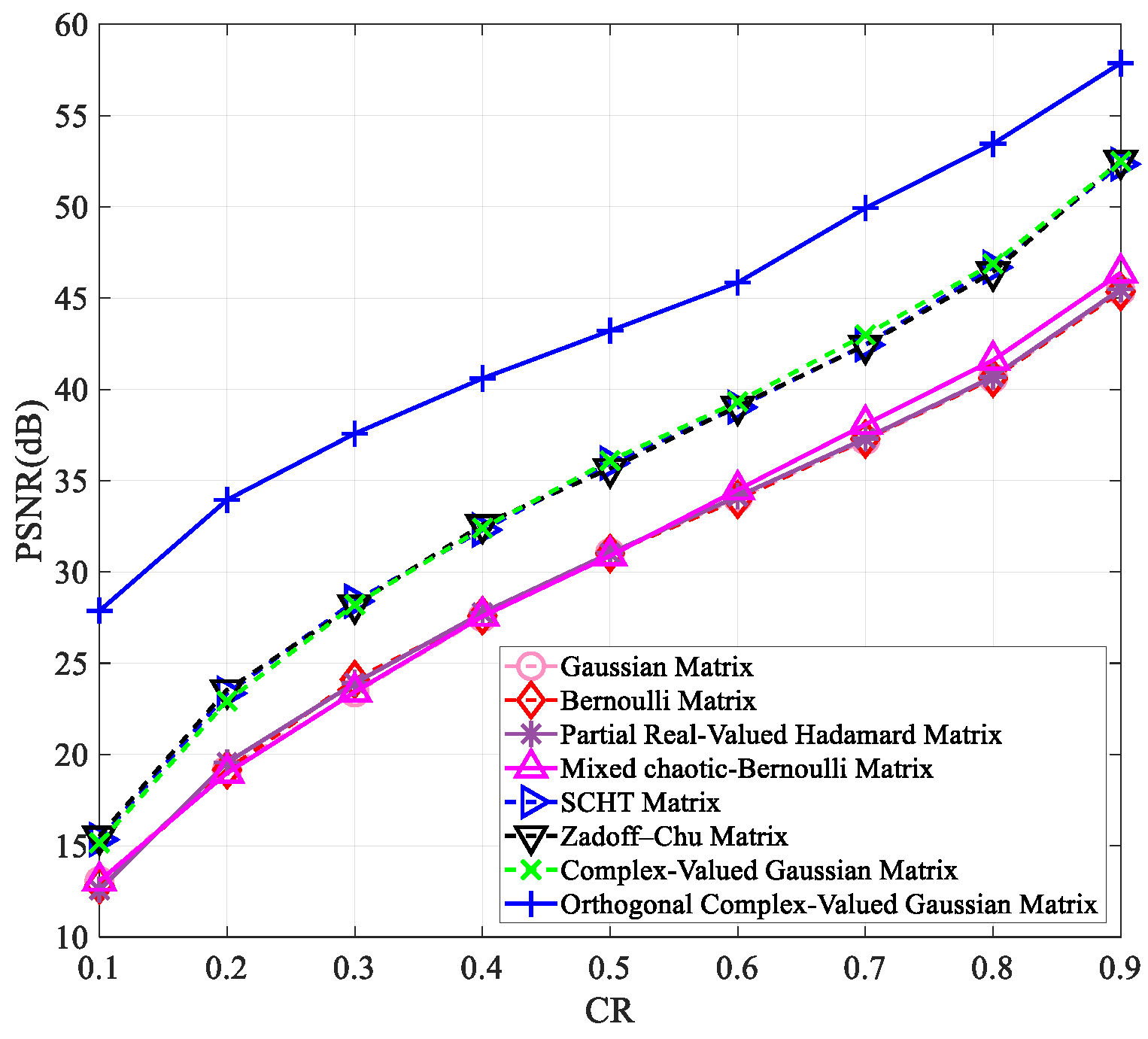
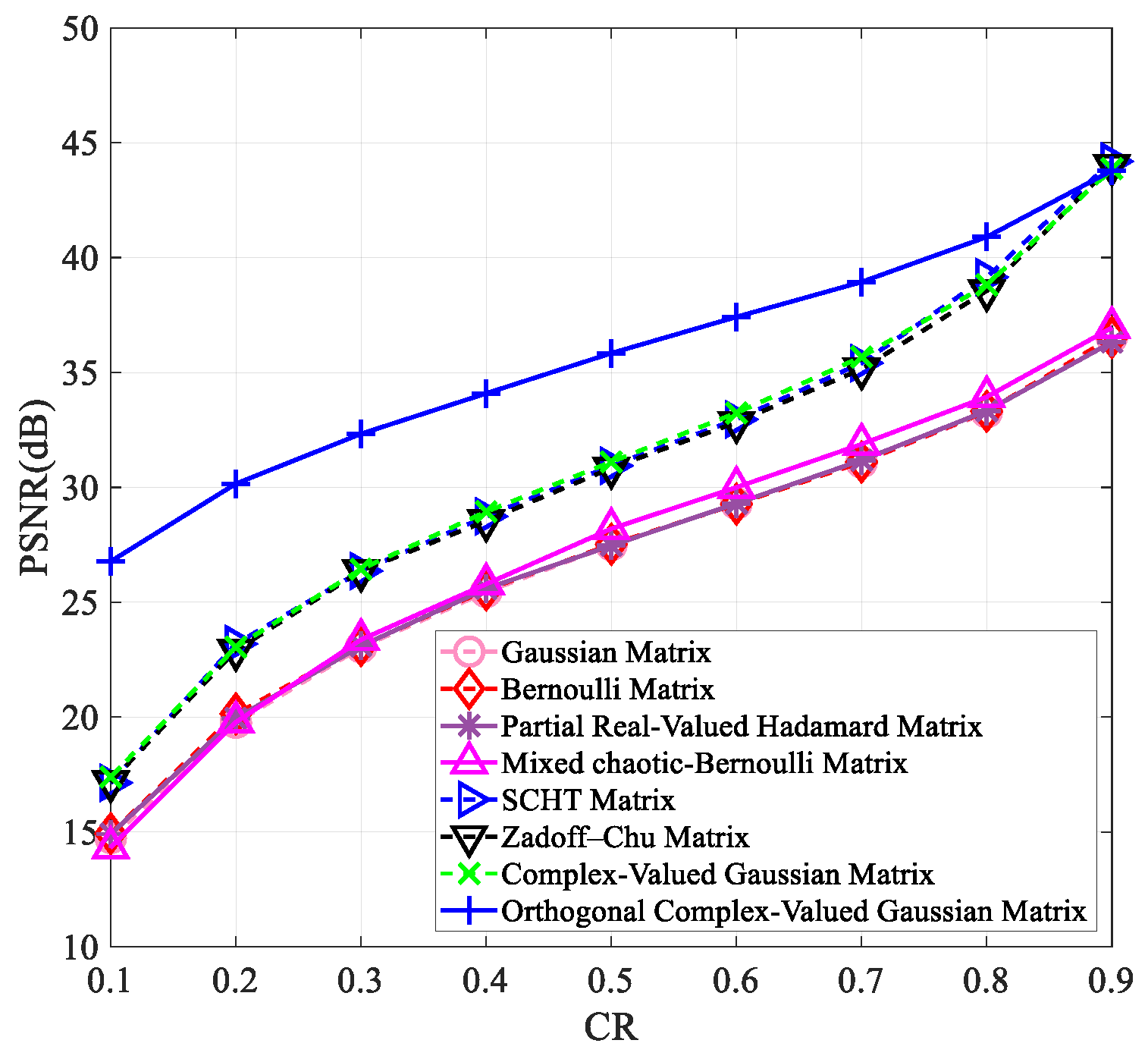




| Measurement Matrix | Lena | Peppers | Woman | Boats |
|---|---|---|---|---|
| Gaussian Matrix [9] | 19.15 | 17.28 | 19.16 | 17.78 |
| Bernoulli Matrix [10] | 19.32 | 17.83 | 19.16 | 17.88 |
| Partial Real-Valued Hadamard Matrix [11] | 19.33 | 17.84 | 19.56 | 17.85 |
| Mixed Chaotic-Bernoulli Matrix [17] | 20.23 | 17.86 | 18.99 | 18.51 |
| SCHT Matrix [27] | 22.03 | 20.61 | 23.35 | 20.90 |
| Zadoff–Chu Matrix [19] | 22.09 | 20.47 | 23.55 | 20.84 |
| Complex-Valued Gaussian Matrix | 22.01 | 20.46 | 22.93 | 20.59 |
| Orthogonal Complex-Valued Gaussian Matrix | 28.64 | 27.92 | 33.95 | 29.12 |
| Measurement Matrix | Lena | Peppers | Woman | Boats |
|---|---|---|---|---|
| Gaussian Matrix [9] | 26.30 | 25.12 | 31.04 | 26.42 |
| Bernoulli Matrix [10] | 26.25 | 25.18 | 31.01 | 26.56 |
| Partial Real-Valued Hadamard Matrix [11] | 26.34 | 25.18 | 31.03 | 26.56 |
| Mixed Chaotic–Bernoulli Matrix [17] | 26.52 | 25.05 | 30.88 | 26.94 |
| SCHT Matrix [27] | 30.40 | 29.16 | 35.96 | 32.09 |
| Zadoff–Chu Matrix [19] | 30.16 | 29.01 | 35.66 | 32.02 |
| Complex-Valued Gaussian Matrix | 30.49 | 29.34 | 36.10 | 32.33 |
| Orthogonal Complex-Valued Gaussian Matrix | 36.85 | 35.38 | 43.21 | 42.23 |
| Measurement Matrix | Lena | Peppers | Woman | Boats |
|---|---|---|---|---|
| Gaussian Matrix [9] | 0.6628 | 0.6067 | 0.7943 | 0.6865 |
| Bernoulli Matrix [10] | 0.6667 | 0.6084 | 0.7965 | 0.6886 |
| Partial Real-Valued Hadamard Matrix [11] | 0.6674 | 0.6120 | 0.7987 | 0.6930 |
| Mixed Chaotic–Bernoulli Matrix [17] | 0.6817 | 0.6558 | 0.8335 | 0.7271 |
| SCHT Matrix [27] | 0.8378 | 0.7883 | 0.9232 | 0.8784 |
| Zadoff–Chu Matrix [19] | 0.8529 | 0.8296 | 0.9360 | 0.8936 |
| Complex-Valued Gaussian Matrix | 0.8235 | 0.7814 | 0.9191 | 0.8699 |
| Orthogonal Complex-Valued Gaussian Matrix | 0.9731 | 0.9681 | 0.9879 | 0.9863 |
| Measurement Matrix | Addition Complexity | Multiplication Complexity |
|---|---|---|
| Haar + Noiselet [7] | 0 | |
| Haar + Noiselet [8] | 0 | |
| Gaussian Matrix [9] | ||
| Bernoulli Matrix [10] | ||
| Partial Real-Valued Hadamard Matrix [11] | 0 | |
| Mixed Chaotic–Bernoulli Matrix [17] | ||
| SCHT Matrix [27] | ||
| Zadoff–Chu Matrix [19] | ||
| Complex-Valued Gaussian Matrix | ||
| Orthogonal Complex-Valued Gaussian Matrix | ||
| Sparse Orthogonal Complex-Valued Gaussian Matrix |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Xue, L.; Yan, Y.; Wang, Z. A Novel Complex-Valued Gaussian Measurement Matrix for Image Compressed Sensing. Entropy 2023, 25, 1248. https://doi.org/10.3390/e25091248
Wang Y, Xue L, Yan Y, Wang Z. A Novel Complex-Valued Gaussian Measurement Matrix for Image Compressed Sensing. Entropy. 2023; 25(9):1248. https://doi.org/10.3390/e25091248
Chicago/Turabian StyleWang, Yue, Linlin Xue, Yuqian Yan, and Zhongpeng Wang. 2023. "A Novel Complex-Valued Gaussian Measurement Matrix for Image Compressed Sensing" Entropy 25, no. 9: 1248. https://doi.org/10.3390/e25091248
APA StyleWang, Y., Xue, L., Yan, Y., & Wang, Z. (2023). A Novel Complex-Valued Gaussian Measurement Matrix for Image Compressed Sensing. Entropy, 25(9), 1248. https://doi.org/10.3390/e25091248





