Abstract
At present, memristive neural networks with various topological structures have been widely studied. However, the memristive neural network with a star structure has not been investigated yet. In order to investigate the dynamic characteristics of neural networks with a star structure, a star memristive neural network (SMNN) model is proposed in this paper. Firstly, an SMNN model is proposed based on a Hopfield neural network and a flux-controlled memristor. Then, its chaotic dynamics are analyzed by using numerical analysis methods including bifurcation diagrams, Lyapunov exponents, phase plots, Poincaré maps, and basins of attraction. The results show that the SMNN can generate complex dynamical behaviors such as chaos, multi-scroll attractors, and initial boosting behavior. The number of multi-scroll attractors can be changed by adjusting the memristor’s control parameters. And the position of the coexisting chaotic attractors can be changed by switching the memristor’s initial values. Meanwhile, the analog circuit of the SMNN is designed and implemented. The theoretical and numerical results are verified through MULTISIM simulation results. Finally, a color image encryption scheme is designed based on the SMNN. Security performance analysis shows that the designed cryptosystem has good security.
1. Introduction
Because of its rich chaotic dynamics, Hopfield neural networks (HNNs) have attracted much attention from chaos scholars [1,2,3]. It is well known that the human brain nervous system has abundant chaotic discharge behaviors [4], which are closely related to advanced intelligence. HNNs are considered to be the best example of studying the dynamics of the brain’s nervous system [5,6]. At the same time, many researchers have found that neural networks with chaotic behavior have a wide range of applications in many fields including associative memory, pattern recognition, and combinatorial optimization [7,8]. Therefore, the study of the chaotic behavior of HNNs has important theoretical and practical significance for brain science and artificial intelligence.
Since the HNN was proposed, various HNNs have been proposed and their chaotic behaviors studied. For example, normal chaos [9,10,11] and hyperchaos [12,13,14] have been detected in some small HNNs with several neurons. Especially in recent years, memristive neural networks have received much attention from many scholars [15,16]. For example, Pham et al. [17] proposed a three-neuron memristive neural network and revealed its hidden chaotic behavior. Bao et al. [18] found that a memristive neural network consisting of three neurons can produce coexisting asymmetric attractors. A memristive neural network with complex chaotic attractors was proposed by Yu et al. in [19]. Furthermore, plenty of similar works have been reported [20,21,22]. To sum up, these studies are mainly focused on the chaotic dynamics of neural networks with mixed structures. Very recently, Lin et al. [23] proposed a memristive neural network with a ring structure, and complex hyperchaos was discovered. However, there are fewer concerns about the chaotic dynamics of neural networks with a star structure.
The multi-scroll attractor is a complex chaos phenomenon [24,25,26], which has irregular scroll trajectories. Multi-scroll attractors have higher tunability and complexity than single-scroll attractors. The multi-scroll attractors of the MNN were first revealed in Ref. [27]. Wan et al. [28] found multi-double-scroll attractors in the MHNN. In addition, grid multi-scroll attractors have been obtained from an MHNN with two memristor synapses [29]. Meanwhile, some similar memristive neural networks with multi-scroll attractors have been investigated and successfully applied in the information security field [30,31,32].
Initial boosting behavior is a kind of complex behavior that shows extreme multistability [33,34]. Generally, this phenomenon has infinite coexisting attractors with the same shape and different positions [35]. More importantly, the initial offset boosting behavior can provide sustained and robust boosted chaotic sequences and their oscillating amplitudes can be non-destructively controlled by switching the initial states flexibly. These merits make them more practical for chaos engineering applications [36,37]. In recent years, some scholars have been devoted to the initial boosting behavior in neural networks [38,39]. Especially, the initial offset boosting coexisting chaos was observed in a two-memristor-based Hopfield neural network [40]. Hyperchaotic initial offset boosting behavior was revealed in a memristive coupling neural network [41].
This paper investigates the chaotic dynamics of the star memristive neural network and its application in color image encryption. To the best of our knowledge, this is the first time that the chaotic dynamics of the star neural network has been investigated. The main novelty and contributions of this study are summarized as follows. (1) We propose a star memristive neural network model based on one Hopfield neural network with four neurons and one memristor. (2) The star memristive neural network exhibits rich and complex multi-scroll attractors and initial boosting dynamics. (3) A star memristive neural network circuit is realized and numerical simulation results are further demonstrated. (4) We design a color image encryption cryptosystem by using the multi-scroll sequences to show the practical application of the presented star memristive neural network.
The rest of this paper is organized as follows. A star memristive neural network model is constructed in Section 2. The chaotic dynamics of the star memristive neural network is studied in Section 3. An analog circuit of the star memristive neural network is implemented in Section 4. An SMNN-based color image encryption scheme is designed in Section 5, and its security performances are analyzed. The full text is summarized in Section 6.
2. Star Memristive Neural Network
2.1. Brief Introduction of the Memristor Model
Memristors are usually used to describe electromagnetic induction in the nervous system caused by electromagnetic radiation. Here, a flux-controlled multi-segment nonlinear memristor is introduced [15]. Its mathematical model can be written by
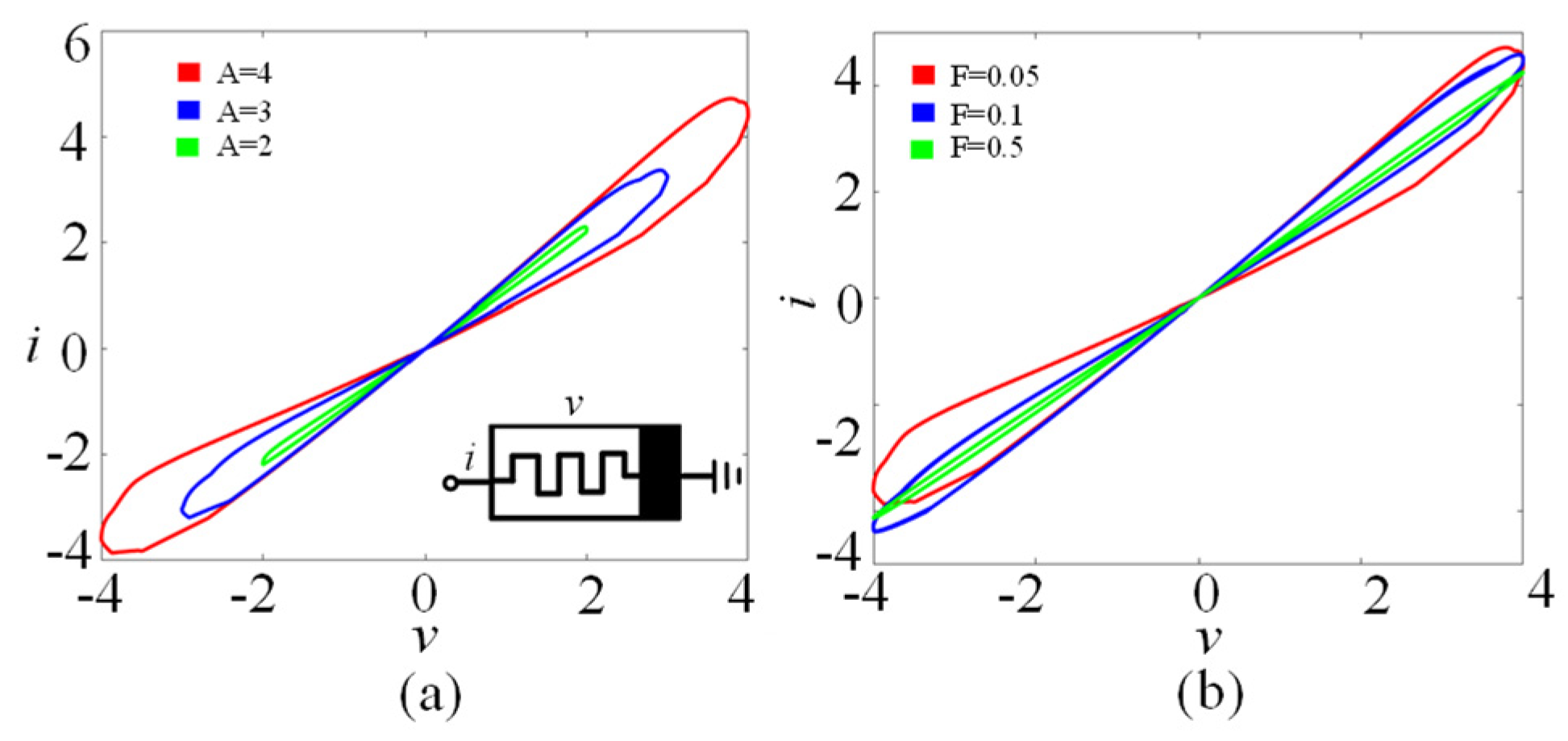
where i, v, and φ are the current, voltage, and state variables of the memristor, respectively. The function h(φ) is the state function of the memristor, where N and M are two control parameters. The memristor model can exhibit typical memristive characteristics, as shown in Figure 1. As can be seen from Figure 1a, the memristor model can generate three tight hysteresis loops under different voltage amplitudes (A = 1, 2, 3). Figure 1b shows that with the increase in voltage frequency (F = 0.05, 0.1, 0.5), the area of the tight hysteresis loop of the memristor decreases gradually.
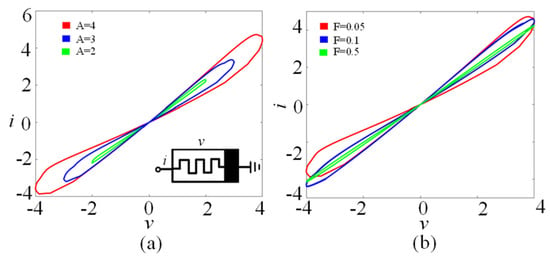
Figure 1.
The fingerprints of the memristor driven by v = Asin(2πFt). (a) Amplitude-related voltage–current loci for A = 2, 3, and 4 with F = 0.05 and x0 = 0. (b) Frequency-related voltage–current loci for F = 0.05, 0.1, and 0.5 with A = 4 and x0 = 0.
2.2. Memristive Star Neural Network Modeling
A Hopfield neural network with a brain-like structure can be used to emulate chaotic behaviors of the biological nervous system. A Hopfield neural network with n neurons can be described by [1]
where Ci, Ri, and xi are the membrane capacitance, membrane resistance, and membrane potential of the neuron i, respectively. wij is the synaptic weight coefficient between neuron j and neuron i. In addition, tanh(.) denotes the neuron activation function, and Ii is an external input current. Based on the original HNN (3), setting Ci = 1, Ri = 1, and Ii = 0, a new HNN with four neurons is proposed as follows:
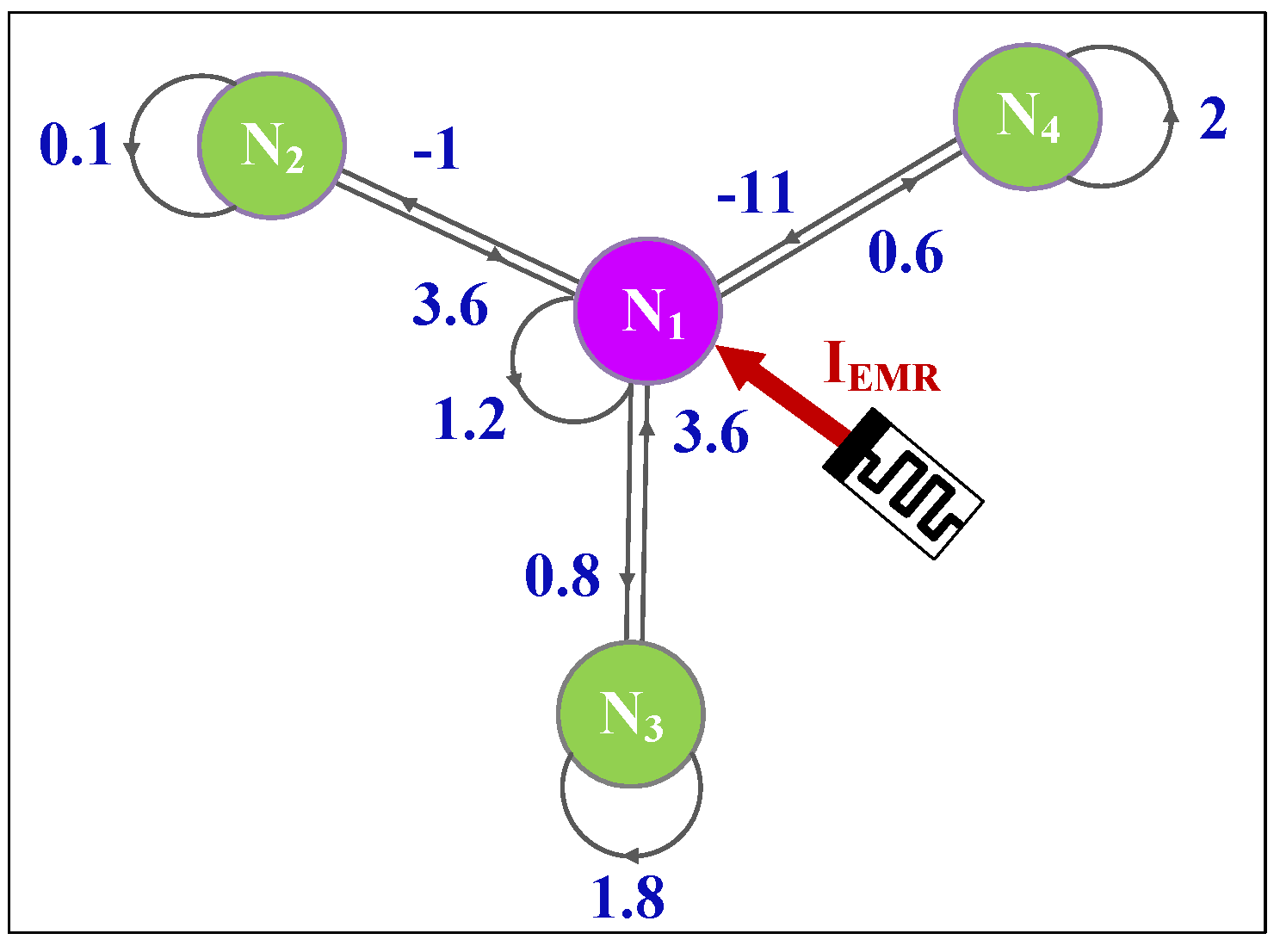
where xi is the membrane potentials of neuron i. As shown in Figure 2, the four neurons are made up of a star neural network. A large number of research results show that the electromagnetic induction effect can be described by a flux-controlled memristor. According to the principle, the effect of external stimuli induced by electromagnetic radiation can be regarded as an additional forcing current IEMR. Consequently, when we consider that neuron 1 is stimulated by external electromagnetic radiation, the memristive star neural network can be modeled and described as follows:
where φ is the magnetic flux across the membrane of neuron 1, µ is the feedback intensity of external stimuli induced by electromagnetic radiation, and µw(φ)x1 is the electromagnetic induction current.
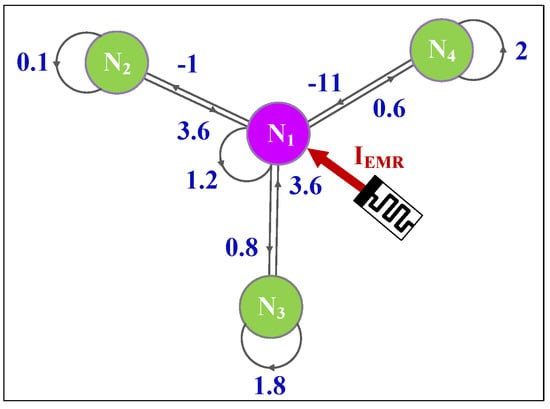
Figure 2.
Concept map of the star memristive neural network.
2.3. Equilibrium Points and Their Stability
The equilibrium points of the star memristive neural network and their stabilities are analyzed in this subsection. Setting the left side of Equation (5) to 0, the equilibrium points are solved by
Solving Equation (6), one can obtain
Obviously, there are infinite discrete equilibrium points. The Jacobian matrix of each equilibrium point can be calculated by
where si = sech2(xi). When setting a = 1, b = 0.01, c = 0.7, and d = 1.3, the corresponding eigenvalues and stabilities are given in Table 1. From Table 1, all the equilibrium points are of unstable saddle type. According to the Shilnikov theorem, the star memristive neural network may have a chaotic phenomenon.

Table 1.
Equilibrium points and their stabilities.
3. Dynamic Analysis
In this section, chaotic dynamics of the proposed star memristive neural network are revealed by using nonlinear dynamics methods including bifurcation diagrams, Lyapunov exponents, phase plots, Poincaré maps, and basins of attraction. It should be noted that the numerical simulations are completed in MATLAB R2017a with the ODE45 algorithm. Meanwhile, the start time, the time step, and the time length are set as 500, 0.01, and 4000, respectively.
3.1. µ-Related Chaotic Dynamics
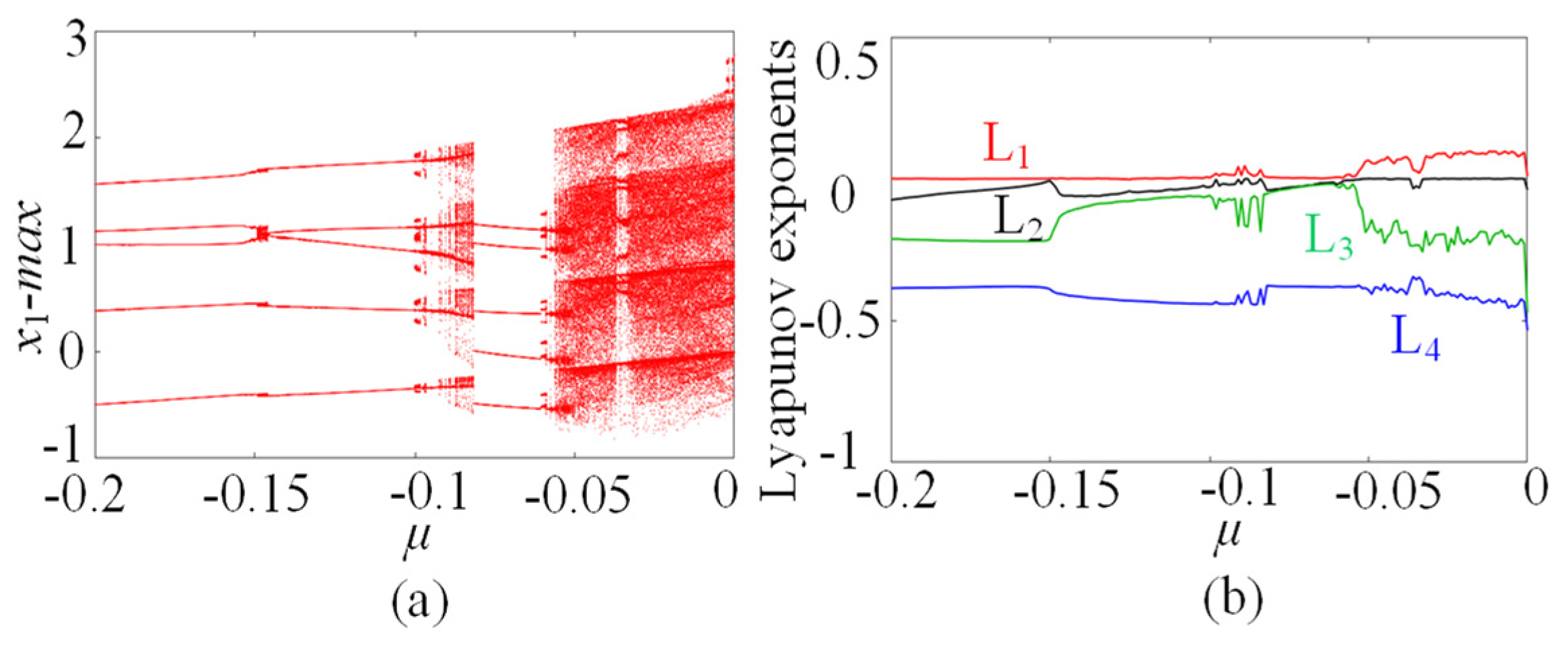
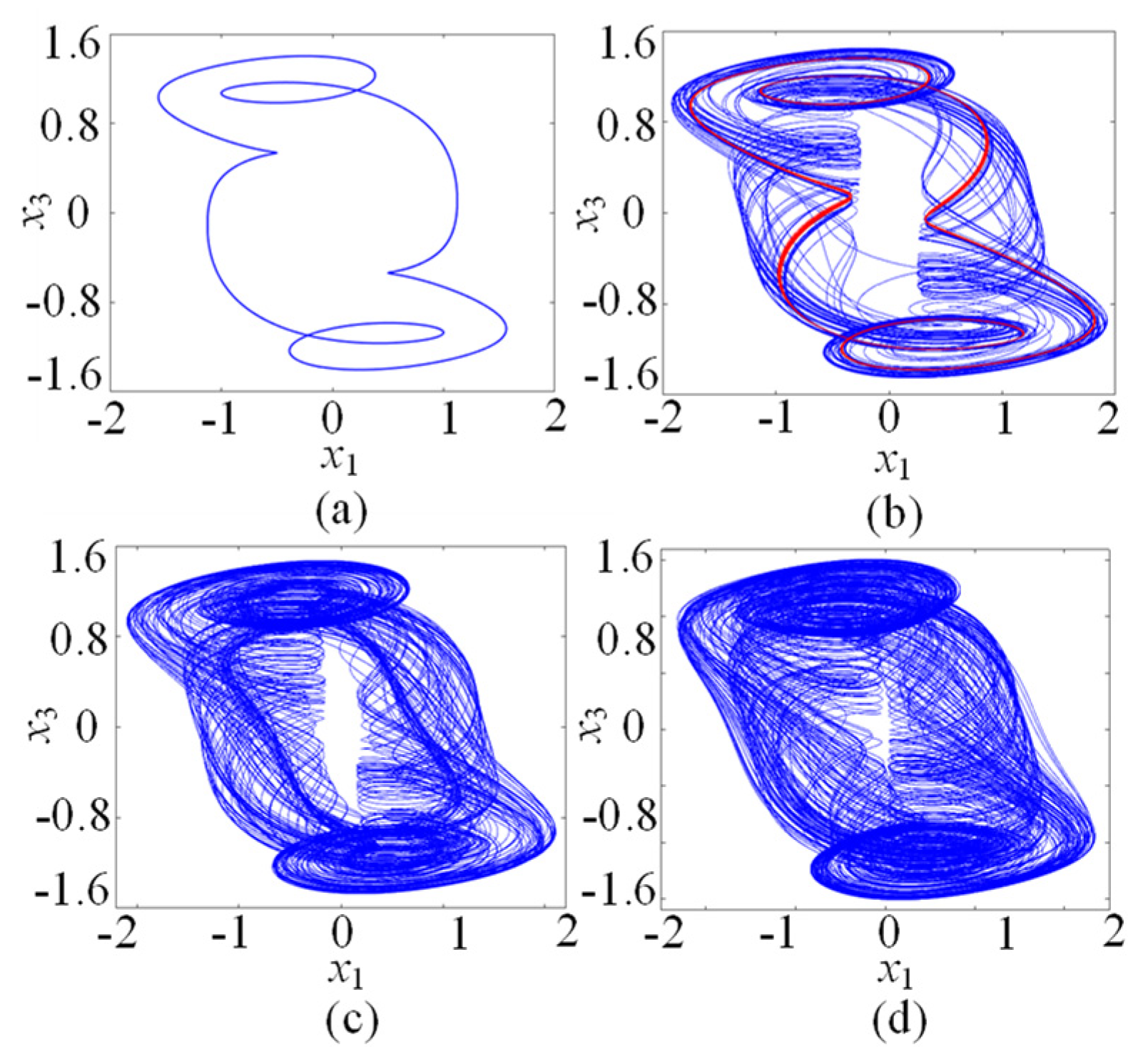
In this subsection, the chaotic dynamics related to the memristive coupling strength µ is analyzed. Setting the parameters a = 1, b = 0.01, c = 0.7, d = 1.3, N = 0, and initial conditions (x10, x20, x30, x40, φ0) = (0.1, 0.1, 0.1, 0.1, 0.1), the parameter µ increases from −0.2 to 0, and the µ-based bifurcation diagram is plotted in Figure 3a, where x1max is the maxima of the membrane potential x1. Moreover, the corresponding Lyapunov exponents are shown in Figure 3b. It can be seen from Figure 3 that the star memristive neural network can generate complex dynamical behaviors including period, transient chaos, and chaos. For example, with µ increasing from −0.2 to 0, the dynamical trajectory of the star memristive neural network starts from the period of entering into transient chaos at µ = −0.1, and then the transient chaotic behavior degrades into periodic behavior at u =−0.08. Interestingly, with the µ increasing to −0.055, the star memristive neural network enters chaos. It can be seen that the star memristive neural network exhibits a wide range of chaos until µ = 0. The phase portraits of the star memristive neural network with different values of u are given to illustrate its dynamical evolution with the parameter µ, as shown in Figure 4. It is obvious that the star memristive neural network successively produces periodic attractors, transient chaotic attractors, and chaotic attractors with the increase in µ.
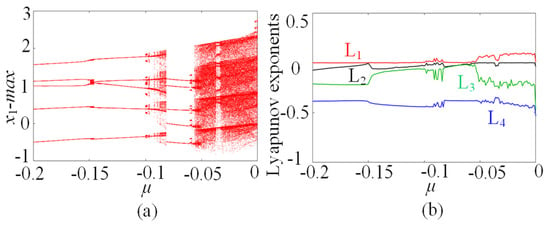
Figure 3.
The µ-dependent dynamics with initial states (0.1, 0.1, 0.1, 0.1, 0.1). (a) Bifurcation diagram. (b) Lyapunov exponents.
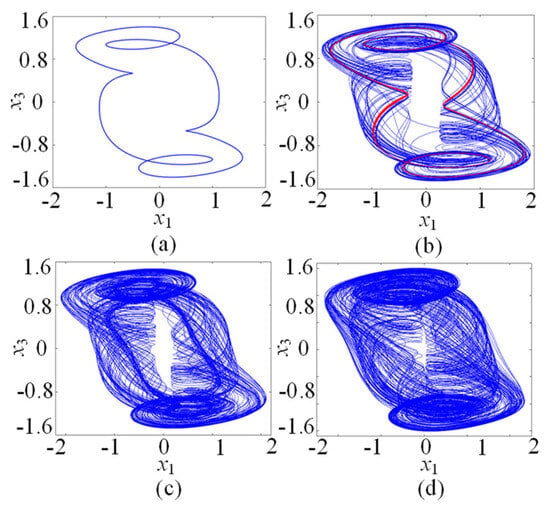
Figure 4.
Dynamical behaviors related to µ. (a) Periodic attractor with µ = −0.2. (b) Transient chaotic attractor with µ = −0.08. (c) Chaotic attractor with µ = −0.05. (d) Chaotic attractor with µ = −0.01.
3.2. N/M-Related Multi-Scroll Attractors
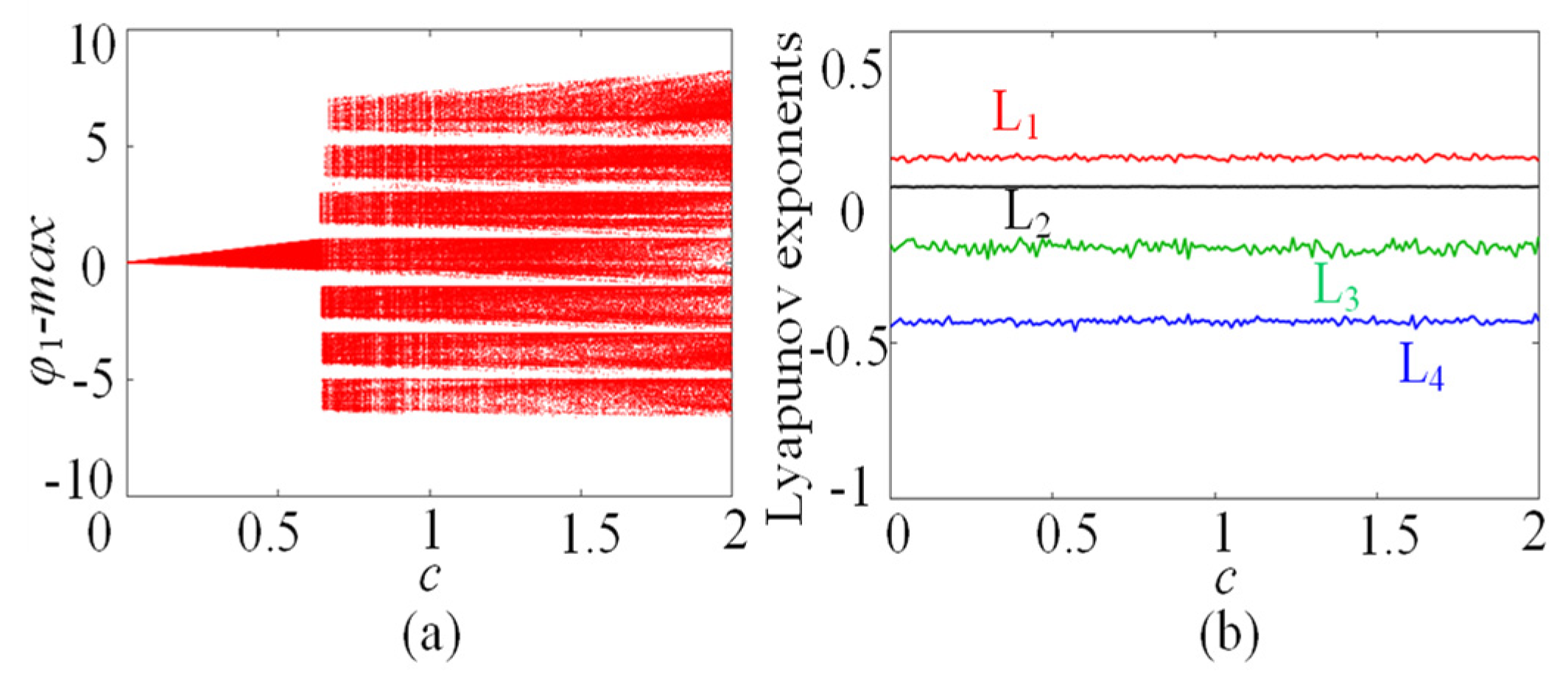
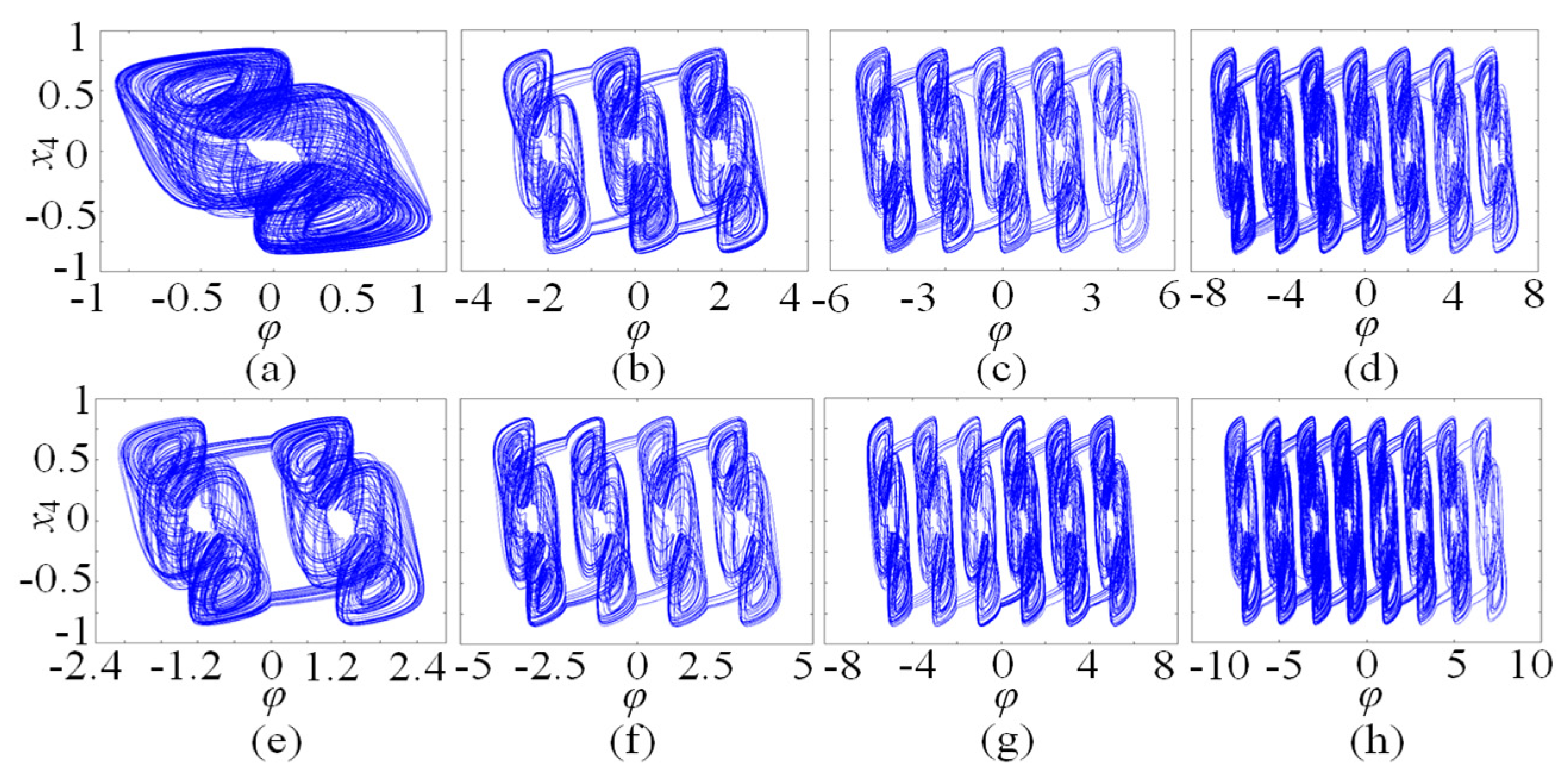
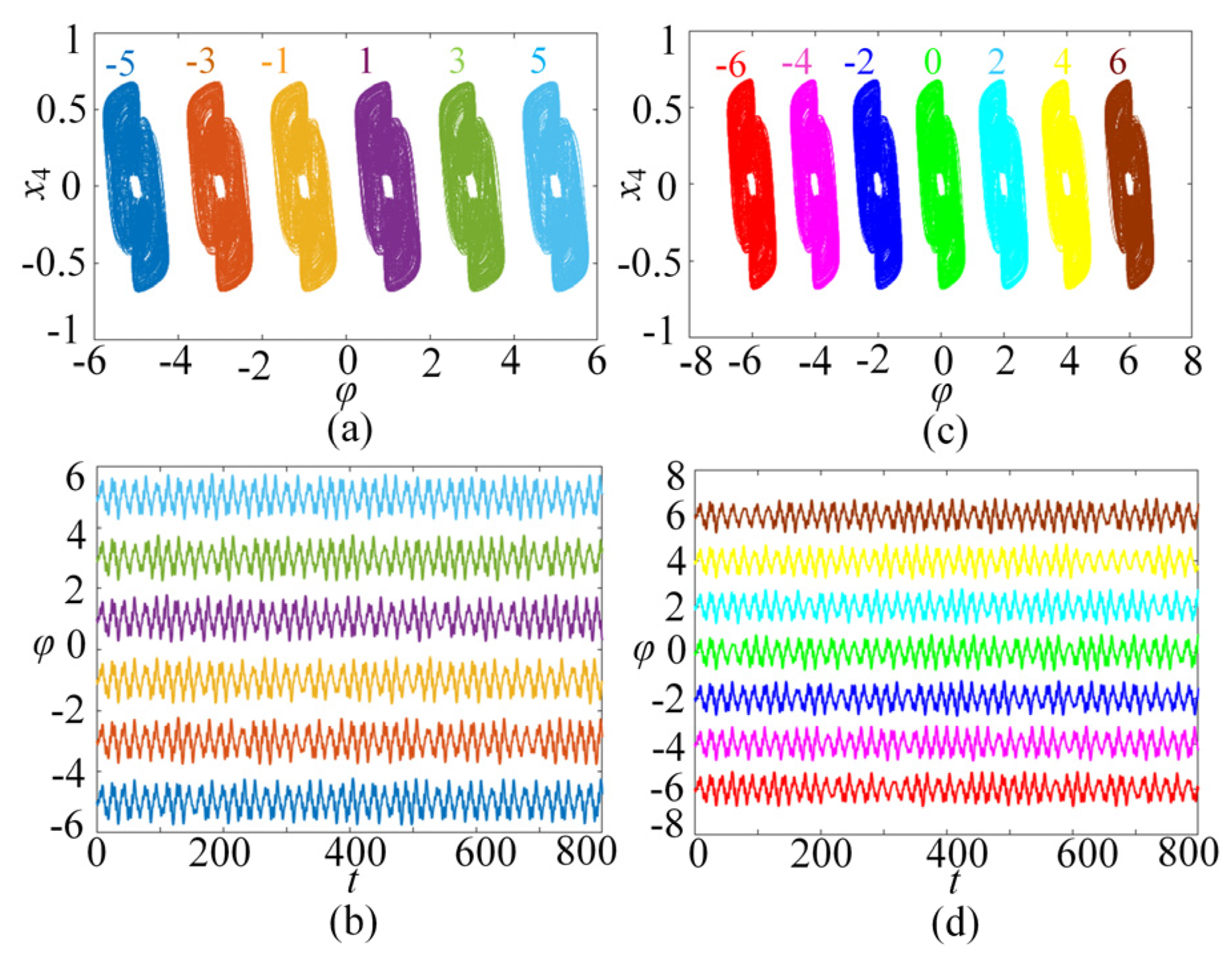
In this subsection, the chaotic dynamics related to memristor control parameters N/M are analyzed. The numerical simulation shows that the SMNN can generate an arbitrary number of multi-scroll chaotic attractors related to N/M. When the parameters a = 1, b = 0.01, d = 1.3, µ = −0.01, N = 3, and initial states are kept unchanged, c is selected as the control parameter. A bifurcation diagram and the corresponding Lyapunov exponents related to parameter c∈(0, 2) are shown in Figure 5a and Figure 5b, respectively. Interestingly, it can be seen from the bifurcation diagram that the bifurcation diagram is made up of a dense patch of points with seven steps. This means that the SMNN not only generates chaotic attractors but also produces seven-scroll attractors. From the Lyapunov exponents, it shows one positive value, namely, it is chaotic behavior. Further research shows that the SMNN can generate an arbitrary number of multi-scroll attractors by selecting different control parameters N/M. To better understand the multi-scroll attractors, Figure 6 gives the phase portraits of multi-scroll attractors under different numbers of scrolls. Obviously, the number of scrolls generated by the star memristive neural network can be controlled by 2N + 1 and 2M + 2.
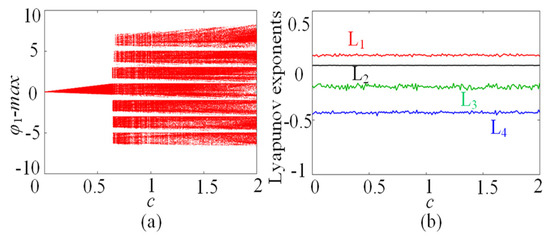
Figure 5.
Dynamics of the SMNN with respect to the parameter c. (a) Bifurcation diagram; (b) Lyapunov exponents.
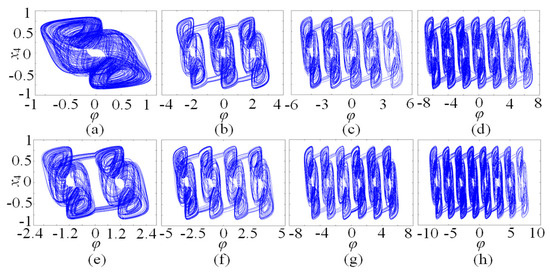
Figure 6.
n-scroll attractors of the SMNN with different values of N and M. (a) 1-scroll attractor with N = 0; (b) 3-scroll attractor with N = 1; (c) 5-scroll attractor with N = 2; (d) 7-scroll attractor with N = 3; (e) 2-scroll attractor with M = 0; (f) 4-scroll attractor with M = 1; (g) 6-scroll attractor with M = 2; (h) 8-scroll attractor with M = 3.
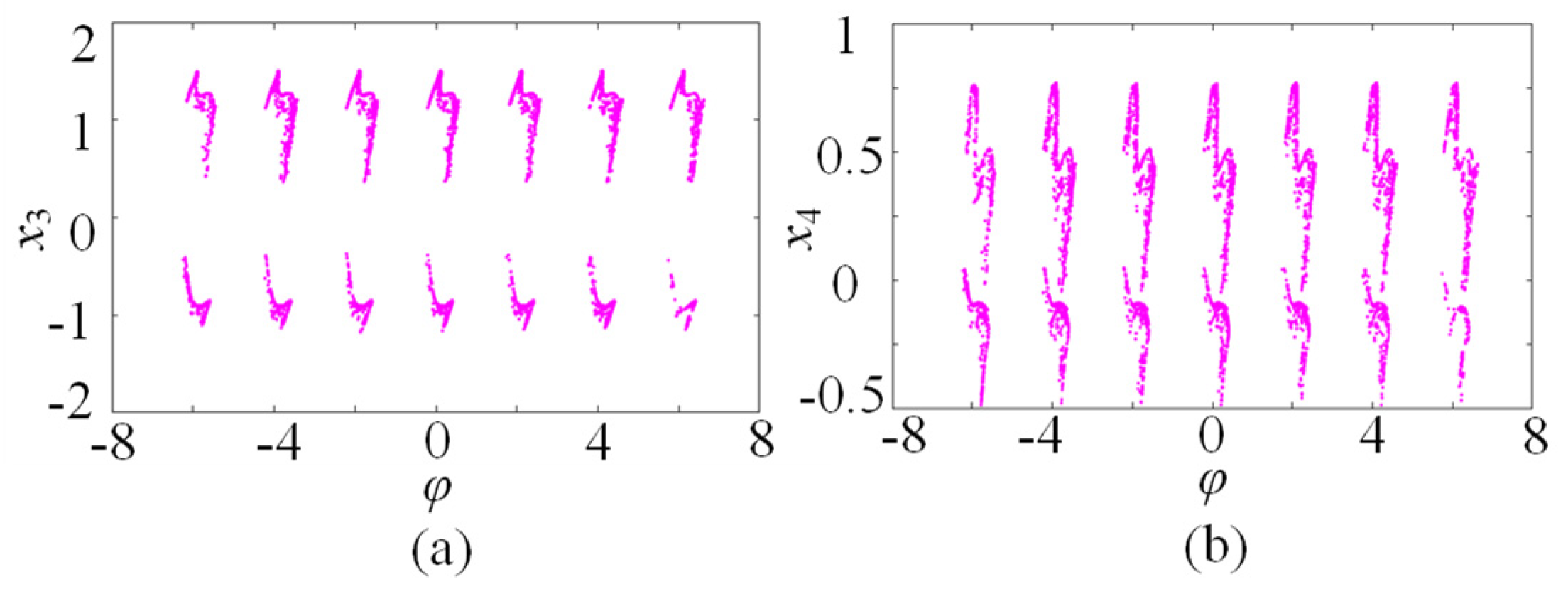
In addition, the Poincaré maps on φ-x3 and φ-x4 phase planes for the 7-scroll attractor with x1 = 0 are depicted in Figure 7a and Figure 7b, respectively. Clearly, the Poincaré maps have approximately 7-scroll maps, implying that the star memristive neural network generates extremely complex multi-scroll attractors.
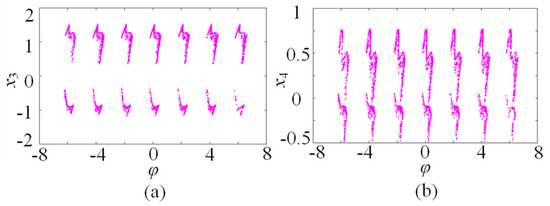
Figure 7.
Poincaré maps of the 7-scroll attractor for x1 = 0. (a) on φ-x3 plane; (b) on φ-x4 plane.
3.3. φ0-Related Initial Boosting Behavior
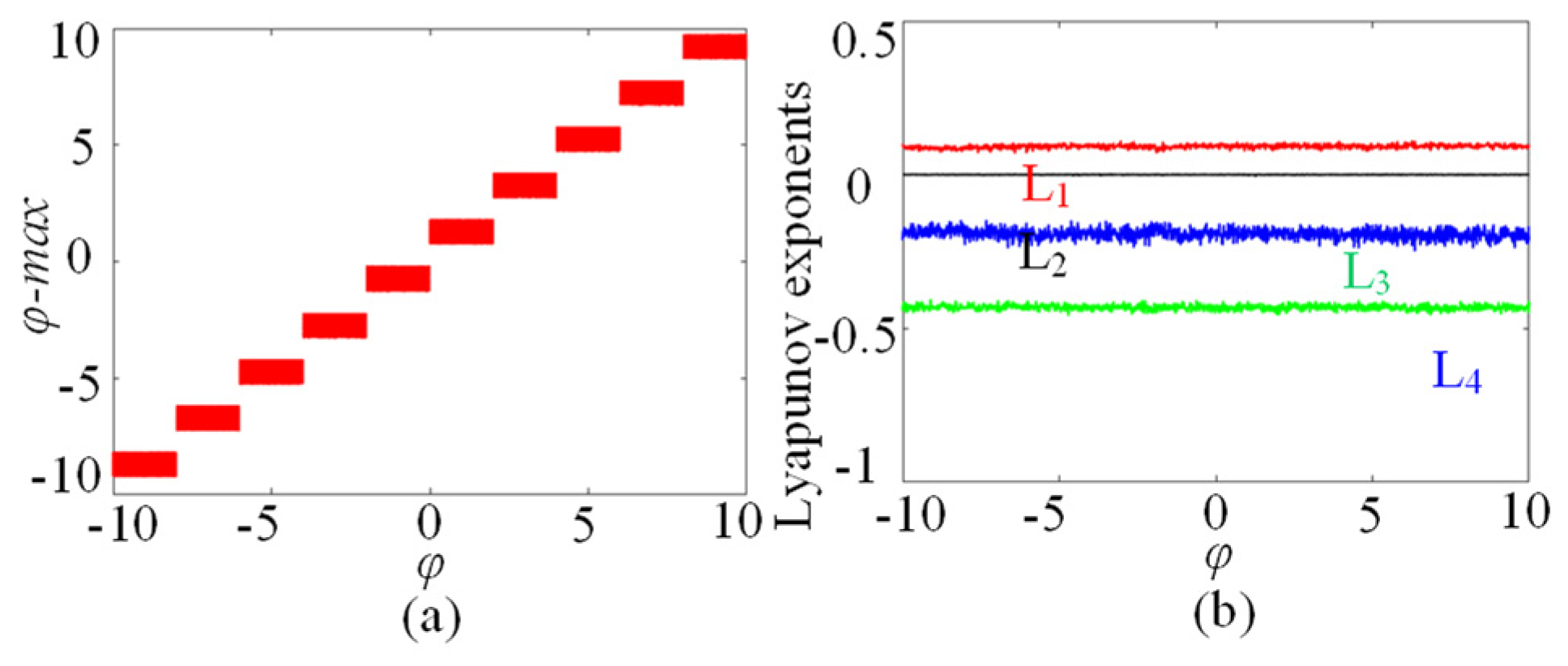
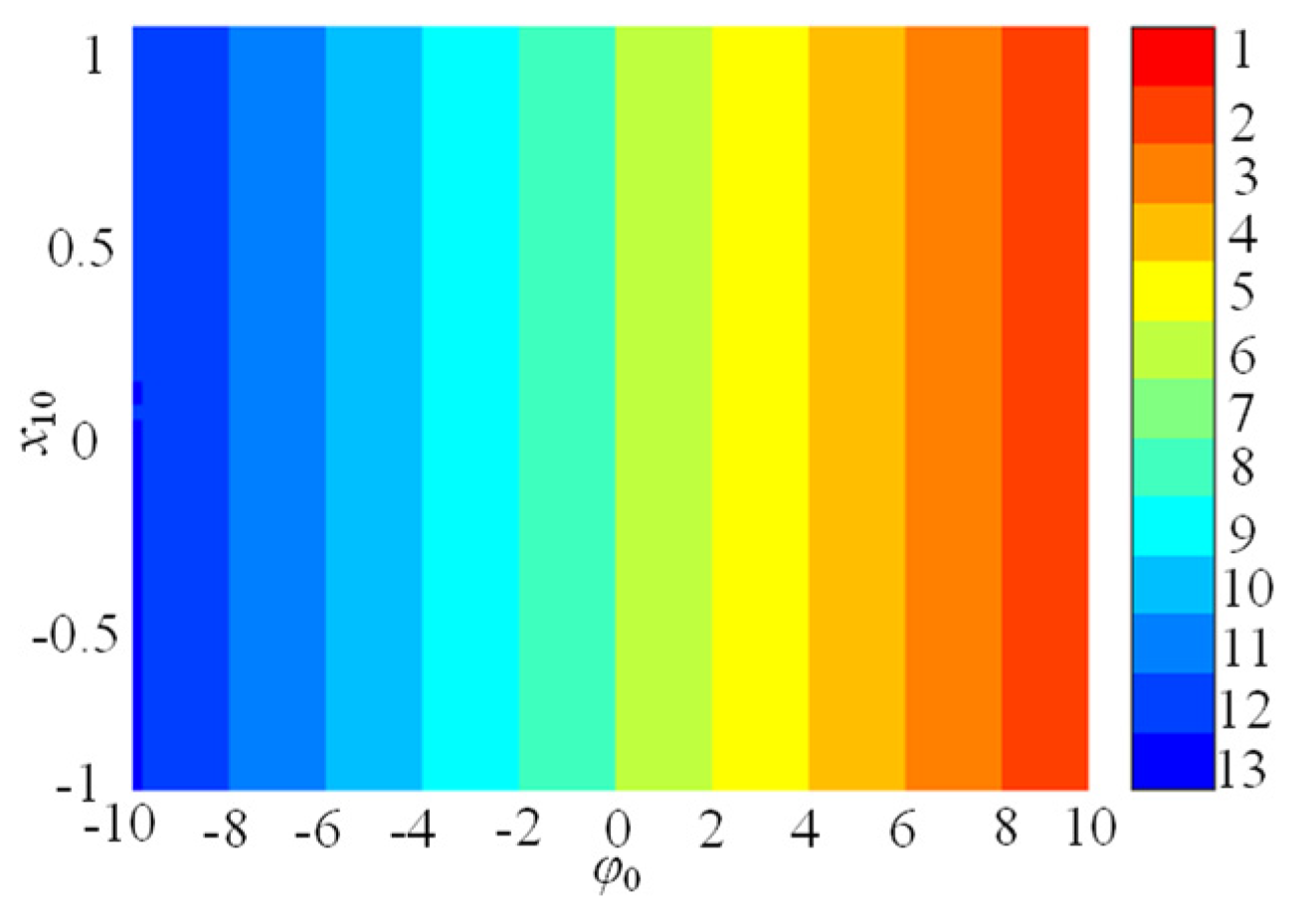
In this subsection, the initial boosting chaotic phenomenon is analyzed. It is wonderful that the presented SMNN can generate initial boosting coexisting chaos. For instance, we plot the bifurcation diagram of the φ0 under a = 1, b = 0.01, c = 0.5, d = 1.3, µ = −0.01, M = 4, and x10 = x20 = x30 = x40 = 0.1, as shown in Figure 8a. As can be seen, the SMNN displays a complicated initial boosting behavior. Meanwhile, the corresponding constant Lyapunov exponents in the whole range of the φ0 variation are given in Figure 8b. Obviously, the SMNN has an infinite wide chaotic range along the φ0-axis. That is to say, the SMNN enjoys complex dynamics of initial boosting coexisting chaos, which means that it has excellent robustness. Moreover, to further verify initial boosting dynamics, the local attraction basin in the φ0-x10 plane is given in Figure 9. From Figure 10, the local attraction basin has complex manifold structures and basin boundaries, and the specified initial value regions are composed of different colored zones marked by 1–13, among which the colored zones marked by 1–13 correspond to the attractors with different positions. Therefore, the star memristive neural network has complex initial boosting behavior.
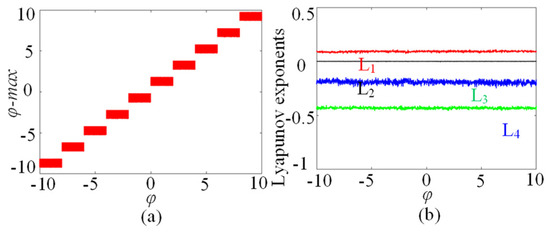
Figure 8.
The φ0-dependent dynamics with the coupling strength µ = 0.5. (a) Bifurcation diagram. (b) Lyapunov exponents.
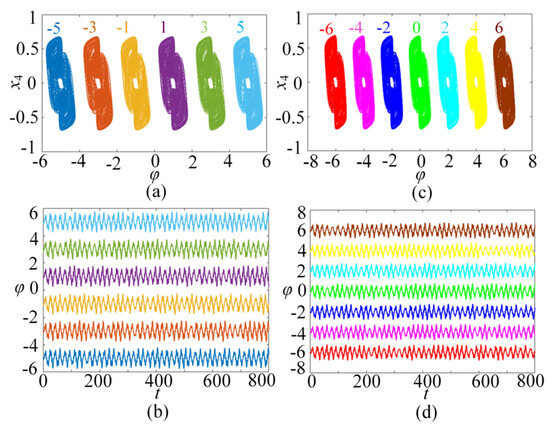
Figure 9.
Coexisting multiple attractors in the SMNN with different φ0. (a) Six Coexisting attractors. (b) Corresponding time series. (c) Seven coexisting attractors. (d) Corresponding time series.
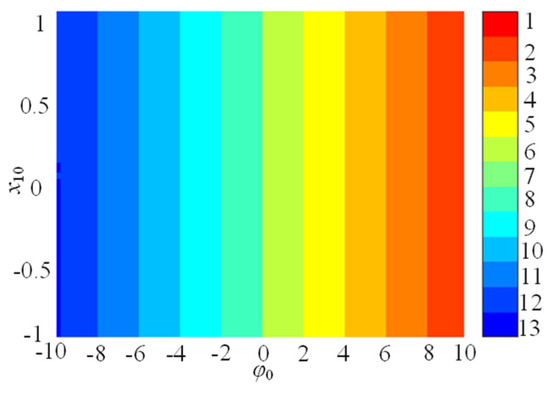
Figure 10.
Basin of attraction for the SMNN.
4. Circuit Validation
With the rapid development of artificial intelligence, the physical realization of neural network models is very important for developing neuromorphic hardware systems [42,43]. It is a reliable way to realize neural network models through analog circuits. This is because the analog neural network circuit can not only achieve real-time calculation but also reproduce the behavior of the real nervous system. In this section, the proposed star memristive neural network model is realized by using basic electronic circuit elements such as resistors, capacitors, operational amplifiers, and analog multipliers. We first design the circuit of the star memristive neural network model and verify its complex behavior in Multisim.
4.1. Design of the SMNN Circuit
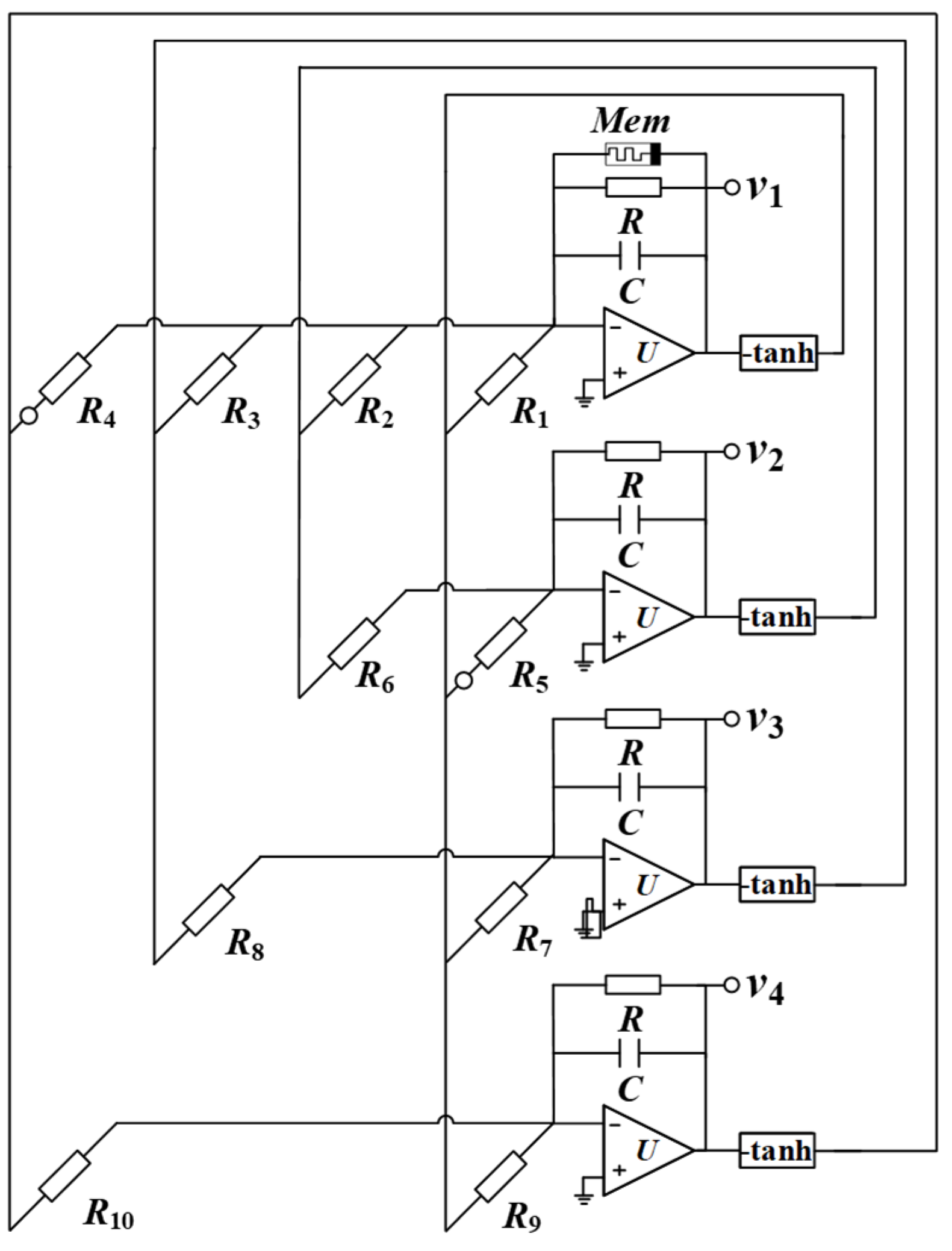
Before implementing the neural network circuit, we first introduce a hyperbolic tangent excitation function circuit [23] and a memristor circuit [15], respectively. Based on the two circuit units, a memristive Hopfield neural network circuit can be designed. According to the star memristive neural network model (5), the circuit structure is designed in Figure 11. Four membrane potentials x1, x2, x3, and x4 are emulated by four out voltages v1, v2, v3, and v4, respectively. All synaptic weight coefficients are simulated by the resistors R1-R10. Based on the circuit in Figure 11, the circuit state equations can be described by
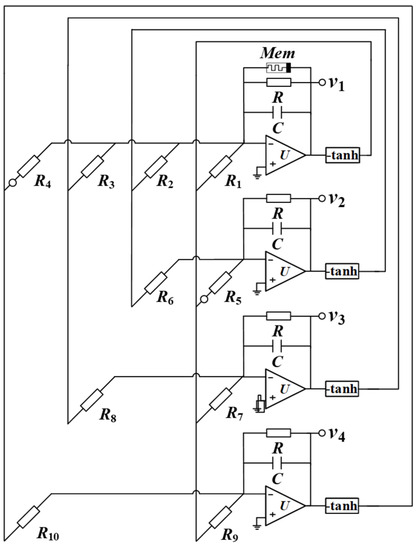
Figure 11.
Circuit implementation.
Assuming that C1 = C2 = C3 = C4 = C = 1 nF, RC = 10 us, and resistance R = 10 kΩ, then C can be chosen as 1 nF. Considering the fixed synaptic weight coefficients, part resistors can be calculated as R1 = 8.3 kΩ, R2 = 2.7 kΩ, R3 = 2.7 kΩ, R4 = 0.9 kΩ, R5 = 10 kΩ, R6 = 100 kΩ, R7 = 12.5 kΩ, R8 = 5.5 kΩ, R9 = 16 kΩ, and R10 = 5 kΩ. In addition, Ra = R/aµ, Rb = Rg/bµ, Rc = R/c, and Rd = R/d are adjustable resistors. In the above formula, g represents the factor of the multiplier M. In this circuit, g is equal to 0.1.
4.2. Measurement of the SMNN Circuit
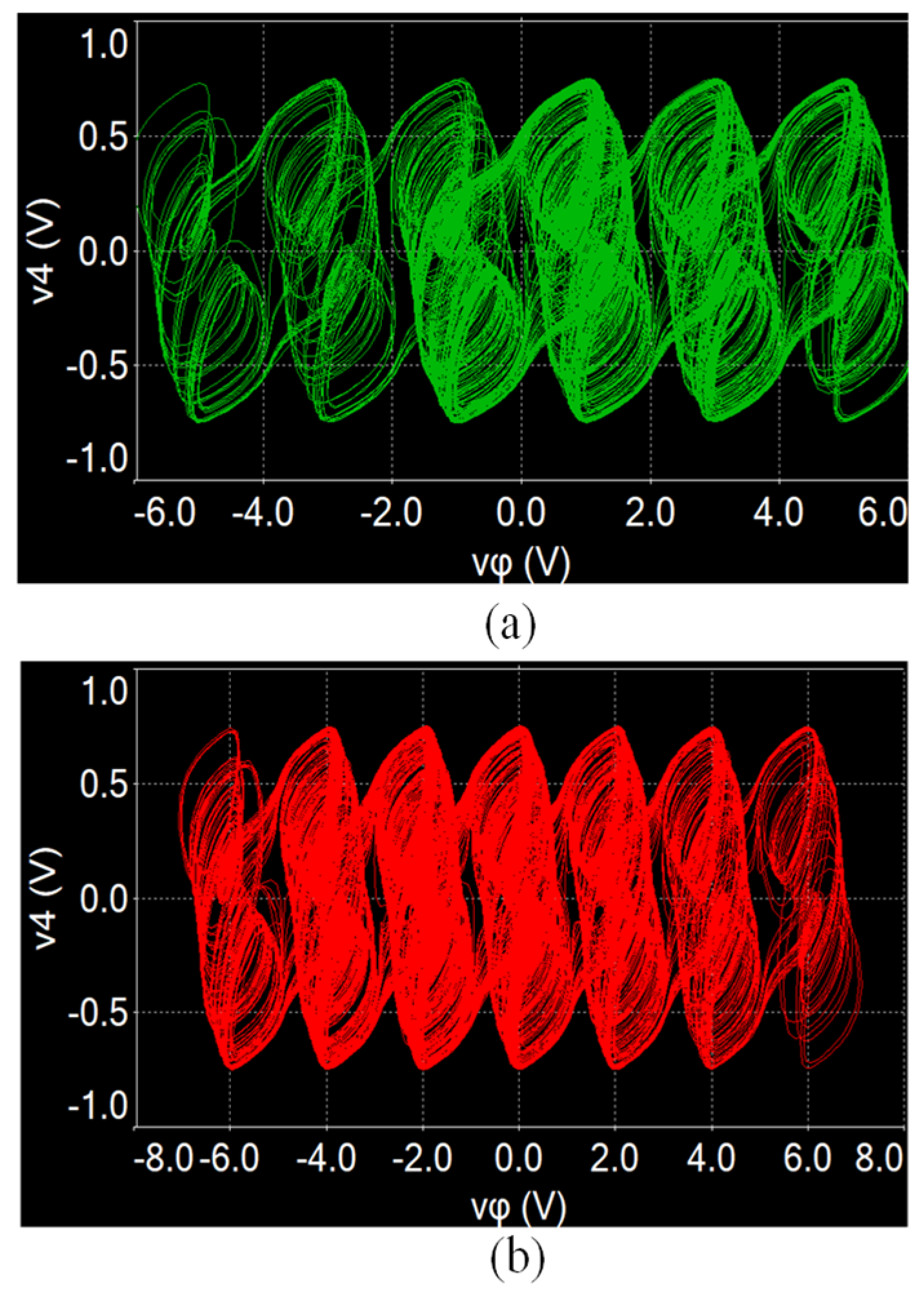
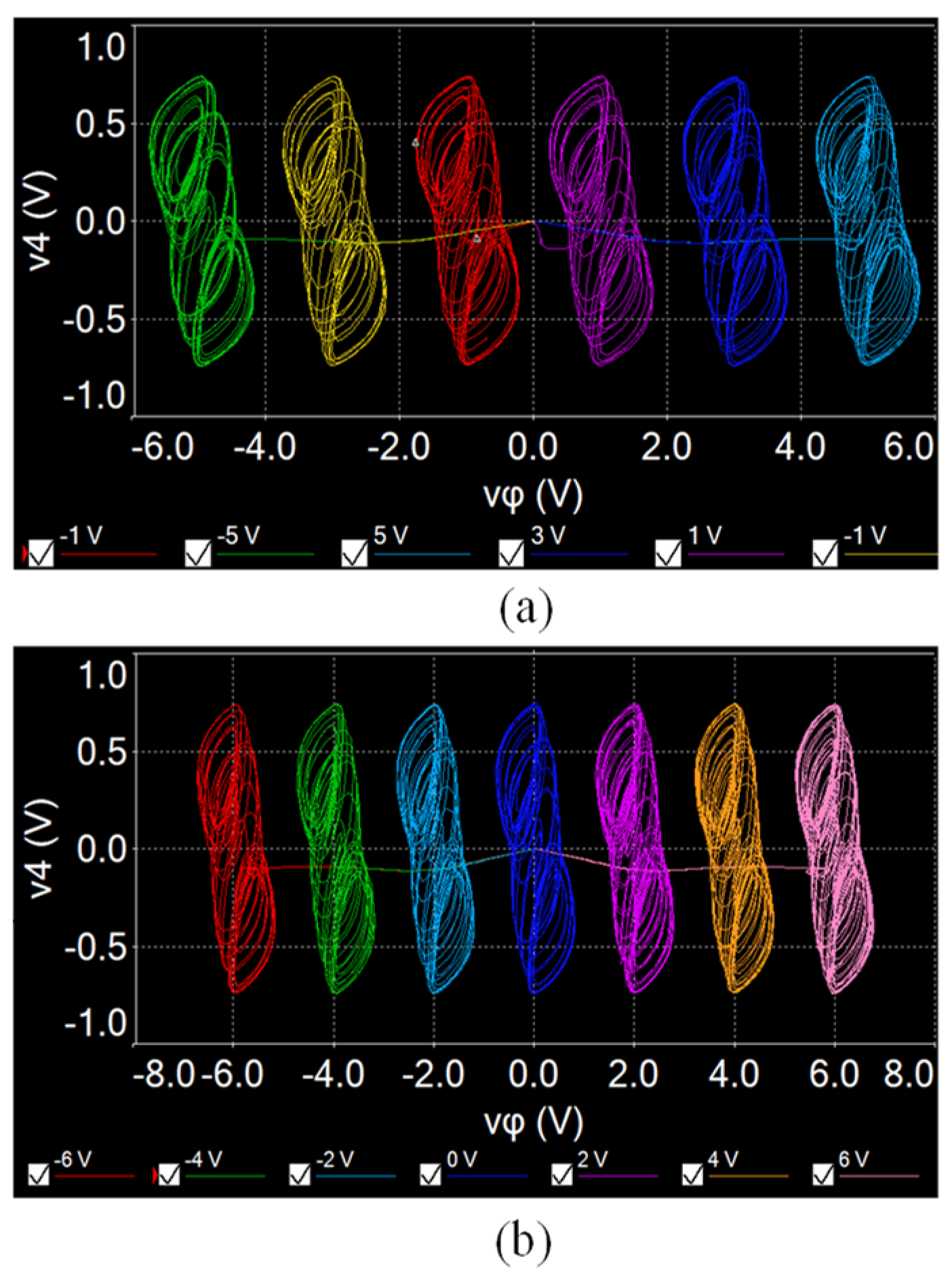
The designed star memristive neural network circuit is verified by using the MULTISIM platform. When a = 1, b = 0.01, µ = 0.01, c = 0.7, d = 1.3, and initial values (0.1, 0.1, 0.1, 0.1, 0.1), and setting Ra = 1 MΩ, Rb = 10 MΩ, Rc = 13.9 kΩ, Rd = 8 kΩ, and initial capacitor voltages to 0.1 V, multi-scroll attractors can be generated by selecting different switches. For example, closing W1, W2, and W3 and setting e1 = 2 V and e2 = 4 V, a six-scroll chaotic attractor can be generated from the designed circuit, as shown in Figure 12a. But when changing Rc = 20 kΩ (c = 0.5), the initial boosting coexisting attractors can be realized by adjusting different initial capacitor voltages vφ0. As shown in Figure 12b, six coexisting chaotic attractors are obtained from the neural network circuit. Similarly, keeping Rc = 13.9 kΩ; closing W2, W3, and W4; and setting e1 = 1 V, e2 = 3 V, and e3 = 5 V, a seven-scroll chaotic attractor can be obtained, as shown in Figure 13a. Keeping Rc = 20 kΩ, seven coexisting chaotic attractors can be obtained as shown in Figure 13b. It should be noted that the circuit simulation results are slightly different from the numerical results because of the computing errors between two different tools.
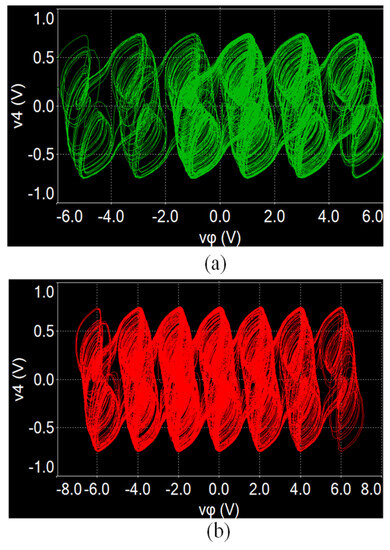
Figure 12.
Experimentally captured multi-scroll attractors from the SMNN circuit with Rc = 13.9 kΩ. (a) Six-scroll attractor. (b) Seven-scroll attractor.
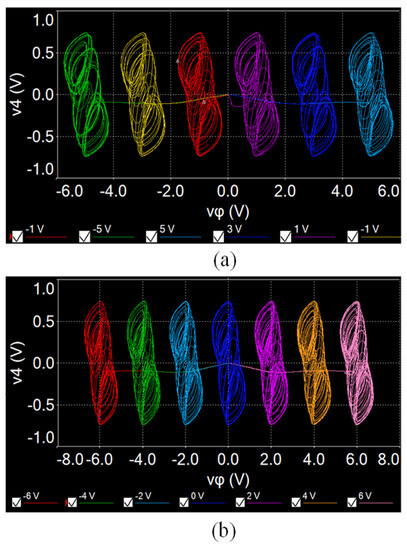
Figure 13.
Experimentally captured coexisting attractors from the SMNN circuit with Rc = 20 kΩ. (a) Six coexisting attractors. (b) Seven coexisting attractors.
5. Application in a Color Cryptosystem
Chaos can be used for information encryption due to its high randomness and sensitivity [44,45]. Chaotic neural networks with complex dynamic behavior have more promising applications for information encryption [46,47,48]. In this section, a new color image encryption scheme is designed based on the proposed star memristive neural network with multi-scroll attractors.
The encryption and decryption process is described in the following steps.
Step 1: Setting a = 1, b = 0.01, c = 0.7, d = 1.3, µ = 0.01, N = 3, and initial states (0.1, 0.1, 0.1, 0.1, 0.1), the proposed SMNN is iterated N0 + mn times, and the last mn iterations are regarded as valid data. Each iteration can generate five chaotic seven-scroll sequences x1(i), x2(i), x3(i), x4(i), and φ(i), where i = [1, mn].
Step 2: To obtain a pseudo-random sequence, the generated sequences are preprocessed as
where mod(x) is the modulo operation and floor(x) is the flooring operation.
Step 3: A chaotic sequence is generated, which can be described as
Step 4: K(i) is used to encrypt the original image using the XOR operation, as follows:
To demonstrate the efficiency of the designed image encryption cryptosystem, three color images “Lena”, “virus”, and “chameleon” with a size of 512 × 512 are chosen as the encryption object. The experimental results and the security performance analyses including the histogram, correlation coefficient, information entropy, key sensitivity, data loss, and noise attacks are given in the following.
(1) Histogram analysis:
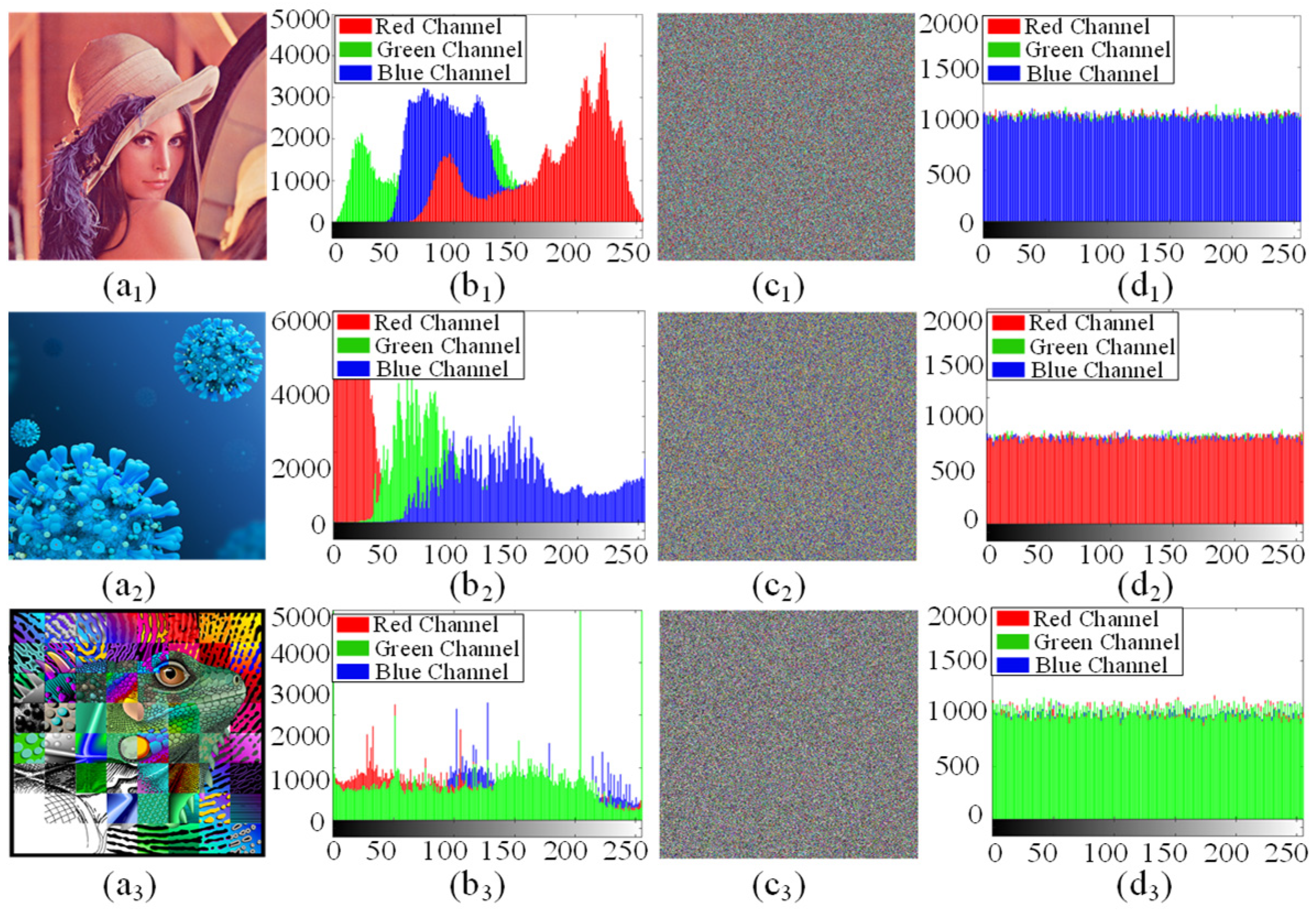
Histograms are used to evaluate the distribution of pixel intensity values in an image. In theory, a good image encryption system should produce a uniform histogram. Figure 14 gives the original images, the encrypted images, and their respective histograms. Obviously, the encrypted images in Figure 14(c1) look cluttered and completely lose their original information. The histograms of the encrypted images in Figure 14(d1–d3) are almost uniform, which means that it is difficult to obtain any useful statistical information from the encrypted image. Therefore, the proposed image encryption scheme is enough to resist statistical attacks.
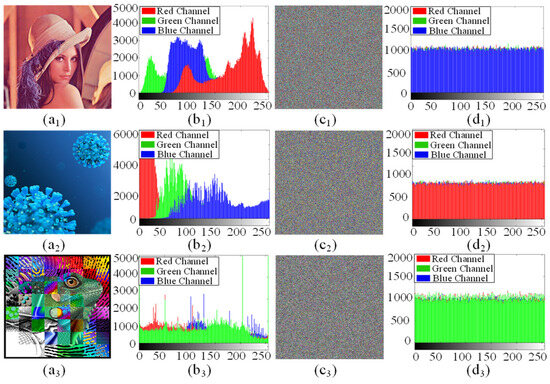
Figure 14.
Encryption results of the proposed encryption scheme: (a1–a3) original images; (b1–b3) histograms of the original images; (c1–c3) encrypted images; (d1–d3) histograms of the encrypted images.
(2) Correlation analysis: The relationship between adjacent pixels in an image can be described using correlation. In general, a stronger correlation indicates a more regular image and a weaker correlation indicates a more chaotic image. The correlation coefficient is computed by [45]
where x and y are the intensity values of two adjacent pixels. Here, 10,000 pairs of pixels were randomly chosen in horizontal, vertical, and diagonal directions from the original image and corresponding encrypted image to evaluate the correlation coefficient. As shown in Table 2, after the original images were encrypted, their relevance was greatly reduced. Therefore, the designed cryptosystem has a strong ability to resist statistical attacks.

Table 2.
Correlation coefficients for different images.
(3) Entropy analysis: Information entropy can be used to evaluate the randomness of image information. The information entropy is calculated as [45]
where P(xi) denotes the probability of xi and 2N represents the number of the information source. The maximum theoretical information entropy is 8. Table 3 gives the calculation results of information entropy under different channels. From the results in Table 3, it can be seen that compared with other similar schemes, the information entropy of this scheme is closer to the theoretical value.

Table 3.
Information entropy in different signal channels and different encryption schemes.
(4) Sensitivity analysis: Key sensitivity is an important indicator for measuring the security of encryption algorithms. A good image encryption scheme should be key-sensitive. The initial values are used as secret keys in this encryption algorithm. The decrypted images are shown in Figure 15(a1–b3) with a slight change of the secret key. Despite the fact that the secret key has been changed a little (10–16), the decrypted images are completely different from the original image. Figure 15(c1–c3) shows the decrypted image with the correct secret key. As shown in Table 4, compared with other similar image encryption schemes, the image encryption scheme proposed in this paper has a higher sensitivity to the key.

Figure 15.
Sensitivity test results with the secret key (x10, x20). (a1–a3) Inaccurate decrypted image with an inaccurate secret key x10 = 0.1 + 10−16; (b1–b3) inaccurate decrypted image with an inaccurate secret key x20 = 0.1 + 10−16; (c1–c3) accurate decrypted image with the secret keys (0.1, 0.1).

Table 4.
Key sensitivity in different encryption schemes.
(5) Data loss and noise attacks
Data loss and noise attacks can seriously affect the decryption effect of encrypted images. To evaluate the ability of data loss and noise attacks, we cut off some parts of the encrypted image and then decrypt it. As shown in Figure 16(a1–b4), data loss attacks for the different lost areas are successfully decrypted for the original image to be recovered. In order to test the resistance of the algorithm to noise attack, salt and pepper noise with different concentrations is added to the encrypted images. It can be seen from Figure 16(c1–c4) that some pixel values in the decrypted images have been changed; however, the approximate information of the original image can still be recovered successfully. Furthermore, when different concentrations of Gaussian noise are added to the encrypted images, these images are still able to be decrypted, as shown in Figure 16(d1–d4). Consequently, we can conclude that the proposed color image encryption scheme is able to withstand data loss and noise attacks and has high security.

Figure 16.
The test results of the proposed scheme for data loss and noise attacks. (a1–a4) The encrypted image with data loss. (b1–b4) Corresponding decrypted images. (c1–c4) The decrypted images under salt and pepper noise. (d1–d4) The decrypted images under Gaussian noise.
6. Conclusions
In this article, the chaotic dynamics of a star memristive neural network are studied. First, based on a Hopfield neural network with four neurons and a flux-controlled memristor, a star memristive neural network model is constructed. Then, its chaotic behaviors are revealed by using various numerical methods. Analysis results show that the star memristive neural network can generate abundant chaotic dynamics including chaos, multi-scroll attractors, and initial boosting coexisting behavior. Especially, the number of scrolls for the multi-scroll attractors can be changed by adjusting the memristor’s control parameters. In addition, the position and number of coexisting attractors can be changed by switching the memristor’s initial value. To further verify these results, an analog neural network circuit is designed and implemented. All numerical results are experimentally verified by MULTISIM circuit simulation. Finally, a color image encryption scheme based on the proposed star memristive neural network is designed. Simulation results such as histograms, correlation, information entropy, key sensitivity, and data loss and noise attacks demonstrate that the designed image encryption scheme has good security.
With the rapid development of memristors, memristor-based neural networks have been widely used in various fields including memristive neurodynamics [51,52], memristive neuromorphic computation [53,54], and so on [55]. In future work, we will devote ourselves to studying the chaotic dynamics of the memristive neural networks with different topology structures. We will also explore the practical applications of the memristive neural network developed here.
Author Contributions
Conceptualization, S.F. and Z.Y.; methodology, C.Q.; software, X.W.; validation, S.F., C.Q. and X.W.; formal analysis, S.F.; investigation, S.F.; resources, S.F.; writing—original draft preparation, S.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Group company integrated innovation projects (No. 2023-JC-13).
Institutional Review Board Statement
Not applicable.
Data Availability Statement
Please contact the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hopfield, J.J. Neural network and physical system with emergent collective computational abilities. Proc. Nat. Acad. Sci. USA 1982, 79, 2554–2558. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Zeng, J.; Dong, W.; Li, X.; Qin, D.; Ding, Q. A novel color image encryption scheme based on hyperchaos and Hopfield chaotic neural network. Entropy 2022, 24, 1474. [Google Scholar] [CrossRef] [PubMed]
- Lin, H.; Wang, C.; Yu, F.; Sun, J.; Du, S.; Deng, Z.; Deng, Q. A review of chaotic systems based on memristive Hopfield neural networks. Mathematics 2023, 11, 1369. [Google Scholar] [CrossRef]
- Korn, H.; Faure, P. Is there chaos in the brain? II. Experimental evidence and related models. Comptes Rendus Biol. 2003, 326, 787–840. [Google Scholar] [CrossRef]
- Akhmet, M.; Tleubergenova, M.; Zhamanshin, A. dynamics of Hopfield-type neural networks with modulo periodic unpredictable synaptic connections, rates and inputs. Entropy 2022, 24, 1555. [Google Scholar] [CrossRef]
- Chen, C.; Bao, H.; Chen, M.; Xu, Q.; Bao, B. Non-ideal memristor synapse-coupled bi-neuron Hopfield neural network: Numerical simulations and breadboard experiments. AEU-Int. J. Electron. Commun. 2019, 111, 152894. [Google Scholar] [CrossRef]
- Yu, F.; Shen, H.; Yu, Q.; Kong, X.; Sharma, P.K.; Cai, S. Privacy protection of medical data based on multi-scroll memristive Hopfield neural network. IEEE Trans. Netw. Sci. Eng. 2022, 10, 845–858. [Google Scholar] [CrossRef]
- Sun, J.; Xiao, X.; Yang, Q.; Liu, P.; Wang, Y. Memristor-based Hopfield network circuit for recognition and sequencing application. AEU-Int. J. Electron. Commun. 2021, 134, 153698. [Google Scholar] [CrossRef]
- Jiang, D.; Njitacke, Z.T.; Nkapkop, J.D.D.; Wang, X.; Awrejcewicz, J. A new cross ring neural network: Dynamic investigations and application to WBAN. IEEE Internet Things J. 2022, 10, 7143–7152. [Google Scholar] [CrossRef]
- Chen, C.; Min, F.; Zhang, Y.; Bao, H. ReLU-type Hopfield neural network with analog hardware implementation. Chaos Solitons Fractals 2023, 167, 113068. [Google Scholar] [CrossRef]
- Xu, Q.; Song, Z.; Qian, H.; Bao, B. Numerical analyses and breadboard experiments of twin attractors in two-neuron-based non-autonomous Hopfield neural network. Eur. Phys. J. Spec. Top. 2018, 227, 777–786. [Google Scholar] [CrossRef]
- Li, Q.; Yang, X.S.; Yang, F. Hyperchaos in Hopfield-type neural networks. Neurocomputing 2005, 67, 275–280. [Google Scholar] [CrossRef]
- Njitacke, Z.T.; Isaac, S.D.; Kengne, J.; Kengne, J.; Negou, A.N.; Leutcho, G.D. Extremely rich dynamics from hyperchaotic Hopfield neural network: Hysteretic dynamics, parallel bifurcation branches, coexistence of multiple stable states and its analog circuit implementation. Eur. Phys. J. Spec. Top. 2020, 229, 1133–1154. [Google Scholar] [CrossRef]
- Liu, Z.; Li, J.; Di, X. A new hyperchaotic 4D-FDHNN system with four positive lyapunov exponents and its application in image encryption. Entropy 2022, 24, 900. [Google Scholar] [CrossRef]
- Lin, H.; Wang, C.; Yu, F.; Hong, Q.; Xu, C.; Sun, Y. A Triple-Memristor Hopfield Neural Network with Space Multi-Structure Attractors and Space Initial-Offset Behaviors. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2023. [Google Scholar] [CrossRef]
- Li, R.; Dong, E.; Tong, J.; Wang, Z. A novel multiscroll memristive Hopfield neural network. Int. J. Bifurc. Chaos 2022, 32, 2250130. [Google Scholar] [CrossRef]
- Pham, V.T.; Jafari, S.; Vaidyanathan, S.; Volos, C.; Wang, X. A novel memristive neural network with hidden attractors and its circuitry implementation. Sci. China Technol. Sci. 2016, 59, 358–363. [Google Scholar] [CrossRef]
- Bao, B.; Qian, H.; Xu, Q.; Chen, M.; Wang, J. Coexisting behaviors of asymmetric attractors in hyperbolic-type memristor based Hopfield neural network. Front. Comput. Neurosci. 2017, 11, 81. [Google Scholar] [CrossRef]
- Yu, F.; Chen, H.; Kong, X.; Yu, Q.; Cai, S. Dynamic analysis and application in medical digital image watermarking of a new multi-scroll neural network with quartic nonlinear memristor. Eur. Phys. J. Plus 2022, 137, 434. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.; Chen, J.; Bao, H.; Chen, M.; Bao, B. Coexisting multi-stable patterns in memristor synapse-coupled Hopfield neural network with two neurons. Nonlinear Dyn. 2019, 95, 3385–3399. [Google Scholar] [CrossRef]
- Lai, Q.; Lai, C.; Kuate, P.D.K.; Li, C.; He, S. Chaos in a simplest cyclic memristive neural network. Int. J. Bifurc. Chaos 2022, 32, 2250042. [Google Scholar] [CrossRef]
- Zhang, S.; Zheng, J.; Wang, X.; Zeng, Z.; He, S. Initial offset boosting coexisting attractors in memristive multi-double-scroll Hopfield neural network. Nonlinear Dyn. 2020, 102, 2821–2841. [Google Scholar] [CrossRef]
- Lin, H.; Wang, C.; Cui, L.; Sun, Y.; Zhang, X.; Yao, W. Hyperchaotic memristive ring neural network and application in medical image encryption. Nonlinear Dyn. 2022, 110, 841–855. [Google Scholar] [CrossRef]
- Dai, S.; Sun, K.; He, S.; Ai, W. Complex chaotic attractor via fractal transformation. Entropy 2019, 21, 1115. [Google Scholar] [CrossRef]
- Lin, H.; Wang, C.; Du, S.; Sun, Y. A family of memristive multibutterfly chaotic systems with multidirectional initial-based offset boosting. Chaos Solitons Fractals 2023, 172, 113518. [Google Scholar] [CrossRef]
- Ye, X.; Wang, X.; Gao, S.; Mou, J.; Wang, Z. A new random diffusion algorithm based on the multi-scroll Chua’s chaotic circuit system. Opt. Lasers Eng. 2020, 127, 105905. [Google Scholar] [CrossRef]
- Lin, H.; Wang, C.; Yao, W.; Tan, Y. Chaotic dynamics in a neural network with different types of external stimuli. Commun. Nonlinear Sci. Numer. Simul. 2020, 90, 105390. [Google Scholar] [CrossRef]
- Wan, Q.; Li, F.; Chen, S.; Yang, Q. Symmetric multi-scroll attractors in magnetized Hopfield neural network under pulse controlled memristor and pulse current stimulation. Chaos Solitons Fractals 2023, 169, 113259. [Google Scholar] [CrossRef]
- Lai, Q.; Wan, Z.; Kuate, P.D.K. Generating grid multi-scroll attractors in memristive neural networks. IEEE Trans. Circuits Syst. I Regul. Pap. 2022, 70, 1324–1336. [Google Scholar] [CrossRef]
- Boya, B.F.B.A.; Kengne, J.; Kenmoe, G.D.; Effa, J.Y. Four-scroll attractor on the dynamics of a novel Hopfield neural network based on bi-neurons without bias current. Heliyon 2022, 8, e11046. [Google Scholar] [CrossRef]
- Yu, F.; Zhang, Z.; Shen, H.; Huang, Y.; Cai, S.; Jin, J. Design and FPGA implementation of a pseudo-random number generator based on a Hopfield neural network under electromagnetic radiation. Front. Phys. 2021, 9, 690651. [Google Scholar] [CrossRef]
- Yu, F.; Kong, X.; Mokbel, A.A.M.; Yao, W. Complex dynamics, hardware implementation and image encryption application of multiscroll memeristive Hopfield neural network with a novel local active memeristor. IEEE Trans. Circuits Syst. II Express Briefs 2022, 70, 326–330. [Google Scholar] [CrossRef]
- Wu, H.G.; Ye, Y.; Bao, B.C.; Chen, M.; Xu, Q. Memristor initial boosting behaviors in a two-memristor-based hyperchaotic system. Chaos Solitons Fractals 2019, 121, 178–185. [Google Scholar] [CrossRef]
- Ding, D.; Shan, X.; Jun, L.; Hu, Y.; Yang, Z. Initial boosting phenomenon of a fractional-order hyperchaotic system based on dual memristors. Mod. Phys. Lett. B 2020, 34, 2050191. [Google Scholar] [CrossRef]
- Song, Y.; Yuan, F.; Li, Y. Coexisting attractors and multistability in a simple memristive Wien-bridge chaotic circuit. Entropy 2019, 21, 678. [Google Scholar] [CrossRef]
- Bao, B.C.; Li, H.Z.; Zhu, L.; Zhang, X.; Chen, M. Initial-switched boosting bifurcations in 2D hyperchaotic map. Chaos Interdiscip. J. Nonlinear Sci. 2020, 30, 033107. [Google Scholar] [CrossRef]
- Almatroud, A.O.; Khennaoui, A.A.; Ouannas, A.; Pham, V.T. Infinite line of equilibriums in a novel fractional map with coexisting infinitely many attractors and initial offset boosting. Int. J. Nonlinear Sci. Numer. Simul. 2023, 24, 373–391. [Google Scholar] [CrossRef]
- Ding, S.; Wang, N.; Bao, H.; Chen, B.; Wu, H.; Xu, Q. Memristor synapse-coupled piecewise-linear simplified Hopfield neural network: Dynamics analysis and circuit implementation. Chaos Solitons Fractals 2023, 166, 112899. [Google Scholar] [CrossRef]
- Doubla, I.S.; Ramakrishnan, B.; Njitacke, Z.T.; Kengne, J.; Rajagopal, K. Hidden extreme multistability and its control with selection of a desired attractor in a non-autonomous Hopfield neuron. AEU-Int. J. Electron. Commun. 2022, 144, 154059. [Google Scholar] [CrossRef]
- Bao, H.; Hua, M.; Ma, J.; Chen, M.; Bao, B. Offset-control plane coexisting behaviors in two-memristor-based Hopfield neural network. IEEE Trans. Ind. Electron. 2022, 70, 10526–10535. [Google Scholar] [CrossRef]
- Lin, H.; Wang, C.; Cui, L.; Sun, Y. Brain-like initial-boosted hyperchaos and application in biomedical image encryption. IEEE Trans. Ind. Inform. 2022, 18, 8839–8850. [Google Scholar] [CrossRef]
- Lai, Q.; Wan, Z.; Zhang, H.; Chen, G. Design and analysis of multiscroll memristive hopfield neural network with adjustable memductance and application to image encryption. IEEE Trans. Neural Netw. Learn. Syst. 2022. [Google Scholar] [CrossRef] [PubMed]
- Leng, Y.; Yu, D.; Hu, Y.; Yu, S.S.; Ye, Z. Dynamic behaviors of hyperbolic-type memristor-based Hopfield neural network considering synaptic crosstalk. Chaos 2020, 30, 033108. [Google Scholar] [CrossRef]
- Zhang, Y.; Dong, W.; Zhang, J.; Ding, Q. An Image Encryption Transmission Scheme Based on a Polynomial Chaotic Map. Entropy 2023, 25, 1005. [Google Scholar] [CrossRef] [PubMed]
- Lin, H.; Wang, C.; Sun, Y. A universal variable extension method for designing multi-scroll/wing chaotic systems. IEEE Trans. Ind. Electron. 2023. [Google Scholar] [CrossRef]
- Wang, X.Y.; Li, Z.M. A color image encryption algorithm based on Hopfield chaotic neural network. Opt. Lasers Eng. 2019, 115, 107–118. [Google Scholar] [CrossRef]
- Tlelo-Cuautle, E.; Díaz-Muñoz, J.D.; González-Zapata, A.M.; Li, R.; Leon, W.D.; Femandez, F.V. Chaotic image encryption using Hopfield and Hindmarsh–Rose neurons implemented on FPGA. Sensors 2020, 20, 1326. [Google Scholar] [CrossRef]
- Xu, X.; Chen, S. An optical image encryption method using Hopfield neural network. Entropy 2022, 24, 521. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, L.; Jiang, D.; Guan, Y.; Zhang, Z. A simultaneous scrambling and diffusion color image encryption algorithm based on Hopfield chaotic neural network. IEEE Access 2019, 7, 185796–185810. [Google Scholar] [CrossRef]
- Bigdeli, N.; Farid, Y.; Afshar, K. A robust hybrid method for image encryption based on Hopfield neural network. Comput. Electr. Eng. 2012, 38, 356–369. [Google Scholar] [CrossRef]
- Wen, Z.; Wang, C.; Deng, Q.; Lin, H. Regulating memristive neuronal dynamical properties via excitatory or inhibitory magnetic field coupling. Nonlinear Dyn. 2022, 110, 3823–3835. [Google Scholar] [CrossRef]
- Yao, W.; Wang, C.; Sun, Y.; Gong, S.; Lin, H. Event-triggered control for robust exponential synchronization of inertial memristive neural networks under parameter disturbance. Neural Netw. 2023, 164, 67–80. [Google Scholar] [CrossRef] [PubMed]
- Hu, M.; Graves, C.E.; Li, C.; Li, Y.; Ge, N.; Montgomery, E.; Davila, N.; Jiang, H.; Williams, R.S.; Yang, J.J.; et al. Memristor-based analog computation and neural network classification with a dot product engine. Adv. Mater. 2018, 30, 1705914. [Google Scholar] [CrossRef] [PubMed]
- Yao, P.; Wu, H.; Gao, B.; Tang, J.; Zhang, Q.; Zhang, W.; Yang, J.J.; Qian, H. Fully hardware-implemented memristor convolutional neural network. Nature 2020, 577, 641–646. [Google Scholar] [CrossRef]
- Liao, M.; Wang, C.; Sun, Y.; Lin, H. Memristor-based affective associative memory neural network circuit with emotional gradual processes. Neural Comput. Appl. 2022, 34, 13667–13682. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).