Generalized Bell Scenarios: Disturbing Consequences on Local-Hidden-Variable Models
Abstract
:1. Introduction
2. Bell Nonlocality and Kochen–Specker Contextuality
2.1. Bell Nonlocality
2.2. Kochen–Specker Contextuality
3. Bell Scenarios with Compatible Measurements
3.1. Non-Signalling and Non-Disturbing Conditions
3.2. Contextuality
3.3. The Many Meanings of Locality in Extended Scenarios
3.4. Locality and Non-Contextuality Together
4. Geometrical Characterization of the Correlation Sets
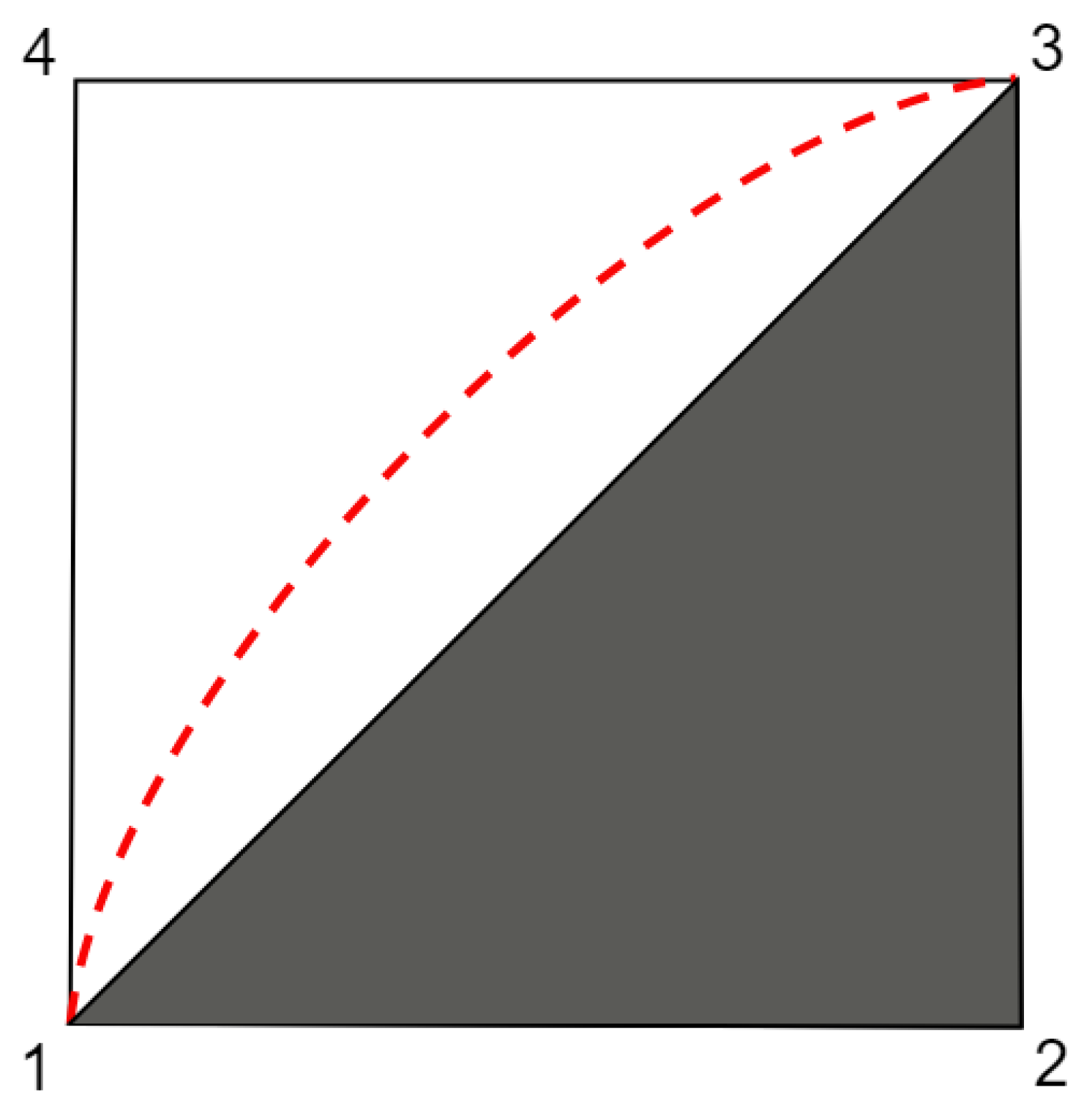
4.1. Digression on Sets of Extreme Response Functions
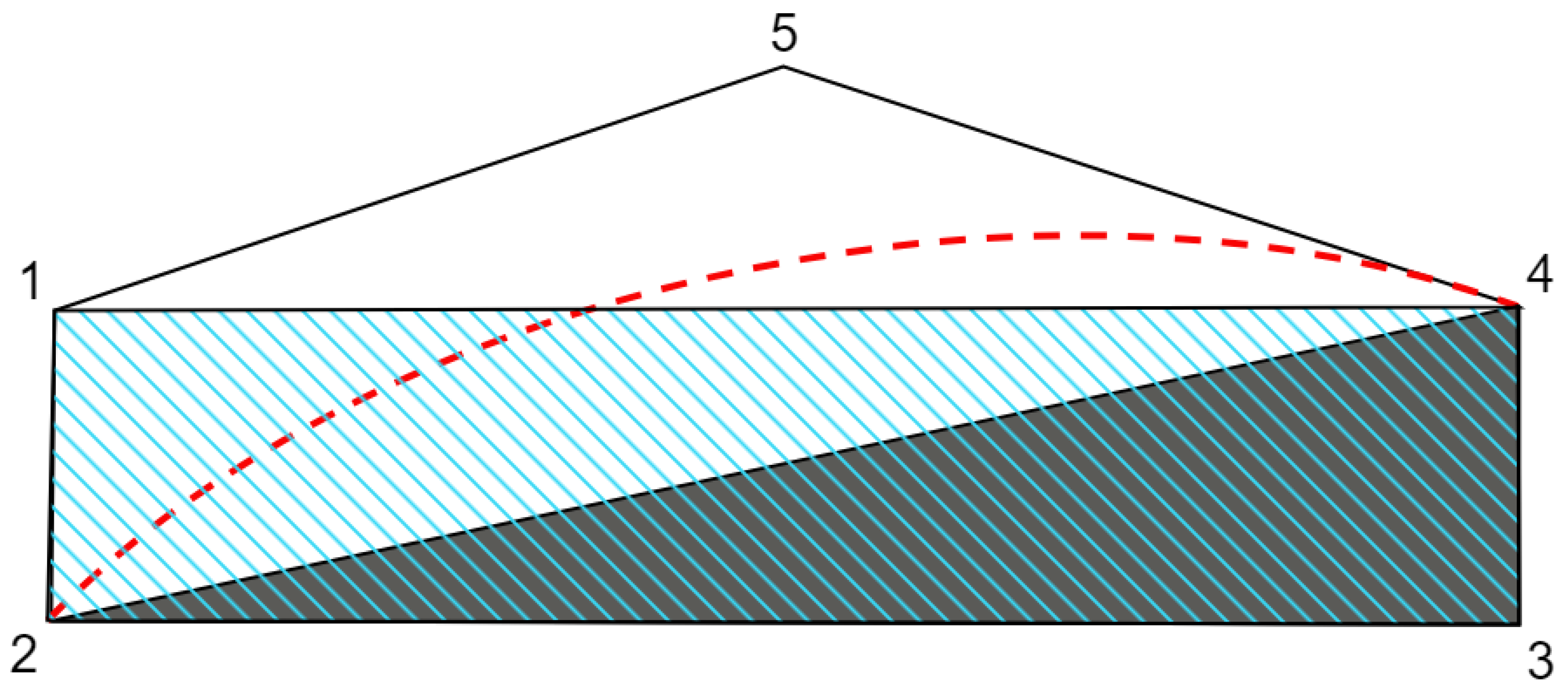
4.2. Polytopes for Standard Scenarios
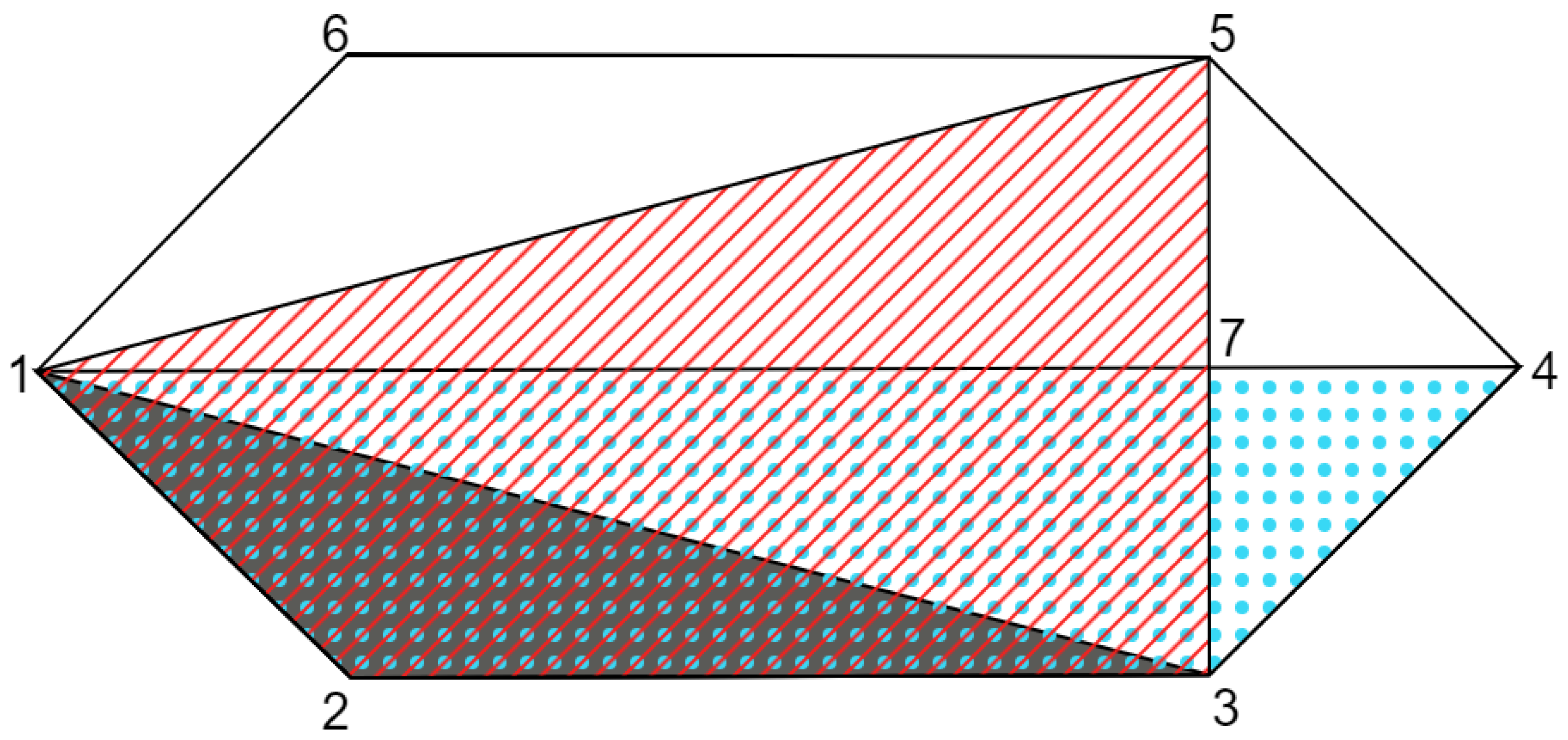
4.3. Polytopes for Extended Scenarios
5. Quantum Correlations
6. Extensions of Fine’s Theorem
7. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Proof of Theorem 1
| 000 | 001 | 010 | 011 | 100 | 101 | 110 | 111 | |
| 0 | 0 | 0 | 0 | 0 | 0 | |||
| 0 | 0 | 0 | 0 | 0 | 0 | |||
| 0 | 0 | 0 | 0 | 0 | 0 | |||
| 0 | 0 | 0 | 0 | 0 | 0 |
| Vertex 1 | 0 | 0 | ||
| Vertex 2 | 0 | 1 |
Appendix B. Proof of Theorem 2
| 000 | 001 | 010 | 011 | 100 | 101 | 110 | 111 | |
| 0 | 0 | 0 | 0 | 0 | ||||
| 0 | 0 | 0 | 0 | 0 | ||||
| 0 | 0 | 0 | 0 | 0 | ||||
| 0 | 0 | 0 | 0 | 0 | ||||
| 0 | 0 | 0 | 0 | 0 | ||||
| 0 | 0 | 0 | 0 | 0 |
| 000 | 001 | 010 | 011 | 100 | 101 | 110 | 111 | |
| 0 | 0 | 0 | 0 | 0 | ||||
| 0 | 0 | 0 | 0 | |||||
| 0 | 0 | 0 | 0 | |||||
| 0 | 0 | 0 | 0 | |||||
| 0 | 0 | 0 | 0 | |||||
| 0 | 0 | 0 | 0 |
References
- Brunner, N.; Cavalcanti, D.; Pironio, S.; Scarani, V.; Wehner, S. Bell nonlocality. Rev. Mod. Phys. 2014, 86, 419. [Google Scholar] [CrossRef]
- Budroni, C.; Cabello, A.; Gühne, O.; Kleinmann, M.; Larsson, J. Kochen–Specker Contextuality. Rev. Mod. Phys. 2022, 94, 045007. [Google Scholar] [CrossRef]
- Bell, J.S. On the Einstein-Podolsky-Rosen paradox. Physics 1964, 1, 195. [Google Scholar] [CrossRef]
- Kochen, S.; Specker, E.P. The problem of hidden variables in quantum mechanics. J. Math. Mech. 1967, 17, 59. [Google Scholar] [CrossRef]
- Freedman, S.J.; Clauser, J.F. Experimental Test of Local Hidden-Variable Theories. Phys. Rev. Lett. 1972, 28, 938. [Google Scholar] [CrossRef]
- Aspect, A.; Dalibard, J.; Roger, G. Experimental Test of Bell’ s Inequalities Using Time-Varying Analyzers’. Phys. Rev. Lett. 1982, 49, 1804. [Google Scholar] [CrossRef]
- Hensen, B.; Bernien, H.; Dréau, A.E.; Reiserer, A.; Kalb, N.; Blok, M.S.; Ruitenberg, J.; Vermeulen, R.F.L.; Schouten, R.N.; Abellan, C.; et al. Loophole-free Bell inequality violation using electron spins separated by 1.3 kilometres. Nature 2015, 526, 682–686. [Google Scholar] [CrossRef] [PubMed]
- Giustina, M.; Versteegh, M.; Wengerowsky, S.; Handsteiner, J.; Hochrainer, A.; Phelan, K.; Steinlechner, F.; Kofler, J.; Larsson, J.; Abellan, C.; et al. Significant-Loophole-Free Test of Bell’s Theorem with Entangled Photons. Phys. Rev. Lett. 2015, 115, 250401. [Google Scholar] [CrossRef]
- Shalm, L.K.; Meyer-Scott, E.; Christensen, B.G.; Bierhorst, P.; Wayne, M.A.; Stevens, M.J.; Gerrits, T.; Glancy, S.; Hamel, D.R.; Allman, M.S.; et al. Strong Loophole-Free Test of Local Realism. Phys. Rev. Lett. 2015, 115, 250402. [Google Scholar] [CrossRef]
- Rosenfeld, W.; Burchardt, D.; Garthoff, R.; Redeker, K.; Ortegel, N.; Rau, M.; Weinfurter, H. Event-ready Bell-test using entangled atoms simultaneously closing detection and locality loopholes. Phys. Rev. Lett. 2017, 119, 010402. [Google Scholar] [CrossRef]
- Kirchmair, G.; Zahringer, F.; Gerritsma, R.; Kleinmann, M.; Guhne, O.; Cabello, A.; Blatt, R.; Roos, C.F. State-independent experimental test of quantum contextuality. Nature 2009, 460, 494–497. [Google Scholar] [CrossRef]
- Amselem, E.; Rådmark, M.; Bourennane, M.; Cabello, A. State-Independent Quantum Contextuality with Single Photons. Phys. Rev. Lett. 2009, 103, 160405. [Google Scholar] [CrossRef]
- Lapkiewicz, R.; Li, P.; Schaeff, C.; Langford, N.K.; Ramelow, S.; Wiesniak, M.; Zeilinger, A. Experimental non-classicality of an indivisible quantum system. Nature 2011, 474, 490–493. [Google Scholar] [CrossRef]
- Cabello, A.; Severini, S.; Winter, A. Graph-Theoretic Approach to Quantum Correlations. Phys. Rev. Lett. 2014, 112, 040401. [Google Scholar] [CrossRef]
- Acín, A.; Fritz, T.; Leverrier, A.; Sainz, A.B. A combinatorial approach to nonlocality and contextuality. Comm. Math. Phys. 2015, 334, 533–628. [Google Scholar] [CrossRef]
- Rabelo, R.; Duarte, C.; López-Tarrida, A.J.; Terra Cunha, M.; Cabello, A. Multigraph approach to quantum non-locality. J. Phys. A Math. Theor. 2014, 47, 424021. [Google Scholar] [CrossRef]
- Kurzyński, P.; Cabello, A.; Kaszlikowski, D. Fundamental Monogamy Relation between Contextuality and Nonlocality. Phys. Rev. Lett. 2014, 112, 100401. [Google Scholar] [CrossRef]
- Temistocles, T.; Rabelo, R.; Terra Cunha, M. Measurement compatibility in Bell nonlocality tests. Phys. Rev. A 2019, 99, 042120. [Google Scholar] [CrossRef]
- Xue, P.; Xiao, L.; Ruffolo, G.; Mazzari, A.; Temistocles, T.; Terra Cunha, M.; Rabelo, R. Synchronous Observation of Bell Nonlocality and State-Dependent Contextuality. Phys. Rev. Lett. 2023, 130, 040201. [Google Scholar] [CrossRef]
- Fine, A. Hidden Variables, Joint Probability, and the Bell Inequalities. Phys. Rev. Lett. 1982, 48, 291. [Google Scholar] [CrossRef]
- Abramsky, S.; Brandenburger, A. The sheaf-theoretic structure of non-locality and contextuality. N. J. Phys. 2011, 13, 113036. [Google Scholar] [CrossRef]
- Clauser, J.F.; Horne, M.A.; Shimony, A.; Holt, R.A. Proposed experiment to test local hidden-variable theories. Phys. Rev. Lett. 1969, 23, 880. [Google Scholar] [CrossRef]
- Klyachko, A.A.; Can, M.A.; Binicioglu, S.; Shumovsky, A.S. Simple Test for Hidden Variables in Spin-1 Systems. Phys. Rev. Lett. 2008, 101, 020403. [Google Scholar] [CrossRef] [PubMed]
- Pitowsky, I. Quantum Probability—Quantum Logic, 1st ed.; Springer: Berlin/Heidelberg, Germany, 1989. [Google Scholar]
- Larwald, S.; Reinelt, G. PANDA: A software for polyhedral transformations. EURO J. Comput. Optim. 2015, 3, 297–308. [Google Scholar] [CrossRef]
- Github Repository. Available online: https://github.com/andremazzari/Generalized-Bell-scenarios-disturbing-consequences-on-local-hidden-variable-models (accessed on 26 July 2023).
- Araújo, M.; Quintino, M.T.; Budroni, C.; Terra Cunha, M.; Cabello, A. All noncontextuality inequalities for the n-cycle scenario. Phys. Rev. A 2013, 88, 022118. [Google Scholar] [CrossRef]
- Navascués, M.; Pironio, S.; Acín, A. A convergent hierarchy of semidefinite programs characterizing the set of quantum correlations. N. J. Phys. 2008, 10, 073013. [Google Scholar] [CrossRef]
- Bowles, J.; Hirsch, F.; Cavalcanti, D. Single-copy activation of Bell nonlocality via broadcasting of quantum states. Quantum 2021, 5, 499. [Google Scholar] [CrossRef]
- Brask, J.B.; Chaves, R. Bell scenarios with communication. J. Phys. A Math. Theor. 2017, 50, 094001. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mazzari, A.; Ruffolo, G.; Vieira, C.; Temistocles, T.; Rabelo, R.; Terra Cunha, M. Generalized Bell Scenarios: Disturbing Consequences on Local-Hidden-Variable Models. Entropy 2023, 25, 1276. https://doi.org/10.3390/e25091276
Mazzari A, Ruffolo G, Vieira C, Temistocles T, Rabelo R, Terra Cunha M. Generalized Bell Scenarios: Disturbing Consequences on Local-Hidden-Variable Models. Entropy. 2023; 25(9):1276. https://doi.org/10.3390/e25091276
Chicago/Turabian StyleMazzari, André, Gabriel Ruffolo, Carlos Vieira, Tassius Temistocles, Rafael Rabelo, and Marcelo Terra Cunha. 2023. "Generalized Bell Scenarios: Disturbing Consequences on Local-Hidden-Variable Models" Entropy 25, no. 9: 1276. https://doi.org/10.3390/e25091276
APA StyleMazzari, A., Ruffolo, G., Vieira, C., Temistocles, T., Rabelo, R., & Terra Cunha, M. (2023). Generalized Bell Scenarios: Disturbing Consequences on Local-Hidden-Variable Models. Entropy, 25(9), 1276. https://doi.org/10.3390/e25091276







