Investigation of Feature Engineering Methods for Domain-Knowledge-Assisted Bearing Fault Diagnosis
Abstract
1. Introduction
2. Fundamentals
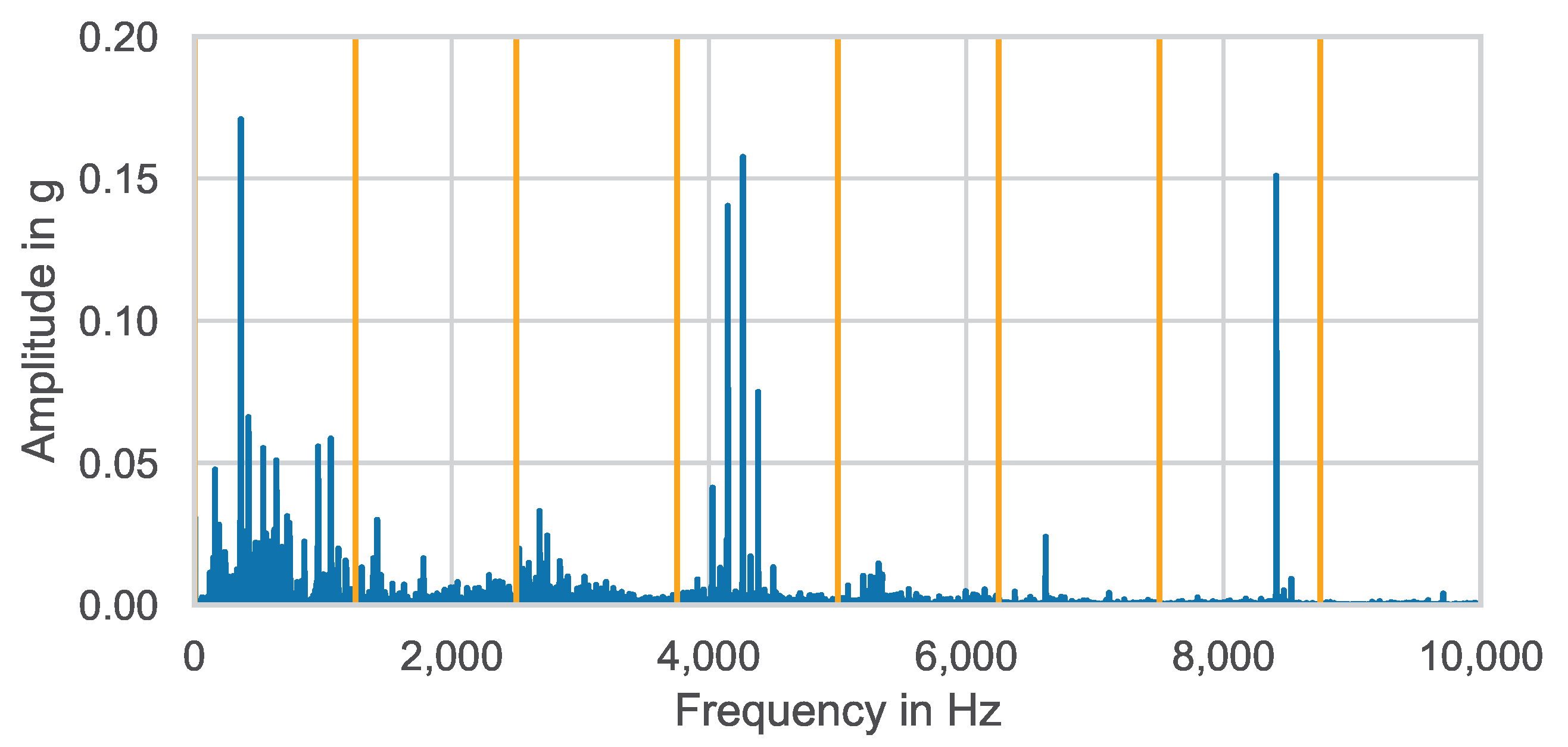
2.1. CWRU Bearing Fault Data
2.2. Feature Formulas
2.3. Signal Processing Methods
2.3.1. Envelope Analysis
2.3.2. Empirical Mode Decomposition
2.3.3. Wavelet Transform
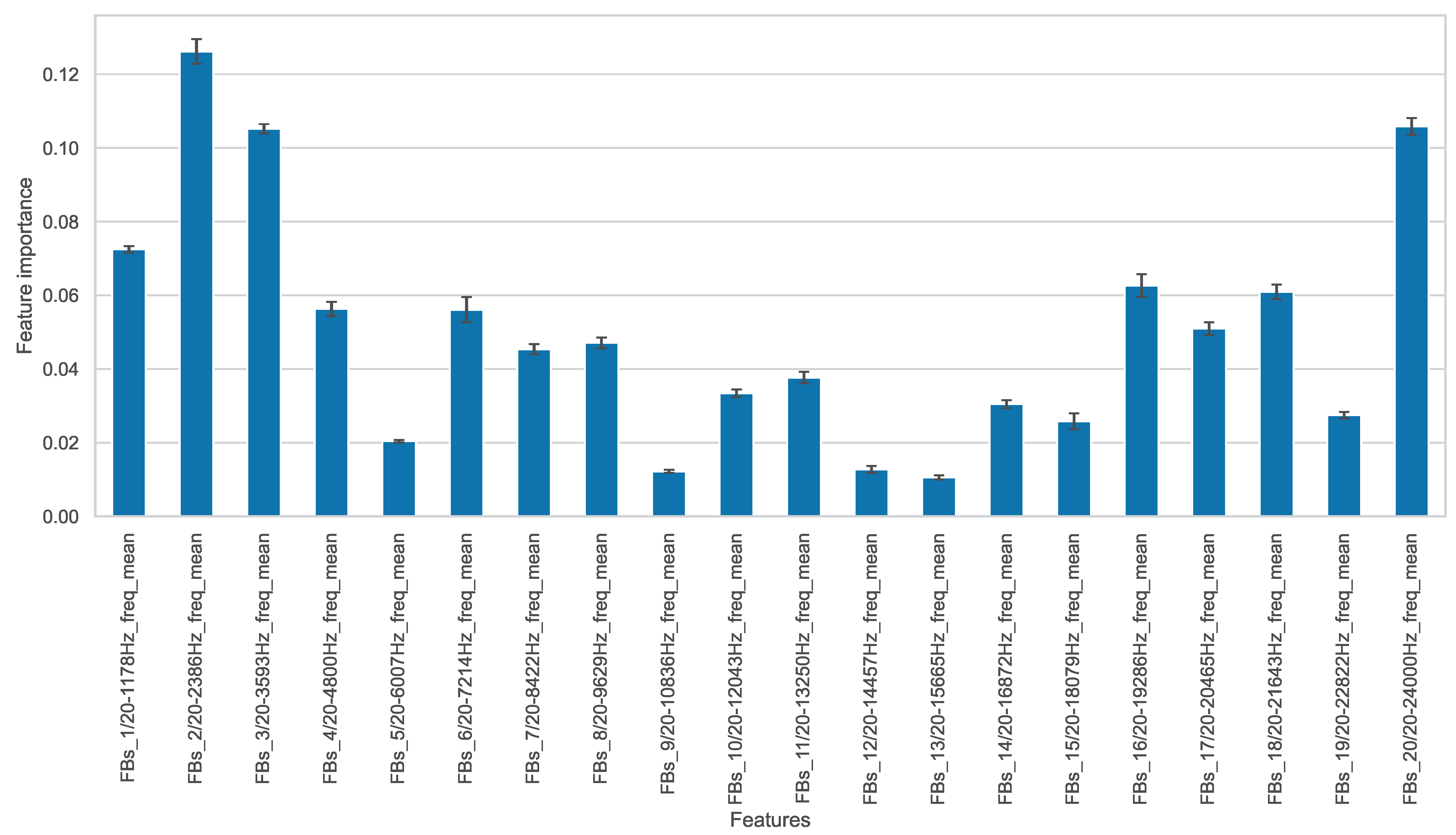
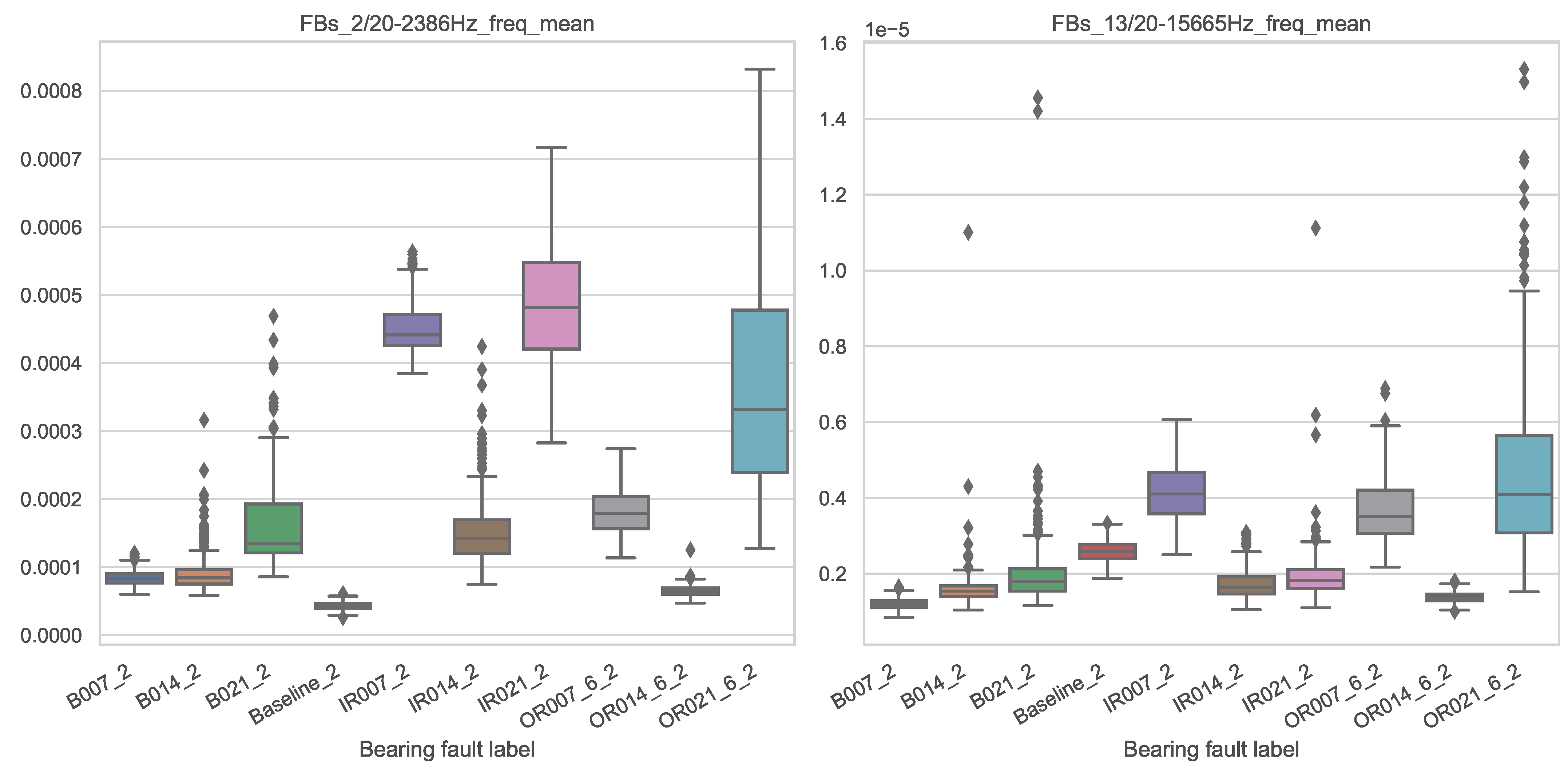
2.3.4. Frequency Bands
3. Methods
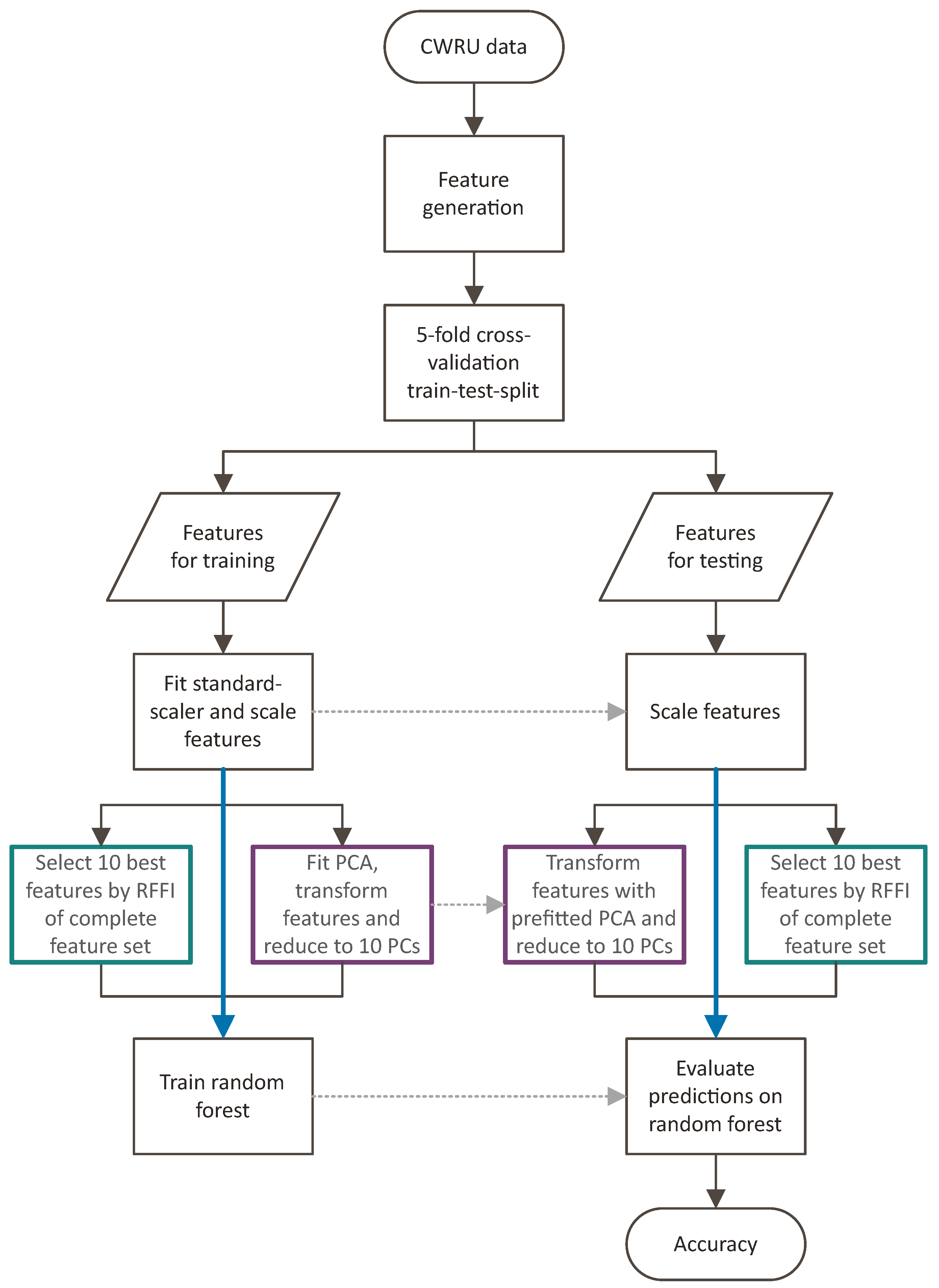
3.1. Data Preparation
- Inner ring faults: IR007_2, IR014_2 and IR021_2;
- Outer ring faults: OR007@6_2, OR014@6_2 and OR021@6_2;
- Ball faults: B007_2, B014_2 and B021_2;
- No fault: Normal_2.
3.2. Machine Learning
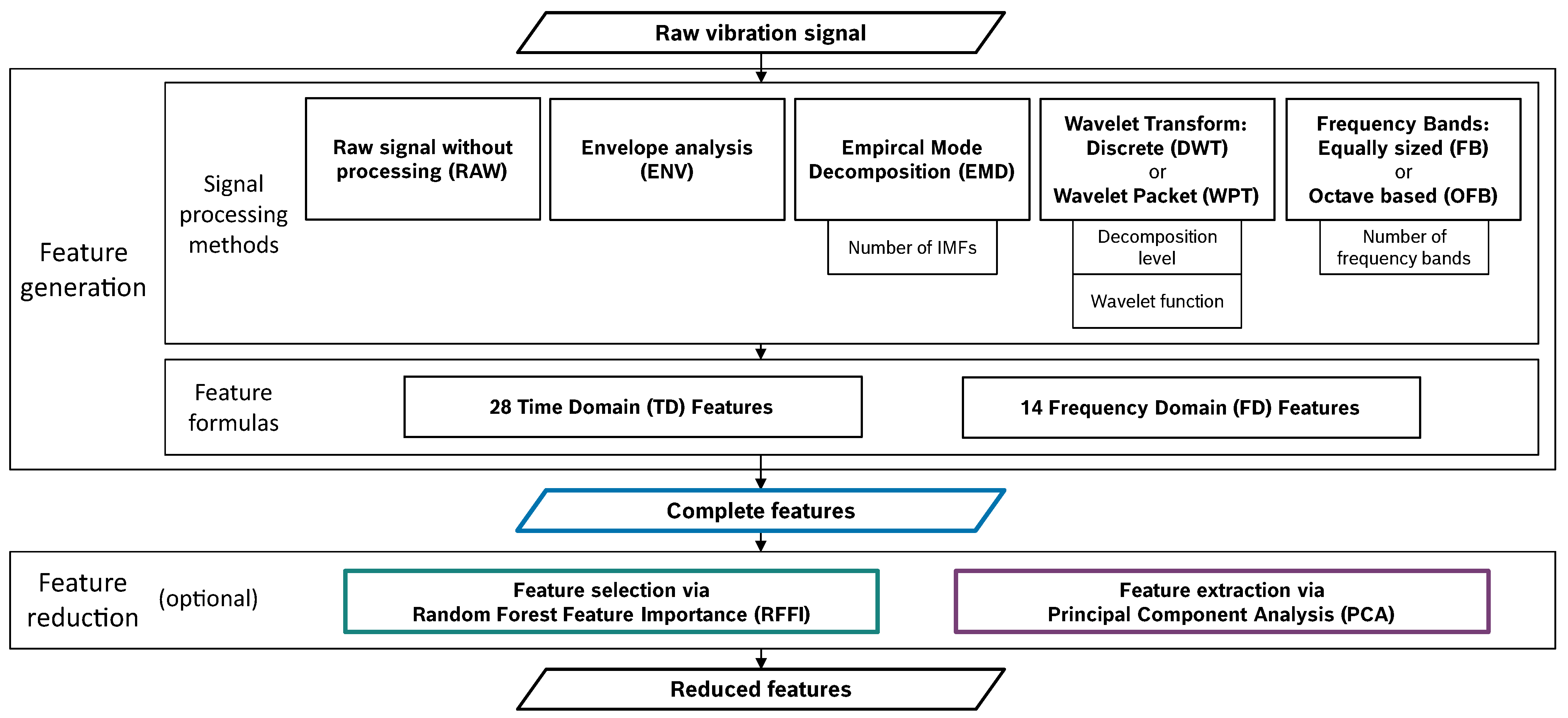
3.3. Feature Engineering
- Selection of an appropriate set of feature formulas based on the raw, unprocessed vibration signal (RAW).
- Comparison of the different processing methods using the feature formulas selected in the previous step.
- Additional investigations of the frequency bands: Consideration of the frequency-domain mean values solely, as proposed in [26].
- All features of the calculated feature set are used for the evaluation of the prediction accuracy—Complete feature set.
- Based on the random forest feature importance evaluated on the complete features set, the 10 most important features are selected and used to evaluate prediction performance—10 most important features (RFFI).
- The feature sets are transformed using a principal component analysis (PCA), and only the 10 principal components representing the largest feature variance are used to evaluate prediction performance—10 principal components (PCA).
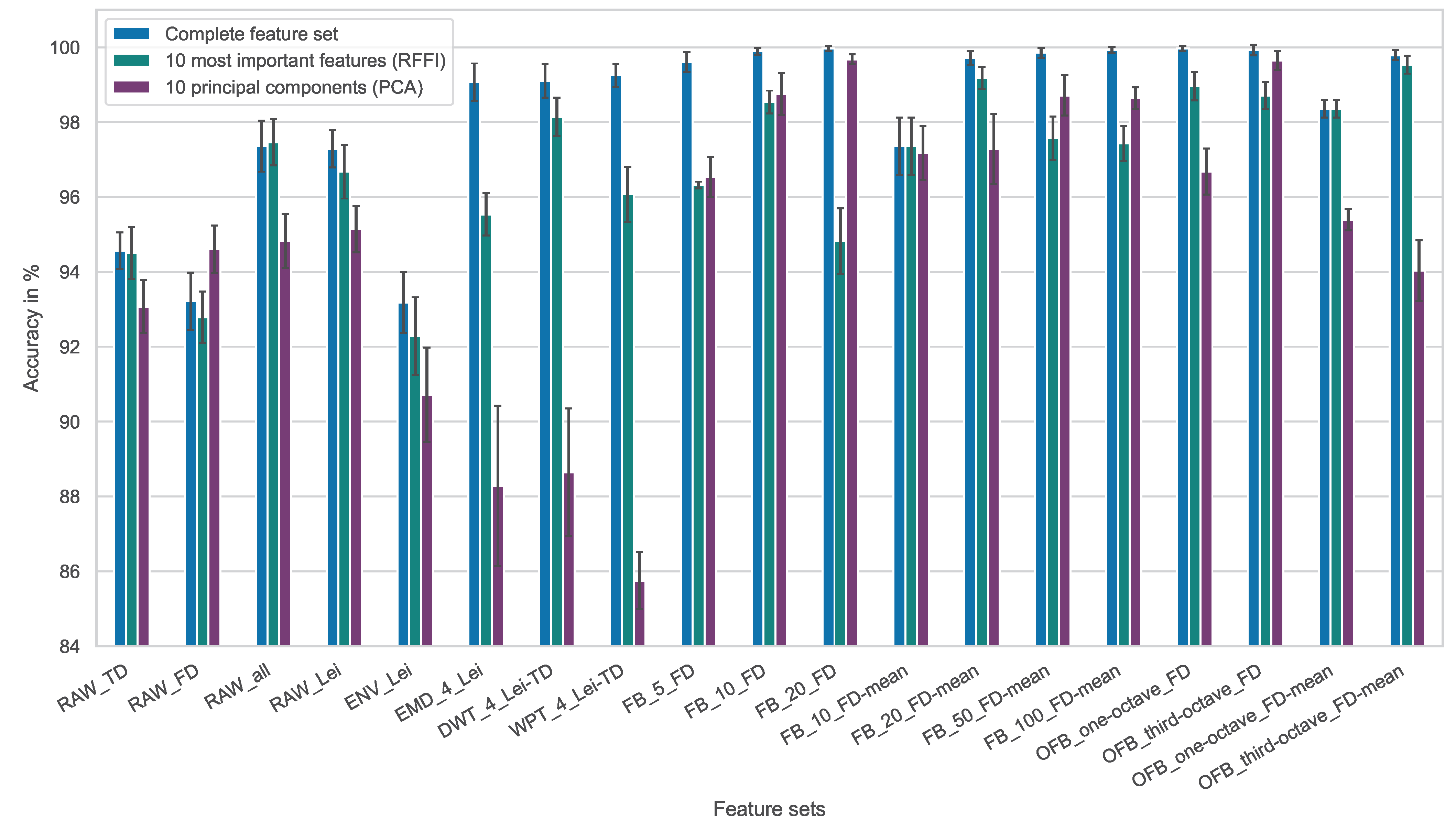
4. Results and Discussion
- FB_20_FD;
- FB_100_FD-mean;
- OFB_one-octave_FD;
- OFB_third-octave_FD.
- FB_20_FD-mean;
- OFB_third-octave_FD-mean.
- FB_20_FD;
- OFB_third-octave_FD.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ML | Machine Learning |
| CWRU | Case Western Reserve University |
| SRM | Square Root Mean |
| RMS | Root Mean Square |
| FFT | Fast Fourier Transform |
| CNN | Convolutional Neural Network |
| RAW | Raw Signal Without Processing |
| ENV | Envelope Analysis |
| EMD | Empirical Mode Decomposition |
| IMF | Intrinsic Mode Function |
| CWT | Continuous Wavelet Transform |
| DWT | Discrete Wavelet Transform |
| WPT | Wavelet Packet Transform |
| FB | Equally Sized Frequency Bands |
| OFB | Octave-based Frequency Bands |
| TD | Time Domain |
| FD | Frequency Domain |
| RFFI | Random Forest Feature Importance |
| PCA | Principal Component Analysis |
References
- Vorwerk-Handing, G.; Martin, G.; Kirchner, E. Integration of Measurement Functions in Existing Systems—Retrofitting as Basis for Digitalization. In Proceedings of the DS 91: Proceedings of NordDesign 2018, Linköping, Sweden, 14–17 August 2018. [Google Scholar]
- Nandi, A.K.; Ahmed, H. Condition Monitoring with Vibration Signals: Compressive Sampling and Learning Algorithms for Rotating Machines; Wiley-IEEE Press: Hoboken, NJ, USA, 2019. [Google Scholar]
- Zhao, Z.; Li, T.; Wu, J.; Sun, C.; Wang, S.; Yan, R.; Chen, X. Deep learning algorithms for rotating machinery intelligent diagnosis: An open source benchmark study. ISA Trans. 2020, 107, 224–255. [Google Scholar] [CrossRef] [PubMed]
- Lei, Y.; Li, N.; Li, X. Big Data-Driven Intelligent Fault Diagnosis and Prognosis for Mechanical Systems; Springer Nature: Singapore, 2023. [Google Scholar] [CrossRef]
- Motahari-Nezhad, M.; Jafari, S.M. Bearing remaining useful life prediction under starved lubricating condition using time domain acoustic emission signal processing. Expert Syst. Appl. 2021, 168, 114391. [Google Scholar] [CrossRef]
- Schwendemann, S.; Amjad, Z.; Sikora, A. A survey of machine-learning techniques for condition monitoring and predictive maintenance of bearings in grinding machines. Comput. Ind. 2021, 125, 103380. [Google Scholar] [CrossRef]
- Hakim, M.; Omran, A.A.B.; Ahmed, A.N.; Al-Waily, M.; Abdellatif, A. A systematic review of rolling bearing fault diagnoses based on deep learning and transfer learning: Taxonomy, overview, application, open challenges, weaknesses and recommendations. Ain Shams Eng. J. 2022, 14, 101945. [Google Scholar] [CrossRef]
- Case Western Reserve University Bearing Data Center. Available online: https://engineering.case.edu/bearingdatacenter (accessed on 7 March 2023).
- Yuan, L.; Lian, D.; Kang, X.; Chen, Y.; Zhai, K. Rolling Bearing Fault Diagnosis Based on Convolutional Neural Network and Support Vector Machine. IEEE Access 2020, 8, 137395–137406. [Google Scholar] [CrossRef]
- Smith, W.A.; Randall, R.B. Rolling element bearing diagnostics using the Case Western Reserve University data: A benchmark study. Mech. Syst. Signal Process. 2015, 64–65, 100–131. [Google Scholar] [CrossRef]
- Lei, Y.; He, Z.; Zi, Y. A new approach to intelligent fault diagnosis of rotating machinery. Expert Syst. Appl. 2008, 35, 1593–1600. [Google Scholar] [CrossRef]
- Lei, Y. Intelligent Fault Diagnosis and Remaining Useful Life Prediction of Rotating Machinery; Butterworth-Heinemann Ltd.: Oxford, UK; Xi’an Jiaotong University Press: Xi’an, China, 2017. [Google Scholar]
- Wang, X.; Zheng, Y.; Zhao, Z.; Wang, J. Bearing Fault Diagnosis Based on Statistical Locally Linear Embedding. Sensors 2015, 15, 16225–16247. [Google Scholar] [CrossRef] [PubMed]
- Tom, K.F. A Primer on Vibrational Ball Bearing Feature Generation for Prognostics and Diagnostics Algorithms. Sens. Electron Devices ARL 2015. Available online: https://apps.dtic.mil/sti/citations/ADA614145 (accessed on 10 February 2023).
- Golbaghi, V.K.; Shahbazian, M.; Moslemi, B.; Rashed, G. Rolling element bearing condition monitoring based on vibration analysis using statistical parameters of discrete wavelet coefficients and neural networks. Int. J. Autom. Smart Technol. 2017, 7, 61–69. [Google Scholar] [CrossRef][Green Version]
- Grover, C.; Turk, N. Optimal Statistical Feature Subset Selection for Bearing Fault Detection and Severity Estimation. Shock Vib. 2020, 2020, 5742053. [Google Scholar] [CrossRef]
- Jain, P.H.; Bhosle, S.P. Study of effects of radial load on vibration of bearing using time-Domain statistical parameters. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1070, 012130. [Google Scholar] [CrossRef]
- Saucedo-Dorantes, J.J.; Zamudio-Ramirez, I.; Cureno-Osornio, J.; Osornio-Rios, R.A.; Antonino-Daviu, J.A. Condition Monitoring Method for the Detection of Fault Graduality in Outer Race Bearing Based on Vibration-Current Fusion, Statistical Features and Neural Network. Appl. Sci. 2021, 11, 8033. [Google Scholar] [CrossRef]
- Brandt, A. Noise and Vibration Analysis: Signal Analysis and Experimental Procedures; Wiley: Chichester, UK, 2011. [Google Scholar]
- VDI. Measurement of Structure-Borne Sound of Rolling Element Bearings in Machines and Plants for Evaluation of Condition; VDI Guideline 3832; Verein Deutscher Ingenieure e.V.: Düsseldorf, Germany, 2013. [Google Scholar]
- Randall, R.B.; Antoni, J. Rolling element bearing diagnostics—A tutorial. Mech. Syst. Signal Process. 2011, 25, 485–520. [Google Scholar] [CrossRef]
- Caesarendra, W.; Tjahjowidodo, T. A Review of Feature Extraction Methods in Vibration-Based Condition Monitoring and Its Application for Degradation Trend Estimation of Low-Speed Slew Bearing. Machines 2017, 5, 21. [Google Scholar] [CrossRef]
- Daubechies, I. Ten Lectures on Wavelets; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1992. [Google Scholar] [CrossRef]
- Patil, A.B.; Gaikwad, J.A.; Kulkarni, J.V. Bearing fault diagnosis using discrete Wavelet Transform and Artificial Neural Network. In Proceedings of the 2016 2nd International Conference on Applied and Theoretical Computing and Communication Technology (iCATccT), Bengaluru, India, 21–23 July 2016; IEEE: Piscataway Township, NJ, USA, 2016; pp. 399–405. [Google Scholar] [CrossRef]
- Prabhakar, S.; Mohanty, A.; Sekhar, A. Application of discrete wavelet transform for detection of ball bearing race faults. Tribol. Int. 2002, 35, 793–800. [Google Scholar] [CrossRef]
- Bienefeld, C.; Vogt, A.; Kacmar, M.; Kirchner, E. Feature-Engineering für die Zustandsüberwachung von Wälzlagern mittels maschinellen Lernens. Tribol. Schmier. 2021, 68, 5–11. [Google Scholar] [CrossRef]
- Bienefeld, C.; Kirchner, E.; Vogt, A.; Kacmar, M. On the Importance of Temporal Information for Remaining Useful Life Prediction of Rolling Bearings Using a Random Forest Regressor. Lubricants 2022, 10, 67. [Google Scholar] [CrossRef]
- Magar, R.; Ghule, L.; Li, J.; Zhao, Y.; Farimani, A.B. FaultNet: A Deep Convolutional Neural Network for Bearing Fault Classification. IEEE Access 2021, 9, 25189–25199. [Google Scholar] [CrossRef]
- Grinsztajn, L.; Oyallon, E.; Varoquaux, G. Why do tree-based models still outperform deep learning on typical tabular data? In Proceedings of the 36th Conference on Neural Information Processing Systems, NeurIPS 2022 Datasets and Benchmarks, New Orleans, LA, USA, 28 November–9 December 2022. [Google Scholar]
- Fernandez-Delgado, M.; Cernadas, E.; Barro, S.; Amorim, D. Do we Need Hundreds of Classifiers to Solve Real World Classification Problems? J. Mach. Learn. Res. 2014, 15, 3133–3181. [Google Scholar]
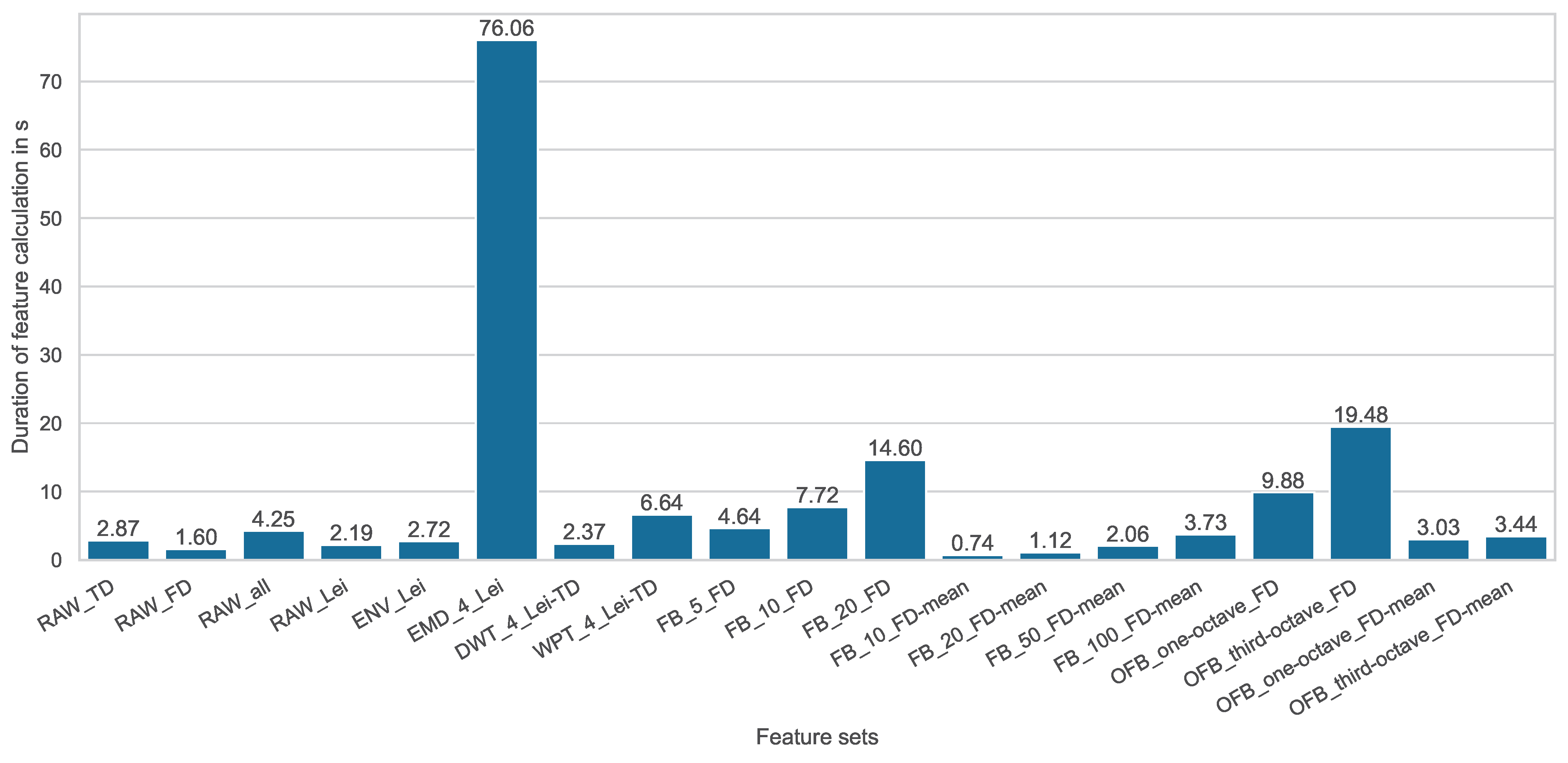
| Feature | Formula | |
|---|---|---|
| Mean | [11] | |
| Standard deviation | [11] | |
| Square root mean (SRM) | [11] | |
| Root mean square (RMS) | [11] | |
| Maximum absolute | [11] | |
| Skewness | [11] | |
| Kurtosis | [11] | |
| Crest factor | [11] | |
| Clearance indicator | [11] | |
| Shape indicator | [11] | |
| Impulse indicator | [11] | |
| Skewness factor | [13] | |
| Kurtosis factor | [13] | |
| Mean absolute | [14] | |
| Variance | [14] | |
| Peak | [14] | |
| K factor | [14] | |
| Energy | [15] | |
| Mean absolute deviation | [16] | |
| Median | [16] | |
| Median absolute deviation | [16] | |
| Rate of zero crossings | [16] | |
| Product RMS kurtosis | [17] | |
| Fifth moment | [18] | |
| Sixth moment | [18] | |
| RMS shape factor | [18] | |
| SRM shape factor | [18] | |
| Latitude factor | [18] |
| Feature | Formula | |
|---|---|---|
| Mean | [11] | |
| Variance | [11] | |
| Third moment | [11] | |
| Fourth moment | [11] | |
| Grand mean | [11] | |
| Standard deviation 1 | [11] | |
| C Factor | [11] | |
| D Factor | [11] | |
| E Factor | [11] | |
| G Factor | [11] | |
| Third moment 1 | [11] | |
| Fourth moment 1 | [11] | |
| H Factor | [11] | |
| J Factor | [12] |
| Feature Set Name | Processing Method | Settings of the Processing Method | Feature Formulas | Complete Feature Count |
|---|---|---|---|---|
| RAW_TD | Raw signal | - | 28 time-domain features: to | 28 |
| RAW_FD | Raw signal | - | 14 frequency-domain features: to | 14 |
| RAW_all | Raw signal | - | All 42 features: to and to | 42 |
| RAW_Lei | Raw signal | - | 25 features according to Lei et al.: to and to | 25 |
| ENV_Lei | Envelope analysis | - | 25 features according to Lei et al.: to and to | 25 |
| EMD_4_Lei | Empirical mode decomposition | Number of extracted IMFs: 4 | 25 features according to Lei et al.: to and to | 125 |
| DWT_4_Lei-TD | Discrete wavelet transform | Decomposition level: 4 Wavelet: Daubechies 13 | 11 time-domain features according to Lei et al.: to | 55 |
| WPT_4_Lei-TD | Wavelet Packet Transform | Decomposition level: 4 Wavelet: Daubechies 13 | 11 time-domain features according to Lei et al.: to | 176 |
| FB_5_FD | Equally sized frequency bands | Number of frequency bands: 5 | 14 frequency -domain features: to | 70 |
| FB_10_FD | Equally sized frequency bands | Number of frequency bands: 10 | 14 frequency -domain features: to | 140 |
| FB_20_FD | Equally sized frequency bands | Number of frequency bands: 20 | 14 frequency domain features: to | 280 |
| FB_10_FD-mean | Equally sized frequency bands | Number of frequency bands: 10 | 1 feature: Mean value in frequency domain: | 10 |
| FB_20_FD-mean | Equally sized frequency bands | Number of frequency bands: 20 | 1 feature: Mean value in frequency domain: | 20 |
| FB_50_FD-mean | Equally sized frequency bands | Number of frequency bands: 50 | 1 feature: Mean value in frequency domain: | 50 |
| FB_100_FD-mean | Equally sized frequency bands | Number of frequency bands: 100 | 1 feature: Mean value in frequency domain: | 100 |
| OFB_one-octave_FD | Octave based frequency bands | Frequency band size: One octave | 14 frequency-domain features: to | 140 |
| OFB_third-octave_FD | Octave based frequency bands | Frequency band size: Third octave | 14 frequency-domain features: to | 336 |
| OFB_one-octave_FD-mean | Octave-based frequency bands | Frequency band size: One octave | 1 feature: Mean value in frequency domain: | 10 |
| OFB_third-octave_FD-mean | Octave-based frequency bands | Frequency band size: Third octave | 1 feature: Mean value in frequency domain: | 24 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bienefeld, C.; Becker-Dombrowsky, F.M.; Shatri, E.; Kirchner, E. Investigation of Feature Engineering Methods for Domain-Knowledge-Assisted Bearing Fault Diagnosis. Entropy 2023, 25, 1278. https://doi.org/10.3390/e25091278
Bienefeld C, Becker-Dombrowsky FM, Shatri E, Kirchner E. Investigation of Feature Engineering Methods for Domain-Knowledge-Assisted Bearing Fault Diagnosis. Entropy. 2023; 25(9):1278. https://doi.org/10.3390/e25091278
Chicago/Turabian StyleBienefeld, Christoph, Florian Michael Becker-Dombrowsky, Etnik Shatri, and Eckhard Kirchner. 2023. "Investigation of Feature Engineering Methods for Domain-Knowledge-Assisted Bearing Fault Diagnosis" Entropy 25, no. 9: 1278. https://doi.org/10.3390/e25091278
APA StyleBienefeld, C., Becker-Dombrowsky, F. M., Shatri, E., & Kirchner, E. (2023). Investigation of Feature Engineering Methods for Domain-Knowledge-Assisted Bearing Fault Diagnosis. Entropy, 25(9), 1278. https://doi.org/10.3390/e25091278






