Exact and Soft Successive Refinement of the Information Bottleneck
Abstract
:1. Introduction
1.1. Conceptualisation and Organisation Outline
1.2. Related Work
1.3. Technical Preliminaries
1.3.1. Notations and Conventions
1.3.2. General Facts and Notions
- A bottleneck must saturate the information constraint, i.e., solutions T to (1) must satisfy . In other words, the primal trade-off parameter is the complexity cost of the corresponding bottleneck.
- The function is constant for . We will thus always assume, without loss of generality, that .
- In the discrete case, choosing a bottleneck cardinality is enough to obtain optimal solutions. Thus, we always assume, without loss of generality, that , where might occur if needed to make T full support.
2. Exact Successive Refinement of the IB
2.1. Formal Framework and First Results
- is a bottleneck with parameter ;
- For every , the variable is a bottleneck with parameter .
- (i)
- There is successive refinement for parameters ;
- (ii)
- There exist bottlenecks , of common source X and relevancy Y, with respective parameters , and an extension of the , such that, under q, we have the Markov chain
- (iii)
- There exist bottlenecks , of common source X and relevancy Y, with respective parameters , and an extension of the , such that, under q, we have the Markov chain
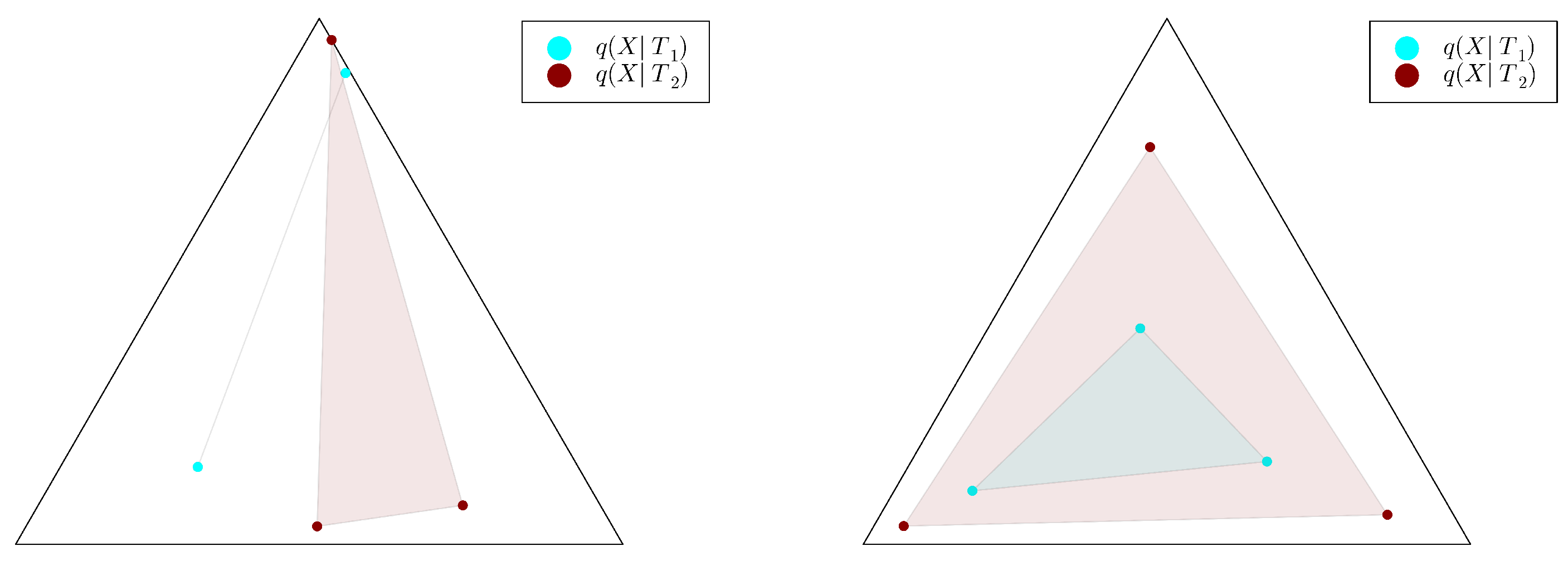
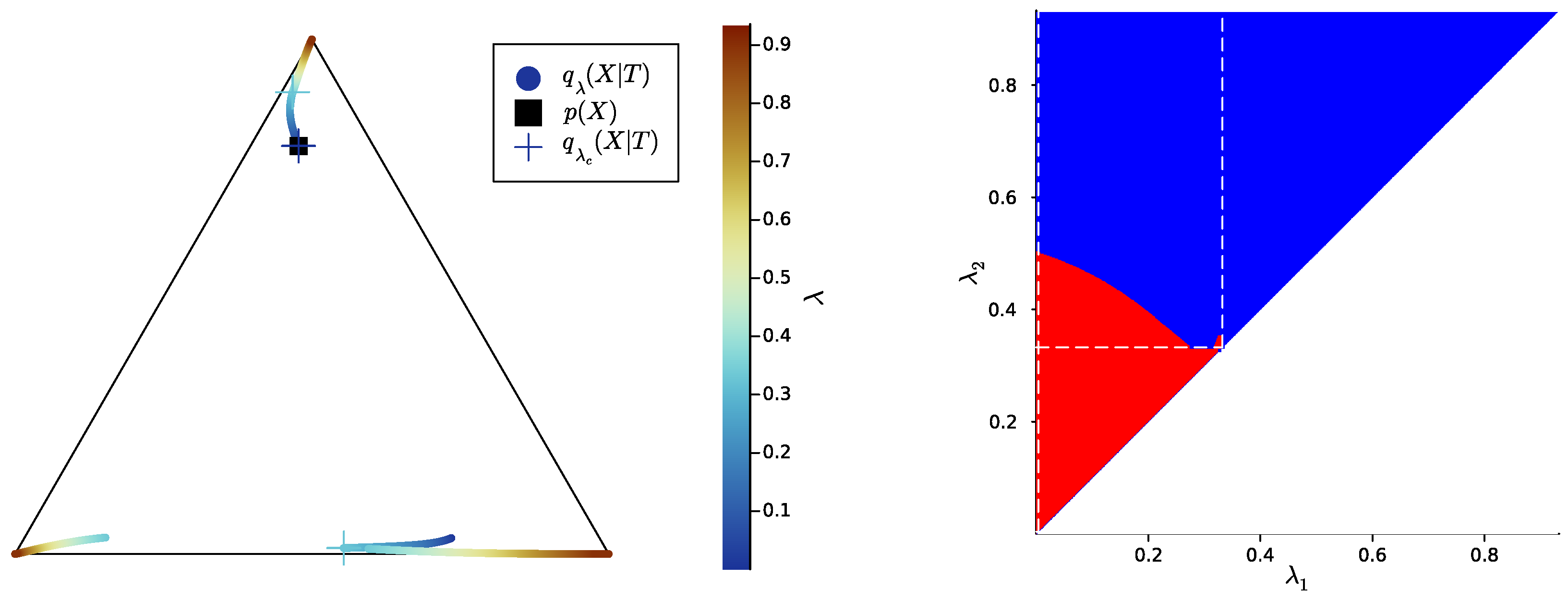
2.2. The Convex Hull Characterisation and the Case
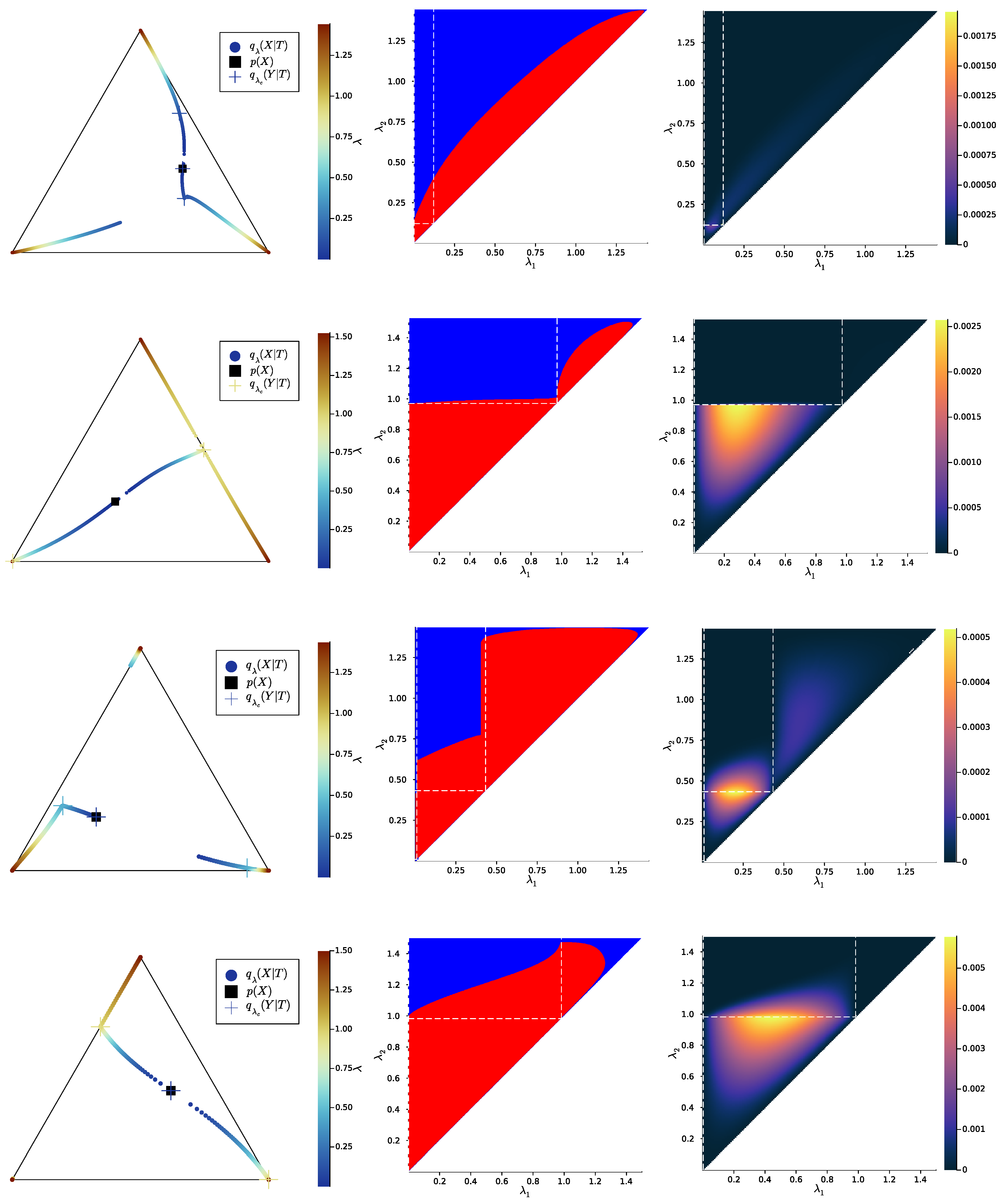
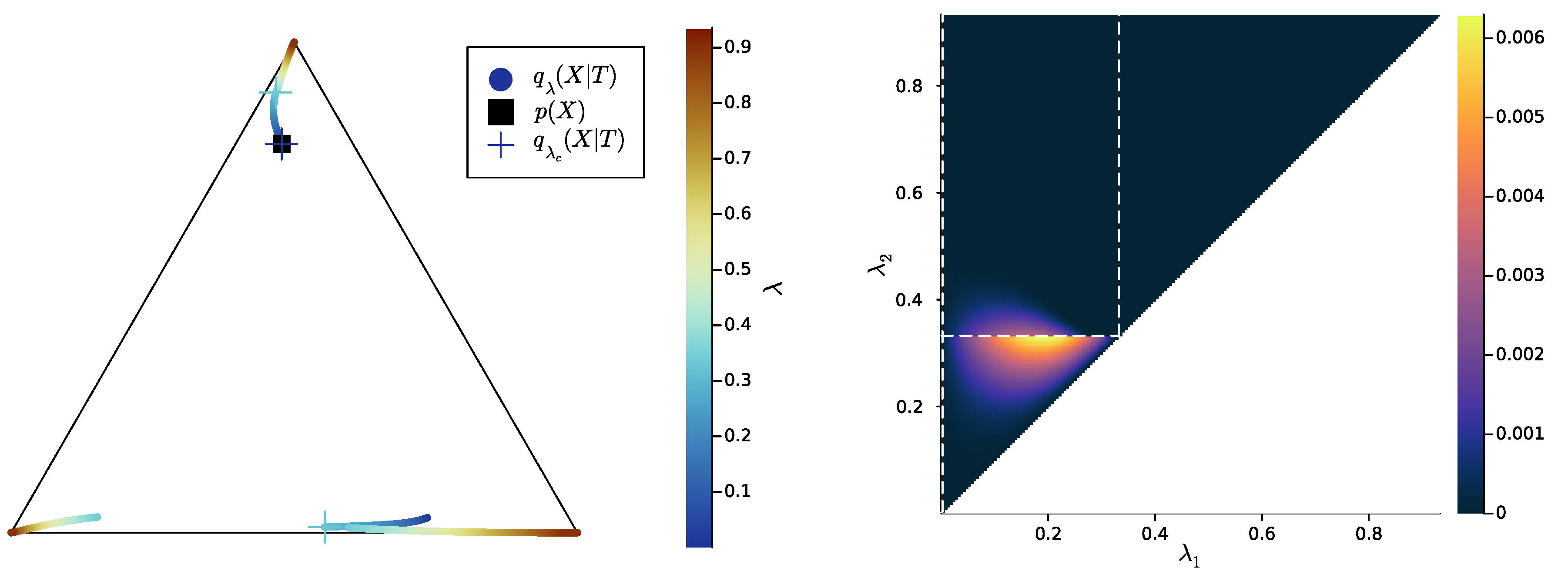
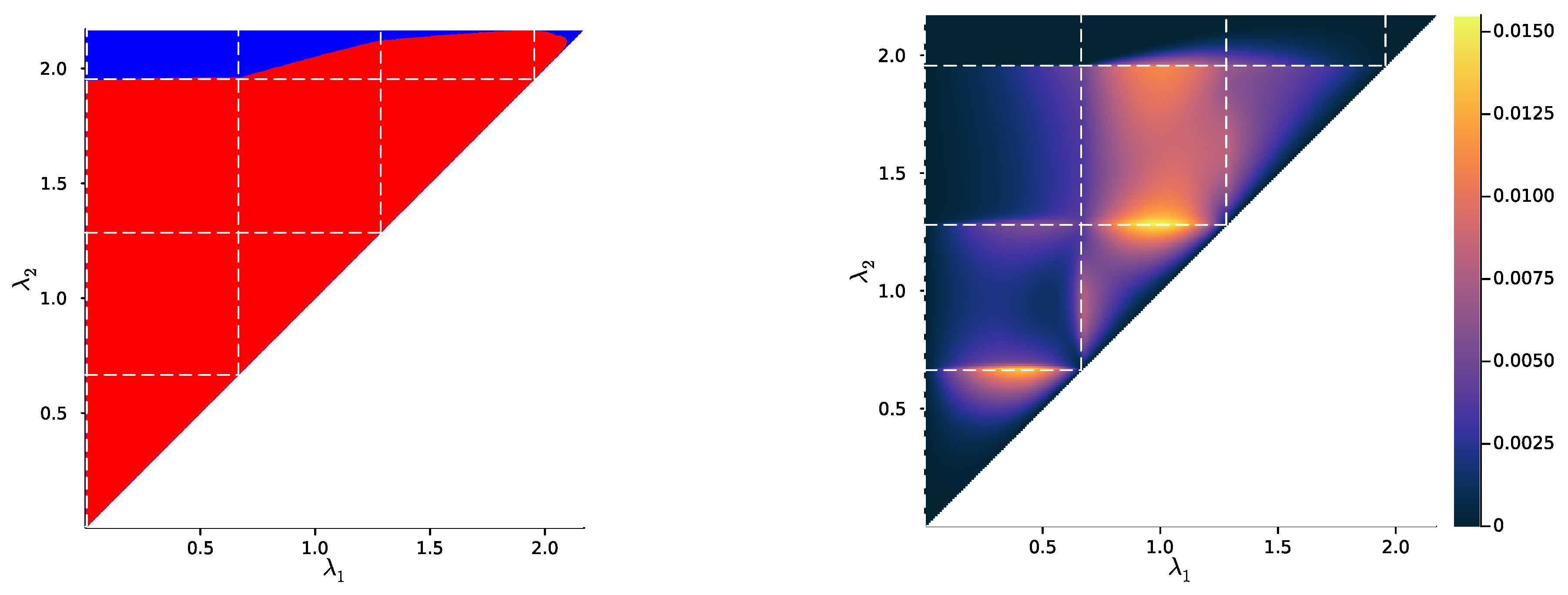
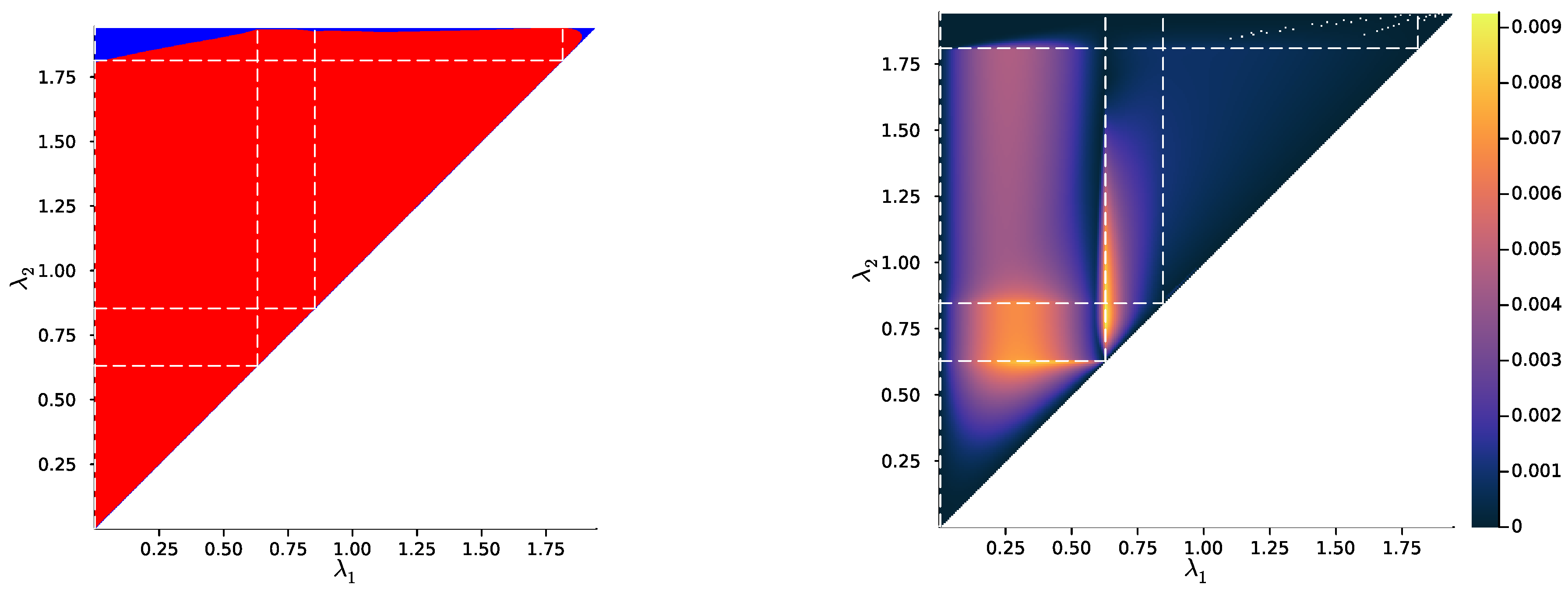
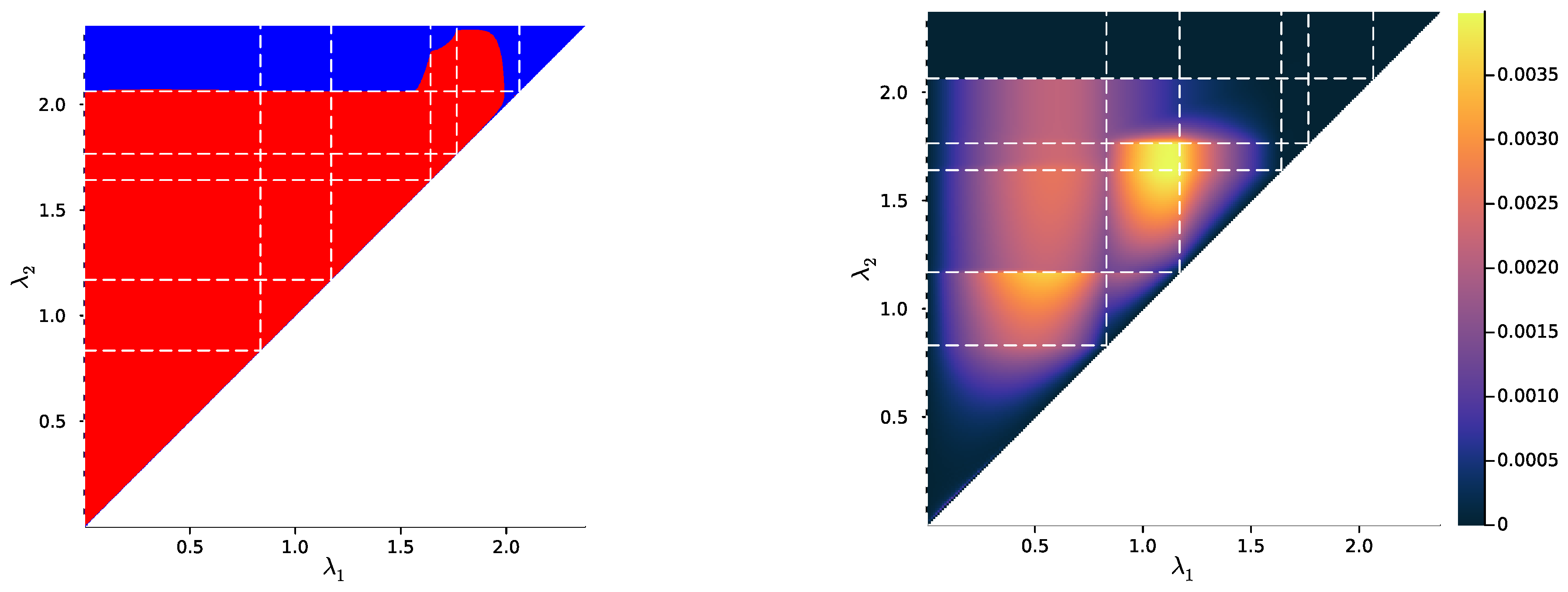
2.3. Numerical Results on Minimal Examples
3. Soft Successive Refinement of the IB
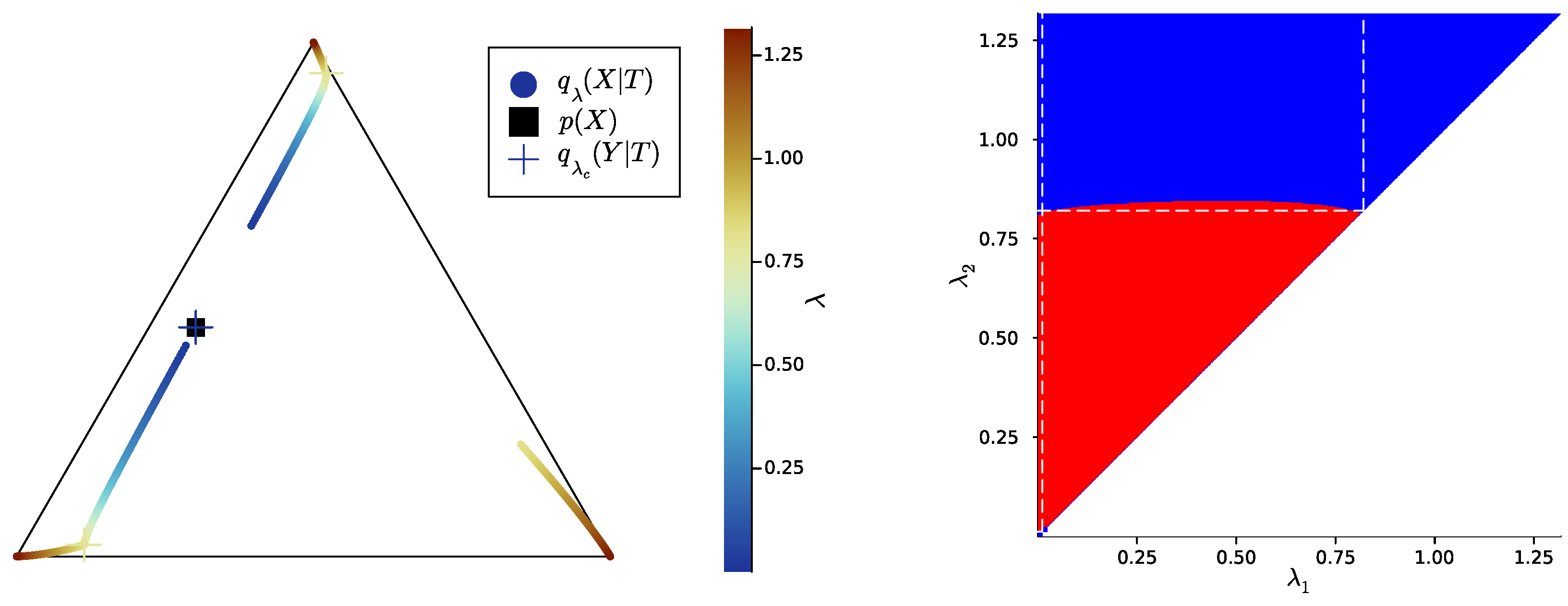
3.1. Formalism
3.2. Numerical Results on Minimal Examples
4. Alternative Interpretations: Decision Problems and Deep Learning
4.1. Successive Refinement, Decision Problems, and Orders on Encoder Channels
- (i)
- There is successive refinement for parameters .
- (ii)
- There are bottlenecks of respective parameters such that
- (iii)
- There are bottlenecks of respective parameters such that
4.2. Successive Refinement and Deep Learning
- (i)
- Satisfy the Markov chain (10); and
- (ii)
- Are each bottlenecks with source X and relevancy Y, for respective trade-off parameters .
- We know that the variables must satisfy , i.e., we know that the joint distribution must be in ;
- And we want to know “how close” we can choose this joint distribution q to one whose marginals coincide with bottleneck distributions , respectively, of parameters , respectively, i.e., we want to know how close we can choose q to the set .
5. Limitations and Future Work
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| IB | Information Bottleneck |
| SR | Successive Refinement |
| UI | Unique Information |
| DNN | Deep Neural Network |
Appendix A. Section 1 Details
Appendix A.1. Effective Cardinality
Appendix B. Section 2 Details
Appendix B.1. Proof of Proposition 1
Appendix B.2. Operational Interpretation of Successive Refinement
- We have the Markov chain ;
- The variables are each bottlenecks with respective parameters .
- We have the Markov chain ; and
- We have, for all ,
Appendix B.3. Proof of Proposition 2
- (i)
- There is successive refinement for Lagrangian parameters .
- (ii)
- There exist Lagrangian bottlenecks , of common source X and relevancy Y, with respective parameters , and an extension of the , such that, under q, we have the Markov chain
Appendix B.4. Proof of Proposition 3
Appendix B.5. Proof of Proposition 4
- (i)
- There exists an extension of and under which the Markov chain holds.
- (ii)
- For each , there exists a family of convex combination coefficients such that
Appendix B.6. Linear Program Used to Compute the Convex Hull Condition (7)
Appendix B.7. Proof of Proposition 5
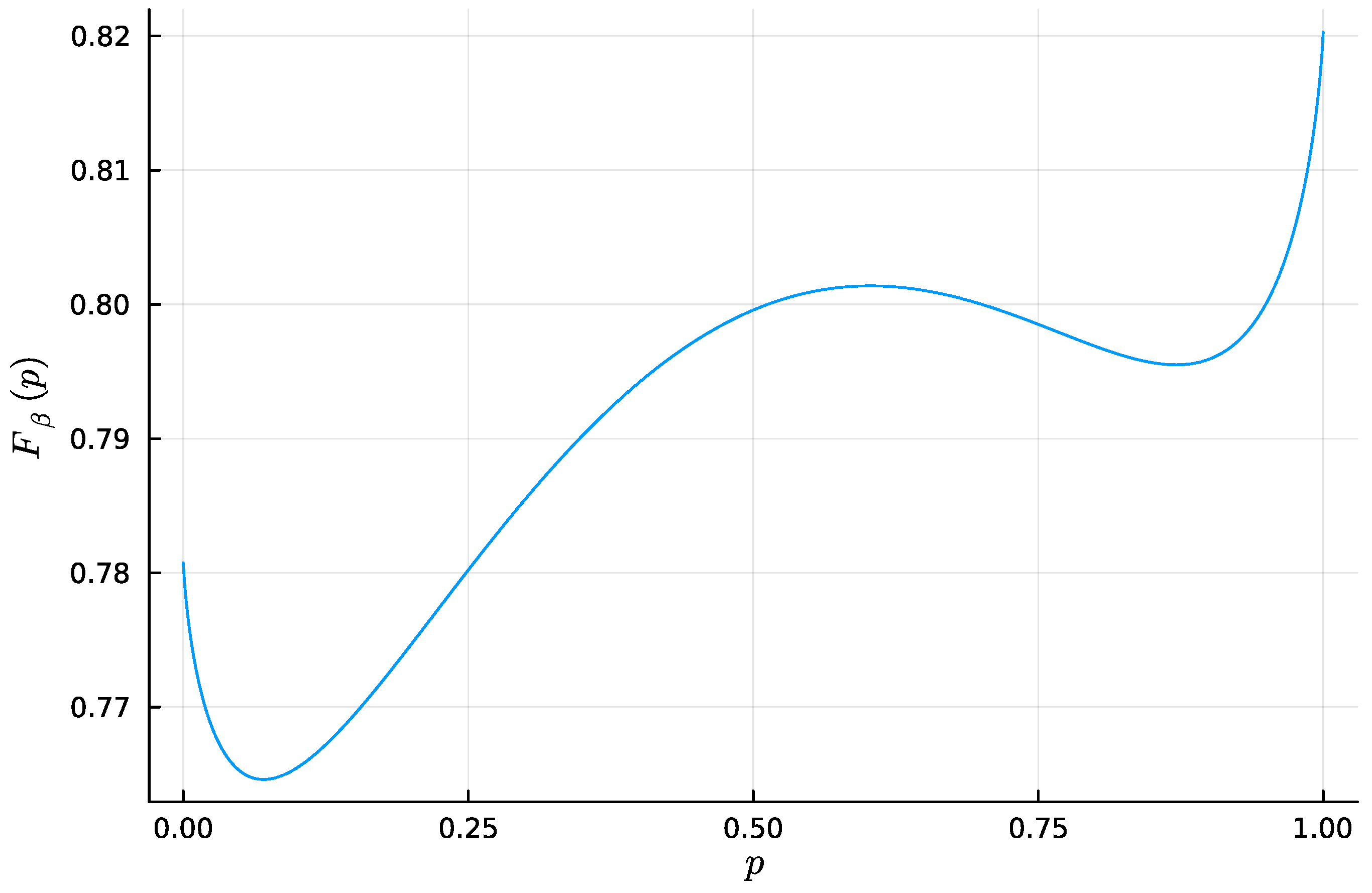
Appendix B.8. Computation of Bifurcations Values
Appendix C. Section 3 Details
Appendix C.1. Proof of Proposition 6
Appendix D. The Unicity and Injectivity Conjecture, and Technical Subtleties It Would Solve
- (i)
- The pair is, up to permuting bottleneck symbols, uniquely determined.
- (ii)
- The channel , seen as a linear operator on probability distributions, is injective.
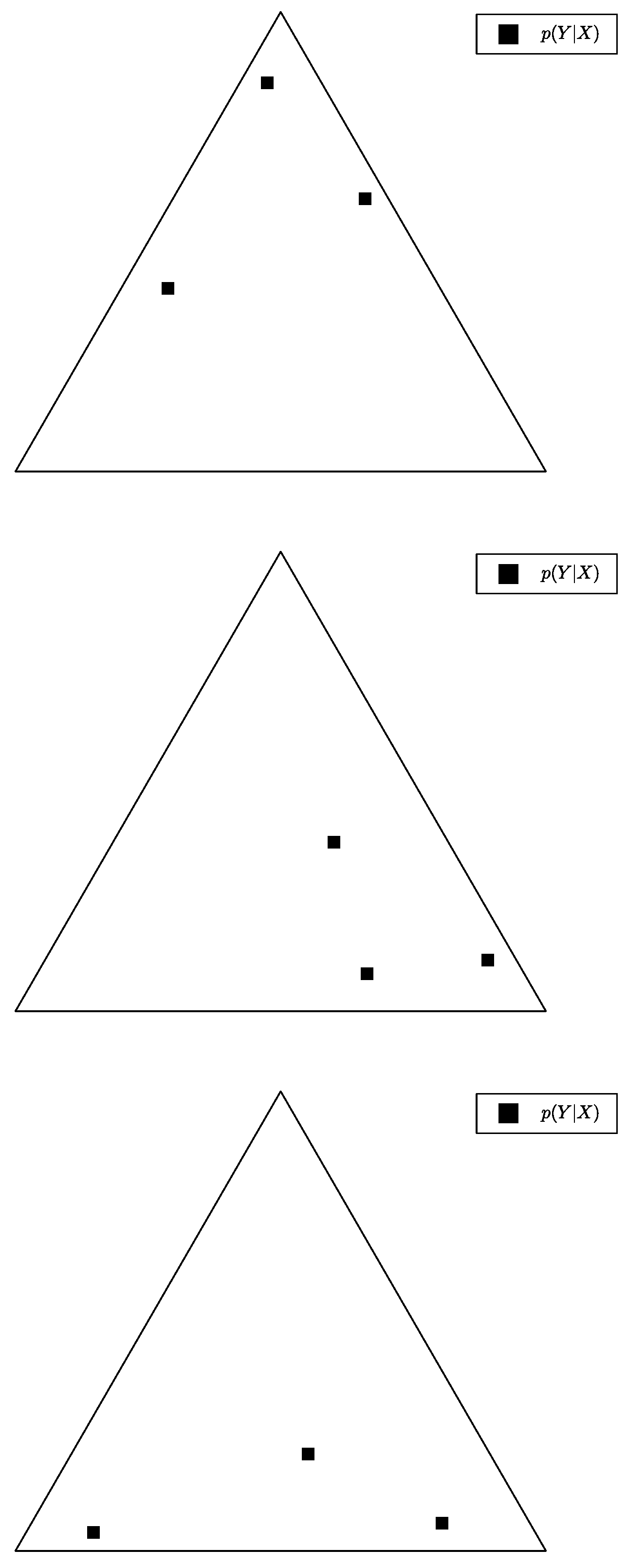
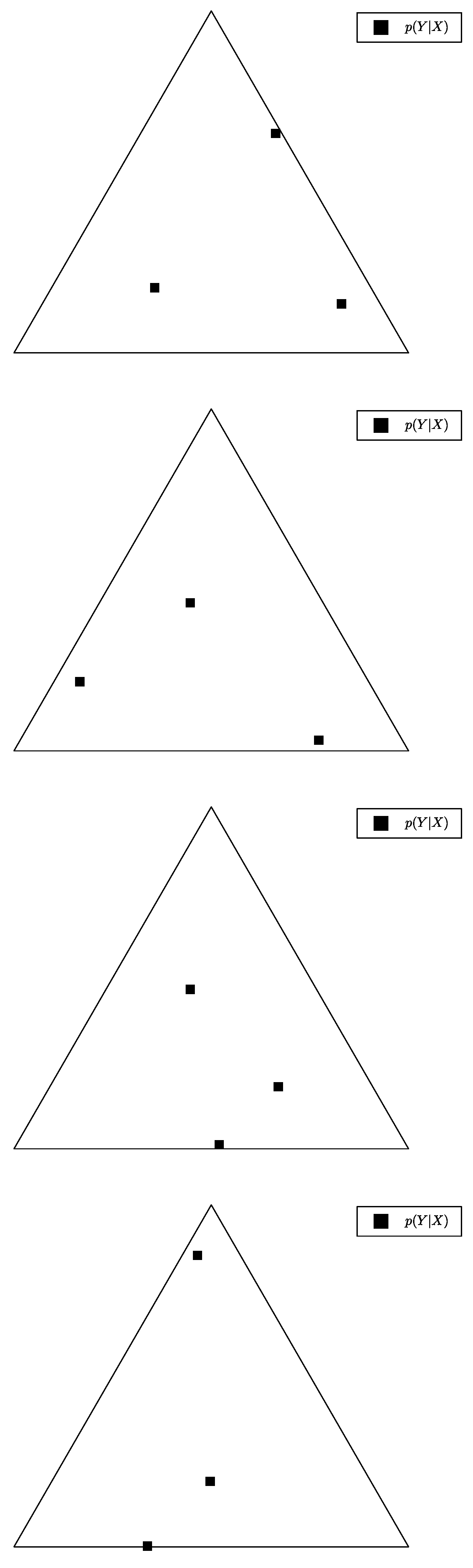
Appendix E. Sample Used in Section 2.3 and Section 3.2
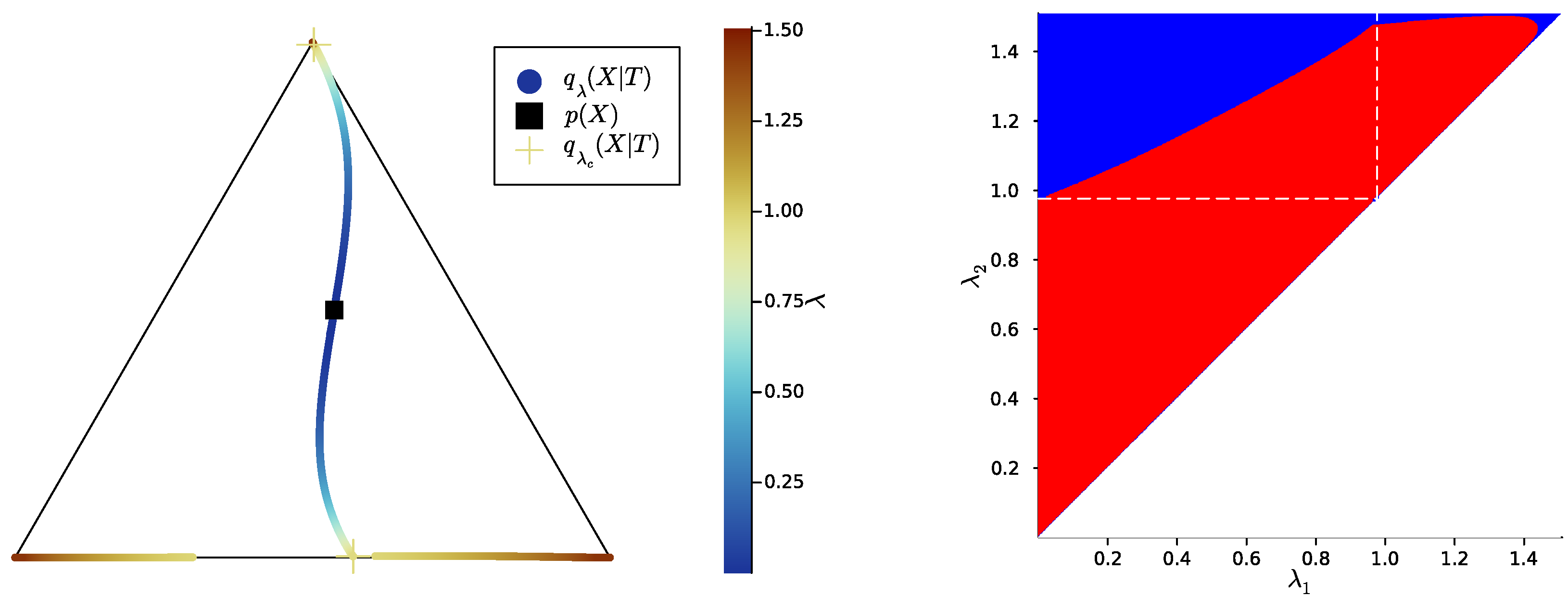
Appendix F. Additional Plots for Exact and Soft Successive Refinement
References
- Tishby, N.; Pereira, F.; Bialek, W. The Information Bottleneck Method. In Proceedings of the 37th Allerton Conference on Communication, Control and Computation, Monticello, IL, USA, 22–24 September 1999; Volume 49. [Google Scholar]
- Gilad-Bachrach, R.; Navot, A.; Tishby, N. An Information Theoretic Tradeoff between Complexity and Accuracy. In Learning Theory and Kernel Machines; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar] [CrossRef]
- Bialek, W.; De Ruyter Van Steveninck, R.R.; Tishby, N. Efficient representation as a design principle for neural coding and computation. In Proceedings of the 2006 IEEE International Symposium on Information Theory, Seattle, WA, USA, 9–14 July 2006; pp. 659–663. [Google Scholar] [CrossRef]
- Creutzig, F.; Globerson, A.; Tishby, N. Past-future information bottleneck in dynamical systems. Phys. Rev. E 2009, 79, 041925. [Google Scholar] [CrossRef]
- Amir, N.; Tiomkin, S.; Tishby, N. Past-future Information Bottleneck for linear feedback systems. In Proceedings of the 2015 54th IEEE Conference on Decision and Control (CDC), Osaka, Japan, 15–18 December 2015; pp. 5737–5742. [Google Scholar] [CrossRef]
- Sachdeva, V.; Mora, T.; Walczak, A.M.; Palmer, S.E. Optimal prediction with resource constraints using the information bottleneck. PLoS Comput. Biol. 2021, 17, e1008743. [Google Scholar] [CrossRef] [PubMed]
- Klampfl, S.; Legenstein, R.; Maass, W. Spiking Neurons Can Learn to Solve Information Bottleneck Problems and Extract Independent Components. Neural Comput. 2009, 21, 911–959. [Google Scholar] [CrossRef] [PubMed]
- Buesing, L.; Maass, W. A Spiking Neuron as Information Bottleneck. Neural Comput. 2010, 22, 1961–1992. [Google Scholar] [CrossRef]
- Chalk, M.; Marre, O.; Tkačik, G. Toward a unified theory of efficient, predictive, and sparse coding. Proc. Natl. Acad. Sci. USA 2018, 115, 186–191. [Google Scholar] [CrossRef]
- Palmer, S.E.; Marre, O.; Berry, M.J.; Bialek, W. Predictive information in a sensory population. Proc. Natl. Acad. Sci. USA 2015, 112, 6908–6913. [Google Scholar] [CrossRef]
- Wang, S.; Segev, I.; Borst, A.; Palmer, S. Maximally efficient prediction in the early fly visual system may support evasive flight maneuvers. PLoS Comput. Biol. 2021, 17, e1008965. [Google Scholar] [CrossRef] [PubMed]
- Buddha, S.K.; So, K.; Carmena, J.M.; Gastpar, M.C. Function Identification in Neuron Populations via Information Bottleneck. Entropy 2013, 15, 1587–1608. [Google Scholar] [CrossRef]
- Kleinman, M.; Wang, T.; Xiao, D.; Feghhi, E.; Lee, K.; Carr, N.; Li, Y.; Hadidi, N.; Chandrasekaran, C.; Kao, J.C. A cortical information bottleneck during decision-making. bioRxiv 2023. [Google Scholar] [CrossRef]
- Nehaniv, C.L.; Polani, D.; Dautenhahn, K.; te Beokhorst, R.; Cañamero, L. Meaningful Information, Sensor Evolution, and the Temporal Horizon of Embodied Organisms. In Artificial life VIII; ICAL 2003; MIT Press: Cambridge, MA, USA, 2002; pp. 345–349. [Google Scholar]
- Klyubin, A.; Polani, D.; Nehaniv, C. Organization of the information flow in the perception-action loop of evolved agents. In Proceedings of the 2004 NASA/DoD Conference on Evolvable Hardware, Seattle, WA, USA, 24–26 June 2004; pp. 177–180. [Google Scholar] [CrossRef]
- van Dijk, S.G.; Polani, D.; Informational Drives for Sensor Evolution. Vol. ALIFE 2012: The Thirteenth International Conference on the Synthesis and Simulation of Living Systems, ALIFE 2022: The 2022 Conference on Artificial Life. 2012. Available online: https://direct.mit.edu/isal/proceedings-pdf/alife2012/24/333/1901044/978-0-262-31050-5-ch044.pdf (accessed on 12 September 2023). [CrossRef]
- Möller, M.; Polani, D. Emergence of common concepts, symmetries and conformity in agent groups—An information-theoretic model. Interface Focus 2023, 13, 20230006. [Google Scholar] [CrossRef]
- Catenacci Volpi, N.; Polani, D. Space Emerges from What We Know-Spatial Categorisations Induced by Information Constraints. Entropy 2020, 20, 1179. [Google Scholar] [CrossRef]
- Zaslavsky, N.; Kemp, C.; Regier, T.; Tishby, N. Efficient compression in color naming and its evolution. Proc. Natl. Acad. Sci. USA 2018, 115, 201800521. [Google Scholar] [CrossRef]
- Zaslavsky, N.; Garvin, K.; Kemp, C.; Tishby, N.; Regier, T. The evolution of color naming reflects pressure for efficiency: Evidence from the recent past. bioRxiv 2022. [Google Scholar] [CrossRef]
- Tucker, M.; Levy, R.P.; Shah, J.; Zaslavsky, N. Trading off Utility, Informativeness, and Complexity in Emergent Communication. Adv. Neural Inf. Process. Syst. 2022, 35, 22214–22228. [Google Scholar]
- Pacelli, V.; Majumdar, A. Task-Driven Estimation and Control via Information Bottlenecks. arXiv 2018, arXiv:1809.07874. [Google Scholar] [CrossRef]
- Lamb, A.; Islam, R.; Efroni, Y.; Didolkar, A.; Misra, D.; Foster, D.; Molu, L.; Chari, R.; Krishnamurthy, A.; Langford, J. Guaranteed Discovery of Control-Endogenous Latent States with Multi-Step Inverse Models. arXiv 2022, arXiv:2207.08229. [Google Scholar] [CrossRef]
- Goyal, A.; Islam, R.; Strouse, D.; Ahmed, Z.; Larochelle, H.; Botvinick, M.; Levine, S.; Bengio, Y. Transfer and Exploration via the Information Bottleneck. In Proceedings of the International Conference on Learning Representations, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Koshelev, V. Hierarchical Coding of Discrete Sources. Probl. Peredachi Inf. 1980, 16, 31–49. [Google Scholar]
- Equitz, W.; Cover, T. Successive refinement of information. IEEE Trans. Inf. Theory 1991, 37, 269–275. [Google Scholar] [CrossRef]
- Rimoldi, B. Successive refinement of information: Characterization of the achievable rates. IEEE Trans. Inf. Theory 1994, 40, 253–259. [Google Scholar] [CrossRef]
- Tuncel, E.; Rose, K. Computation and analysis of the N-Layer scalable rate-distortion function. IEEE Trans. Inf. Theory 2003, 49, 1218–1230. [Google Scholar] [CrossRef]
- Kostina, V.; Tuncel, E. Successive Refinement of Abstract Sources. IEEE Trans. Inf. Theory 2019, 65, 6385–6398. [Google Scholar] [CrossRef]
- Tian, C.; Chen, J. Successive Refinement for Hypothesis Testing and Lossless One-Helper Problem. IEEE Trans. Inf. Theory 2008, 54, 4666–4681. [Google Scholar] [CrossRef]
- Tuncel, E. Capacity/Storage Tradeoff in High-Dimensional Identification Systems. In Proceedings of the 2006 IEEE International Symposium on Information Theory, Seattle, WA, USA, 9–14 July 2006; pp. 1929–1933. [Google Scholar] [CrossRef]
- Mahvari, M.M.; Kobayashi, M.; Zaidi, A. On the Relevance-Complexity Region of Scalable Information Bottleneck. arXiv 2020, arXiv:2011.01352. [Google Scholar] [CrossRef]
- Kline, A.G.; Palmer, S.E. Gaussian information bottleneck and the non-perturbative renormalization group. New J. Phys. 2022, 24, 033007. [Google Scholar] [CrossRef]
- Kolchinsky, A.; Tracey, B.D.; Van Kuyk, S. Caveats for information bottleneck in deterministic scenarios. arXiv 2018, arXiv:1808.07593. [Google Scholar] [CrossRef]
- Witsenhausen, H.; Wyner, A. A conditional entropy bound for a pair of discrete random variables. IEEE Trans. Inf. Theory 1975, 21, 493–501. [Google Scholar] [CrossRef]
- Hsu, H.; Asoodeh, S.; Salamatian, S.; Calmon, F.P. Generalizing Bottleneck Problems. In Proceedings of the 2018 IEEE International Symposium on Information Theory (ISIT), Vail, CO, USA, 17–22 June 2018; pp. 531–535. [Google Scholar] [CrossRef]
- Asoodeh, S.; Calmon, F. Bottleneck Problems: An Information and Estimation-Theoretic View. Entropy 2020, 22, 1325. [Google Scholar] [CrossRef]
- Dikshtein, M.; Shamai, S. A Class of Nonbinary Symmetric Information Bottleneck Problems. arXiv 2021, arXiv:cs.IT/2110.00985. [Google Scholar]
- Benger, E.; Asoodeh, S.; Chen, J. The Cardinality Bound on the Information Bottleneck Representations is Tight. arXiv 2023, arXiv:cs.IT/2305.07000. [Google Scholar]
- Bertschinger, N.; Rauh, J.; Olbrich, E.; Ay, N. Quantifying Unique Information. Entropy 2013, 16, 2161–2183. [Google Scholar] [CrossRef]
- Parker, A.E.; Gedeon, T.; Dimitrov, A. The Lack of Convexity of the Relevance-Compression Function. arXiv 2022, arXiv:2204.10957. [Google Scholar] [CrossRef]
- Wu, T.; Fischer, I. Phase Transitions for the Information Bottleneck in Representation Learning. arXiv 2020, arXiv:2001.01878. [Google Scholar]
- Zaslavsky, N.; Tishby, N. Deterministic Annealing and the Evolution of Information Bottleneck Representations. 2019. Available online: https://www.nogsky.com/publication/2019-evo-ib/2019-evo-IB.pdf (accessed on 12 September 2023).
- Ngampruetikorn, V.; Schwab, D.J. Perturbation Theory for the Information Bottleneck. Adv. Neural Inf. Process. Syst. 2021, 34, 21008–21018. [Google Scholar]
- Bertschinger, N.; Rauh, J. The Blackwell relation defines no lattice. In Proceedings of the 2014 IEEE International Symposium on Information Theory, Honolulu, HI, USA, 29 June–4 July 2014; pp. 2479–2483. [Google Scholar] [CrossRef]
- Yang, Q.; Piantanida, P.; Gündüz, D. The Multi-layer Information Bottleneck Problem. arXiv 2017, arXiv:1711.05102. [Google Scholar] [CrossRef]
- Cover, T.; Thomas, J. Elements of Information Theory; Wiley-Interscience: Hoboken, NJ, USA, 2006. [Google Scholar]
- Zaidi, A.; Estella-Aguerri, I.; Shamai (Shitz), S. On the Information Bottleneck Problems: Models, Connections, Applications and Information Theoretic Views. Entropy 2020, 22, 151. [Google Scholar] [CrossRef] [PubMed]
- Tishby, N.; Zaslavsky, N. Deep Learning and the Information Bottleneck Principle. In Proceedings of the 2015 IEEE Information Theory Workshop, ITW 2015, Jerusalem, Israel, 26 April–1 May 2015. [Google Scholar] [CrossRef]
- Shwartz-Ziv, R.; Tishby, N. Opening the Black Box of Deep Neural Networks via Information. 2017. Available online: http://xxx.lanl.gov/abs/1703.00810 (accessed on 12 September 2023).
- Shwartz-Ziv, R.; Painsky, A.; Tishby, N. Representation Compression and Generalization in Deep Neural Networks. 2019. Available online: https://openreview.net/pdf?id=SkeL6sCqK7 (accessed on 12 September 2023).
- Saxe, A.M.; Bansal, Y.; Dapello, J.; Advani, M.; Kolchinsky, A.; Tracey, B.D.; Cox, D.D. On the information bottleneck theory of deep learning. J. Stat. Mech. Theory Exp. 2019, 2019, 124020. [Google Scholar] [CrossRef]
- Achille, A.; Soatto, S. Emergence of Invariance and Disentanglement in Deep Representations. In Proceedings of the 2018 Information Theory and Applications Workshop (ITA), San Diego, CA, USA, 11–16 February 2018; pp. 1–9. [Google Scholar] [CrossRef]
- Elad, A.; Haviv, D.; Blau, Y.; Michaeli, T. Direct Validation of the Information Bottleneck Principle for Deep Nets. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision Workshop (ICCVW), Seoul, Republic of Korea, 27–28 October 2019; pp. 758–762. [Google Scholar] [CrossRef]
- Lorenzen, S.S.; Igel, C.; Nielsen, M. Information Bottleneck: Exact Analysis of (Quantized) Neural Networks. In Proceedings of the International Conference on Learning Representations, Virtual Event, 25–29 April 2022. [Google Scholar]
- Kawaguchi, K.; Deng, Z.; Ji, X.; Huang, J. How Does Information Bottleneck Help Deep Learning? 2023. Available online: https://proceedings.mlr.press/v202/kawaguchi23a/kawaguchi23a.pdf (accessed on 12 September 2023).
- Yousfi, Y.; Akyol, E. Successive Information Bottleneck and Applications in Deep Learning. In Proceedings of the 2020 54th Asilomar Conference on Signals, Systems, and Computers, Pacific Grove, CA, USA, 1–4 November 2020; pp. 1210–1213. [Google Scholar] [CrossRef]
- No, A. Universality of Logarithmic Loss in Successive Refinement. Entropy 2019, 21, 158. [Google Scholar] [CrossRef]
- Nasser, R. On the input-degradedness and input-equivalence between channels. In Proceedings of the 2017 IEEE International Symposium on Information Theory (ISIT), Aachen, Germany, 25–30 June 2017; pp. 2453–2457. [Google Scholar] [CrossRef]
- Lastras, L.; Berger, T. All sources are nearly successively refinable. IEEE Trans. Inf. Theory 2001, 47, 918–926. [Google Scholar] [CrossRef]
- Williams, P.L.; Beer, R.D. Nonnegative Decomposition of Multivariate Information. 2010. Available online: https://arxiv.org/pdf/1004.2515 (accessed on 12 September 2023).
- Bertschinger, N.; Rauh, J.; Olbrich, E.; Jost, J. Shared Information—New Insights and Problems in Decomposing Information in Complex Systems. In Proceedings of the European Conference on Complex Systems, 2012; Springer International Publishing: Berlin/Heidelberg, Germany, 2013; pp. 251–269. [Google Scholar] [CrossRef]
- Griffith, V.; Koch, C. Quantifying Synergistic Mutual Information. In Guided Self-Organization: Inception; Prokopenko, M., Ed.; Springer: Berlin/Heidelberg, Germany, 2014; pp. 159–190. [Google Scholar] [CrossRef]
- Harder, M.; Salge, C.; Polani, D. Bivariate measure of redundant information. Phys. Rev. E 2013, 87, 012130. [Google Scholar] [CrossRef] [PubMed]
- Blackwell, D. Equivalent Comparisons of Experiments. Ann. Math. Stat. 1953, 24, 265–272. [Google Scholar] [CrossRef]
- Lemaréchal, C. Lagrangian Relaxation. In Computational Combinatorial Optimization: Optimal or Provably Near-Optimal Solutions; Jünger, M., Naddef, D., Eds.; Springer: Berlin/Heidelberg, Germany, 2001; pp. 112–156. [Google Scholar] [CrossRef]
- Kolchinsky, A.; Tracey, B.; Wolpert, D. Nonlinear Information Bottleneck. Entropy 2017, 21, 1181. [Google Scholar] [CrossRef]
- Matousek, J.; Gärtner, B. Understanding and Using Linear Programming, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- van den Brand, J. A Deterministic Linear Program Solver in Current Matrix Multiplication Time. In Proceedings of the Thirty-First Annual ACM-SIAM Symposium on Discrete Algorithms; Society for Industrial and Applied Mathematics (SODA’20), Salt Lake City, UT, USA, 5–8 January 2020; pp. 259–278. [Google Scholar]
- Rose, K. Deterministic annealing for clustering, compression, classification, regression, and related optimization problems. Proc. IEEE 1998, 86, 2210–2239. [Google Scholar] [CrossRef]
- Gedeon, T.; Parker, A.E.; Dimitrov, A.G. The Mathematical Structure of Information Bottleneck Methods. Entropy 2012, 14, 456–479. [Google Scholar] [CrossRef]
- Shamir, O.; Sabato, S.; Tishby, N. Learning and generalization with the information bottleneck. Theor. Comput. Sci. 2010, 411, 2696–2711. [Google Scholar] [CrossRef]
- Rauh, J.; Banerjee, P.K.; Olbrich, E.; Jost, J. Unique Information and Secret Key Decompositions. In Proceedings of the 2019 IEEE International Symposium on Information Theory (ISIT), Paris, France, 7–12 July 2019. [Google Scholar] [CrossRef]
- Banerjee, P.; Rauh, J.; Montufar, G. Computing the Unique Information. In Proceedings of the 2018 IEEE International Symposium on Information Theory (ISIT), Vail, CO, USA, 17–22 June 2018; pp. 141–145. [Google Scholar] [CrossRef]
- Chechik, G.; Globerson, A.; Tishby, N.; Weiss, Y. Information bottleneck for Gaussian variables. J. Mach. Learn. Res. 2005, 6, 165–188. [Google Scholar]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction, 2nd ed.; The MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Goldfeld, Z.; Polyanskiy, Y. The Information Bottleneck Problem and its Applications in Machine Learning. IEEE J. Sel. Areas Inf. Theory 2020, 1, 19–38. [Google Scholar] [CrossRef]
- Mahvari, M.M.; Kobayashi, M.; Zaidi, A. Scalable Vector Gaussian Information Bottleneck. In Proceedings of the 2021 IEEE International Symposium on Information Theory (ISIT), Melbourne, Australia, 12–20 July 2021; pp. 37–42. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Charvin, H.; Catenacci Volpi, N.; Polani, D. Exact and Soft Successive Refinement of the Information Bottleneck. Entropy 2023, 25, 1355. https://doi.org/10.3390/e25091355
Charvin H, Catenacci Volpi N, Polani D. Exact and Soft Successive Refinement of the Information Bottleneck. Entropy. 2023; 25(9):1355. https://doi.org/10.3390/e25091355
Chicago/Turabian StyleCharvin, Hippolyte, Nicola Catenacci Volpi, and Daniel Polani. 2023. "Exact and Soft Successive Refinement of the Information Bottleneck" Entropy 25, no. 9: 1355. https://doi.org/10.3390/e25091355
APA StyleCharvin, H., Catenacci Volpi, N., & Polani, D. (2023). Exact and Soft Successive Refinement of the Information Bottleneck. Entropy, 25(9), 1355. https://doi.org/10.3390/e25091355








