Assessing Credibility in Bayesian Networks Structure Learning
Abstract
1. Introduction
- We introduce a new algorithm that utilises MCMC methods to assess learning about BN structures. Our method overcomes the drawbacks of conventional score-based algorithms, which often do not provide insight into the reasons behind selecting a particular structure over others. Instead, our approach offers a more thorough analysis of possible structures by treating the BN’s structure as changeable and treating the presence or absence of each edge as random variables.
- We propose the usage of a bootstrapping method for generating multiple subsets of the data, in order to learn a collection of BNs from distinct data samples, which helps capture various aspects of the underlying relationships and enhances the reliability of the learned model.
- We suggest a Dirichlet-Multinomial model to represent the probability distribution of edge characteristics. This model is based on the observed counts in the learned BNs, providing a robust and flexible framework for quantifying the uncertainty associated with each edge.
- We demonstrate the effectiveness of our approach on both synthetic and real-life datasets. By comparing the structure of the learned BNs with previously known structures and evaluating the inference capabilities of the final BN, we show that our method achieves competitive results while providing valuable information on the model’s credibility.
2. Brief Overview on Bayesian Networks
2.1. Mathematical Framework
2.2. Learning a Bayesian Network from Data
2.3. Bayesian Network Uncertainty Metrics
3. Materials and Methods
- Resample in smaller subsets with independent and identically distributed samples;
- Learn a set of Bayesian networks using the data for each of the data subsets;
- Use MCMC to approximate a multinomial distribution for each pair of variables , with the count of occurrence of the edges or in B.
Proposed Approach
| Algorithm 1: Generating a set B containing k Bayesian networks from a dataset , which are learned from n samples each. In a stationary and complete dataset, using an ideal scoring method, all networks would be identical. However, real-world data often deviate from this ideal. This algorithm captures small statistical differences within the dataset that may be missed when evaluating it as a whole. |
 |
- State 1, a left-direction edge:
- State 2, no edge:
- State 3, a right-direction edge:
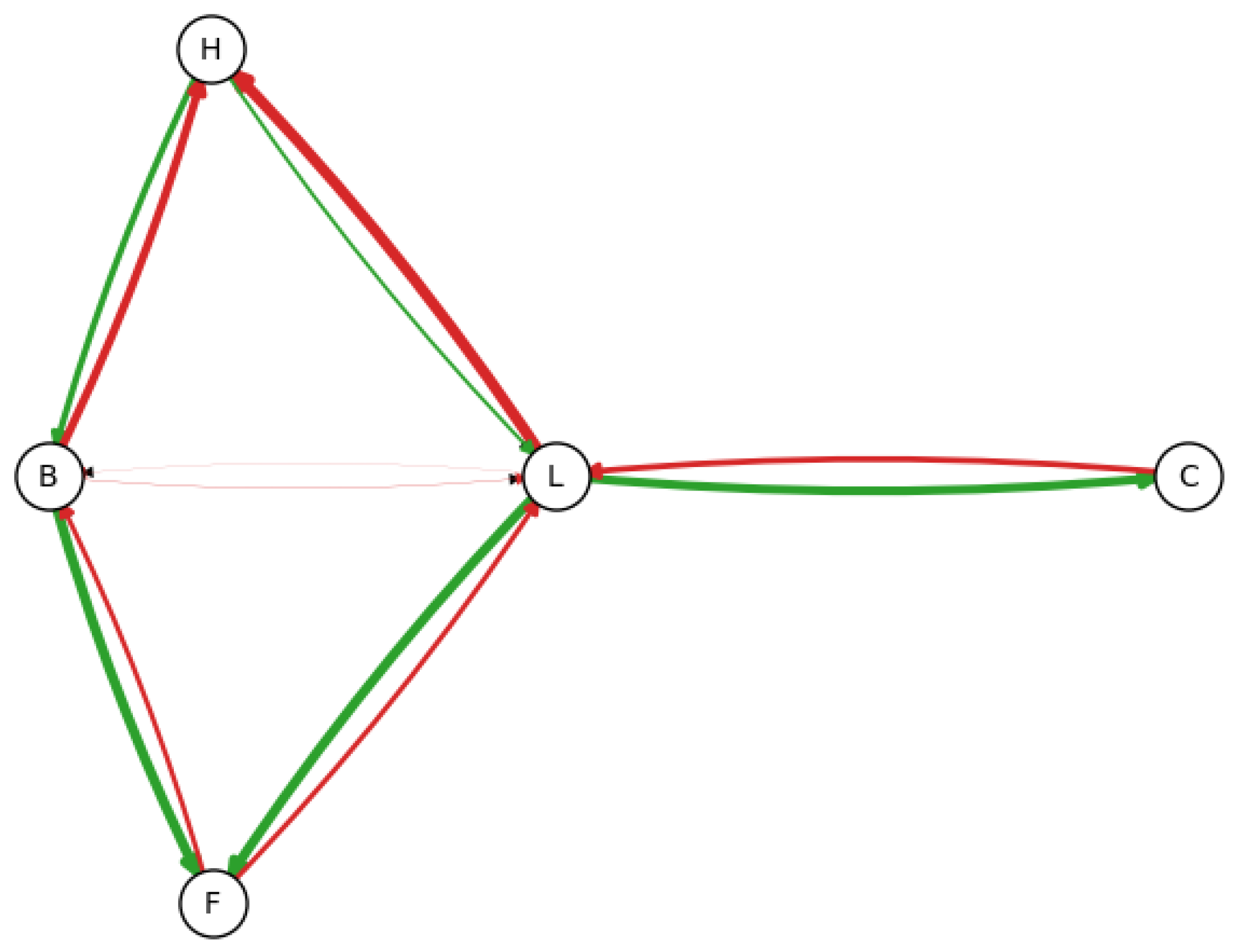
| Algorithm 2: Counting the frequency of each edge appearance in B (). This result can later be used as a source in a count data model, so the frequency of each edge is independently analyzed. |
 |
| Algorithm 3: Sampling the distribution of each edge appearance. In this example, a 3-event Dirichlet-Multinomial model is built from an uninformative prior using MCMC. |
 |
4. Results and Discussion
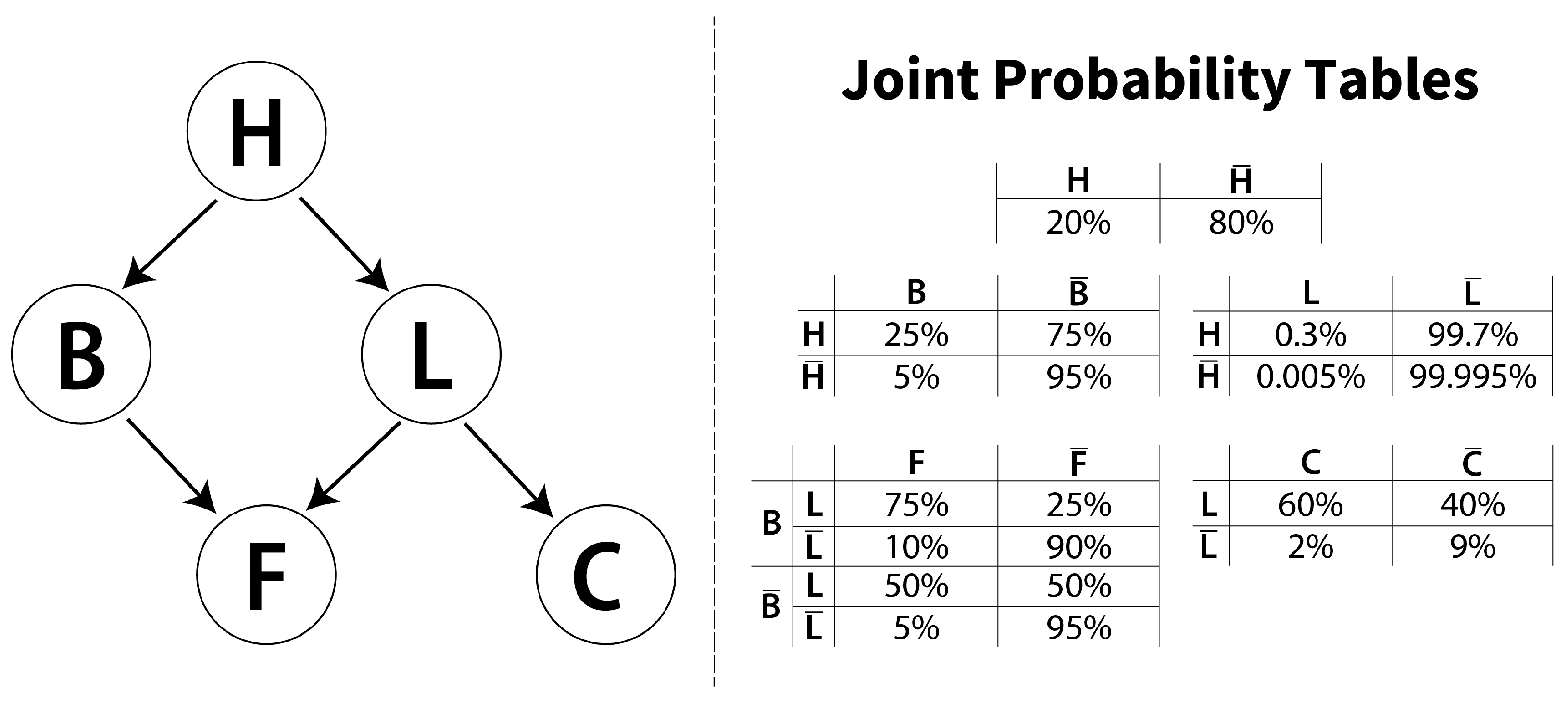
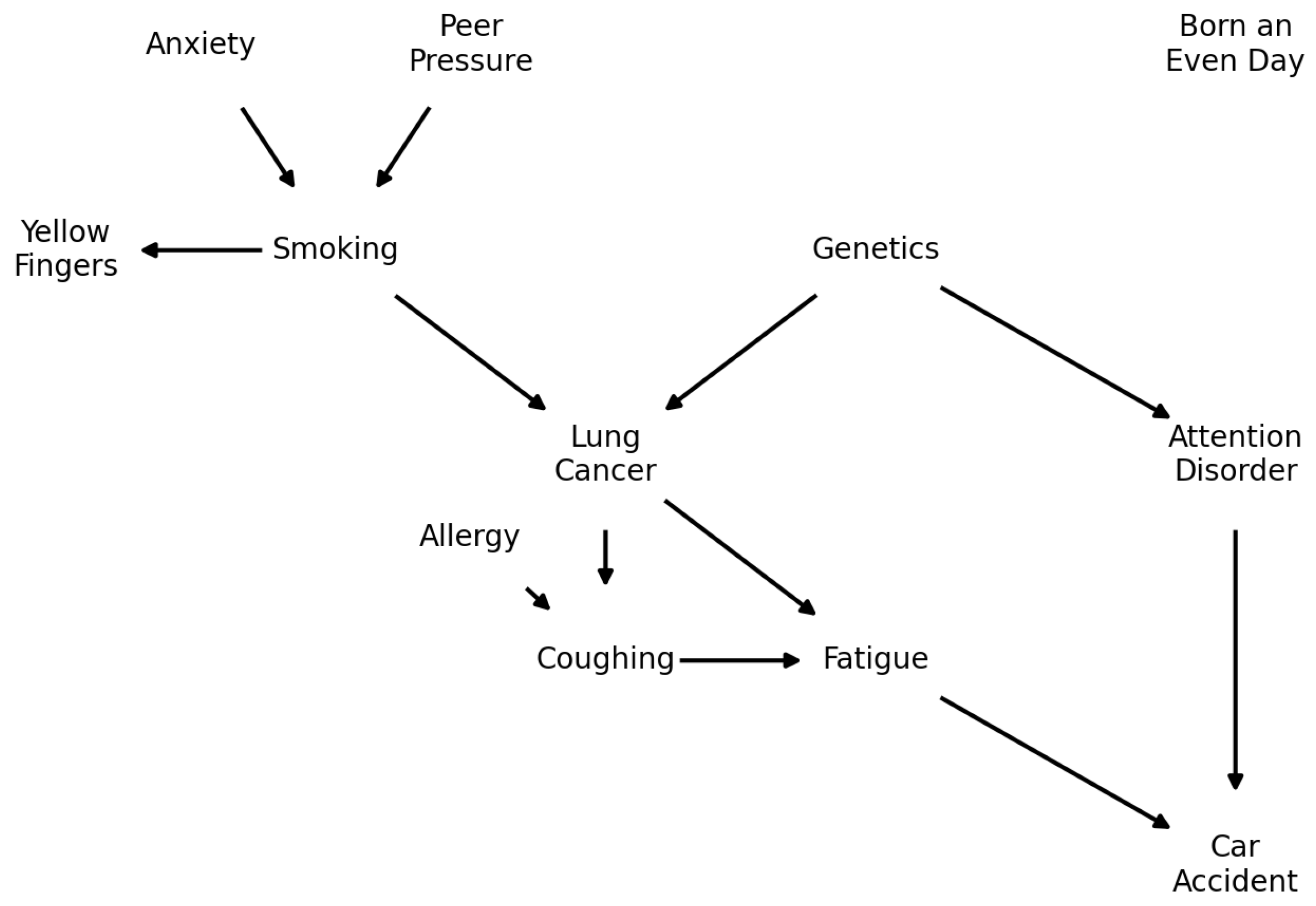
- Experiment 1: Sample size. A synthetic dataset with 5 variables was utilized. The significant variability of probabilistic dependencies (0.005% being the rarest) theoretically requires 187,500 samples to achieve 95% confidence that the rarest event (, 1 in 62,500 events) will happen at least once.
- Experiment 2: Network complexity. A well-documented synthetic dataset with 12 variables and 12 edges was utilized, which makes possible to verify the behavior of the proposed method in DAG spaces that cannot be fully explored in reasonable time.
- Experiment 3: Real-world case. The proposed methodology was applied to electromyography (EMG) data during gait of 70 individuals, with and without patellofemoral pain syndrome (PFP). The cause of PFP is unknown, but indications of changes in EMG are known to exist.
4.1. Experiment 1: Sample Size
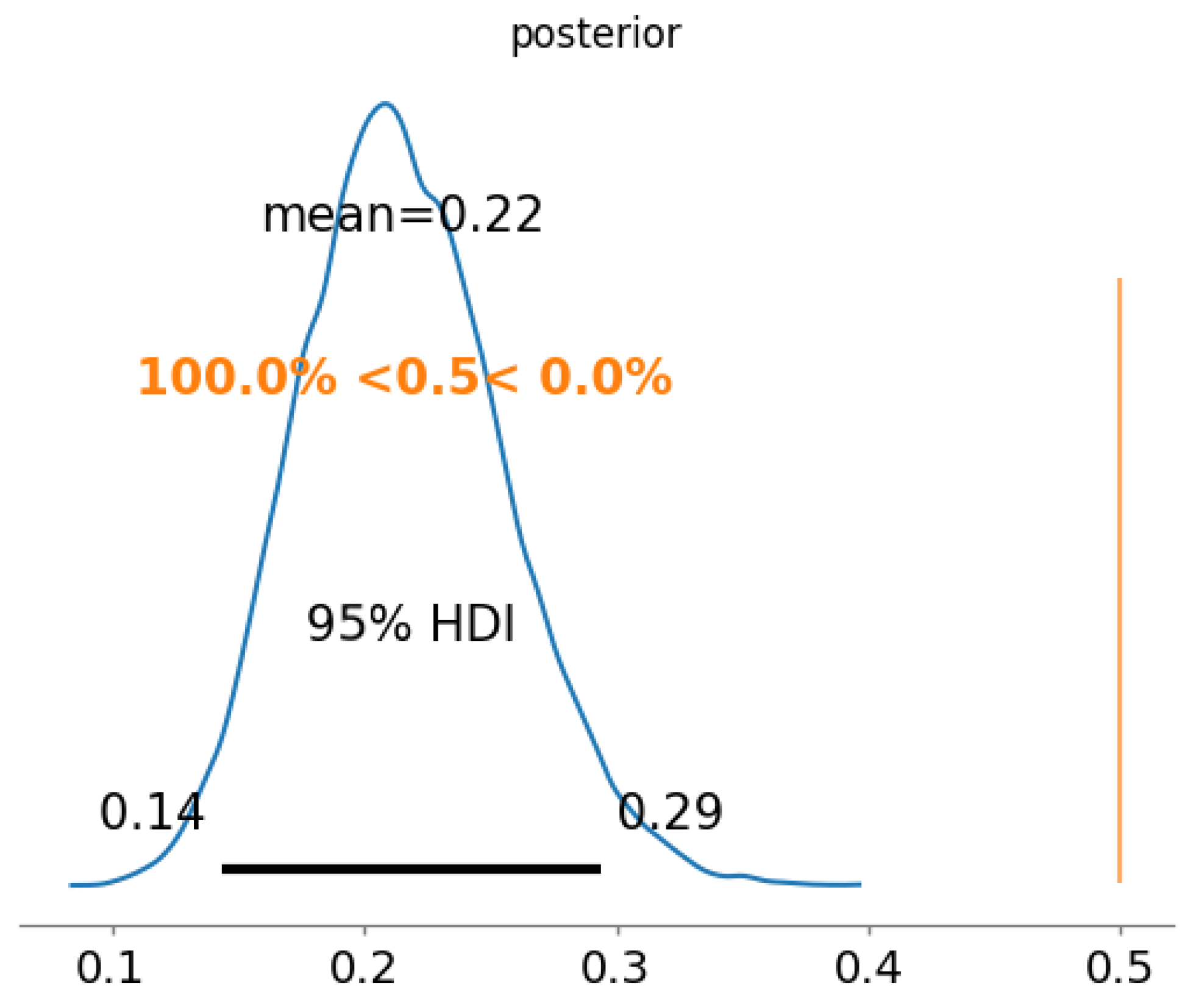
- Beta-Binomial approach: verify the probability that each edge exists, being a and b dataset variables, and . Therefore, for 5 nodes, distributions would be obtained.
- Dirichlet-Multinomial approach: verify the probability that a pair of variables are correlated in direction , correlated in direction , or are uncorrelated. Therefore, for 5 nodes, distributions would be obtained.
4.1.1. The Beta-Binomial Approach
4.1.2. The Dirichlet-Multinomial Approach
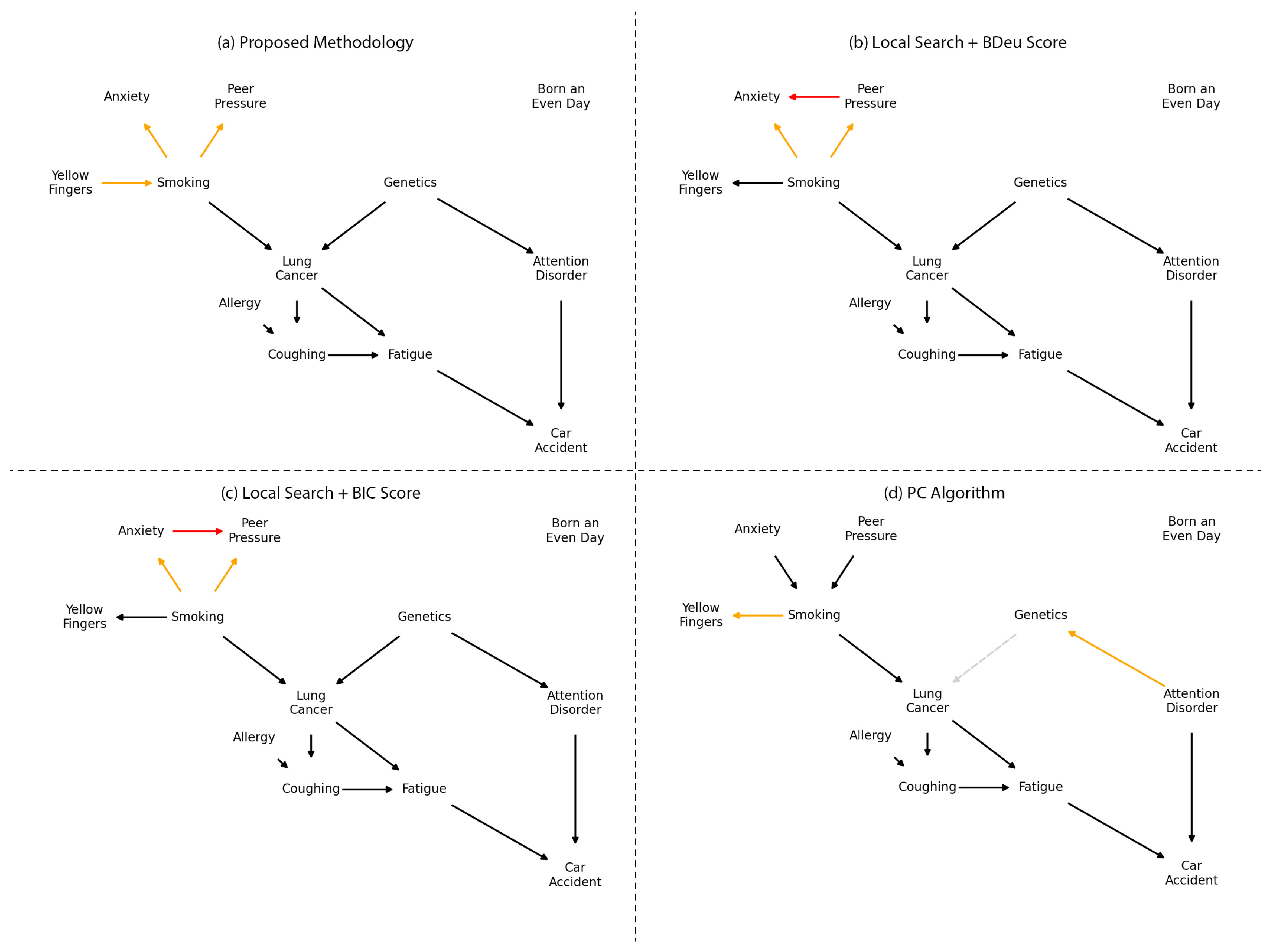
4.2. Comparison with Alternative Methods
4.3. Experiment 2: Network Complexity
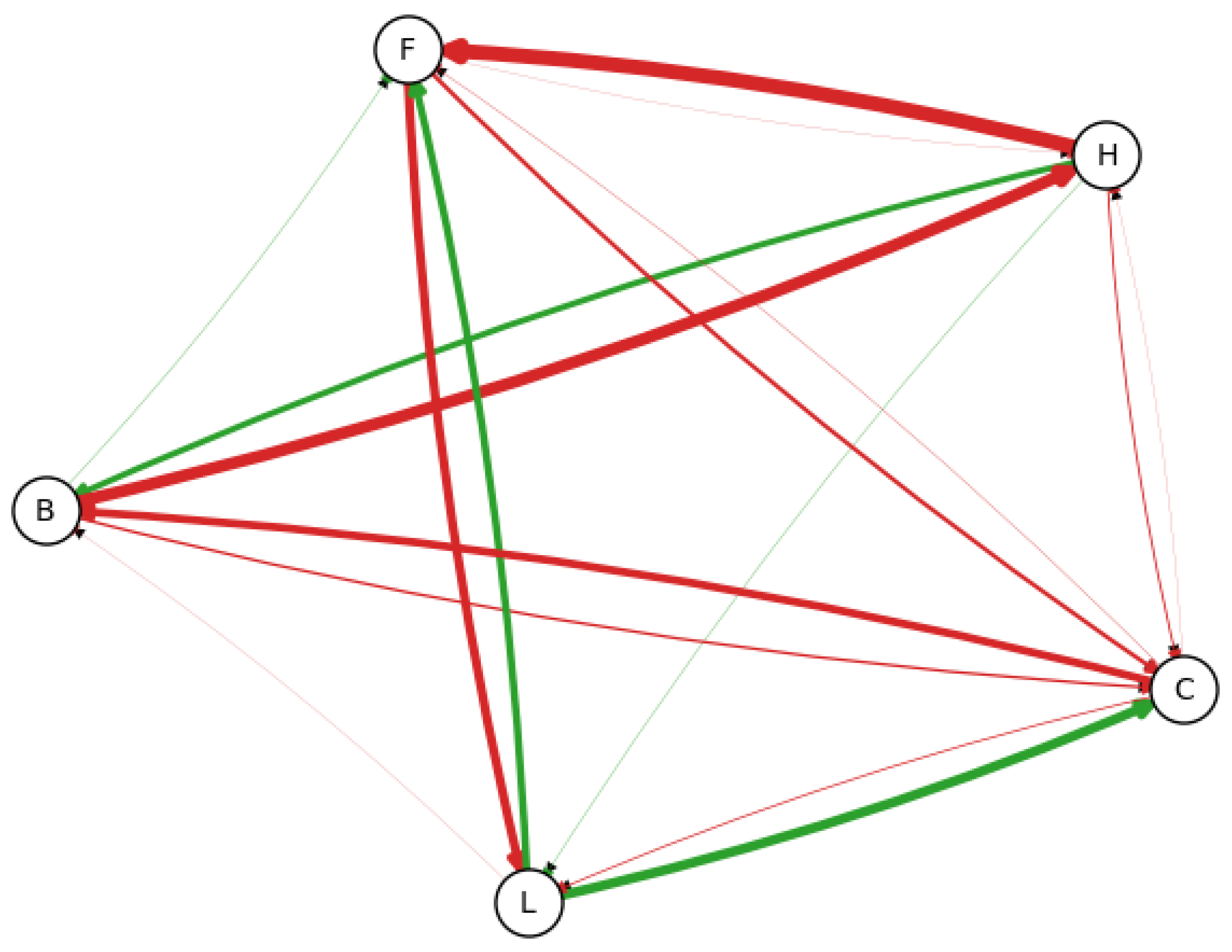
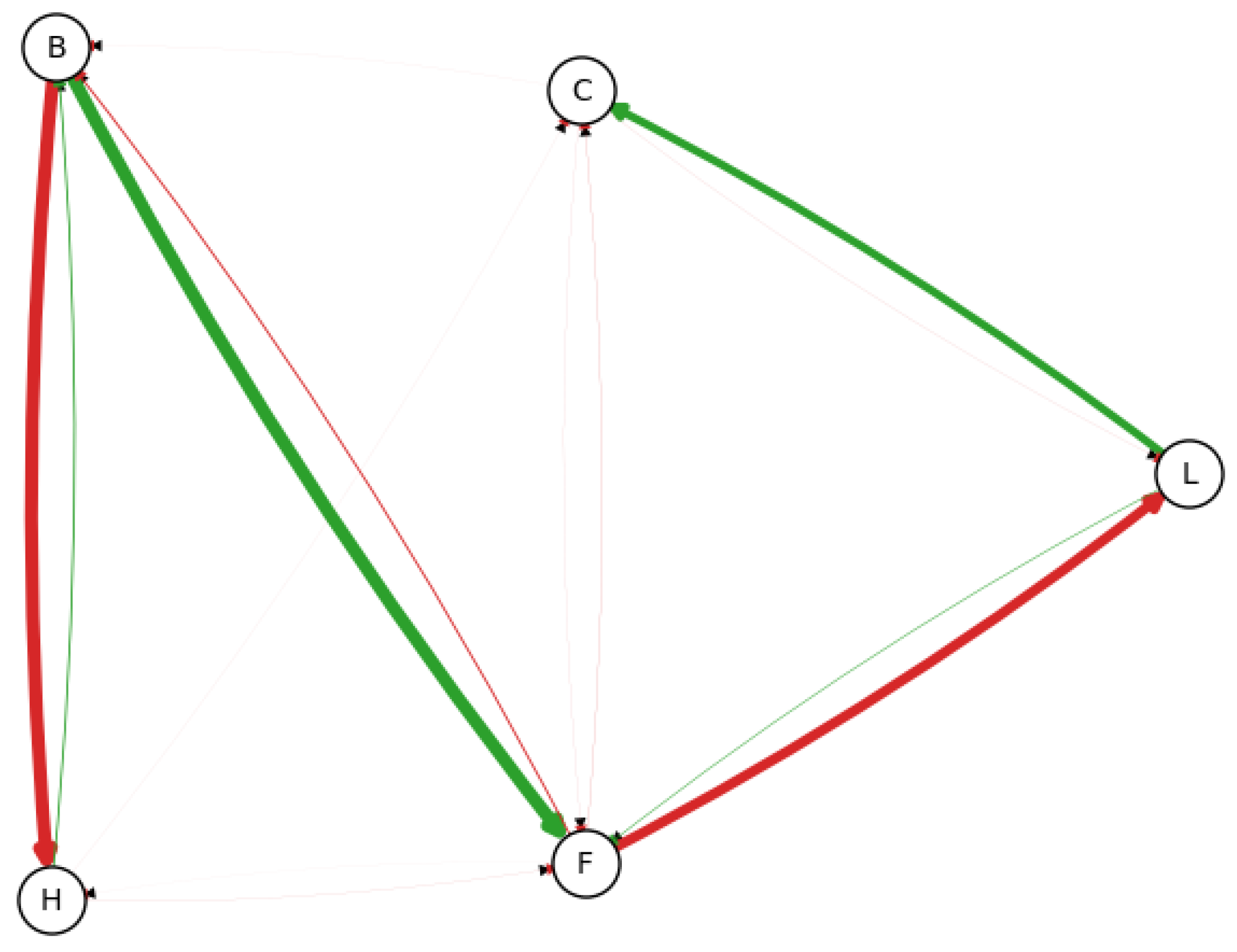
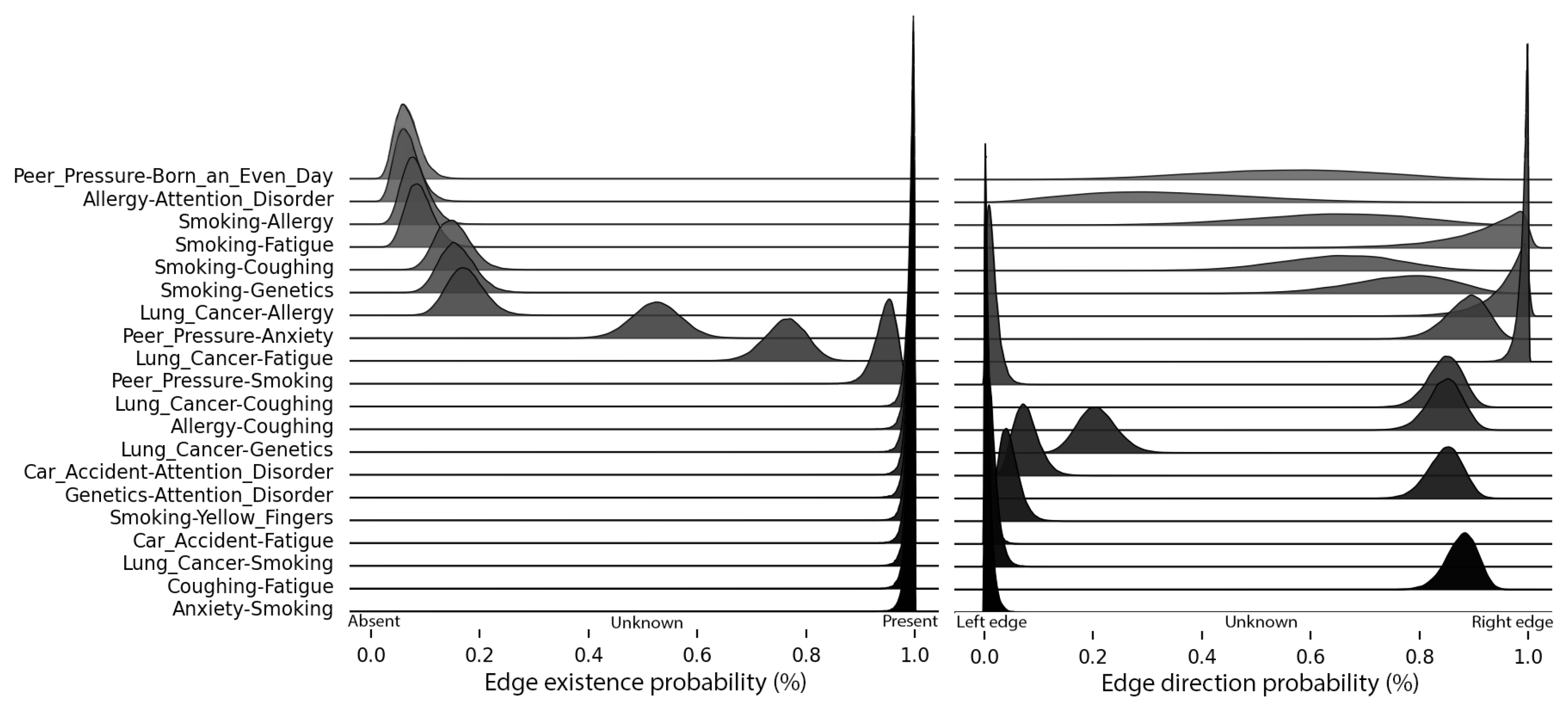
- Edge existence probability: summing the distributions for and , then calculating a binomial distribution against ;
- Edge direction probability: assuming a binomial distribution when merging and ).
Impact of Dataset Size on Inference Tasks
4.4. Experiment 3: Real-Use Case
4.4.1. Data Preprocessing
4.4.2. Per-Subject Model
4.4.3. Combined Model
- there is no relevant connection present in the data: the No edge case is always the most likely when identifying the maxima a posteriori;
- the dataset is too small to uncover any relevant connections: the credible intervals are broad and exhibit significant overlap.
4.5. Challenges and Opportunities in Real-World Scenarios
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AI | Artificial Intelligence |
| BF | Biceps femoris muscle |
| BN | Bayesian Network |
| CPT | Conditional Probability Table |
| DAG | Directed Acyclic Graph |
| EMG | Electromyography |
| GASTRO | Gastrocnemius muscle |
| GMAX | Gluteus maximus muscle |
| GMED | Gluteus medius muscle |
| JPT | Joint Probability Table |
| MAP | Maxima a Posteriori |
| MCMC | Markov chain Monte Carlo |
| ML | Machine Learning |
| PFP | Patellofemoral Pain Syndrom |
| RF | Rectus femoris muscle |
| TA | Tibialis anterior muscle |
| VL | Vastus lateralis muscle |
| VM | Vastus medialis muscle |
References
- Koller, D.; Friedman, N. Probabilistic Graphical Models: Principles and Techniques; Adaptive computation and machine learning; MIT Press: Cambridge, MA, USA, 2009. [Google Scholar]
- Lin, J.H.; Haug, P.J. Exploiting missing clinical data in Bayesian network modeling for predicting medical problems. J. Biomed. Inform. 2008, 41, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Mihaljević, B.; Bielza, C.; Larrañaga, P. Bayesian networks for interpretable machine learning and optimization. Neurocomputing 2021, 456, 648–665. [Google Scholar] [CrossRef]
- Tang, X.; Chen, A.; He, J. A modelling approach based on Bayesian networks for dam risk analysis: Integration of machine learning algorithm and domain knowledge. Int. J. Disaster Risk Reduct. 2022, 71, 102818. [Google Scholar] [CrossRef]
- Heckerman, D. A tutorial on learning with Bayesian networks. In Innovations in Bayesian Networks: Theory and Applications; Springer: Dordrecht, The Netherlands, 2008; pp. 33–82. [Google Scholar]
- Daly, R.; Shen, Q.; Aitken, S. Learning Bayesian networks: Approaches and issues. Knowl. Eng. Rev. 2011, 26, 99–157. [Google Scholar] [CrossRef]
- Ji, Z.; Xia, Q.; Meng, G. A review of parameter learning methods in Bayesian network. In Proceedings of the Advanced Intelligent Computing Theories and Applications: 11th International Conference, ICIC 2015, Fuzhou, China, 20–23 August 2015; Proceedings, Part III 11. Springer: Cham, Switzerland, 2015; pp. 3–12. [Google Scholar]
- Boudali, H.; Dugan, J.B. A continuous-time Bayesian network reliability modeling, and analysis framework. IEEE Trans. Reliab. 2006, 55, 86–97. [Google Scholar] [CrossRef]
- Zemplenyi, M.; Miller, J.W. Bayesian optimal experimental design for inferring causal structure. Bayesian Anal. 2023, 18, 929–956. [Google Scholar] [CrossRef]
- Cheng, J.; Greiner, R.; Kelly, J.; Bell, D.; Liu, W. Learning Bayesian networks from data: An information-theory based approach. Artif. Intell. 2002, 137, 43–90. [Google Scholar] [CrossRef]
- Oniśko, A.; Druzdzel, M.J. Impact of precision of Bayesian network parameters on accuracy of medical diagnostic systems. Artif. Intell. Med. 2013, 57, 197–206. [Google Scholar] [CrossRef][Green Version]
- Rodrigues Mendes Ribeiro, R.; Natal, J.; Polpo de Campos, C.; Dias Maciel, C. Conditional probability table limit-based quantization for Bayesian networks: Model quality, data fidelity and structure score. Appl. Intell. 2024, 54, 4668–4688. [Google Scholar] [CrossRef]
- Glymour, C.; Zhang, K.; Spirtes, P. Review of Causal Discovery Methods Based on Graphical Models. Front. Genet. 2019, 10. [Google Scholar] [CrossRef]
- Spirtes, P. An Anytime Algorithm for Causal Inference. In Proceedings of Machine Learning Research, Proceedings of the Eighth International Workshop on Artificial Intelligence and Statistics, Key West, FL, USA, 4–7 January 2001; Richardson, T.S., Jaakkola, T.S., Eds.; PMLR: London, UK, 2001; Volume R3, pp. 278–285. [Google Scholar]
- Murphy, K.P. Machine Learning: A Probabilistic Perspective; Adaptive Computation and Machine Learning Series; MIT Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Neapolitan, R.E. Learning Bayesian Networks; Prentice-Hall, Inc.: Upper Saddle River, NJ, USA, 2003. [Google Scholar]
- Pearl, J.; Glymour, M.; Jewell, N. Causal Inference in Statistics: A Primer; Wiley: Hoboken, NJ, USA, 2016. [Google Scholar]
- Scutari, M.; Graafland, C.E.; Gutiérrez, J.M. Who learns better bayesian network structures: Constraint-based, score-based or hybrid algorithms? In Proceedings of the International Conference on Probabilistic Graphical Models, Prague, Czech Republic, 11–14 September 2018; PMLR: London, UK, 2018; pp. 416–427. [Google Scholar]
- Rodrigues Mendes Ribeiro, R.; Dias Maciel, C. Bayesian Network Structural Learning Using Adaptive Genetic Algorithm with Varying Population Size. Mach. Learn. Knowl. Extr. 2023, 5, 1877–1887. [Google Scholar] [CrossRef]
- Gross, T.J.; Bessani, M.; Darwin Junior, W.; Araújo, R.B.; Vale, F.A.C.; Maciel, C.D. An analytical threshold for combining Bayesian Networks. Knowl.-Based Syst. 2019, 175, 36–49. [Google Scholar] [CrossRef]
- Wang, X.; Pan, J.; Ren, Z.; Zhai, M.; Zhang, Z.; Ren, H.; Song, W.; He, Y.; Li, C.; Yang, X.; et al. Application of a novel hybrid algorithm of Bayesian network in the study of hyperlipidemia related factors: A cross-sectional study. BMC Public Health 2021, 21, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Contaldi, C.; Vafaee, F.; Nelson, P.C. Bayesian network hybrid learning using an elite-guided genetic algorithm. Artif. Intell. Rev. 2019, 52, 245–272. [Google Scholar] [CrossRef]
- Constantinou, A.C.; Fenton, N.; Neil, M. Integrating expert knowledge with data in Bayesian networks: Preserving data-driven expectations when the expert variables remain unobserved. Expert Syst. Appl. 2016, 56, 197–208. [Google Scholar] [CrossRef] [PubMed]
- Friedman, N.; Koller, D. Being Bayesian About Network Structure. A Bayesian Approach to Structure Discovery in Bayesian Networks. Mach. Learn. 2003, 50, 95–125. [Google Scholar] [CrossRef]
- Kitson, N.K.; Constantinou, A.C.; Guo, Z.; Liu, Y.; Chobtham, K. A survey of Bayesian Network structure learning. Artif. Intell. Rev. 2023, 56, 8721–8814. [Google Scholar] [CrossRef]
- Murphy, K.P. Dynamic Bayesian Networks: Representation, Inference and Learning. Ph.D. Thesis, University of California, Berkeley Berkeley, CA, USA, 2002. [Google Scholar]
- Marcot, B.G. Metrics for evaluating performance and uncertainty of Bayesian network models. Ecol. Model. 2012, 230, 50–62. [Google Scholar] [CrossRef]
- Marcot, B.G.; Hanea, A.M. What is an optimal value of k in k-fold cross-validation in discrete Bayesian network analysis? Comput. Stat. 2021, 36, 2009–2031. [Google Scholar] [CrossRef]
- Guo, Y.; Gravina, R.; Gu, X.; Fortino, G.; Yang, G.Z. EMG-based Abnormal Gait Detection and Recognition. In Proceedings of the 2020 IEEE International Conference on Human-Machine Systems (ICHMS), Rome, Italy, 7–9 September 2020; pp. 1–6. [Google Scholar]
- Agostini, V.; Ghislieri, M.; Rosati, S.; Balestra, G.; Knaflitz, M. Surface Electromyography Applied to Gait Analysis: How to Improve Its Impact in Clinics? Front. Neurol. 2020, 11, 994. [Google Scholar] [CrossRef]
- Dicharry, J. Kinematics and Kinetics of Gait: From Lab to Clinic. Clin. Sports Med. 2010, 29, 347–364. [Google Scholar] [CrossRef] [PubMed]
- Cruz-Montecinos, C.; Pérez-Alenda, S.; Querol, F.; Cerda, M.; Maas, H. Changes in Muscle Activity Patterns and Joint Kinematics During Gait in Hemophilic Arthropathy. Front. Physiol. 2020, 10, 1575. [Google Scholar] [CrossRef] [PubMed]
- Jorge, G.; Faria, A.N.d.; Furtado, D.A.; Pereira, A.A.; Carvalho, E.M.d.; Dionísio, V.C. Kinematic and electromyographic analysis of school children gait with and without load in the backpack. Res. Biomed. Eng. 2018, 34, 9–18. [Google Scholar] [CrossRef]
- Kelencz, C.A.; Muñoz, I.S.S.; de Oliveira, P.R.; Mazziotti, B.; Amorim, C.F. Kinematics and Electromyographic Analysis of Gait with Different Footwear. Arch. Pharm. Pharm. Sci. 2017, 1, 001–006. [Google Scholar]
- Stokes, H.E.; Thompson, J.D.; Franz, J.R. The Neuromuscular Origins of Kinematic Variability during Perturbed Walking. Sci. Rep. 2017, 7, 808. [Google Scholar] [CrossRef]
- Patikas, D.A. EMG Activity in Gait: The Influence of Motor Disorders. In Handbook of Human Motion; Springer International Publishing: Cham, Switzerland, 2016; pp. 1–26. [Google Scholar]
- Hong, S.R.; Hullman, J.; Bertini, E. Human Factors in Model Interpretability: Industry Practices, Challenges, and Needs. Proc. ACM Hum.-Comput. Interact. 2020, 4, 68. [Google Scholar] [CrossRef]
- Liu, J. Adaptive myoelectric pattern recognition toward improved multifunctional prosthesis control. Med. Eng. Phys. 2015, 37, 424–430. [Google Scholar] [CrossRef]
- Meng, M.; She, Q.; Gao, Y.; Luo, Z. EMG signals based gait phases recognition using hidden Markov models. In Proceedings of the 2010 IEEE International Conference on Information and Automation, Harbin, China, 20–23 June 2010; pp. 852–856. [Google Scholar]
- Morbidoni, C.; Cucchiarelli, A.; Fioretti, S.; Di Nardo, F. A Deep Learning Approach to EMG-Based Classification of Gait Phases during Level Ground Walking. Electronics 2019, 8, 894. [Google Scholar] [CrossRef]
- Senanayake, S.M.N.A.; Triloka, J.; Malik, O.A.; Iskandar, M. Artificial neural network based gait patterns identification using neuromuscular signals and soft tissue deformation analysis of lower limbs muscles. In Proceedings of the 2014 International Joint Conference on Neural Networks (IJCNN), Beijing, China, 6–11 July 2014; pp. 3503–3510. [Google Scholar]
- Rechy-Ramirez, E.J.; Hu, H. Bio-signal based control in assistive robots: A survey. Digit. Commun. Netw. 2015, 1, 85–101. [Google Scholar] [CrossRef]
- Trigili, E.; Grazi, L.; Crea, S.; Accogli, A.; Carpaneto, J.; Micera, S.; Vitiello, N.; Panarese, A. Detection of movement onset using EMG signals for upper-limb exoskeletons in reaching tasks. J. NeuroEng. Rehab. 2019, 16, 1–16. [Google Scholar] [CrossRef]
- Vellido, A. The importance of interpretability and visualization in machine learning for applications in medicine and health care. Neural Comput. Appl. 2020, 32, 18069–18083. [Google Scholar] [CrossRef]
- Lauritsen, S.M.; Kristensen, M.; Olsen, M.V.; Larsen, M.S.; Lauritsen, K.M.; Jørgensen, M.J.; Lange, J.; Thiesson, B. Explainable artificial intelligence model to predict acute critical illness from electronic health records. Nat. Commun. 2020, 11, 3852. [Google Scholar] [CrossRef]
- Amann, J.; Blasimme, A.; Vayena, E.; Frey, D.; Madai, V.I. Explainability for artificial intelligence in healthcare: A multidisciplinary perspective. BMC Med. Inform. Decis. Mak. Vol. 2020, 20, 310. [Google Scholar] [CrossRef] [PubMed]
- Davenport, T.; Kalakota, R. The potential for artificial intelligence in healthcare. Future Healthc. J. 2019, 6, 94–98. [Google Scholar] [CrossRef] [PubMed]
- Graham, J. Artificial Intelligence, Machine Learning, and the FDA; Forbes: Jersey City, NJ, USA, 2016. [Google Scholar]
- Turpin, N.A.; Uriac, S.; Dalleau, G. How to improve the muscle synergy analysis methodology? Eur. J. Appl. Physiol. 2021, 121, 1009–1025. [Google Scholar] [CrossRef] [PubMed]
- Purves, S. Phase and the Hilbert transform. Lead. Edge 2014, 33, 1164–1166. [Google Scholar] [CrossRef]
- Acharya, D.; Rani, A.; Agarwal, S.; Singh, V. Application of adaptive Savitzky–Golay filter for EEG signal processing. Perspect. Sci. 2016, 8, 677–679. [Google Scholar] [CrossRef]
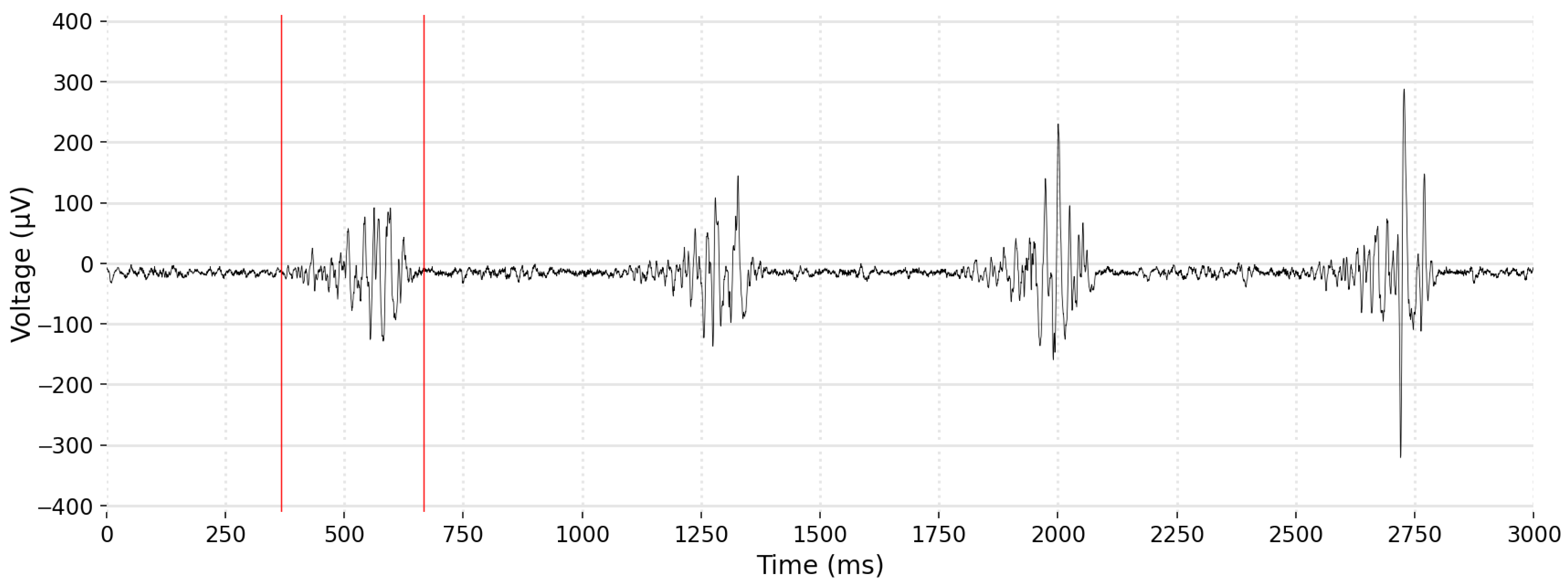
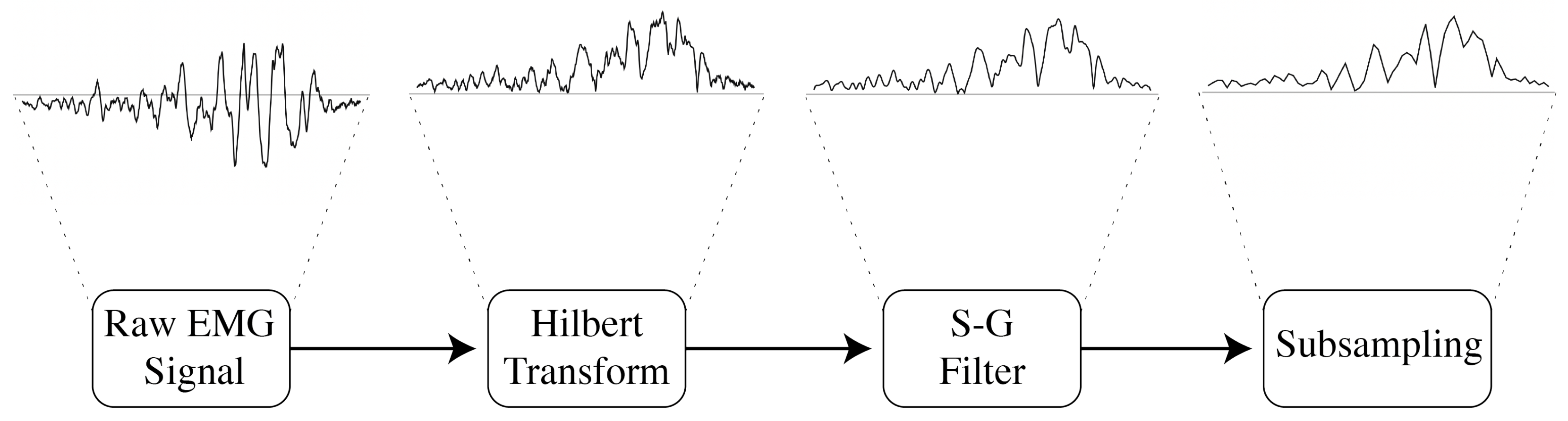
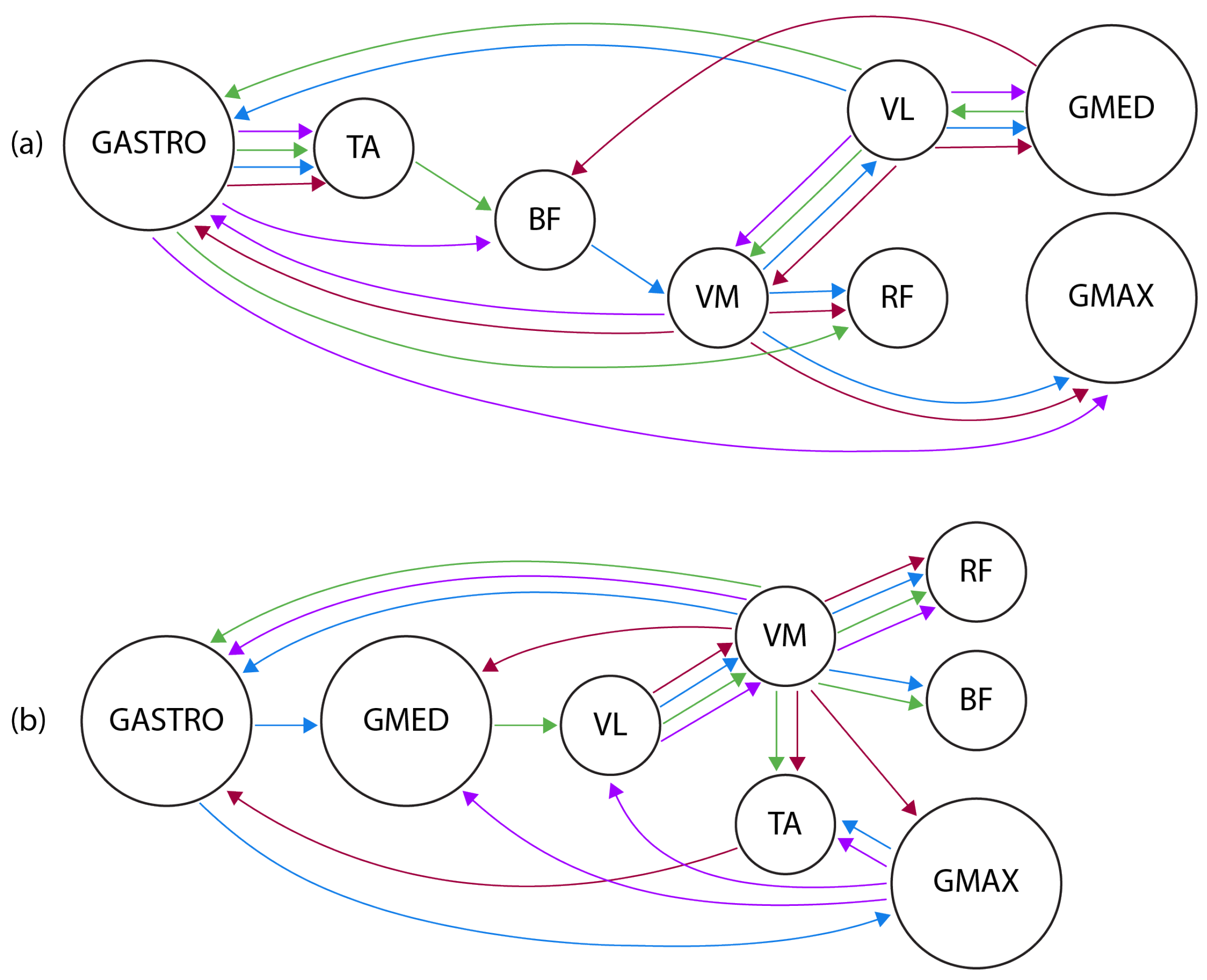
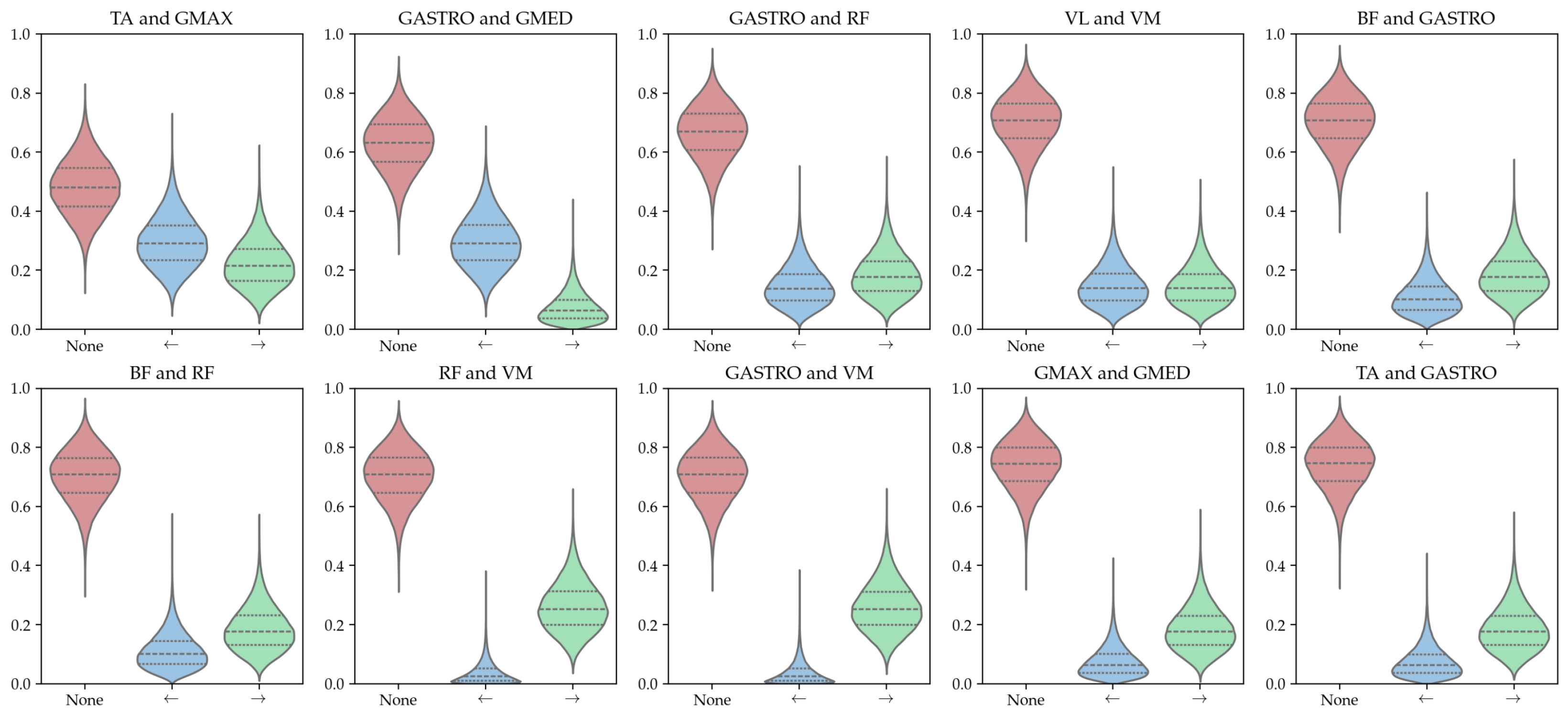
| Algorithm | Limitations When Applied Small Sample Sizes |
|---|---|
| Score-based methods | Tend to overfit when data are scarce because they search for the highest-scoring DAG, potentially capturing spurious relationships. |
| Constraint-based methods | Independence tests used in PC and FCI algorithms can be unreliable with small sample sizes, leading to incorrect structures. |
| Threshold-based approaches | The threshold for selecting an edge will not be achievable, leading to structures with a small number of edges. |
| Metric | Comparison |
|---|---|
| Analytic threshold |
|
| Bayesian credible interval |
|
| Information scores (BDeu and BIC) |
|
| K-fold cross validation |
|
| Num. of Samples | TP | TN | FP | FN |
|---|---|---|---|---|
| 65% | 21% | 7% | 7% | |
| 65% | 21% | 7% | 7% | |
| 68% | 17% | 10% | 5% | |
| 72% | 0% | 28% | 0% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barth, V.; Serrão, F.; Maciel, C. Assessing Credibility in Bayesian Networks Structure Learning. Entropy 2024, 26, 829. https://doi.org/10.3390/e26100829
Barth V, Serrão F, Maciel C. Assessing Credibility in Bayesian Networks Structure Learning. Entropy. 2024; 26(10):829. https://doi.org/10.3390/e26100829
Chicago/Turabian StyleBarth, Vitor, Fábio Serrão, and Carlos Maciel. 2024. "Assessing Credibility in Bayesian Networks Structure Learning" Entropy 26, no. 10: 829. https://doi.org/10.3390/e26100829
APA StyleBarth, V., Serrão, F., & Maciel, C. (2024). Assessing Credibility in Bayesian Networks Structure Learning. Entropy, 26(10), 829. https://doi.org/10.3390/e26100829







