RBFNN-PSO Intelligent Synchronisation Method for Sprott B Chaotic Systems with External Noise and Its Application in an Image Encryption System
Abstract
1. Introduction
- A controller based on RBFNN is constructed, considering the influence of external noise on the performance of the system, and the controller parameters are optimized by the group intelligent optimization algorithm to realize the suppression of the influence of external noise on the performance of the synchronous system.
- The PSO optimization algorithm is selected and improved, and the linear dynamic adjustment of the optimization parameters is used to update the weights, so as to overcome the problem of the PSO optimization algorithm being prone to falling into the local optimal situation; meanwhile, the characteristics of the rich dynamics behaviour of the multi-attractor chaotic system are taken into account, the Sprott B system is selected as the synchronization object, and the parameters of the synchronization controller of the Sprott B chaotic system are introduced into the training process, so as to achieve the optimal solution of the controller parameters of the chaotic system, which is the best solution for the chaotic system. The optimal solution of the controller parameters realizes the consistent synchronization of the two Sprott B systems.
- In order to enhance the complexity of image encryption, an improved Zigzag top-angle rotation image disruption algorithm is proposed to overcome the problem of the first data in the first place not changing and being easily recognized when the Zigzag is disrupted; at the same time, the method in which the mean size of the image determines the disruption channel is adopted to expand the encrypted secret key space; an analysis of the security performance of the image encryption is carried out, and the encryption system has a better resistance to the differential attack and statistical analysis.
2. Proposed Model and Preliminary Work
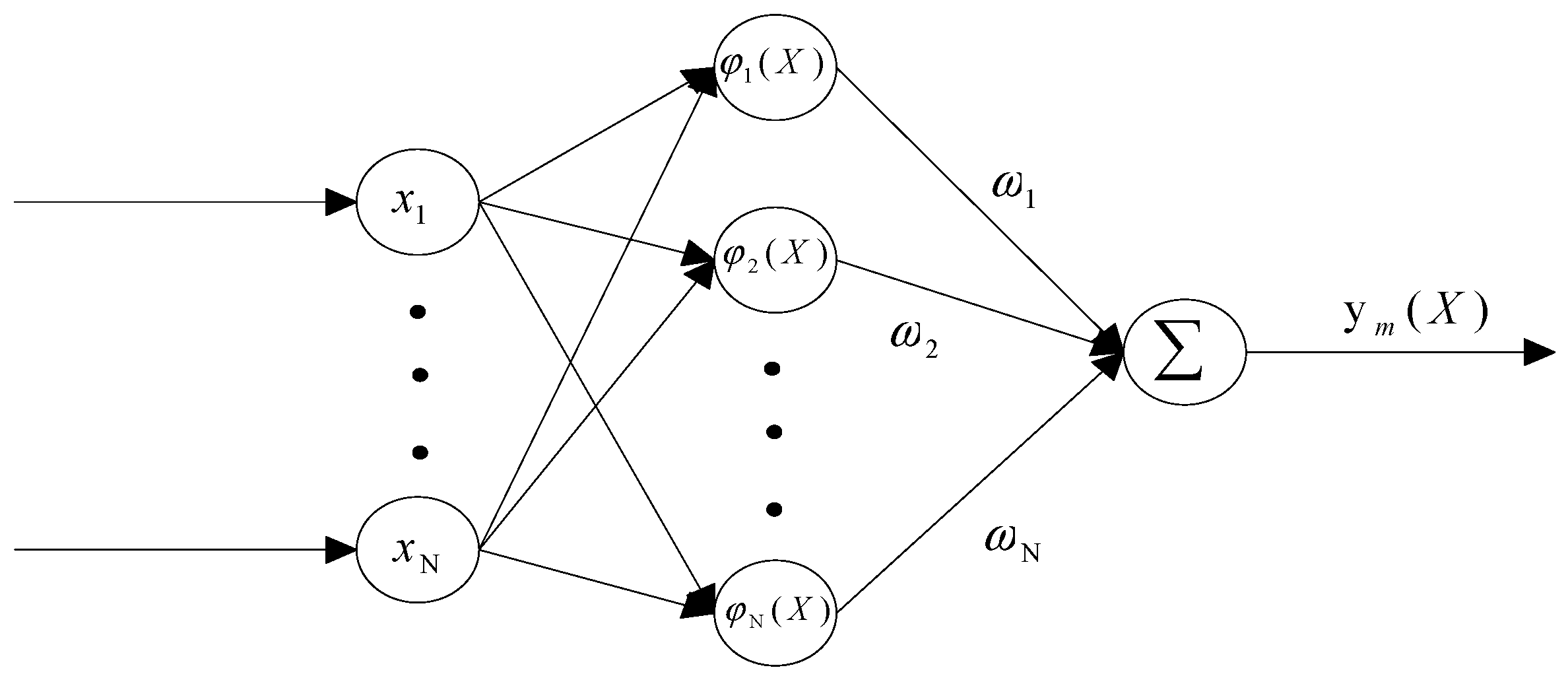
2.1. RBF Neural Network
2.2. The PSO Algorithm
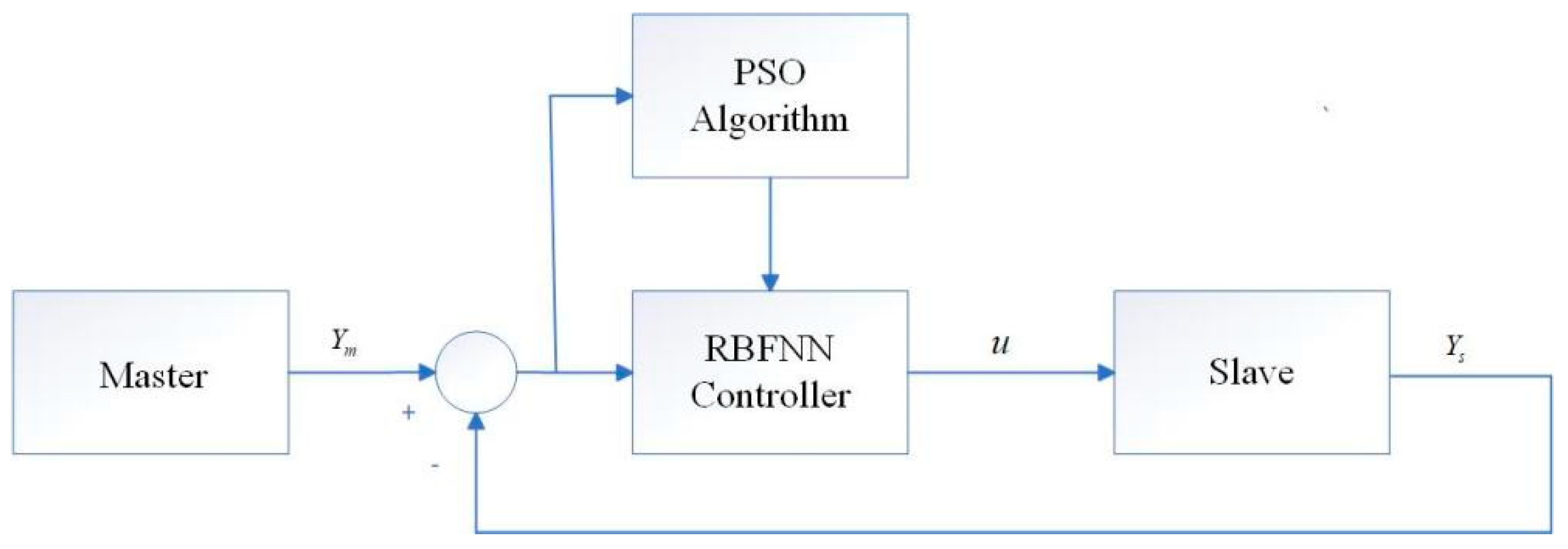
2.3. Design Methodology for Synchronous System Controllers
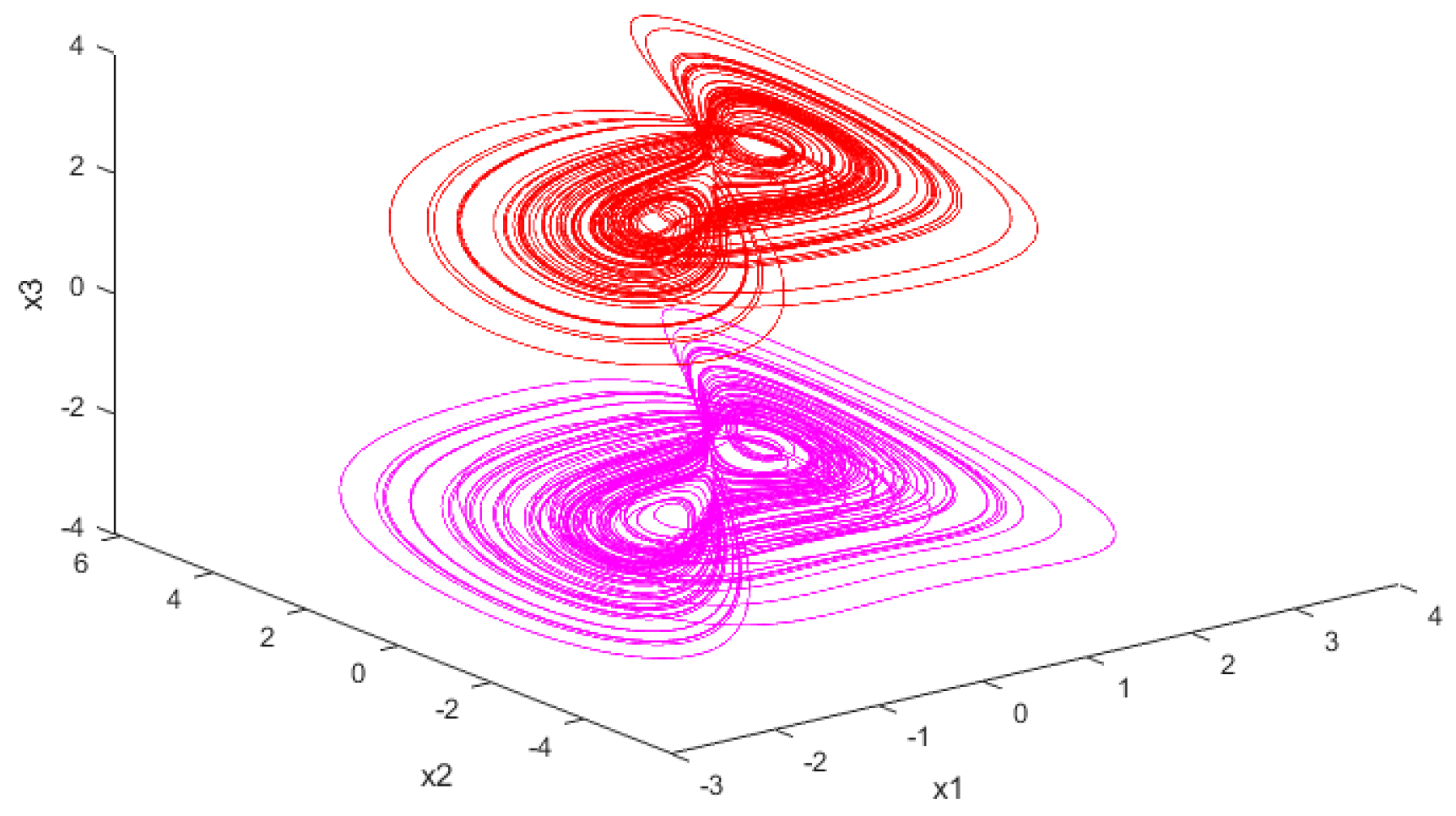
2.4. Constructed Chaotic System Models
3. Synchronisation Schemes for Master–Slave Sprott B Chaotic Systems with Additional Noise
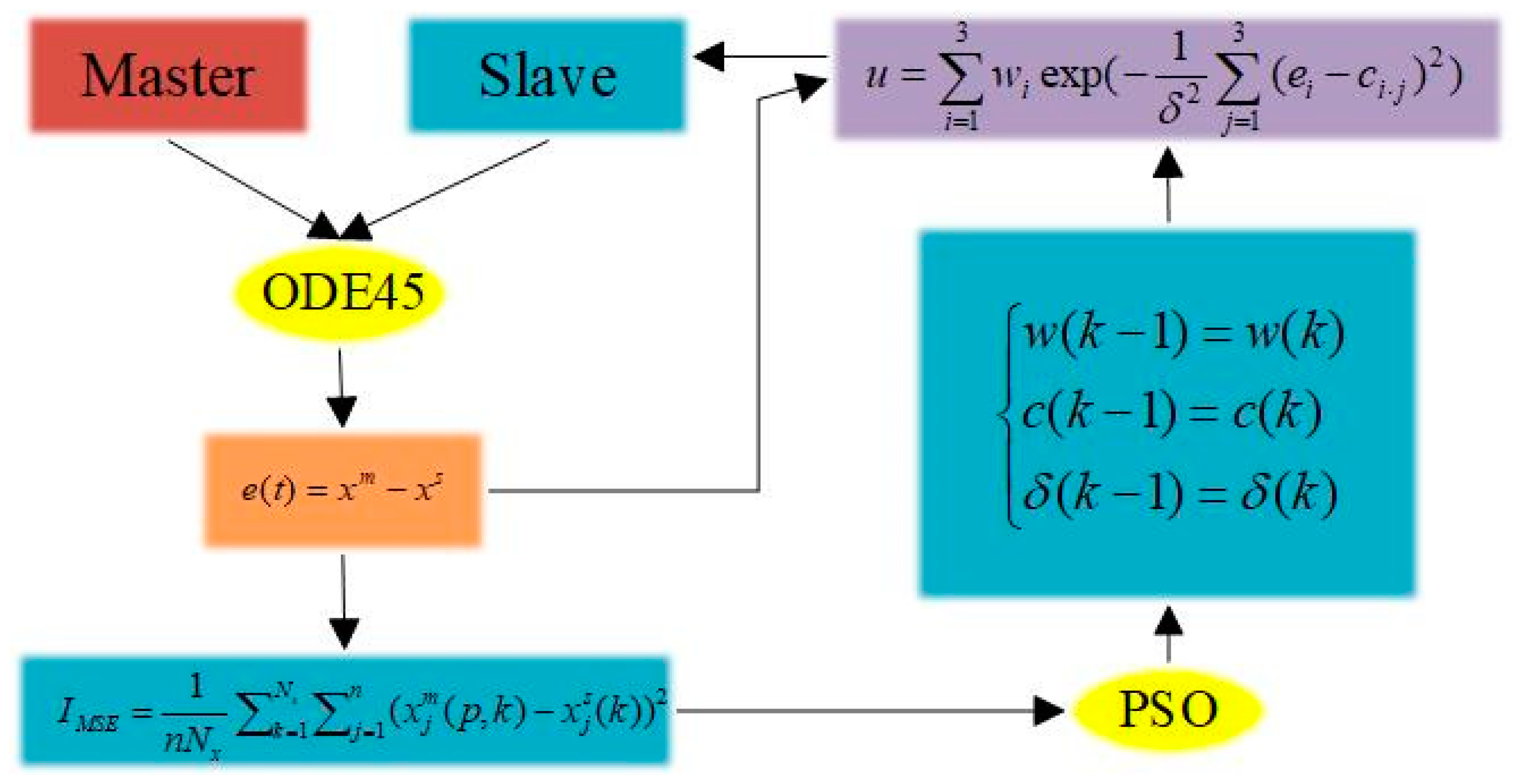
3.1. Training Process for PSO Parameters
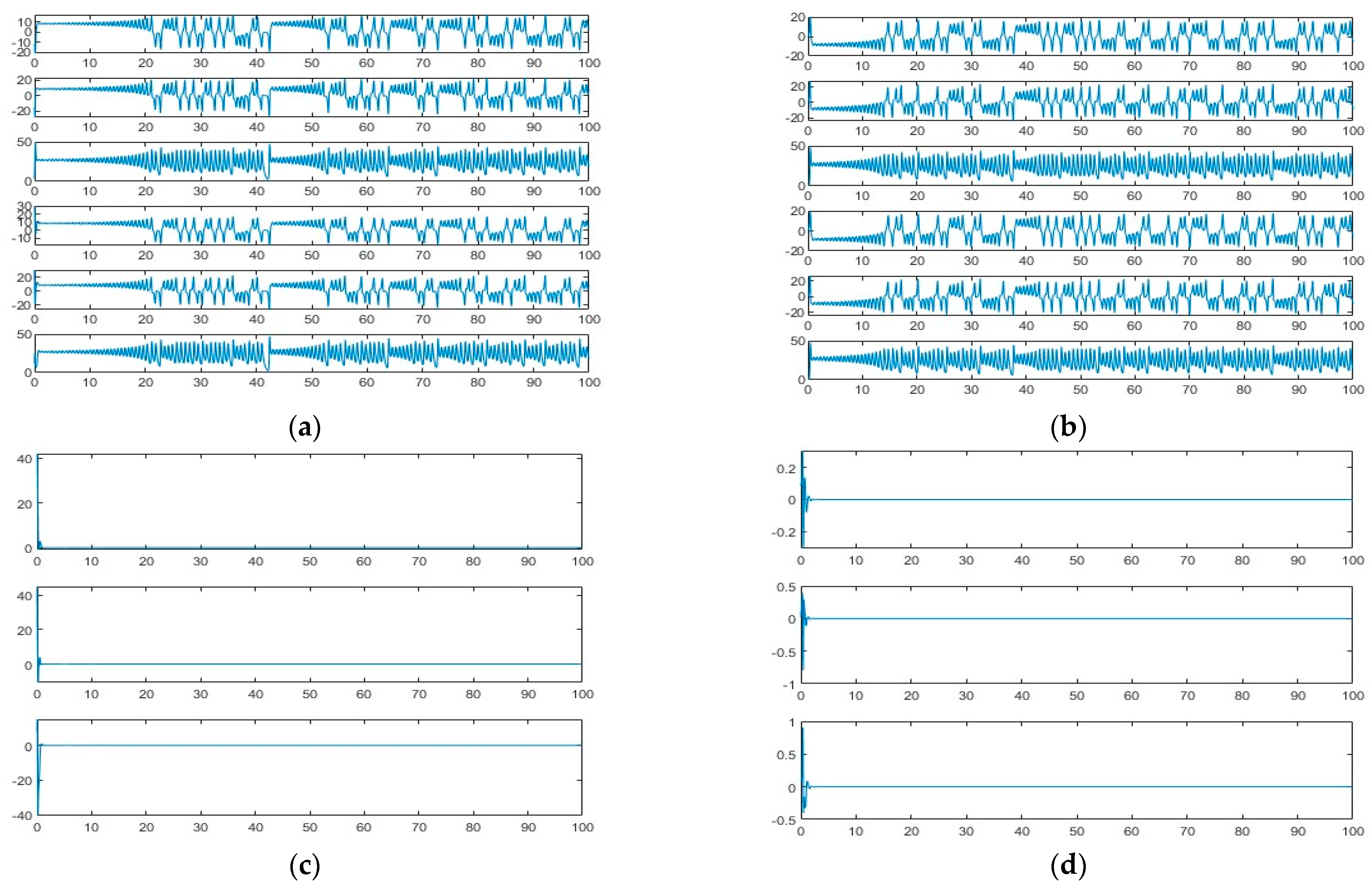
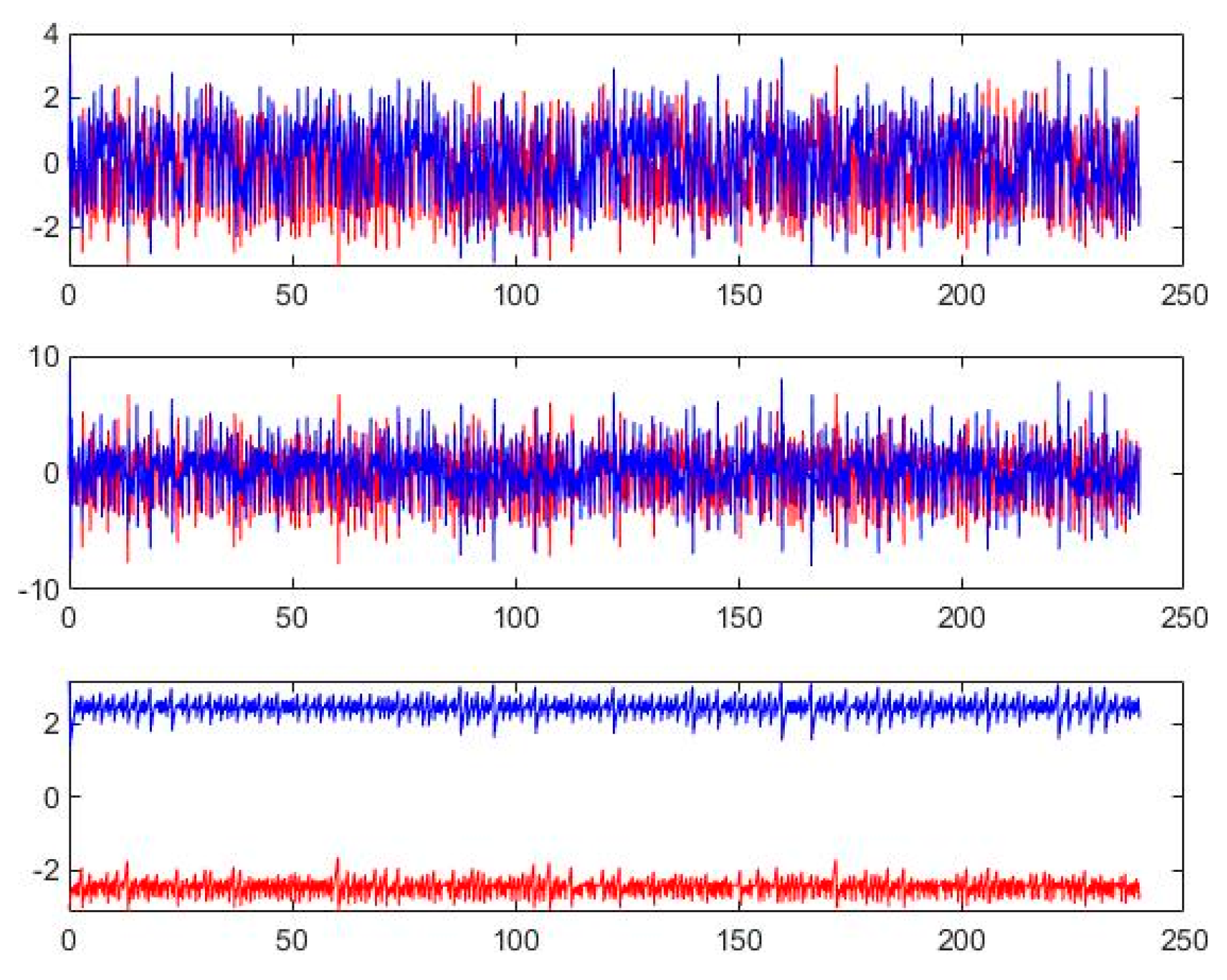
3.2. Synchronisation Characterisation of Chaotic Systems
4. Application of the Introduced Synchronization Scheme in Image Encryption System
4.1. Proposed Image Encryption Scheme
4.2. Zigzag Image Scrambling Scheme
4.3. Image Diffusion Program
4.4. Simulation Results of the Encryption System
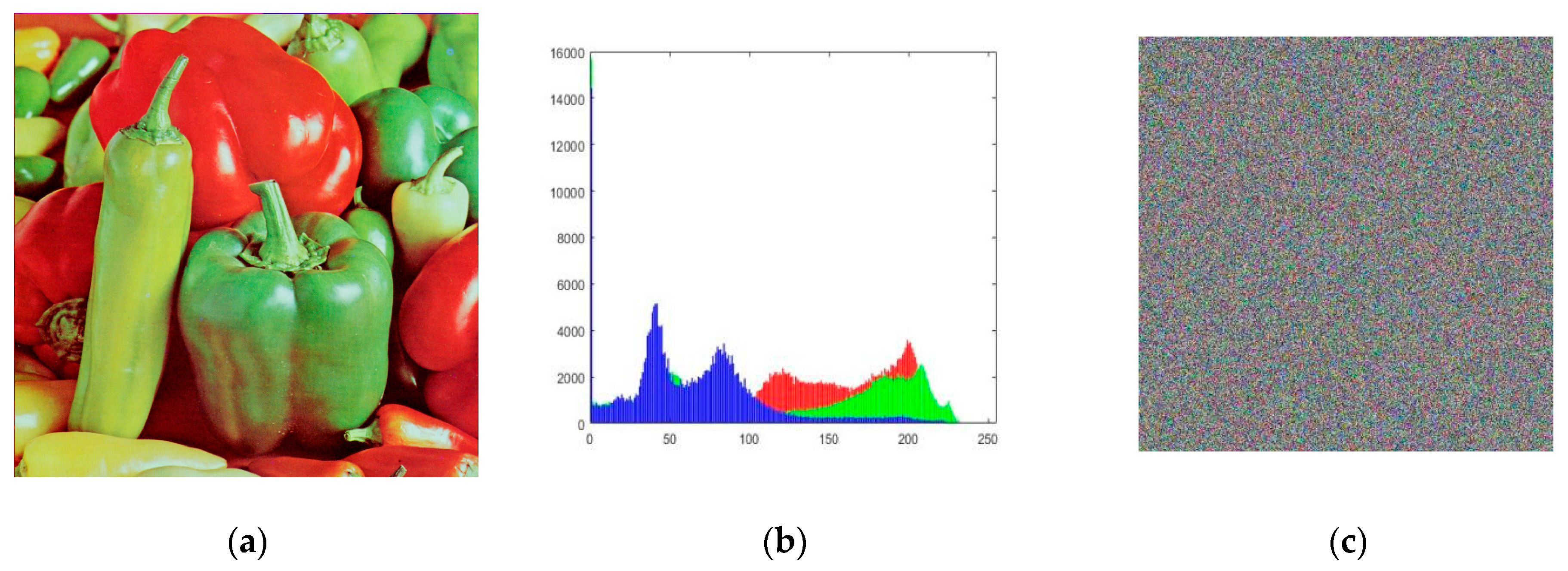
4.4.1. Analysis of Encryption and Decryption Results
4.4.2. Histogram Analysis
4.4.3. Shannon Entropy of Encrypted Images
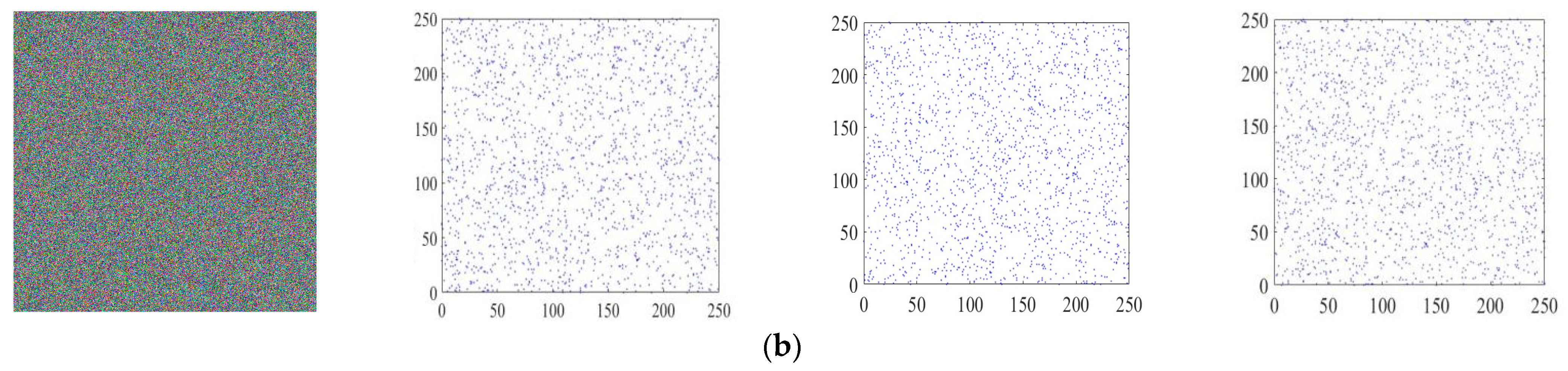
4.4.4. Correlation Analysis
4.4.5. Differential Attack
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, X.; Chen, X. An image encryption algorithm based on dynamic row scrambling and Zigzag transformation. Chaos Solitons Fractals 2021, 147, 110962. [Google Scholar] [CrossRef]
- Zhang, Y.; Yan, W.; Dong, W.; Ding, Q. Linear Feedback Synchronization of High-Dimensional Discrete Chaotic Systems and Their Application to Image Encryption Systems. In Proceedings of the 2nd International Joint Conference on Information and Communication Engineering (JCICE), Chengdu, China, 12–14 May 2023; pp. 100–104. [Google Scholar]
- Luo, L.; Wang, Y.; Deng, S. Adaptive synchronization on uncertain dynamics of high-order nonlinear multi-agent systems with partition of unity approach. Int. J. Control. Autom. Syst. 2014, 12, 259–264. [Google Scholar] [CrossRef]
- Li, D.; Li, J.; Di, X. A novel exponential one-dimensional chaotic map enhancer and its application in an image encryption scheme using modified ZigZag transform. J. Inf. Secur. Appl. 2022, 69, 103304. [Google Scholar] [CrossRef]
- Deng, Q.; Wang, C.; Sun, Y.; Deng, Z.; Yang, G. Memristive Tabu Learning Neuron Generated Multi-Wing Attractor with FPGA Implementation and Application in Encryption. IEEE Trans. Circuits Syst. I Regul. Pap. 2024, 1–12. [Google Scholar] [CrossRef]
- Wang, C.; Luo, D.; Deng, Q.; Yang, G. Dynamics analysis and FPGA implementation of discrete memristive cellular neural network with heterogeneous activation functions. Chaos Solitons Fractals 2024, 187, 115471. [Google Scholar] [CrossRef]
- Li, J.; Wang, C.; Deng, Q. Symmetric multi-double-scroll attractors in Hopfield neural network under pulse controlled memristor. Nonlinear Dyn. 2024, 112, 14463–14477. [Google Scholar] [CrossRef]
- Wang, C.; Liang, J.; Deng, Q. Dynamics of heterogeneous Hopfield neural network with adaptive activation function based on memristor. Neural Netw. 2024, 178, 106408. [Google Scholar] [CrossRef]
- Pecora, L.M.; Carroll, T.L. Synchronization in chaotic systems. Phys. Rev. Lett. 1990, 64, 821–824. [Google Scholar] [CrossRef]
- Pecora, L.M.; Carroll, T.L. Driving systems with chaotic signals. Phys. Rev. A 1991, 44, 2374–2383. [Google Scholar] [CrossRef]
- Guo, P.; Shi, Q.; Jian, Z.; Zhang, J.; Ding, Q.; Yan, W. An intelligent controller of homo-structured chaotic systems under noisy conditions and applications in image encryption. Chaos Solitons Fractals 2024, 180, 114524. [Google Scholar] [CrossRef]
- Cheng, C.-J. Robust synchronization of uncertain unified chaotic systems subject to noise and its application to secure communication. Appl. Math. Comput. 2012, 219, 2698–2712. [Google Scholar] [CrossRef]
- Yang, J.; Chen, Y.; Zhu, F. Associated observer-based synchronization for uncertain chaotic systems subject to channel noise and chaos-based secure communication. Neurocomputing 2015, 167, 587–595. [Google Scholar] [CrossRef]
- Xu, G.; Zhao, S.; Cheng, Y. Chaotic synchronization based on improved global nonlinear integral sliding mode control. Comput. Electr. Eng. 2021, 96, 107497. [Google Scholar] [CrossRef]
- Sprott, J.C. Some simple chaotic flows. Phys. Rev. E 1994, 50, R647–R650. [Google Scholar] [CrossRef] [PubMed]
- Carroll, T.; Pecora, L. Using Multiple Attractor Chaotic Systems for Communication. In Proceedings of the 1998 IEEE International Conference on Electronics, Circuits and Systems: Surfing the Waves of Science and Technology, Lisbon, Portugal, 7–10 September 1998. [Google Scholar]
- Qiang, L.; Chen, S. Generating Multiple Chaotic Attractors from Sprott B System. Int. J. Bifurc. Chaos 2016, 26, 1650177. [Google Scholar] [CrossRef]
- Ramamoorthy, R.; Rajagopal, K.; Leutcho, G.D.; Krejcar, O.; Namazi, H.; Hussain, I. Multistable dynamics and control of a new 4D memristive chaotic Sprott B system. Chaos Solitons Fractals 2022, 156, 111834. [Google Scholar] [CrossRef]
- Li, C.; Duan, H. Information granulation-based fuzzy RBFNN for image fusion based on chaotic brain storm optimization. Optik 2015, 126, 1400–1406. [Google Scholar] [CrossRef]
- Ding, R.; Yan, P.; Cheng, M.; Xu, B. A flow inferential measurement of the independent metering multi-way valve based on an improved RBF neural network. Measurement 2023, 223, 113750. [Google Scholar] [CrossRef]
- Zheng, S.; Feng, R. A variable projection method for the general radial basis function neural network. Appl. Math. Comput. 2023, 451, 128009. [Google Scholar] [CrossRef]
- Dehdarinejad, E.; Bayareh, M. Performance analysis of a novel cyclone separator using RBFNN and MOPSO algorithms. Powder Technol. 2023, 426, 118663. [Google Scholar] [CrossRef]
- Darani, A.Y.; Yengejeh, Y.K.; Navarro, G.; Pakmanesh, H.; Sharafi, J. Optimal location using genetic algorithms for chaotic image steganography technique based on discrete framelet transform. Digit. Signal Process. 2024, 144, 104228. [Google Scholar] [CrossRef]
- Yanzhuang, X.; Shibin, X. Grey Wolf Optimization algorithm with random local optimal regulation and first-element dominance. Egypt. Inform. J. 2024, 27, 100486. [Google Scholar] [CrossRef]
- Zhang, J.; Dai, Y.; Shi, Q. An improved grey wolf optimization algorithm based on scale-free network topology. Heliyon 2024, 10, e35958. [Google Scholar] [CrossRef] [PubMed]
- Chen, K.; Zhou, F.; Liu, A. Chaotic dynamic weight particle swarm optimization for numerical function optimization. Knowl. Based Syst. 2018, 139, 23–40. [Google Scholar] [CrossRef]
- Luo, T.; Xie, J.; Zhang, B.; Zhang, Y.; Li, C.; Zhou, J. An improved levy chaotic particle swarm optimization algorithm for energy-efficient cluster routing scheme in industrial wireless sensor networks. Expert Syst. Appl. 2024, 241, 122780. [Google Scholar] [CrossRef]
- Akbilgic, O.; Bozdogan, H.; Balaban, M.E. A novel Hybrid RBF Neural Networks model as a forecaster. Stat. Comput. 2013, 24, 365–375. [Google Scholar] [CrossRef]
- Seshagiri, S.; Khalil, H. Output feedback control of nonlinear systems using RBF neural networks. IEEE Trans. Neural Netw. 2000, 11, 69–79. [Google Scholar] [CrossRef]
- Wang, B.; Jahanshahi, H.; Volos, C.; Bekiros, S.; Khan, M.A.; Agarwal, P.; Aly, A.A. A New RBF Neural Network-Based Fault-Tolerant Active Control for Fractional Time-Delayed Systems. Electronics 2021, 10, 1501. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar] [CrossRef]
- Sheikhan, M.; Shahnazi, R.; Garoucy, S. Synchronization of general chaotic systems using neural controllers with application to secure communication. Neural Comput. Appl. 2011, 22, 361–373. [Google Scholar] [CrossRef]
- Zhang, X.; Hu, Y. Multiple-image encryption algorithm based on the 3D scrambling model and dynamic DNA coding. Opt. Laser Technol. 2021, 141, 107073. [Google Scholar] [CrossRef]
- Zhang, Y.; Dong, W.; Zhang, J.; Ding, Q. An Image Encryption Transmission Scheme Based on a Polynomial Chaotic Map. Entropy 2023, 25, 1005. [Google Scholar] [CrossRef] [PubMed]






| Input: ,, y0; Output: IMSE; |
| initialize , ; |
| [t, ym] = ODE45 (Sprott B (), tpan, y0); [t, ys] = ODE45 (Sprott B (), tpan, y0); |
| L = length(t); |
| initialize IMSE = 0; |
| for k: 1 to L |
| end for |
| IMSE = IMSE/(n*L); |
| Input: FP; Output: p*; |
| intonation: N = 5, Np = 5*N, num_particles = 1000, num_iteration = 50, rp = rq = 2, wl = 0.3, wu = 0.95, y0 = [y01,y02], xpan, lb = −125, ub = 125, p_position,g_positionϵR5*N, cost, vp, vg = inf; |
| generate randomly: p = p_position = g_position = p0; |
| for i = 1 to num_particles; |
| cost(i) = FP(p(i), y0, xpan); |
| update vp and vg according to comparative result with cost; |
| end for |
| for ite = 1 to num_iterationt; |
| w1 = wb(2) − (wb(2) − wb(1)) * ite/num_iteration; |
| for i = 1 to num_particles; |
| q(i) = w1 * q(i − 1) + cp * rp * (pp − p(i − 1)) + cq * rq * (pq − p(i − 1)); |
| restric the scope of q; |
| p(i) = q(i); restic the scope of p; |
| cost(i) = FP(p(i), y0, xpan); |
| update vp and vg according to comparative result with cost or the cost small enough; |
| end for |
| end for |
| Images | Lena | Ruler | Gray | Pepper | Boat |
|---|---|---|---|---|---|
| 247.985 | 242.063 | 237.382 | 217.067 | 245.313 |
| File Name | Original Image | Encrypted Image |
|---|---|---|
| Lena | 7.7319 | 7.9920 |
| Ruler | 0.5000 | 7.9956 |
| Gray | 4.3923 | 7.9970 |
| Pepper | 7.6698 | 7.9920 |
| Boat | 7.1941 | 7.9833 |
| Mean value | 5.4973 | 7.9920 |
| Schemes | Horizontal | Vertical | Diagonal |
|---|---|---|---|
| “Pepper” image | 0.9831 | 0.9835 | 0.9723 |
| Proposed method | −0.00100 | −0.00093 | 0.00100 |
| Images | NPCR (%) | UACI (%) | ||||
|---|---|---|---|---|---|---|
| R | G | B | R | G | B | |
| Pepper | 99.37 | 99.62 | 99.58 | 33.42 | 33.37 | 33.41 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Zeng, J.; Yan, W.; Ding, Q. RBFNN-PSO Intelligent Synchronisation Method for Sprott B Chaotic Systems with External Noise and Its Application in an Image Encryption System. Entropy 2024, 26, 855. https://doi.org/10.3390/e26100855
Zhang Y, Zeng J, Yan W, Ding Q. RBFNN-PSO Intelligent Synchronisation Method for Sprott B Chaotic Systems with External Noise and Its Application in an Image Encryption System. Entropy. 2024; 26(10):855. https://doi.org/10.3390/e26100855
Chicago/Turabian StyleZhang, Yanpeng, Jian Zeng, Wenhao Yan, and Qun Ding. 2024. "RBFNN-PSO Intelligent Synchronisation Method for Sprott B Chaotic Systems with External Noise and Its Application in an Image Encryption System" Entropy 26, no. 10: 855. https://doi.org/10.3390/e26100855
APA StyleZhang, Y., Zeng, J., Yan, W., & Ding, Q. (2024). RBFNN-PSO Intelligent Synchronisation Method for Sprott B Chaotic Systems with External Noise and Its Application in an Image Encryption System. Entropy, 26(10), 855. https://doi.org/10.3390/e26100855





