Permutation Entropy: An Ordinal Pattern-Based Resilience Indicator for Industrial Equipment
Abstract
:1. Introduction
2. Theoretical Background
2.1. The Concept of Resilience
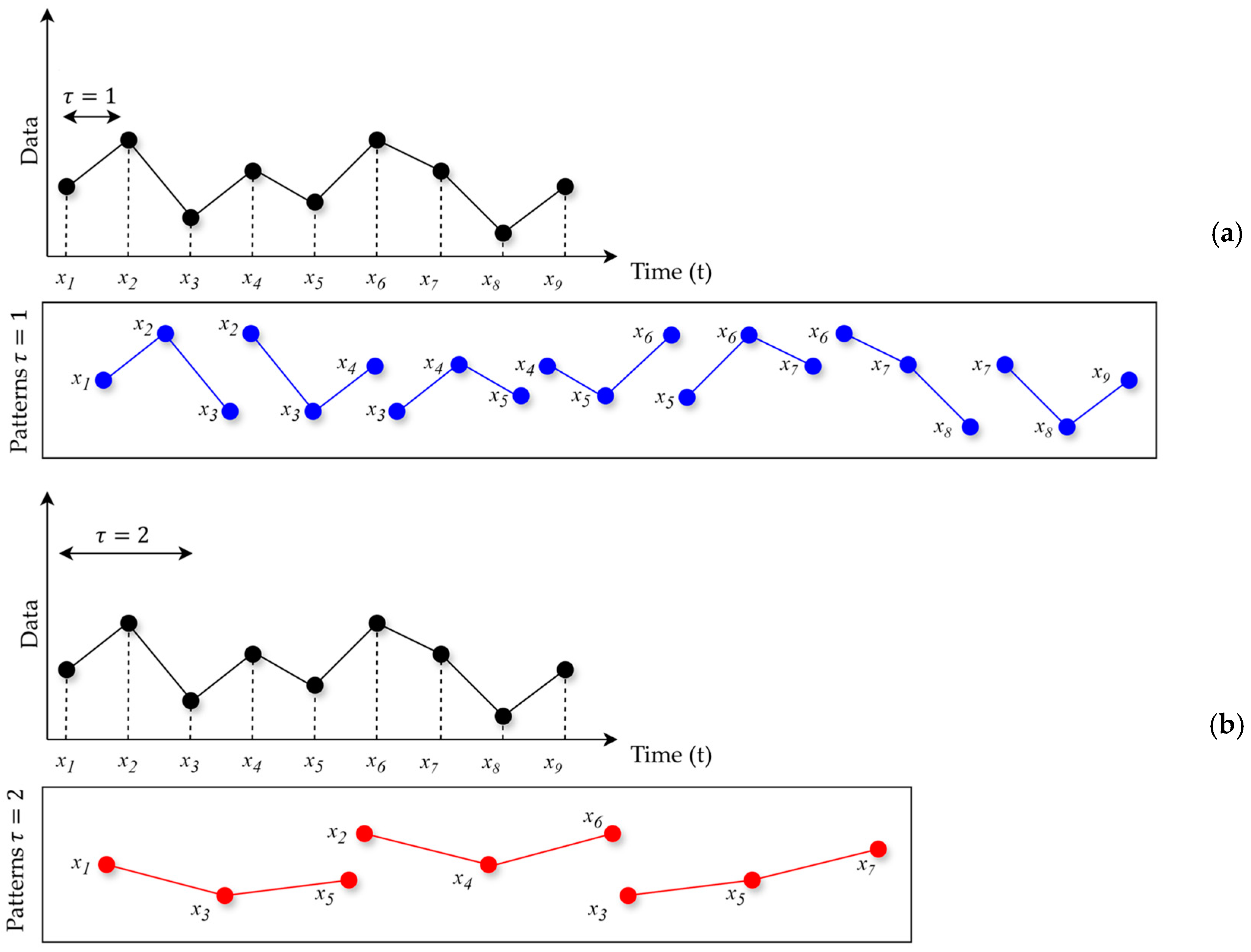
2.2. Ordinal Patterns
2.3. Permutation Entropy
3. Methodology
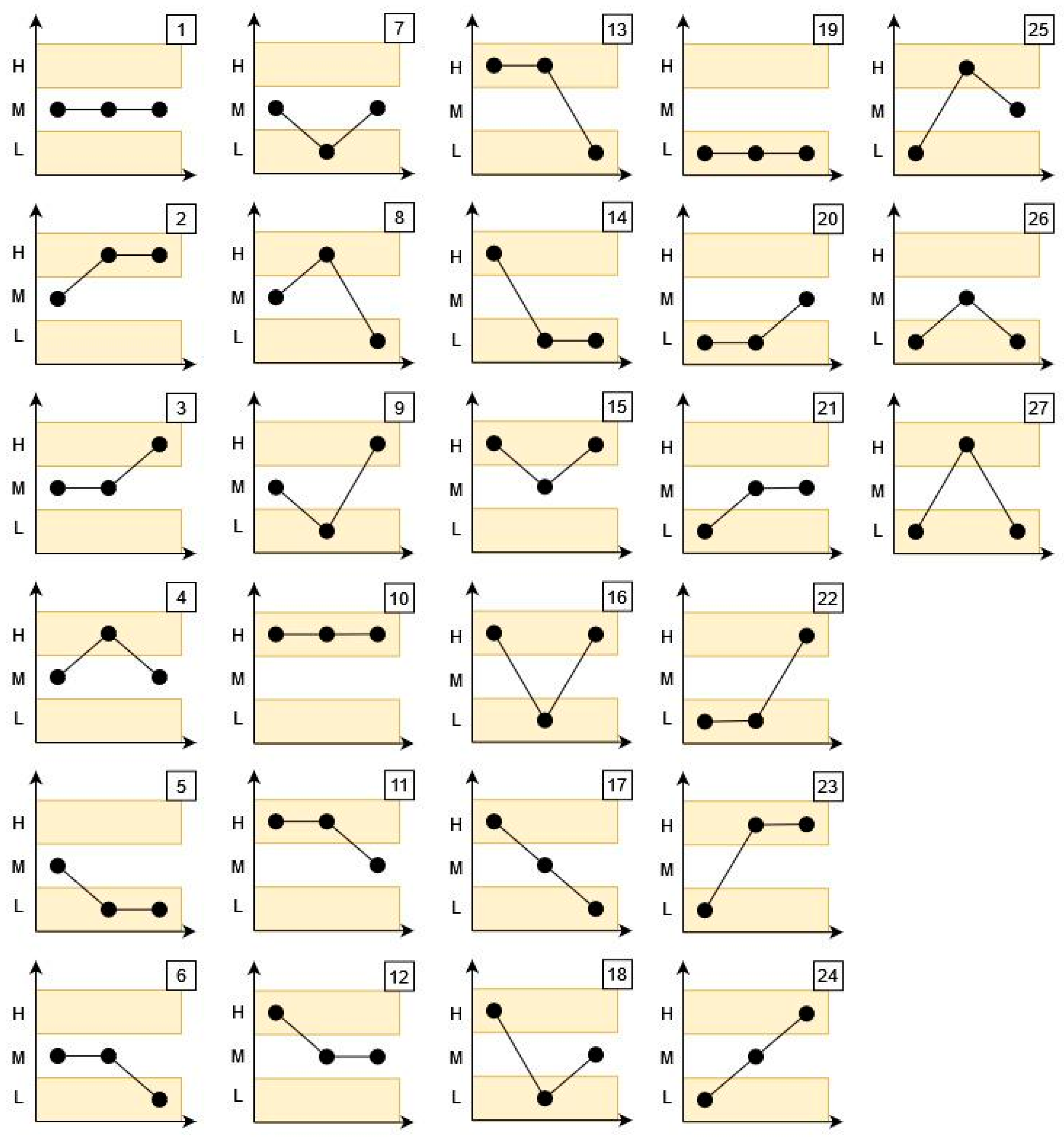
3.1. Ordinal Pattern Identification
3.2. Definition of Lookback
3.3. Resilience Factors
- Normal Performance: In this stage, the system operates regularly with an availability A0.
- Performance Drop: Due to a disruptive event, the system degrades from A0 to AD between times tI and tII.
- Disrupted Performance: The system stabilizes at a lower-than-acceptable availability level, AL. During this stage, corrective and maintenance actions are applied to begin recovering the system’s performance at time tIII.
- Recovery: Due to the recovery efforts, the system’s availability increases, surpassing the acceptable availability limit and reaching an acceptable level by time tIV.
- Recovered Performance: The system returns to normal operation, regaining its initial availability or something close to A0.
- ▪
- i is the pattern number between 1 and 27.
- ▪
- is the contribution of the first transition between nodes and .
- ▪
- is the contribution of the second transition between nodes and .
- ▪
- and are importance factors that modify the weight of the transitions intra-pattern and depending on how the pattern ends.
4. Application Example
- ▪
- ▪
- Lookback = 10
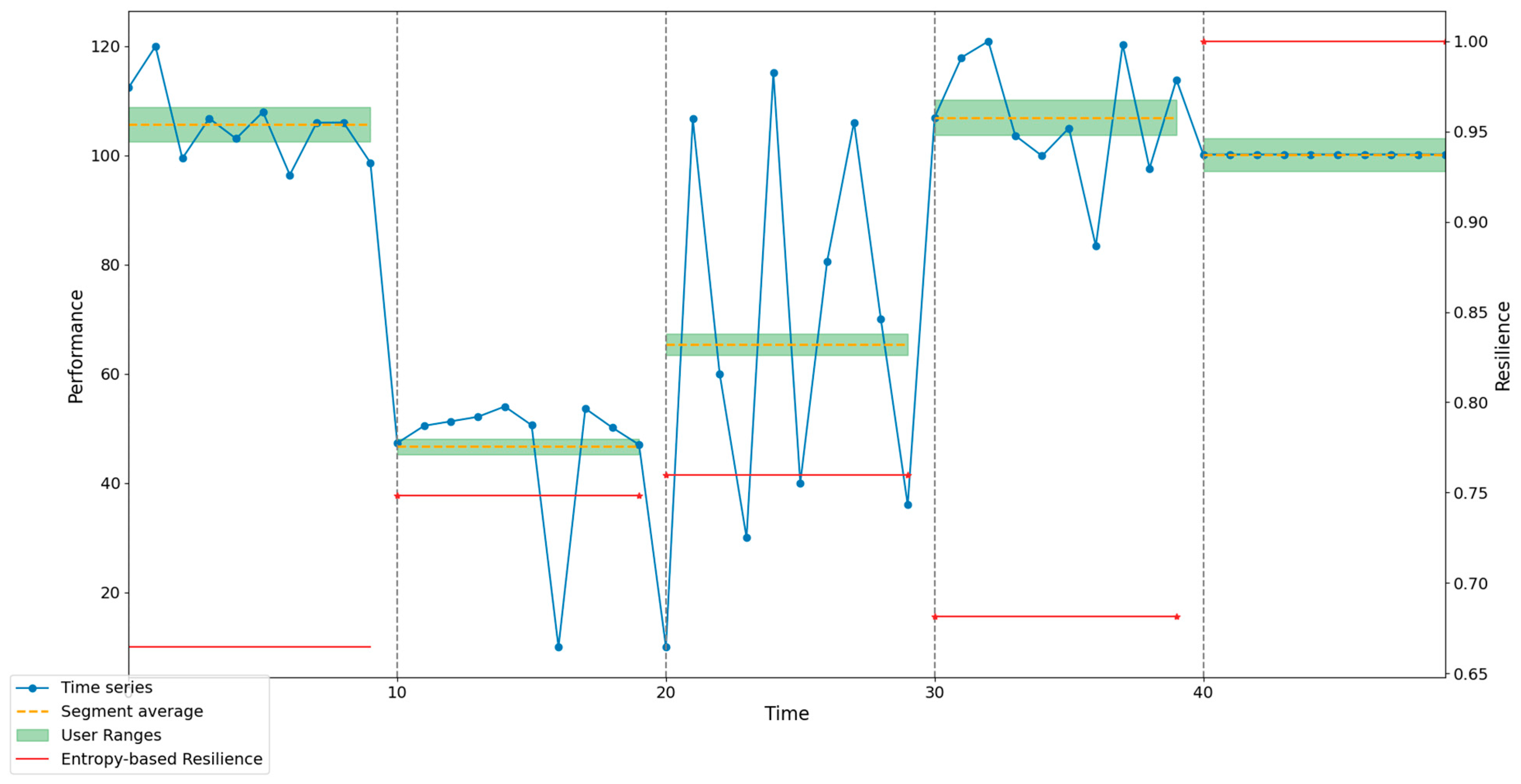
5. Case Study
- ▪
- is the system’s availability in a steady state before the shock.
- ▪
- is the time required to reach the initial steady state.
- ▪
- is the transient availability of the system immediately after shock .
- ▪
- is the system’s availability in the new steady state after shock .
- ▪
- and are the times corresponding to the states and , respectively.
- ▪
- is the system’s normalized performance over time .
- ▪
- is the normalized duration time of segment m.
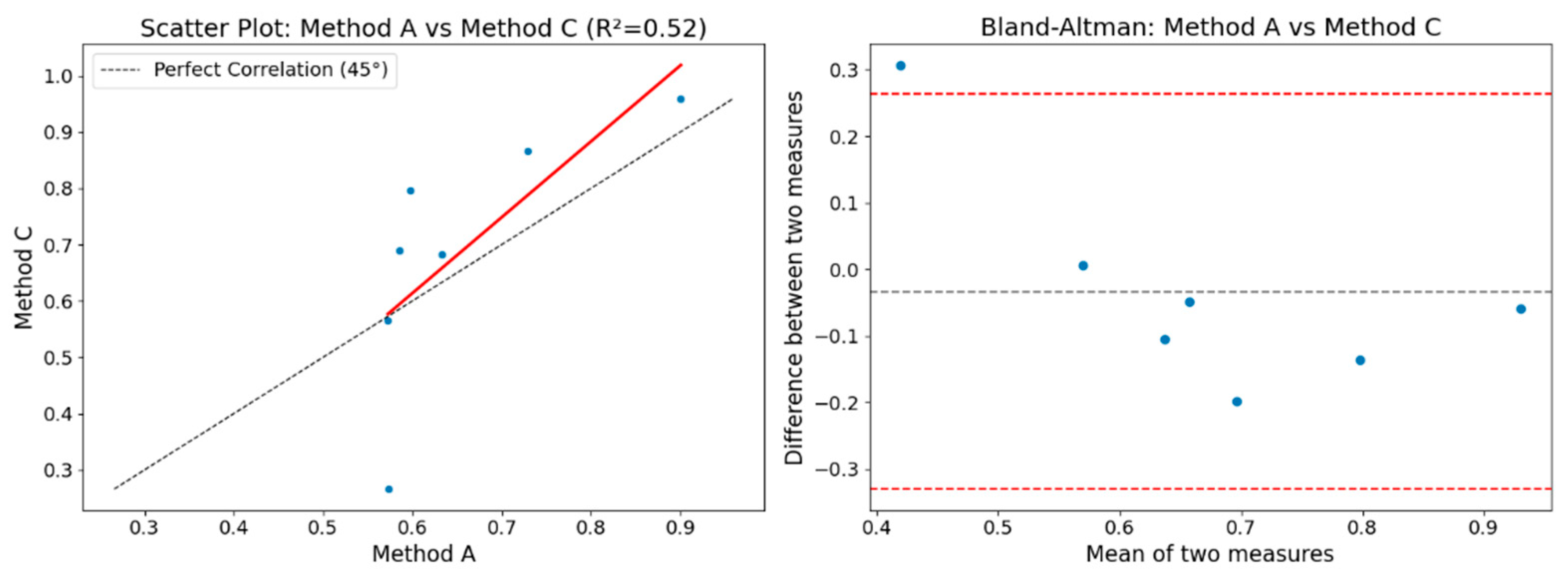
- Coefficient of Determination (R2): This method measures how well the observed outcomes are replicated by the model, indicating the proportion of the variance in the dependent variable that is predictable from the independent variable.
- Bland–Altman Model: This approach evaluates the agreement between two measurement methods by plotting the differences between the measures against their mean, allowing for the identification of any systematic bias [30].
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bhamra, R.; Dani, S.; Burnard, K. Resilience: The Concept, a Literature Review and Future Directions. Int. J. Prod. Res. 2011, 49, 5375–5393. [Google Scholar] [CrossRef]
- Hutchison, D.; Sterbenz, J.P.G. Architecture and Design for Resilient Networked Systems. Comput. Commun. 2018, 131, 13–21. [Google Scholar] [CrossRef]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Fiksel, J.; Polyviou, M.; Croxton, K.L.; Pettit, T.J. From Risk to Resilience: Learning to Deal with Disruption; MIT Sloan Management Review: Cambridge, MA, USA, 2015. [Google Scholar]
- Holling, C.S. Resilience of Ecological Systems. Annu. Rev. Ecol. Syst. 1973, 4, 1–23. [Google Scholar] [CrossRef]
- Callister, W.D.; Rethwisch, D.G. Fundamentals of Materials Science and Engineering: SI Version; John Wiley & Sons: Hoboken, NJ, USA, 2022. [Google Scholar]
- Pawar, B.; Park, S.; Hu, P.; Wang, Q.; Kay O’connor, M. Applications of Resilience Engineering Principles in Different Fields with a Focus on Industrial Systems: A Literature Review. J. Loss Prev. Process Ind. 2021, 69, 104366. [Google Scholar] [CrossRef]
- Hu, Z.; Mahadevan, S. Resilience Assessment Based on Time-Dependent System Reliability Analysis. J. Mech. Des. Trans. ASME 2016, 138, 111404. [Google Scholar] [CrossRef]
- Tierney, K.J.; Bruneau, M. Conceptualizing and Measuring Resilience. TR News: All-Hazards, Preparedness, Response, and Recovery. 2007. Available online: https://onlinepubs.trb.org/onlinepubs/trnews/trnews250_p14-17.pdf (accessed on 11 September 2024).
- Yodo, N.; Wang, P. Engineering Resilience Quantification and System Design Implications: A Literature Survey. J. Mech. Des. Trans. ASME 2016, 138, 1148. [Google Scholar] [CrossRef]
- Cholda, P.; Tapolcai, J.; Cinkler, T.; Wajda, K.; Jajszczyk, A. Quality of Resilience as a Network Reliability Characterization Tool. IEEE Netw. 2009, 23, 11–19. [Google Scholar] [CrossRef]
- Albasrawi, M.N.; Jarus, N.; Joshi, K.A.; Sarvestani, S.S. Analysis of Reliability and Resilience for Smart Grids. In Proceedings of the 2014 IEEE 38th Annual Computer Software and Applications Conference, Vasteras, Sweden, 21–25 July 2014. [Google Scholar]
- Ibrahim, M.; Alkhraibat, A. Resiliency Assessment of Microgrid Systems. Appl. Sci. 2020, 10, 1824. [Google Scholar] [CrossRef]
- Attoh-Okine, N.O.; Cooper, A.T.; Mensah, S.A. Formulation of Resilience Index of Urban Infrastructure Using Belief Functions. IEEE Syst. J. 2009, 3, 147–153. [Google Scholar] [CrossRef]
- Durán, O.; Aguilar, J.; Capaldo, A.; Arata, A. Fleet Resilience: Evaluating Maintenance Strategies in Critical Equipment. Appl. Sci. 2020, 11, 38. [Google Scholar] [CrossRef]
- Novak, B.S.; Aragoneses, A. Unveiling Dynamical Symmetries in 2D Chaotic Iterative Maps with Ordinal-Patterns-Based Complexity Quantifiers. Dynamics 2023, 3, 750–763. [Google Scholar] [CrossRef]
- Suriano, M.; Caram, L.F.; Rosso, O.A. Daily Streamflow of Argentine Rivers Analysis Using Information Theory Quantifiers. Entropy 2024, 26, 56. [Google Scholar] [CrossRef] [PubMed]
- Keller, K.; Sinn, M.; Emonds, J. Time Series from the Ordinal Viewpoint. Stoch. Dyn. 2007, 7, 247–272. [Google Scholar] [CrossRef]
- Keller, K.; Unakafov, A.M.; Unakafova, V.A. Ordinal Patterns, Entropy and EEG. Entropy 2014, 16, 6212–6239. [Google Scholar] [CrossRef]
- Neuman, Y.; Cohen, Y. Unveiling Herd Behavior in Financial Markets. J. Stat. Mech. Theory Exp. 2023, 2023, 083407. [Google Scholar] [CrossRef]
- Barbosa, K.; Frery, A. Temporal Assessment of Terrain Complexity through Ordinal Patterns in LiDAR Data. In Proceedings of the 2024 International Conference on Machine Intelligence for GeoAnalytics and Remote Sensing (MIGARS), Wellington, New Zealand, 8–10 April 2024; pp. 1–4. [Google Scholar]
- Osara, J.A. Thermodynamics of Manufacturing Processes—The Workpiece and the Machinery. Inventions 2019, 4, 28. [Google Scholar] [CrossRef]
- Zubair, M. A Brief History of Information Theory by Claude Shannon in Data Communication. J. Appl. Emerg. Sci. 2023, 13, 23–30. [Google Scholar]
- Bandt, C.; Pompe, B. Permutation Entropy: A Natural Complexity Measure for Time Series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef]
- Riedl, M.; Müller, A.; Wessel, N. Practical Considerations of Permutation Entropy: A Tutorial Review. Eur. Phys. J. Spec. Top. 2013, 222, 249–262. [Google Scholar] [CrossRef]
- Vajapeyam, S. Understanding Shannon’s Entropy Metric for Information. arXiv 2014, arXiv:1405.2061. [Google Scholar]
- Cai, B.; Xie, M.; Liu, Y.; Liu, Y.; Feng, Q. Availability-Based Engineering Resilience Metric and Its Corresponding Evaluation Methodology. Reliab. Eng. Syst. Saf. 2018, 172, 216–224. [Google Scholar] [CrossRef]
- Cheng, Y.; Elsayed, E.A.; Huang, Z. Systems Resilience Assessments: A Review, Framework and Metrics. Int. J. Prod. Res. 2022, 60, 595–622. [Google Scholar] [CrossRef]
- Merriam-Webster.com. Available online: https://www.merriam-webster.com/dictionary (accessed on 30 October 2024).
- Bland, J.M.; Altman, D.G. Statistical Methods for Assessing Agreement between Two Methods of Clinical Measurement. Int. J. Nurs. Stud. 2010, 47, 931–936. [Google Scholar] [CrossRef]

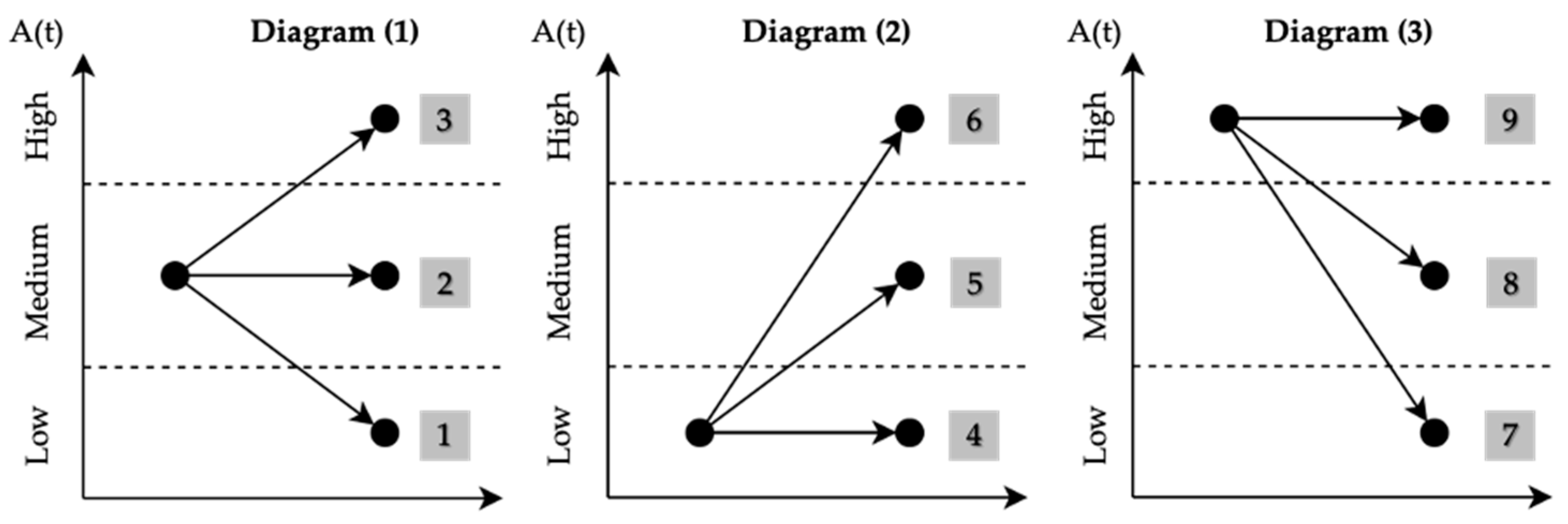

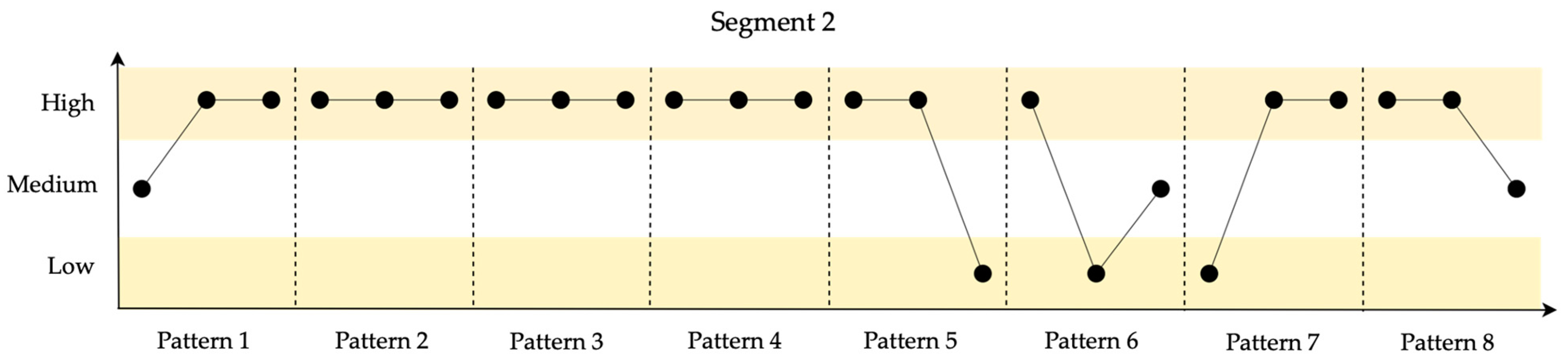


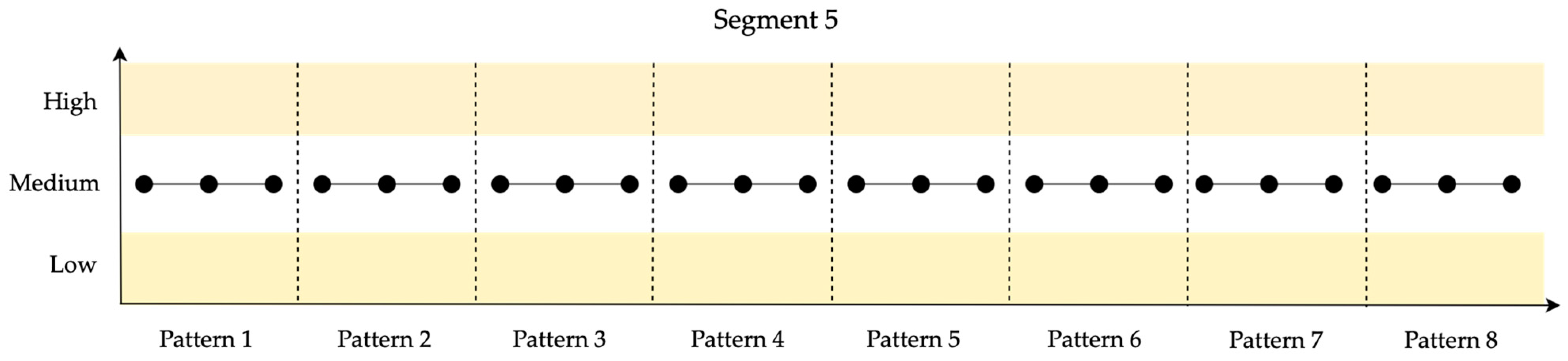
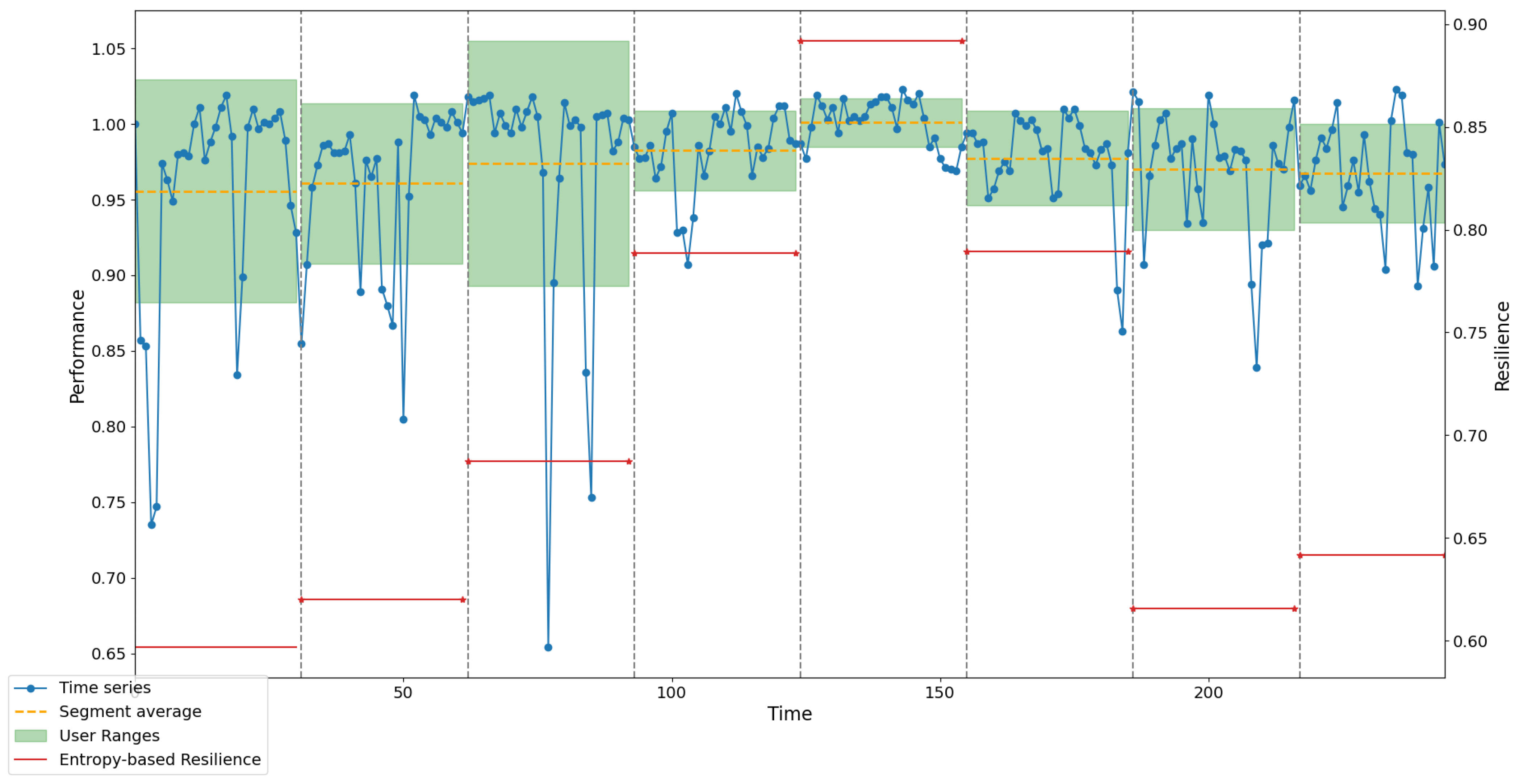
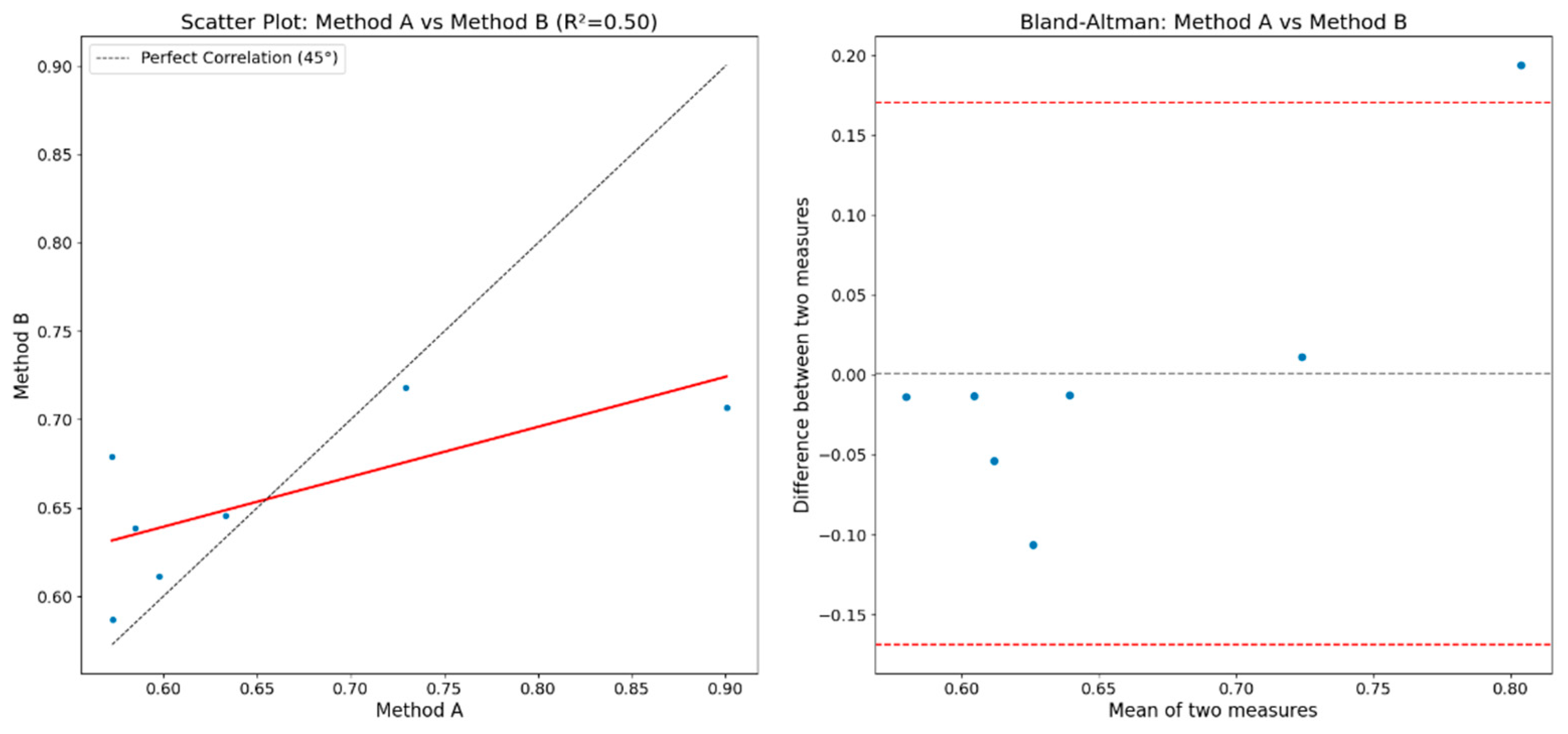
| Transition | Stage Name | Description | Contribution |
|---|---|---|---|
| 1 | Moderate drop | Performance reduction due to a disruptive event. | 5 |
| 2 | Stable at a medium level | The system operates within the expected range without significant changes in performance. | 3 |
| 3 | Sharp rise | The system’s performance improves. | 2 |
| 4 | Stable at a low level | After a disruptive event, the system stabilizes at a vulnerable performance level. | 4 |
| 5 | Gradual recovery | The system recovers to an expected performance state. | 2 |
| 6 | Rapid recovery | The system not only recovers but reaches a superior performance level. | 1 |
| 7 | Disruptive drop | Significant performance reduction from a high state to a vulnerable state. | 5 |
| 8 | Moderate decline | Performance reduces to a medium or expected level. | 3 |
| 9 | Stable at a high level | Performance improves and maintains at a high level. | 1 |
| Segment | Patterns [Pattern ID: Frequency] | Average | Standard Deviation | Resilience |
|---|---|---|---|---|
| 1 | {13: 1, 18: 1, 21: 2, 1: 1, 6: 2, 7: 1} | 105,660 | 6.606 | 0.635 |
| 2 | {2: 1, 10: 3, 13: 1, 16: 1, 23: 1, 11: 1} | 46,662 | 12.413 | 0.691 |
| 3 | {27: 2, 14: 1, 22: 1, 16: 1, 23: 1, 10: 1, 13: 1} | 65,439 | 34.551 | 0.631 |
| 4 | {2: 1, 13: 1, 14: 1, 20: 1, 26: 1, 9: 1, 27: 1, 16: 1} | 106,941 | 11.168 | 0.592 |
| 5 | {1: 8} | 100,161 | 0.000 | 1.000 |
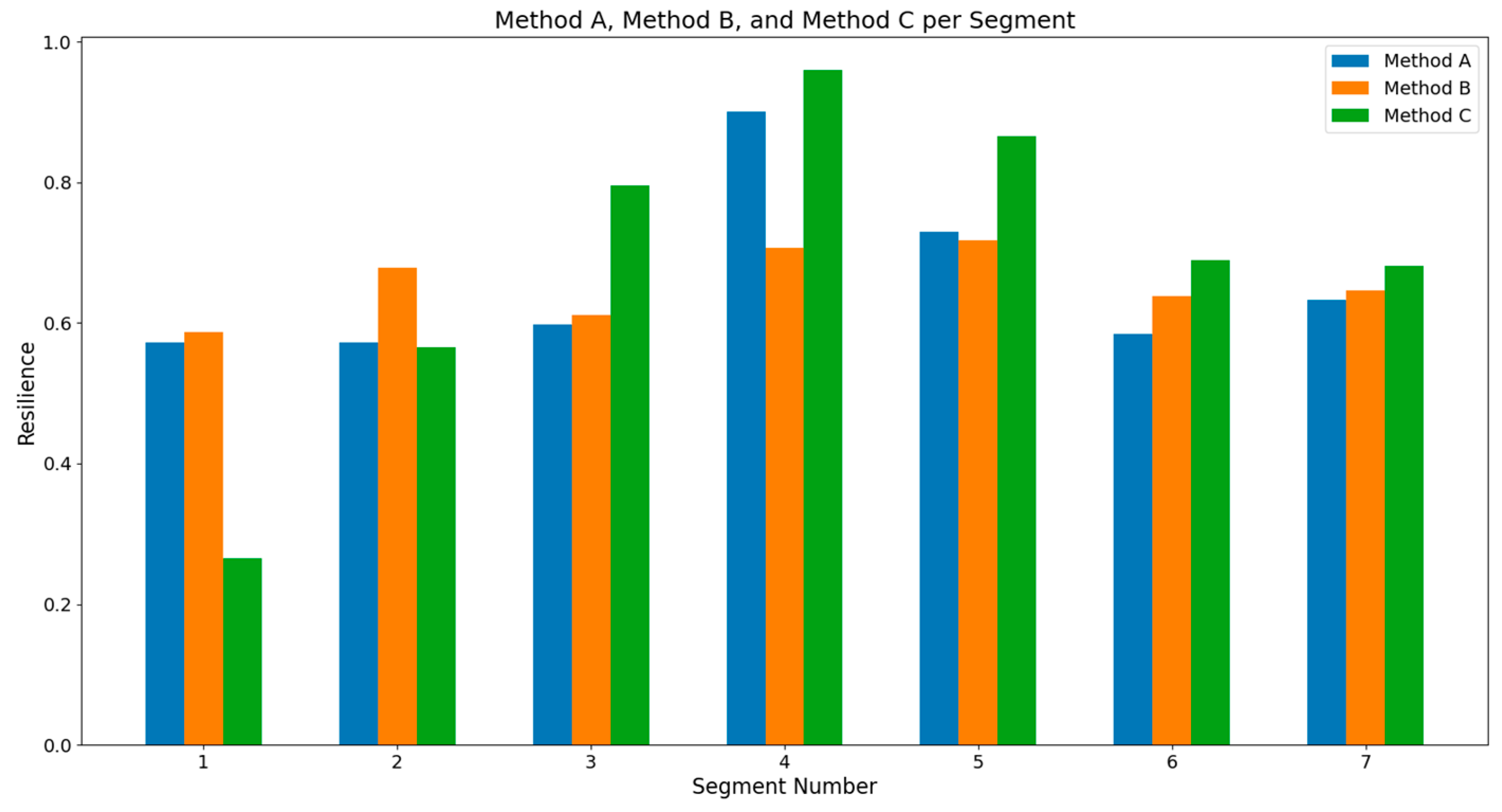
| Segment | Method A | Method B | Method C |
|---|---|---|---|
| 1 | 0.573 | 0.587 | 0.266 |
| 2 | 0.573 | 0.679 | 0.566 |
| 3 | 0.598 | 0.611 | 0.796 |
| 4 | 0.901 | 0.707 | 0.960 |
| 5 | 0.729 | 0.718 | 0.866 |
| 6 | 0.585 | 0.639 | 0.689 |
| 7 | 0.633 | 0.646 | 0.682 |
| 8 | 0.573 | 0.587 | 0.266 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salas, C.; Durán, O.; Vergara, J.I.; Arata, A. Permutation Entropy: An Ordinal Pattern-Based Resilience Indicator for Industrial Equipment. Entropy 2024, 26, 961. https://doi.org/10.3390/e26110961
Salas C, Durán O, Vergara JI, Arata A. Permutation Entropy: An Ordinal Pattern-Based Resilience Indicator for Industrial Equipment. Entropy. 2024; 26(11):961. https://doi.org/10.3390/e26110961
Chicago/Turabian StyleSalas, Christian, Orlando Durán, José Ignacio Vergara, and Adolfo Arata. 2024. "Permutation Entropy: An Ordinal Pattern-Based Resilience Indicator for Industrial Equipment" Entropy 26, no. 11: 961. https://doi.org/10.3390/e26110961
APA StyleSalas, C., Durán, O., Vergara, J. I., & Arata, A. (2024). Permutation Entropy: An Ordinal Pattern-Based Resilience Indicator for Industrial Equipment. Entropy, 26(11), 961. https://doi.org/10.3390/e26110961







