Quantum Circuit Architecture Search on a Superconducting Processor
Abstract
:1. Introduction
2. Materials and Methods
2.1. The Mechanism of QAS
2.2. Experimental Implementation
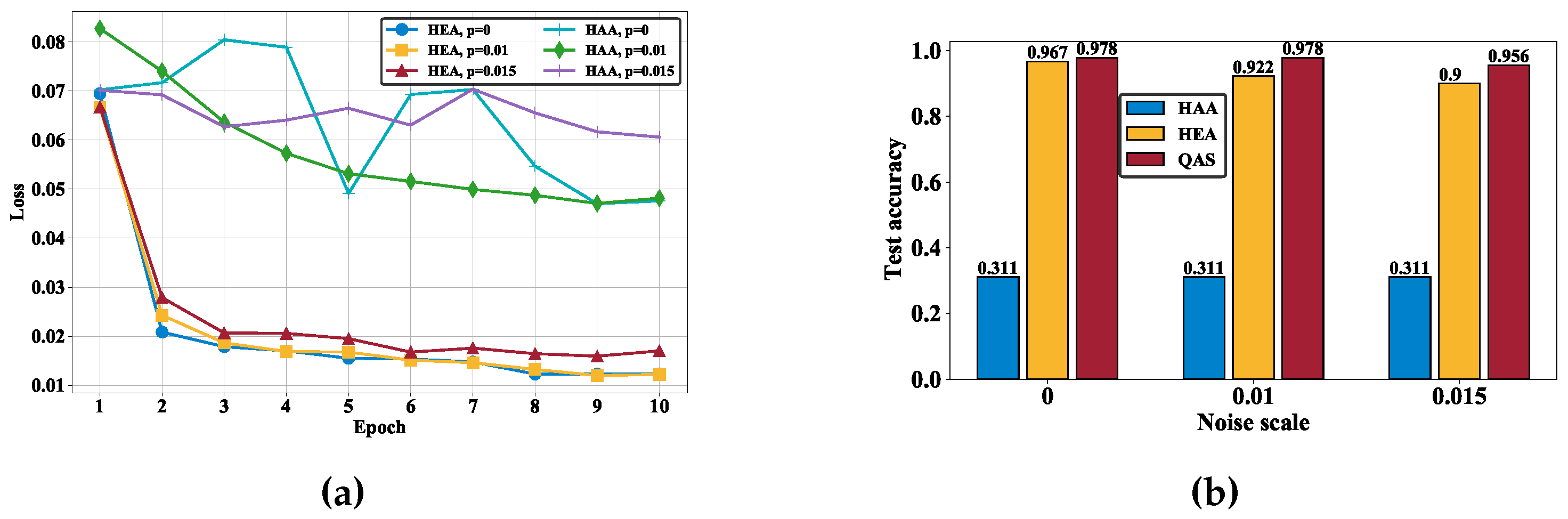
3. Results
4. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Experiment Setup
Appendix A.1. Device Parameters
Appendix A.2. Electronics and Control Wiring
| Parameter | Q1 | Q2 | Q3 | Q4 | Q5 | Q6 | Q7 | Q8 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (GHz) | |||||||||||||||
| (GHz) | |||||||||||||||
| () | |||||||||||||||
| () | |||||||||||||||
| () | 37 | 37 | 37 | 35 | 35 | 37 | 37 | 35 | |||||||
| () |

Appendix A.3. Noise Setup
| Parameter | Q1 | Q2 | Q3 | Q4 | Q5 | Q6 | Q7 | Q8 |
|---|---|---|---|---|---|---|---|---|
| (s) | ||||||||
| (s) | ||||||||
| (s) | ||||||||
| (s) |
Appendix A.4. Readout Correction
Appendix B. Implementation of Quantum Classifiers
Appendix B.1. Dataset
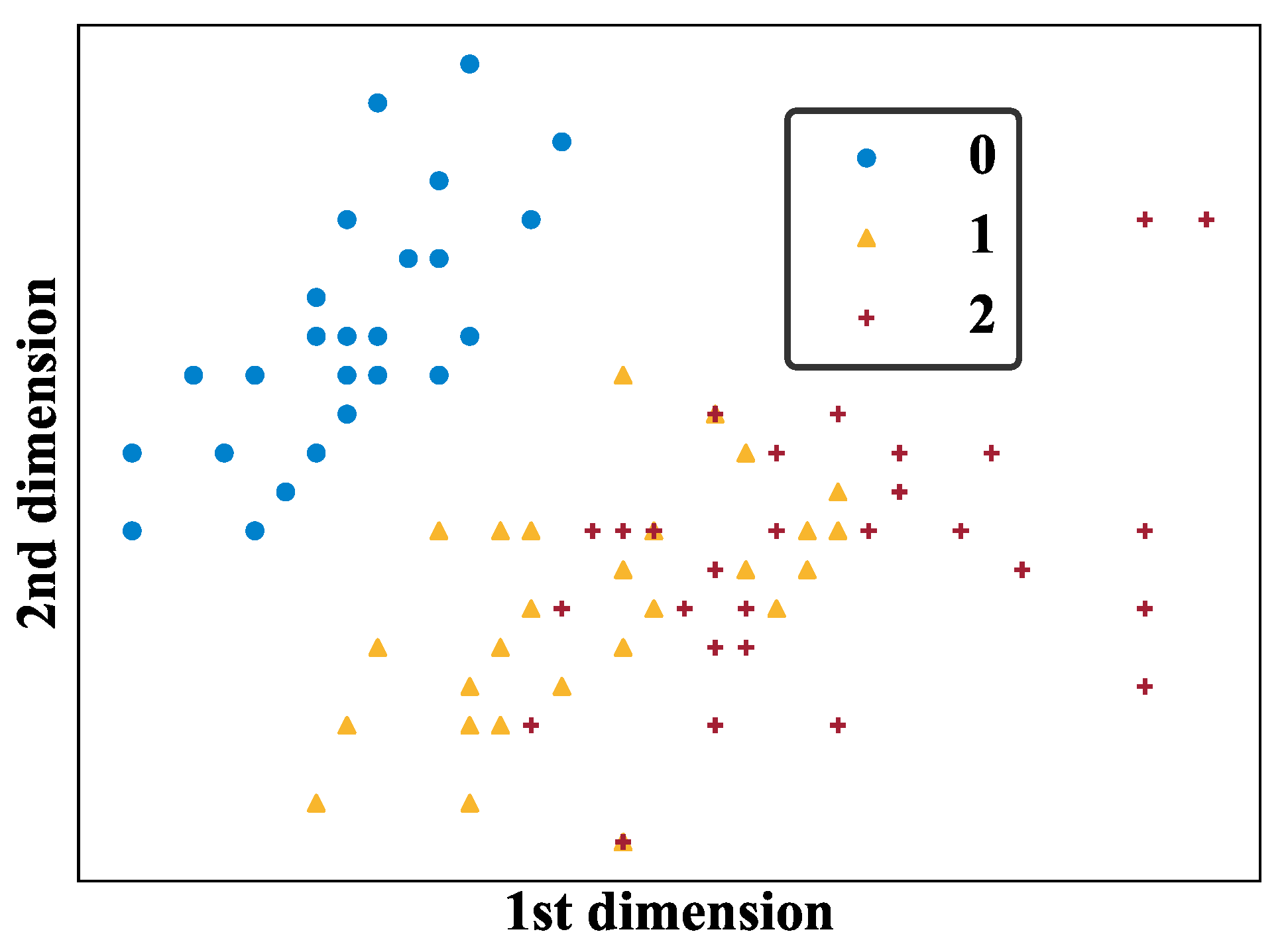
Appendix B.2. Objective Function and Accuracy Measure
Appendix B.3. Training Hyper-Parameters
Appendix C. More Details of the Results
Appendix C.1. PCA Used in the Visualization of Loss Landscape
Appendix C.2. Simulation Results
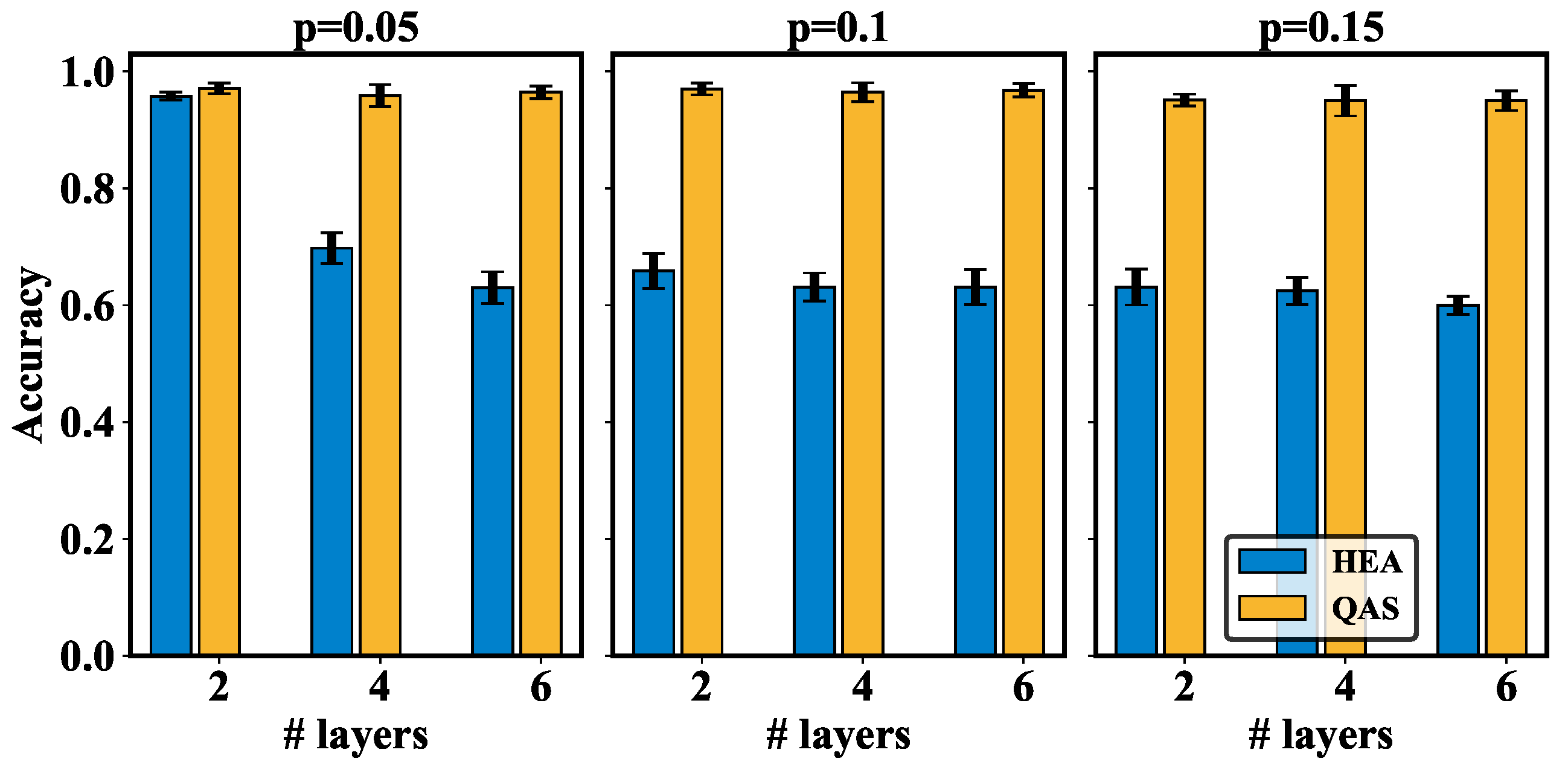
Appendix C.3. QAS in Quantum Approximate Optimization Algorithm (QAOA)
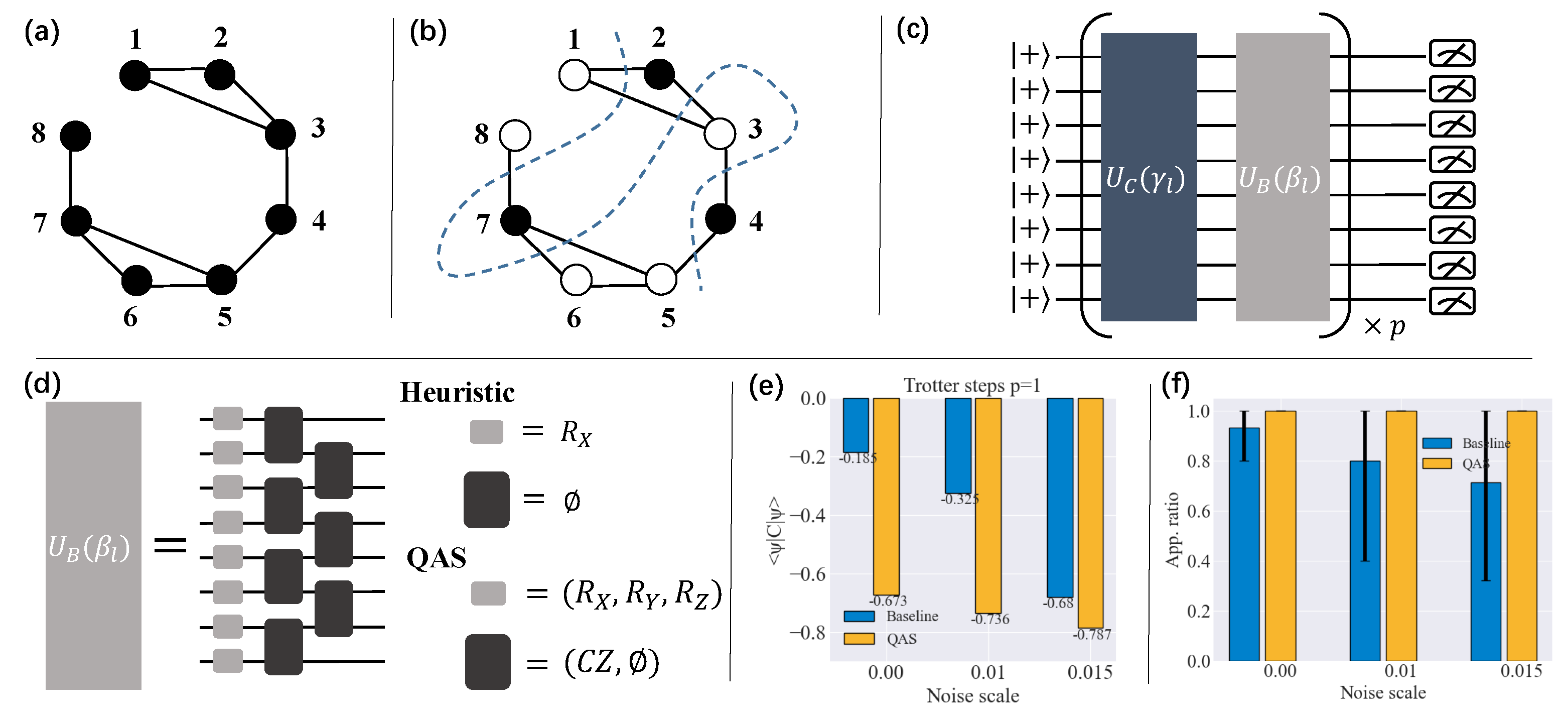
References
- Arute, F.; Arya, K.; Babbush, R.; Bacon, D.; Bardin, J.C.; Barends, R.; Biswas, R.; Boixo, S.; Brandao, F.G.; Buell, D.A.; et al. Quantum supremacy using a programmable superconducting processor. Nature 2019, 574, 505–510. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Bao, W.S.; Cao, S.; Chen, F.; Chen, M.C.; Chen, X.; Chung, T.H.; Deng, H.; Du, Y.; Fan, D.; et al. Strong quantum computational advantage using a superconducting quantum processor. Phys. Rev. Lett. 2021, 127, 180501. [Google Scholar] [CrossRef] [PubMed]
- Zhong, H.S.; Wang, H.; Deng, Y.H.; Chen, M.C.; Peng, L.C.; Luo, Y.H.; Qin, J.; Wu, D.; Ding, X.; Hu, Y.; et al. Quantum computational advantage using photons. Science 2020, 370, 1460–1463. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Q.; Cao, S.; Chen, F.; Chen, M.C.; Chen, X.; Chung, T.H.; Deng, H.; Du, Y.; Fan, D.; Gong, M.; et al. Quantum computational advantage via 60-qubit 24-cycle random circuit sampling. Sci. Bull. 2021, 67, 240–245. [Google Scholar] [CrossRef]
- Bharti, K.; Cervera-Lierta, A.; Kyaw, T.H.; Haug, T.; Alperin-Lea, S.; Anand, A.; Degroote, M.; Heimonen, H.; Kottmann, J.S.; Menke, T.; et al. Noisy intermediate-scale quantum algorithms. Rev. Mod. Phys. 2022, 94, 015004. [Google Scholar] [CrossRef]
- Cerezo, M.; Arrasmith, A.; Babbush, R.; Benjamin, S.C.; Endo, S.; Fujii, K.; McClean, J.R.; Mitarai, K.; Yuan, X.; Cincio, L.; et al. Variational quantum algorithms. Nat. Rev. Phys. 2021, 3, 625–644. [Google Scholar] [CrossRef]
- Preskill, J. Quantum computing in the NISQ era and beyond. Quantum 2018, 2, 79. [Google Scholar] [CrossRef]
- Abbas, A.; Sutter, D.; Zoufal, C.; Lucchi, A.; Figalli, A.; Woerner, S. The power of quantum neural networks. Nat. Comput. Sci. 2021, 1, 403–409. [Google Scholar] [CrossRef]
- Banchi, L.; Pereira, J.; Pirandola, S. Generalization in quantum machine learning: A quantum information standpoint. PRX Quantum 2021, 2, 040321. [Google Scholar] [CrossRef]
- Bu, K.; Koh, D.E.; Li, L.; Luo, Q.; Zhang, Y. Statistical complexity of quantum circuits. Phys. Rev. A 2022, 105, 062431. [Google Scholar] [CrossRef]
- Caro, M.C.; Datta, I. Pseudo-dimension of quantum circuits. Quantum Mach. Intell. 2020, 2, 14. [Google Scholar] [CrossRef]
- Caro, M.C.; Huang, H.Y.; Cerezo, M.; Sharma, K.; Sornborger, A.; Cincio, L.; Coles, P.J. Generalization in quantum machine learning from few training data. Nat. Commun. 2022, 13, 4919. [Google Scholar] [CrossRef]
- Du, Y.; Hsieh, M.H.; Liu, T.; You, S.; Tao, D. Learnability of Quantum Neural Networks. PRX Quantum 2021, 2, 040337. [Google Scholar] [CrossRef]
- Du, Y.; Tu, Z.; Yuan, X.; Tao, D. Efficient measure for the expressivity of variational quantum algorithms. Phys. Rev. Lett. 2022, 128, 080506. [Google Scholar] [CrossRef]
- Huang, H.Y.; Kueng, R.; Preskill, J. Information-theoretic bounds on quantum advantage in machine learning. Phys. Rev. Lett. 2021, 126, 190505. [Google Scholar] [CrossRef] [PubMed]
- Huang, H.Y.; Broughton, M.; Mohseni, M.; Babbush, R.; Boixo, S.; Neven, H.; McClean, J.R. Power of data in quantum machine learning. Nat. Commun. 2021, 12, 1–9. [Google Scholar] [CrossRef]
- Huang, H.Y.; Kueng, R.; Torlai, G.; Albert, V.V.; Preskill, J. Provably efficient machine learning for quantum many-body problems. Science 2022, 377, eabk3333. [Google Scholar] [CrossRef] [PubMed]
- Endo, S.; Sun, J.; Li, Y.; Benjamin, S.C.; Yuan, X. Variational quantum simulation of general processes. Phys. Rev. Lett. 2020, 125, 010501. [Google Scholar] [CrossRef]
- Kandala, A.; Mezzacapo, A.; Temme, K.; Takita, M.; Brink, M.; Chow, J.M.; Gambetta, J.M. Hardware-efficient variational quantum eigensolver for small molecules and quantum magnets. Nature 2017, 549, 242–246. [Google Scholar] [CrossRef]
- Pagano, G.; Bapat, A.; Becker, P.; Collins, K.S.; De, A.; Hess, P.W.; Kaplan, H.B.; Kyprianidis, A.; Tan, W.L.; Baldwin, C.; et al. Quantum approximate optimization of the long-range Ising model with a trapped-ion quantum simulator. Proc. Natl. Acad. Sci. USA 2020, 117, 25396–25401. [Google Scholar] [CrossRef]
- Cerezo, M.; Poremba, A.; Cincio, L.; Coles, P.J. Variational quantum fidelity estimation. Quantum 2020, 4, 248. [Google Scholar] [CrossRef]
- Du, Y.; Tao, D. On exploring practical potentials of quantum auto-encoder with advantages. arXiv 2021, arXiv:2106.15432. [Google Scholar]
- Carolan, J.; Mohseni, M.; Olson, J.P.; Prabhu, M.; Chen, C.; Bunandar, D.; Niu, M.Y.; Harris, N.C.; Wong, F.N.; Hochberg, M.; et al. Variational quantum unsampling on a quantum photonic processor. Nat. Phys. 2020, 16, 322–327. [Google Scholar] [CrossRef]
- Holmes, Z.; Sharma, K.; Cerezo, M.; Coles, P.J. Connecting ansatz expressibility to gradient magnitudes and barren plateaus. PRX Quantum 2022, 3, 010313. [Google Scholar] [CrossRef]
- McClean, J.R.; Boixo, S.; Smelyanskiy, V.N.; Babbush, R.; Neven, H. Barren plateaus in quantum neural network training landscapes. Nat. Commun. 2018, 9, 4812. [Google Scholar] [CrossRef]
- Cerezo, M.; Sone, A.; Volkoff, T.; Cincio, L.; Coles, P.J. Cost function dependent barren plateaus in shallow parametrized quantum circuits. Nat. Commun. 2021, 12, 1–12. [Google Scholar] [CrossRef]
- Pesah, A.; Cerezo, M.; Wang, S.; Volkoff, T.; Sornborger, A.T.; Coles, P.J. Absence of Barren Plateaus in Quantum Convolutional Neural Networks. Phys. Rev. X 2021, 11, 041011. [Google Scholar] [CrossRef]
- Grant, E.; Wossnig, L.; Ostaszewski, M.; Benedetti, M. An initialization strategy for addressing barren plateaus in parametrized quantum circuits. Quantum 2019, 3, 214. [Google Scholar] [CrossRef]
- Bravyi, S.; Kliesch, A.; Koenig, R.; Tang, E. Obstacles to variational quantum optimization from symmetry protection. Phys. Rev. Lett. 2020, 125, 260505. [Google Scholar] [CrossRef]
- Havlíček, V.; Córcoles, A.D.; Temme, K.; Harrow, A.W.; Kandala, A.; Chow, J.M.; Gambetta, J.M. Supervised learning with quantum-enhanced feature spaces. Nature 2019, 567, 209–212. [Google Scholar] [CrossRef]
- Huang, H.L.; Du, Y.; Gong, M.; Zhao, Y.; Wu, Y.; Wang, C.; Li, S.; Liang, F.; Lin, J.; Xu, Y.; et al. Experimental quantum generative adversarial networks for image generation. Phys. Rev. Appl. 2021, 16, 024051. [Google Scholar] [CrossRef]
- Peters, E.; Caldeira, J.; Ho, A.; Leichenauer, S.; Mohseni, M.; Neven, H.; Spentzouris, P.; Strain, D.; Perdue, G.N. Machine learning of high dimensional data on a noisy quantum processor. npj Quantum Inf. 2021, 7, 161. [Google Scholar] [CrossRef]
- Rudolph, M.S.; Toussaint, N.B.; Katabarwa, A.; Johri, S.; Peropadre, B.; Perdomo-Ortiz, A. Generation of high-resolution handwritten digits with an ion-trap quantum computer. Phys. Rev. X 2022, 12, 031010. [Google Scholar] [CrossRef]
- Arute, F.; Arya, K.; Babbush, R.; Bacon, D.; Bardin, J.C.; Barends, R.; Boixo, S.; Broughton, M.; Buckley, B.B.; Buell, D.A.; et al. Hartree-Fock on a superconducting qubit quantum computer. Science 2020, 369, 1084–1089. [Google Scholar]
- Robert, A.; Barkoutsos, P.K.; Woerner, S.; Tavernelli, I. Resource-efficient quantum algorithm for protein folding. npj Quantum Inf. 2021, 7, 38. [Google Scholar] [CrossRef]
- Kais, S. Introduction to quantum information and computation for chemistry. In Quantum Information and Computation for Chemistry; Wiley: Hoboken, NJ, USA, 2014; pp. 1–38. [Google Scholar]
- Wecker, D.; Hastings, M.B.; Wiebe, N.; Clark, B.K.; Nayak, C.; Troyer, M. Solving strongly correlated electron models on a quantum computer. Phys. Rev. A 2015, 92, 062318. [Google Scholar] [CrossRef]
- Cai, X.; Fang, W.H.; Fan, H.; Li, Z. Quantum computation of molecular response properties. Phys. Rev. Res. 2020, 2, 033324. [Google Scholar] [CrossRef]
- Harrigan, M.P.; Sung, K.J.; Neeley, M.; Satzinger, K.J.; Arute, F.; Arya, K.; Atalaya, J.; Bardin, J.C.; Barends, R.; Boixo, S.; et al. Quantum approximate optimization of non-planar graph problems on a planar superconducting processor. Nat. Phys. 2021, 17, 332–336. [Google Scholar] [CrossRef]
- Lacroix, N.; Hellings, C.; Andersen, C.K.; Di Paolo, A.; Remm, A.; Lazar, S.; Krinner, S.; Norris, G.J.; Gabureac, M.; Heinsoo, J.; et al. Improving the performance of deep quantum optimization algorithms with continuous gate sets. PRX Quantum 2020, 1, 110304. [Google Scholar] [CrossRef]
- Zhou, L.; Wang, S.T.; Choi, S.; Pichler, H.; Lukin, M.D. Quantum approximate optimization algorithm: Performance, mechanism, and implementation on near-term devices. Phys. Rev. X 2020, 10, 021067. [Google Scholar] [CrossRef]
- Hadfield, S.; Wang, Z.; O’Gorman, B.; Rieffel, E.G.; Venturelli, D.; Biswas, R. From the quantum approximate optimization algorithm to a quantum alternating operator ansatz. Algorithms 2019, 12, 34. [Google Scholar] [CrossRef]
- Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef]
- Poland, K.; Beer, K.; Osborne, T.J. No free lunch for quantum machine learning. arXiv 2020, arXiv:2003.14103. [Google Scholar]
- Gard, B.T.; Zhu, L.; Barron, G.S.; Mayhall, N.J.; Economou, S.E.; Barnes, E. Efficient symmetry-preserving state preparation circuits for the variational quantum eigensolver algorithm. npj Quantum Inf. 2020, 6, 10. [Google Scholar] [CrossRef]
- Ganzhorn, M.; Egger, D.J.; Barkoutsos, P.; Ollitrault, P.; Salis, G.; Moll, N.; Roth, M.; Fuhrer, A.; Mueller, P.; Woerner, S.; et al. Gate-efficient simulation of molecular eigenstates on a quantum computer. Phys. Rev. Appl. 2019, 11, 044092. [Google Scholar] [CrossRef]
- Choquette, A.; Di Paolo, A.; Barkoutsos, P.K.; Sénéchal, D.; Tavernelli, I.; Blais, A. Quantum-optimal-control-inspired ansatz for variational quantum algorithms. Phys. Rev. Res. 2021, 3, 023092. [Google Scholar] [CrossRef]
- Cao, Y.; Romero, J.; Olson, J.P.; Degroote, M.; Johnson, P.D.; Kieferová, M.; Kivlichan, I.D.; Menke, T.; Peropadre, B.; Sawaya, N.P.; et al. Quantum chemistry in the age of quantum computing. Chem. Rev. 2019, 119, 10856–10915. [Google Scholar] [CrossRef] [PubMed]
- Romero, J.; Babbush, R.; McClean, J.R.; Hempel, C.; Love, P.J.; Aspuru-Guzik, A. Strategies for quantum computing molecular energies using the unitary coupled cluster ansatz. Quantum Sci. Technol. 2018, 4, 014008. [Google Scholar] [CrossRef]
- Cervera-Lierta, A.; Kottmann, J.S.; Aspuru-Guzik, A. Meta-Variational Quantum Eigensolver: Learning Energy Profiles of Parameterized Hamiltonians for Quantum Simulation. PRX Quantum 2021, 2, 020329. [Google Scholar] [CrossRef]
- Parrish, R.M.; Hohenstein, E.G.; McMahon, P.L.; Martínez, T.J. Quantum computation of electronic transitions using a variational quantum eigensolver. Phys. Rev. Lett. 2019, 122, 230401. [Google Scholar] [CrossRef]
- Petit, L.; Eenink, H.; Russ, M.; Lawrie, W.; Hendrickx, N.; Philips, S.; Clarke, J.; Vandersypen, L.; Veldhorst, M. Universal quantum logic in hot silicon qubits. Nature 2020, 580, 355–359. [Google Scholar] [CrossRef] [PubMed]
- DiVincenzo, D.P. The physical implementation of quantum computation. Fortschritte Phys. Prog. Phys. 2000, 48, 771–783. [Google Scholar] [CrossRef]
- Devoret, M.H.; Schoelkopf, R.J. Superconducting circuits for quantum information: An outlook. Science 2013, 339, 1169–1174. [Google Scholar] [CrossRef] [PubMed]
- Cincio, L.; Rudinger, K.; Sarovar, M.; Coles, P.J. Machine learning of noise-resilient quantum circuits. PRX Quantum 2021, 2, 010324. [Google Scholar] [CrossRef]
- Chivilikhin, D.; Samarin, A.; Ulyantsev, V.; Iorsh, I.; Oganov, A.; Kyriienko, O. MoG-VQE: Multiobjective genetic variational quantum eigensolver. arXiv 2020, arXiv:2007.04424. [Google Scholar]
- Rattew, A.G.; Hu, S.; Pistoia, M.; Chen, R.; Wood, S. A domain-agnostic, noise-resistant, hardware-efficient evolutionary variational quantum eigensolver. arXiv 2019, arXiv:1910.09694. [Google Scholar]
- He, Z.; Chen, C.; Li, L.; Zheng, S.; Situ, H. Quantum Architecture Search with Meta-Learning. Adv. Quantum Technol. 2022, 5, 2100134. [Google Scholar] [CrossRef]
- Meng, F.X.; Li, Z.T.; Yu, X.T.; Zhang, Z.C. Quantum Circuit Architecture Optimization for Variational Quantum Eigensolver via Monto Carlo Tree Search. IEEE Trans. Quantum Eng. 2021, 2, 3103910. [Google Scholar] [CrossRef]
- Kuo, E.J.; Fang, Y.L.L.; Chen, S.Y.C. Quantum Architecture Search via Deep Reinforcement Learning. arXiv 2021, arXiv:2104.07715. [Google Scholar]
- Zhang, S.X.; Hsieh, C.Y.; Zhang, S.; Yao, H. Differentiable quantum architecture search. Quantum Sci. Technol. 2022, 7, 045023. [Google Scholar] [CrossRef]
- Zhang, S.X.; Hsieh, C.Y.; Zhang, S.; Yao, H. Neural predictor based quantum architecture search. Mach. Learn. Sci. Technol. 2021, 2, 045027. [Google Scholar] [CrossRef]
- Ostaszewski, M.; Trenkwalder, L.M.; Masarczyk, W.; Scerri, E.; Dunjko, V. Reinforcement learning for optimization of variational quantum circuit architectures. Adv. Neural Inf. Process. Syst. 2021, 34, 18182–18194. [Google Scholar]
- Pirhooshyaran, M.; Terlaky, T. Quantum circuit design search. Quantum Mach. Intell. 2021, 3, 25. [Google Scholar] [CrossRef]
- Lei, C.; Du, Y.; Mi, P.; Yu, J.; Liu, T. Neural Auto-designer for Enhanced Quantum Kernels. In Proceedings of the Twelfth International Conference on Learning Representations, Vienna, Austria, 7–11 May 2024. [Google Scholar]
- Bilkis, M.; Cerezo, M.; Verdon, G.; Coles, P.J.; Cincio, L. A semi-agnostic ansatz with variable structure for variational quantum algorithms. Quantum Mach. Intell. 2023, 5, 43. [Google Scholar] [CrossRef]
- Grimsley, H.R.; Economou, S.E.; Barnes, E.; Mayhall, N.J. An adaptive variational algorithm for exact molecular simulations on a quantum computer. Nat. Commun. 2019, 10, 3007. [Google Scholar] [CrossRef] [PubMed]
- Tang, H.L.; Shkolnikov, V.; Barron, G.S.; Grimsley, H.R.; Mayhall, N.J.; Barnes, E.; Economou, S.E. qubit-ADAPT-VQE: An adaptive algorithm for constructing hardware-efficient ansätze on a quantum processor. PRX Quantum 2021, 2, 020310. [Google Scholar] [CrossRef]
- Du, Y.; Huang, T.; You, S.; Hsieh, M.H.; Tao, D. Quantum circuit architecture search for variational quantum algorithms. npj Quantum Inf. 2022, 8, 62. [Google Scholar] [CrossRef]
- Farhi, E.; Goldstone, J.; Gutmann, S. A quantum approximate optimization algorithm. arXiv 2014, arXiv:1411.4028. [Google Scholar]
- Mckay, D.C.; Wood, C.J.; Sheldon, S.; Chow, J.M.; Gambetta, J.M. Efficient Z-Gates for Quantum Computing. Phys. Rev. A 2017, 96, 022330. [Google Scholar] [CrossRef]
- Pearson, K. LIII. On lines and planes of closest fit to systems of points in space. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1901, 2, 559–572. [Google Scholar] [CrossRef]
- Rudolph, M.S.; Sim, S.; Raza, A.; Stechly, M.; McClean, J.R.; Anschuetz, E.R.; Serrano, L.; Perdomo-Ortiz, A. ORQVIZ: Visualizing High-Dimensional Landscapes in Variational Quantum Algorithms. arXiv 2021, arXiv:2111.04695. [Google Scholar]
- Peruzzo, A.; McClean, J.; Shadbolt, P.; Yung, M.H.; Zhou, X.Q.; Love, P.J.; Aspuru-Guzik, A.; O’brien, J.L. A variational eigenvalue solver on a photonic quantum processor. Nat. Commun. 2014, 5, 4213. [Google Scholar] [CrossRef] [PubMed]
- Yan, F.; Campbell, D.; Krantz, P.; Kjaergaard, M.; Kim, D.; Yoder, J.L.; Hover, D.; Sears, A.; Kerman, A.J.; Orlando, T.P.; et al. Distinguishing coherent and thermal photon noise in a circuit quantum electrodynamical system. Phys. Rev. Lett. 2018, 120, 260504. [Google Scholar] [CrossRef] [PubMed]
- Fisher, R.A. The use of multiple measurements in taxonomic problems. Ann. Eugen. 1936, 7, 179–188. [Google Scholar] [CrossRef]
- Kiefer, J.; Wolfowitz, J. Stochastic estimation of the maximum of a regression function. Ann. Math. Stat. 1952, 23, 462–466. [Google Scholar] [CrossRef]
- Mitarai, K.; Negoro, M.; Kitagawa, M.; Fujii, K. Quantum circuit learning. Phys. Rev. A 2018, 98, 032309. [Google Scholar] [CrossRef]
- Govia, L.; Poole, C.; Saffman, M.; Krovi, H. Freedom of mixer rotation-axis improves performance in the quantum approximate optimization algorithm. arXiv 2021, arXiv:2107.13129. [Google Scholar] [CrossRef]
- Farhi, E.; Goldstone, J.; Gutmann, S.; Neven, H. Quantum algorithms for fixed qubit architectures. arXiv 2017, arXiv:1703.06199. [Google Scholar]
- Bapat, A.; Jordan, S. Bang-bang control as a design principle for classical and quantum optimization algorithms. arXiv 2018, arXiv:1812.02746. [Google Scholar] [CrossRef]
- Yu, Y.; Cao, C.; Dewey, C.; Wang, X.B.; Shannon, N.; Joynt, R. Quantum Approximate Optimization Algorithm with Adaptive Bias Fields. arXiv 2021, arXiv:2105.11946. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Linghu, K.; Qian, Y.; Wang, R.; Hu, M.-J.; Li, Z.; Li, X.; Xu, H.; Zhang, J.; Ma, T.; Zhao, P.; et al. Quantum Circuit Architecture Search on a Superconducting Processor. Entropy 2024, 26, 1025. https://doi.org/10.3390/e26121025
Linghu K, Qian Y, Wang R, Hu M-J, Li Z, Li X, Xu H, Zhang J, Ma T, Zhao P, et al. Quantum Circuit Architecture Search on a Superconducting Processor. Entropy. 2024; 26(12):1025. https://doi.org/10.3390/e26121025
Chicago/Turabian StyleLinghu, Kehuan, Yang Qian, Ruixia Wang, Meng-Jun Hu, Zhiyuan Li, Xuegang Li, Huikai Xu, Jingning Zhang, Teng Ma, Peng Zhao, and et al. 2024. "Quantum Circuit Architecture Search on a Superconducting Processor" Entropy 26, no. 12: 1025. https://doi.org/10.3390/e26121025
APA StyleLinghu, K., Qian, Y., Wang, R., Hu, M.-J., Li, Z., Li, X., Xu, H., Zhang, J., Ma, T., Zhao, P., Liu, D. E., Hsieh, M.-H., Wu, X., Du, Y., Tao, D., Jin, Y., & Yu, H. (2024). Quantum Circuit Architecture Search on a Superconducting Processor. Entropy, 26(12), 1025. https://doi.org/10.3390/e26121025






