Infinite-Dimensional Quantum Entropy: The Unified Entropy Case
Abstract
1. Introduction
1.1. On the Standard Notation Used
1.2. Entropy-Based Entanglement Measures in Bipartite Systems
- :
- The map H is concave (or convex) and finite (or continuous in -norm) on ;
- :
- ;
- :
- ;
- :
- H is non-increasing under the action of quantum operations;
- :
- If , , then .
- :
- For :
- :
- If is separable, then
- :
- is non-increasing under local quantum operations;
- :
- The measure should be invariant under the action of local unitary groups.
2. Quantum von Neumann Entropy and Fredholm Determinants
3. The Unified Quantum Entropies in Terms of the Fredholm Determinants
3.1. The Hu–Ye Unified Entropy for the Finite-Dimensional Case
3.2. HY Entropy Summary ()
- :
- Connection with other entropies:
- (i)
- where stands for the Tsallis entropy functional and the limit is taken pointwise on .
- (ii)
- For any admissible value of r and :
- (iii)
- And for any admissible value of r:where is the Rényi entropy.
- :
- Non-negativity and boundness for any admissible values of r and s:and:
- (i)
- if (see [20]),
- (ii)
- iff , where .
- :
- If , then for any :
- (i)
- (ii)
- Letthen,where .
- (iii)
- if , then for any admissible :
- :
- Continuity. It is known [20] that for and :
- :
- Concavity. Let , , and or , , and let , , . Then (see [20]),
- :
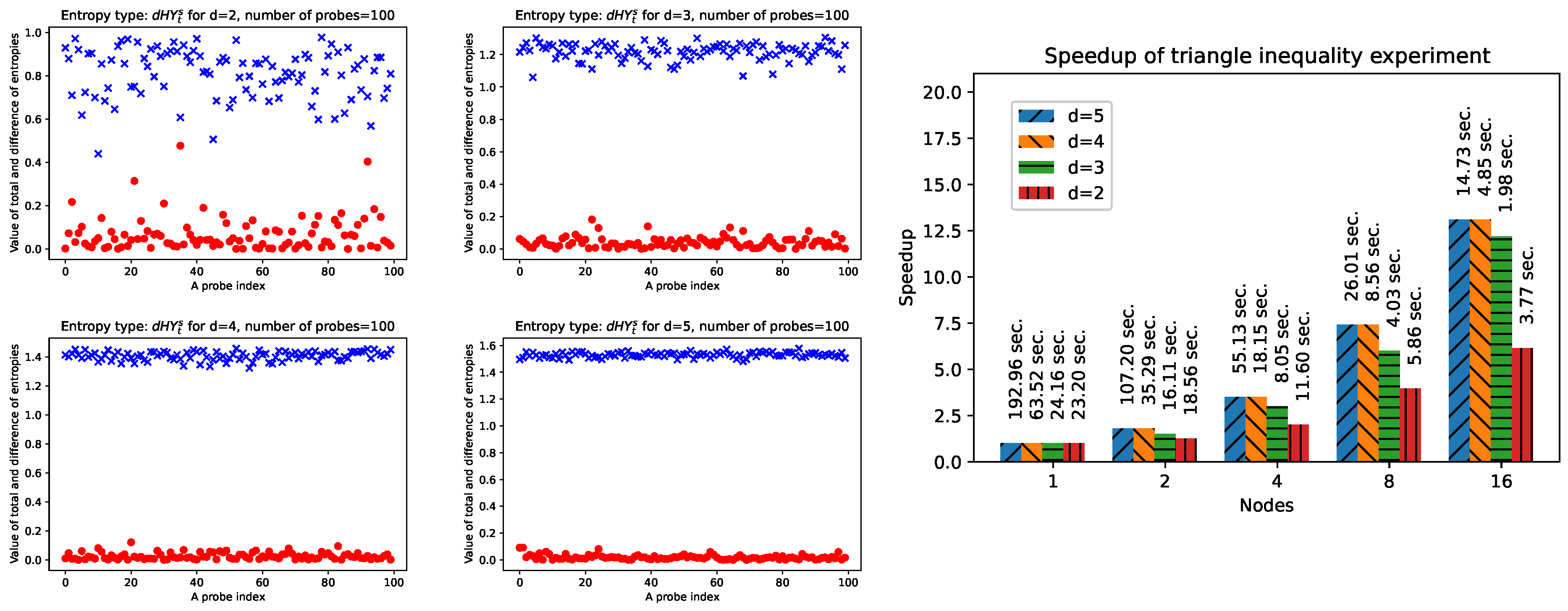
- Triangle inequality. Let and . Then, for and (see [21]):
3.3. The Hu–Ye Entropy in an Infinite-Dimensional Case
3.3.1. The Case
- (i)
- For any ,
- (ii)
- If is a sequence of states, i.e., , such thatthen
- (iii)
- The following equalities are valid:where is the n-th skew tensor power of .
- ()
- is a two-sided ⋆-ideal in the -algebra of bounded linear operators acting in and equipped with the operator norm . For any and , the following estimates are valid:
- ()
- If , then(see, e.g., [18]).
- :
- for any , , and :
3.3.2. The Case
- (i)
- For any , ;
- (ii)
- If , then ;
- (iii)
- Let ; then, .
- (1)
- For any , the following Fredholm determinant:is well defined on the space , and is continuous on this space.
- (2)
- For any and , as defined in Equation (72), the renormalised Fredholm determinantis finite and obeys the bound
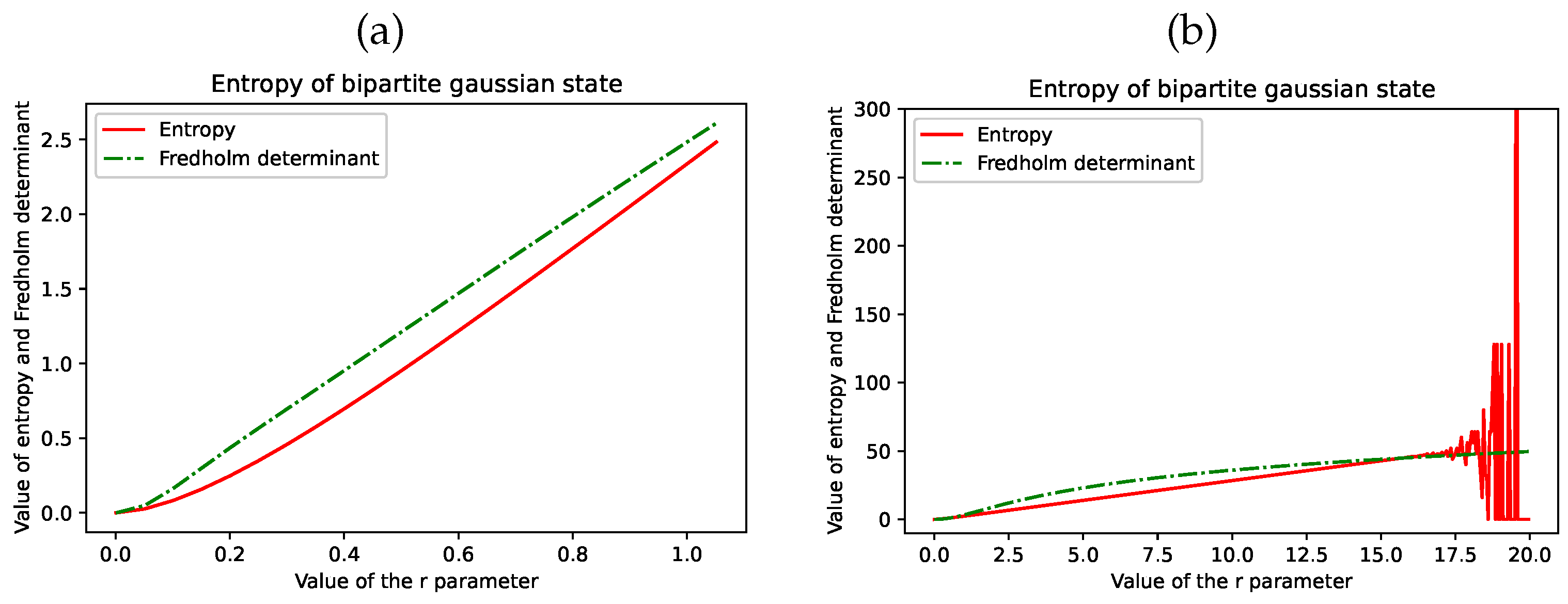
4. Numerical Examples
| def fredholm_det(K, z, a, b, m): |
| w,x=gauss_legendre_quadrature(a,b,m) |
| w = np.sqrt(w) |
| xi,xj = np.meshgrid(x, x, indexing=’ij’) |
| d = np.linalg.det( np.eye(m) + z * np.outer(w,w) * K(xi,xj) ) |
| return d |
4.1. The d-Dimensional Isotropic State
4.2. The d-Dimensional X Quantum State
| m = create_x_state( d ) |
| pt0 = ed.PT(m, [d,d], 1 ) |
| pt1 = ed.PT(m, [d,d], 0 ) |
| ent_m = HY_by_d( m, s, r ) |
| ent_pt0 = HY_by_d( pt0, s, r ) |
| ent_pt1 = HY_by_d( pt1, s, r ) |
4.3. The Infinite Bipartite Case
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
- (i)
- If , then and
- (ii)
- If , then ,and
- (iii)
- Let , , and . Then, , where and
- (iv)
- For 0 < p < q < 1:
References
- Neumann, J. Thermodynamik quantenmechanischer Gesamtheiten. Nachrichten Von Der Ges. Der Wiss. GöTtingen-Math.-Phys. Kl. 1927, 1927, 273–291. [Google Scholar]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information: 10th Anniversary Edition; Cambridge University Press: Cambridge, UK, 2010; p. 702. [Google Scholar] [CrossRef]
- Bengtsson, I.; Życzkowski, K. Geometry of Quantum States: An Introduction to Quantum Entanglement, 2nd ed.; Cambridge University Press: Cambridge, UK, 2017; p. 636. [Google Scholar] [CrossRef]
- Lloyd, S.; Braunstein, S.L. Quantum Computation over Continuous Variables. Phys. Rev. Lett. 1999, 82, 1784–1787. [Google Scholar] [CrossRef]
- Braunstein, S.L.; van Loock, P. Quantum information with continuous variables. Rev. Mod. Phys. 2005, 77, 513–577. [Google Scholar] [CrossRef]
- Serafini, A. Quantum Continuous Variables: A Primer of Theoretical Methods, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2023. [Google Scholar] [CrossRef]
- Andersen, U.; Leuchs, G.; Silberhorn, C. Continuous-variable quantum information processing. Laser Photonics Rev. 2010, 4, 337–354. [Google Scholar] [CrossRef]
- Weedbrook, C.; Pirandola, S.; García-Patrón, R.; Cerf, N.J.; Ralph, T.C.; Shapiro, J.H.; Lloyd, S. Gaussian quantum information. Rev. Mod. Phys. 2012, 84, 621–669. [Google Scholar] [CrossRef]
- Castellanos-Beltran, M.A.; Irwin, K.D.; Hilton, G.C.; Vale, L.R.; Lehnert, K.W. Amplification and squeezing of quantum noise with a tunable Josephson metamaterial. Nat. Phys. 2008, 4, 929–931. [Google Scholar] [CrossRef]
- Estève, J.; Gross, C.; Weller, A.; Giovanazzi, S.; Oberthaler, M.K. Squeezing and entanglement in a Bose–Einstein condensate. Nature 2008, 455, 1216–1219. [Google Scholar] [CrossRef]
- Eichler, C.; Bozyigit, D.; Lang, C.; Baur, M.; Steffen, L.; Fink, J.M.; Filipp, S.; Wallraff, A. Observation of Two-Mode Squeezing in the Microwave Frequency Domain. Phys. Rev. Lett. 2011, 107, 113601. [Google Scholar] [CrossRef]
- Rudner, M.S.; Vandersypen, L.M.K.; Vuletić, V.; Levitov, L.S. Generating Entanglement and Squeezed States of Nuclear Spins in Quantum Dots. Phys. Rev. Lett. 2011, 107, 206806. [Google Scholar] [CrossRef]
- Fredholm, E.I. Les équations intégrales linéaires. C. R. Congrés des Math. Tenu à Stockholm 1909. [Google Scholar]
- Harris, C.R.; Millman, K.J.; Van Der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J.; et al. Array programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef]
- Sawerwain, M.; Wiśniewska, J.; Wróblewski, M.; Gielerak, R. Source Code of Examples of Entropy Calculations. Available online: https://github.com/qMSUZ/EntDetector/tree/main/examples-entropy (accessed on 2 October 2024).
- Plenio, M.B.; Virmani, S. An introduction to entanglement measures. Quantum Inf. Comput. 2007, 7, 1–51. [Google Scholar] [CrossRef]
- Gielerak, R. Renormalized Von Neumann entropy with application to entanglement in genuine infinite dimensional systems. Quantum Inf. Process. 2023, 22, 311. [Google Scholar] [CrossRef]
- Simon, B. Notes on infinite determinants of Hilbert space operators. Adv. Math. 1977, 24, 244–273. [Google Scholar] [CrossRef]
- Simon, B. Trace Ideals and Their Applications, 2nd ed.; Mathematical Surveys and Monographs; American Mathematical Society: Providence, RI, USA, 2005; Volume 120, p. 150. [Google Scholar]
- Hu, X.; Ye, Z. Generalized quantum entropy. J. Math. Phys. 2006, 47, 023502. [Google Scholar] [CrossRef]
- Rastegin, A.E. Some General Properties of Unified Entropies. J. Stat. Phys. 2011, 143, 1120–1135. [Google Scholar] [CrossRef]
- Bornemann, F. On the numerical evaluation of Fredholm determinants. Math. Comp. 2010, 79, 871–915. [Google Scholar] [CrossRef]
- Plemelj, J. Zur Theorie der Fredholmschen Funktionalgleichung. Monatshefte Für Math. Und Phys. 1904, 15, 93–128. [Google Scholar] [CrossRef]
- Grothendieck, A. La théorie de Fredholm. Bull. SociÉtÉ MathÉmatique Fr. 1956, 84, 319–384. [Google Scholar] [CrossRef]
- Berry, M.V. Riemann’s Zeta function: A model for quantum chaos? In Quantum Chaos and Statistical Nuclear Physics; Seligman, T.H., Nishioka, H., Eds.; Springer: Berlin/Heidelberg, Germany, 1986; pp. 1–17. [Google Scholar] [CrossRef]
- Berry, M.V.; Keating, J.P. H=xp and the Riemann Zeros. In Supersymmetry and Trace Formulae: Chaos and Disorder; Lerner, I.V., Keating, J.P., Khmelnitskii, D.E., Eds.; Springer: Boston, MA, USA, 1999; pp. 355–367. [Google Scholar] [CrossRef]
- Bender, C.M.; Brody, D.C.; Müller, M.P. Hamiltonian for the Zeros of the Riemann Zeta Function. Phys. Rev. Lett. 2017, 118, 130201. [Google Scholar] [CrossRef]
- Melech, P. p-Schatten Embeddings. Master’s Thesis, FernUniversität in Hagen, Hagen, Germany, 2017. [Google Scholar]
- Hilbert, D. Grundzüge einer allgeminen Theorie der linaren Integralrechnungen. (Erste Mitteilung). Nachrichten Von Der Ges. Der Wiss. GöTtingen-Math.-Phys. Kl. 1904, 1904, 49–91. [Google Scholar]
- Poincaré, H. Remarques diverses sur l’équation de Fredholm. Acta Math. 1910, 33, 57–86. [Google Scholar] [CrossRef]
- Giedke, G.; Wolf, M.M.; Krüger, O.; Werner, R.F.; Cirac, J.I. Entanglement of Formation for Symmetric Gaussian States. Phys. Rev. Lett. 2003, 91, 107901. [Google Scholar] [CrossRef] [PubMed]
- Dunford, N.; Schwartz, J. Linear Operators, Part II; Spectral Theory; Interscience: New York, NY, USA, 1963. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gielerak, R.; Wiśniewska, J.; Sawerwain, M. Infinite-Dimensional Quantum Entropy: The Unified Entropy Case. Entropy 2024, 26, 1070. https://doi.org/10.3390/e26121070
Gielerak R, Wiśniewska J, Sawerwain M. Infinite-Dimensional Quantum Entropy: The Unified Entropy Case. Entropy. 2024; 26(12):1070. https://doi.org/10.3390/e26121070
Chicago/Turabian StyleGielerak, Roman, Joanna Wiśniewska, and Marek Sawerwain. 2024. "Infinite-Dimensional Quantum Entropy: The Unified Entropy Case" Entropy 26, no. 12: 1070. https://doi.org/10.3390/e26121070
APA StyleGielerak, R., Wiśniewska, J., & Sawerwain, M. (2024). Infinite-Dimensional Quantum Entropy: The Unified Entropy Case. Entropy, 26(12), 1070. https://doi.org/10.3390/e26121070





