Efficiently Characterizing the Quantum Information Flow, Loss, and Recovery in the Central Spin System
Abstract
:1. Introduction
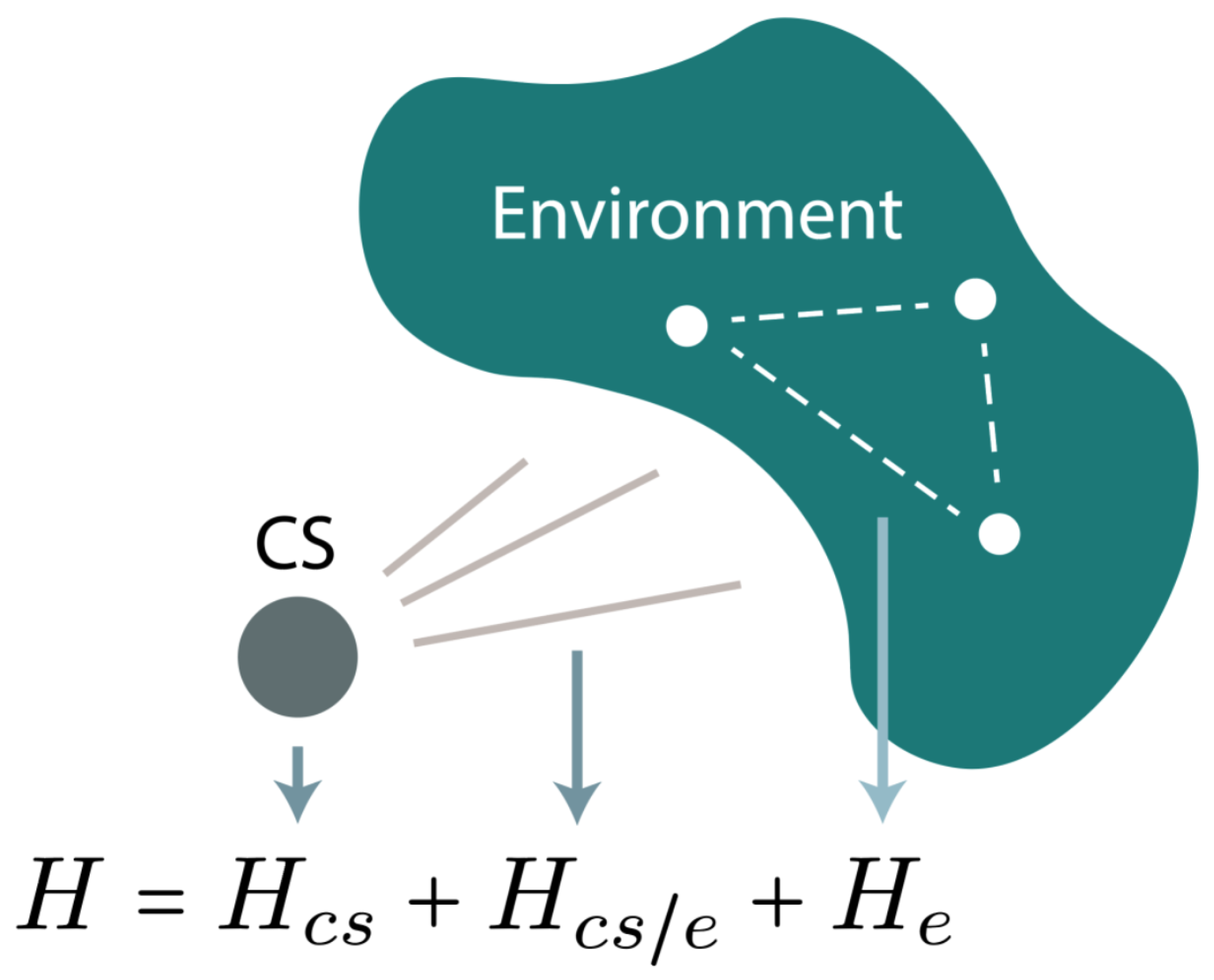
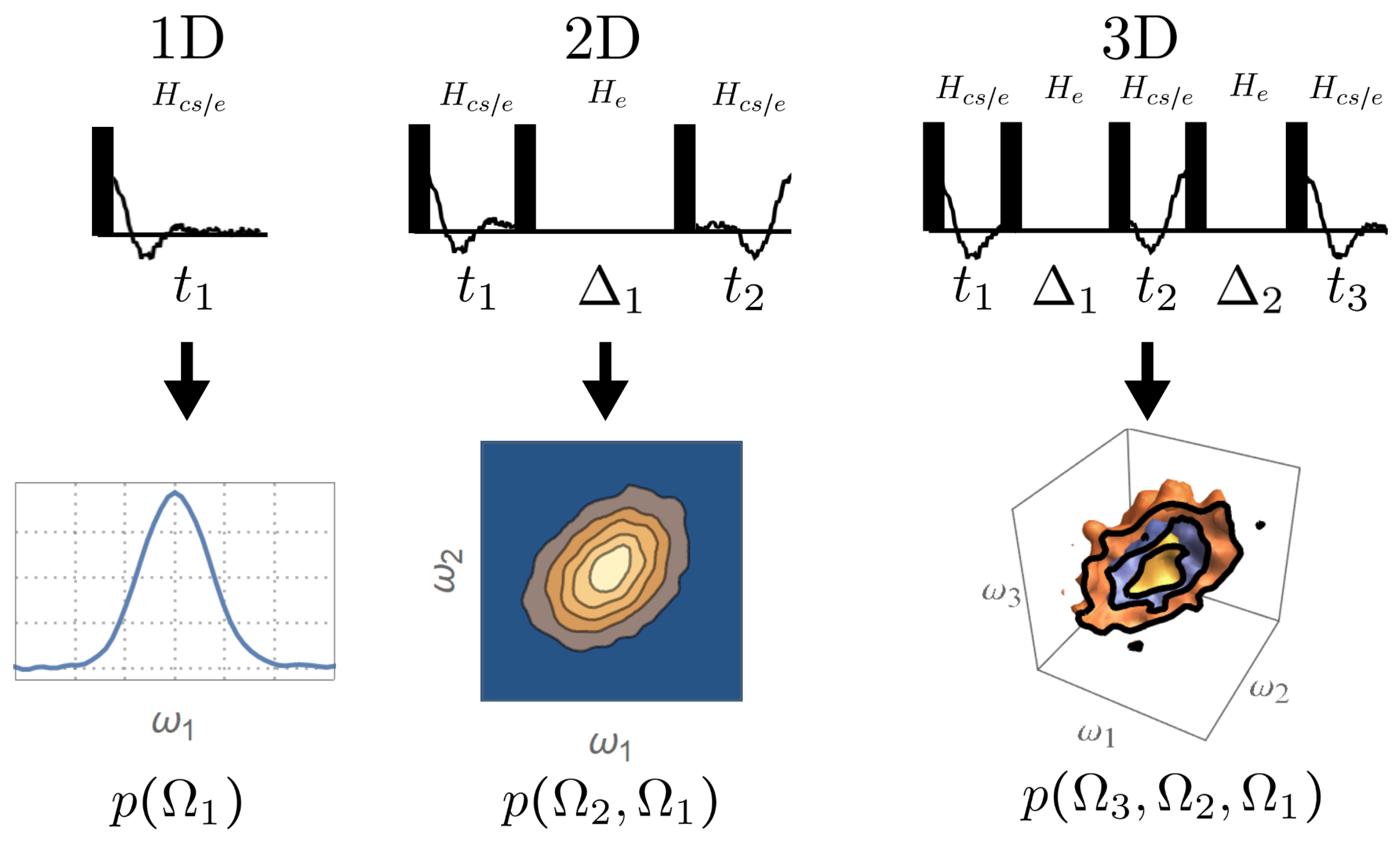
2. Theory
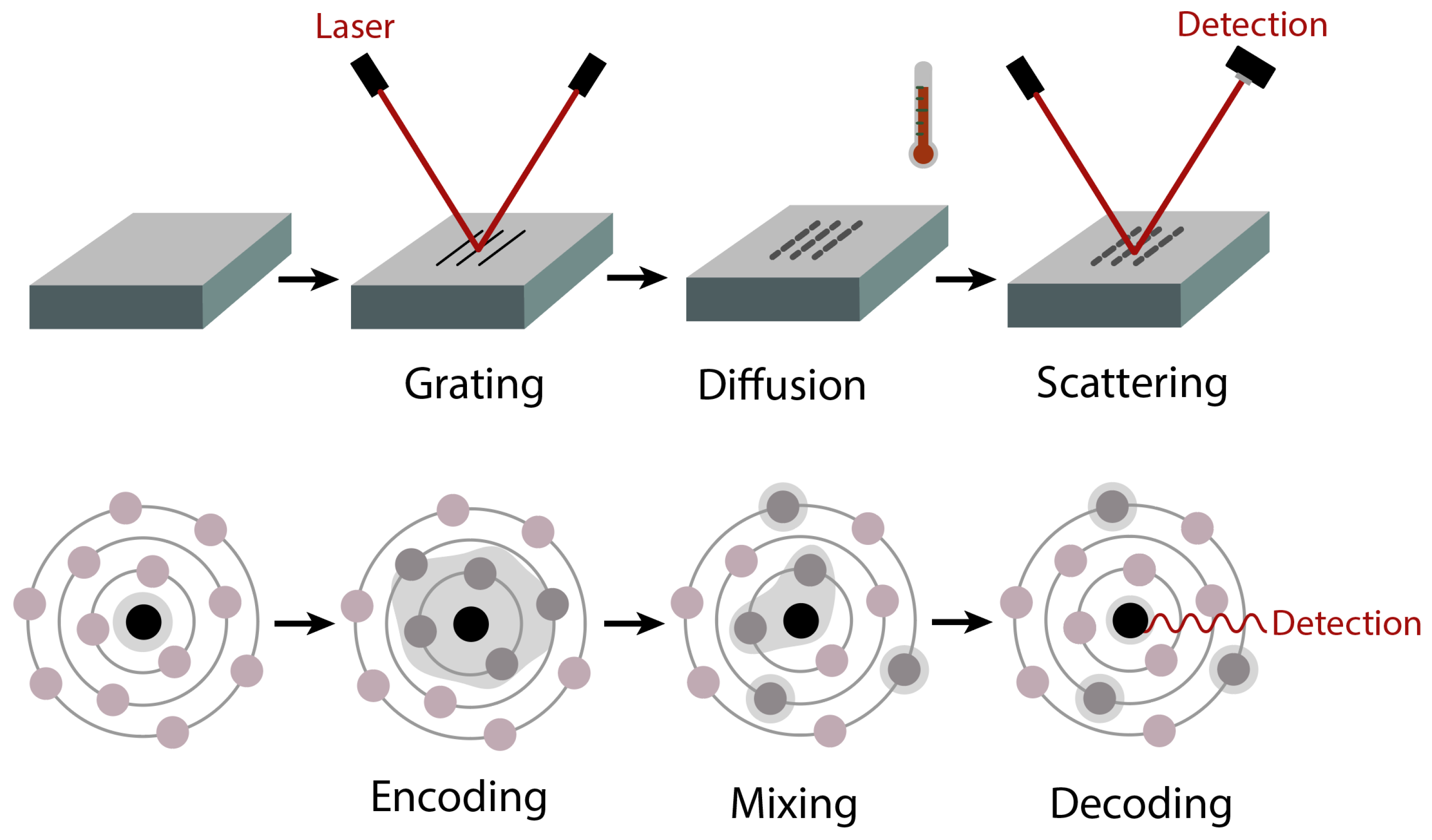
- Creation of spatial grating: A structured spatial grating is created within the material by intersecting two coherent laser beams.
- Thermal diffusion and grating decay: The material is then allowed to undergo thermal diffusion, which causes the grating to blur.
- Monitoring diffusion via scattered light: A monitoring laser beam (with the same frequency as the initial grating-forming lasers) is applied to the material. The intensity of the scattered light from this probe beam is measured, which indicates the state of the grating. The decay in the scattered intensity corresponds to the extent of diffusion, reflecting the material’s diffusion properties.
- Creation of the CS/environment correlation: The CS interacts with the environment via , forming a correlation with it.
- Environment mixing and correlation decay: The CS undergoes a mixing period under , which perturbs the CS/environment correlation.
- Measuring mixing through echo: The CS evolves under to form an echo, and the echo intensity is measured to reflect the extent of mixing and reveal properties of the environment.
3. Method
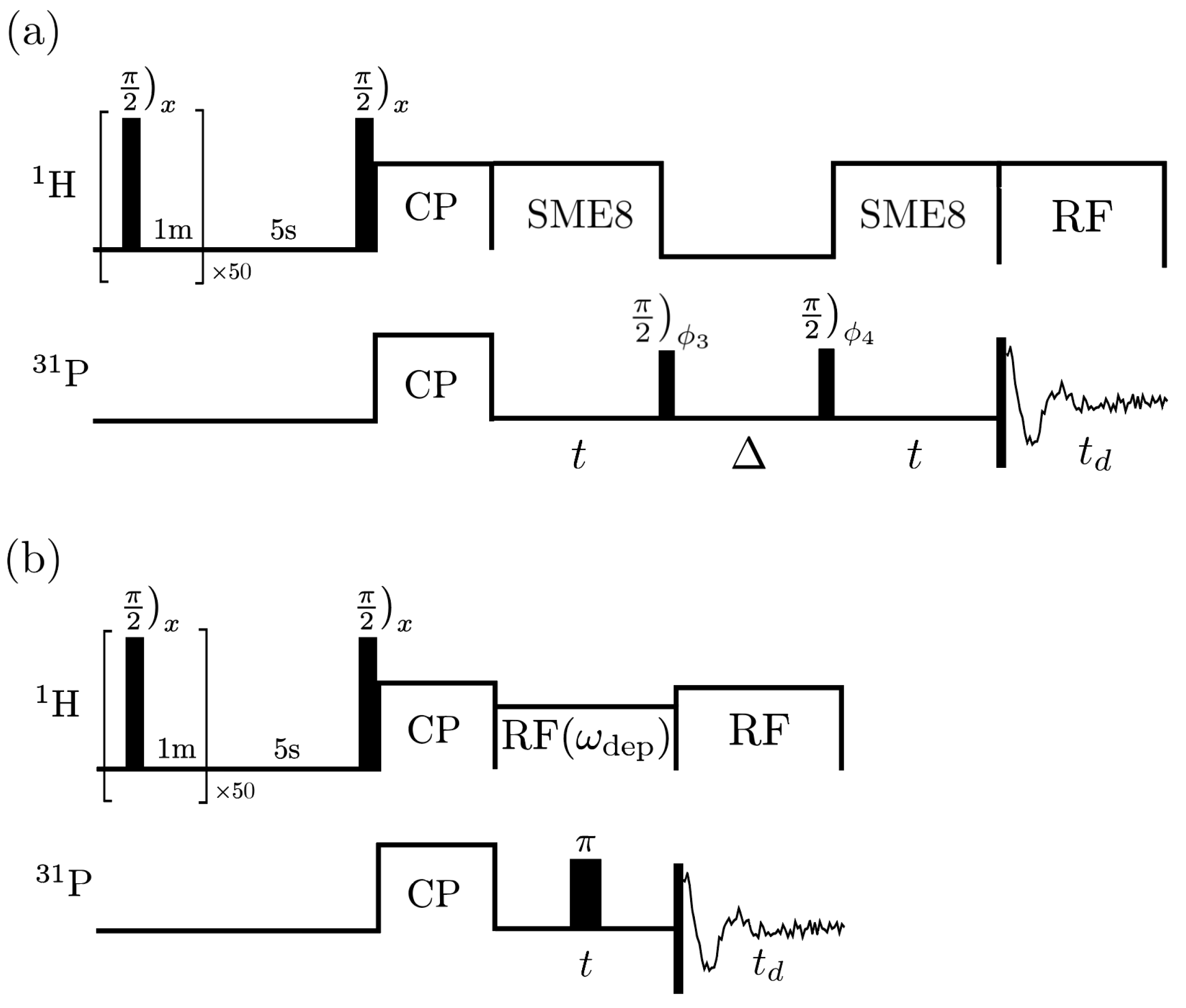
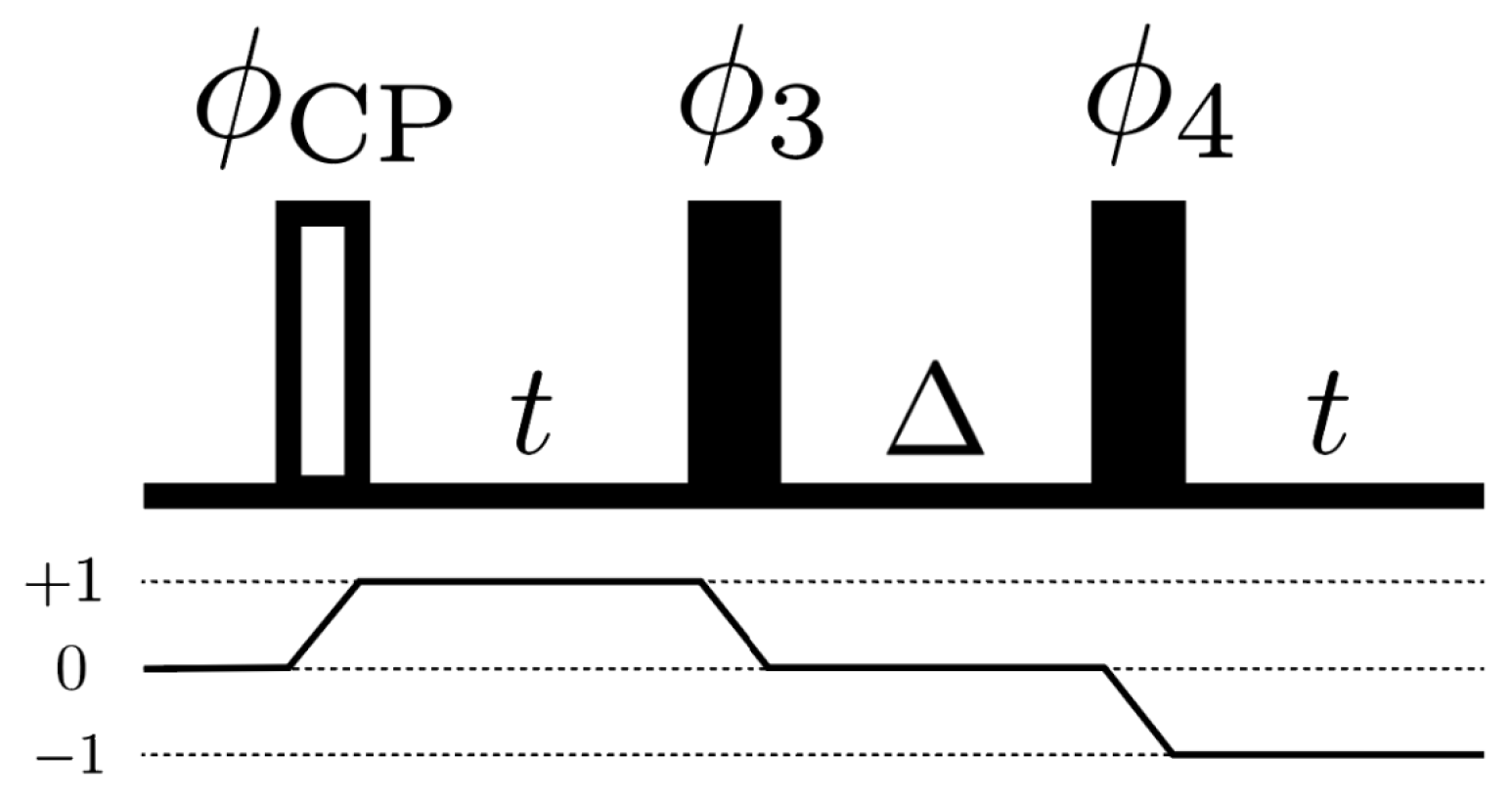
4. Results
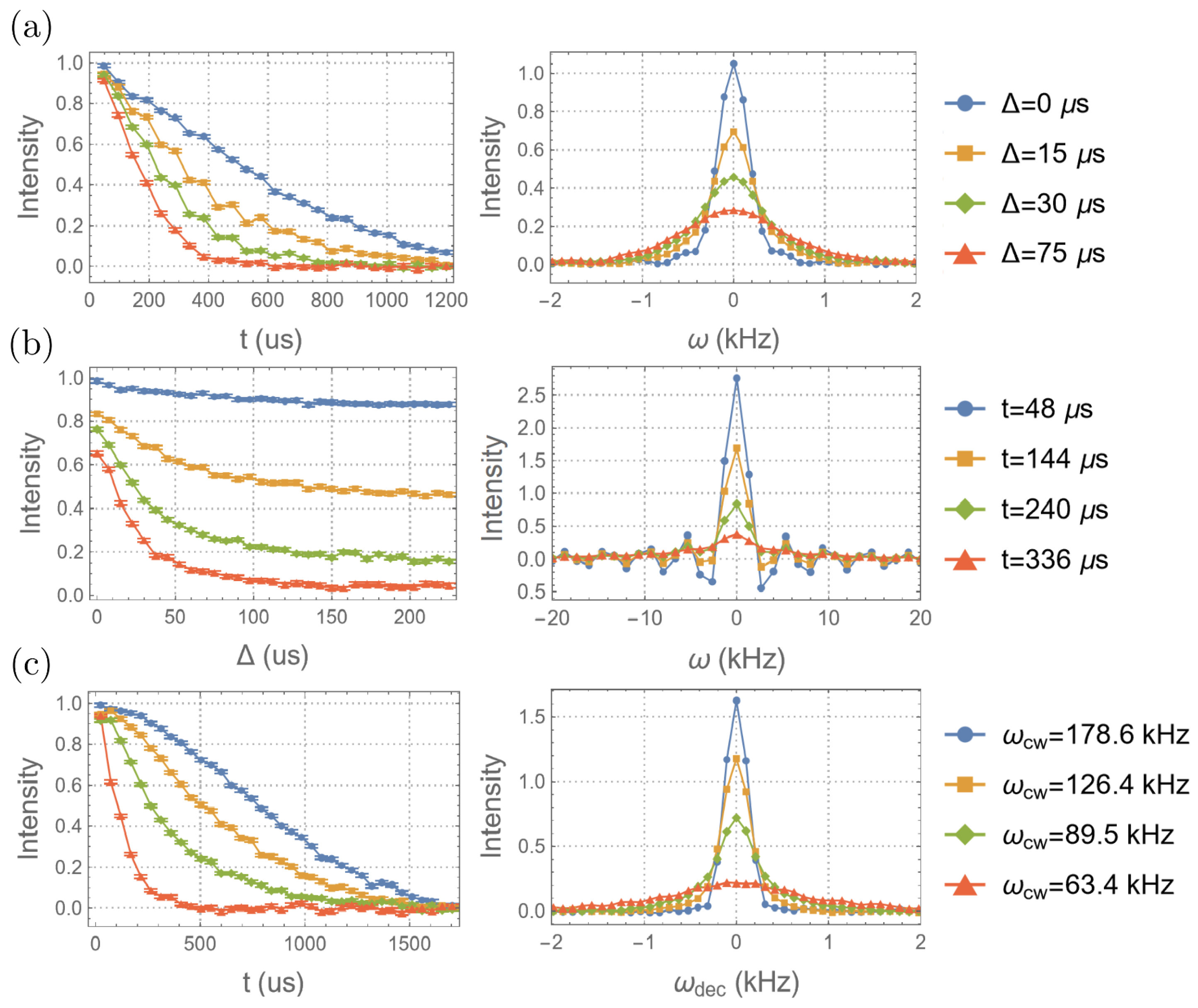
4.1. Measuring the Change in the Local Field
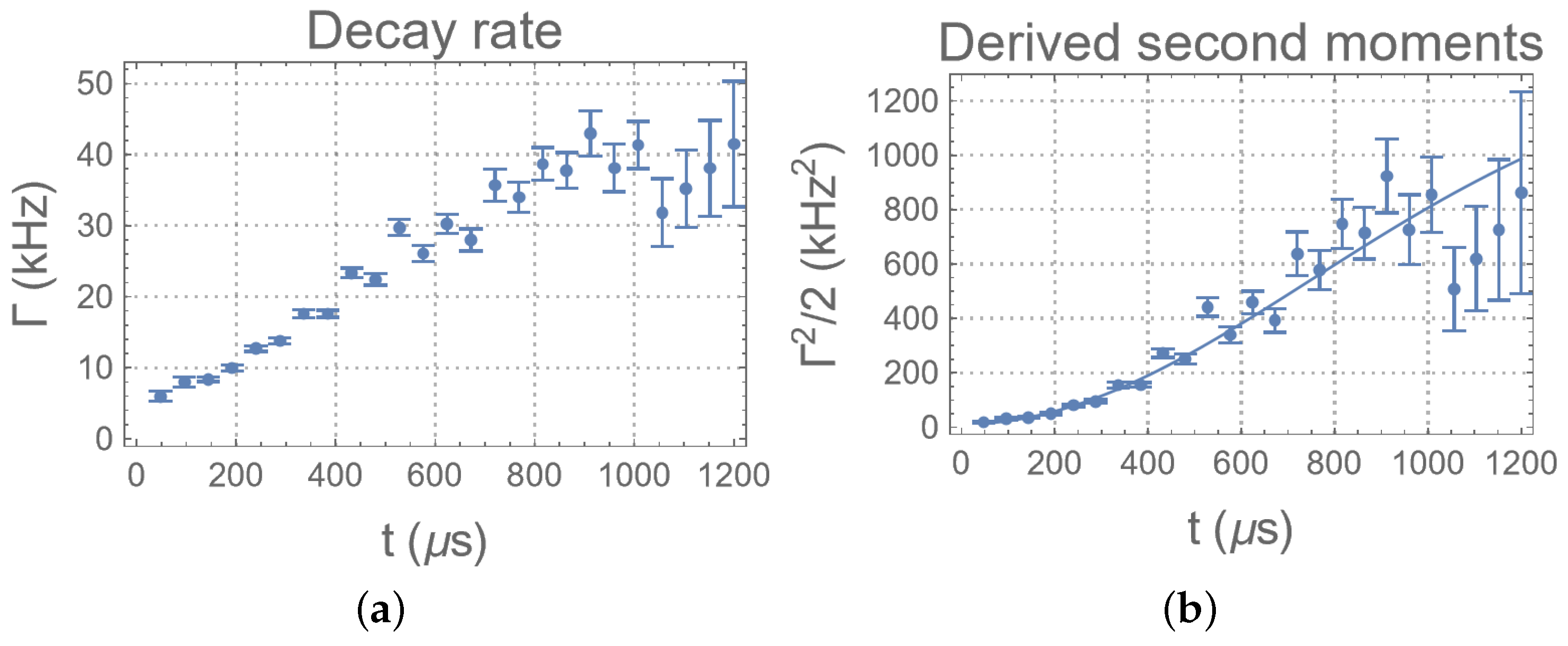
4.2. Measuring the Change in the Sensitivity
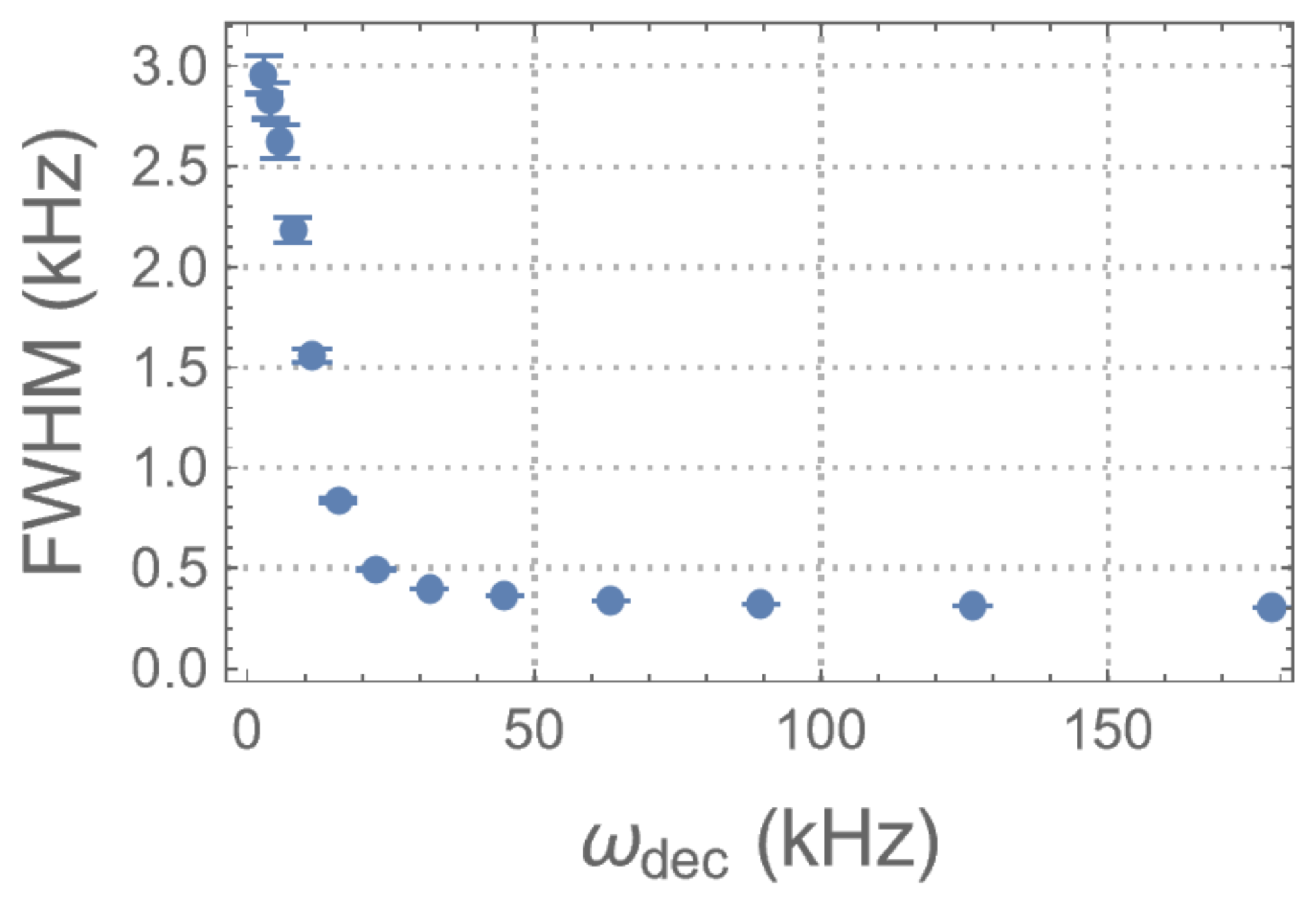
4.3. Measuring the Strength of
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
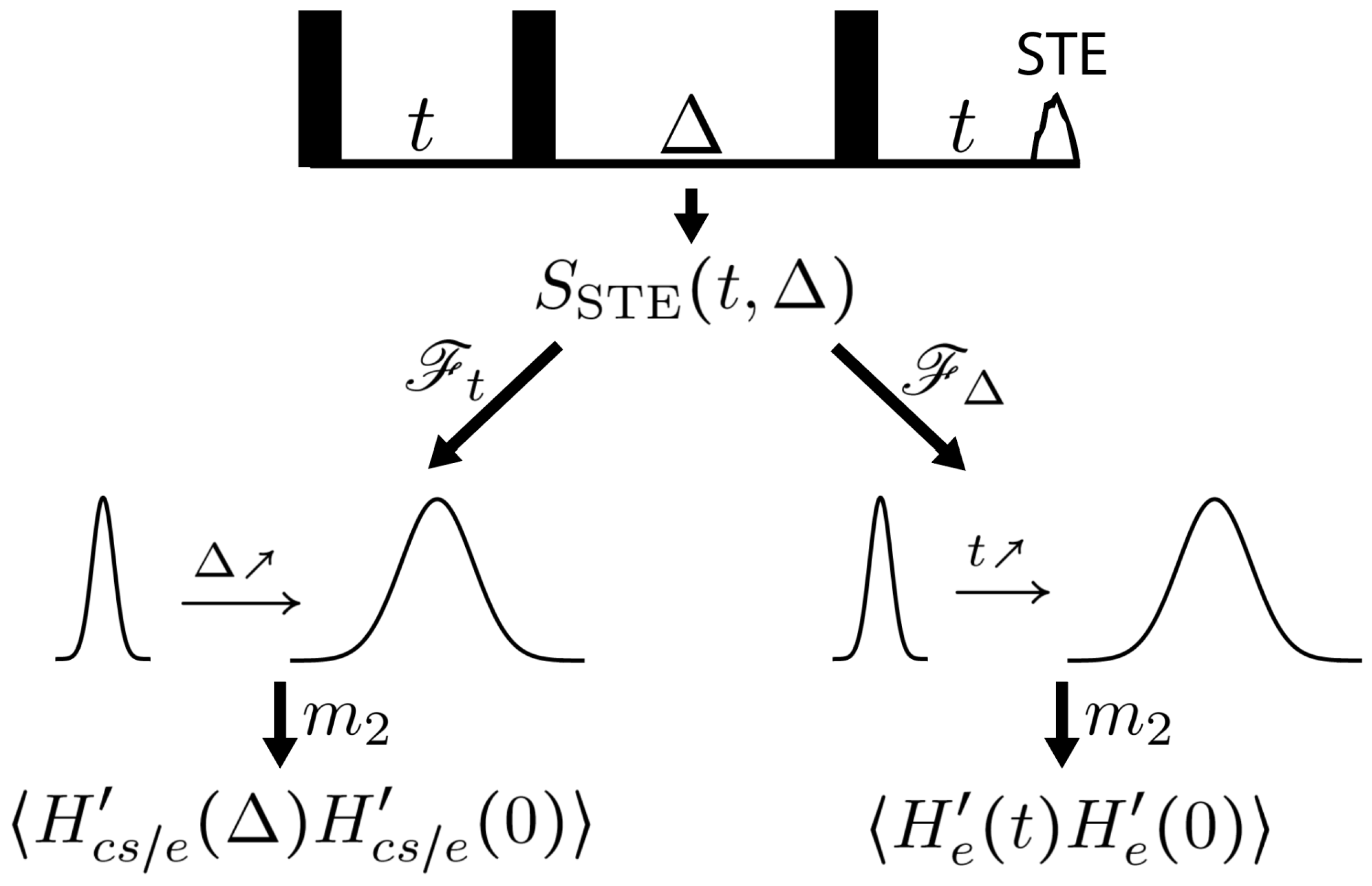
Appendix A. Detailed Analysis of the Stimulated Echo
Appendix B. Bayesian Analysis for the Stimulated Echo
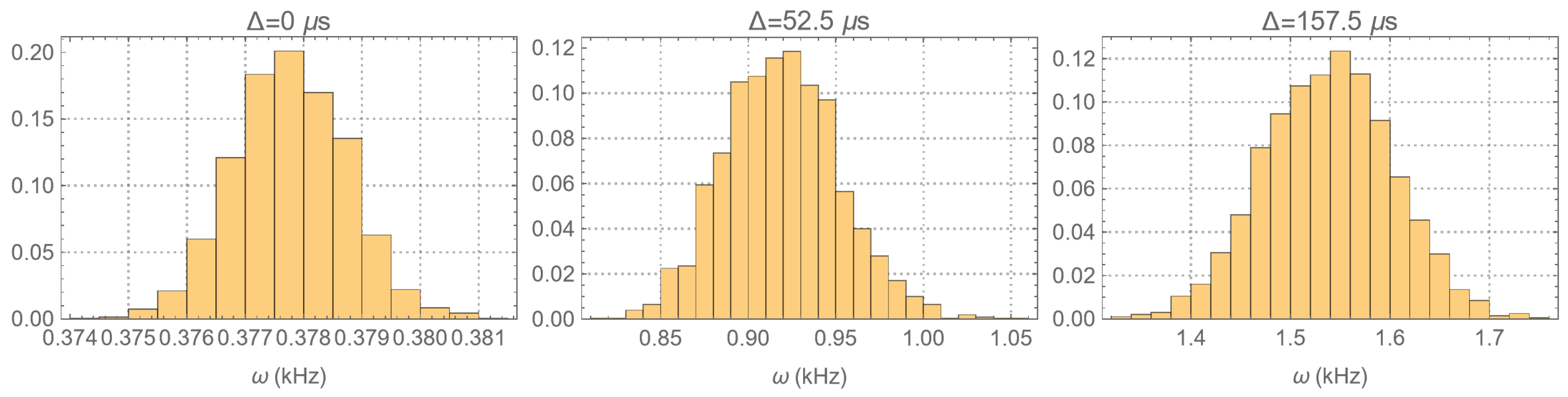

References
- Gisin, N.; Thew, R. Quantum communication. Nat. Photonics 2007, 1, 165–171. [Google Scholar] [CrossRef]
- Degen, C.L.; Reinhard, F.; Cappellaro, P. Quantum sensing. Rev. Mod. Phys. 2017, 89, 035002. [Google Scholar] [CrossRef]
- Georgescu, I.M.; Ashhab, S.; Nori, F. Quantum simulation. Rev. Mod. Phys. 2014, 86, 153–185. [Google Scholar] [CrossRef]
- Bian, J.; Lu, P.; Liu, T.; Wu, H.; Rao, X.; Wang, K.; Lao, Q.; Liu, Y.; Zhu, F.; Luo, L. Quantum simulation of a general anti-PT-symmetric Hamiltonian with a trapped ion qubit. Fundam. Res. 2023, 3, 904–908. [Google Scholar] [CrossRef]
- Haas, H.; Puzzuoli, D.; Zhang, F.; Cory, D.G. Engineering effective hamiltonians. New J. Phys. 2019, 21, 103011. [Google Scholar] [CrossRef]
- Chen, X.Y.; Zhang, N.N.; He, W.T.; Kong, X.Y.; Tao, M.J.; Deng, F.G.; Ai, Q.; Long, G.L. Global correlation and local information flows in controllable non-Markovian open quantum dynamics. npj Quantum Inf. 2022, 8, 22. [Google Scholar] [CrossRef]
- Zhang, F.; Xing, J.; Hu, X.; Pan, X.; Long, G. Coupling-selective quantum optimal control in weak-coupling NV-13 C system. AAPPS Bull. 2023, 33, 2. [Google Scholar] [CrossRef]
- Terhal, B.M. Quantum error correction for quantum memories. Rev. Mod. Phys. 2015, 87, 307–346. [Google Scholar] [CrossRef]
- Lindblad, G. On the generators of quantum dynamical semigroups. Commun. Math. Phys. 1976, 48, 119–130. [Google Scholar] [CrossRef]
- De Gennes, P. Sur la relaxation nucleaire dans les cristaux ioniques. J. Phys. Chem. Solids 1958, 7, 345–350. [Google Scholar] [CrossRef]
- Anderson, P. Spectral diffusion, phonons, and paramagnetic spin-lattice relaxation. Phys. Rev. 1959, 114, 1002. [Google Scholar] [CrossRef]
- Niknam, M.; Santos, L.F.; Cory, D.G. Sensitivity of quantum information to environment perturbations measured with a nonlocal out-of-time-order correlation function. Phys. Rev. Res. 2020, 2, 013200. [Google Scholar] [CrossRef]
- Itano, W.M.; Heinzen, D.J.; Bollinger, J.J.; Wineland, D.J. Quantum zeno effect. Phys. Rev. A 1990, 41, 2295. [Google Scholar] [CrossRef] [PubMed]
- Bylander, J.; Gustavsson, S.; Yan, F.; Yoshihara, F.; Harrabi, K.; Fitch, G.; Cory, D.G.; Nakamura, Y.; Tsai, J.S.; Oliver, W.D. Noise spectroscopy through dynamical decoupling with a superconducting flux qubit. Nat. Phys. 2011, 7, 565–570. [Google Scholar] [CrossRef]
- Paz-Silva, G.A.; Norris, L.M.; Viola, L. Multiqubit spectroscopy of Gaussian quantum noise. Phys. Rev. A 2017, 95, 022121. [Google Scholar] [CrossRef]
- Biercuk, M.; Doherty, A.; Uys, H. Dynamical decoupling sequence construction as a filter-design problem. J. Phys. B At. Mol. Opt. Phys. 2011, 44, 154002. [Google Scholar] [CrossRef]
- Álvarez, G.A.; Suter, D. Measuring the spectrum of colored noise by dynamical decoupling. Phys. Rev. Lett. 2011, 107, 230501. [Google Scholar] [CrossRef]
- Yan, F.; Gustavsson, S.; Bylander, J.; Jin, X.; Yoshihara, F.; Cory, D.G.; Nakamura, Y.; Orlando, T.P.; Oliver, W.D. Rotating-frame relaxation as a noise spectrum analyser of a superconducting qubit undergoing driven evolution. Nat. Commun. 2013, 4, 2337. [Google Scholar] [CrossRef]
- Sung, Y.; Beaudoin, F.; Norris, L.M.; Yan, F.; Kim, D.K.; Qiu, J.Y.; von Lüpke, U.; Yoder, J.L.; Orlando, T.P.; Gustavsson, S.; et al. Non-Gaussian noise spectroscopy with a superconducting qubit sensor. Nat. Commun. 2019, 10, 3715. [Google Scholar] [CrossRef]
- Norris, L.M.; Paz-Silva, G.A.; Viola, L. Qubit noise spectroscopy for non-Gaussian dephasing environments. Phys. Rev. Lett. 2016, 116, 150503. [Google Scholar] [CrossRef]
- Niknam, M.; Santos, L.F.; Cory, D.G. Experimental detection of the correlation Rényi entropy in the central spin model. Phys. Rev. Lett. 2021, 127, 080401. [Google Scholar] [CrossRef] [PubMed]
- Hahn, E.L. Spin echoes. Phys. Rev. 1950, 80, 580. [Google Scholar] [CrossRef]
- Tanner, J.E. Use of the stimulated echo in NMR diffusion studies. J. Chem. Phys. 1970, 52, 2523–2526. [Google Scholar] [CrossRef]
- Jaynes, E.T. Probability Theory: The Logic of Science; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Gelman, A.; Carlin, J.B.; Stern, H.S.; Rubin, D.B. Bayesian Data Analysis; Chapman and Hall/CRC: Boca Raton, FL, USA, 1995. [Google Scholar]
- Bloembergen, N.; Purcell, E.M.; Pound, R.V. Relaxation effects in nuclear magnetic resonance absorption. Phys. Rev. 1948, 73, 679. [Google Scholar] [CrossRef]
- Schmidt-Rohr, K.; Spiess, H. Nature of nonexponential loss of correlation above the glass transition investigated by multidimensional NMR. Phys. Rev. Lett. 1991, 66, 3020. [Google Scholar] [CrossRef]
- Bloembergen, N. On the interaction of nuclear spins in a crystalline lattice. Physica 1949, 15, 386–426. [Google Scholar] [CrossRef]
- Zhang, W.; Cory, D. First direct measurement of the spin diffusion rate in a homogenous solid. Phys. Rev. Lett. 1998, 80, 1324. [Google Scholar] [CrossRef]
- Pohl, D.; Schwarz, S.; Irniger, V. Forced rayleigh scattering. Phys. Rev. Lett. 1973, 31, 32. [Google Scholar] [CrossRef]
- Haeberlen, U. High Resolution NMR in Solids Selective Averaging: Supplement 1 Advances in Magnetic Resonance; Elsevier: Amsterdam, The Netherlands, 2012; Volume 1. [Google Scholar]
- Bodenhausen, G.; Kogler, H.; Ernst, R. Selection of coherence-transfer pathways in NMR pulse experiments. J. Magn. Reson. 1984, 58, 370–388. [Google Scholar] [CrossRef]
- Sodickson, A.; Cory, D.G. A generalized k-space formalism for treating the spatial aspects of a variety of NMR experiments. Prog. Nucl. Magn. Reson. Spectrosc. 1998, 33, 77–108. [Google Scholar] [CrossRef]
- Keeler, J. Understanding NMR Spectroscopy; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Hartmann, S.; Hahn, E. Nuclear double resonance in the rotating frame. Phys. Rev. 1962, 128, 2042. [Google Scholar] [CrossRef]
- Pines, A.; Gibby, M.; Waugh, J. Proton-Enhanced Nuclear Induction Spectroscopy: A Method for High-Resolution NMR of Dilute Spins in Solids; Technical Report; Massachusetts Inst. of Tech.: Cambridge, MA, USA, 1972. [Google Scholar]
- Boutis, G.; Cappellaro, P.; Cho, H.; Ramanathan, C.; Cory, D. Pulse error compensating symmetric magic-echo trains. J. Magn. Reson. 2003, 161, 132–137. [Google Scholar] [CrossRef] [PubMed]
- Stejskal, E.; Schaefer, J. Removal of artifacts from cross-polarization NMR experiments. J. Magn. Reson. 1975, 18, 560–563. [Google Scholar] [CrossRef]
- Wasserman, L. Bayesian model selection and model averaging. J. Math. Psychol. 2000, 44, 92–107. [Google Scholar] [CrossRef]
- Kooijman, H.; Spek, A.L.; Van Bommel, K.; Verboom, W.; Reinhoudt, D.N. A triclinic modification of triphenylphosphine. Acta Crystallogr. Sect. C Cryst. Struct. Commun. 1998, 54, 1695–1698. [Google Scholar] [CrossRef]
- Di Franco, C.; Paternostro, M.; Palma, G.; Kim, M. Information-flux approach to multiple-spin dynamics. Phys. Rev. A—At. Mol. Opt. Phys. 2007, 76, 042316. [Google Scholar] [CrossRef]
- Di Franco, C.; Paternostro, M.; Kim, M. Nested entangled states for distributed quantum channels. Phys. Rev. A—At. Mol. Opt. Phys. 2008, 77, 020303. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the dimension of a model. In The Annals of Statistics; JSTOR: New York, NY, USA, 1978; pp. 461–464. [Google Scholar]
- Rouder, J.N.; Speckman, P.L.; Sun, D.; Morey, R.D.; Iverson, G. Bayesian t tests for accepting and rejecting the null hypothesis. Psychon. Bull. Rev. 2009, 16, 225–237. [Google Scholar] [CrossRef]
- Kass, R.E.; Raftery, A.E. Bayes factors. J. Am. Stat. Assoc. 1995, 90, 773–795. [Google Scholar] [CrossRef]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Tsallis, C.; Stariolo, D.A. Generalized simulated annealing. Phys. A Stat. Mech. Its Appl. 1996, 233, 395–406. [Google Scholar] [CrossRef]
- Schanze, T. An exact D-dimensional Tsallis random number generator for generalized simulated annealing. Comput. Phys. Commun. 2006, 175, 708–712. [Google Scholar] [CrossRef]
- Haario, H.; Saksman, E.; Tamminen, J. An adaptive Metropolis algorithm. Bernoulli 2001, 7, 223–242. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.; Niknam, M.; Cory, D. Efficiently Characterizing the Quantum Information Flow, Loss, and Recovery in the Central Spin System. Entropy 2024, 26, 1077. https://doi.org/10.3390/e26121077
Chen J, Niknam M, Cory D. Efficiently Characterizing the Quantum Information Flow, Loss, and Recovery in the Central Spin System. Entropy. 2024; 26(12):1077. https://doi.org/10.3390/e26121077
Chicago/Turabian StyleChen, Jiahui, Mohamad Niknam, and David Cory. 2024. "Efficiently Characterizing the Quantum Information Flow, Loss, and Recovery in the Central Spin System" Entropy 26, no. 12: 1077. https://doi.org/10.3390/e26121077
APA StyleChen, J., Niknam, M., & Cory, D. (2024). Efficiently Characterizing the Quantum Information Flow, Loss, and Recovery in the Central Spin System. Entropy, 26(12), 1077. https://doi.org/10.3390/e26121077






