Comparison of Graph Distance Measures for Movie Similarity Using a Multilayer Network Model
Abstract
:1. Introduction
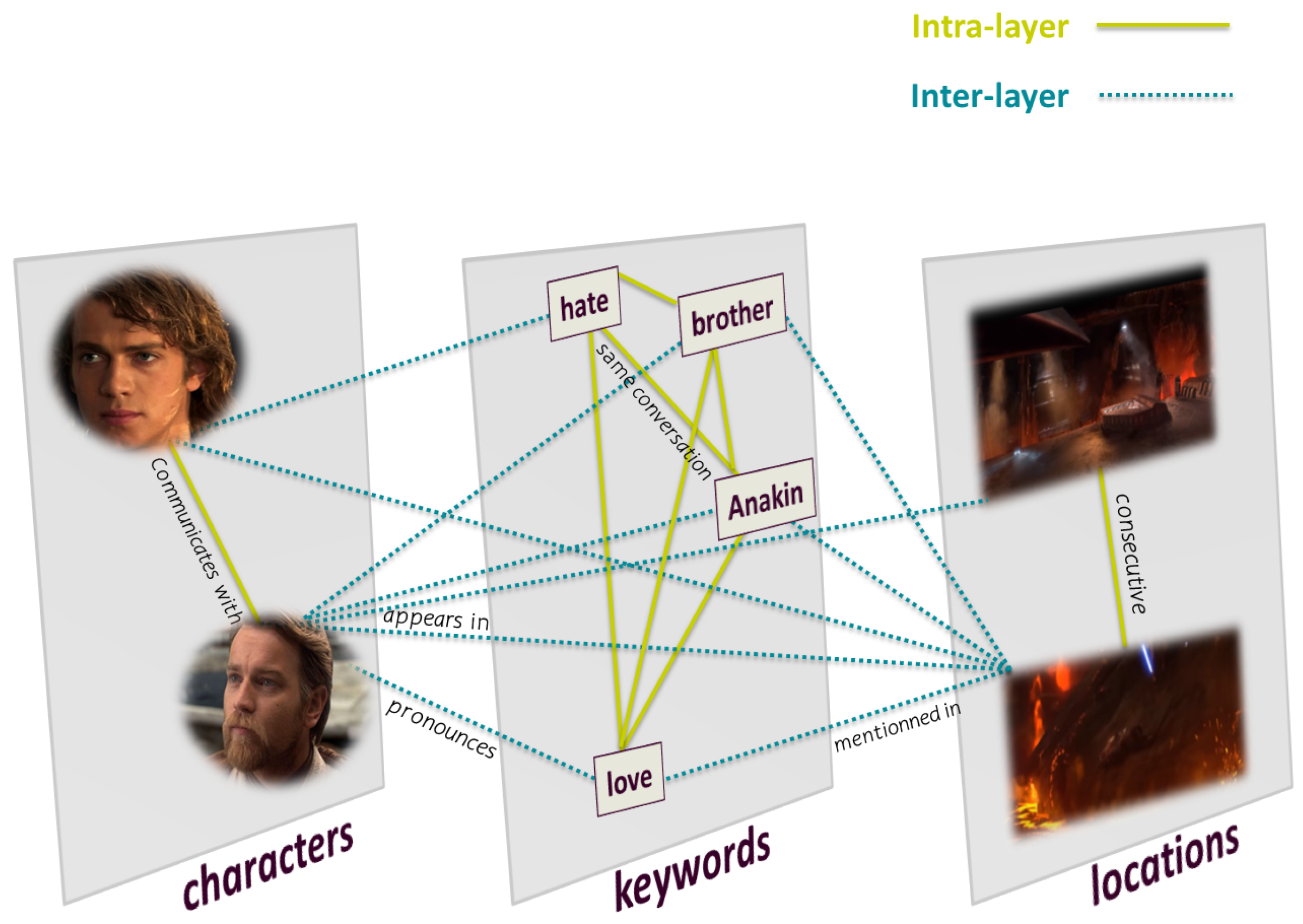
2. Multilayer Movie Model
2.1. Definition
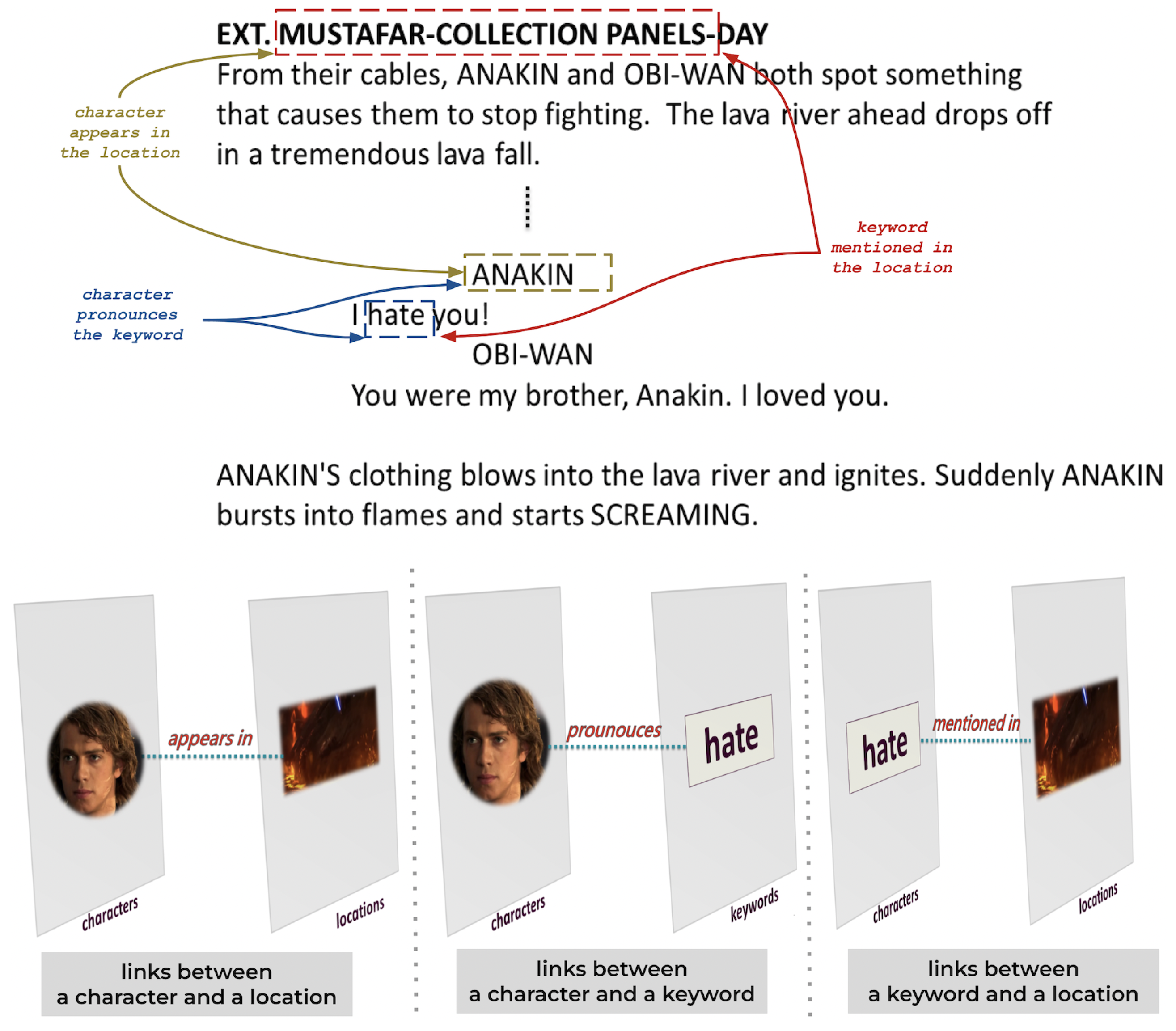
- Nodes
- A character refers to an actor in a movie.
- A location is a place where a scene turns.
- A keyword is a significant word uttered by a character during dialogues.
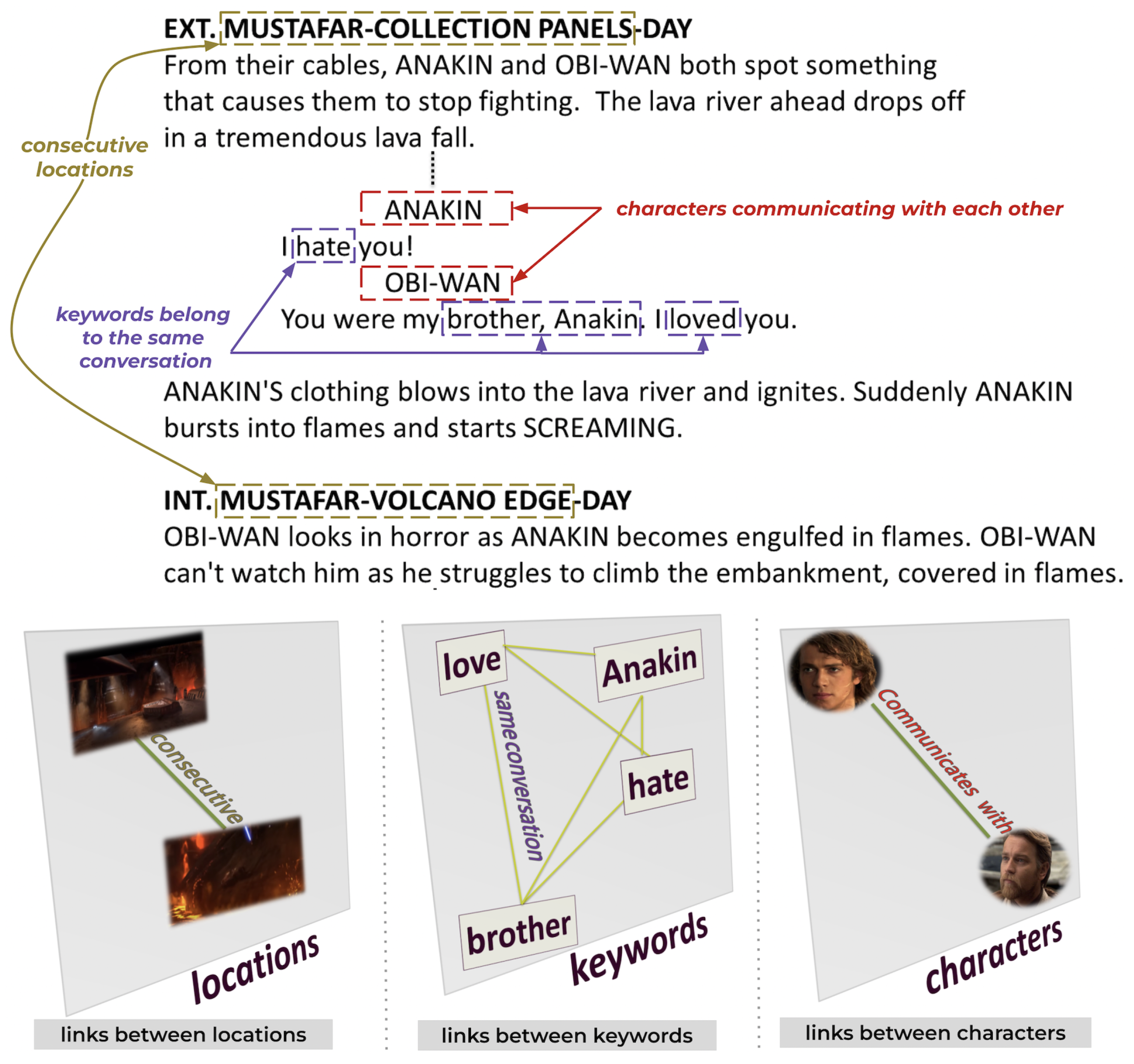
- Links
- Intralayer link connects nodes of the same entity:
- -
- A link when two characters communicate with each other.
- -
- A link when two locations are consecutive.
- -
- A link when two keywords belong to the same conversation.
- Interlayer link connects nodes of different entities:
- -
- A link between a character and a location if the character appears in the location in a scene.
- -
- A link between a character and a keyword if the character pronounces the keyword.
- -
- A link between a location and a keyword if the keyword is mentioned in a conversation taking place in the location.
2.2. Network Extraction
| Term | Definition |
| Script (Screenplay) | A document includes technical information about scenes, dialogues, and settings. |
| Scene heading | The start of a scene in a screenplay. A scene heading describes the physical spaces (INT or EXT), location, and time of the day (DAY or NIGHT). |
| Scene | A piece of the script. Each script is divided into scenes, which are separated by scene headings. |
| Dialogue | The lines of a speech a character must say in a scene. |
| Conversation | An interchange of dialogue between two or more characters in a script. |
| Action | Lines describe visual and audible actions in a scene. |
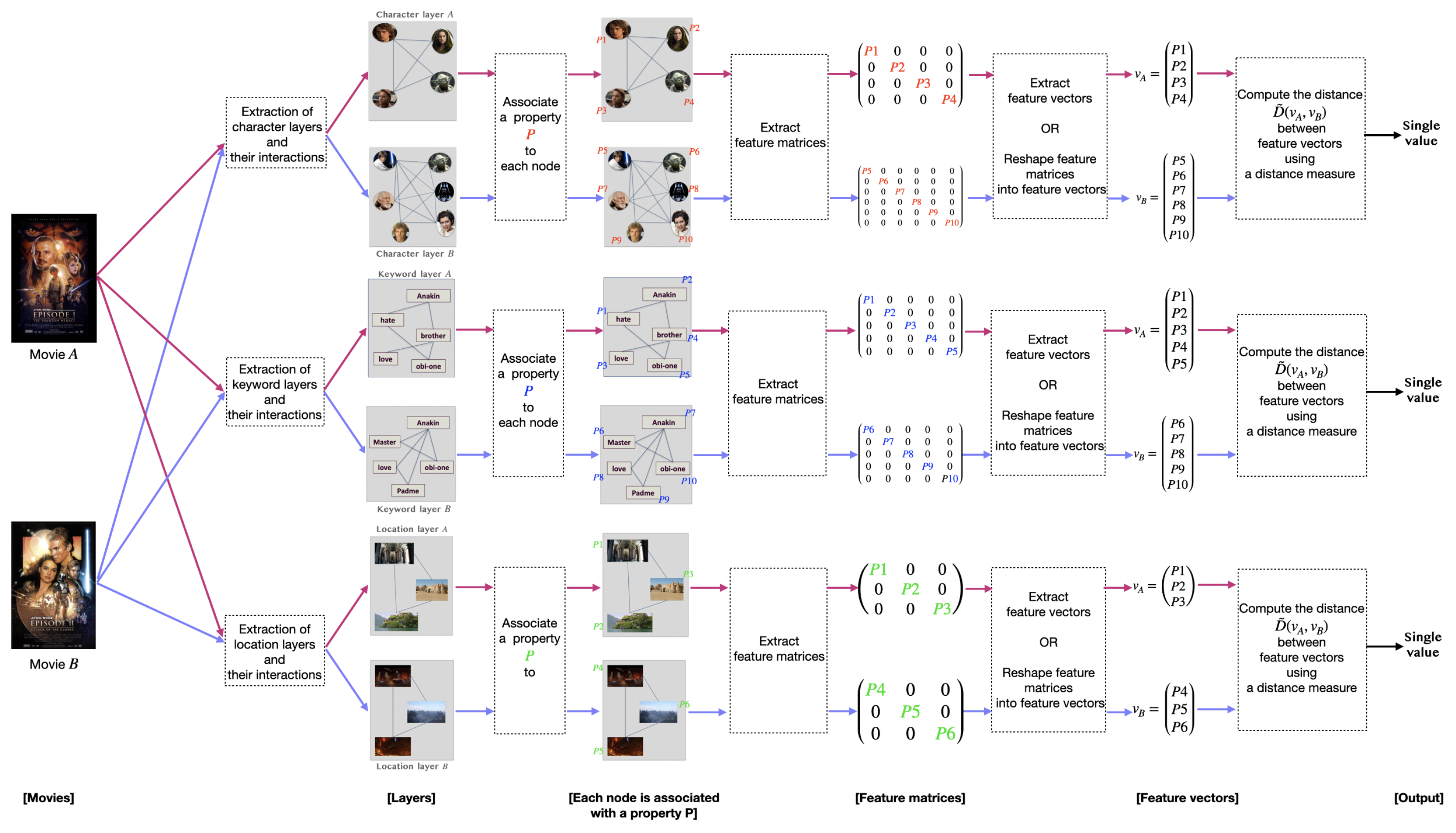
3. Network Similarity Measures
3.1. Spectral Methods
3.1.1. Euclidean Distance between Spectra
| Algorithm 1 Compute the distance between two networks across Laplacian spectra. |
| input: and output: single value Compute //Return the Laplacian Matrix of Compute //Return the Laplacian Matrix of Compute //Extract Spectra of as a vector Compute //Extract Spectra of as a vector return //The output is a single value |
3.1.2. Network Laplacian Spectral Descriptor
- Permutation-invariant: A distance on a graph representation is permutation-invariant if, despite permuting two given networks and , their graph representations remain identical:As seen in Equation (2), we note that the inherits properties from . Since the normalized Laplacian spectrum () verifies the permutation property, the heat matrix () also verifies the permutation property.
- Scale-adaptive: A graph representation is scale adaptive if it contains both local feature and global feature :
- -
- Local feature () captures information about the graph structure at the local level:
- -
- Global feature () captures information about the graph structure at the global level:The heat kernel matrix can encode global and local connectivities thanks to its diagonal matrix.
- Size-invariant: Let be a domain. A distance on a graph representation is size-invariant if it verifies:
| Algorithm 2 Compute the distance between two networks across NetLSD. |
| input: and output: single value Compute //Return the NetLSD of as a matrix Compute //Return the NetLSD of as a matrix Compute //Convert heat kernel matrix into vector Compute //Convert heat kernel matrix into vector return //The output is a single value |
3.2. Embedding Methods
| Algorithm 3 Compute the distance between two networks across network NetMF. |
| input: and output: single value Compute //Return the Network Embedding of as a matrix Compute //Return the Network Embedding of as a matrix Compute //Convert Network Embedding into vector Compute //Convert Network Embedding into vector return //The output is a single value |
3.3. Statistical Methods
3.3.1. Portrait Divergence
| Algorithm 4 Compute the distance between two networks across portrait divergence. |
| input: and output: single value Compute ) //Return the network portrait of as matrix Compute ) //Return the network portrait of as matrix Compute = () //Return the Probability Distribution of Compute = () //Return the Probability Distribution of Compute //Convert into vector Compute //Convert into vector return , //The output is a single value |
3.3.2. D-Measure
| Algorithm 5 Compute the distance between two networks across D-measure. |
| input: , , , , and // = = 0.35 and = 0.3 output: single value Compute //Return network node distribution of as matrix Compute //Return network node distribution of as matrix Compute = Reshape() //Convert into vector Compute = Reshape() //Convert into vector Compute //Distance between and Compute //Return network node dispersion of as vector Compute //Return network node dispersion of as vector Compute //Distance between and Compute //Return alpha-centrality distribution of as matrix Compute //Return alpha-centrality distribution of as matrix Compute //Return alpha-centrality distribution of as matrix Compute //Return alpha-centrality distribution of as matrix Compute //Convert into vector Compute //Convert into vector Compute //Convert into vector Compute //Convert into vector Compute //Compute the distance between , , , and return //The output is a single value |
4. Data
5. Methodology
| Methods | Local Feature | Global Feature | Distance |
|---|---|---|---|
| NetLSD | Permutation-invariance Scale-adaptivity | Size-invariant Scale-adaptivity | Euclidean |
| Laplacian spectra | ✗ | Eigenvalue spectrum of the Laplacian matrix | Euclidean |
| NetMF | Random walks | ✗ | Euclidean |
| D-measure | Node dispersion | Node distance distribution Alpha centrality | Jensen–Shannon |
| Network portrait divergence | ✗ | Node degree distribution Shortest path length distribution Next-nearest neighbors distribution | Jensen–Shannon |
6. Experimental Evaluation
6.1. What Is the Best Measure for Comparing Horror Movies?
6.2. What Is the Best Measure for Comparing Romance Movies?
6.3. What Is the Best Measure for Comparing Sci-Fi Movies?
6.4. What Is the Best Measure for Comparing Comedy Movies?
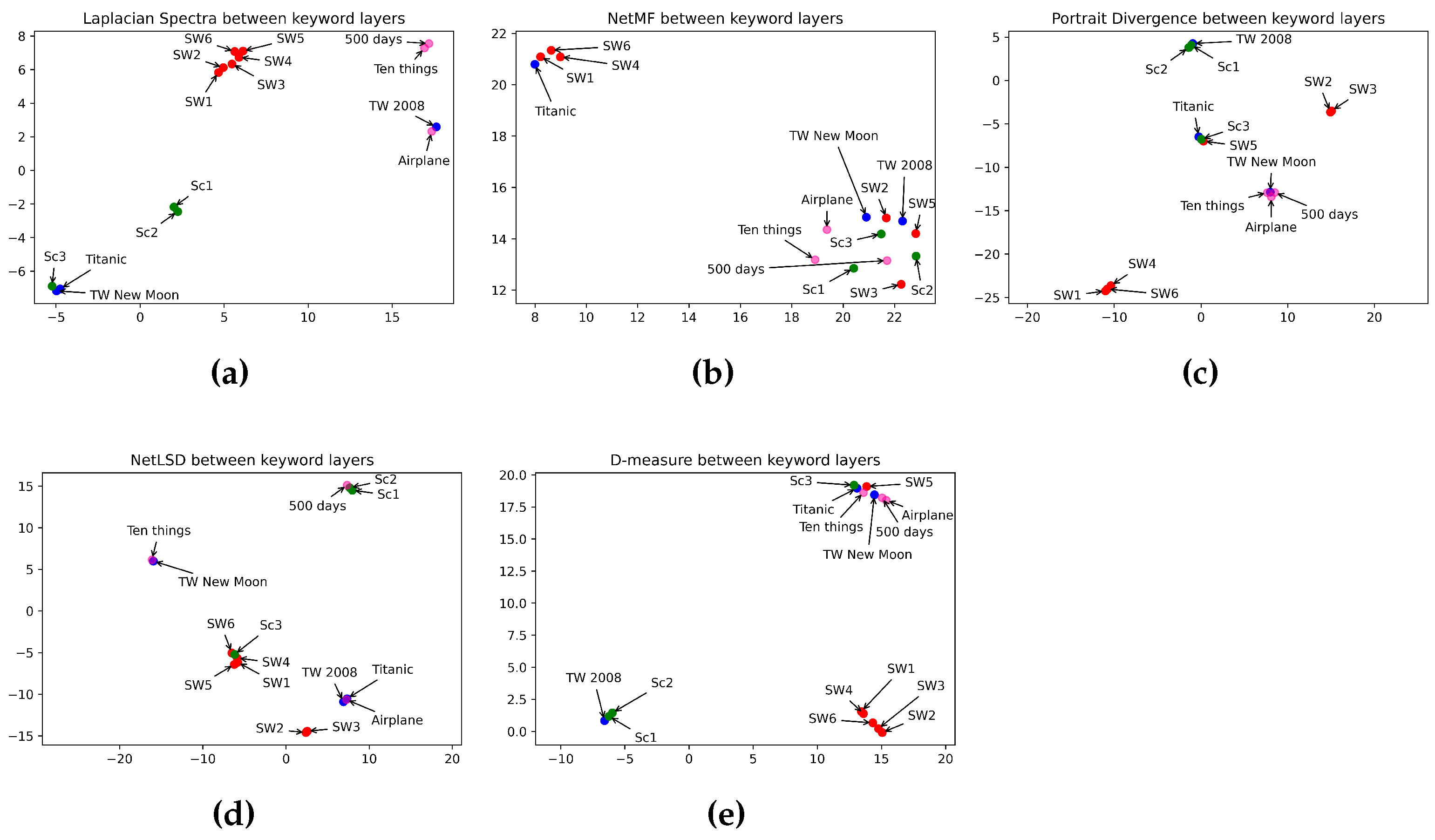
6.5. What Is the Best Measure for Measuring the Similarity between Character Layers?
| Categories | Movies | Methods | ||||
|---|---|---|---|---|---|---|
| Laplacian Spectra Distance | Network Portrait Divergence | NetLSD | NetMF | D-Measure | ||
| Horror | SC1 & SC2 SC2 & SC3 SC1 & SC3 | 192.60 (0.99) 90.15 (0.46) 177.85 (0.92) | 0.98 0.890 0.97 | 2.27 (0.45) 2.34 (0.46) 4.60 (0.92) | 3.50 (0.18) 11.42 (0.6) 8.45 (0.44) | 0.67 0.31 0.44 |
| Romance | TW1 & TW2 TW1 & Titanic TW2 & Titanic | 11.90 (0.06) 11.14 (0.05) 5.73 (0.02) | 0.91 0.96 0.98 | 3.18 (0.63) 4.88 (0.97) 1.70 (0.34) | 15.28 (0.8) 11.68 (0.61) 14.70 (0.77) | 0.13 0.07 0.12 |
| Sci-Fi | SW5 & SW6 SW4 & SW5 SW4 & SW6 SW2 & SW3 SW1 & SW2 SW1 & SW3 SW3 & SW4 SW3 & SW5 SW2 & SW4 SW2 & SW5 SW1 & SW4 SW3 & SW6 SW1 & SW5 SW2 & SW6 SW1 & SW6 | 21.25 (0.11) 27.75 (0.14) 13.25 (0.06) 30.53 (0.15) 46.10 (0.23) 23.84 (0.12) 36.59 (0.18) 27.00 (0.13) 46.51 (0.24) 29.90 (0.15) 43.10 (0.22) 29.36 (0.15) 35.92 (0.18) 28.00 (0.14) 41.67 (0.21) | 0.13 0.19 0.22 0.27 0.28 0.30 0.13 0.15 0.26 0.32 0.34 0.21 0.37 0.33 0.39 | 0.65 (0.13) 0.04 (0.008) 0.69 (0.14) 0.62 (0.12) 0.42 (0.08) 1.04 (0.2) 0.19 (0.4) 0.23 (0.05) 0.80 (0.16) 0.84 (0.17) 1.22 (0.24) 0.88 (0.18) 1.26 (0.25) 1.50 (0.3) 1.92 (0.38) | 15.56 (0.82) 14.82 (0.78) 14.23 (0.74) 16.55 (0.87) 15.46 (0.81) 16.88 (0.89) 18.08 (0.95) 14.80 (0.78) 16.53 (0.87) 15.17 (0.79) 18.01 (0.94) 14.32 (0.75) 13.50 (0.71) 15.19 (0.8) 13.30 (0.7) | 0.06 0.1 0.12 0.13 0.07 0.11 0.07 0.16 0.15 0.23 0.15 0.18 0.22 0.25 0.25 |
| Comedy | Airplane & 10 Things I Hate About You 500 Days of Summer & 10 Things I Hate About You Airplane & 500 Days of Summer | 64.30 (0.33) 72.90 (0.37) 80.59 (0.41) | 0.81 0.94 0.90 | 2.26 (0.45) 0.10 (0.02) 2.16 (0.43) | 16.35 (0.86) 11.18 (0.59) 12.59 (0.66) | 0.12 0.25 0.30 |
| Type of Methods | Measures | Horror | Romance | Sci-Fi | Comedy |
|---|---|---|---|---|---|
| Spectral | NetLSD | ✓ | ✗ | ✗ | ✓ |
| Laplacian Spectra | ✗ | ✗ | ✗ | ✗ | |
| Embedding | NetMF | ✗ | ✗ | ✗ | ✗ |
| Statistical | D-measure | ✗ | ✗ | ✓ | ✓ |
| Network Portrait Divergence | ✗ | ✓ | ✓ | ✓ |
6.6. What Is the Best Measure for Measuring the Similarity between Keyword Layers?
| Categories | Movies | Methods | ||||
|---|---|---|---|---|---|---|
| Laplacian Spectra | Network Portrait Divergence | NetLSD | NetMF | D-Measure | ||
| Horror | SC1 & SC2 SC2 & SC3 SC1 & SC3 | 2.68 (0.006) 4.68 (0.01) 9.43 (0.02) | 0.23 0.89 0.81 | 1.20 (0.15) 7.99 (0.99) 6.79 (0.85) | 25.91 (0.63) 24.42 (0.6) 25.27 (0.61) | 0.10 0.69 0.61 |
| Romance | TW1 & TW2 TW1 & Titanic TW2 & Titanic | 11.14 (0.02) 11.89 (0.03) 11.14 (0.02) | 0.69 0.71 0.44 | 3.75 (0.47) 0.78 (0.09) 2.97 (0.38) | 29.99 (0.73) 29.72 (0.72) 28.84 (0.7) | 0.43 0.47 0.12 |
| Sci-Fi | SW5 & SW6 SW4 & SW5 SW4 & SW6 SW2 & SW3 SW1 & SW2 SW1 & SW3 SW3 & SW4 SW3 & SW5 SW2 & SW4 SW2 & SW5 SW1 & SW4 SW3 & SW6 SW1 & SW5 SW2 & SW6 SW1 & SW6 | 200.77 (0.52) 136.05 (0.35) 142.04 (0.37) 139.77 (0.36) 271.94 (0.7) 377.72 (0.98) 124.80 (0.32) 102.60 (0.27) 125.14 (0.32) 211.24 (0.55) 316.06 (0.82) 203.02 (0.53) 383.35 (0.99) 142.34 (0.37) 213.98 (0.55) | 0.72 0.46 0.54 0.29 0.61 0.61 0.65 0.81 0.68 0.82 0.41 0.56 0.66 0.59 0.33 | 1.13 (0.14) 0.64 (0.08) 0.48 (0.06) 0.06 (0.007) 2.00 (0.25) 2.06 (0.26) 1.91 (0.23) 2.55 (0.31) 1.86 (0.23) 2.49 (0.31) 0.15 (0.02) 1.43 (0.17) 0.51 (0.06) 1.37 (0.17) 0.63 (0.08) | 37.50 (0.91) 39.13 (0.95) 36.49 (0.89) 32.57 (0.79) 35.55 (0.87) 36.19 (0.88) 37.62 (0.92) 35.64 (0.87) 37.18 (0.76) 34.56 (0.84) 40.05 (0.98) 32.96 (0.8) 38.49 (0.94) 31.56 (0.76) 35.68 (0.87) | 0.26 0.14 0.15 0.04 0.12 0.11 0.16 0.28 0.18 0.30 0.11 0.06 0.23 0.06 0.09 |
| Comedy | Airplane & 10 Things I Hate About You 500 Days of Summer & 10 Things I Hate About You Airplane & 500 Days of Summer | 17.05 (0.04) 14.67 (0.03) 12.73 (0.03) | 0.56 0.47 0.43 | 2.12 (0.26) 6.58 (0.82) 4.46 (0.56) | 29.30 (0.71) 28.47 (0.7) 29.63 (0.72) | 0.19 0.09 0.15 |
| Type of Methods | Measures | Horror | Romance | Sci-Fi | Comedy |
|---|---|---|---|---|---|
| Spectral | NetLSD | ✗ | ✗ | ✗ | ✗ |
| Laplacian Spectra | ✓ | ✗ | ✗ | ✓ | |
| Embedding | NetMF | ✗ | ✗ | ✗ | ✗ |
| Statistical | D-measure | ✗ | ✗ | ✗ | ✗ |
| Network Portrait Divergence | ✗ | ✗ | ✗ | ✓ |
6.7. What Is the Best Measure for Measuring the Similarity between Location Layers?
| Categories | Movies | Methods | ||||
|---|---|---|---|---|---|---|
| Laplacian Spectra | Network Portrait Divergence | NetLSD | NetMF | D-Measure | ||
| Horror | SC1 & SC2 SC2 & SC3 SC1 & SC3 | 5.76 (0.11) 5.03 (0.1) 5.46 (0.1) | 0.87 0.33 0.85 | 3.57 (0.39) 5.02 (0.56) 8.59 (0.95) | 17.74 (0.55) 16.23 (0.5) 15.73 (0.49) | 0.65 0.12 0.67 |
| Romance | TW1 & TW2 TW1 & Titanic TW2 & Titanic | 3.74 (0.07) 18.82 (0.38) 18.82 (0.38) | 0.59 0.62 0.37 | 0.44 (0.05) 0.46 (0.05) 0.05 (0.005) | 24.16 (0.75) 19.74 (0.62) 20.56 (0.64) | 0.35 0.31 0.19 |
| Sci-Fi | SW5 & SW6 SW4 & SW5 SW4 & SW6 SW2 & SW3 SW1 & SW2 SW1 & SW3 SW3 & SW4 SW3 & SW5 SW2 & SW4 SW2 & SW5 SW1 & SW4 SW3 & SW6 SW1 & SW5 SW2 & SW6 SW1 & SW6 | 22.08 (0.44) 49.91 (0.99) 18.21 (0.36) 8.05 (0.16) 5.80 (0.12) 13.73 (0.27) 10.34 (0.2) 9.73 (0.19) 5.60 (0.11) 10.90 (0.21) 10.35 (0.2) 19.71 (0.39) 16.55 (0.33) 16.75 (0.33) 15.40 (0.31) | 0.08 0.23 0.26 0.00 0.01 0.02 0.58 0.30 0.55 0.26 0.50 0.15 0.20 0.13 0.10 | 1.16 (0.13) 0.76 (0.08) 1.92 (0.21) 0.33 (0.04) 0.20 (0.02) 0.53 (0.06) 2.91 (0.32) 2.15 (0.23) 2.58 (0.28) 1.82 (0.2) 2.38 (0.2) 0.99 (0.11) 1.61 (0.18) 0.66 (0.07) 0.46 (0.05) | 20.56 (0.64) 31.64 (0.98) 21.85 (0.68) 23.24 (0.73) 25.22 (0.78) 23.37 (0.73) 28.50 (0.89) 29.38 (0.92) 27.30 (0.85) 25.91 (0.8) 27.44 (0.85) 18.93 (0.59) 26.21 (0.81) 19.96 (0.62) 20.13 (0.62) | 0.12 0.09 0.16 0.07 0.08 0.07 0.18 0.15 0.20 0.18 0.16 0.11 0.12 0.13 0.06 |
| Comedy | Airplane & 10 Things I Hate About You 500 Days of Summer & 10 Things I Hate About You Airplane & 500 Days of Summer | 15.45 (0.3) 11.14 (0.22) 10.80 (0.22) | 0.57 0.61 0.67 | 7.06 (0.78) 0.33 (0.03) 6.74 (0.75) | 17.12 (0.53) 5.20 (0.16) 5.56 (0.17) | 0.25 0.32 0.25 |
| Type of Methods | Measures | Horror | Romance | Sci-Fi | Comedy |
|---|---|---|---|---|---|
| Spectral | NetLSD | ✓ | ✗ | ✗ | ✓ |
| Laplacian Spectra | ✗ | ✓ | ✗ | ✗ | |
| Embedding | NetMF | ✗ | ✗ | ✗ | ✗ |
| Statistical | D-measure | ✗ | ✗ | ✗ | ✗ |
| Network Portrait Divergence | ✗ | ✗ | ✗ | ✗ |
6.8. What Is the Best Measure for Comparing the Similarity between Movies from Different Categories?

| Measures | Horror | Romance | Sci-fi | Comedy | Horror vs. Romance | Horror vs. Sci-fi | Horror vs. Comedy | Romance vs. Sci-fi | Romance vs. Comedy | Sci-fi vs. Comedy |
|---|---|---|---|---|---|---|---|---|---|---|
| NetLSD | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✗ |
| Laplacian Spectra | ✗ | ✓ | ✓ | ✓ | ✗ | ✗ | ✓ | ✓ | ✓ | ✓ |
| NetMF | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ |
| D-measure | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ |
| Network Portrait Divergence | ✓ | ✓ | ✓ | ✓ | ✗ | ✓ | ✗ | ✓ | ✓ | ✓ |
| Measures | Horror | Romance | Sci-fi | Comedy | Horror vs. Romance | Horror vs. Sci-fi | Horror vs. Comedy | Romance vs. Sci-fi | Romance vs. Comedy | Sci-fi vs. Comedy |
|---|---|---|---|---|---|---|---|---|---|---|
| NetLSD | ✓ | ✓ | ✓ | ✗ | ✗ | ✗ | ✗ | ✓ | ✗ | ✓ |
| Laplacian Spectra | ✓ | ✓ | ✓ | ✓ | ✗ | ✓ | ✓ | ✓ | ✓ | ✓ |
| NetMF | ✓ | ✓ | ✗ | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ |
| D-measure | ✓ | ✗ | ✓ | ✓ | ✗ | ✓ | ✓ | ✓ | ✗ | ✓ |
| Network Portrait Divergence | ✓ | ✗ | ✗ | ✓ | ✗ | ✓ | ✓ | ✗ | ✗ | ✓ |

7. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| NetLSD | Network Laplacian spectral descriptor |
| NetMF | Network embedding as matrix factorization |
| SW | Star Wars |
| SC | Scream |
Appendix A
Appendix A.1. Movie Stories
“The Scream Saga follows a series of murders, where killers wear a ghost face.
Scream 1: The first part of the story follows Casey, a young student in a Woodsboro High School. Casey was in her house when the phone rang for the first time. Casey answered the phone and thought the man’s voice (Stu) had the wrong number. The phone rang again when Casey was in the kitchen. The man’s voice asked her for her favorite scary movie. When Casey answered the question, he asked her to see her boyfriend dead in the front yard. The killer (Stu) followed Casey and killed her in the front yard. When Casey’s parents returned home, they tried to call the police but failed. Casey’s mother was screaming when she found her daughter dead. The second part follows Sidney, a teenage student in Woodsboro high school. Billy Loomis, the boyfriend of Sidney, had killed her mother with the help of Stu. That is because Sidney’s mother was the cause of the separation of Billy’s parents. One year later, Billy informed Casey about her mother’s murder and killed Stu. Sidney survived under her fight with Billy and Stu. Finally, Sidney killed Billy by shooting him with a gun.
Scream 2: The events of the screams reached in theatres. Luke Wilson played the role of Billy Loomis, and Tori Spelling played Sidney’s character. A series of murders began. Sidney survived again by confronting the new Ghostface killers. With the help of Mickey (Sidney’s friend), Mrs. Loomis (Billy’s mother) tried to avenge her son’s died. Mickey killed Derek, the new boyfriend of Sidney. Mrs. Loomis killed Randy (Sidney’s friend) because he bad-mounted Billy. Then, she killed Mickey because she found him useless. Mrs. Loomis confronted Sidney. Mrs. Loomis was killed by Cotton Weary, who was accused of murdering Sidney’s mother.
Scream 3: Sidney went to the mountain to hide from the killers. She received a call from the Ghostface (Roman). First, she was thinking the caller’s voice was of her mother. Roman, Ghostface’s new killer, had executed a series of murders. He killed Cotton, Steven, and others. In the end, he was killed by Sidney and Dewey.” [28]
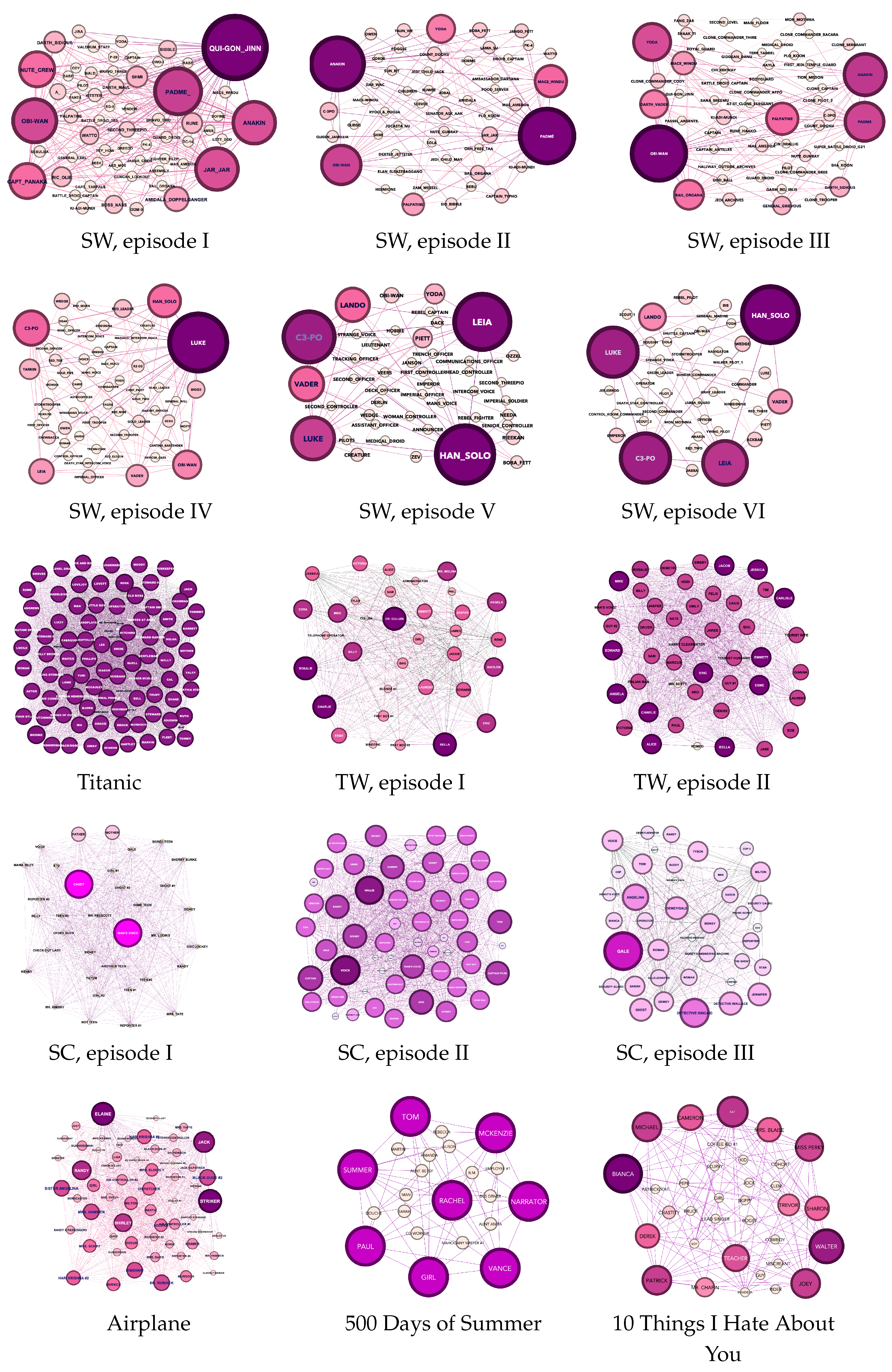
Appendix A.2. Movie Networks Visualization


References
- Kardan, A.A.; Ebrahimi, M. A novel approach to hybrid recommendation systems based on association rules mining for content recommendation in asynchronous discussion groups. Inf. Sci. 2013, 219, 93–110. [Google Scholar] [CrossRef]
- Drif, A.; Zerrad, H.E.; Cherifi, H. Ensvae: Ensemble variational autoencoders for recommendations. IEEE Access 2020, 8, 188335–188351. [Google Scholar] [CrossRef]
- Drif, A.; Guembour, S.; Cherifi, H. A sentiment enhanced deep collaborative filtering recommender system. In Proceedings of the Complex Networks & Their Applications IX: Volume 2, Proceedings of the Ninth International Conference on Complex Networks and Their Applications COMPLEX NETWORKS 2020, Madrid, Spain, 1–3 December 2020; Springer International Publishing: Berlin/Heidelberg, Germany, 2021; pp. 66–78. [Google Scholar]
- Drif, A.; Cherifi, H. Migan: Mutual-interaction graph attention network for collaborative filtering. Entropy 2022, 24, 1084. [Google Scholar] [CrossRef]
- Sang, J.; Xu, C. Character-based movie summarization. In Proceedings of the 18th ACM international conference on Multimedia, Firenze, Italy, 25–29 October 2010; pp. 855–858. [Google Scholar]
- Tran, Q.D.; Hwang, D.; Lee, O.J.; Jung, J.E. Exploiting character networks for movie summarization. Multimed. Tools Appl. 2017, 76, 10357–10369. [Google Scholar] [CrossRef]
- Li, Y.; Narayanan, S.; Kuo, C.C.J. Content-based movie analysis and indexing based on audiovisual cues. IEEE Trans. Circuits Syst. Video Technol. 2004, 14, 1073–1085. [Google Scholar] [CrossRef]
- Adams, B.; Dorai, C.; Venkatesh, S. Toward automatic extraction of expressive elements from motion pictures: Tempo. IEEE Trans. Multimed. 2002, 4, 472–481. [Google Scholar] [CrossRef]
- Weng, C.Y.; Chu, W.T.; Wu, J.L. Rolenet: Movie analysis from the perspective of social networks. IEEE Trans. Multimed. 2009, 11, 256–271. [Google Scholar] [CrossRef]
- Jung, J.J.; You, E.; Park, S.B. Emotion-based character clustering for managing story-based contents: A cinemetric analysis. Multimed. Tools Appl. 2013, 65, 29–45. [Google Scholar] [CrossRef]
- Weng, C.Y.; Chu, W.T.; Wu, J.L. Movie analysis based on roles’ social network. In Proceedings of the 2007 IEEE International Conference on Multimedia and Expo, Beijing, China, 2–5 July 2007; IEEE: Piscataway, NJ, USA, 2007; pp. 1403–1406. [Google Scholar]
- Mourchid, Y.; Renoust, B.; Cherifi, H.; El Hassouni, M. Multilayer network model of movie script. In Proceedings of the Complex Networks and Their Applications VII: Volume 1 Proceedings The 7th International Conference on Complex Networks and Their Applications COMPLEX NETWORKS, Cambridge, UK, 11–13 December 2018; Springer: Berlin/Heidelberg, Germany, 2019; pp. 782–796. [Google Scholar]
- Markovič, R.; Gosak, M.; Perc, M.; Marhl, M.; Grubelnik, V. Applying network theory to fables: Complexity in Slovene belles-lettres for different age groups. J. Complex Netw. 2019, 7, 114–127. [Google Scholar] [CrossRef]
- Lv, J.; Wu, B.; Zhou, L.; Wang, H. Storyrolenet: Social network construction of role relationship in video. IEEE Access 2018, 6, 25958–25969. [Google Scholar] [CrossRef]
- Chen, R.G.; Chen, C.C.; Chen, C.M. Unsupervised cluster analyses of character networks in fiction: Community structure and centrality. Knowl.-Based Syst. 2019, 163, 800–810. [Google Scholar] [CrossRef]
- Mourchid, Y.; Renoust, B.; Roupin, O.; Văn, L.; Cherifi, H.; Hassouni, M.E. Movienet: A movie multilayer network model using visual and textual semantic cues. Appl. Netw. Sci. 2019, 4, 1–37. [Google Scholar] [CrossRef]
- Xiao, Q. A method for measuring node importance in hypernetwork model. Res. J. Appl. Sci. Eng. Technol. 2013, 5, 568–573. [Google Scholar] [CrossRef]
- Das, K.; Samanta, S.; Pal, M. Study on centrality measures in social networks: A survey. Soc. Netw. Anal. Min. 2018, 8, 1–11. [Google Scholar] [CrossRef]
- Abdelsadek, Y.; Chelghoum, K.; Herrmann, F.; Kacem, I.; Otjacques, B. Community extraction and visualization in social networks applied to Twitter. Inf. Sci. 2018, 424, 204–223. [Google Scholar] [CrossRef]
- Grandjean, M. Comparing the Relational Structure of the Gospels. Network Analysis as a Tool for Biblical Sciences. Society of Biblical Literature. 2013. Available online: https://hal.science/hal-01525574/file/Grandjean-2013.pdf (accessed on 1 December 2023).
- Bastian, M.; Heymann, S.; Jacomy, M. Gephi: An open source software for exploring and manipulating networks. In Proceedings of the Third international AAAI Conference on Weblogs and Social Media, San Jose, CA, USA, 17–20 May 2009. [Google Scholar]
- Schieber, T.A.; Carpi, L.; Díaz-Guilera, A.; Pardalos, P.M.; Masoller, C.; Ravetti, M.G. Quantification of network structural dissimilarities. Nat. Commun. 2017, 8, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Zhang, R.J.; Fred, Y.Y. Measuring similarity for clarifying layer difference in multiplex ad hoc duplex information networks. J. Inf. 2020, 14, 100987. [Google Scholar] [CrossRef]
- Saxena, R.; Kaur, S.; Bhatnagar, V. Identifying similar networks using structural hierarchy. Phys. A Stat. Mech. Appl. 2019, 536, 121029. [Google Scholar] [CrossRef]
- Bródka, P.; Chmiel, A.; Magnani, M.; Ragozini, G. Quantifying layer similarity in multiplex networks: A systematic study. R. Soc. Open Sci. 2018, 5, 171747. [Google Scholar] [CrossRef]
- Lafhel, M.; Cherifi, H.; Renoust, B.; El Hassouni, M.; Mourchid, Y. Movie Script Similarity Using Multilayer Network Portrait Divergence. In Proceedings of the International Conference on Complex Networks and Their Applications, Madrid, Spain, 1–3 December 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 284–295. [Google Scholar]
- Bagrow, J.P.; Bollt, E.M.; Skufca, J.D.; Ben-Avraham, D. Portraits of complex networks. EPL (Europhys. Lett.) 2008, 81, 68004. [Google Scholar] [CrossRef]
- Lafhel, M.; Abrouk, L.; Cherifi, H.; El Hassouni, M. The similarity between movie scripts using Multilayer Network Laplacian Spectra Descriptor. In Proceedings of the 2022 IEEE Workshop on Complexity in Engineering (COMPENG), Florence, Italy, 18–20 July 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–5. [Google Scholar]
- Blei, D.M.; Ng, A.Y.; Jordan, M.I. Latent dirichlet allocation. J. Mach. Learn. Res. 2003, 3, 993–1022. [Google Scholar]
- Wilson, R.C.; Zhu, P. A study of graph spectra for comparing graphs and trees. Pattern Recognit. 2008, 41, 2833–2841. [Google Scholar] [CrossRef]
- Zhu, P.; Wilson, R.C. A study of graph spectra for comparing graphs. In Proceedings of the BMVC, Oxford, UK, 5–8 September 2005. [Google Scholar]
- Tsitsulin, A.; Mottin, D.; Karras, P.; Bronstein, A.; Müller, E. Netlsd: Hearing the shape of a graph. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, London, UK, 19–23 August 2018; pp. 2347–2356. [Google Scholar]
- Goyal, P.; Ferrara, E. Graph embedding techniques, applications, and performance: A survey. Knowl.-Based Syst. 2018, 151, 78–94. [Google Scholar] [CrossRef]
- Cui, P.; Wang, X.; Pei, J.; Zhu, W. A survey on network embedding. IEEE Trans. Knowl. Data Eng. 2018, 31, 833–852. [Google Scholar] [CrossRef]
- Cai, H.; Zheng, V.W.; Chang, K.C.C. A comprehensive survey of graph embedding: Problems, techniques, and applications. IEEE Trans. Knowl. Data Eng. 2018, 30, 1616–1637. [Google Scholar] [CrossRef]
- Li, B.; Pi, D. Learning deep neural networks for node classification. Expert Syst. Appl. 2019, 137, 324–334. [Google Scholar] [CrossRef]
- Liao, L.; He, X.; Zhang, H.; Chua, T.S. Attributed social network embedding. IEEE Trans. Knowl. Data Eng. 2018, 30, 2257–2270. [Google Scholar] [CrossRef]
- Wang, C.; Pan, S.; Hu, R.; Long, G.; Jiang, J.; Zhang, C. Attributed graph clustering: A deep attentional embedding approach. arXiv 2019, arXiv:1906.06532. [Google Scholar]
- Ding, C.H.; He, X.; Zha, H.; Gu, M.; Simon, H.D. A min-max cut algorithm for graph partitioning and data clustering. In Proceedings of the 2001 IEEE International Conference on Data Mining, San Jose, CA, USA, 29 November–2 December 2001; IEEE: Piscataway, NJ, USA, 2001; pp. 107–114. [Google Scholar]
- Chen, H.; Yu, Z.; Yang, Q.; Shao, J. Attributed graph clustering with subspace stochastic block model. Inf. Sci. 2020, 535, 130–141. [Google Scholar] [CrossRef]
- Liu, F.; Xue, S.; Wu, J.; Zhou, C.; Hu, W.; Paris, C.; Nepal, S.; Yang, J.; Yu, P.S. Deep learning for community detection: Progress, challenges and opportunities. arXiv 2020, arXiv:2005.08225. [Google Scholar]
- Van der Maaten, L.; Hinton, G. Visualizing data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- Chen, X.; Heimann, M.; Vahedian, F.; Koutra, D. CONE-Align: Consistent Network Alignment with Proximity-Preserving Node Embedding. In Proceedings of the 29th ACM International Conference on Information & Knowledge Management, Virtual Event, 19–23 October 2020; pp. 1985–1988. [Google Scholar]
- Asta, D.; Shalizi, C.R. Geometric network comparison. arXiv 2014, arXiv:1411.1350. [Google Scholar]
- Huang, W.; Ribeiro, A. Network comparison: Embeddings and interiors. IEEE Trans. Signal Process. 2017, 66, 412–427. [Google Scholar] [CrossRef]
- Koren, Y.; Bell, R.; Volinsky, C. Matrix factorization techniques for recommender systems. Computer 2009, 42, 30–37. [Google Scholar] [CrossRef]
- Van Loan, C.F. Generalizing the singular value decomposition. SIAM J. Numer. Anal. 1976, 13, 76–83. [Google Scholar] [CrossRef]
- Perozzi, B.; Al-Rfou, R.; Skiena, S. Deepwalk: Online learning of social representations. In Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 24–27 August 2014; pp. 701–710. [Google Scholar]
- Qiu, J.; Dong, Y.; Ma, H.; Li, J.; Wang, K.; Tang, J. Network embedding as matrix factorization: Unifying deepwalk, line, pte, and node2vec. In Proceedings of the Eleventh ACM International Conference on Web Search and Data Mining, Marina Del Rey, CA, USA, 5–9 February 2018; pp. 459–467. [Google Scholar]
- Bagrow, J.P.; Bollt, E.M. An information-theoretic, all-scales approach to comparing networks. Appl. Netw. Sci. 2019, 4, 45. [Google Scholar] [CrossRef]


| Symbol | Description |
|---|---|
| G | Undirected and unweighted network |
| V, n | Set of vertices, Number of nodes |
| E, m | Set of edges, Number of edges |
| A | adjacency matrix |
| D | diagonal matrix |
| I | identity matrix |
| L | Laplacian matrix |
| Normalized Laplacian matrix | |
| Orthogonal matrix | |
| Graph representation | |
| d | Graph’s diameter |
| Eigenvalue | |
| v | Feature vector |
| Distance | |
| Jensen–Shannon divergence |
| Categories | Movies |
|---|---|
| Horror | Scream: Episode I (SC1) in 1995 |
| Scream: Episode II (SC2) in 1997 | |
| Scream: Episode III (SC3) in 1999 | |
| Romance | Twilight: Fascination (TW1) in 2008 |
| Twilight: New Moon (TW2) in 2009 | |
| Titanic in 1997 | |
| Comedy | 500 Days of Summer in 2009 |
| Ten Things I Hate About You in 1997 | |
| Airplane in 1979 | |
| Sci-Fi | Star Wars: A New Hope (SW1) in 1977 |
| Star Wars: The Empire Strikes Back (SW2) in 1980 | |
| Star Wars: Return of the Jedi (SW3) in 1983 | |
| Star Wars: The Phantom Menace (SW4) in 1999 | |
| Star Wars: Attack of the Clones (SW5) in 2002 | |
| Star Wars: Revenge of the Sith (SW6) in 2005 |
| Categories | Movies | Rank of Similarity | ||
|---|---|---|---|---|
| Characters | Keywords | Locations | ||
| Horror | SC1 & SC2 | order 1 | order 1 | order 1 |
| SC2 & SC3 | order 2 | order 2 | order 2 | |
| SC1 & SC3 | order 3 | order 3 | order 3 | |
| Romance | TW1 & TW2 | order 1 | order 1 | order 1 |
| TW1 & Titanic | order 2 | order 2 | order 2 | |
| TW2 & Titanic | order 2 | order 2 | order 2 | |
| Sci-Fi | SW5 & SW6 | order 1 | order 1 | order 1 |
| SW4 & SW5 | order 2 | order 2 | order 2 | |
| SW4 & SW6 | order 3 | order 3 | order 3 | |
| SW2 & SW3 | order 4 | order 4 | order 4 | |
| SW1 & SW2 | order 5 | order 5 | order 5 | |
| SW1 & SW3 | order 6 | order 6 | order 6 | |
| SW3 & SW4 | order 7 | order 7 | order 7 | |
| SW3 & SW5 | order 8 | order 8 | order 8 | |
| SW2 & SW4 | order 9 | order 9 | order 9 | |
| SW2 & SW5 | order 10 | order 10 | order 10 | |
| SW1 & SW4 | order 11 | order 11 | order 11 | |
| SW3 & SW6 | order 12 | order 12 | order 12 | |
| SW1 & SW5 | order 13 | order 13 | order 13 | |
| SW2 & SW6 | order 14 | order 14 | order 14 | |
| SW1 & SW6 | order 15 | order 15 | order 15 | |
| Comedy | Airplane & Ten Things I Hate About You | order 3 | order 3 | order 2 |
| 500 Days of Summer & Ten Things I Hate About You | order 3 | order 2 | order 1 | |
| Airplane & 500 Days of Summer | order 3 | order 1 | order 2 | |
| Measures | Horror | Romance | Sci-fi | Comedy | Horror vs. Romance | Horror vs. Sci-fi | Horror vs. Comedy | Romance vs. Sci-fi | Romance vs. Comedy | Sci-fi vs. Comedy |
|---|---|---|---|---|---|---|---|---|---|---|
| NetLSD | ✗ | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | ✓ | ✗ | ✗ |
| Laplacian Spectra | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✗ | ✗ | ✓ | ✓ |
| NetMF | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ |
| D-measure | ✗ | ✗ | ✓ | ✓ | ✗ | ✓ | ✓ | ✓ | ✗ | ✓ |
| Network Portrait Divergence | ✓ | ✗ | ✓ | ✓ | ✓ | ✗ | ✓ | ✓ | ✓ | ✓ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lafhel, M.; Cherifi, H.; Renoust, B.; El Hassouni, M. Comparison of Graph Distance Measures for Movie Similarity Using a Multilayer Network Model. Entropy 2024, 26, 149. https://doi.org/10.3390/e26020149
Lafhel M, Cherifi H, Renoust B, El Hassouni M. Comparison of Graph Distance Measures for Movie Similarity Using a Multilayer Network Model. Entropy. 2024; 26(2):149. https://doi.org/10.3390/e26020149
Chicago/Turabian StyleLafhel, Majda, Hocine Cherifi, Benjamin Renoust, and Mohammed El Hassouni. 2024. "Comparison of Graph Distance Measures for Movie Similarity Using a Multilayer Network Model" Entropy 26, no. 2: 149. https://doi.org/10.3390/e26020149
APA StyleLafhel, M., Cherifi, H., Renoust, B., & El Hassouni, M. (2024). Comparison of Graph Distance Measures for Movie Similarity Using a Multilayer Network Model. Entropy, 26(2), 149. https://doi.org/10.3390/e26020149








