Gas Kinetic Scheme Coupled with High-Speed Modifications for Hypersonic Transition Flow Simulations
Abstract
:1. Introduction
2. Mesoscopic Transition Prediction Method Framework
2.1. Gas Kinetic Scheme
2.2. Langtry–Menter Transition Model
2.3. High-Speed Modification Methods
2.3.1. Hypersonic Crossflow Extension
2.3.2. The Pressure–Dilatation Correlation
2.3.3. Pressure Gradient Parameter Correction
3. Coupling Mechanism in the Mesoscopic Transition Prediction Method
4. Results and Discussion
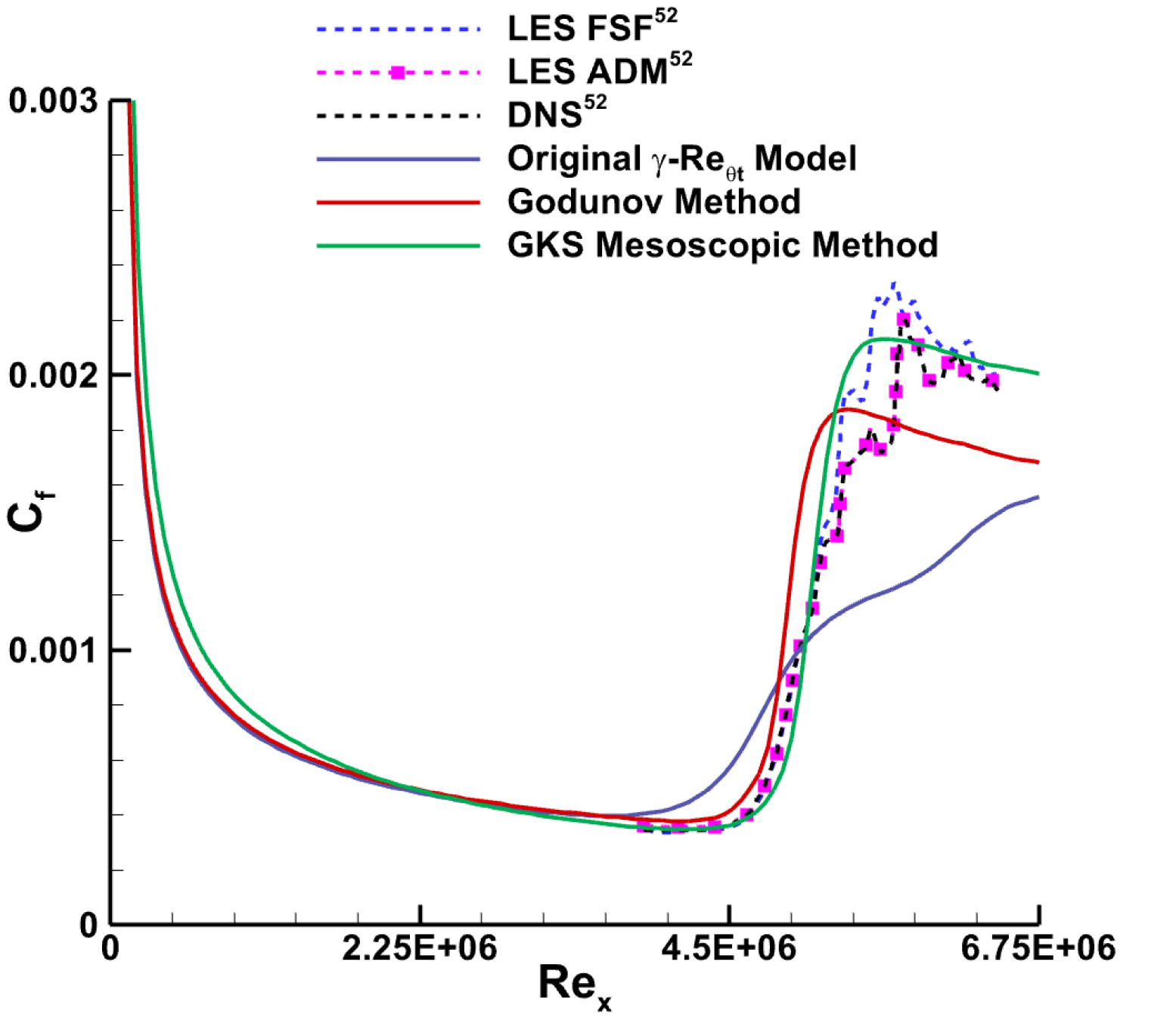
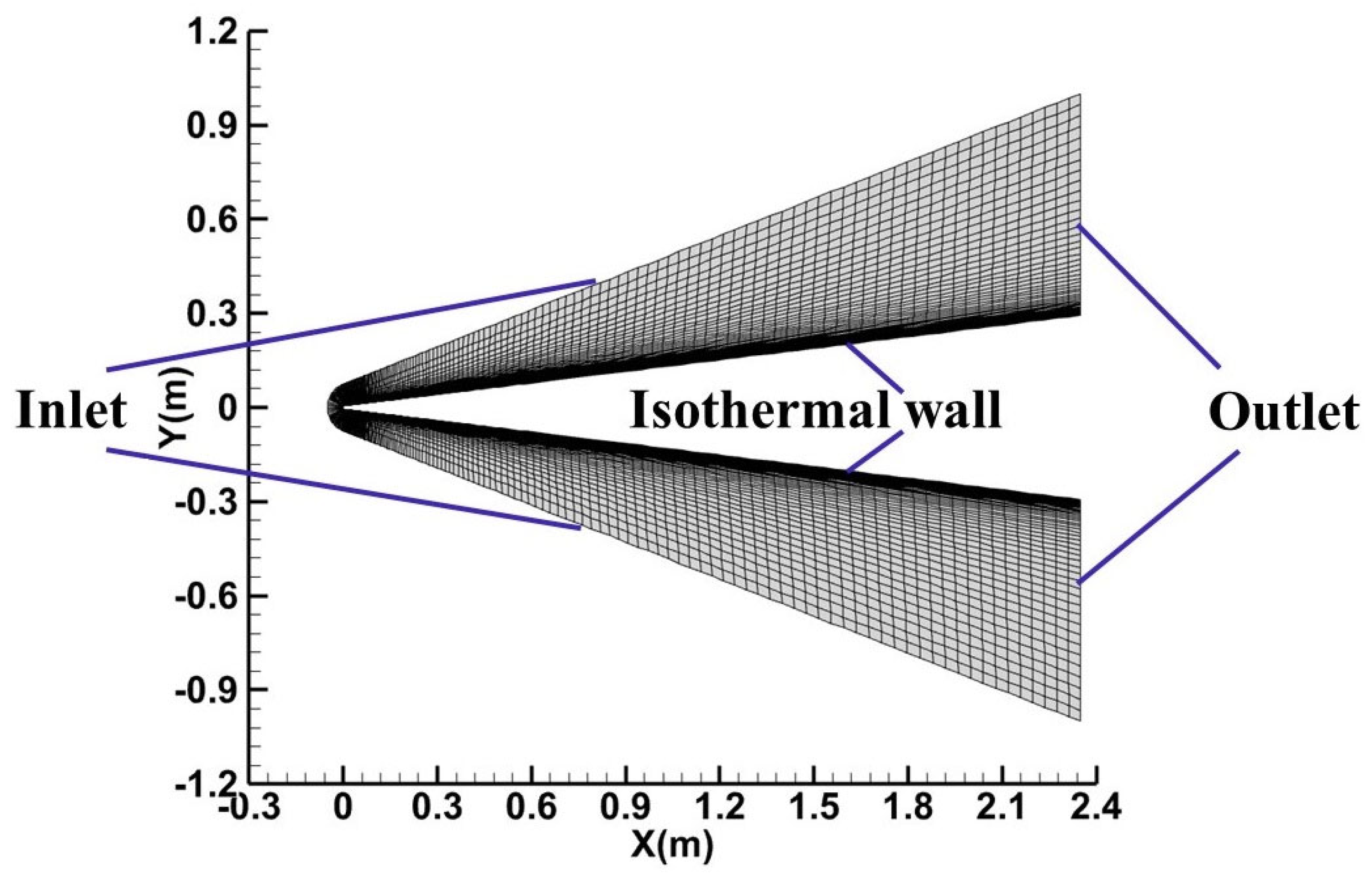
4.1. Supersonic Adiabatic Flat Plate with Ma∞ = 4.5
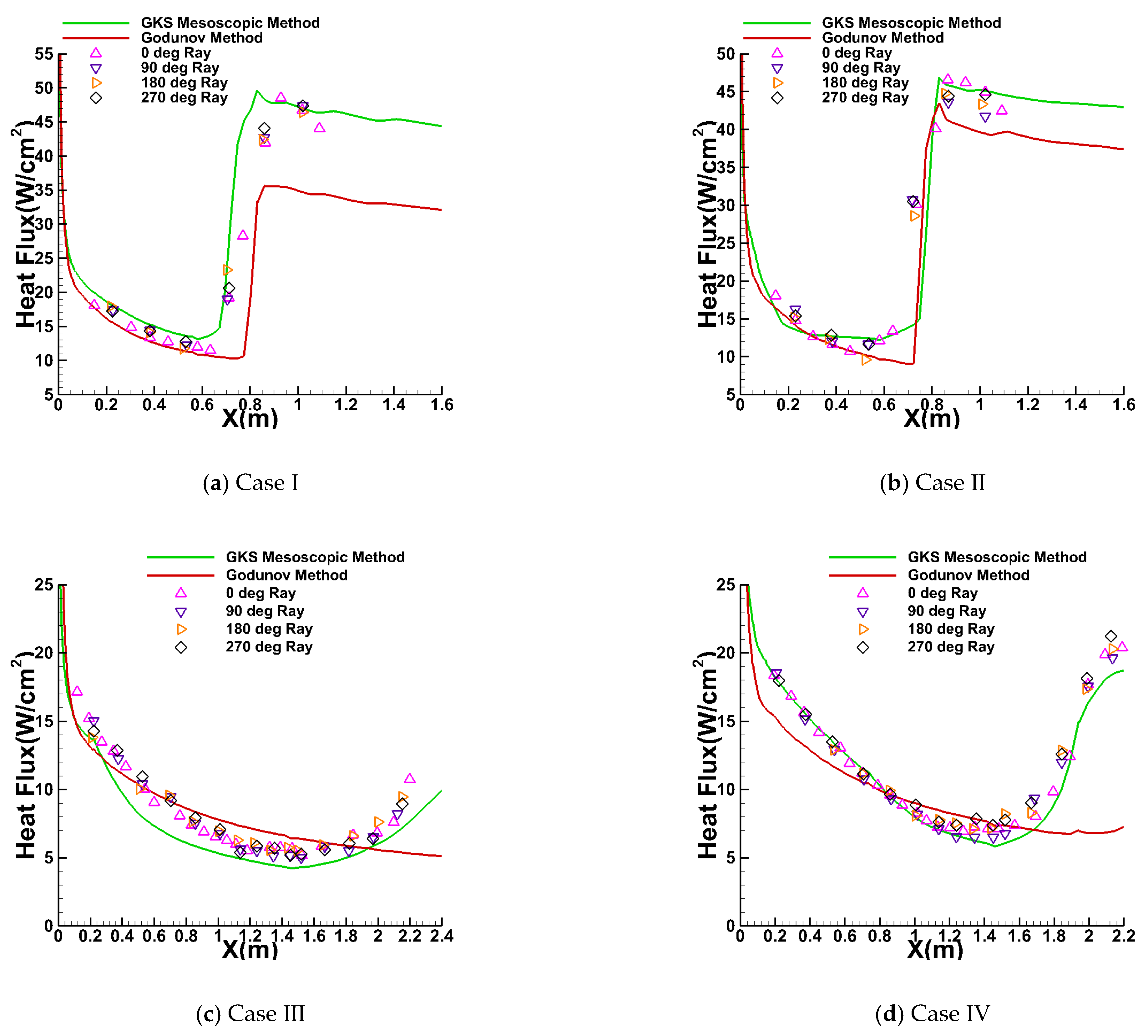
4.2. Hypersonic Transition on Cones
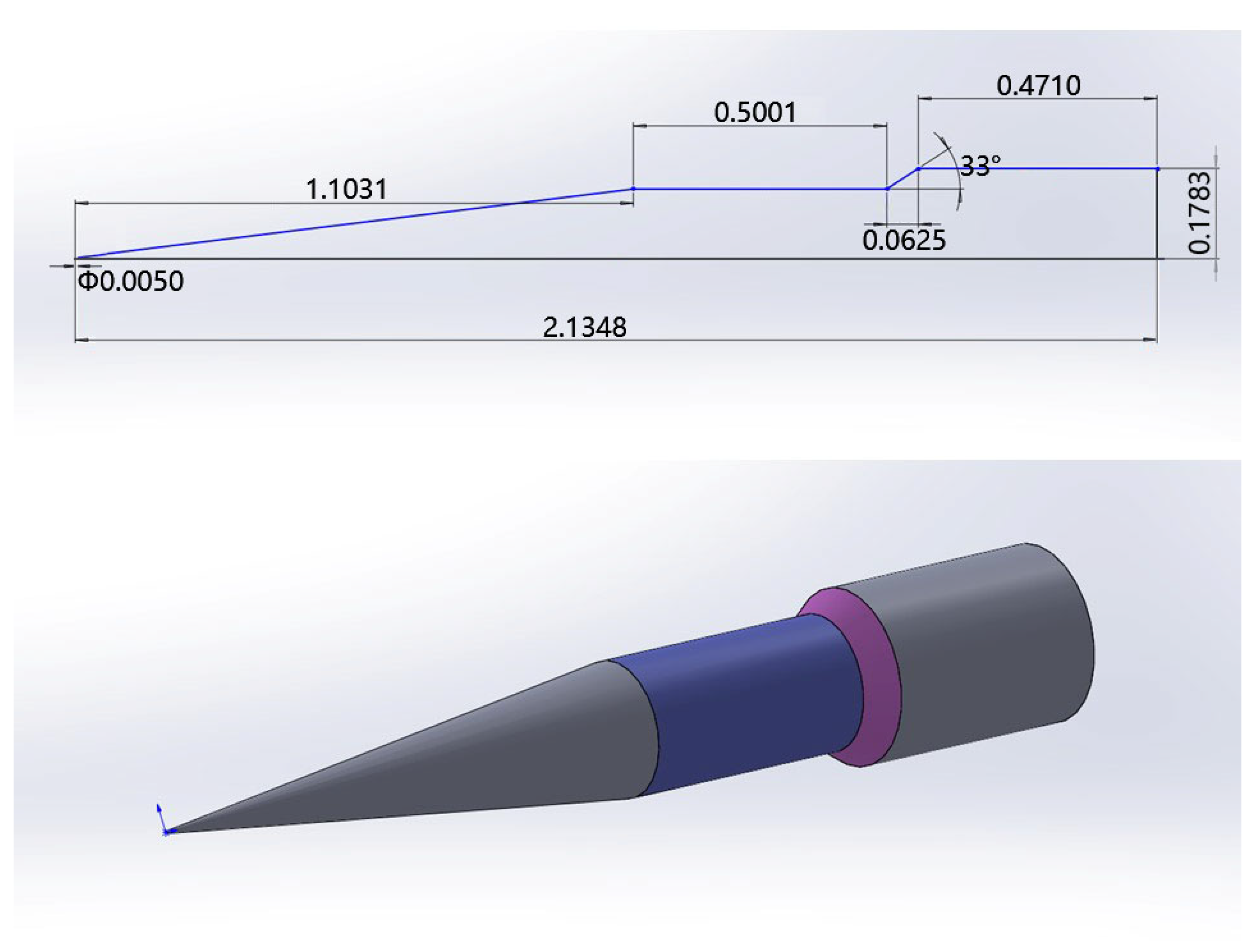
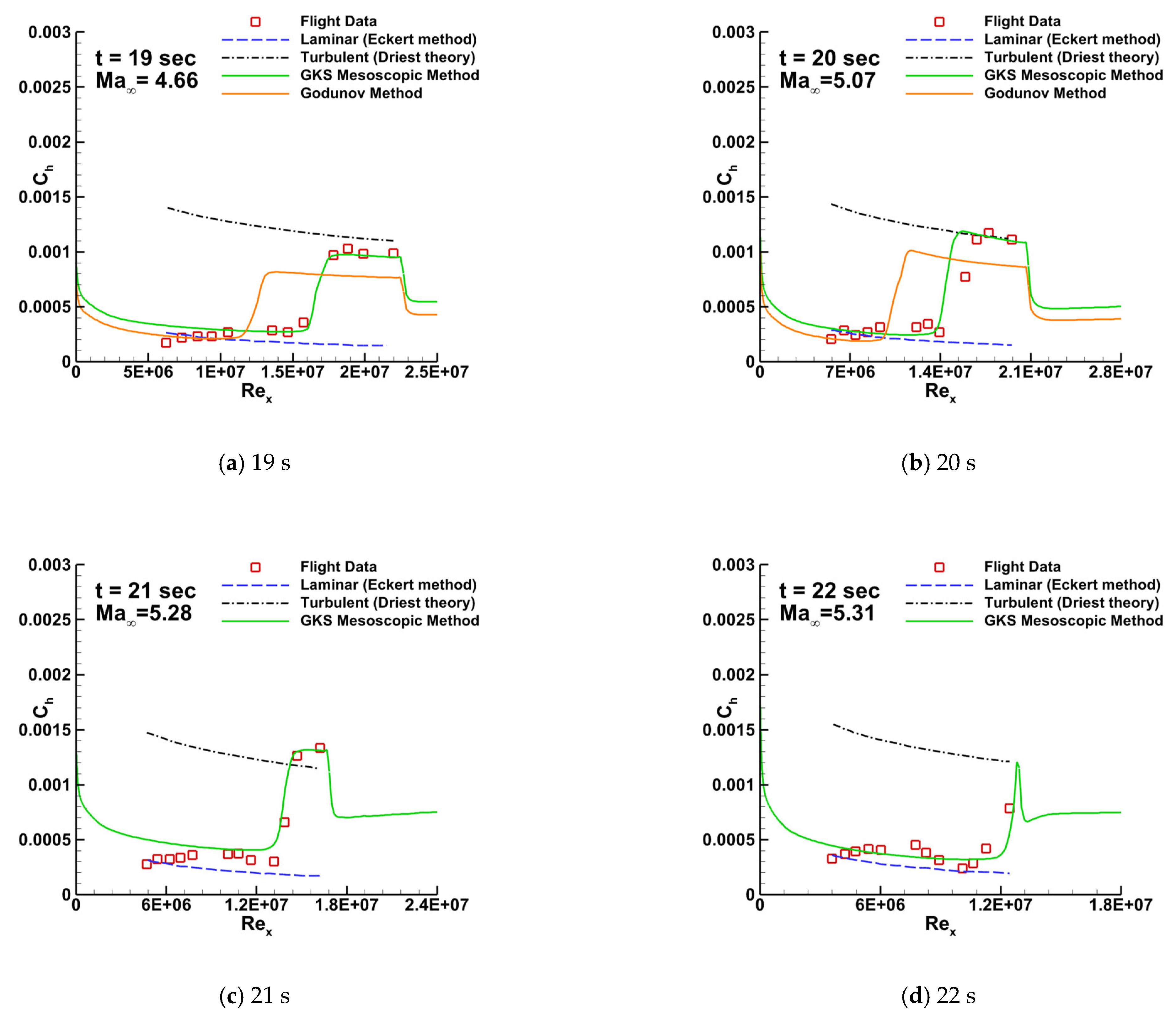
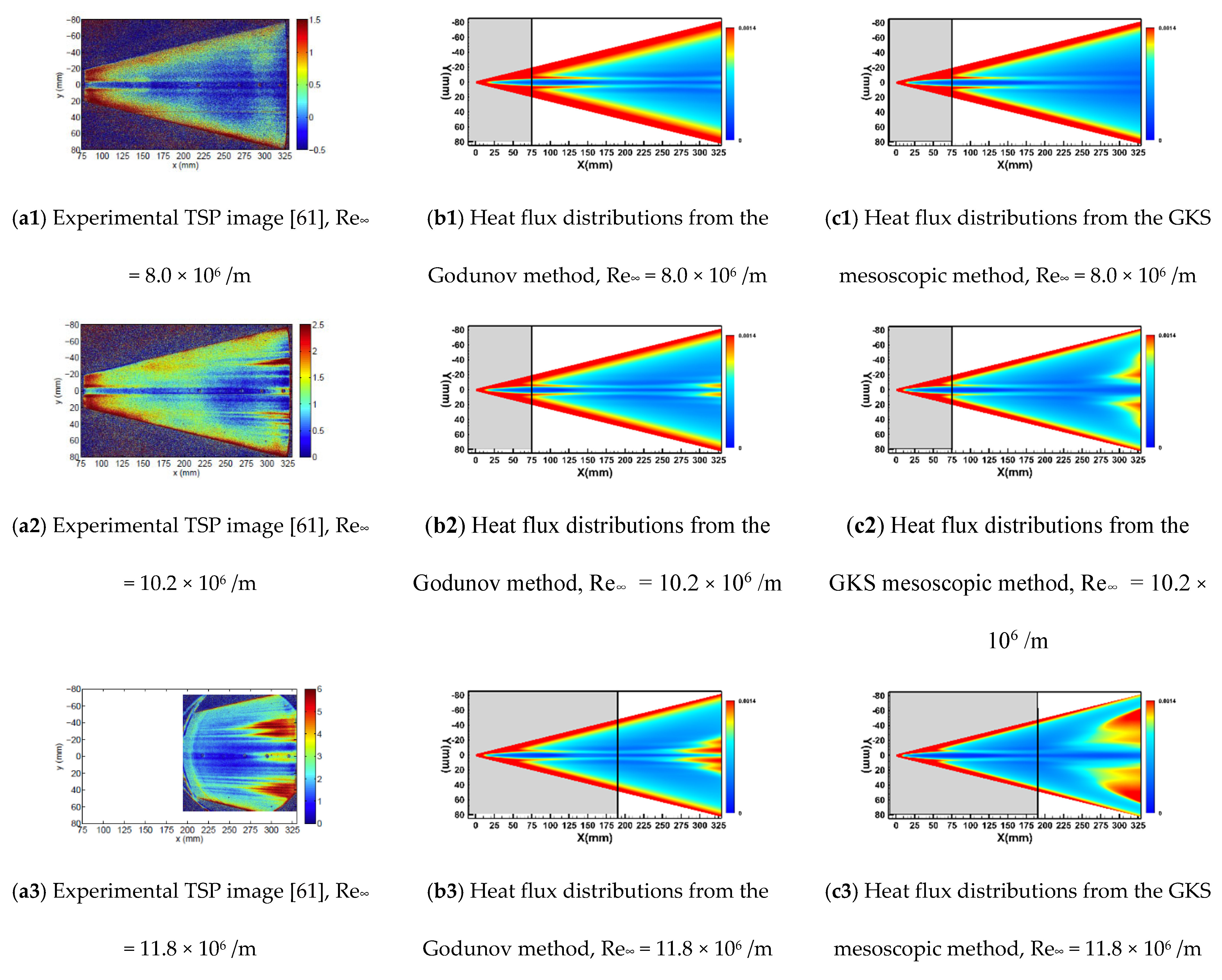
4.3. HIFiRE-1 Hypersonic Flight
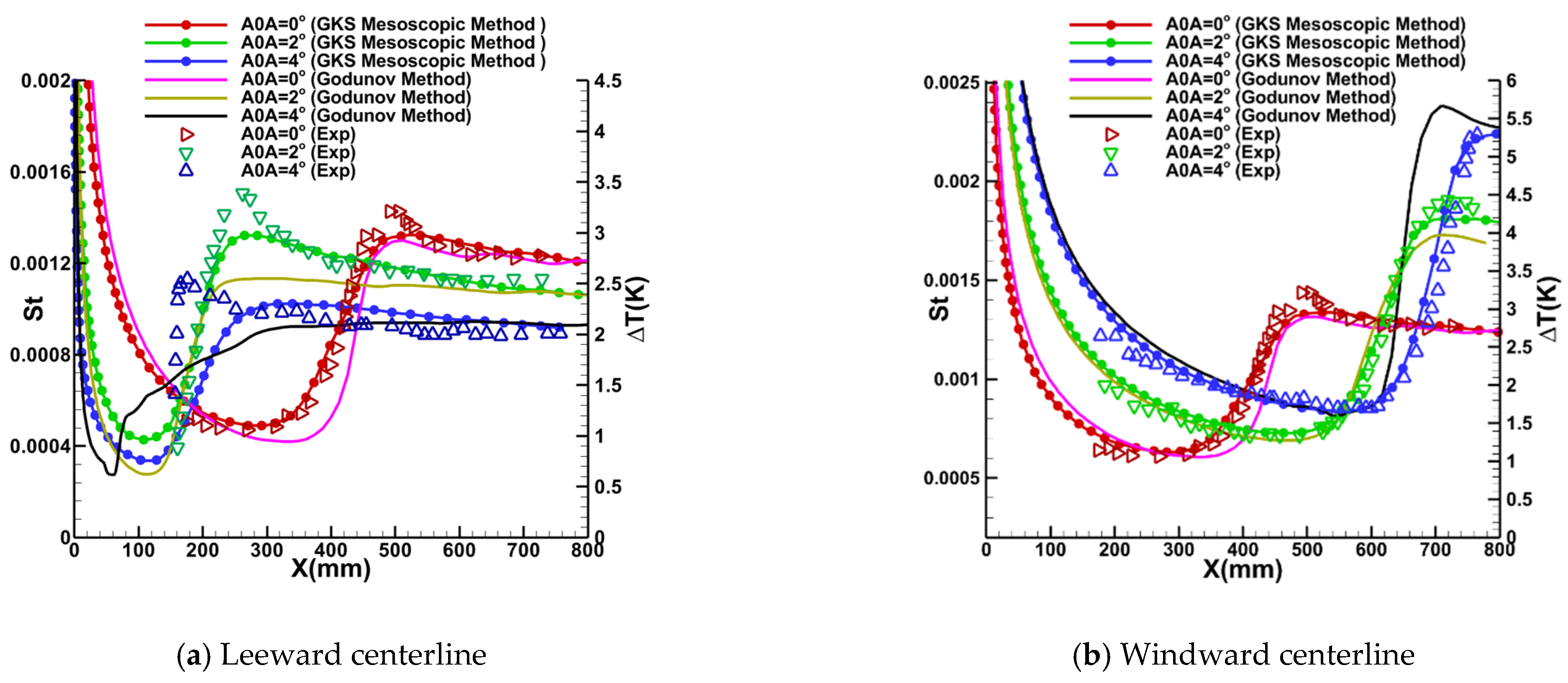
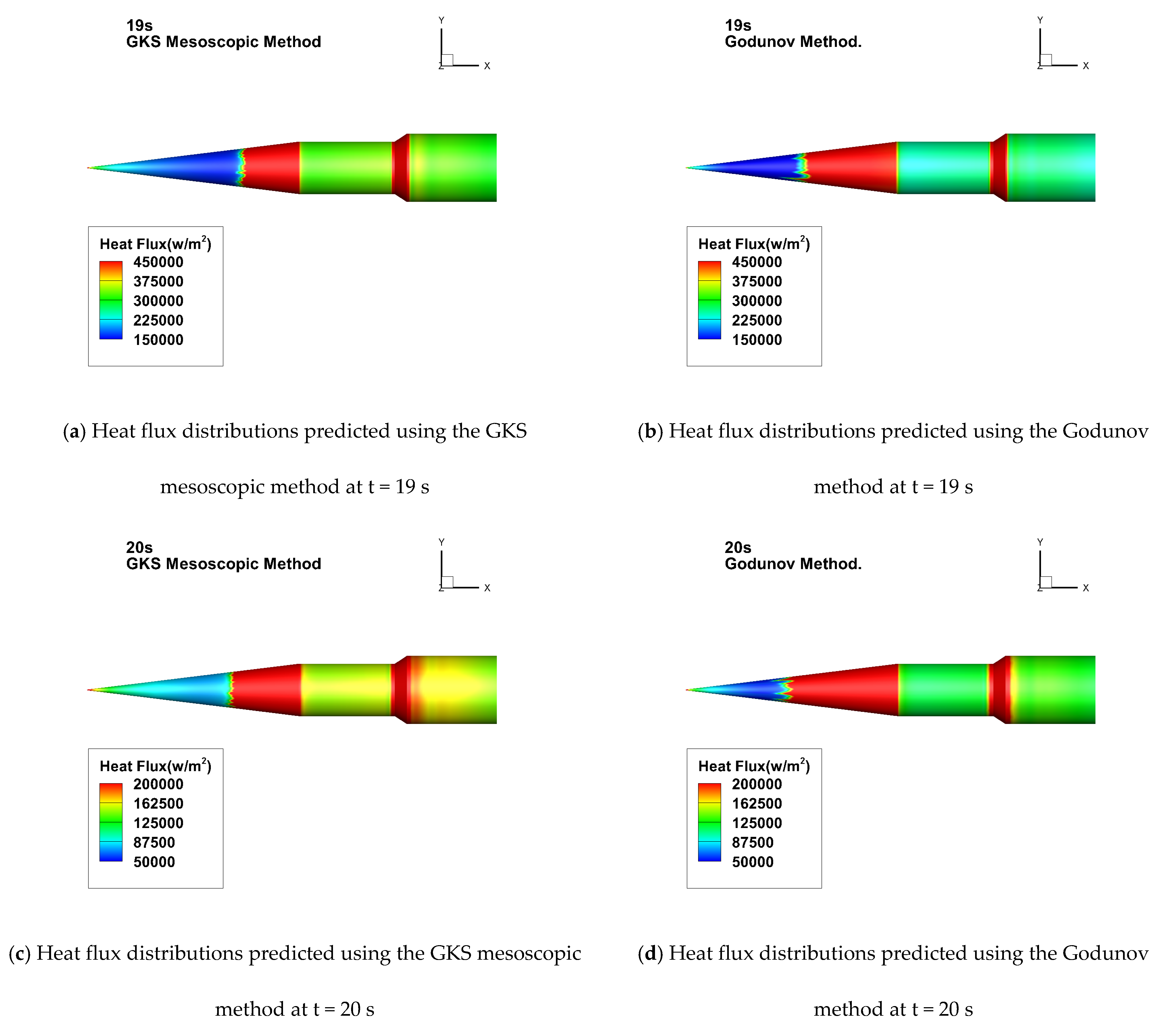
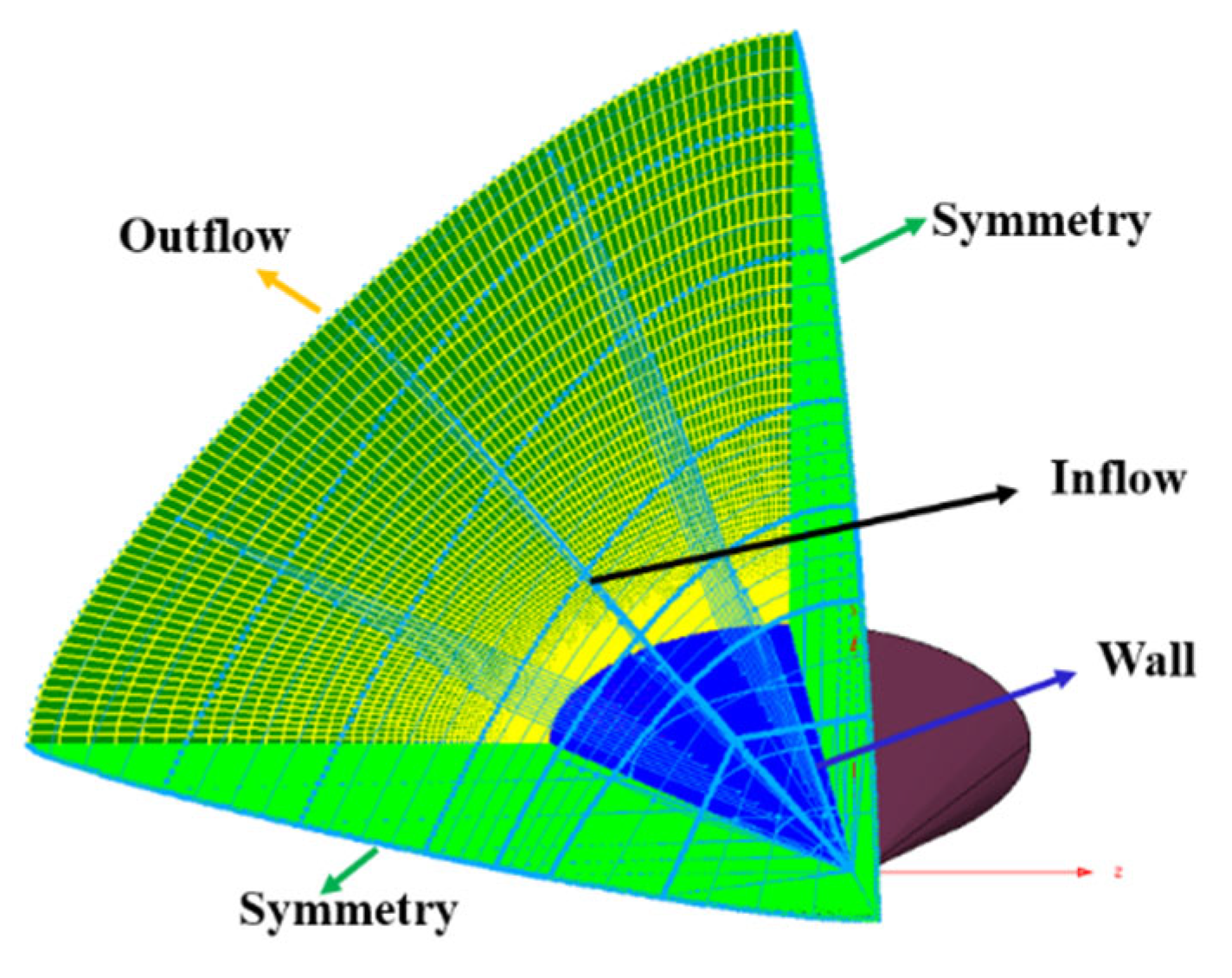
4.4. HIFiRE-5
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, Q.; Luo, Z.; Wang, L.; Tu, G.; Deng, X.; Zhou, Y. Direct numerical simulations of supersonic turbulent boundary layer with streamwise-striped wall blowing. Aerosp. Sci. Technol. 2021, 110, 106510. [Google Scholar] [CrossRef]
- White, F.M. Viscous Fluid Flow; McGraw-Hill: New York, NY, USA, 1974. [Google Scholar]
- Heeg, J.; Zeiler, T.A.; Pototzky, A.S.; Spain, C.V.; Engelund, W.C. Aerothermoelastic Analysis of a NASP Demonstrator Model. In Proceedings of the 34th Structures, Structural Dynamics and Materials Conference, La Jolla, CA, USA, 19–22 April 1993; pp. 617–627. [Google Scholar]
- Li, X.; Fu, D.; Ma, Y. Direct numerical simulation of hypersonic boundary layer transition over a blunt cone with a small angle of attack. Phys. Fluids 2010, 22, 025105. [Google Scholar] [CrossRef]
- Men, H.; Li, X. Direct numerical simulations of hypersonic boundary layer transition over a hypersonic transition research vehicle model lifting body at different angles of attack. Phys. Fluids 2023, 35, 044111. [Google Scholar] [CrossRef]
- Piomelli, U. Large-Eddy Simulation: Achievements and Challenges. Prog. Aerosp. Sci. 1999, 35, 335–362. [Google Scholar] [CrossRef]
- Menter, F.R.; Langtry, R.B.; Likki, S.R.; Suzen, Y.B.; Huang, P.G.; Völker, S. A Correlation-Based Transition Model Using Local Variables—Part I: Model Formulation. J. Turbomach. 2006, 128, 413–422. [Google Scholar] [CrossRef]
- Langtry, R.B.; Menter, F.R.; Likki, S.R.; Suzen, Y.B.; Huang, P.G.; Völker, S. A Correlation-Based Transition Model Using Local Variables—Part II: Test Cases and Industrial Applications. J. Turbomach. 2006, 128, 423–434. [Google Scholar] [CrossRef]
- Liu, Y.; Li, P.; Jiang, K. Comparative assessment of transitional turbulence models for airfoil aerodynamics in the low Reynolds number range. J. Wind. Eng. Ind. Aerodyn. 2021, 217, 104726. [Google Scholar] [CrossRef]
- Menter, F.R. Review of the shear-stress transport turbulence model experience from an industrial perspective. Int. J. Comput. Fluid Dyn. 2009, 23, 305–316. [Google Scholar] [CrossRef]
- Dick, E.; Kubacki, S. Transition Models for Turbomachinery Boundary Layer Flows: A Review. Int. J. Turbomach. Propuls. Power 2017, 2, 4. [Google Scholar] [CrossRef]
- You, Y.; Luedeke, H.; Eggers, T.; Hannemann, K. Application of the γ-Reθt Transition Model in High Speed Flows. In Proceedings of the 18th AIAA/3AF International Space Planes and Hypersonic Systems and Technologies Conference, Tours, France, 24–28 September 2012. [Google Scholar]
- Zangeneh, R. Assessment of RANS Models for Numerical Prediction of Laminar-turbulent Transition in Hypersonic Flows. In Proceedings of the AIAA AVIATION 2021 FORUM, Virtual Event, 2–6 August 2021. [Google Scholar]
- Hao, Z.; Yan, C.; Qin, Y.; Zhou, L. Improved γ-Reθt model for heat transfer prediction of hypersonic boundary layer transition. Int. J. Heat Mass Tran. 2017, 107, 329–338. [Google Scholar] [CrossRef]
- Liu, Z.; Yan, C.; Cai, F.; Yu, J.; Lu, Y. An improved local correlation-based intermittency transition model appropriate for high-speed flow heat transfer. Aerosp. Sci. Technol. 2020, 106, 106122. [Google Scholar] [CrossRef]
- Wang, L.; Fu, S. Development of an Intermittency Equation for the Modeling of the Supersonic/Hypersonic Boundary Layer Flow Transition. Flow Turbul. Combust. 2011, 87, 165–187. [Google Scholar] [CrossRef]
- Zhou, L.; Zhao, R.; Li, R. A combined criteria-based method for hypersonic three-dimensional boundary layer transition prediction. Aerosp. Sci. Technol. 2018, 73, 105–117. [Google Scholar] [CrossRef]
- Frauholz, S.; Reinartz, B.U.; Müller, S.; Behr, M. Transition Prediction for Scramjets Using γ-Reθt Model Coupled to Two Turbulence Models. J. Propul. Power 2015, 31, 1404–1422. [Google Scholar] [CrossRef]
- Eisfeld, B. Computation of Complex Compressible Aerodynamic Flows with a Reynolds Stress Turbulence Model. In Proceedings of the International Conference on Boundary and Interior, Gottingen, Germany, 24–28 July 2006. [Google Scholar]
- Xia, C.; Chen, W. Boundary-layer transition prediction using a simplified correlation-based model. Chin. J. Aeronaut. 2016, 29, 66–75. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Y.; Chen, J.; Mao, M.; Jiang, Y. Numerical Simulations of Hypersonic Boundary Layer Transition Based on the Flow Solver Chant 2.0. In Proceedings of the 21st AIAA International Space Planes and Hypersonics Technologies Conference, Xiamen, China, 6–9 March 2017. [Google Scholar]
- Zhang, Y.; He, K.; Zhang, Y.; Mao, M.; Chen, J. Improvement and Validation of Menter’s Transition Model for Hyper-sonic Flow Simulation. J. Astronaut. 2016, 37, 397–402. [Google Scholar]
- Xiang, X.; Zhang, Y.; Yuan, X.; TU, G.; Wan, B.; Chen, J. C-γ-Reθ model for hyperson in three-dimensional boundary layer transition prediction. Acta Aeronaut. Astronaut. Sin. 2021, 42, 188–196. [Google Scholar]
- Xiang, X.-H.; Chen, J.-Q.; Yuan, X.-X.; Wan, B.-B.; Zhuang, Y.; Zhang, Y.-F.; Tu, G.-H. Cross-flow transition model predictions of hypersonic transition research vehicle. Aerosp. Sci. Technol. 2022, 122, 107327. [Google Scholar] [CrossRef]
- Zhang, T.-X.; Chen, J.-Q.; Zeng, F.-Z.; Tang, D.-G.; Yan, C. Improvement of transition prediction model in hypersonic boundary layer based on field inversion and machine learning framework. Phys. Fluids 2023, 35, 24104. [Google Scholar] [CrossRef]
- Duraisamy, K.; Spalart, P.R.; Rumsey, C.L. Status, Emerging Ideas and Future Directions of Turbulence Modeling Research in Aeronautics; NASA Technical Report No. NASA/TM-2017-219682; NASA: Washington, DC, USA, 2017. [Google Scholar]
- Runsey, C.L.; Coleman, G.N. NASA Symposium on Turbulence Modeling: Roadblocks, and the Potential for Machine Learning; NASA Technical Report No. NASA/TM–20220015595; NASA: Washington, DC, USA, 2022. [Google Scholar]
- Xu, K. A Gas-Kinetic BGK Scheme for the Navier–Stokes Equations and Its Connection with Artificial Dissipation and Godu-nov Method. J. Comput. Phys. 2001, 171, 289–335. [Google Scholar] [CrossRef]
- Xu, K. Direct Modeling for Computational Fluid Dynamics: Construction and Application of Unified Gas-Kinetic Schemes; World Scientific: Singapore, 2015; pp. 11–48. [Google Scholar]
- Xu, K.; Mao, M.; Tang, L. A multidimensional gas-kinetic BGK scheme for hypersonic viscous flow. J. Comput. Phys. 2005, 203, 405–421. [Google Scholar] [CrossRef]
- Cao, G.; Pan, L.; Xu, K. Three dimensional high-order gas-kinetic scheme for supersonic isotropic turbulence II: Coarse-graining analysis of compressible Ksgs budget. J. Comput. Phys. 2021, 439, 110402. [Google Scholar] [CrossRef]
- Kun, X.U.; Songze, C. Gas kinetic scheme in hypersonic flow simulation. Acta Aeronaut. ET Astronaut. Sin. 2015, 36, 135–146. [Google Scholar]
- Shu, C.; Yang, L.; Liu, Y.; Liu, W.; Zhang, Z. High-order implicit RBF-based differential quadrature-finite volume method on unstructured grids: Application to inviscid and viscous compressible flows. J. Comput. Phys. 2023, 478, 111962. [Google Scholar] [CrossRef]
- Liu, Y.Y.; Yang, L.M.; Shu, C.; Zhang, H.W. Three-dimensional high-order least square-based finite difference-finite volume method on unstructured grids. Phys. Fluids 2020, 32, 123604. [Google Scholar] [CrossRef]
- Li, Q.; Fu, S. High-order accurate gas-kinetic scheme and turbulence simulation. Sci. Sin. Phys. Mech. Astron. 2014, 44, 278–284. [Google Scholar]
- Pan, L.; Cao, G.; Xu, K. Fourth-order gas-kinetic scheme for turbulence simulation with multi-dimensional WENO reconstruction. Comput. Fluids 2021, 221, 104927. [Google Scholar] [CrossRef]
- Cao, G.; Pan, L.; Xu, K. High-order gas-kinetic scheme with parallel computation for direct numerical simulation of turbulent flows. J. Comput. Phys. 2022, 448, 110739. [Google Scholar] [CrossRef]
- Righi, M. A Modified Gas-Kinetic Scheme for Turbulent Flow. Commun. Comput. Phys. 2014, 16, 239–263. [Google Scholar] [CrossRef]
- Righi, M. A Gas-Kinetic Scheme for Turbulent Flow. Flow Turbul. Combust. 2016, 97, 121–139. [Google Scholar] [CrossRef]
- Tan, S.; Li, Q.; Xiao, Z.; Fu, S. Gas kinetic scheme for turbulence simulation. Aerosp. Sci. Technol. 2018, 78, 214–227. [Google Scholar] [CrossRef]
- Bhatnagar, P.L.; Gross, E.P.; Krook, M. A Model for Collision Processes in Gases. I. Small Amplitude Processes in Charged and Neutral One-Component Systems. Phys. Rev. B 1954, 94, 511–525. [Google Scholar] [CrossRef]
- Li, J.; Zhong, C.; Pan, D.; Zhuo, C. A gas-kinetic scheme coupled with SST model for turbulent flows. Comput. Math. Appl. 2019, 78, 1227–1242. [Google Scholar] [CrossRef]
- Cao, G.; Su, H.; Xu, J.; Xu, K. Implicit high-order gas kinetic scheme for turbulence simulation. Aerosp. Sci. Technol. 2019, 92, 958–971. [Google Scholar] [CrossRef]
- Liu, H.; Cao, G.; Chen, W.; Agarwal, R.K.; Zhao, W. Gas-Kinetic Scheme Coupled with Turbulent Kinetic Energy Equation for Computing Hypersonic Turbulent and Transitional Flows. Int. J. Comput. Fluid Dyn. 2021, 35, 319–330. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Langtry, R.B.; Sengupta, K.; Yeh, D.T.; Dorgan, A.J. Extending the γ-Reθt Local Correlation based Transition Model for Crossflow Effects. In Proceedings of the 45th AIAA Fluid Dynamics Conference, Dallas, TX, USA, 22–26 June 2015; pp. 2015–2474. [Google Scholar]
- Zhou, L.; Li, R.; Hao, Z.; Zaripov, D.I.; Yan, C. Improved k-ω-γ model for crossflow-induced transition prediction in hyper-sonic flow. Int. J. Heat Mass Tran. 2017, 115, 115–130. [Google Scholar] [CrossRef]
- Qiao, L.; Xu, J.; Bai, J.; Zhang, Y. Fully Local Transition Closure Model for Hypersonic Boundary Layers Considering Cross-flow Effects. Aiaa J. 2021, 59, 1692–1706. [Google Scholar] [CrossRef]
- Krishnamurty, V.S.; Shyy, W. Study of compressibility modifications to the k−ε turbulence model. Phys. Fluids 1997, 9, 2769–2788. [Google Scholar] [CrossRef]
- Sarkar, S. The pressure–dilatation correlation in compressible flows. Phys. Fluids A Fluid Dyn. 1992, 4, 2674–2682. [Google Scholar] [CrossRef]
- Yang, W.; Shen, Q.; Zhu, D.; Min, Y.; Liu, Z. Tendency and current status of hypersonic boundary layer transition. J. Aerodyn. 2018, 36, 180–195. [Google Scholar]
- Jiang, L.; Choudhari, M.; Chang, C.-L.; Liu, C. Numerical Simulations of Laminar-Turbulent Transition in Supersonic Boundary Layer. In Proceedings of the 36th AIAA Fluid Dynamics Conference and Exhibit, San Francisco, CA, USA, 5–8 June 2006. [Google Scholar]
- Wadhams, T.; MacLean, M.; Holden, M.; Mundy, E. Pre-Flight Ground Testing of the Full-Scale FRESH FX-1 at Fully Duplicated Flight Conditions. In Proceedings of the 37th AIAA Fluid Dynamics Conference and Exhibit, Miami, FL, USA, 25–28 June 2007. [Google Scholar]
- Johnson, H.; Alba, C.; Candler, G.; MacLean, M.; Wadhams, T.; Holden, M. Boundary Layer Stability Analysisto Support the HIFiRE Transition Experiment. In Proceedings of the 45th AIAA Aerospace Sciences Meeting and Exhibi, Reno, Nevada, 8–11 January 2007. [Google Scholar]
- Chen, J.; Ling, G.; Zhang, Q.; Xie, F.; Xv, X.; Zhang, Y. Infrared thermography experiments of hypersonic boundary-layer transition on a 7° half-angle sharp cone. J. Exp. Fluid Mech. 2020, 34, 60–66. [Google Scholar]
- Dolvin, D. Hypersonic International Flight Research and Experimentation Technology Development and Flight Certification Strategy. In Proceedings of the 16th AIAA/DLR/DGLR International Space Planes and Hypersonic Systems and Technologies Conference, Bremen, Germany, 19–22 October 2009. Paper No. AIAA 2009-7228. [Google Scholar]
- Kimmel, R.; Adamczak, D. HIFiRE-1 Preliminary Aerothermodynamic Measurements. In Proceedings of the 41st AIAA Fluid Dynamics Conference and Exhibit, Honolulu, HI, USA, 27–30 June 2011. Paper No. AIAA 2011-3413. [Google Scholar]
- Van Driest, E.R. Turbulent Boundary Layer in Compressible Fluids. J. Aeronaut. Sci. 1951, 18, 145–160. [Google Scholar] [CrossRef]
- Eckert, E.R.G. Engineering Relations for Friction and Heat Transfer to Surfaces in High Velocity Flow. J. Aero-Naut. Sci. 1955, 22, 585–587. [Google Scholar]
- Kimmel, R.; Adamczak, D.; Berger, K.; Choudhari, M. HIFiRE-5 Flight Vehicle Design. In Proceedings of the 40th Fluid Dynamics Conference and Exhibit, Chicago, IL, USA, 28 June–1 July 2010. Paper No. AIAA 2010-4985. [Google Scholar]
- Juliano, T.J.; Borg, M.P.; Schneider, S.P. Quiet Tunnel Measurements of HIFiRE-5 Boundary-Layer Transition. AIAA J. 2015, 53, 832–846. [Google Scholar] [CrossRef]

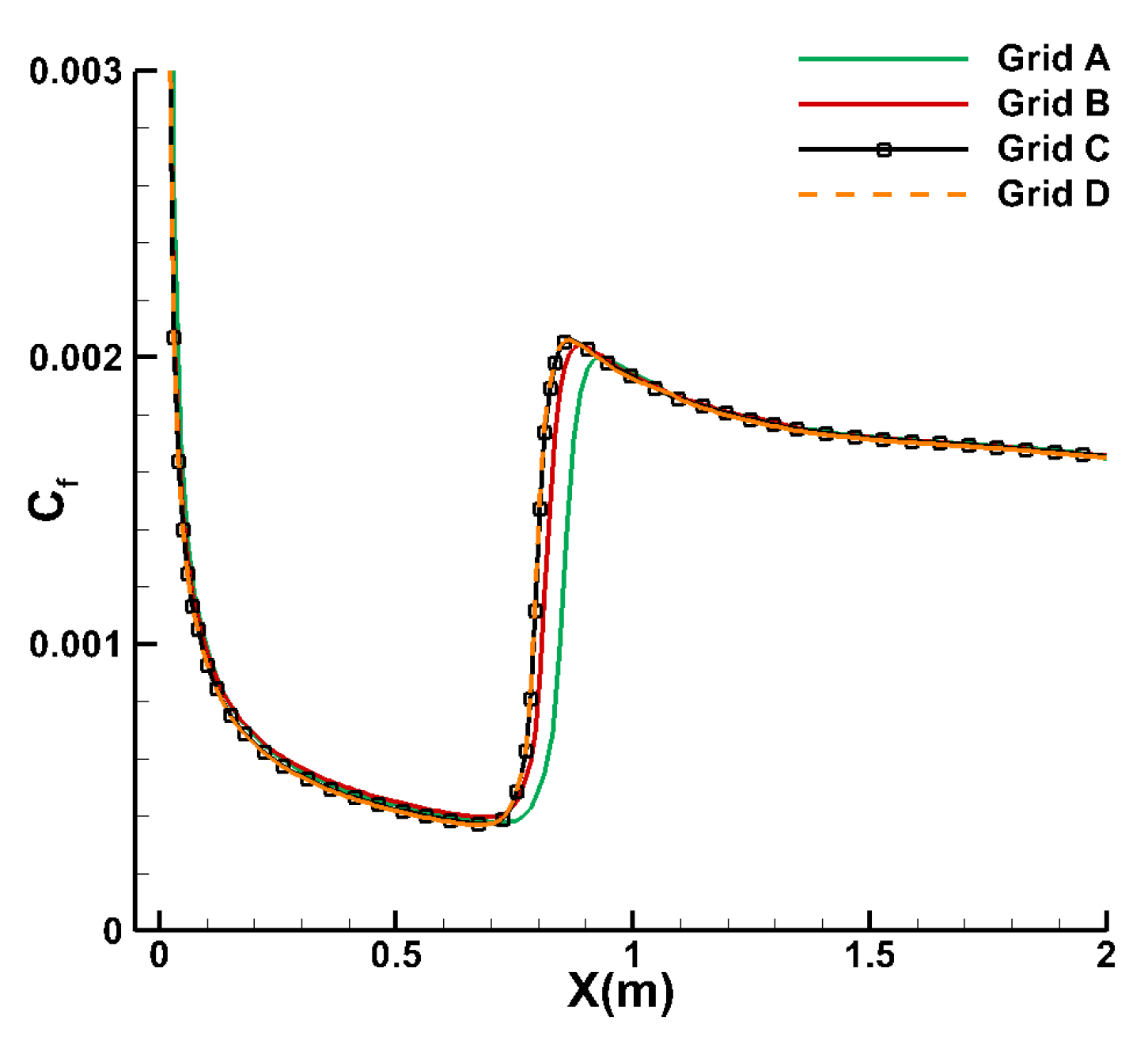

| Mesh | Computational Mesh Dimensions (Streamwise × Normal) | First Layer Grid Spacing (m) |
|---|---|---|
| Grid A | 175 × 120 | 1 × 10−5 |
| Grid B | 219 × 190 | 5 × 10−6 |
| Grid C | 259 × 200 | 1 × 10−6 |
| Grid D | 329 × 220 | 5 × 10−7 |
| H0 (MJ/kg) | Ma∞ | T∞ (K) | ρ∞ (kg/m3) | Re∞ (1/m) | Twall (K) | Rn (mm) | |
|---|---|---|---|---|---|---|---|
| Case I | 2.62 | 7.15 | 231.1 | 0.07060 | 9.92 × 106 | 301.0 | 5.0 |
| Case II | 2.09 | 6.58 | 214.0 | 0.12568 | 1.67 × 107 | 301.3 | 5.0 |
| Case III | 4.49 | 9.91 | 206.71 | 0.0121 | 2.52 × 106 | 295.61 | 6.35 |
| Case IV | 4.56 | 9.93 | 209.33 | 0.0160 | 3.33 × 106 | 299.00 | 6.35 |
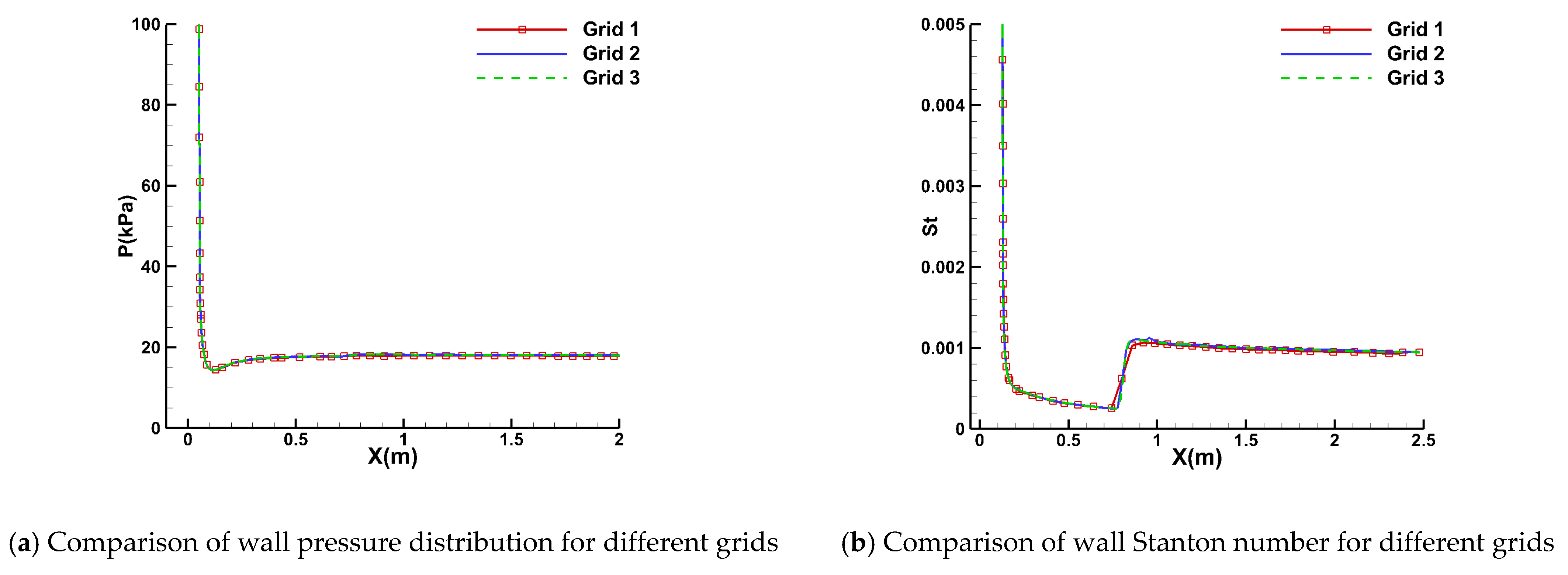
| Mesh | Computational Mesh Dimensions (Streamwise × Normal × Circumferential) | First Layer Grid Spacing (m) |
|---|---|---|
| Grid 1 | 104 × 60 × 13 | 1 × 10−5 |
| Grid 2 | 186 × 101 × 31 | 1 × 10−6 |
| Grid 3 | 226 × 150 × 37 | 5 × 10−7 |
| Time(s) | Altitude (km) | P∞ (Pas) | T∞ (K) | Ma∞ | Unit Re (106/m) |
|---|---|---|---|---|---|
| 19.00 | 15.42 | 12317.90 | 205.30 | 4.66 | 20.58 |
| 20.00 | 16.75 | 9851.90 | 201.00 | 5.07 | 18.46 |
| 21.00 | 18.15 | 7753.70 | 199.20 | 5.28 | 15.28 |
| 22.00 | 19.58 | 6102.50 | 203.70 | 5.31 | 11.74 |
| Noise level | Ma∞ | Re∞ (106/m) | T∞ (K) | Twall (K) | Tu∞ |
|---|---|---|---|---|---|
| Quiet flow | 6.0 | 8.0, 10.2, 11.8 | 52.8 | 300 | 0.05% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, C.; Zhao, W.; Liu, H.; Xue, Y.; Yang, Y.; Chen, W. Gas Kinetic Scheme Coupled with High-Speed Modifications for Hypersonic Transition Flow Simulations. Entropy 2024, 26, 173. https://doi.org/10.3390/e26020173
Li C, Zhao W, Liu H, Xue Y, Yang Y, Chen W. Gas Kinetic Scheme Coupled with High-Speed Modifications for Hypersonic Transition Flow Simulations. Entropy. 2024; 26(2):173. https://doi.org/10.3390/e26020173
Chicago/Turabian StyleLi, Chengrui, Wenwen Zhao, Hualin Liu, Youtao Xue, Yuxin Yang, and Weifang Chen. 2024. "Gas Kinetic Scheme Coupled with High-Speed Modifications for Hypersonic Transition Flow Simulations" Entropy 26, no. 2: 173. https://doi.org/10.3390/e26020173
APA StyleLi, C., Zhao, W., Liu, H., Xue, Y., Yang, Y., & Chen, W. (2024). Gas Kinetic Scheme Coupled with High-Speed Modifications for Hypersonic Transition Flow Simulations. Entropy, 26(2), 173. https://doi.org/10.3390/e26020173









