A Eulerian Numerical Model to Predict the Enhancement Effect of the Gravity-Driven Motion Melting Process for Latent Thermal Energy Storage
Abstract
:1. Introduction
2. Materials and Methods
- The liquid phase flow is assumed to be Newtonian, laminar and incompressible. Therefore, pressure and flow terms in the momentum equation are not considered;
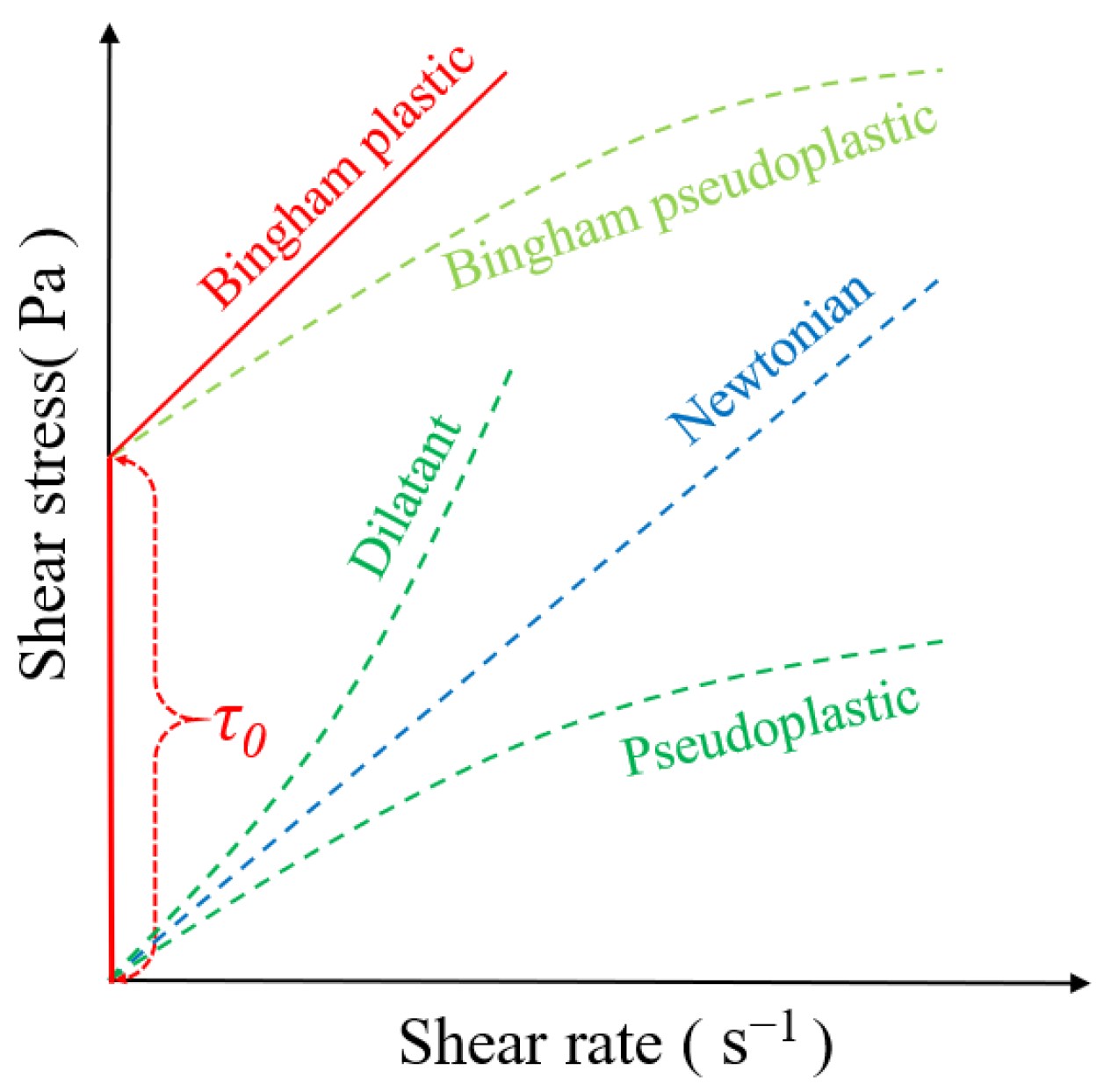
- The substance in the “solid phase” domain is assumed to be the Bingham fluid that can withstand a certain level of shear stress [19];
- There is a mass transfer in the mushy zone. The physical properties are expressed through the volume fraction of the liquid phase;
- The Boussinesq approximation is introduced by using the gravitational term to simulate the buoyancy effect of the pure liquid phase [20];
- The phase transition energy related to the transfer of solid–liquid mass in the mushy zone is added to the energy equation as a source term.
2.1. Governing Equations
2.2. “Solid Phase” Property Equation
2.3. Defined Mass Transfer Function
2.4. Solution Method
3. Model Verification
3.1. Meshing Independence
3.2. Macroscopic Settling Velocity of “Solid Phase”
3.3. Verification Case 1: Vertical Cylinder Melting
3.3.1. Referenced Experimental Data
3.3.2. Model Development
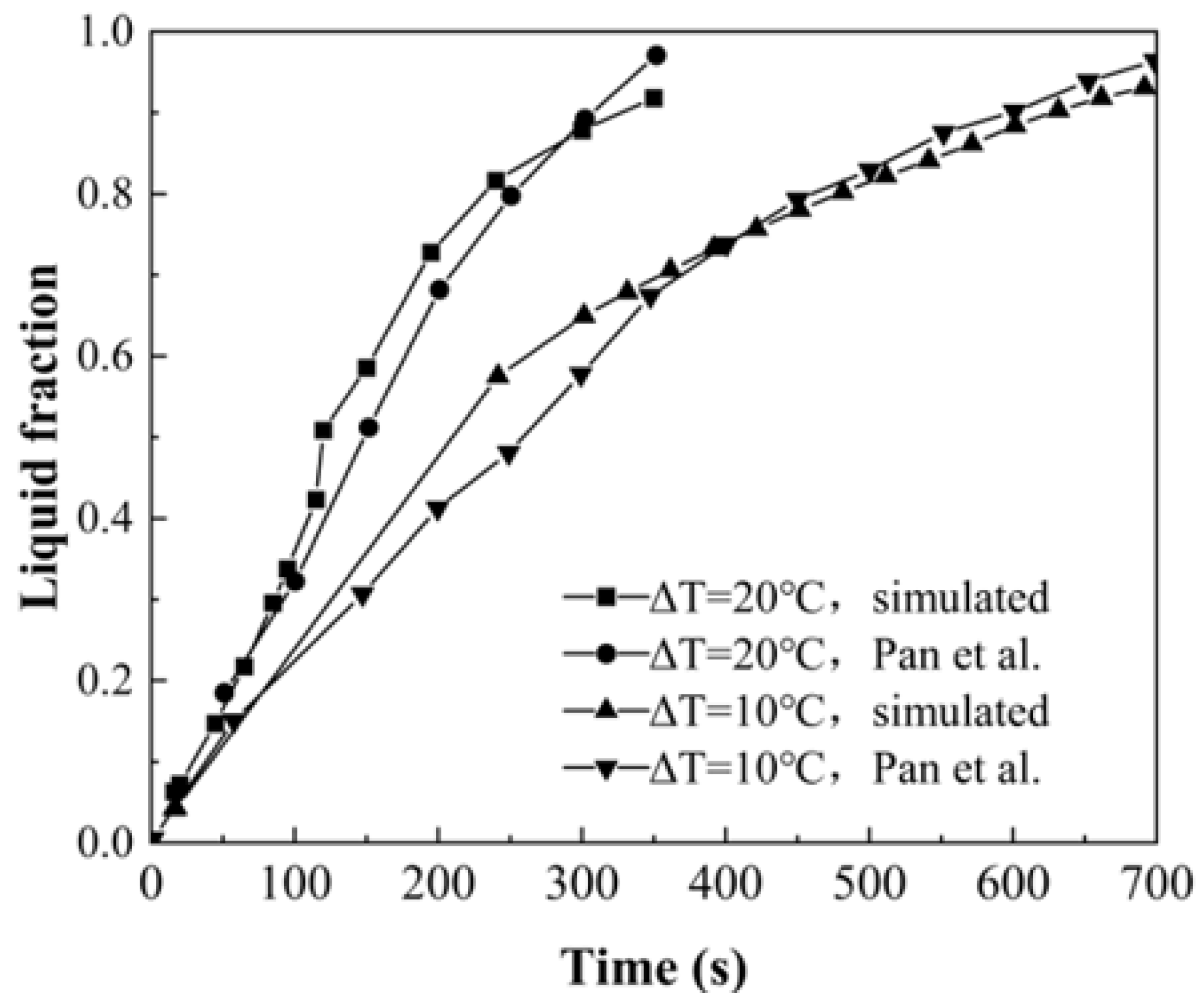
3.3.3. Verification Results
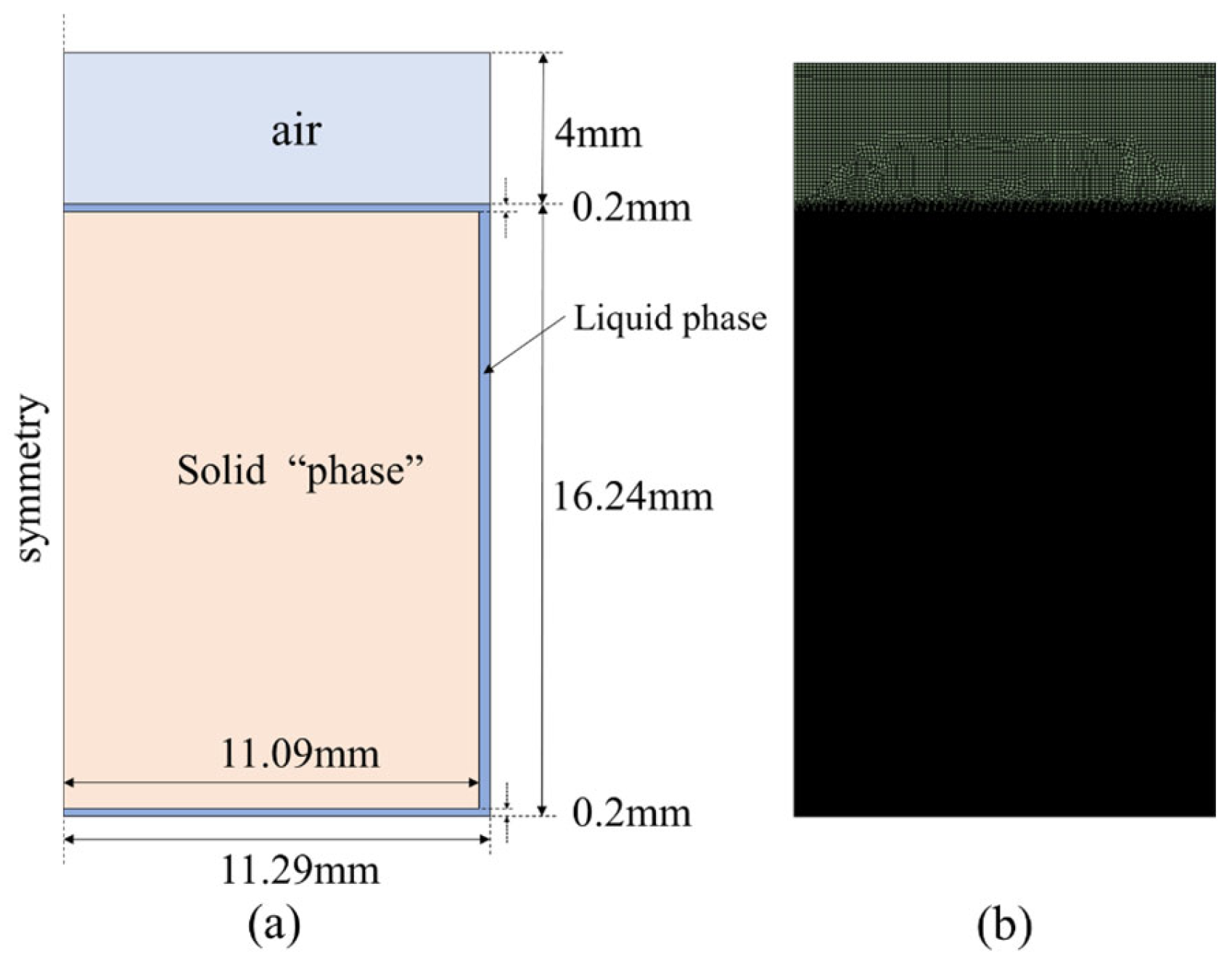
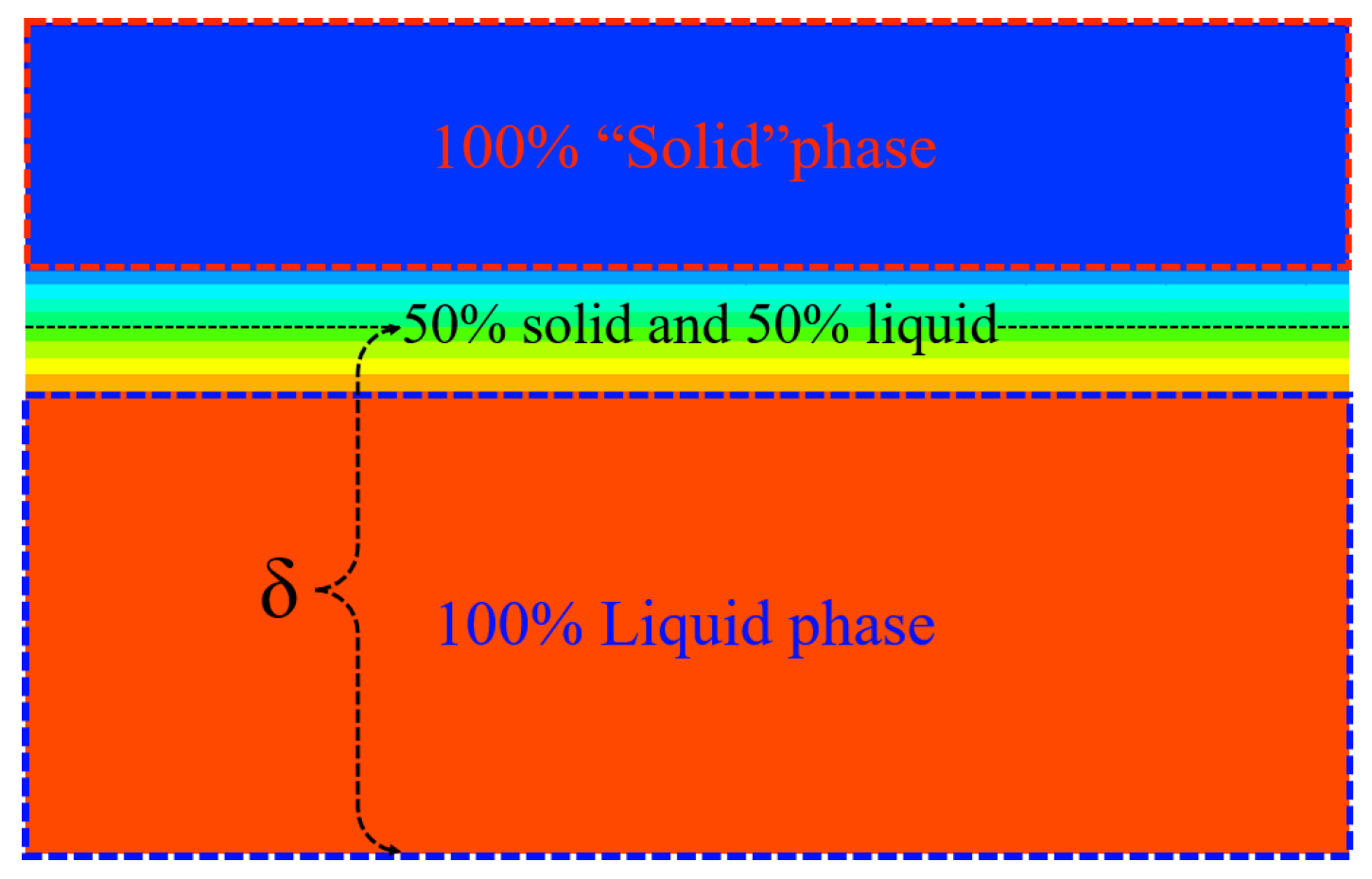
3.4. Verification Case 2: Thin Liquid-Film Thickness
3.4.1. Referenced Experimental Data
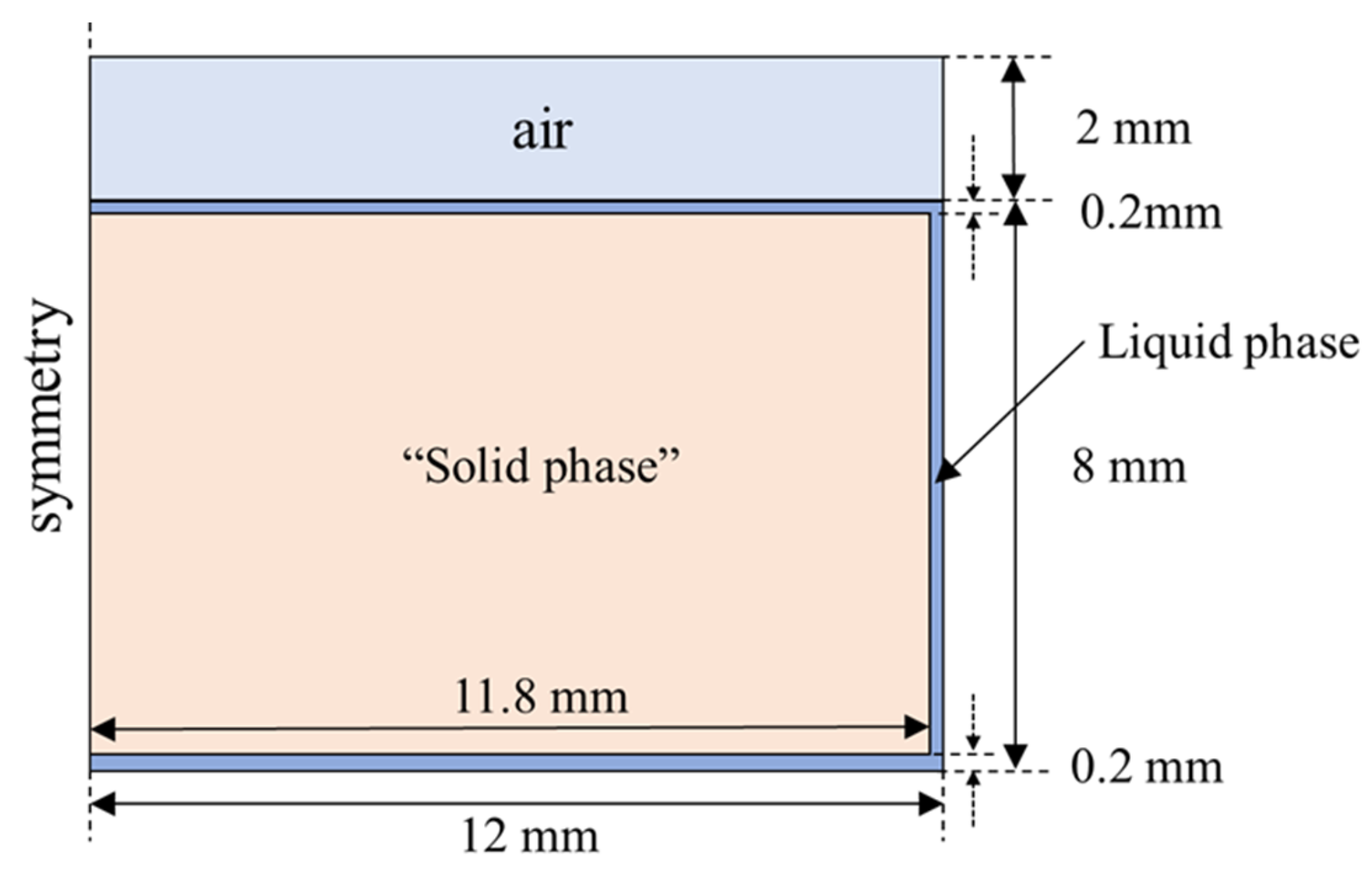
3.4.2. Model Development
3.4.3. Verification Result
4. Numerical Analysis and Results
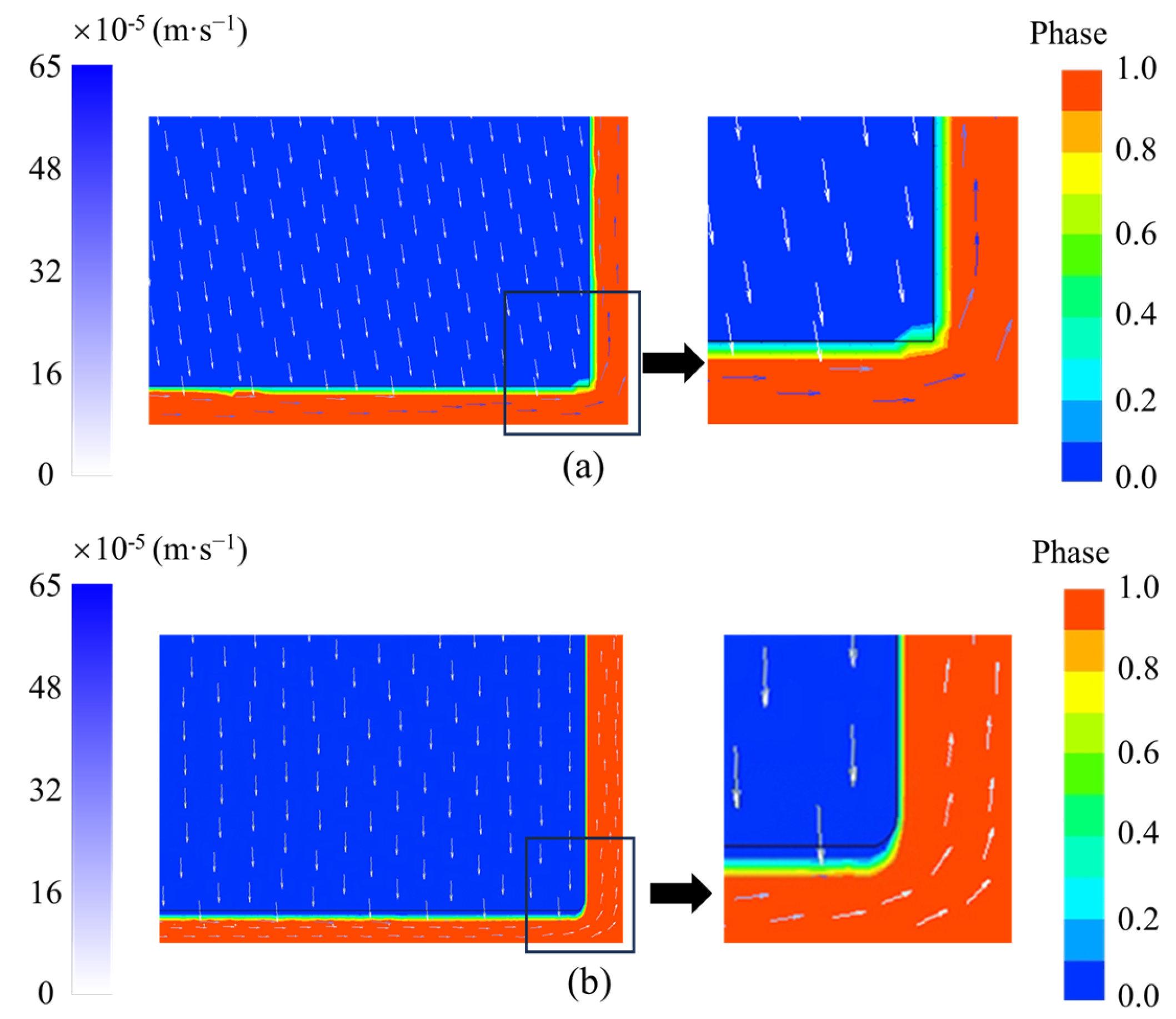
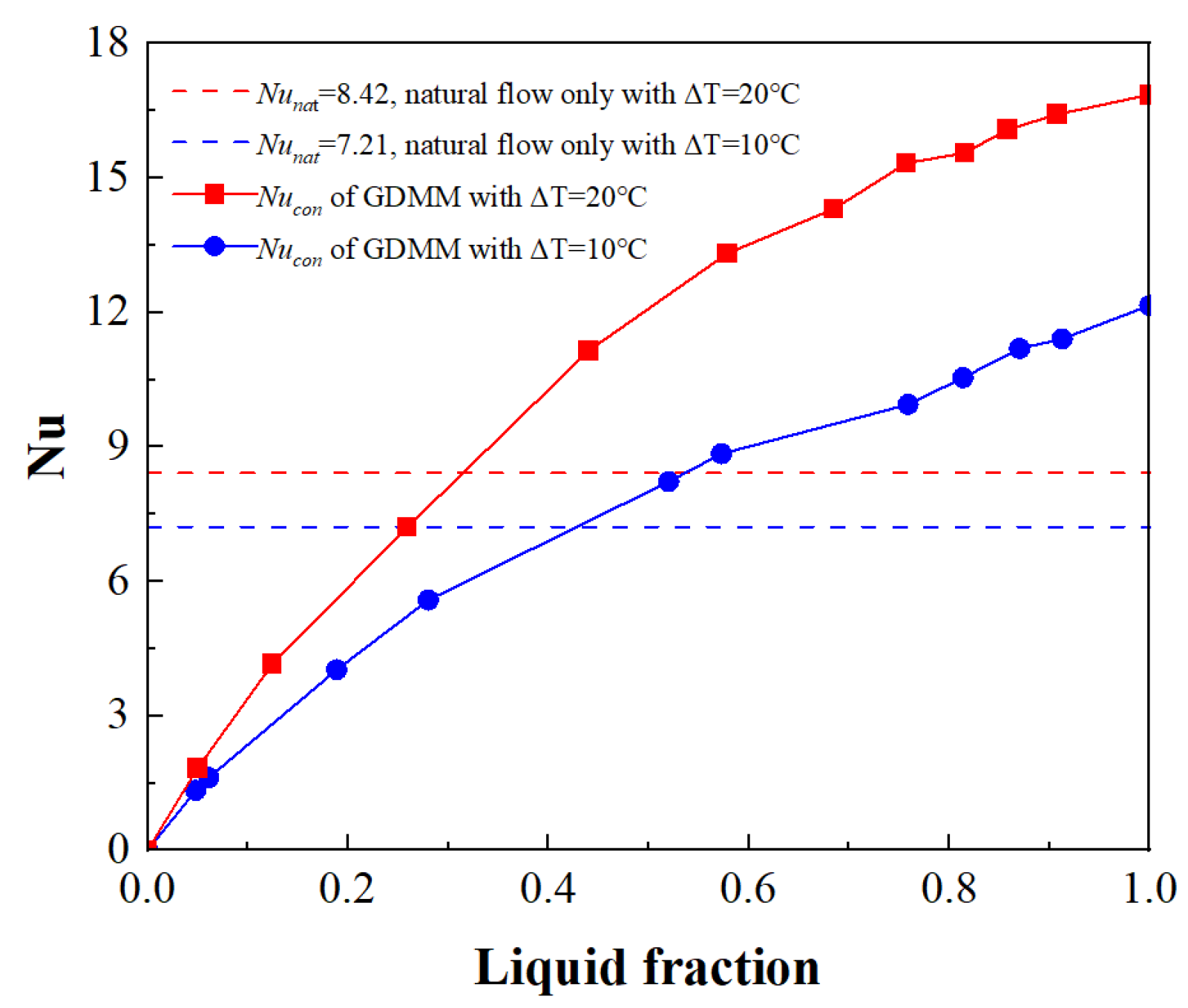
4.1. Convective Heat Transfer within the Thin Liquid Film
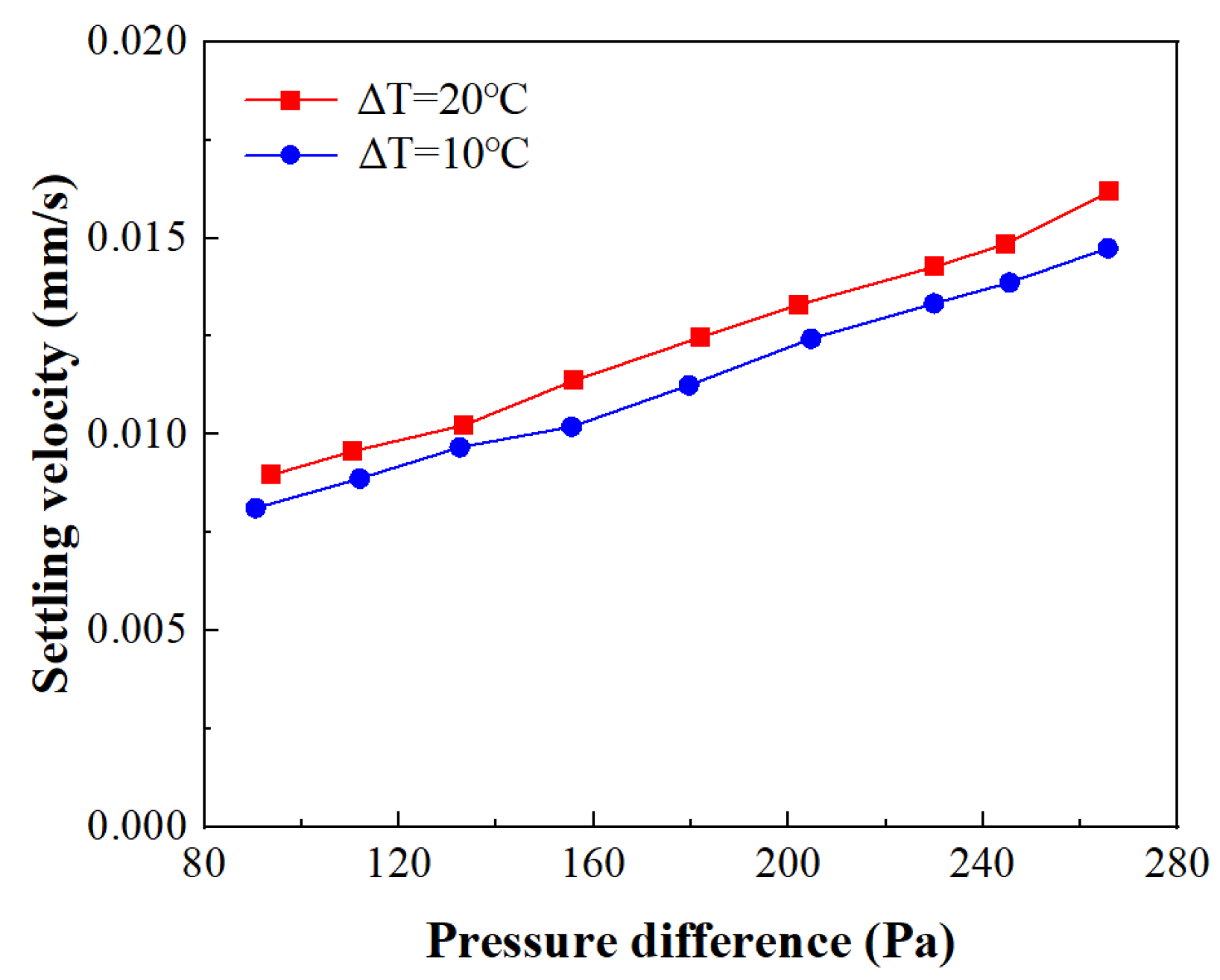
4.2. The Settling Velocity Variation with Pressure Difference
5. Conclusions
- Based on the Bingham fluid assumption, it can be seen in the simulation results that the flow deformation of the “solid phase” can be controlled by setting the threshold value to the shear stress term. The model is used to predict the melting processes in closed cylindrical containers. The prediction error of the transient volume fraction is less than 10.88%. The predicted melting pattern for the “solid phase” indicates good consistency with the experiment. Selection criteria for the simulated liquid-film thickness were proposed, for which the predictions provided rational results;
- The estimation of the convective enhancement ability of the GDMM process on the liquid phase shows that the GDMM process can accomplish a flow-strengthening effect in the middle and later stages of melting. This explains the mechanism of the high melting rate. In addition, a linear relationship between the settling velocity and the pressure difference of the “solid phase” is observed, which is consistent with the results of Fu et al., obtained under external pressure conditions.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| GDMM | Gravity-driven motion melting |
| LTES | Latent thermal energy storage |
| PCM | Phase-change material |
| RMSE | Root mean squared error |
| VOF | Volume of fluid |
| C | Specific heat capacity (J K−1 kg−1) |
| d | Characteristic length (m) |
| f | Unit mass force (N) |
| g | Gravitational acceleration (m s−2) |
| h | Enthalpy (J kg−1) |
| Δh | Latent heat capacity (J kg−1) |
| k | Consistency index (Pa sn) |
| L | Latent heat of fusion (J kg−1) |
| m | Mass (kg) |
| n | Power law index |
| p | Pressure (Pa) |
| T | Temperature (K) |
| Tf | Reference temperature (K) |
| ΔT | Driving temperature difference (K) |
| t | Time (s) |
| Δt | Time step (s) |
| Convective heat transfer coefficient (w m−2 K−1) | |
| Velocity vector (m s−1) | |
| V | Volume (m3) |
| α | Volume fraction |
| β | Coefficient of thermal expansion (K−1) |
| γ | Shear rate (s−1) |
| δ | Liquid-film thickness (m) |
| λ | Thermal conductivity (W m−1 K−1) |
| ν | Dynamic viscosity (m2 s−1) |
| ρ | Density (kg m−3) |
| τ | Shear stress (Pa) |
| τ0 | Yield stress (Pa) |
| ω | Under relaxation factor |
| Subscripts | |
| con | Convective |
| l | Liquid |
| ls | Liquid–solid |
| nat | Nature |
| s | Solid |
| sat | Start |
| Superscript | |
| ′ | Next time step |
References
- Xiao, X.; Zhang, P.; Li, M. Experimental and numerical study of heat transfer performance of nitrate/expanded graphite composite PCM for solar energy storage. Energy Convers. Manag. 2015, 105, 272–284. [Google Scholar] [CrossRef]
- Selvakumar, R.D.; Wu, J.; Afgan, I.; Ding, Y.; Alkaabi, A.K. Melting performance enhancement in a thermal energy storage unit using active vortex generation by electric field. J. Energy Storage 2023, 67, 107593. [Google Scholar] [CrossRef]
- Zhao, Q.; Sun, Q.; Xin, S.; Chen, Y.; Wu, C.; Wang, H.; Xu, J.; Wan, M.; Zeng, W.; Zhao, Y. High-strength titanium alloys for aerospace engineering applications: A review on melting-forging process. Mater. Sci. Eng. A 2022, 845, 143260. [Google Scholar] [CrossRef]
- Ghosh, D.; Ghose, J.; Datta, P.; Kumari, P.; Paul, S. Strategies for phase change material application in latent heat thermal energy storage enhancement: Status and prospect. J. Energy Storage 2022, 53, 105179. [Google Scholar] [CrossRef]
- IRENA. Innovation Outlook: Thermal Energy Storage; International Renewable Energy Agency: Masdar City, Abu Dhabi, 2020. [Google Scholar]
- Lacroix, M. Contact melting of a phase change material inside a heated parallelepedic capsule. Energy Convers. Manag. 2001, 42, 35–47. [Google Scholar] [CrossRef]
- Zhao, Y.; Chen, W.; Sun, F. Effects of convection and density difference on contact melting around a cylinder. Energy Convers. Manag. 2010, 51, 253–257. [Google Scholar] [CrossRef]
- Hu, N.; Li, Z.R.; Xu, Z.W.; Fan, L.W. Rapid charging for latent heat thermal energy storage: A state-of-the-art review of close-contact melting. Renew. Sustain. Energy Rev. 2022, 155, 111918. [Google Scholar] [CrossRef]
- Li, Z.R.; Baghaei Oskouei, S.; Fu, G.T.; Bayer, Ö.; Fan, L.-W. Enhanced power density during energy charging of a shell-and-tube thermal storage unit: Comparison between the inclusion of metal fins and foams. J. Energy Storage 2022, 55, 105576. [Google Scholar] [CrossRef]
- Rabienataj Darzi, A.A.; Jourabian, M.; Farhadi, M. Melting and solidification of PCM enhanced by radial conductive fins and nanoparticles in cylindrical annulus. Energy Convers. Manag. 2016, 118, 253–263. [Google Scholar] [CrossRef]
- Kozak, Y.; Rozenfeld, T.; Ziskind, G. Close-contact melting in vertical annular enclosures with a non-isothermal base: Theoretical modeling and application to thermal storage. Int. J. Heat Mass Transf. 2014, 72, 114–127. [Google Scholar] [CrossRef]
- Jaisatia Varthani, A.; Shasthri, S.; Baljit, S.; Kausalyah, V. A systematic review of metal foam and heat pipe enhancement in Latent Heat Thermal Energy Storage system. J. Energy Storage 2022, 56, 105888. [Google Scholar] [CrossRef]
- Aljaghtham, M.; Premnath, K.; Alsulami, R. Investigation of Time-Dependent Microscale Close Contact Melting. Int. J. Heat Mass Transf. 2021, 166, 120742. [Google Scholar] [CrossRef]
- Rozenfeld, T.; Kozak, Y.; Hayat, R.; Ziskind, G. Close-contact melting in a horizontal cylindrical enclosure with longitudinal plate fins: Demonstration, modeling and application to thermal storage. Int. J. Heat Mass Transf. 2015, 86, 465–477. [Google Scholar] [CrossRef]
- Pan, C.; Charles, J.; Vermaak, N.; Romero, C.; Neti, S.; Zheng, Y.; Chen, C.-H.; Bonner, R. Experimental, numerical and analytic study of unconstrained melting in a vertical cylinder with a focus on mushy region effects. Int. J. Heat Mass Transf. 2018, 124, 1015–1024. [Google Scholar] [CrossRef]
- Kozak, Y.; Ziskind, G. Novel enthalpy method for modeling of PCM melting accompanied by sinking of the solid phase. Int. J. Heat Mass Transf. 2017, 112, 568–586. [Google Scholar] [CrossRef]
- Faden, M.; König-Haagen, A.; Höhlein, S.; Brüggemann, D. An implicit algorithm for melting and settling of phase change material inside macrocapsules. Int. J. Heat Mass Transf. 2018, 117, 757–767. [Google Scholar] [CrossRef]
- Oskouei, S.B.; Li, Z.R.; Bayer, Ö.; Fan, L.-W. Close-contact melting and natural convection in unconstrained melting: A parametric study. Int. J. Heat Mass Transf. 2024, 218, 124795. [Google Scholar] [CrossRef]
- Kozak, Y. Close-contact melting of phase change materials with a non-Newtonian power-law fluid liquid phase-Modeling and analysis. J. Non-Newton. Fluid Mech. 2023, 318, 105062. [Google Scholar] [CrossRef]
- Lee, J.H.; Shin, J.H.; Chang, S.M.; Min, T. Numerical Analysis on Natural Convection Heat Transfer in a Single Circular Fin-Tube Heat Exchanger (Part 1): Numerical Method. Entropy 2020, 22, 363. [Google Scholar] [CrossRef]
- Liu, Z.; Huang, S.M.; Wang, C.; Zhuang, Y. A review on non-Newtonian effects and structure-activity relationship of nanoparticles enhanced phase change materials in porous media. J. Energy Storage 2023, 64, 107221. [Google Scholar] [CrossRef]
- Rogovyi, A.; Korohodskyi, V.; Medvediev, Y. Influence of Bingham fluid viscosity on energy performances of a vortex chamber pump. Energy 2021, 218, 119432. [Google Scholar] [CrossRef]
- Hu, N.; Zhang, R.H.; Zhang, S.T.; Liu, J.; Fan, L.-W. A laser interferometric measurement on the melt film thickness during close-contact melting on an isothermally-heated horizontal plate. Int. J. Heat Mass Transf. 2019, 138, 713–718. [Google Scholar] [CrossRef]
- Fu, W.; Yan, X.; Gurumukhi, Y.; Garimella, V.S.; King, W.P.; Miljkovic, N. High power and energy density dynamic phase change materials using pressure-enhanced close contact melting. Nat. Energy 2022, 7, 270–280. [Google Scholar] [CrossRef]

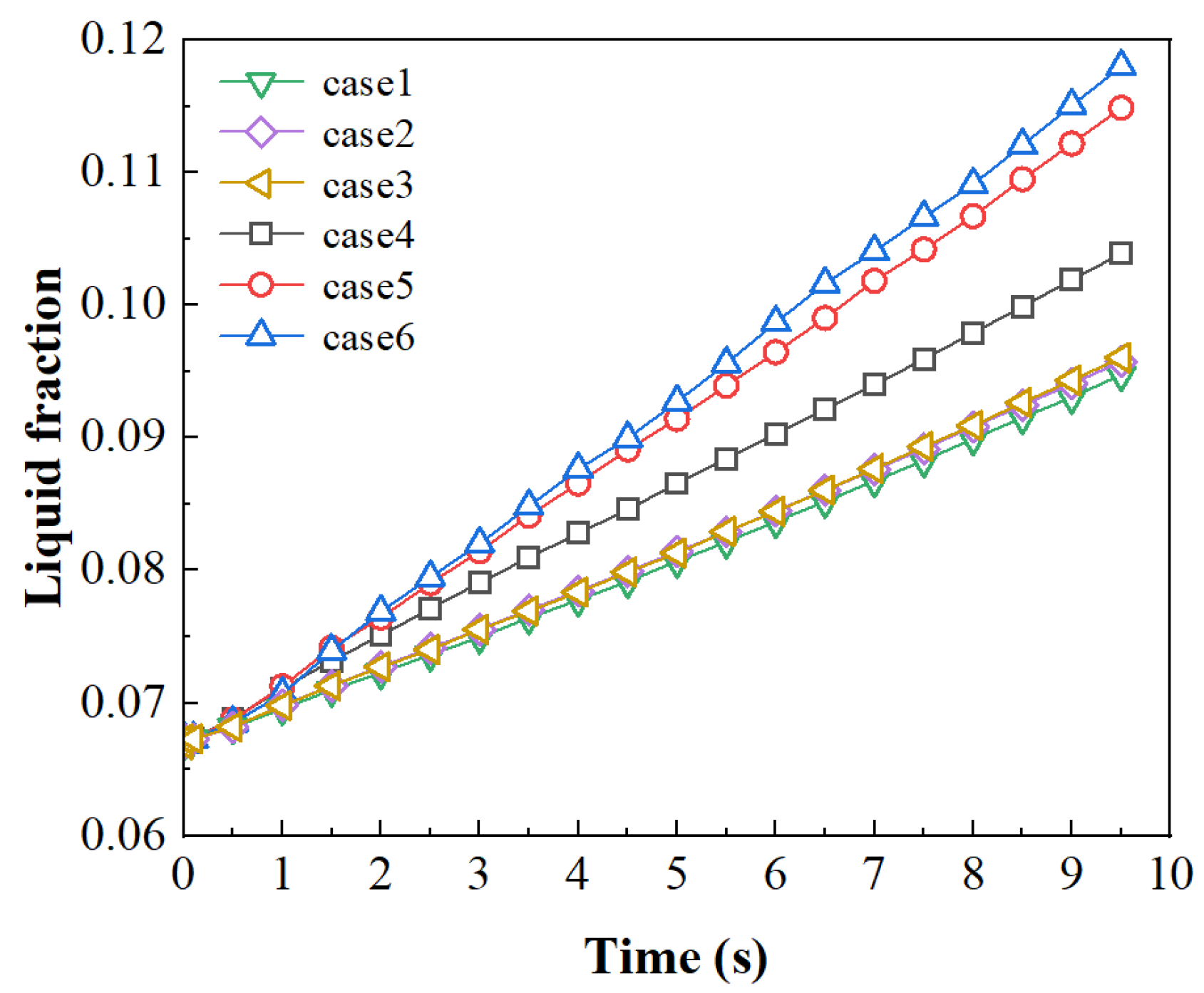



| Case | Average Mesh Size in the Solid Phase Region (mm) | Refined Mesh Size in the Liquid Phase Region (mm) | Total Number of Mesh Cells |
|---|---|---|---|
| 1 | 0.02 | 0.006 | 384,680 |
| 2 | 0.02 | 0.008 | 323,596 |
| 3 | 0.02 | 0.01 | 295,984 |
| 4 | 0.02 | 0.02 | 232,976 |
| 5 | 0.03 | 0.03 | 108,466 |
| 6 | 0.04 | 0.04 | 64,923 |
| Properties | Values |
|---|---|
| Melting temperature | 29 (°C) |
| Density (solid/liquid) | 1706/1538 (kg m−3) |
| Thermal conductivity (solid/liquid) | 1.09/0.546 (W m−1 K−1) |
| Specific heat (solid/liquid) | 2060/2230 (J kg−1 K−1) |
| Molecular weight | 219.08 |
| Coefficient of thermal expansion | 0.0005 (K−1) |
| Latent heat | 170 (kJ kg−1) |
| Dynamic viscosity | 0.01 (Pa s) |
| Properties | Values |
|---|---|
| Melting temperature | 39 (°C) |
| Density (solid/liquid) | 869/802.70 (kg m−3) |
| Thermal conductivity (solid/liquid) | 0.85/0.35 (W m−1 K−1) |
| Specific heat (solid/liquid) | 376.66/704.51 (J kg−1 K−1) |
| Molecular weight | 214.39 |
| Coefficient of thermal expansion | 0.0032 (K−1) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, S.; Tan, B.; Lin, Y.; Wang, T.; Hu, K. A Eulerian Numerical Model to Predict the Enhancement Effect of the Gravity-Driven Motion Melting Process for Latent Thermal Energy Storage. Entropy 2024, 26, 175. https://doi.org/10.3390/e26020175
Tian S, Tan B, Lin Y, Wang T, Hu K. A Eulerian Numerical Model to Predict the Enhancement Effect of the Gravity-Driven Motion Melting Process for Latent Thermal Energy Storage. Entropy. 2024; 26(2):175. https://doi.org/10.3390/e26020175
Chicago/Turabian StyleTian, Shen, Bolun Tan, Yuchen Lin, Tieying Wang, and Kaiyong Hu. 2024. "A Eulerian Numerical Model to Predict the Enhancement Effect of the Gravity-Driven Motion Melting Process for Latent Thermal Energy Storage" Entropy 26, no. 2: 175. https://doi.org/10.3390/e26020175
APA StyleTian, S., Tan, B., Lin, Y., Wang, T., & Hu, K. (2024). A Eulerian Numerical Model to Predict the Enhancement Effect of the Gravity-Driven Motion Melting Process for Latent Thermal Energy Storage. Entropy, 26(2), 175. https://doi.org/10.3390/e26020175





