Magnetic Black Hole Thermodynamics in an Extended Phase Space with Nonlinear Electrodynamics
Abstract
:1. Introduction
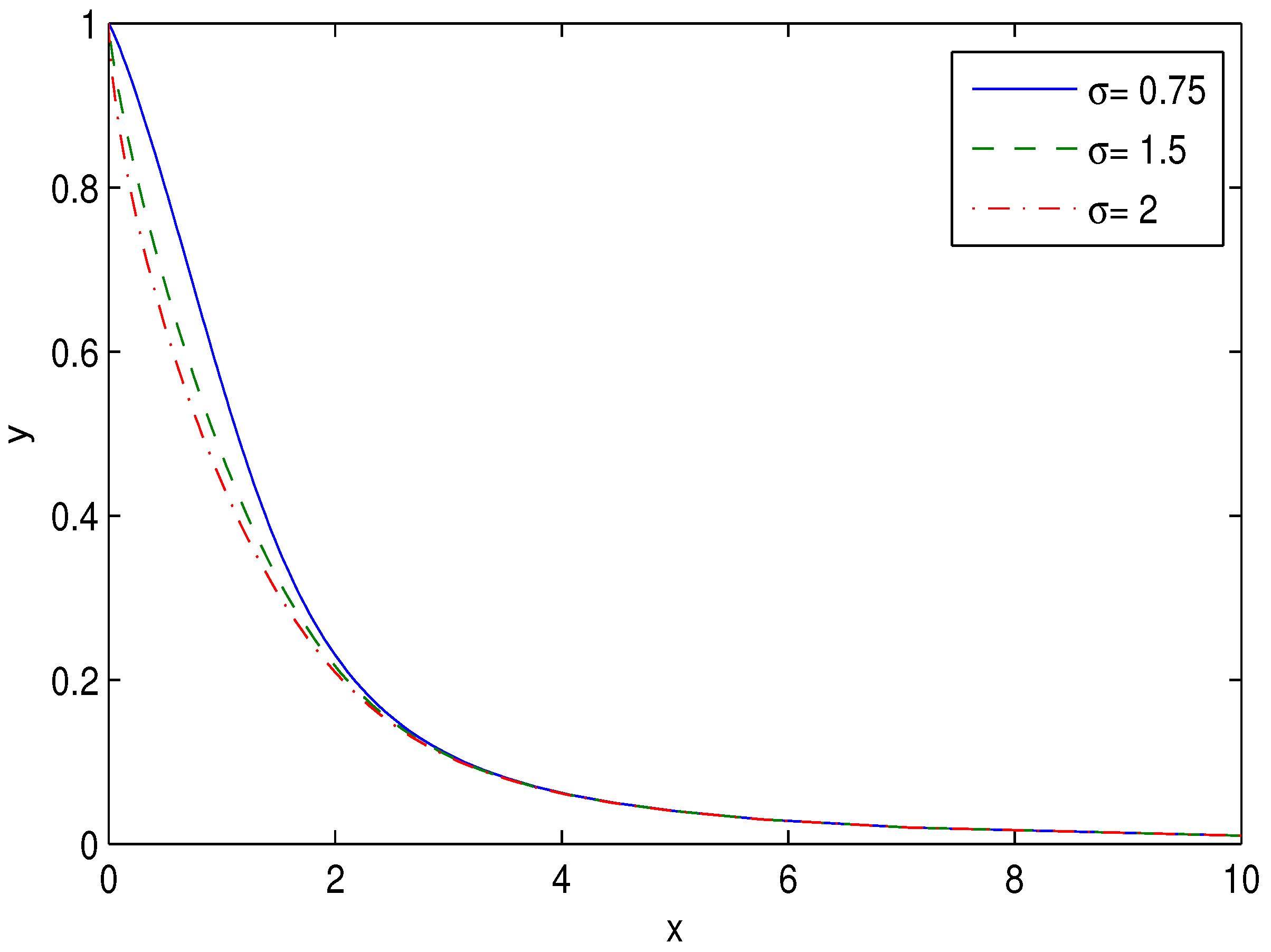
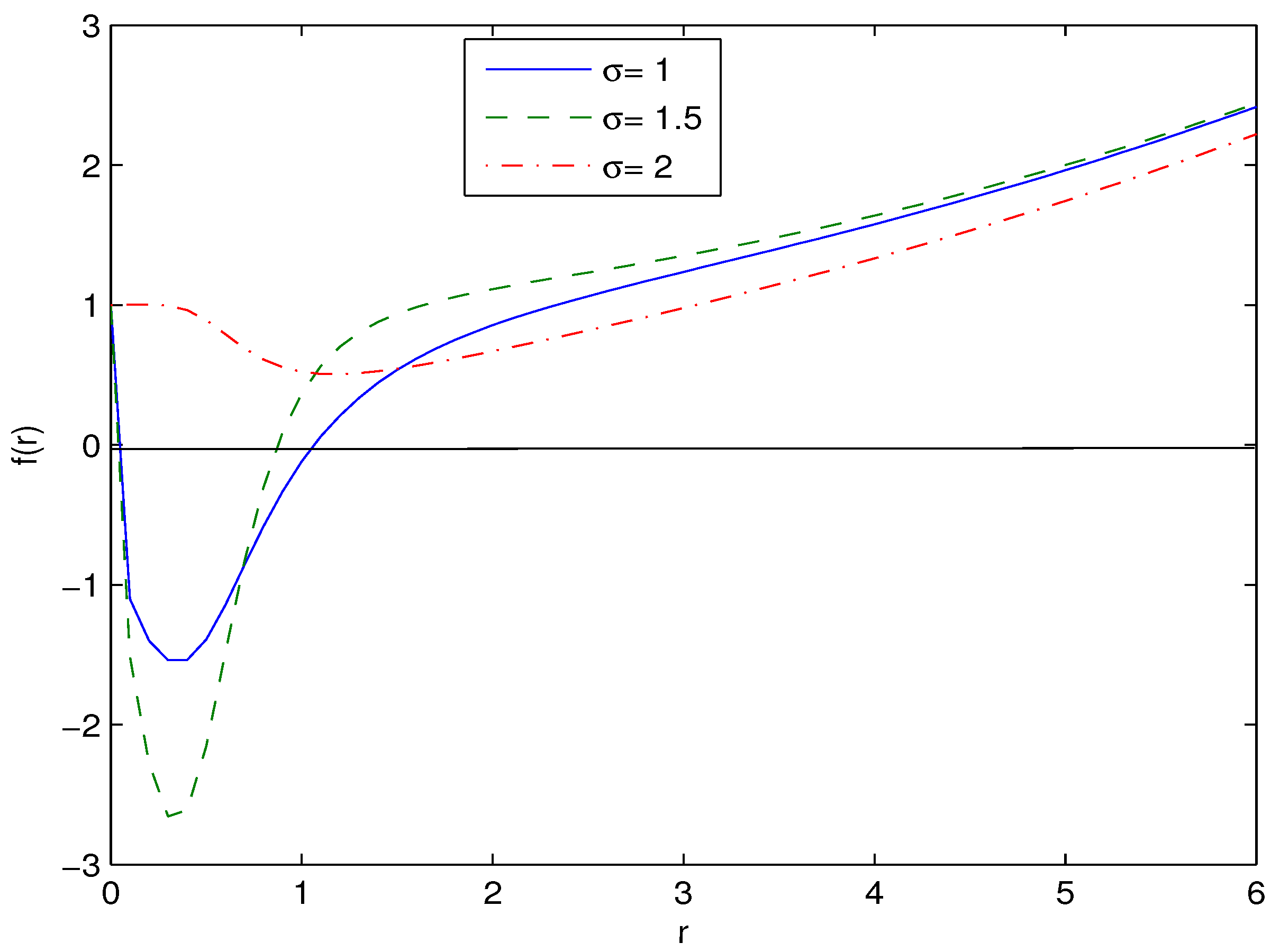
2. Einstein–AdS Black Hole Solution
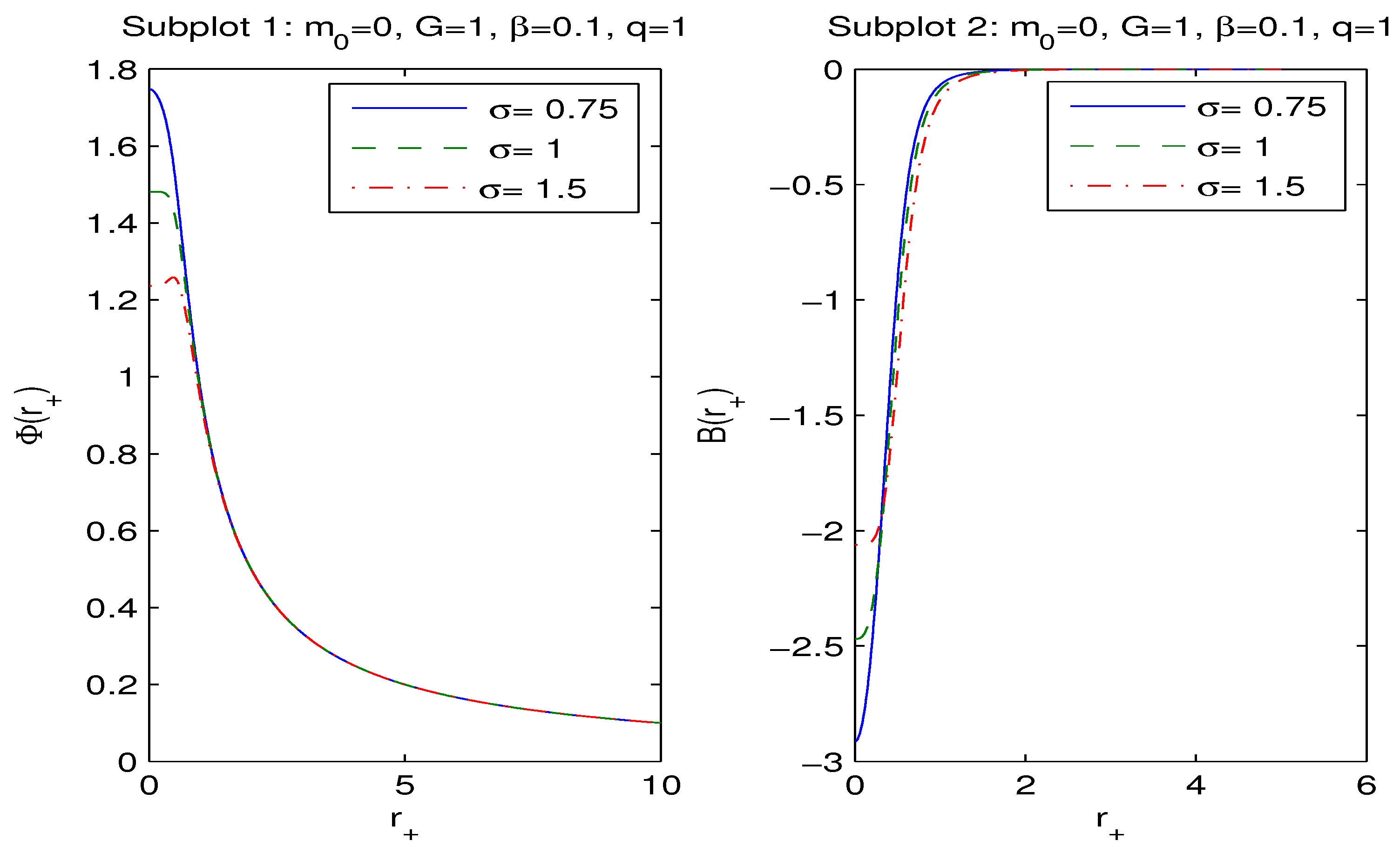
3. First Law of Black Hole Thermodynamics
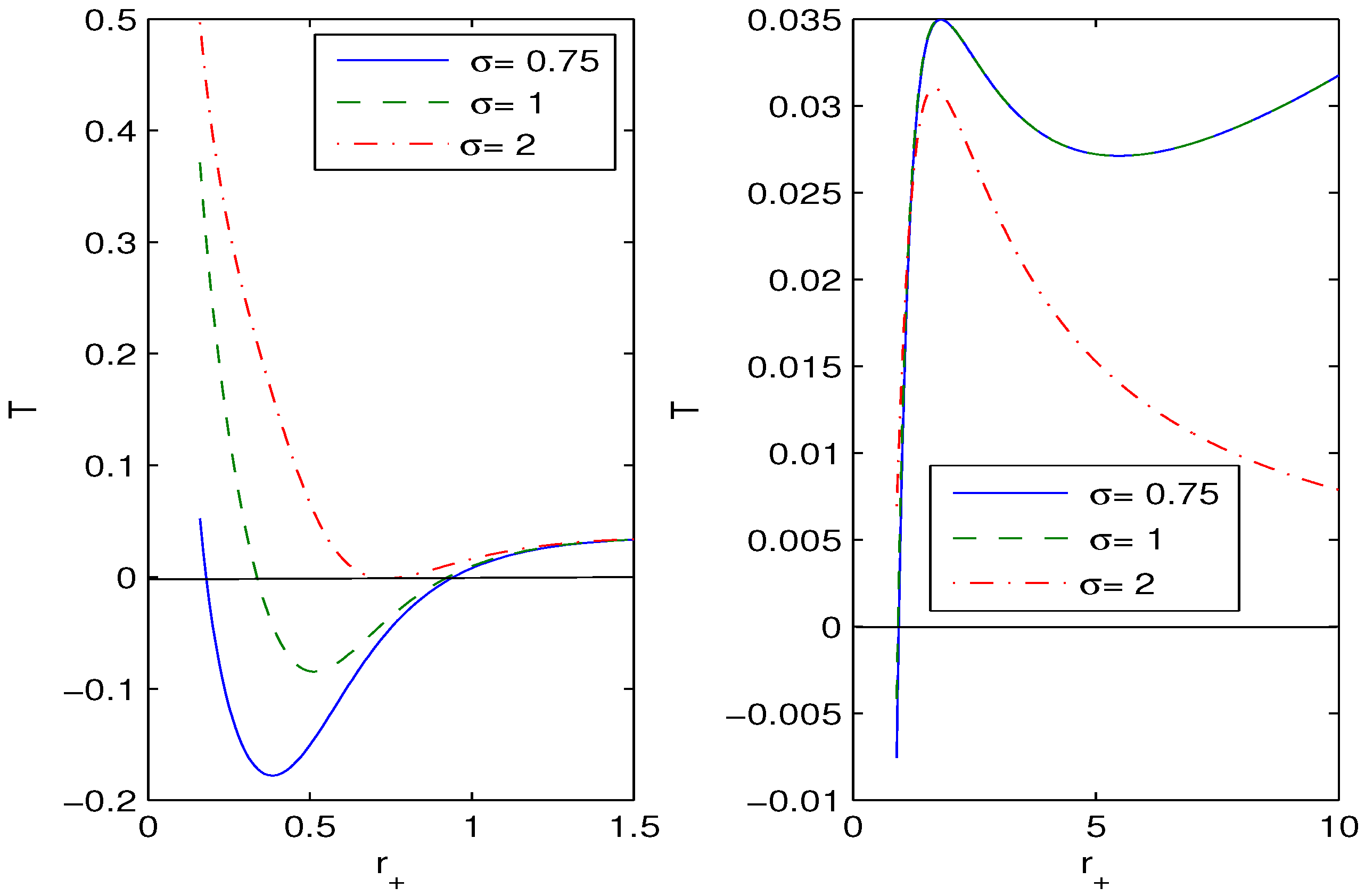
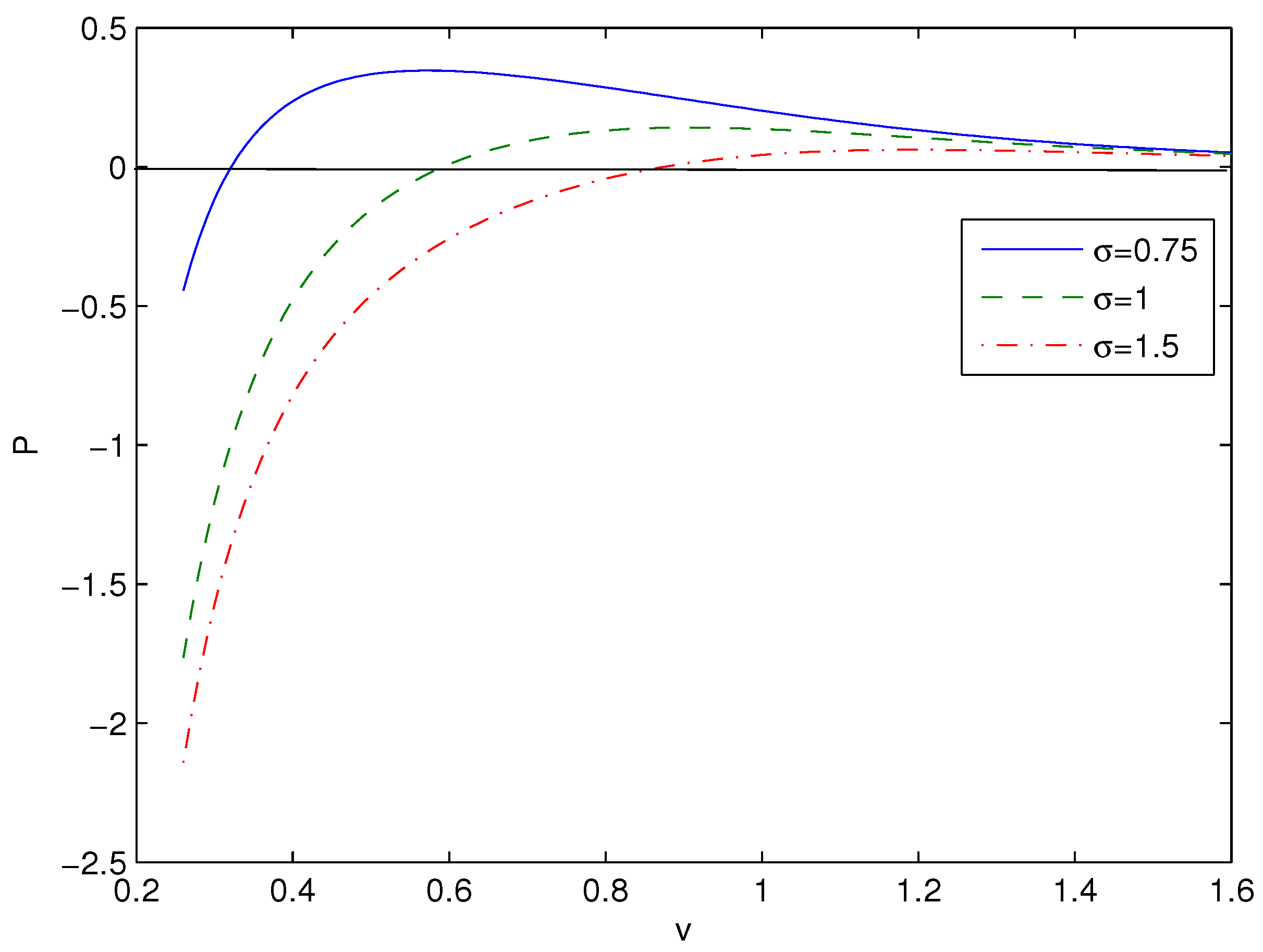
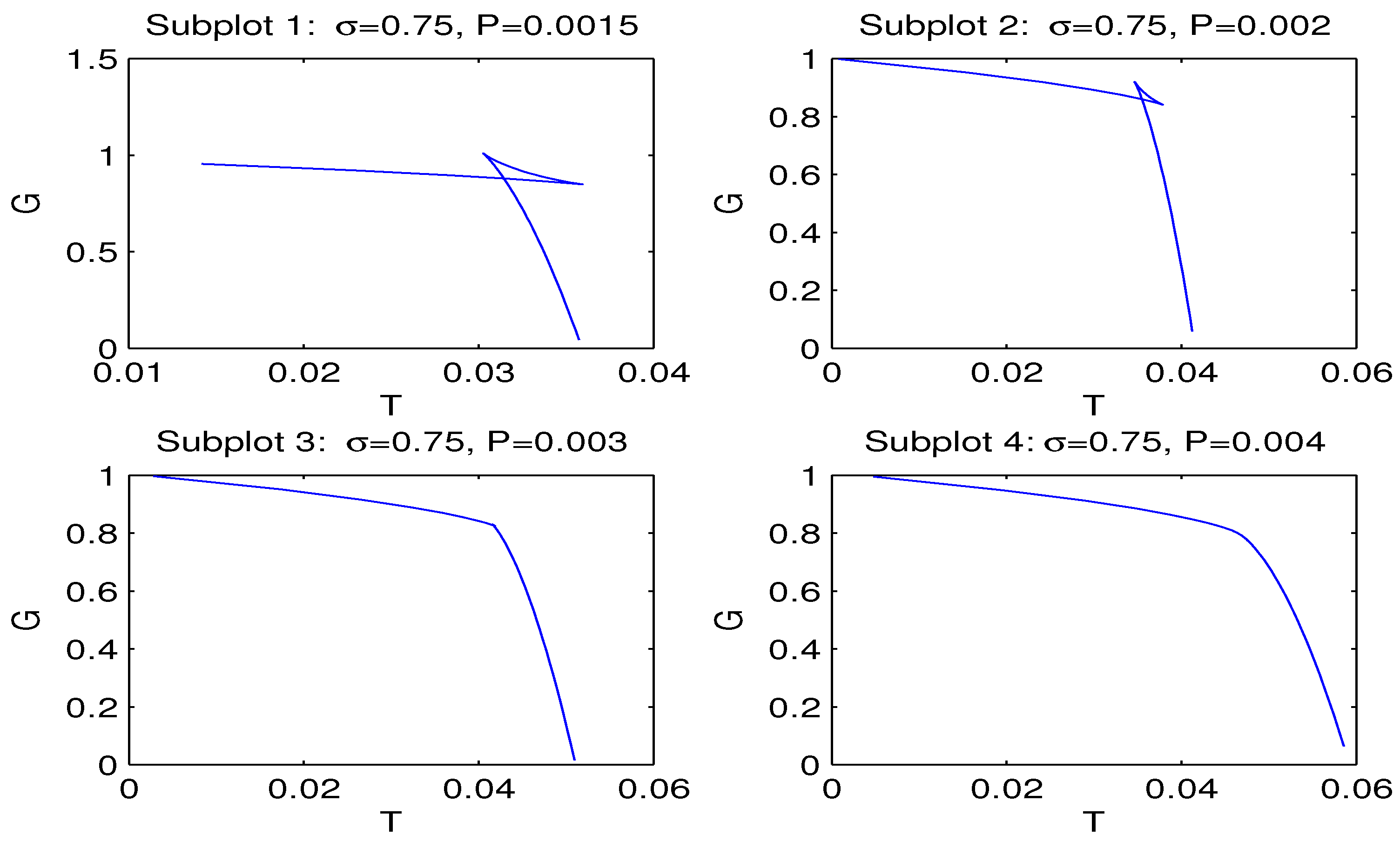
4. Thermodynamics of Black Holes
5. Summary
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
| 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 1.272 | 1.233 | 1.202 | 1.176 | 1.153 | 1.132 | 1.108 | 1.097 | 1.081 | 1.067 |
Appendix C
References
- Bekenstein, J.D. Black holes and entropy. Phys. Rev. D 1973, 7, 2333–2346. [Google Scholar] [CrossRef]
- Hawking, S.W. Particle Creation by Black Holes. Commun. Math. Phys. 1975, 43, 199–220. [Google Scholar] [CrossRef]
- Bardeen, J.M.; Carter, B.; Hawking, S.W. The four laws of black hole mechanics. Commun. Math. Phys. 1973, 31, 161–170. [Google Scholar] [CrossRef]
- Jacobson, T. Thermodynamics of space-time: The Einstein equation of state. Phys. Rev. Lett. 1995, 75, 1260–1263. [Google Scholar] [CrossRef] [PubMed]
- Padmanabhan, T. Thermodynamical Aspects of Gravity: New insights. Rept. Prog. Phys. 2010, 73, 046901. [Google Scholar] [CrossRef]
- Maldacena, J.M. The Large N limit of superconformal field theories and supergravity. Int. J. Theor. Phys. 1999, 38, 1113–1133. [Google Scholar] [CrossRef]
- Hawking, S.W.; Page, D.N. Thermodynamics of Black Holes in anti-de Sitter Space. Commun. Math. Phys. 1983, 87, 577. [Google Scholar] [CrossRef]
- Dolan, B.P. Black holes and Boyle’s law? The thermodynamics of the cosmological constant. Mod. Phys. Lett. A 2015, 30, 1540002. [Google Scholar] [CrossRef]
- Kubiznak, D.; Mann, R.B. Black hole chemistry. Can. J. Phys. 2015, 93, 999–1002. [Google Scholar] [CrossRef]
- Kubiznak, D.; Mann, R.B.; Teo, M. Black hole chemistry: Thermodynamics with Lambda. Class. Quant. Grav. 2017, 34, 063001. [Google Scholar] [CrossRef]
- Gunasekaran, S.; Mann, R.B.; Kubiznak, D. Extended phase space thermodynamics for charged and rotating black holes and Born—Infeld vacuum polarization. J. High Energy Phys. 2012, 1211, 110. [Google Scholar] [CrossRef]
- Caldarelli, M.M.; Cognola, G.; Klemm, D. Thermodynamics of Kerr-Newman-AdS black holes and conformal field theories. Class. Quant. Grav. 2000, 17, 399–420. [Google Scholar] [CrossRef]
- Kastor, D.; Ray, S.; Traschen, J. Enthalpy and the Mechanics of AdS Black Holes. Class. Quant. Grav. 2009, 26, 195011. [Google Scholar] [CrossRef]
- Dolan, B. The cosmological constant and the black hole equation of state. Class. Quant. Grav. 2011, 28, 125020. [Google Scholar] [CrossRef]
- Dolan, B.P. Pressure and volume in the first law of black hole thermodynamics. Class. Quant. Grav. 2011, 28, 235017. [Google Scholar] [CrossRef]
- Dolan, B.P. Compressibility of rotating black holes. Phys. Rev. D 2011, 84, 127503. [Google Scholar] [CrossRef]
- Cvetic, M.; Gibbons, G.; Kubiznak, D.; Pope, C. Black Hole Enthalpy and an Entropy Inequality for the Thermodynamic Volume. Phys. Rev. D 2011, 84, 024037. [Google Scholar] [CrossRef]
- Gibbons, G.W.; Kallosh, R.; Kol, B. Moduli, scalar charges, and the first law of black hole thermodynamics. Phys. Rev. Lett. 1996, 77, 4992–4995. [Google Scholar] [CrossRef]
- Creighton, J.; Mann, R.B. Quasilocal thermodynamics of dilaton gravity coupled to gauge fields. Phys. Rev. D 1995, 52, 4569–4587. [Google Scholar] [CrossRef]
- Born, M.; Infeld, L. Foundations of the new field theory. Proc. Royal Soc. 1934, 144, 425–451. [Google Scholar] [CrossRef]
- Kruglov, S.I. Rational non-linear electrodynamics of AdS black holes and extended phase space thermodynamics. Eur. Phys. J. C 2022, 82, 292. [Google Scholar] [CrossRef]
- Kruglov, S.I. A model of nonlinear electrodynamics. Ann. Phys. 2014, 353, 299–306. [Google Scholar] [CrossRef]
- Kruglov, S.I. Rational nonlinear electrodynamics causes the inflation of the universe. Int. J. Mod. Phys. A 2020, 35, 2050168. [Google Scholar] [CrossRef]
- Kruglov, S.I. Inflation of universe due to nonlinear electrodynamics. Int. J. Mod. Phys. A 2017, 32, 1750071. [Google Scholar] [CrossRef]
- Kruglov, S.I. Universe acceleration and nonlinear electrodynamics. Phys. Rev. D 2015, 92, 123523. [Google Scholar] [CrossRef]
- Bronnikov, K.A. Regular magnetic black holes and monopoles from nonlinear electrodynamics. Phys. Rev. D 2001, 63, 044005. [Google Scholar] [CrossRef]
- Handbook of Mathematical Functions with Formulas, Graphs and Mathematical Tables. In Applied Mathematics Series; Abramowitz, M.; Stegun, I. (Eds.) National Bureau of Standarts: Gaithersburg, MD, USA, 1972; Volume 55. [Google Scholar]
- Viatcheslav, M. Physical Foundations of Cosmology; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Cong, W.; Kubiznak, D.; Mann, R.B.; Visser, M. Holographic CFT Phase Transitions and Criticality for Charged AdS Black Holes. J. High Energy Phys. 2022, 2022, 174. [Google Scholar] [CrossRef]
- Smarr, L. Mass Formula for Kerr Black Holes. Phys. Rev. Lett. 1973, 30, 71–73, Erratum in Phys. Rev. Lett. 1973, 30, 521. [Google Scholar] [CrossRef]
- Rohrlich, F. Classical Charged Particles; Addison Wesley: Redwood City, CA, USA, 1990. [Google Scholar]
- Spohn, H. Dynamics of Charged Particles and Their Radiation Field; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Dirac, P.A.M. An extensible model of the electron. Proc. R. Soc. A 1962, 268, 57–67. [Google Scholar]
- Boas, M.L. Mathematical Methods in the Physical Sciences; Jonn Wiley and Sons, Inc.: Hoboken, NJ, USA, 2006. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kruglov, S.I. Magnetic Black Hole Thermodynamics in an Extended Phase Space with Nonlinear Electrodynamics. Entropy 2024, 26, 261. https://doi.org/10.3390/e26030261
Kruglov SI. Magnetic Black Hole Thermodynamics in an Extended Phase Space with Nonlinear Electrodynamics. Entropy. 2024; 26(3):261. https://doi.org/10.3390/e26030261
Chicago/Turabian StyleKruglov, Sergey Il’ich. 2024. "Magnetic Black Hole Thermodynamics in an Extended Phase Space with Nonlinear Electrodynamics" Entropy 26, no. 3: 261. https://doi.org/10.3390/e26030261
APA StyleKruglov, S. I. (2024). Magnetic Black Hole Thermodynamics in an Extended Phase Space with Nonlinear Electrodynamics. Entropy, 26(3), 261. https://doi.org/10.3390/e26030261







