Exploration of Resonant Modes for Circular and Polygonal Chladni Plates
Abstract
:1. Introduction
2. Resonant Mode Chladni Patterns
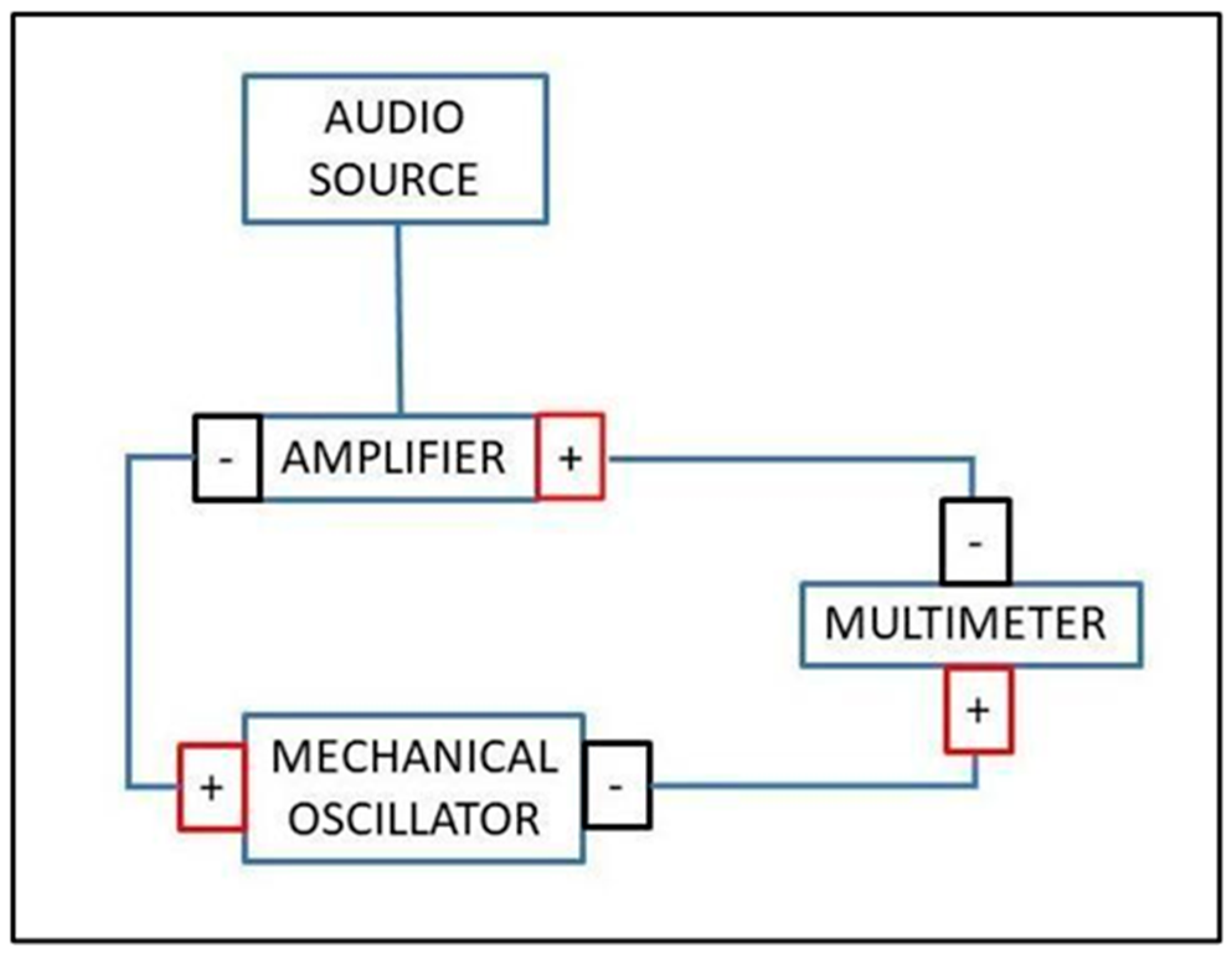
2.1. Impedance Experiment to Determine Resonant Modes
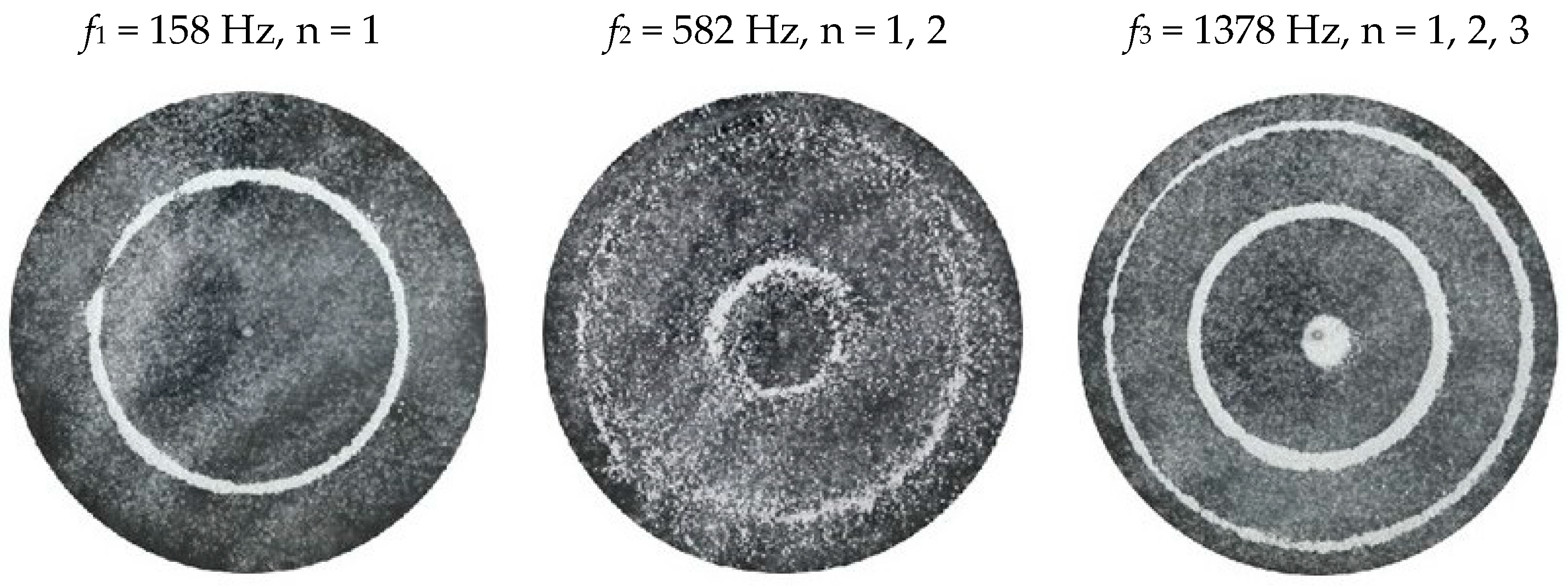
2.2. Chladni Plate Vibration at Resonant Mode Frequencies
3. Theoretical Determination of the Nodal Line Patterns
3.1. Circular Chladni Plate
3.2. Square Chladni Plate
3.3. Triangular Chladni Plate
3.4. Pentagon Chladni Plate
3.5. Hexagon Chladni Plate
4. Summary
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Flores, J. Nodal patterns in the seismic response of sedimentary valleys. Eur. Phys. J. Spec. Top. 2007, 145, 63–75. [Google Scholar] [CrossRef]
- Schaadt, K.; Kudrolli, A. Experimental investigation of universal parametric correlators using a vibrating plate. Phys. Rev. E 1999, 60, R3479–R3482. [Google Scholar] [CrossRef]
- Dorrestijn, M.; Bietsch, A.; Açıkalın, T.; Raman, A.; Hegner, M.; Meyer, E.; Gerber, C. Chladni Figures Revisited Based on Nanomechanics. Phys. Rev. Lett. 2007, 98, 026102. [Google Scholar] [CrossRef]
- Chakram, S.; Patil, Y.S.; Chang, L.; Vengalattore, M. Dissipation in Ultrahigh Quality Factor SiN Membrane Resonators. Phys. Rev. Lett. 2014, 112, 127201. [Google Scholar] [CrossRef]
- Chladni, E.F.F. Entdeckungen uber die Theorie des Klanges; Weidmanns Erben und Reich: Leipzig, Germany, 1787. [Google Scholar]
- Chladni, E.F.F. Die Akustik; Breitkopf und Härtel: Leipzig, Germany, 1802. [Google Scholar]
- Chladni, E.F.F. Neue Beitruge zur Akustik; Breitkopf und Härtel: Leipzig, Germany, 1817. [Google Scholar]
- Galilei, G. Dialogues Concerning Two New Sciences; Crew, H.; de Salvio, A., Translators; Macmillan: London, UK, 1914; pp. 209–221. [Google Scholar]
- Andrade, E.N.D.C. Wilkins Lecture—Robert Hooke. Proc. R. Soc. Lond. Ser. B Biol. Sci. 1997, 137, 153–187. [Google Scholar] [CrossRef]
- Waller, M.D. Vibrations produced in bodies by contact with solid carbon dioxide. Proc. Phys. Soc. 1933, 45, 101–116. [Google Scholar] [CrossRef]
- Waller, M.D. The production of sounds from heated metals by contact with ice and other substances. Proc. Phys. Soc. 1934, 46, 116–123. [Google Scholar] [CrossRef]
- Waller, M.D. The production of chladni figures by means of solid carbon dioxide. Part 1: Bars and other metal bodies. Proc. Phys. Soc. 1937, 49, 522–531. [Google Scholar] [CrossRef]
- Waller, M.D. Vibrations of free circular plates. Part 3: A study of Chladni’s original figures. Proc. Phys. Soc. 1938, 50, 83–86. [Google Scholar] [CrossRef]
- Jenny, H. CYMATICS—A Study of Wave Phenomena and Vibration; Macromedia Press: Newmarket, NH, USA, 2001; Volume 1 & Volume 2. [Google Scholar]
- Kirchhoff, G. Über das Gleichgewicht und die Bewegung einer elastischen Scheibe. J. Reine Angew. Math. 1850, 40, 51–88. [Google Scholar]
- Rayleigh, J.W.S. (Ed.) Chapter 10. Vibrations of Plates. In The Theory of Sound; Macmillan and Co.: London, UK, 1877; Volume 1, pp. 203–326. [Google Scholar]
- Leissa, A.W. (Ed.) Vibration of Plates; Ohio State University: Columbus, OH, USA, 1969. [Google Scholar]
- Timoshenko, S. Vibration Problems in Engineering, 3rd ed.; D. Van Nostrand Company, Inc.: Princeton, NJ, USA, 1961. [Google Scholar]
- Wah, T. Vibration of Circular Plates. J. Acoust. Soc. Am. 1962, 34, 275–281. [Google Scholar] [CrossRef]
- Waller, M.D. Vibrations of free circular plates. Part 2: Compounded normal modes. Proc. Phys. Soc. 1938, 50, 77–82. [Google Scholar] [CrossRef]
- Tuan, P.H.; Wen, C.P.; Yu, Y.T.; Liang, H.C.; Huang, K.F.; Chen, Y.F. Exploring the distinction between experimental resonant modes and theoretical eigenmodes: From vibrating plates to laser cavities. Phys. Rev. E 2014, 89, 022911. [Google Scholar] [CrossRef]
- Waller, M.D. Vibrations of free square plates: Part I. Normal vibrating modes. Proc. Phys. Soc. 1939, 51, 831–844. [Google Scholar] [CrossRef]
- Waller, M.D. Vibrations of free square plates: Part II, compounded normal modes. Proc. Phys. Soc. 1940, 52, 452–455. [Google Scholar] [CrossRef]
- Tuan, P.H.; Wen, C.P.; Chiang, P.Y.; Yu, Y.T.; Liang, H.C.; Huang, K.F.; Chen, Y.F. Exploring the resonant vibration of thin plates: Reconstruction of Chladni patterns and determination of resonant wave numbers. J. Acoust. Soc. Am. 2015, 137, 2113–2123. [Google Scholar] [CrossRef]
- Tuan, P.H.; Tung, J.C.; Liang, H.C.; Chiang, P.Y.; Huang, K.F.; Chen, Y.F. Resolving the formation of modern Chladni figures. EPL Europhys. Lett. 2015, 111, 64004. [Google Scholar] [CrossRef]
- Tuan, P.H.; Liang, H.C.; Tung, J.C.; Chiang, P.Y.; Huang, K.F.; Chen, Y.F. Manifesting the evolution of eigenstates from quantum billiards to singular billiards in the strongly coupled limit with a truncated basis by using RLC networks. Phys. Rev. E 2015, 92, 062906. [Google Scholar] [CrossRef]
- Tuan, P.H.; Lai, Y.H.; Wen, C.P.; Huang, K.F.; Chen, Y.F. Point-driven modern Chladni figures with symmetry breaking. Sci. Rep. 2018, 8, 10844. [Google Scholar] [CrossRef]
- Shu, Y.-H.; Tseng, Y.-C.; Lai, Y.-H.; Yu, Y.-T.; Huang, K.-F.; Chen, Y.-F. Exploring the Origin of Maximum Entropy States Relevant to Resonant Modes in Modern Chladni Plates. Entropy 2022, 24, 215. [Google Scholar] [CrossRef]
- Amore, P. Solving the Helmholtz equation for membranes of arbitrary shape: Numerical results. J. Phys. A Math. Theor. 2008, 41, 265206. [Google Scholar] [CrossRef]
- Amore, P.; Cervantes, M.; Fernández, F.M. Variational collocation on finite intervals. J. Phys. A Math. Theor. 2007, 40, 13047–13062. [Google Scholar] [CrossRef]
- Amore, P. Alternative representation for nonlocal operators and path integrals. Phys. Rev. A 2007, 75, 032111. [Google Scholar] [CrossRef]
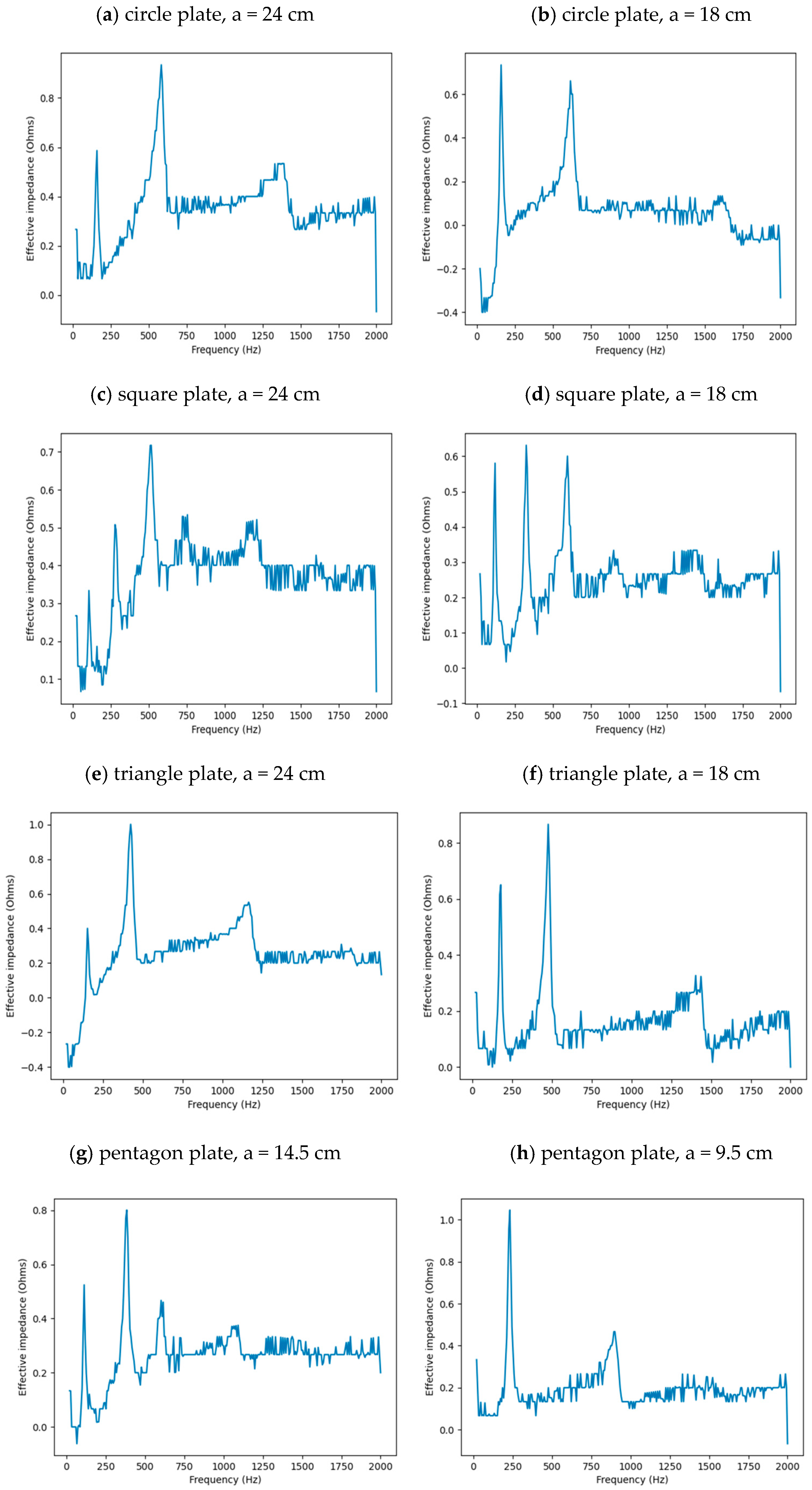
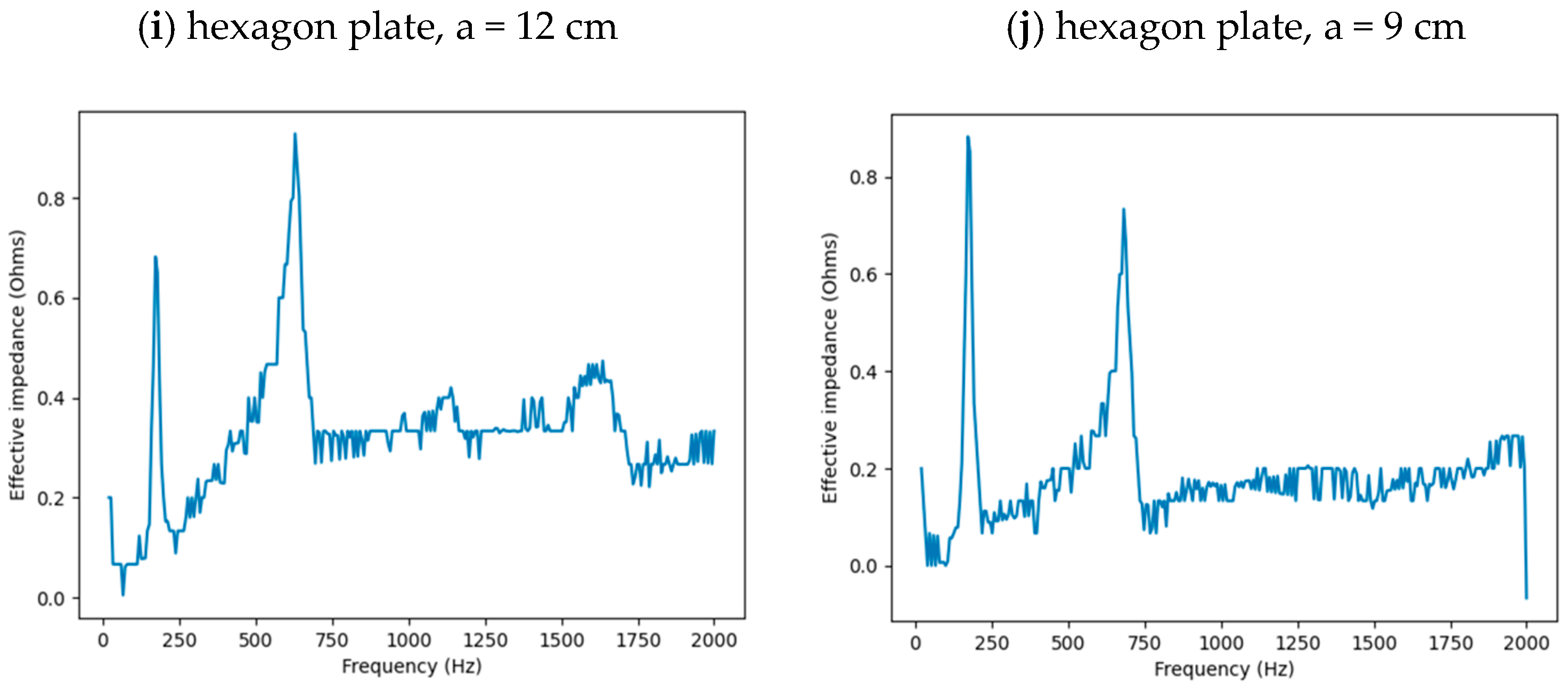
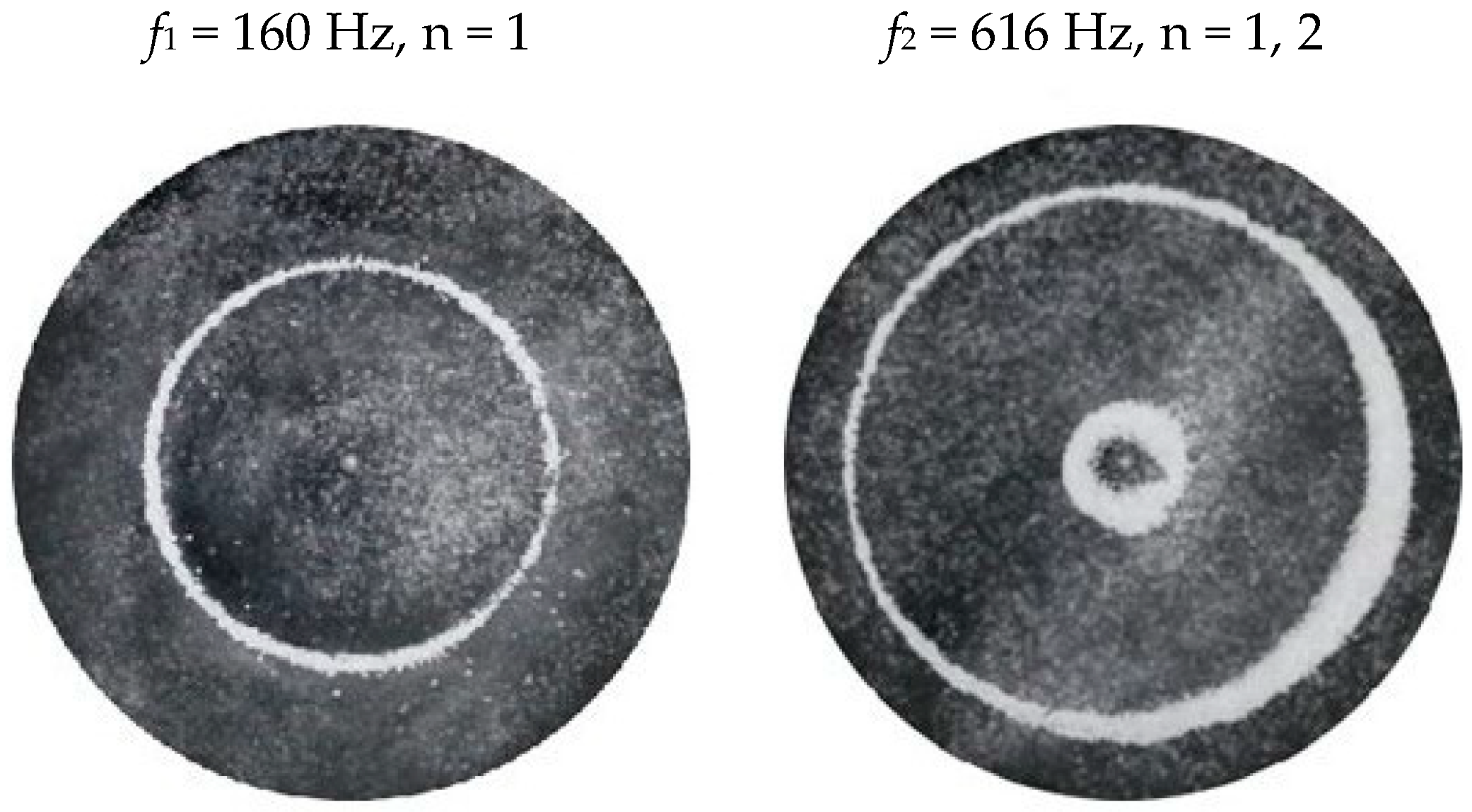
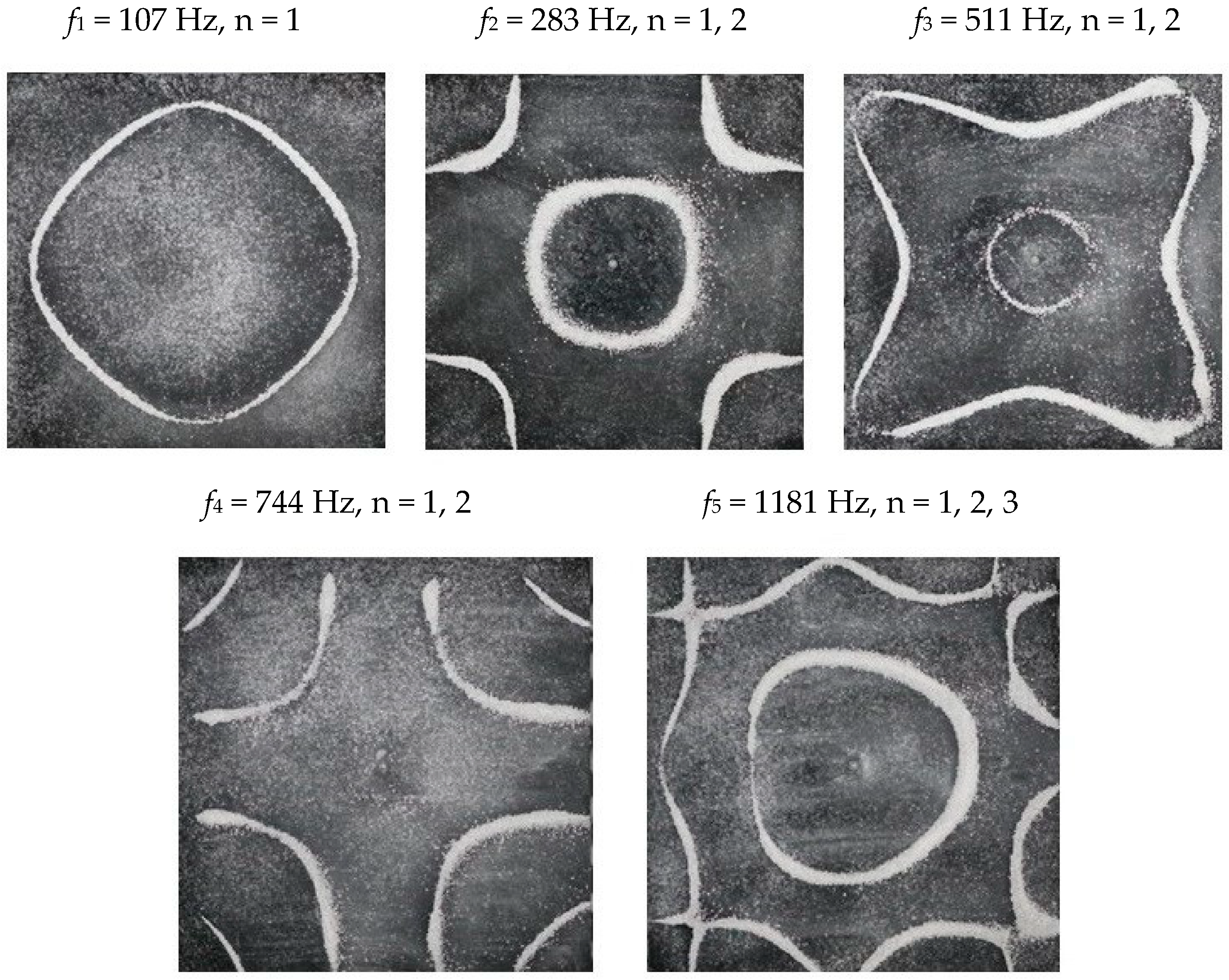
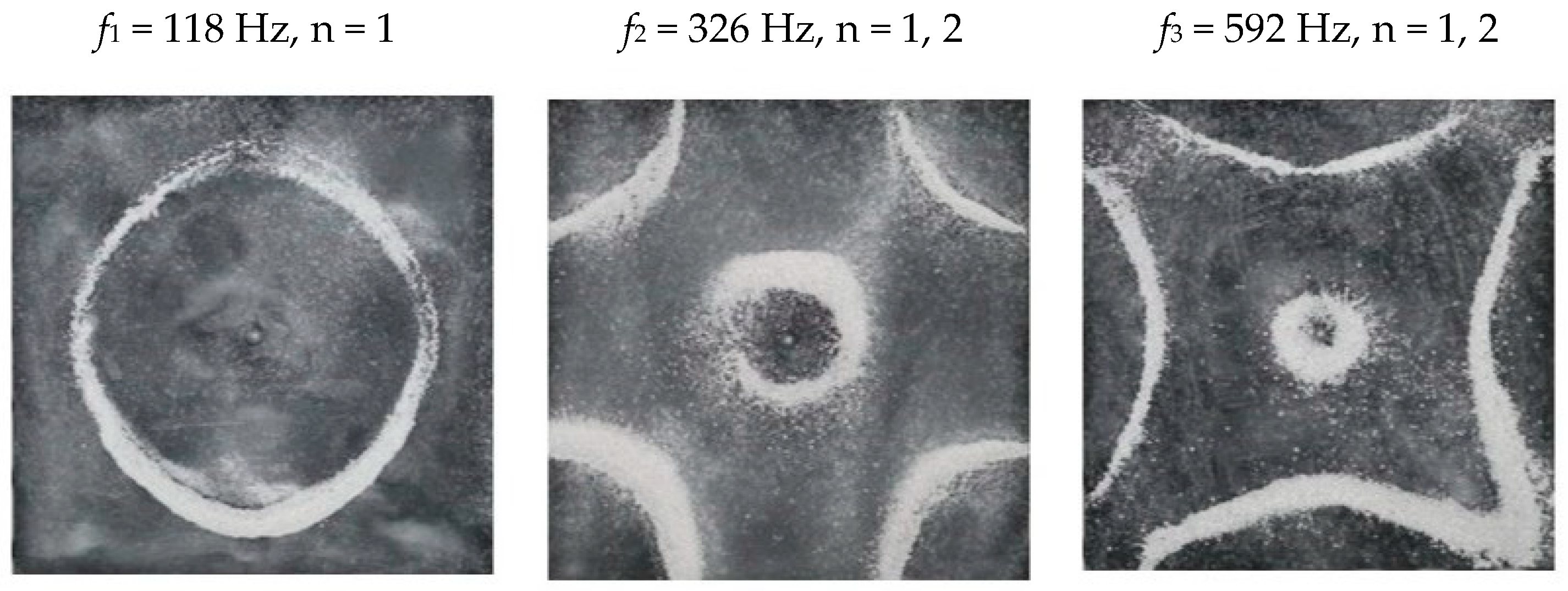




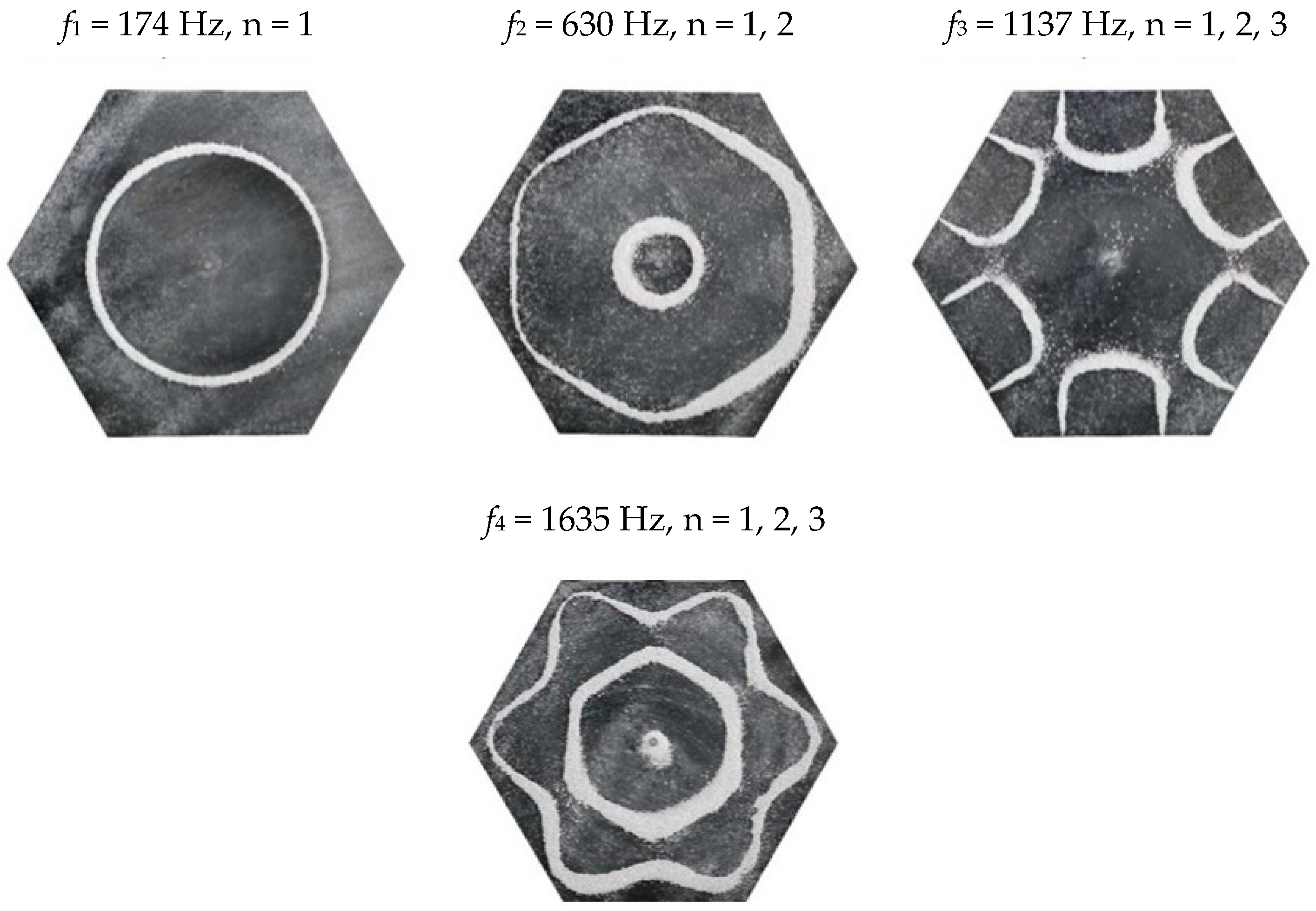

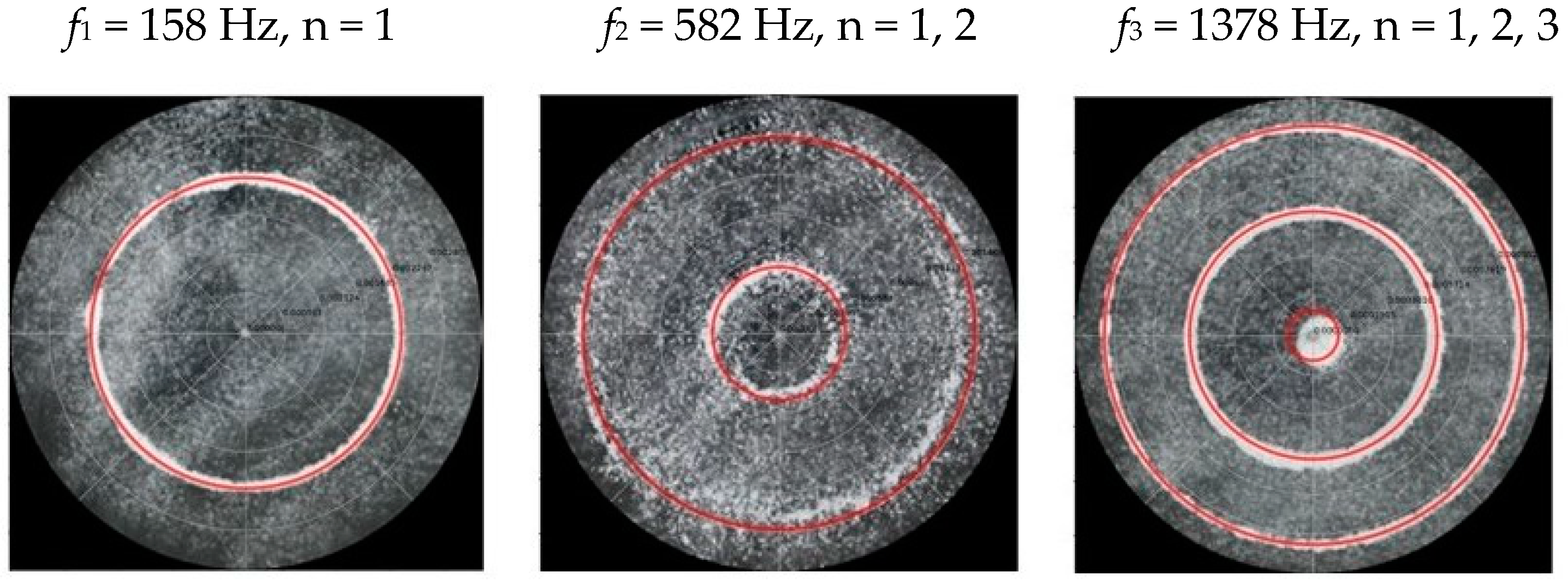

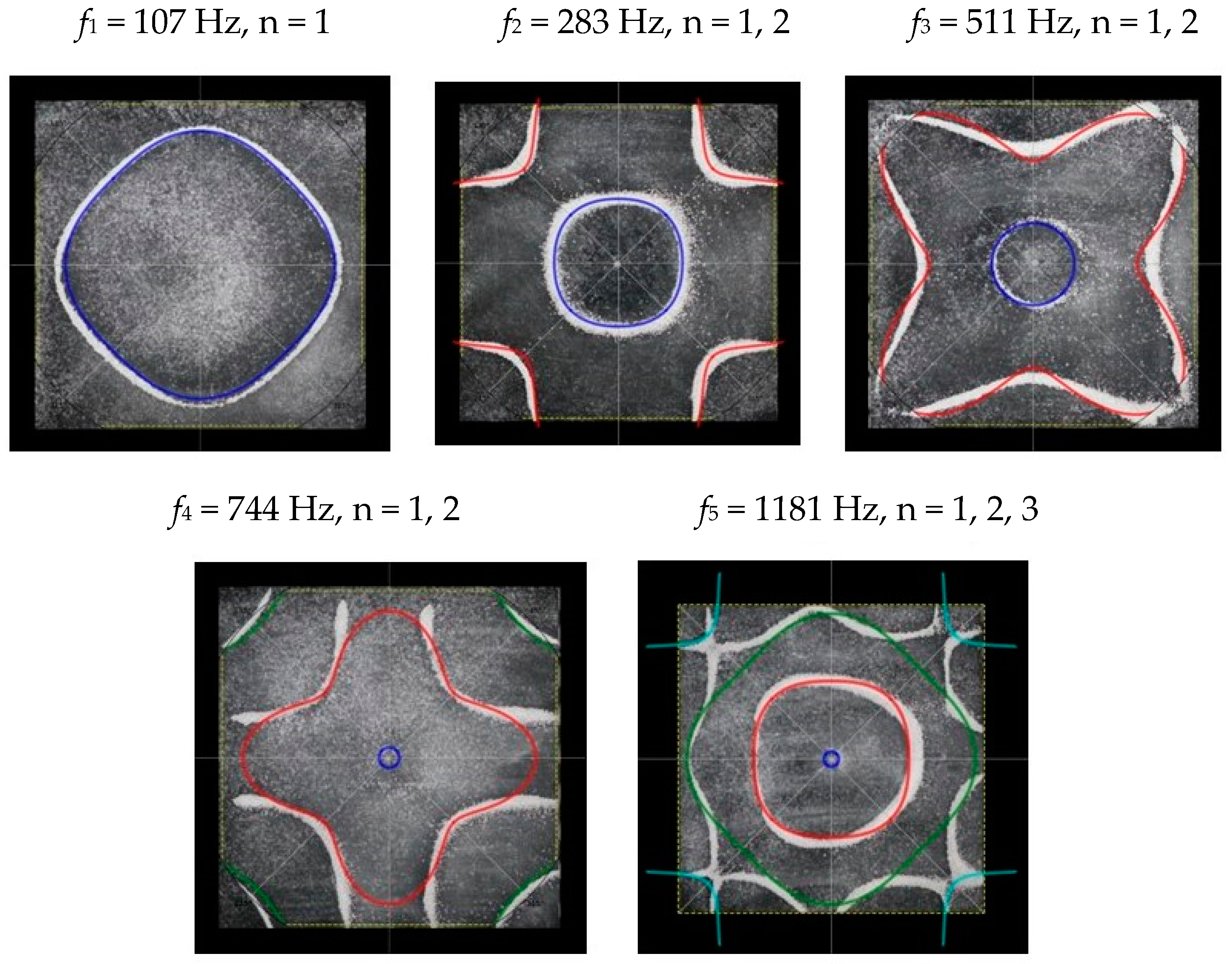

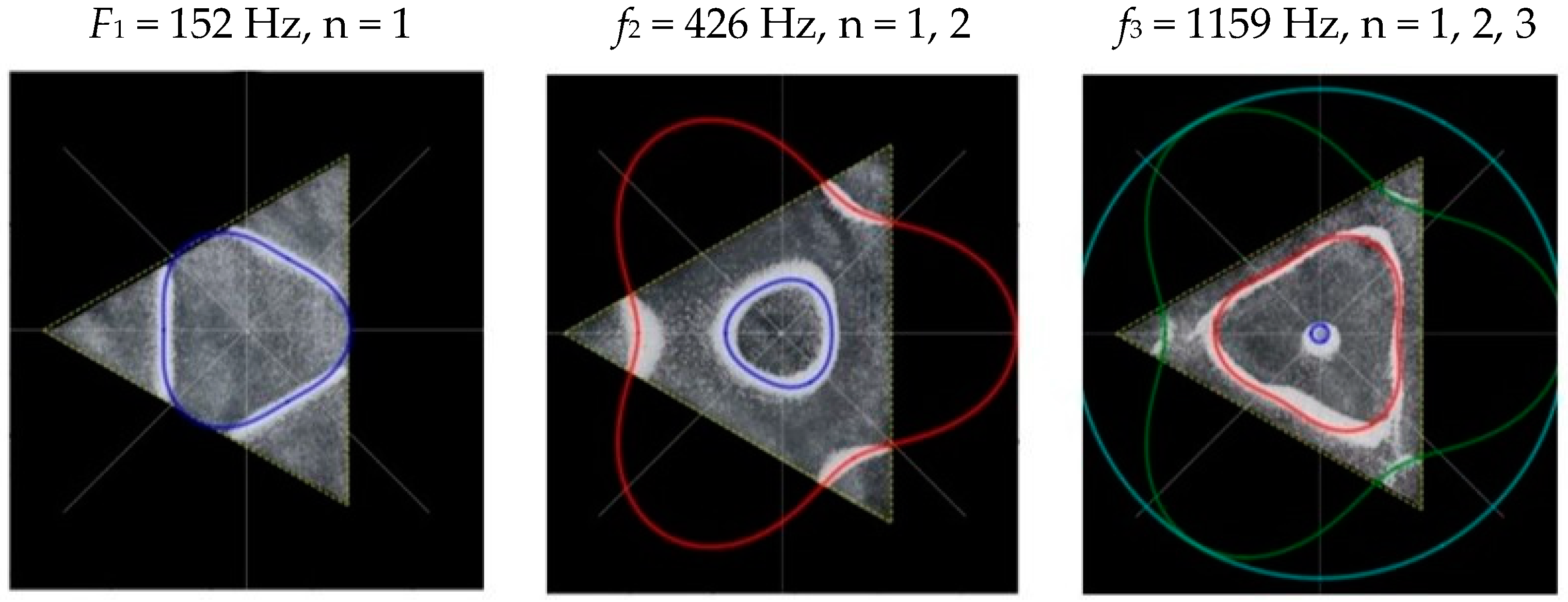





| Shape | Circle | Square | Triangle | Pentagon | Hexagon | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Size (cm) | 24 | 18 | 24 | 18 | 24 | 18 | 14.5 | 9.5 | 12 | 9 |
| f1 (Hz) | 158 | 160 | 107 | 118 | 152 | 176 | 112 | 228 | 174 | 174 |
| f2 (Hz) | 582 | 616 | 283 | 326 | 426 | 477 | 381 | 895 | 630 | 682 |
| f3 (Hz) | 1378 | 511 | 592 | 1159 | 1402 | 604 | 1137 | |||
| f4 (Hz) | 744 | 1071 | 1635 | |||||||
| f5 (Hz) | 1181 | |||||||||
| Coefficients | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Shape (cm) | Frequency (Hz) | Velocity (m/s) | A1 | A2 | A3 | A4 | C1 | C2 | C3 | C4 |
| circle 24 | 158 | 35.6 | 0.95 | |||||||
| 582 | 68.2 | 1.35 | 1 | |||||||
| 1378 | 105.0 | 2.1 | 1.15 | 0.75 | ||||||
| circle 18 | 160 | 35.8 | 1.65 | |||||||
| 616 | 70.2 | 2.4 | 2.25 | |||||||
| square 24 | 107 | 29.3 | −0.1 | 0.95 | ||||||
| 283 | 47.6 | 0.05 | −1.85 | 1.25 | 0.6 | |||||
| 511 | 63.9 | 0 | 1.7 | 1.6 | 0.7 | |||||
| 744 | 77.1 | 0 | −1.2 | −1.3 | 2.7 | 1.1 | 0 | |||
| 1181 | 97.2 | 0 | 0.2 | −0.55 | −5.8 | 2.7 | 1.45 | 1.35 | −3.65 | |
| square 18 | 118 | 30.7 | −0.05 | 1.55 | ||||||
| 326 | 51.1 | 0 | −0.9 | 2.3 | 2.2 | |||||
| 592 | 68.8 | 0 | 0.6 | 2.5 | 2.4 | |||||
| triangle 24 | 152 | 34.9 | −0.2 | 1.4 | ||||||
| 426 | 58.4 | 0.1 | −1.4 | 1.6 | 0.8 | |||||
| 1159 | 96.3 | 0 | 0.7 | −2.3 | 2.7 | 1.6 | −0.8 | |||
| triangle 18 | 176 | 37.5 | −0.2 | 1.75 | ||||||
| 477 | 61.8 | 0 | −0.95 | 2.15 | 2 | |||||
| 1402 | 105.9 | 0 | 0.6 | −2.8 | 2.8 | 2.6 | 0 | |||
| pentagon 14.5 | 112 | 29.9 | 0 | 1.7 | ||||||
| 381 | 55.2 | 0 | −0.4 | 2.3 | 2.3 | |||||
| 604 | 69.5 | 0 | 0.7 | −2.9 | 2.8 | 2.4 | 2 | |||
| 1071 | 92.6 | 0 | −0.2 | 1.1 | 2.9 | 2.6 | 2.6 | |||
| pentagon 9.5 | 228 | 42.7 | 0 | 2 | ||||||
| 895 | 84.6 | 0 | −0.3 | 2.7 | 2.35 | |||||
| hexagon 12 | 174 | 37.3 | 0 | 1.1 | ||||||
| 630 | 71.0 | 0 | −2 | 1.85 | 1.25 | |||||
| 1137 | 95.4 | 0 | 0.5 | −2.5 | 2.55 | 1.4 | 1.3 | |||
| 1635 | 114.4 | 0 | −0.15 | 1 | 2.8 | 1.6 | 1.1 | |||
| hexagon 9 | 174 | 37.3 | 0 | 1.9 | ||||||
| 682 | 73.9 | 0 | −0.1 | 2.65 | 2.45 | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Val Baker, A.; Csanad, M.; Fellas, N.; Atassi, N.; Mgvdliashvili, I.; Oomen, P. Exploration of Resonant Modes for Circular and Polygonal Chladni Plates. Entropy 2024, 26, 264. https://doi.org/10.3390/e26030264
Val Baker A, Csanad M, Fellas N, Atassi N, Mgvdliashvili I, Oomen P. Exploration of Resonant Modes for Circular and Polygonal Chladni Plates. Entropy. 2024; 26(3):264. https://doi.org/10.3390/e26030264
Chicago/Turabian StyleVal Baker, Amira, Mate Csanad, Nicolas Fellas, Nour Atassi, Ia Mgvdliashvili, and Paul Oomen. 2024. "Exploration of Resonant Modes for Circular and Polygonal Chladni Plates" Entropy 26, no. 3: 264. https://doi.org/10.3390/e26030264
APA StyleVal Baker, A., Csanad, M., Fellas, N., Atassi, N., Mgvdliashvili, I., & Oomen, P. (2024). Exploration of Resonant Modes for Circular and Polygonal Chladni Plates. Entropy, 26(3), 264. https://doi.org/10.3390/e26030264







